Abstract
This paper proposes an advanced simulation-optimization approach to evaluate and optimize the passenger flows within international airports. This approach allocates resources intelligently during the simulation process and balances demand and service quality. The resource allocation performed by our Advanced Resource Management (ARM) algorithm was used to develop an integrated system for arranging resources, identifying the proper resources, and allocating them throughout the model. It was used to investigate the influences of different staff allocation techniques on the inbound and outbound processes of an airport terminal. The purpose of the proposed simulation-optimization approach is to enhance passenger satisfaction through ensuring reasonable wait times during processing at the lowest cost possible (minimal staff hours).
1. Introduction
In recent years, airports have played a significant role in economic growth, connecting cities and countries around the world. Numerous passengers choose to travel by airline in preference to other transportation modes such as trains, buses, and private cars [1]. Based on the International Civil Aviation Organization [2] report for 2017, the number of airline travellers exceeded 4 billion globally, a growth in global air transport demand of about 8.1% compared with the previous year [3]. An international airport terminal is a large and complex system, since it involves inbound and outbound passenger flow processes, each with its own unique operations. Some airports have a slightly different process, and new airports designed in the future may require further changes to the standard process in light of new security concerns faced in our modern world. In addition, airport management and airlines have discussed the possibility of changing and updating several policies related to flight schedules, staff allocation, and other operational policies to accommodate future demand for growth and to provide better quality services and security. The solution to this problem requires the development of a new generation of fast, reliable decision-making tools to quickly mobilise the human and technical resources available at modern airports.
The passengers in an airport terminal can be divided into three types based on how they are handled inside the terminal: departing passengers, arriving passengers, and transferring or transiting passengers. Each type of passenger behaves differently depending on why they are using the airport’s facilities. An Australian international airport terminal has been used as an example to demonstrate a common layout of airport terminals. According to Ma’s [4] definition, departing passengers start with the check-in process in the international terminal and transfer to their airplane within the same terminal. These passengers arrive at the airport terminal based on their flight schedule, normally at least two hours before their departure time. Departing passengers complete three main processes, check-in, security screening, and immigration, and then they wait to board the airplane at their specified gate. In contrast, transferring passengers merely pass through the security screening control and then go directly to their specified boarding gate. The other type of passenger flow is that of arriving passengers, who can be defined as people who disembark from the aircraft after landing at the airport terminal. This includes services provided to transit passengers, and the time taken to complete this process is often significantly longer than that of the arrival process [5]. Inbound passenger flow is smoother than outbound passenger flow, although delays can occur in the inbound system depending on the time it takes to deliver baggage from the aircraft to the baggage claim area [4].
Our review of the literature suggests that operational issues within individual airport processes have predominantly been focused upon, and models have not holistically assessed an entire airport [6], while there have been few attempts to develop holistic models that provide an integrated view of the processes and sub-processes of the whole airport that help with the analysis and evaluation of various measures of the efficiency of the airport. Hence, the primary contribution of this paper is the development of the Advanced Resource Management (ARM) model to improve the flow of passengers within the inbound and outbound processes of airports. By facilitating and integrating inbound and outbound processes, an integrated view of overall airport operations can be achieved [7]. This model provides a clear idea of passenger flow through the entire airport terminal processing procedure. The objective of developing this model was to examine the possible bottlenecks in arriving and departing passenger flows. It also provides a platform for studying more complex processing behaviours and operational strategies using the simulation environment. Consequently, insight into current and future situations of airport systems will be gained.
2. Related Work
Congestion is a major problem in airports around the world. Congestion and delays are predominantly caused by ground operations, and the efficiency of terminal processes is assumed to have huge importance. To resolve these inefficiencies, and to improve passenger travel experience and airport management performance, one area of focus has been staff scheduling, which can be defined as the allocation of activities or actions to resources according to specific performance criteria [8]. A number of papers have studied staff scheduling and staff rostering problems. For example, Rodic [9] proposed the idea of workforce shift allocation and rapid rescheduling based on dynamic flight scheduling. In [10], staff scheduling issues in security operations are discussed. The memetic algorithm is used to solve the problem. They found that it is possible to open and close counters depending on demand, using a dynamic programming approach.
Dowling and Krishnamoorthy [11] discussed the development of an optimization approach to roster nearly 500 staff of a major international airline at one of the busiest airports in the world. The key issue was to establish a robust algorithm that offers optimized monthly rosters for airport service employees. The study was successful in describing an overall system and an algorithm to solve rostering issues linked to the system. Soukour and Devendeville [12] proposed an approach to resolve realistic scheduling issues in the airport security service domain. The authors divided the problem into three steps: days off schedule, shift scheduling, and staff assignment. Then, for staff assignment they propose two algorithms, the global assignment and greedy algorithms, to offer an initial solution. Sabar and Montreuil [13] aimed to use a multi-agent-based algorithm model for personnel scheduling and rescheduling in the dynamic setting of a fast-paced multi-product assembly center.
Effective allocation of Ground Service Equipment (GSE) to aircraft standing on the apron is determined with the help of a framework (Integrated Airport Apron Safety Fleet Management—AAS) that emerged from a European sponsored project [14]. An integer programming model was formulated for the Ground-Service Resource Allocation Problem (GRAP). Andreatta and De Giovanni [14] proposed a fast heuristic approach to show how the issue can be broken down into sub-issues. It was recommended that GRAP should be improved to make it robust against the unforeseen delays which often happen in airport aprons. Parlar and Sharafali [15] conducted research to determine the optimal number of open counters over a specified period. Lin and Xin [16] described problems with ground crew rostering and shift allocation in an attempt to better manage the opening and closing of check-in counters. Recent research by Rodic and Baggia [17] attempted to solve the problem of a lack of schedules for airport check-in employees, especially regarding work groups and overlapping skills.
3. Modelling Approach and Design
This section introduces a generic framework for modelling the flow of passengers through an airport terminal involving both inbound and outbound processing points (see Figure 1). Each system has its own particular flow, and each system requires different infrastructure and services [18].
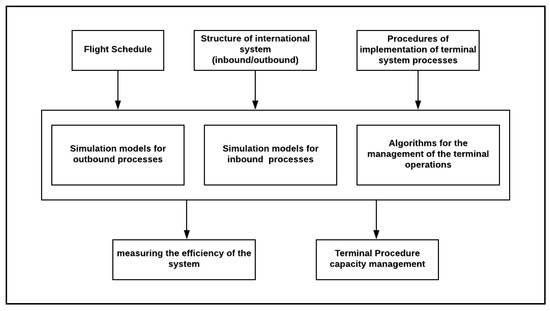
Figure 1.
Airport system model [19].
The model describes the potential interactions between inbound passengers and outbound passengers, resulting in competing priorities regarding physical space. This competition results in the need to model and optimize these interactions under realistic terminal conditions. Most international airports have inbound and outbound processes. The outbound processes include check-in, security, immigration and boarding. The inbound processes include disembarkation, baggage claim, immigration, and quarantine. To generically model an airport, it is best to divide the airport processes hierarchically into smaller and more manageable pieces. The workstations and queuing in different airport facilities (including between operational sections) were included using the simulation software package ExtendSim. The developed model has been applied to Brisbane International Airport (BNE). The model describes the main characteristics of BNE in terms of the flight schedule, passenger-flow processes, and a variety of functional areas and facilities [1].
3.1. Outbound Extendsim Module
A hierarchical model:
In this context, the proposed model is organized into two hierarchical levels:
- (1)
- The first level of the hierarchy reflects the airport departure system, which is broken down into the main departure procedures, including check-in, security, immigration, and boarding.
- (2)
- The second level describes the intricate details of the different sub-processes in the airport terminal. Specifically, the main departure procedures that the airport terminal model includes are as follows:
- Arrival characteristics, including the distribution of arrivals, method of arrival (car, bus, or train), number of bags, class of travel, and time of travel;
- The check-in process, including the type of check-in, e.g., at the kiosk or online with a bag, business or economy, and the assignment of each flight to specific check-in counters;
- Security screening, including X-ray checks conducted in the common security screening line, X-ray checks for diplomats, and secondary screening checks (i.e., random checks);
- Immigration processing, including SmartGate services and manned counters for passport control; and
- Boarding procedures, including boarding time, waiting time at the gate, boarding strategy, jetway capacity, and flight capacity.
3.2. Inbound Extendsim Module
The inbound simulation models can be organized into two hierarchical levels. The first level of the hierarchy reflects the inbound airport system broken down into a set of the main inbound procedures. The second level describes the intricate details of the different sub-processes in the airport terminal. Specifically, the main inbound procedures that the airport terminal model consists of are as follows:
- Passengers disembarking, including the generation of inbound passengers’ attributes, such as the number of SmartGate users, walking speed, number of bags, etc.;
- An inbound security screening checkpoint for inbound passengers, assuming that 15% of total transfer passengers fail on their first attempt. This module takes into consideration X-ray checks and secondary screening checks (i.e., random checks);
- Inbound immigration processing points, including SmartGate services and manned counters for passport control;
- Quarantine processing checking points, including two separate queues to process arriving passengers: one for passengers who have something to declare and another for passengers who have nothing to declare.
3.3. Advanced Resource Management (ARM) Approach
This section discusses the development of an advanced resource management model. Figure 2 gives an overview of passenger flow at the international terminal building as well as departure processes from check-in to boarding and arrival processes from de-boarding to baggage claim and exiting the airport. As we can see from the figure below, the left-hand side of the figure represents outbound flow processes and the right-hand side is inbound flow processes. The two lines of inbound and outbound passengers interact with each other using limited resources that are mutual for both lines (see red arrows in Figure 2).

Figure 2.
Flowchart framework for the Advanced Resource Management (ARM) model.
Many issues mean that managing airport staff can be difficult [20]. One of these issues is that each process is operated by a different stakeholder, for instance, check-in and boarding is performed by the related airlines and the ground handlers [21,22]. Another important issue for managing terminal staff is that each airport domain behaves differently in terms of the skills required to perform the tasks of particular workstations. Chuin Lau [23] argued that “manpower scheduling is concerned with the scheduling of manpower resources to meet temporal operational requirements in ways that satisfy the goals and policies imposed by the management, labor union, and the government”. Furthermore, each process has its own rules for allocating staff and methods of sharing the staff resources between related areas. Given the complexity of an international terminal system, algorithms have been developed to manage staff dynamically across the international terminal [24]. Algorithms can be divided into two different levels:
- Algorithms for managing staff that are working on one system (outbound/inbound) and can be shared with another process in the same system, such as airline staff responsible for operating check-in, who share tasks with boarding and quarantine;
- Algorithms to control staff who work on a particular process that is located on both sides (outbound/inbound), such as immigration and security.
3.3.1. The Logic of Algorithm Development
The proposed approach performs dynamic management of where the staff can be controlled and allocated based on a given rule, such as the queue length threshold. The logic that has been followed to develop such algorithms is categorized into three options. The first option is adding staff to a particular workstation. That can be done by looping across the queues of processing points and reading the status of the queue: if the queue length exceeds the threshold, check if there are staff available in the resource pool and add them to the first available spot. The second option is removing the staff from the processing point and shutting down the workstation. This can be done if the queue length is less than a given threshold. The last option is more complicated because the staff need to be shared between related processes. This option is considered after the loop through the staff resource pool “global array” databases is done and no available staff have been found. Then, we need to share resources between areas based on the queue threshold for each process; for example, airline staff will be shared between economy and business counters with more priority given to the business class queue. The purpose of developing such algorithms is to operate airport terminal processes at the optimum level.
3.3.2. Data Requirements
- Staff attributes
Since each process has different characteristics, staff attributes can be classified into general and specific. As seen in Figure 3, there are four types of staff that operate airport operational elements in this model. The first type is airlines, which are responsible for operating check-in and boarding domains of the outbound system [22]. The second type is security, which is operated by the airport owner. In Australia, security is contracted out to expert companies to perform this terminal domain. The third type is immigration and customs staff, who are responsible for controlling Australian customs and passport checks; this is the responsibility of an Australian government agency. The last type is quarantine staff for border protection, which is operated by distinct stakeholders of a government agency.

Figure 3.
Staff attributes for the ARM model.
- ii
- Rules given for managing staff
The proposed approach allocates staff based on two different techniques. The first type is a schedule-based method. In this method, the staff are allocated and used all the time to observe what the results are in terms of queue lengths and waiting time. The second type is demand-based allocation. Unlike the first type, demand-based methods allocate and reallocate staff based on queue length rules. Additionally, in this method, the staff are not only shared between two processes but there are also passengers arriving at the particular processing point every 30 min. Regarding the queue threshold rule, action will be taken if the queue length reaches X value, as explained above.
3.3.3. Categories of Algorithms
In this section, we provide further explanation of the development algorithms, including the aims and objectives, the functionalities, and the conditions of the algorithms. The algorithms were developed to meet the needs of the behaviors of airport terminal operations that occur in real life and have been classified into two categories, as explained below.
- Algorithms developed for non-integrated processes
Check-in/boarding gates module
This section discusses the algorithms that were developed for the airport terminal elements that are located on only one side, without integration between outbound and inbound processes. Examples of these elements are check-in/boarding and quarantine.
Figure 4 illustrates algorithms used to allocate airline staff to check-in desks and boarding gates. Airline staff allow passengers to drop their baggage and submit their passports and tickets to be processed. The operating procedures of airline staff dynamic allocation are based on the following algorithmic steps:

Figure 4.
Algorithmic approach for airline staff allocation module.
- Step 1: Loop through the economy and business queues and read the queue status.
- Step 2: Check if the queue length exceeds the queue threshold, and if there are staff available in the resource pool, assign them to the first spot. If not, and the queue length is less than the minimum limit, then remove the staff and shutdown the workstation.
- Step 3: (When step 1 and step 2 are not applicable), share staff between economy and immigration counters if there are no available staff in the resource pool. This procedure is done based on the given policy and always prioritises business class. The mechanism of moving staff is that if the business queue length exceeds the queue threshold, such as five passengers, and there is more than one staff member at the economy counters, then move the staff from economy to business counters and vice versa.
The notations used in the algorithmic approach are defined as follows:
: Queue length at business check-in counters
: Queue length at economy check-in counters
: Threshold for business queue
: Threshold for economy queue
: Number of airline staff available in the database of the global array
: Airline staff for check-in counters assigned
: Airline staff for business counters
: Airline staff for economy counters
: Airline staff for boarding gate
: Departure gate
: Start shift of airline staff
: End shift of airline staff
The airline staff are also the operators of boarding. Thus, an integrated module to share staff between check-in and boarding was developed. Before developing the code for this algorithm, a global array database was created for boarding procedures and to define and declare the related variables, such as flight code, boarding time, boarding strategy, and gate number. As we can see in Figure 5, the first step of the algorithm is to check the gate status by looping through all gates and seeing which one is active based on the departure time. The second step is that if the gate is active and there are staff available in the global array database, the staff who are not at the end of their shift are assigned to it.
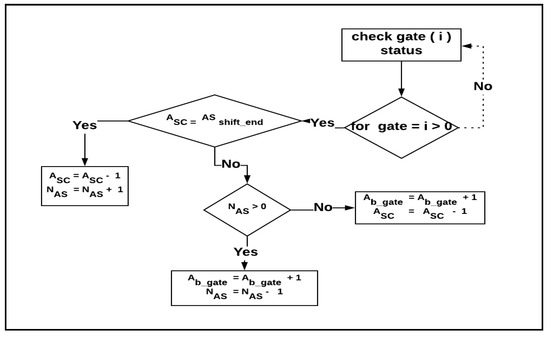
Figure 5.
Algorithmic approach for the integrated module for the boarding procedure.
- Algorithms for integrated processes
Security staff management module
This section discusses the integrated model that is used to manage staff working in the processes that are located on both sides of an international terminal. Examples of these processes are immigration and security screening. As explained earlier, security is operated by the owner of the airport, but in Australia, security is contracted to third-party companies to process passengers. The developed algorithm considers a VIP lane in the security system to process diplomatic passengers. Moreover, the passengers disembarking from arrived flights who have connecting flights have to pass through inbound security before reaching their outbound boarding gates. Thus, the security staff need to be shared not only between two lines in the outbound system but also with inbound security to process transiting passengers. The algorithm of the security sharing resource is presented in Figure 6.

Figure 6.
Phase one of algorithmic approach for security resource allocation management.
: Queue length at diplomatic security screening checkpoint
: Queue length at non-diplomatic security screening checkpoint
: Queue length for inbound security
: Threshold for diplomatic security screening checkpoint
: Threshold for non-diplomatic security screening checkpoint
: Threshold for inbound security screening checkpoint
: Number of security screening staff available in the database of the global array
: Security staff assigned
: Security staff for diplomatic lane
: Security staff for non-diplomatic lane
: Security staff for inbound lane
: Start of shift for security staff
: End of shift for Security staff
For the demand-based allocation method, the procedure of moving and managing security staff is summarised by the following algorithmic steps:
- Create a global array database to declare variables related to staff attributes, such as start of shift, end of shift, and staff availability. In addition, the global array is used to exchange interface data with the internal data structure needed for ModL programming language.
- Read the queue statuses of both sides, inbound and outbound, every minute of a simulation run and record which queue status is exceeded.
- Determine the available staff members who are not at the end of their shift and assign them to the area where the queue has reached its maximum limit, and remove staff if the queue size is less than the minimum limit. If steps one and two are not applicable, move to step four.
- Share the staff based on the given rules and priority. According to Odoni and de Neufville [5], the departure process, which sometimes involves services provided to transit passengers, typically requires a significantly longer time than the arrival process. The queue length of outbound security is observed; if the queue exceeds the maximum length, then move staff from inbound to outbound security screening processing points, and vice versa, as shown in Figure 7.
 Figure 7. Phase two of the algorithmic approach for security resource allocation management.
Figure 7. Phase two of the algorithmic approach for security resource allocation management.
4. Model Demonstration
The proposed model was developed to accurately mimic real-world situations, since terminal operations are dynamic and involve a range of services, e.g., check-in, passport control, boarding pass control, and security screening. To demonstrate the model’s capability, a set of experiments was conducted to analyze staff allocation methods under the same conditions and input data. The following phases were performed:
- Two experimental scenarios, each with a total of 81 simulation runs, were conducted to test the variable of staff number for each processing station. Experiment 1 considered the base case (static method) of allocating staff, while experiment 2 allocated the terminal staff dynamically, i.e., staff were assigned when and where needed.
- To obtain insight into stochastic variations, the simulation was run more than 200 times for each method (static and dynamic) using the same input data.
For comparative purposes, the experimental scenarios were conducted under the same conditions. The first type of data used were the flight schedules for both types of flight: departure and arrival. The second type of data related to the operational characteristics of the system, for example, the processing distribution at the various airport processing points and the number of checking points available. The required data related to time statistics and operational characteristics were collected by [22]. Table 1 summarizes the operational input data.

Table 1.
Summary of common operational input data for the experiments.
Simulation Results and Analyses
This section discusses the results of the initial experiments conducted to demonstrate the developed dynamic staff allocation and to ensure the reliability of the results. Since there are four types of staff—airline, security, immigration, and quarantine—the simulation was run with various staffing levels for each process to ensure that we investigated the operation of the terminal for all possible scenarios, as shown in Table 1. The results were collected from 81 multi-simulation runs for the two types of allocation method: (1) allocating staff according to a static base and (2) allocating staff dynamically—staff allocated when needed. For each simulation run, the Key Performance Indicators (KPIs) considered in this study were recorded for each processing point, both outbound and inbound. The KPIs included the maximum/average queue length, the maximum/average waiting time, the number of late flights/average time delay for late flights, and the total staff hours.
The airport terminal is operated as one single system with multiple elements located in the different types of outbound and inbound passenger flow processes. For this study, staff types were grouped into four different groups: airline staff, immigration staff, security staff, and quarantine staff. The number of scenarios was set based on the Cartesian product of the staff sets, which is defined as [25]:
It was assumed that set A represented airline staff = {8, 9, 10}, set B represented security staff = {3, 4, 5}, set C represented immigration staff = {6, 7, 8}, and set D represented quarantine staff = {5, 7, 8}. Since each set had three elements, the Cartesian products of these four sets had 81 ordered pairs. The same order of pairs was used for both experiments for two reasons: (i) to determine the significance of the dynamic allocation approach and how it improves the efficiency of all processes, and (ii) to obtain insight into the best policy for airport operations and management.
- Impacts of static and dynamic allocation approaches on delayed flights
Figure 8 presents the status of boarding procedures by employing the static method. In general, the time from the start of boarding until flight departure is about 30 min [26]. Hence, any flight departing more than 30 min after the original time is considered to be a delayed flight. This figure also demonstrates considerable fluctuation in the number of delayed flights and the average delay time. The number of delayed flights reached a peak of 18 flights in the 19th simulation run with an average delay time of 28 min.

Figure 8.
Influence of the static method on boarding procedures.
Figure 9 illustrates the impacts of the dynamic resource allocation technique on the boarding time. The dynamic method provided better results in regard to fewer delayed flights. There was little variation in the number of delayed flights over the first 28 scenarios when eight airline staff members were allocated to boarding processes. When more staff were added, the number of delayed flights experienced a slight drop followed by considerable variation. The highest number of delayed flights was 13 with 8 staff members available. The maximum delay time for delayed flights was around 18 min with a minimum delay time of 4 min.

Figure 9.
Influence of the dynamic resource allocation method on boarding procedures.
- Sharing staff policy for the Immigration and security domains
This section discusses the results of the simulation referring to staff sharing policies. Immigration is discussed first as it is located on both the inbound and outbound sides. Staff are shared between the two sides with outbound immigration having priority. The criteria for selecting the best policy is based on [22]; the author found that the average time spent in the immigration domain is between 6 and 7 min. Thus, any policy within this range or lower is acceptable. From Figure 10, it is clear to see that the average waiting time for outbound immigration is in the range of 5 to 7 min for the first 16 scenarios and the last nine scenarios. The policies that can provide acceptable waiting times are summarized in Table 2.

Figure 10.
Outcomes of simulated immigration staff sharing rules.

Table 2.
Summary of eligible sharing polices.
Results suggest that to decrease the number of passengers waiting in the queue, the number of staff hours must increase. Waiting times for both sides exhibit similar behavior for the first nine scenarios including the maximum and average waiting times. From scenario 11, there was a sharp rise in the maximum waiting time until the peak waiting time was reached in scenario 41. The swapping policy of scenario 41 is that if the number of passengers waiting at outbound immigration is greater than 100 and the number of passengers waiting at the inbound domain is less than 50, staff are moved from inbound to outbound processing. If the number of outbound passengers is 20 or less, staff are moved from outbound to inbound processing.
The second integrated process is security screening, since it is located in both outbound and inbound process flows. The same policies were applied to the immigration domain for this investigation. The results were compared with the actual data collected by Kirk [22] to determine the acceptable queue time at security. Based on Kirk [22], the average queue time at security screening was 3.75 min, while the maximum queue time was 17.09 min. Hence, the best rules will be those where the resulting wait times are equal to or lower than these limits.
Figure 11 demonstrates the outcomes of the simulation considering the performance metrics of the 65 sharing policies including the maximum/average waiting time of inbound and outbound security screening and the total staffing hours. The maximum/average waiting time of outbound security in the first nine scenarios and in the last 19 scenarios represent acceptable policies. The average waiting time ranged from 3.80 to 4.86 min in the first nine scenarios and from 3.71 to 5.7 min in the last 19 scenarios. The maximum waiting time ranged from 17.18 to 22.89 min for the first nine scenarios and from 16.47 to 30 min for the last 19 scenarios. Scenario 5 is considered to be the best policy since it provides the minimum waiting time for both outbound and inbound security with average waiting times of 3.92 and 6.70 min, respectively, and maximum waiting times of 17.18 and 25.42 min, respectively.
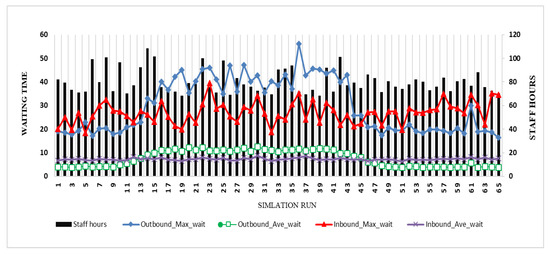
Figure 11.
Security screening facility results for shared staffing policies.
The developed approach is significant because it can be used to manage entire airport systems and provide better results than existing approaches. For example, the results obtained from our model demonstrated better improvement than those of Kierzkowski and Kisiel [27], especially in regard to the total average waiting time and staffing hours of security screening, as summarised in Table 3.

Table 3.
Comparison with ARM results from Kierzkowski and Kisiel [27].
- Comparison of overall impact of static and dynamic allocation approaches
The dynamic approach was found to provide better results, because it mimics real-life scenarios, including adding and removing staff and sharing staff between related processes. This section compares the results for the total average waiting time and the total staff hours using both methods of allocating staff, as shown in Figure 12 and Figure 13. The static results show considerable variation in regard to the outbound average waiting time compared with the dynamic allocation method using the same inputs, especially in terms of the number of personnel available. The dynamic approach can significantly impact the total staffing hours (time spent serving passengers), halving the hours produced by the static method. The proposed dynamic algorithms also have less variation associated with the total staff hours, where the minimum number of staffing hours is 625.78 h and the maximum is 777.15 h. In comparison, the minimum number of working hours for the static method is 1432 h and the maximum is 1781 h.

Figure 12.
Static allocation method results.

Figure 13.
Dynamic resource allocation method results.
After employing the dynamic resource allocation method, the total average waiting time in the outbound system was stable over all scenarios with a maximum of 24.52 min and a minimum of 17.38 min. The most interesting finding was that the check-in process plays a significant role in the performance of the entire outbound system in the case of the dynamic allocation method. According to the literature, the check-in process is considered to be the major factor causing delays and congestion at airport terminals, with more than 60% of the total time spent at check-in [28,29,30].
5. Conclusions
This paper proposes that a resource management approach can be embedded within an airport simulation model to reduce the likely delays incurred by passengers as they move through the inbound and outbound processes of an airport. The model can dynamically allocate/reallocate or add and remove airport personnel based on the given queue threshold policies. The results showed that the static allocation method can provide shorter queueing times for all terminal processes only if the upper limit of employees is chosen. However, the static allocation method has a significant impact on the operating time, which leads to long staffing hours. Allocating staff dynamically provides better outcomes in terms of representing flows of both passenger types—departing and arriving service processes. It is also able to manage the operations significantly better by allocating the staff if needed, which balances the queuing time of passengers and the operating hours of staff. The results of this investigation show that the total staffing hours are halved or sometimes 65% lower when the dynamic allocation approach is used.
The proposed model was developed for a specific Australian international airport. This is an issue as airports are operated in different ways [31]. For example, international airports commonly open check-in counters 3 h prior to departure, while domestic airports open check-in counters just 90 min beforehand [26]. Therefore, passenger arrival distribution patterns can vary between local airports and international airports. The simulation model of passenger flows considers all aspects of international airports. Hence, it can be adapted widely. Since domestic airports are considered to be a subset of international airports, the proposed model can be utilized to simulate all scenarios that may occur in domestic airports after adjustment of the processes in the model based on empirical data. To address this limitation, the following future research directions are recommended:
- How to employ the developed models in larger airports with two or more terminals should be determined. For example, Dubai International Airport has three separate terminals, and Terminal 3 alone has four concourses, each with 26 gates, including five A380 gates, and a total capacity of 60 million passengers. Similarly, further research could study the problem of passenger flow within airports dealing with international and domestic passengers in the same terminal, such as the Gold Coast Airport.
- As previously mentioned, the holistic framework proposed in this paper was developed based on the available data (Airport of the Future Project undertaken by Queensland University of Technology (QUT) and available literature. The lack of real-world data or scenarios make this topic significant; hence, further research is needed to validate the developed model by comparing its results with real-life scenarios to increase the model’s accuracy and robustness as well as to meet practical requirements.
Author Contributions
Conceptualization, S.A., P.K.D.V.Y.; formal analysis, S.A. and R.L.B.; project administration, S.A.; methodology, R.L.B.; supervision, funding acquisition, P.K.D.V.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Australian Research Council’s Linkage Project “Improving Productivity and Efficiency of Australian Airports” (140100282). The authors would also like to thank QUT High Performance Computing (HPC) for providing the computational resources for this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alodhaibi, S.; Burdett, R.L.; Yarlagadda, P.K.D.V. Impact of passenger-arrival patterns in outbound processes of airports. Procedia Manuf. 2019, 30, 323–330. [Google Scholar] [CrossRef]
- ICAO. Continued Passenger Traffic Growth and Robust Air Cargo Demand in 2017 2018. Available online: https://www.icao.int/Newsroom/Pages/Continued-passenger-traffic-growth-and-robust-air-cargo-demand-in-2017.aspx (accessed on 20 July 2018).
- Statista. Annual Growth in Global Air Traffic Passenger Demand from 2005 to 2018. Available online: https://www.statista.com/statistics/193533/growth-of-global-air-traffic-passenger-demand/ (accessed on 8 January 2018).
- Ma, W. Agent-Based Model of Passenger Flows in Airport Terminals. Ph.D. Thesis, Queensland University of Technology, Brisbane, Australia, 2013. [Google Scholar]
- Odoni, A.R.; De Neufville, R. Passenger terminal design. Transp. Res. Part A Policy Pract. 1992, 26, 27–35. [Google Scholar] [CrossRef]
- Zografos, K.G.; Madas, M.A.; Salouras, Y. A decision support system for total airport operations management and planning. J. Adv. Transp. 2010, 47, 170–189. [Google Scholar] [CrossRef]
- Yamada, H.; Ohori, K.; Iwao, T.; Kira, A.; Kamiyama, N.; Yoshida, H.; Anai, H. Modeling and Managing Airport Passenger Flow under Uncertainty: A Case of Fukuoka Airport in Japan; Springer Science and Business Media LLC: Cham, Switzerland, 2017. [Google Scholar]
- Spyropoulos, C.D. AI planning and scheduling in the medical hospital environment. Artif. Intell. Med. 2000, 20, 101–111. [Google Scholar] [CrossRef]
- Blaz Rodic, A.B. Dynamic airport ground crew scheduling. In Proceedings of the 21st Central European Conference on Information and Intelligent Systems, Varazdin, Croatia, 22–24 September 2010. [Google Scholar]
- Soukour, A.A.; Devendeville, L.; Lucet, C.; Moukrim, A. A memetic algorithm for staff scheduling problem in airport security service. Expert Syst. Appl. 2013, 40, 7504–7512. [Google Scholar] [CrossRef]
- Dowling, D.; Krishnamoorthy, M.; MacKenzie, H.; Sier, D. Staff rostering at a large international airport. Ann. Oper. Res. 1997, 72, 125–147. [Google Scholar] [CrossRef]
- Soukour, A.A.; Devendeville, L.; Lucet, C.; Moukrim, A. Staff scheduling in airport security service. IFAC Proc. Vol. 2012, 45, 1413–1418. [Google Scholar] [CrossRef]
- Sabar, M.; Montreuil, B.; Frayret, J.-M. An agent-based algorithm for personnel shift-scheduling and rescheduling in flexible assembly lines. J. Intell. Manuf. 2011, 23, 2623–2634. [Google Scholar] [CrossRef]
- Andreatta, G.; De Giovanni, L.; Monaci, M. A fast heuristic for airport ground-service equipment–and–staff allocation. Procedia Soc. Behav. Sci. 2014, 108, 26–36. [Google Scholar] [CrossRef]
- Parlar, M.; Sharafali, M. Dynamic allocation of airline check-in counters: A queueing optimization approach. Manag. Sci. 2008, 54, 1410–1424. [Google Scholar] [CrossRef]
- Lin, D.; Xin, Z.; Huang, Y. Ground crew rostering for the airport check-in counter. In Proceedings of the 2015 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Institute of Electrical and Electronics Engineers (IEEE), Singapore, 6–9 December 2015; pp. 1462–1466. [Google Scholar]
- Rodic, B.; Baggia, A. Airport ground crew scheduling using heuristics and simulation. In Applied Simulation and Optimization 2: New Applications in Logistics, Industrial and Aeronautical Practice; Mota, M.M., de la Mota, I.F., Eds.; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Alodhaibi, S.; Burdett, R.L.; Yarlagadda, P.K.D.V. Framework for airport outbound passenger flow modelling. Procedia Eng. 2017, 174, 1100–1109. [Google Scholar] [CrossRef]
- Alodhaibi, S.; Burdett, R.L.; Yarlagadda, P.K. A model to simulate passenger flow congestion in airport environment. Int. J. Eng. Technol. 2018, 7, 6943–6946. [Google Scholar]
- Wu, P.; Mengersen, K.L. A review of models and model usage scenarios for an airport complex system. Transp. Res. Part A Policy Pract. 2013, 47, 124–140. [Google Scholar] [CrossRef]
- Manataki, I.E.; Zografos, K.G. Development and demonstration of a modeling framework for airport terminal planning and performance evaluation. Transp. Res. Rec. J. Transp. Res. Board 2009, 2106, 66–75. [Google Scholar] [CrossRef]
- Kirk, P.J. Passenger Experience at Airports: An Activity-Centred Approach. Ph.D. Thesis, Queensland University of Technology, Brisbane, Australia, 2013. [Google Scholar]
- Lau, H.C. On the complexity of manpower shift scheduling. Comput. Oper. Res. 1996, 23, 93–102. [Google Scholar] [CrossRef]
- Ip, W.; Ho, G.T.S.; Chung, S.-H. Using integer programming for airport service planning in staff scheduling. Int. J. Eng. Bus. Manag. 2010, 2, 8. [Google Scholar] [CrossRef]
- Imrich, W.; Klavzar, S.; Rall, D.F. Topics in Graph Theory: Graphs and Their Cartesian Product; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Cheng, L. Modelling Airport Passenger Group Dynamics Using an Agent-Based Method. Ph.D. Thesis, Queensland University of Technology, Brisbane, Australia, 2014. [Google Scholar]
- Kierzkowski, A.; Kisiel, T. Simulation model of security control system functioning: A case study of the Wroclaw Airport terminal. J. Air Transp. Manag. 2017, 64, 173–185. [Google Scholar] [CrossRef]
- Park, Y.; Ahn, S.B. Optimal assignment for check-in counters based on passenger arrival behaviour at an airport. Transp. Plan. Technol. 2003, 26, 397–416. [Google Scholar] [CrossRef]
- Guizzi, G.; Murino, T.; Romano, E. A discrete event simulation to model passenger flow in the airport terminal. In Proceedings of the 11th WSEAS International Conference on Mathematical Methods and Computational Techniques in Electrical Engineering (MMACTEE’09), WI, USA, September 2009; Available online: https://dl.acm.org/doi/10.5555/1949006.1949078 (accessed on 25 January 2020).
- Schultz, M.; Fricke, H. Managing passenger handling at airport terminals. In Proceedings of the 9th Air Traffic Management Research and Development Seminars, Berlin, Germany, 14–17 June 2011. [Google Scholar]
- Fernandes, E.; Pacheco, R.R. Efficient use of airport capacity. Transp. Res. Part A Policy Pract. 2002, 36, 225–238. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).