1. Introduction
Matrices in max–min algebra (fuzzy matrices), in which the binary operations of addition and multiplication are replaced by binary operations of maximum and minimum, are useful when modeling fuzzy discrete dynamic systems. They are also useful for graph theory, scheduling, knowledge engineering, cluster analysis, fuzzy systems and when describing the diagnosis of technical devices [
1,
2] or medical diagnosis [
3]. The problem studied in [
3] leads to the problem of finding the greatest invariant of the fuzzy system.
Fuzzy DES combine fuzzy set theory with discrete events systems and are represented by vectors and matrices having entries between 0 and 1 and describing uncertain and vague values. The papers [
4,
5] are devoted to a generalization of DES into fuzzy DES and spreading optimal control of discrete event systems to fuzzy discrete event systems. The authors of [
6] deal with predictability in fuzzy DES. In particular, these papers are motivated by an ambition to clear a difficulty with vagueness and subjectivity in real medical applications. The other possibility how to treat the possible inaccuracy of DES entries is to use interval data in combination with forall–exists quantification of values. Namely, some elements of the interval vector and the interval matrix are taken into account for each value of the interval, and some of them are only considered for at least one value. This approach allows to obtain alternative solutions.
The research of fuzzy algebra is also motivated by max-plus interaction discrete-events systems (DESs) whereby applications on the system of processors and multi-machine interactive production process were presented in [
7,
8], respectively. In these systems, we have
n entities (e.g., processors, servers, machines, etc.) which that work in stages. In the algebraic model of their interactive work, the entry
of the state vector
represents the start-time of the
kth stage on entity
i,
, and the entry
of the transition matrix encodes the influence of the work of entity
j in the previous stage on the work of entity
i in the current stage. The system is assumed to be homogeneous, in the sense that
A does not change from stage to stage.
Summing up all the influence effects multiplied by the results of previous stages, we have
, where
and
. In max-plus algebra, the maximum is often interpreted as waiting until all works of the system are finished and all of the necessary influence constraints are satisfied. The problem of finding the vectors for which the DES reaches the steady state leads to the eigenproblem
, and is one of the most intensively studied questions (see max–min case study in
Section 3.2.
Analogously, in max–min algebra. The summing is then interpreted as computing the maximal capacity of the path leading to the next state of the system. Because the operations max and min do not create new values, a DES in max–min algebra necessarily comes to periodic repetition of the state vector (i.e., to a steady state) if the period is 1. The eigenproblem then has the form . In comparison with the max–plus algebra, the eigenvalue is omitted (in other words, we assume that is equal to the maximal value I).
In practice, the values of the matrix entries obtained as a result of roundoff, truncation, or data errors are not exact numbers and they are usually contained in some intervals. Interval arithmetic is an efficient way to represent matrices in a guaranteed way on a computer. Meanwhile, fuzzy algebra is a convenient algebraic setting for some types of optimization problems, see [
9]. Matrices and vectors with interval entries play important role in practice. They can be applied in several branches of applied mathematics, as for instance, a solvability of systems of linear interval equations in classical linear algebra [
10] and in max-plus algebra [
11] or the stability of the matrix orbit in max–min algebra [
12,
13].
The motivation for the basic questions studied in this paper comes from an investigation of the steady states of max–min systems with interval coefficients. Suppose that X is an interval vector and A is an interval matrix, then X is called a strong eigenvector of A if holds for every and for every . The eigenvectors correspond to steady states, and it may happen in reality that this interpretation—with the universal quantifier for every index and for every pair —is too strong for all of the entries.
In other words, in some model situations only the existence of some (some ) is required for for , while all possible values of (of ) must be considered for for .
Hence, we assume that X and A can be split into two subsets according to the exists/forall quantification of its interval entries; that is, or (or both splittings simultaneously) take place.
According to the first two cases, the properties of various types of the strong EA/AE-eigenvectors, or the EA/AE-strong eigenvectors, are studied in this paper. In addition, their characterizations by equivalent conditions are given. Moreover, polynomial recognition algorithms for the described conditions are presented. The mixed case (the EA/AE-strong EA/AE-eigenvectors) is briefly considered without recognition algorithms.
Related concepts of robustness (when an eigenvector of
A is reached with any starting vector) and strong robustness (when the greatest eigenvector of
A is reached with any starting vector) in fuzzy algebra were introduced and studied in [
14,
15]. Equivalent conditions for the robustness of interval matrix were presented in [
11] and efficient algorithms for checking of strong robustness were described in [
16]. The papers by [
12,
13] deal with AE/EA robustness of interval circulant matrices and
/
robustness of max–min matrices. Polynomial procedures for the recognition of weak robustness were described in [
15].
The rest of this paper is organized as follows. The next section contains the basic definitions and notation.
Section 3 and
Section 4 deal with the definitions and equivalent conditions for the EA/AE-eigenvectors. In particular,
Section 3 is divided into two subsections, where
Section 3.1 contains the methodology and
Section 3.2 presents a study case application based on a numerical example.
Section 5 describes the strong EA/AE-eigenvectors. Meanwhile,
Section 6 is devoted to characterization of the necessary and sufficient conditions for the EA/AE-strong eigenvectors. Finally, the generalization to the mixed case of EA/AE-strong EA/AE-eigenvectors is briefly sketched in
Appendix A.
2. Preliminaries and Basic Definitions
Let be a bounded linearly ordered set with the least element in denoted by O and the greatest element denoted by I. For given natural numbers , we use the notation and , respectively. The set of matrices over is denoted by , the set of vectors over is denoted by and, for , the constant vector is denoted by .
The max–min algebra is defined as a triple , where and The operations are extended to the matrix-vector algebra over by the direct analogy to the conventional linear algebra. If each entry of a matrix (a vector ) is equal to O, then we write ().
The ordering from is naturally extended to vectors and matrices. For example, for and we write , if holds for each .
For
and
, the interval matrix
A with bounds
,
and the interval vector
X with bounds
,
are defined as follows
In the rest of this paper we assume that subsets are given with and . In other words, we consider a partition . If (), then we say that the index i is associated with the existential (universal) quantifier.
Using the given partition , we can split the interval vector X as , where is the interval vector comprising the universally quantified entries and concerns the existentially quantified entries. In the other words, every vector can be written in the form , with , .
More precisely, for , for ; and similarly, for , for .
Definition 1. Let interval vector and partition be given. Interval vector is called
E-subvector of X, if for each and for each ,
and interval vector is called
A-subvector of X, if for each and for each ,
Example 1. Suppose that , . Consider interval vector X which has the form Then subvectors and have the form For given , we say that x is eigenvector of A, if In the rest of this paper, we assume that a partition is given. The corresponding subvectors , and entries will always be related to this fixed N, without explicit formulation. The same is true for the EA/AE-eigenvectors that are defined as follows.
Definition 2. Let matrix and interval vector be given. We say that X is
All matrices belonging to
A and vectors belonging to
X can be represented as max–min linear combinations of so-called
generators, which are defined as follows. For every
,
and
are defined by putting, for every
,
Furthermore, we denote and . Notice that .
Lemma 1. Let and . Then,
- (i)
if and only if for some with ,
- (ii)
if and only if for some with .
Proof. For the proof of statement (i), let us suppose that ; that is, the inequalities hold for every . Denoting we get and for every . It can be easily verified that . The proof of statement (ii) is analogous. □
3. EA-Eigenvector
3.1. Description of the Methodology
The first result is the characterization of an interval EA-eigenvector of a given (non-interval) matrix A, with the help of generators.
Theorem 1. Let and be given. Then, X is EA-eigenvector of A if and only if Proof. Suppose that there is
such that
holds for all
. For fixed
define the auxiliary interval vector
as follows:
Notice that vectors
of
have the form
or equivalently,
for each
and
for each
. It is easy to see that
X is EA-eigenvector if and only if
holds for each
. By Lemma 1, an arbitrary vector
is defined as the max–min linear combination
We will then prove that the equality
holds for each
. Thus, we get
The reverse implication is trivial. □
The next result shows that the conditions in Theorem 1 can be equivalently formulated as the solvability condition of a system of two-sided max–min linear equations. Hence, the interval EA-eigenvectors of a given non-interval matrix can be recognized in polynomial time.
Without loss of generality, suppose that
and
; that is,
and
Define the matrices
as follows
and
Theorem 2. Let A and be given. Then, X is EA-eigenvector of A if and only if the system is solvable with for and for .
Proof. By Lemma 1, if for , then belongs to ; and if , then we can find for such that .
We also have that the system
is solvable with
for
and
for
if and only if the following equivalences hold true:
because of
for
. Thus by Theorem 1, the assertion follows. □
A polynomial algorithm for solving a general two-sided system
of max–min linear equations with
, is presented in [
17]. This method finds the maximum possible solution,
, of the system. If this possible solution does not satisfy all of the conditions of the system, then the system is not solvable. In our case, the insolvability means that the considered
X is not an EA-eigenvector of
A. The computational complexity of the proposed algorithm is
.
Theorem 3. Suppose that we are given a matrix A and an interval vector . The recognition problem of whether a given interval vector X of A is EA-eigenvector is then solvable in time.
Proof. According to Theorem 2, the recognition problem of EA-eigenvector of
A is equivalent to recognizing whether the system
is solvable with
for
and
for
. In the general case, the computation of the needs
time (see [
17]). In our case, we have
,
; therefore, the computation of
is done in
time. □
3.2. Case Study Application of the Methodology Based on Numerical Example
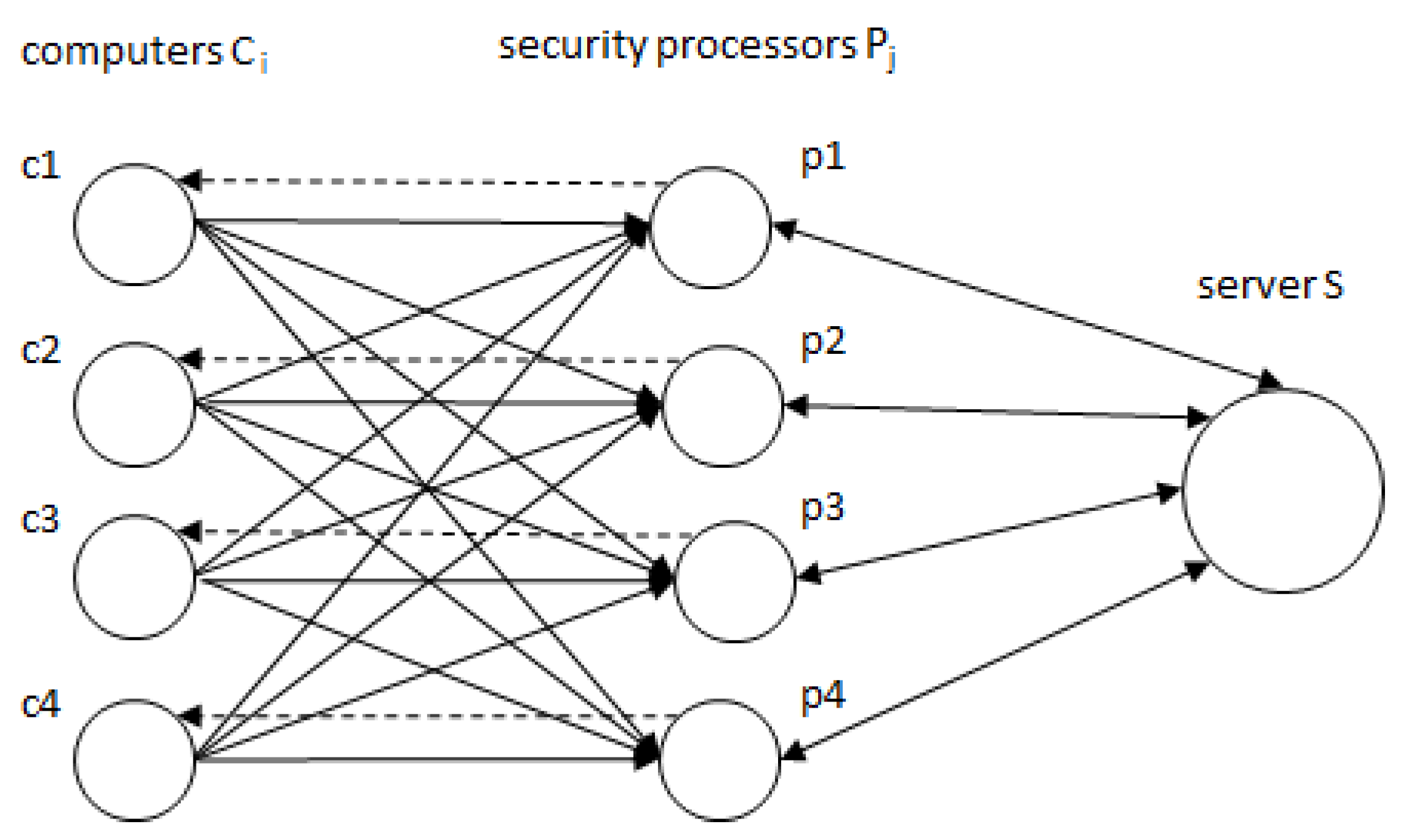
Consider a data transfer system consisting of n computers and one server S. The computed data from computer , are sent to S whereby the corrected data have to return to . We assume that the connection between and S is only possible via one of n security processors , the connections between and are one-way connections, and the capacity of the connection between and is equal to . Moreover, suppose that security processors are connected with S by two-way connections with capacities in both directions. The data are transmitted in data packets, and every data packet is transmitted over just one connection as an inseparable unit. Therefore, the total capacity of the connection between i and S is equal to , that is, different used connections are comprised as the maximum of capacities (not as their sum).
The transfer from S to i is carried out via other one-way connections between security processors and with capacities between j and i equal to the constant I (the greatest element) if , and equal to O (the least element), otherwise. Since the connections between S and j are two-way connections, the total capacity of the connection between S and i is equal to for every . The goal is to find optimal capacities , such that the maximal capacity of all connections between i and S via j is equal to the maximal capacity of connections between S and i on the way back, that is, we have to choose , in such a way that for all .
Consider a data transfer system which consists of 4 computers, 4 security processors and one server (see
Figure 1). To find optimal capacities
,
means to solve an eigenproblem for a matrix
A. Then for
and the matrix
A we look for a solution of the equality
, or in matrix-vector form, we have
One solution of the set of all solutions describing optimal capacities , of the data transfer system is vector .
Assume now that the capacities , are limited by the lower bound and upper bound . Furthermore, we assume that not all of the processed data have the same importance: whereby, for some more important types of data, all values of the interval must be taken into account (all capacities of the data transfer system have to be involved in optimal solutions), and for some—less important data types—it is sufficient to be considered for at least one value (some value of these capacities of the data transfer system are optimal). In the above defined terminology, the optimal solution has to satisfy the definition of the EA-eigenvector of A.
For numerical illustration of this situation suppose that interval vector
X has the form
with
,
and
.
Then generators of
X and its matrix-vector products can be computed as follows:
and
By Theorem 2 we will show that
X is EA-eigenvector. At first we shall construct matrices
C and
D and after that we shall solve the system
with
for
and
for
, i.e.,
with
To obtain a solution of the system (
3), we use the Algorithm 1 presented in [
17]. For the convenience of the reader, the algorithm is described in the original notation.
Let
be given matrices. Denote
| Algorithm 1: Solving a general two-sided system. |
Input: . Output: . begin 1 If , then , STOP; 2 Change notation so that for all ; 3 Compute ; 4 Set if otherwise; 5 If , then , STOP; 6 Put go to 2 ; end
|
We will now apply the items of the Algorithm 2 to obtain the greatest solution of the system (
3) whereby
will be substituted by
, respectively:
| Algorithm 2: Solving a general two-sided system - example. |
Input: . Output: 1 ; 2 ; 3 ; 4 ; 5 , , STOP.
|
The output of the Algorithm 2 is vector
, which is the greatest possible solution of the system (
3). It is easy to verify that the possible solution
satisfies all conditions of (
3). In other words,
is the solution, and we can conclude that
X is an EA-eigenvector of
A.
4. AE-Eigenvector
As in the previous section, we characterize an interval AE-eigenvector of a given non-interval matrix
A with the help of generators. We recall that
, where
for
, and
.
Theorem 4. Let and be given. Then, X is an AE-eigenvector of A if and only if Proof. Suppose that
X is not an AE-eigenvector of
A; that is,
or equivalently
We shall prove that either there is such that for each the inequality holds true or there is such that for each the inequality is fulfilled.
We will next analyze four cases:
Case (i).
Suppose that
and
We then have
and for
we obtain
Case(ii).
Suppose that
and
We then have
and hence
because
. Moreover, there exists
such that
We will consider two subcases:
Subcase 1:
. Then, for
, we obtain
Subcase 2:
. Then, for
, we obtain
Case (iii).
Suppose that
and
We then have
and hence it follows that
Thus, for
we obtain
Case (iv).
Suppose that
and
We then have
hence there is
such that
because
We will consider two subcases:
Subcase 1:
. Then, for
, we obtain
Subcase 2:
. Then, for
, we obtain
The reverse implication is trivial. □
The last theorem can be rewritten in the following form:
Corollary 1. Let and be given. Then, X is AE-eigenvector of A if and only if The next two theorems show that the conditions in Corollary 1 can be equivalently formulated as the solvability conditions of a finite set of two-sided max–min linear systems. Consequently, the interval AE-eigenvectors of a given non-interval matrix can be recognized in polynomial time.
Without loss of generality suppose that
, where
and
; that is,
and
Define matrices
, for
, as follows
Also, denote
Theorem 5. Let , and be given. Then
if and only if the system with for and is solvable,
if and only if the system with for and is solvable.
Proof. By Lemma 1, if for , then belongs to , and if then we can find for such that .
We also have the following equivalences for an arbitrary
because
.
Similarly, we can prove the second part of the theorem. □
Theorem 6. Suppose that we are given a matrix and an interval vector . Then, X is an AE-eigenvector of A if and only if for each the systems and are solvable with for , and for , , respectively.
Proof. The assertion follows from Theorems 4 and 5. □
Theorem 7. Suppose that we are given a matrix and an interval vector . The recognition problem of whether a given interval vector X is an AE-eigenvector of A is then solvable in time.
Proof. According to Theorem 6, the recognition problem of whether a given interval vector
X is an AE-eigenvector of
A is equivalent to recognizing if the system
is solvable for each
with
for
and
. The computation of a system
needs
time (see [
17]), where
. Therefore, the computation of at most
n such systems is done in
time. □
5. Strong Eigenvectors
In this section, we study various eigenvector types for the interval matrix and the interval vector . The basic type, which is called a strong eigenvector, is related to all matrices in A and all vectors in X. Further types, which are called strong EA-eigenvectors (strong AE-eigenvectors), are related to all matrices and to EA-eigenvectors (AE-eigenvectors) derived from X.
Definition 3. Let be given. The interval vector X is called strong eigenvector of A if
Theorem 8. Let be given. Then, X is a strong eigenvector of A if and only if and for all .
Proof. Let us assume that
,
and
for all
. Then, for arbitrary
we get
and
The assertion follows from the monotonicity of operations; that is, for each . The converse implication is trivial. □
Remark 1. It is easy to see that the conditions in Theorem 8 can be verified in time.
Definition 4. Let be given. Then interval vector X is called
a strong EA-eigenvector
of A ifand a strong AE-eigenvector
of A if
Theorem 9. Let be given. The following conditions are equivalent
- (i)
X is a strong EA-eigenvector of A,
- (ii)
,
- (iii)
.
Proof. These assertions follow from Theorems 1 and 8. □
Theorem 10. Let be given. The following conditions are equivalent
- (i)
X is a strong AE-eigenvector of A,
- (ii)
,
- (iii)
.
Proof. These assertions follow from Theorems 4 and 8. □
Remark 2. By Theorems 9 and 10, the verification of whether
- (i)
X is a strong EA-eigenvector,
- (ii)
X is a strong AE-eigenvector,
reduces to finding a vector satisfying some linear max–min equations, similar to Theorems 2 and 6. Hence, the recognition problem for these types of strong eigenvectors is polynomially solvable.
6. EA/AE-Strong Eigenvectors
In the previous sections, we worked with a fixed partition , with and . In other words, every index is associated either with the existential, or with the universal quantifier. According to partition N, the interval vector X is presented as a sum of subintervals . The interpretation of this partition is such that, for technical reasons, the vector entries in subinterval only require the existence of one possible value , while the entries in subinterval require all possible values .
A similar interpretation can be applied to the matrix entries. Suppose that each interval of A is associated either with the universal or with the existential quantifier. We can then split the interval matrix as , where is the interval matrix comprising universally quantified coefficients and concerns existentially quantified coefficients.
Hence, we work with partition , where and . In other words, for each pair and for each
Definition 5. Let A, X be given. Interval vector X is called
EA-strong eigenvector of A if there is such that for any the vector X is a strong eigenvector of ,
AE-strong eigenvector of A if for any there is such that X is a strong eigenvector of .
6.1. EA-Strong Eigenvector
Theorem 11. Let A, X be given. Then, X is an EA-strong eigenvector of A if and only if Proof. Suppose that there is
such that
and
hold for each
. By monotonicity of the operations ⊕ and ⊗ for an arbitrary matrix
, we get
The reverse implication trivially holds. □
Theorem 12. Let A, X be given. Then, X is an EA-strong eigenvector of A if and only if Proof. By Lemma 1, if
for
then
belongs to
X; and if
, then we can find
for
such that
. Then, we have
Similarly, we can prove the second equality and by Theorem 11 the assertion follows. The reverse implication trivially holds. □
The last theorem enables us to check the equivalent conditions of Theorem 12 in practice, whereby and are joined into one system of equalities.
Let
A and
X be given and
. We denote the block matrix
and vectors
,
as follows
and
where
is a variable corresponding to the last column of
Theorem 13. Let A, X be given. Then X is EA-strong eigenvector of A if and only if the system has a solution α such that and
Proof. The system
is solvable if and only if there is a vector
such that
for all
with
and
Put
and by Theorem 12 the assertion holds true. □
Theorem 14. Suppose that we are given a matrix A and interval vector . The recognition problem of whether a given interval vector X is EA-strong eigenvector of A is solvable in time.
Proof. According to Theorem 13, the recognition problem of whether a given interval vector
X is EA-strong eigenvector of
A is equivalent to recognizing if the system
has a solution
with
and
The computation of a system
needs
time (see [
18]), where
. Therefore, the computation of such systems is done in
time. □
6.2. AE-Strong Eigenvector
Denote
Theorem 15. Let A, X be given. Then, X is an AE-strong eigenvector of A if and only if Proof. Suppose that for
there is
such that for all
the equality
holds true and for
there is
such that for all
the equality
is fulfilled. Moreover, assume that
is arbitrary but fixed. Then, for any
there is
such that the following
holds for any
.
We will prove that for an arbitrary but fixed matrix , there is such that
Put
. Then, there is
such that
Consider two cases.
Case 1. For
, we get
The reverse inequality follows from the monotonicity of operations
Case 2. For
, we get
Because the reverse inequality trivially follows from (
4), the equality
is proven.
The reverse implication is trivial. □
Theorem 16. Let A, X be given. Then, X is AE-strong eigenvector of A if and only if Proof. By Lemma 1, if
for
, then
belongs to
X; and if
, then we can find
for
such that
. Then, for any
there is
such that for and fixed
we have
and by Theorem 15 the implication follows. The reverse implication trivially holds true. □
Let
A and
X be given and
. For each
and
, we denote the block matrix
and
as follows
and
where
is a variable corresponding to the last column of
Theorem 17. Let A, X be given. Then, X is an AE-strong eigenvector of A if and only if each and for each the system has a solution α such that and
Proof. Suppose that
and
are fixed. The system
is solvable if and only if there is a vector
such that
with
and
Put
and by Theorem 16 the assertion holds true. □
Theorem 18. Let A, X be given. The recognition problem of whether a given interval vector X is an AE-strong eigenvector of A is solvable in time.
Proof. According to Theorem 17, the recognition problem of whether a given interval vector
X is an AE-strong eigenvector of
A is equivalent to recognizing if the system
has a solution
with
and
The computation of a system
needs
time (see [
18]), where
. Therefore, the computation of such systems is done in
time. □
7. Conclusions
In this paper, we have presented the properties of steady states in max–min discrete event systems. This concept, in connection with inexact entries and its exists/forall quantification, represents an alternating version to fuzzy discrete events systems which are using vectors and matrices with entries between 0 and 1, and are describing uncertain and vague values. The practical significance of this approach is that some elements of the vector X and the matrix A are taken into account for all values of the interval (corresponding to A-index), and some of them are only considered for at least one value (corresponding to E-index).
The concept of various types of the strong EA/AE-eigenvectors and the EA/AE-strong eigenvectors have been studied. In addition, their characterizations by equivalent conditions are given. All findings have been formally analyzed with a target to estimate the computational complexity of checking the obtained equivalent conditions. The results have been illustrated by an application of the obtained methodology on a numerical example.
The investigation of AE/EA concepts for steady state of discrete events systems with interval data has brought new efficient equivalent conditions. There is a good reason to continue the study of exists/forall quantification method for tolerable, universal and weak eigenvectors which are still unexplored and stay open for future research.