A Philosophical Treatise on the Connection of Scientific Reasoning with Fuzzy Logic

Abstract

The present article studies the connection of scientific reasoning with fuzzy logic. Induction and deduction are the two main types of human reasoning. Although deduction is the basis of the scientific method, almost all the scientific progress (with pure mathematics being probably the unique exception) has its roots to inductive reasoning. Fuzzy logic gives to the disdainful by the classical/bivalent logic induction its proper place and importance as a fundamental component of the scientific reasoning. The error of induction is transferred to deductive reasoning through its premises. Consequently, although deduction is always a valid process, it is not an infallible method. Thus, there is a need of quantifying the degree of truth not only of the inductive, but also of the deductive arguments. In the former case, probability and statistics and of course fuzzy logic in cases of imprecision are the tools available for this purpose. In the latter case, the Bayesian probabilities play a dominant role. As many specialists argue nowadays, the whole science could be viewed as a Bayesian process. A timely example, concerning the validity of the viruses’ tests, is presented, illustrating the importance of the Bayesian processes for scientific reasoning.

“Doubt is not a pleasant situation, but the excessive certainty is an unreasonable situation”

Voltaire (1694–1778)

1. Introduction

It is hard to deny that the rapid and impressive advances of the last 100–150 years in science and technology have been greatly based on the principles of the bivalent logic of Aristotle, which has played (and plays) a dominant role for more than 23 centuries for the progress of the Western civilization. On the contrary, ideas of multi-valued logics were traditionally connected to the culture and customs of the Eastern countries of Asia, being inherent in the philosophy of Buddha Siddhartha Gautama, who lived in India during the fifth century BC. Nevertheless, the formalization of those logics was performed in the West with the Zadeh’s Fuzzy Logic (FL), an infinite-valued logic based on the mathematical theory of fuzzy set (FS) [1]. The instantaneous switch from truth (1) to falsity (0) can easily distinguish propositions of classical logic from those in FL with values lying in the interval [0, 1]. As it usually happens in science with such radical ideas, FL, when first introduced during the 1970s, was confronted with distrust and reserve by most mathematicians and other positive scientists. However, it has been eventually proved to be an effective generalization and complement of the classical logic and has found many and important applications to almost all sectors of human activity, e.g., [2]: Chapters 4–8, [3], etc.

Human reasoning is characterized by inaccuracies and uncertainties, which stem from the nature of humans and the world. In fact, none of our senses and observation instruments allows us to reach an absolute precision in a world which is based on the principle of continuity, as opposed to discrete values. Consequently, FL, introducing the concept of membership degree that allows a condition to be in a state other than true or false, provides a flexibility to formalize human reasoning. Another advantage of FL is that rules are set in natural language with the help of linguistic, and therefore fuzzy, variables. In this way, the potential of FL becomes strong enough to enable developing a model of human reasoning proceeding in natural language. Furthermore, since at the basis of reasoning in expert systems are human notions and concepts, the success of these systems depends upon the correspondence between human reasoning and their formalization. Thus, FL appears as a powerful theoretical framework for studying not only human reasoning, but also the structure of expert systems.

However, only a limited number of reports appear in the literature connecting FL to human reasoning; e.g., see [4,5,6]. This was our main motivation for performing the present study by continuing our previous analogous efforts. In fact, in a recent book written in the Greek language, the first author of this article studies the inductive reasoning under the light of FL and criticizes the excessive accusations of the Philosophy of Science against it [7]. Additionally, in an earlier work [8], the second author has introduced a model for analyzing human reasoning by representing its steps as fuzzy sets on a set of linguistic labels characterizing the individual’s performance in each of those steps.

The target of the article at hand is to analyze the scientific method of reasoning under the light of FL. The rest of the article is organized as follows: Section 2 examines the inductive and deductive reasoning from the scope of FL. Section 3 explains how these two fundamental components of human reasoning act together for creating, improving and expanding the scientific knowledge and presents a graphical representation of the scientific progress through the centuries. Section 4 studies the unreasonable effectiveness of mathematics in the natural sciences (Winger’s enigma), while Section 5 quantifies the degree of truth of the inductive and deductive arguments. 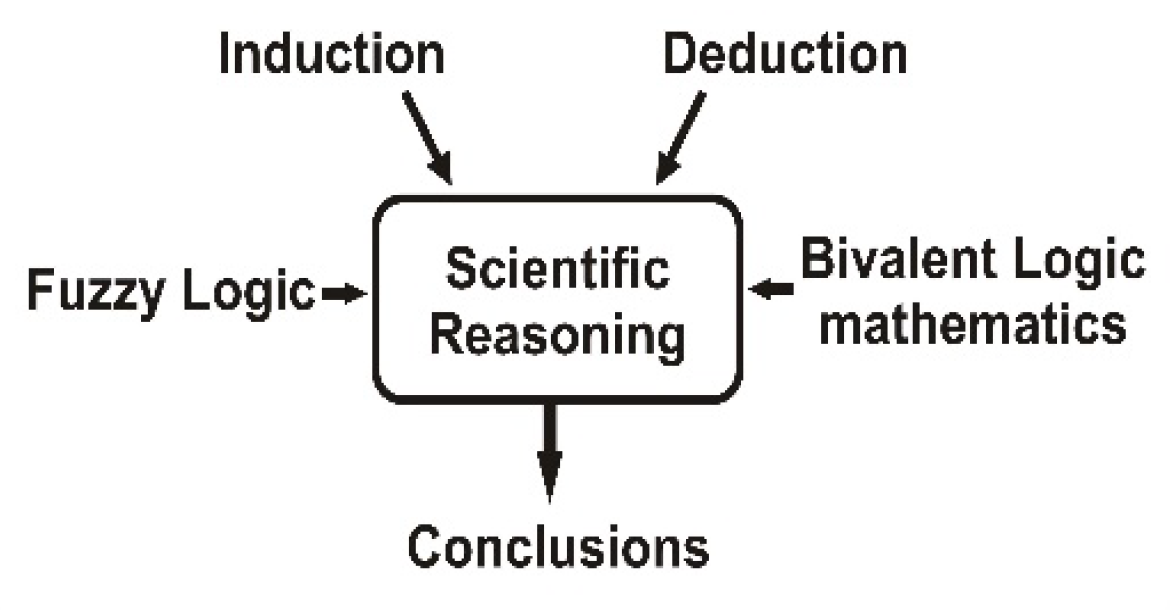The article closes with the general conclusions presented in Section 6. A schematic diagram of the proposed study is presented in Figure 1.

The novelty of the present article is that it brings together philosophy, mathematics and fuzzy logic, thus becoming a challenge for further scientific discussion on the subject. This is the added value of this work.

2. Human Reasoning and Fuzzy Logic

Induction and deduction are the two fundamental mechanisms of human reasoning. Roughly speaking, induction is the process of going from the specific to general, whereas deduction is exactly the opposite process of going from the general to the specific. A third form of reasoning that does not fit to induction and deduction is the abduction. It starts with a series of incomplete observations and proceeds to the most possible conclusion. For example, abduction is often used by jurors, who make decisions based on the evidence presented to them, by doctors, who make a diagnosis based on test results, etc.

A typical form of a deductive argument is the following:

• If “Every A is B” and “C is an A”, then “C is B”.

For example, “All dogs are animals” and “Snoopy is a dog”, therefore, “Snoopy is an animal”. That is, deductive reasoning starts from a first premise and based on a second premise reaches a logical inference.

A deductive argument is always valid/consistent in the sense that, if its premises are true, then its inference is also true. However, if at least one of its premises is false, then the inference may also be false. For example, “All positive integers are even numbers”, “5 is a positive integer”, therefore “5 is an even number”. In that case, the inference is false due to the fact that the first premise is false. However, the deductive argument remains a valid logical procedure. This is better understood, if one restates the above argument in the form: “If all positive integers were even numbers, then 5 would be an even number”. In conclusion, the typical logic is interested only for the validity and not for the truth of an argument. Therefore, a deductive argument is always compatible to the principles of the bivalent logic, regardless whether or not its inference is true.

A characteristic example of the deductive mechanism can be found in the function of computers. A computer is unable to judge if the input data inserted to it is correct and, therefore, if the result obtained is correct and useful for the user. The only thing that it guarantees is that, if the input is correct, then the output will be correct too. Thus, the credo that was popular in the early days of computing, “Garbage in, garbage out” (GIGO), or “Rubbish in, rubbish out” (RIRO), is still valid.

An inductive argument makes generalizations from specific observations. It starts with a series of observations on the specific cases of a phenomenon and reaches a conclusion by making a broad/imperfect generalization. A typical form of an inductive argument is the following:

• The element x₁ of the set A has the property B.
• The element x₂ of the set A has the property B.
• ……………………………………………………
• …………………………………………………...
• The element x_n of the set A has the property B.
• Therefore, all the elements of the set A have the property B.

The inference of an inductive argument could be either true or false. However, an inductive argument is never valid/consistent, even if its inference is true, because it is not a procedure compatible to the principles of the typical logic. In fact, if all the premises of an inductive argument are true, there is always the possibility for its inference to be false.

Let us now restate the previous inference as follows:

• Therefore, all the elements of the set A possibly have the property B.

This is not an acceptable by the bivalent logic statement, because it does not satisfy the principle of the excluded middle. However, it is compatible to FL, which does not adopt the above principle. It is evident that the greater the value of n in the last premise of the above inductive argument (i.e., the greater the number of observations performed), the greater the degree of truth of its inference. In other words, an inductive argument, although not a logical process according to the standards of the bivalent logic, is acceptable when its inference is “translated” in the language of FL.

The validity of the deductive reasoning is very important for scientific research, because it enables the construction of extended arguments. An extended argument is understood to be a chain of simple deductive arguments A₁, A₂, …, An, which has been built by putting as first premise of the next argument the inference of the previous one. In this way the validity of the argument A₁ is transferred to the final argument A_n.

In everyday life, however, people always want to know the truth in order to organize better, or even to protect their lives. Consequently, in such cases the significance of an argument has greater importance than its validity/precision. In Figure 2, retrieved from https://complementarytraining.net/strength-training-categorization/figure-6-precision-vs-significance, the extra precision on the left actually makes things worse for the poor man in danger, who has to spend too much time trying to understand the data and misses the opportunity to take the much needed action of getting out of the way. On the contrary, the rough/fuzzy warning on the right could save his life.

Figure 2 illustrates very successfully the importance of FL for real-life situations. Real-world knowledge generally has a different structure and requires different formalization than existing formal systems. FL, which according to Zadeh is “a precise logic of imprecision and approximate reasoning”, serves as a link between classical logic and human reasoning/experience, which are two incommensurable approaches. Having a much higher generality than bivalent logic, FL is capable of generalizing any bivalent logic-based theory. Linguistic variables and fuzzy if-then rules are in effect a powerful modelling tool used widely in FL applications. In addition, FL is the basis for computing with words, i.e., computation with information described in the natural language. This is particularly useful when dealing with second order uncertainty, i.e., uncertainty about uncertainty [9].

Some important details about the history and evolution of FL, like Plato’s ideas about the existence of a third area beyond “true” and “false”, the Lukasiewicz’s [10] and Tarski’s multi-valued logics, etc., can be found in Section 2 of [11]. In addition, it is useful to notice here the connection of FL to the Reiter’s logic for default reasoning [12]. An example of default reasoning is the following: “Whenever x is a bird, then in the absence of any information about the contrary (e.g., that x is a penguin or an ostrich or a Maltese falcon, etc.) one may assume that x flies”.

Fuzzy mathematics is trying to cover an inherent weakness of crisp mathematics, which was very successfully stated by Einstein during his speech in the Prussian Academy of Sciences in 1921 as follows: “So far as lows of mathematics refer to reality, they are not certain. And so far as they are certain, they do not refer to reality”.

FL, however, should not be viewed as the final solution for representing human knowledge about the world. Simply, it has offered a model that could easily be grasped by scientists and researchers alike as a step toward formalizing human reasoning. Because of this, Zadeh’s basic notion of FS stimulated enormous research activity that has generated various extensions and generalizations (type-2 FS, interval-valued FS, intuitionistic FS, hesitant FS, Pythagorean FS, complex FS, neutrosophic sets, etc.), as well as several alternative theories for dealing with the several forms of the existing in the real world uncertainty (grey systems, rough sets, soft sets, etc.) [13]. Although none of those generalizations/theories look to be perfect for tackling all the types of uncertainty existing in the real word, the combination of all of them provides a powerful framework for this purpose.

It is of worth noting here that, before the development of FL by Zadeh, the unique tool to deal with the uncertainty appearing in everyday life and science used to be probability theory. Nevertheless, probability, which is based on the principles of the bivalent logic, is only capable to tackle the cases of uncertainty which are due to randomness. On the contrary, FL, its generalizations and all the alternative theories mentioned above, can also manage the several types of uncertainty that are due to imprecision. Probabilities and membership degrees, although they both function on the same interval [0, 1], they are completely different notions ([14], Remark 3, p.22). An additional example illustrating this difference is presented in Section 5 of the present article.

3. The Scientific Method of Thinking and the Curve of the Scientific Error

As we have previously seen, the truth of a deductive argument depends upon the truth or not of its premises. However, the premises must be true not only in a particular moment, but forever. The following example illustrates the significance of this remark:

• All swans are white.
• The bird in the lake is a swan.
  _______________________________________________________________________
• The bird in the lake is white.

This used to be a true deductive argument before the discovery of Australia, where a kind of black swan was traced in 1697 (Figure 3). Since then the argument turned to be false.

Unfortunately, only a few arguments are known that could be used as premises, which remain true forever. Even the premise that “all humans are mortal” could be put under dispute. In fact, there is a theoretical possibility that the continuous progress of science and technology could enable in the remote future humans to live forever. Then, we would have a fact analogous to the case of the swans! In Physics, the classical law of “conservation of the energy” has been transformed now to “conservation of energy and mass”. This seems, however, as a premise that could remain true forever.

Some premises of such kind can also be found in mathematics, which is considered as the most “solid” among the sciences; e.g., the arithmetic of the natural numbers. However, problems exist even in the area of mathematics. For example, the target of the leader of formalism David Hilbert (1862–1943) anticipated a complete and consistent (i.e., not permitting the existence of paradoxes) axiomatic development of all branches of mathematics [15]. Gödel’s (1906–1978) two incompleteness theorems [16], however, put a definite end to Hilbert’s ambitious plans. In fact, as a consequence of the second theorem, there is no formal system with a finite set of axioms and rules that can prove the consistency of another system, since it must prove its own consistency first, which is impossible. Thus, for a given system the best to hope is that, although by the first theorem is not complete (i.e., there exist propositions which cannot either proved or refuted inside it), it is consistent. Of course, this happens due to the inherent deficiencies of the formal systems and does not imply that the human ability to understand is restricted and therefore some truths will never be known.

Evolutionary anthropologists have estimated that the modern human (homo sapiens, which means wise man) occurred on the earth roughly to 200 thousand years ago. However, the existing witnesses lead to the conclusion that the first smart human behavior, connected to the stone-made tools and the isolation of fire, appeared much earlier, in the time of the homo erectus (upright man). The earliest occurrence of the homo erectus, who is the archaic ancestor of homo sapiens, is estimated about two million years ago. Homo erectus appears to be much more similar to modern humans than to his ancestors, the australopithecines, with a more humanlike gait, body proportions, height, and brain capacity. He was capable of starting speech, hunting and gathering in coordinated groups, caring for injured or sick group members, and possibly making art. However, his IQ remained at a constantly low level, being slightly higher than that of his ancestors.

Curiosity was a dominant characteristic of humans from the time of their occurrence on the earth. They made continuous observations trying to understand the world around them and they searched for explanations about the various natural phenomena. Inductive reasoning helped them on that step to create such explanations by making hypotheses, which were eventually transformed to empirical theories and applications for improving their lives and security; e.g., constructing stone and wood-made weapons and tools for hunting and cultivating the earth, using the fire for heating and cooking, etc.

Deductive arguments started to appear in human reasoning since the time of occurrence of the homo sapiens. Deductive reasoning became eventually the dominant component of human reasoning that led through the centuries to the development of the human civilization. In the first place, humans tried to verify by deduction the empirical theories created on the basis of earlier observations and inductive arguments. For this, they used as premises intuitively profound truths, which much later have been called axioms. On the basis of the axioms, whose number should be as small as possible, they proved, using deductive arguments, all the other inferences (laws, propositions, etc.) of the empirical theory. They also created new deductive inferences on the basis of the corresponding theory, usually leading to various useful applications.

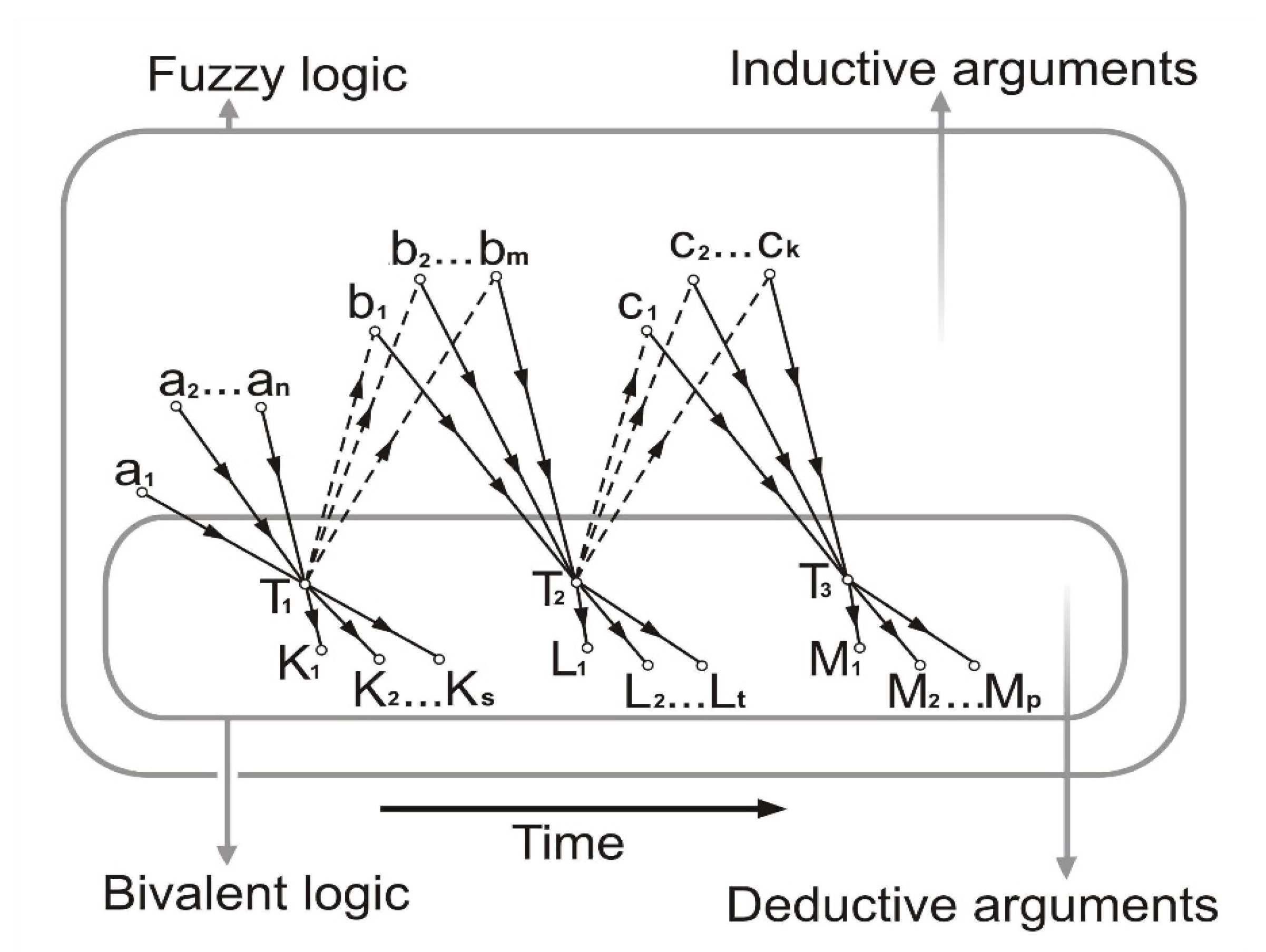
This process is graphically represented on the left side of Figure 4, where α₁, α₂, α₃, α₄, … are observations of the real world that have been transformed, by induction, to the theory T₁. Theory T₁ was verified by deduction and additional deductive inferences K₁, K₂, …, K_s, …, K_n were obtained. Next, a new series of observations b₁, b₂, b₃, …, follow. If some of those observations are not compatible to the laws of theory T₁, a new theory T₂ is formed by induction (intuitively) to replace/extend T₁. The deductive verification of T₂ is based on axioms partially or even completely different to those of theory T₁ and new deductive inferences L₁, L₂, …, L_s, …, L_m follow. The same process could be repeated (observations c₁, c₂, c₃, …, theory T₃, inferences M₁, M₂, …, M_s, …, M_k, etc.) one or more times. In each case the new theory extends or rejects the previous one approaching more and more the absolute truth.

This procedure is known as the scientific method. The term was introduced in the 19th century, when significant terminologies appeared establishing clear boundaries between science and non-science. However, the scientific method characterizes the development of science since at least the 17th century. Aristotle (384–322 BC) is recognized as the inventor of the scientific method due to his refined analysis of the logical implications contained in demonstrative discourse.

James Ladyman, Professor of Philosophy at the University of Bristol, UK, notes that the relationship between observations and theory is much more composite than it looks at first glance [17]. Our illustration of the scientific method in Figure 4 reveals that there exists a continuous “ping pong” between induction and deduction that characterizes this relationship.

The first book in the history of human civilization written on the basis of the principles of the scientific method is, according to the existing witnesses, the “Elements” of Euclid (365–300 BC) addressing the axiomatic foundation of Geometry. However, although the Euclidean Geometry remains still valid for small distances on the earth, the non-Euclidean Geometries of Lobachevsky (1792–1856) and Riemann (1826–1866), which were developed by changing the fifth Euclid’s axiom of the parallel lines (for more details see Section 4), have replaced it for the great distances on the earth’s surface and of the Universe ([18]: Section 3).

The non-Euclidean geometries helped Einstein to prove on a theoretical basis (deductively) his general relativity theory (alternatively termed as the new theory of gravity), which corrected the Newton’s law of gravity in case of very strong gravitational forces (for more details see Section 4). Einstein’s theory was experimentally verified by the irregularity of the Hermes’ orbit around the sun, although at that time many scientists argued that this irregularity was due to the existence of an unknown planet near Hermes or a satellite of Hermes or a group of asteroids near the planet. However, the magnitude of the divergence of the light’s journey, which was calculated during the eclipse of the sun on 29 May, 1919, was the definite evidence for the soundness of Einstein’s theory. In fact, the eclipse let some stars, which normally should be behind the sun, to appear beside it on the sky [19].

In many cases, a new theory knocks completely down a previously existing one. This happened, for example, with the geocentric theory (Almagest) of Ptolemy of Alexandria (100–170). That theory, being able to satisfactorily predict the movements of the planets and the moon, was considered to be true for centuries. However, it was finally proved to be wrong and has been replaced by the heliocentric theory of Copernicus (1473–1543). The Copernicus’ theory was supported and enhanced a hundred years later by the observations/studies of Kepler and Galileo. But, although the idea of the earth and the other planets rotating around the sun has its roots at least in the time of the ancient Greek astronomer Aristarchus of Samos (310–230 BC), the heliocentric theory faced many obstacles for a long period of time, especially from the part of the church, before its final justification [20].

It becomes evident that the scientific method is highly based on the “Trial and Error” procedure. According to W. H. Thrope ([21]: p. 26), this term was devised by C. Lloyd Morgan (1852–1936). This procedure is characterized by repeated attempts, which are continued until success or until the subject stops trying. Sir Karl Raimund Popper (1902–1994), one of the 20th century’s most influential philosophers of science, suggested the principle of falsification according to which a proposition can be characterized as scientific, only if it includes all the necessary criteria for its control, and therefore only if it could be falsified [22]. This principle gives actual emphasis to the second component of the “Trial and Error” procedure. Critiques on the ideas of Popper report that he used the principle of falsification to decrease the importance of induction for the scientific method [7,17].

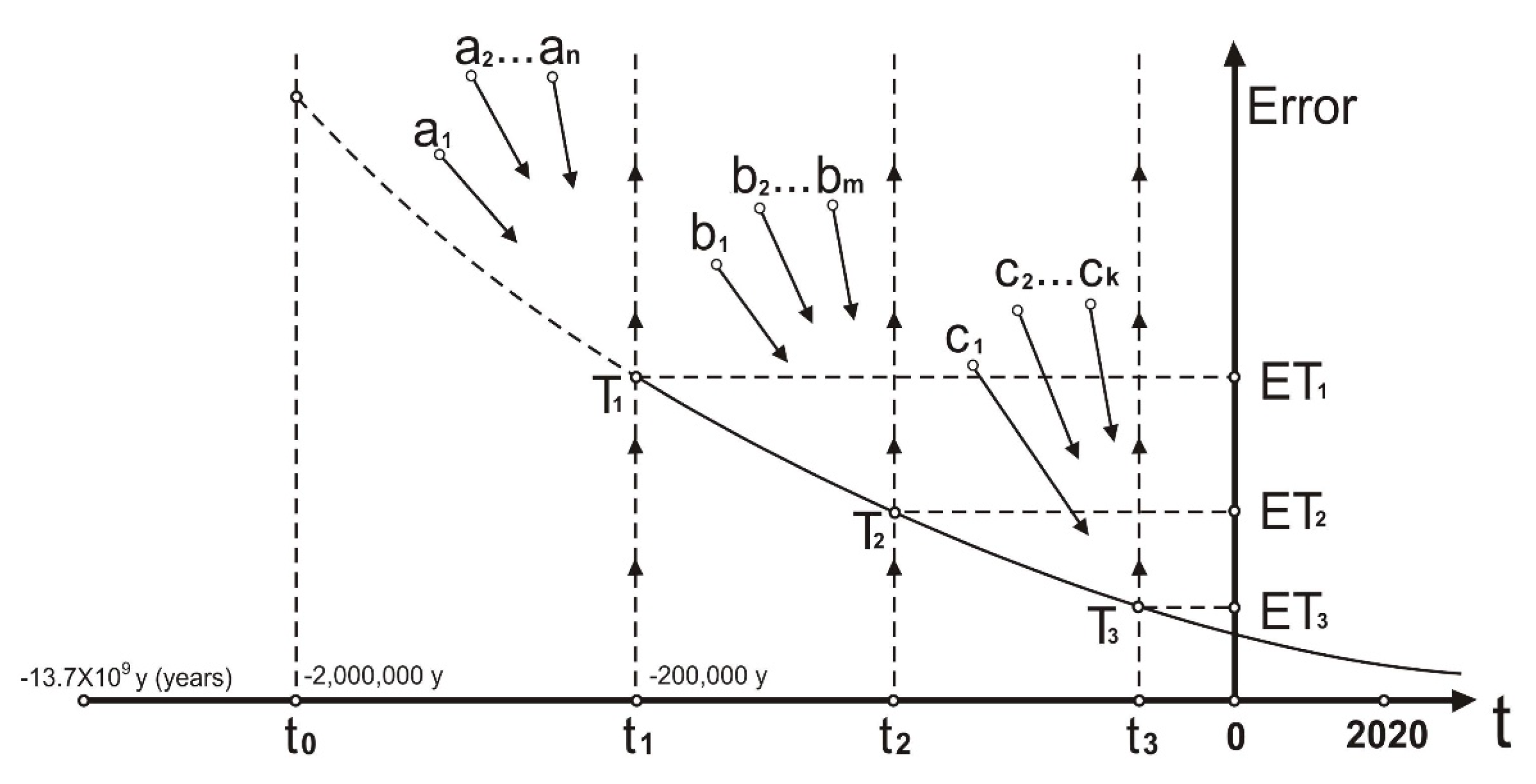
All those discussed in this Section are depicted in Figure 5, representing the curve of the scientific error. This curve, which is connected to the scientific method illustrated in Figure 4, represents the scientific progress through the centuries (the smaller the error, the greater the progress). The horizontal axis in Figure 5 corresponds to the time (t) and the vertical one to the value of the scientific error (E). The starting point M of the curve, giving the maximal value of the scientific error, corresponds to the time t₀ of occurrence of the homo erectus on the earth. The curve is decreasing asymptotically to the axis of time approaching continuously the absolute truth, where the value of the scientific error is zero. The part MT₁ of the curve has been designed with dots, because no evidence of deductive reasoning existed before, which means that only empirical but not scientific progress was realized during that period. The point T₁ of the curve corresponds to the time t₁ of occurrence of the homo sapiens, while the value of −13.7 × 10⁹ years is approximately the time of creation of the Universe (Big Bang) [19].

In conclusion, although deduction is the basis of the scientific method, almost all the scientific progress (with pure mathematics being probably the unique exception; see Section 4) has its roots to inductive reasoning. To put it on a different basis, quantifying the scientific reasoning within the interval [0, 1], only the values 0 and 1 correspond to deductive reasoning, which is connected to the bivalent logic. All the other, values correspond to inductive reasoning, which is supported by the FL.

It is worth emphasizing here that the error of induction is transferred to deductive reasoning through its premises. Therefore, the scientific error in its final form is actually a deductive and not an inductive error. However, many philosophers consider deduction as being an infallible method. This consideration is due to the following two reasons:

• Deduction is always a consistent method
• The existing theories are considered as being always true, which leads frequently to surprises.

The Scottish philosopher David Hume (1711–1776) argued that, with deductive reasoning only, humans would be starving. Although this could not happen nowadays due to our past knowledge obtained with the help of induction, without inductive reasoning no further scientific progress could be achieved. Therefore, a proper balance must exist between induction and deduction, the two fundamental forms of human reasoning.

4. The Unreasonable Effectiveness of Mathematics in the Natural Sciences

Mathematics is the fundamental tool for the development of science and technology. In fact, a single equation (or another mathematical representation) frequently has the potential to replace hundreds of written pages in explaining a phenomenon or situation. For example, the famous Einstein’s equation E = mC² is enough to explain the relationship between mass (m) and energy (E) with the help of the light’s speed (C).

The success of mathematics in the natural sciences appears in two forms, the energetic and the pathetic one. In the former case, the laws of nature are expressed mathematically by developing the corresponding mathematical theories so that they fit the existing observations. In the latter case, however, completely abstract mathematical theories, without any visible applications at the time of their creation, are utilized in unsuspicious time for the construction of physical models!

The Nobelist E. P. Winger, in his famous Richard Courant lecture at the New York University on May, 11, 1959, characterized the success of mathematics in describing the architecture of the Universe as the “unreasonable effectiveness of mathematics in the natural sciences” [23]. Since then, this is usually referred as the Winger’s enigma.

The Winger’s enigma is the main argument of the philosophical school of mathematical realism in supporting the idea that mathematics exists independently of human reasoning. Consequently, the supporters of this idea believe that mathematics is actually discovered and not invented by humans. Although mathematical realism is nowadays under dispute by those arguing, under the light of various indications from the history of mathematics and the data of experiments performed by cognitive scientists and psychologists, that mathematics is a human invention or at least a mixture of inventions and discoveries ([18]: Section 4), it still has many supporters. Among those are the Platonists, arguing the existence of an eternal and unchanged “universe” of mathematical forms, the supporters of the MIT’s cosmologist Max Tegmark theory that Universe is not simply described by mathematics, but IT IS mathematics, etc. ([18]: Section 2).

As it has already mentioned in Section 3, Euclid created the theoretical foundation of the traditional Geometry on the basis of 10 axioms, which were used to prove all the other known on that time geometric propositions and theorems. It is recalled that a fifth of those axioms, stated in its present form by Proclus (412–485), says that from a point outside a given straight line only one parallel can be drawn to this line. However, this axiom does not have the plainness of the rest of the Euclid’s axioms. This gave during the centuries to many mathematicians the impulsion to try to prove the fifth axiom with the help of the other Euclid’s axioms.

One of the latest among those mathematicians was the Russian Lobachevsky, who, when he failed to do so, decided to investigate what happens if the fifth axiom does not hold. Thus, replacing (on a theoretical basis) that axiom by the statement that AT LEAST TWO parallels can be drawn from the given point to the given line, he created the Hyperbolic Geometry, which is developed on a hyperbolic paraboloid’s (saddle’s) surface. The Riemann’s Elliptic Geometry on the surface of a sphere followed, which is based on the assumption that NO PARALLEL can be drawn from the given point to the given straight line. Several other types of non-Euclidean Geometries can be also developed in an analogous way.

Approximately 50 years later, Einstein expressed his strong belief that the Newton’s calculation of the gravitational force F between two masses m₁ and m₂ by the formula

$$\mathrm{F}=\mathrm{G}\frac{{\mathrm{m}}_1{\mathrm{m}}_2}{{\mathrm{r}}^2}$$

(1)

where G stands for the gravitational constant, was not correct for the existing in the Universe (outside the earth) strong gravitational forces (general relativity theory; see Section 3). This new approach was based on the fact that, according to Einstein’s special theory of relativity (1905), the distance (r) and the time (t) are changing in a different way with respect to a motionless and to a moving observer.

To support his argument, Einstein introduced the concept of the four-dimensional time–space and after a series of intensive efforts (1908–1915) he finally managed to prove that the geometry of this space is non-Euclidean! For example, the non-Euclidean divergence of the radius r of a sphere of total surface S and mass m is, according to Einstein’s theory, equal to r − $\sqrt{\frac{\mathrm{S}}{4\mathsf{\pi }}}$ = $\frac{\mathrm{Gm}}{3{\mathrm{C}}^2}$. The theoretical foundation of the general relativity theory made Einstein to state with relief and surprise: “How is it possible for mathematics to fit so eminently to the natural reality?”

The non-Euclidian form of time–space is physically explained by its distortion created by the presence of mass or of an equivalent amount of energy. The level projection of this distortion is represented in Figure 6, retrieved from http://physics4u.gr/blog/2017/04/21. This appears analogous to the distortion created by a ball of bowling on the level of a trampoline.

Another characteristic example of the interaction between the energetic and the pathetic form of mathematics is the Knot Theory, initiated through an unsuccessful effort to represent the atom’s structure. However, the theoretical research on the structure and properties of knots led eventually to the understanding of the mechanisms of the DNA!

It is probably useful to add here a personal experience about the Winger’s enigma. The Ph.D. research of the second author of this article during the early 1980′s was focused on “Iterated Skew Polynomial Rings “ [24], a purely theoretical topic of abstract algebra. To the great surprise of the specialists on the subject, however, this topic has found recently two very important applications to the theory of Quantum Groups (a basic tool of Theoretical Physics) [25] and to Cryptography for analyzing the structure of certain codes [26].

Today the distinction between Pure and Applied Mathematics tends to lose its meaning, because almost all the known mathematical topics have already found applications to science, technology and/or to the everyday life situations. However, the research process that the pathetic approach of mathematics follows, could be considered as an exception (possibly the unique) of the general process followed by the scientific method. In fact, although the axioms introduced for the study of a mathematical topic via the pathetic approach are sometimes based on intuitional criteria or beliefs, the method that this approach follows is purely deductive. The results obtained are considered as correct, if the mathematical manipulation is proved to be correct and regardless whether or not they have a physical meaning. The amazing thing is, however, as said before, that those results are more or less finding unexpected practical applications in the near or remote future. This made the famous astrophysicist and bestselling author M. Livio wonder: “Is God a mathematician?” [27].

Thus, although inductive reasoning is actually the “mother” of the scientific and technological progress and mathematics is the main tool promoting this progress, the pathetic approach of mathematics is a “pure product” of deduction and the connected to it bivalent logic. On the other hand, FL and the related to it generalizations/theories give to the disdainful by the bivalent logic inductive reasoning its proper place and importance as a fundamental component of scientific reasoning.

5. Quantification of the Inductive and Deductive Inferences

As we have previously seen, according to bivalent logic, a given proposition is either true or false. This is really useful in case of a deductive inference, but it says almost nothing in case of an inductive argument, which is based on a series of observations. In fact, as we have seen in Section 2, from the scope of the bivalent logic an inductive argument is never valid, even if it is true. However, what really counts in practice is not the validity, but the degree of truth of the inductive argument. There is, therefore, a need to quantify the inductive arguments, i.e., to calculate their degree of truth. The main tools being available for making those calculations are Probability and Statistics, as well as FL and the related to it generalizations/theories.

Probability and Statistics are related areas of mathematics which, however, have fundamental differences. Probability is a theoretical branch of mathematics which deals with predicting the likelihood of future events. On the contrary, Statistics is an applied branch of mathematics, which tries to make sense of observations in the real world by analyzing the frequency of past events. The distinction between Probability and Statistics could be clarified better by tracing the thoughts of a gambler mathematician during a game with dice. If the gambler is a probabilist, he will think that each face of the dice comes up with probability $\frac{1}{6}$. If instead he is a statistician, he will think: “How I know that the dice are not loaded? I keep track how often each number comes up and once I am confident that the dice are fair I’ll decide how to play”. In other words, Probability enables one to predict the consequences of an ideal world, whereas Statistics enables him/her to measure the extent to which our world is ideal.

Consider, for example, the following argument: “The sun will always rise in the morning”. From the statistical point of view this is a true argument, because the sun rises every morning from the time that humans occurred on earth and have started observing it. Therefore, the number of positive cases of this “experiment” is equal to the number of the total cases, which means that the corresponding frequency is equal to 1. Things, however, are not exactly the same for the probabilistic approach. In fact, it has been estimated by the cosmologists that the sun will “extinguish” in about 7 billion years from now, becoming a small white dwarf star, after being transformed to a red giant first. Therefore, setting t = 7 × 10⁹ × 365 days, the probability that the given statement is true is equal to $\mathrm{p}=\frac{\mathrm{t}-1}{\mathrm{t}}=1-\frac{1}{\mathrm{t}}$. Since t is a very large number, $\frac{1}{\mathrm{t}}$ is very close to 0, therefore, p is very close, but not equal, to 1. Thus, the previous argument is not absolutely true. The difference between the statistical and the probabilistic inference in this case is due to the fact that an experiment cannot be repeated an infinite number of times, which means that the value 1 of the corresponding frequency is not exact.

The A. F. Chalmer’s generalization, however, that no scientific knowledge can be considered as being absolutely true, cannot be justified in the way that he attempts to do in [28]: Chapter 2. In fact, his argument that the corresponding probability is equal to the quotient of a finite number (positive observations) by an infinite number (total observations) is not correct, for the very simple reason that an experiment could not be repeated an infinite number of times.

Edwin T. Jaynes (1922–1998), Professor of Physics at the University of Washington, was one of the first suggesting in the middle of 1990s that probability theory is a generalization of the bivalent logic reducing to it in the special case that our hypotheses are considered to be either absolutely true or absolutely false [29]. Many eminent scientists have been inspired by the ideas of Jaynes. Among those is the Fields medalist David Mumford, who believes that Probability theory and statistical inference are emerging now as a better foundation of scientific models and even as essential ingredients for the foundation of mathematics [30]. Mumford reveals in [30] that he takes back his advice given to a graduate student during his Algebraic Geometry days in the 1970s: “Good grief, don’t waste your time studying Statistics, it’s all cookbook nonsense”!

But what happens in the everyday life? As we have already seen in Section 2, Probability, being a “child” of the bivalent logic, is effective in tackling only the cases of uncertainty which are due to randomness, but not those due to imprecision. For example, consider the expression “John is a good football player”. According to the statistical approach, one should attend John playing in a series of games in order to decide if this argument is true. However, different observers could have different opinions about his playing skills. The probabilistic approach is also not suitable. The statement, for example, that “The probability for John to be a good player is 80%” means that John, being or not, according to the law of the excluded middle, a good player, is probably a good one, perhaps because his coach believes so. In such cases, FL comes to bridge the gap through the use of a suitable membership function. Saying for example, that “The membership degree of John in the fuzzy set of the good players is 0.8”, one understands that John is a rather good player.

Nevertheless, the problem with FL is that the definition of the membership function, although it should always be compatible with the common logic, is not unique, depending on the observer’s subjective criteria. The generalizations/extensions of the concept of fuzzy set and the related theories (see Section 2) have been developed on the purpose of managing better this weakness of FL, but each one of them succeeds to do so in certain cases only. However, the combination of FL with all those generalizations/theories provides a framework that treats satisfactorily all the existing in the real-world types of uncertainty.

Let us now turn our attention to the deductive arguments. As we have seen in Section 3, the error of the inductive reasoning is transferred to deduction through its premises. Therefore, the quantification of the deductive arguments becomes also a necessity. But, as it has already been discussed, the inference of a deductive argument is true under the CONDITION that its premises are true. In other words, if H denotes the hypothesis imposed by its premises and I denotes its inference, then the conditional probability P(I/H) expresses the degree of truth of the deductive argument. Then, by the Bayes’s (1701–1761) formula, one finds that

$$\mathrm{P}(\mathrm{I}/\mathrm{H})=\frac{\mathrm{P}(\mathrm{H}/\mathrm{I})\mathrm{P}\left(\mathrm{H}\right)}{\mathrm{P}\left(\mathrm{I}\right)}$$

(2)

Equation (2), connects P(I/H) with the conditional probability P(H/I) of the inverse process. The final outcome depends on the value of the independent probability P(H) about the truth of the existing hypothesis, usually referred as the prior probability. The Bayes formula, although at first glance looks as a salient generalization of the original concept of probability, has been proved to be very important for scientific reasoning. Many philosophers assert that science as a whole could be viewed as a Bayesian process! (e.g., see [31,32], etc.) The New York Times reports that “Bayesian statistics are rippling through everything from physics to cancer research, ecology to psychology”; see also Figure 7, retrieved from [32]. Artificial Intelligence specialists utilize Bayesian software for helping machines to recognize patterns and make decisions. In a conference held at the New York University on November 2014 with title “Are Brains Bayesian?”, specialists from all around the world had the opportunity to discuss how the human mind employs Bayesian algorithms to pre-check and decide.

The following example, inspired from [32] and properly adapted here, illustrates the importance of the Bayes’s theorem in real life situations. This is a timely example due to the current COVID-19 pandemic, because it concerns the creditability of medical tests.

EXAMPLE: In a town of 10,000 inhabitants, Mr. X makes a test for checking whether or not he is infected by a dangerous virus. It has been statistically estimated that 1% of the town’s population has been infected by the virus, while the test has a 96% statistical success to diagnose both positive and negative cases of infections. The result of the test was positive and Mr. X concluded that the probability to be a carrier of the virus is 96%. Is that a correct?

The answer is no! For explaining this, let us consider the following two events:

• H: The test is positive, and
• I: The subject is a carrier of the virus.

From the given data it turns out that P(I) = 0.1 and P(H/I) = 0.96. Further, from the 10,000 inhabitants of the town, 100 are carriers of the virus and 9900 are not. Assume (on a theoretical basis) that all the inhabitants make the test. Then we should have 9900 × 4% = 396 positive results from the non-carriers and 96 positive results from the carriers, i.e., 492 in total positive results. Therefore P(H) 0.492. Replacing the values of P(I), P(H/I) and P(H) to formula (1) one finds that P(I/H) ≈ 0.1951. Therefore, the probability for Mr. X to be a carrier of the virus is only 19.51%!

On the contrary, assuming that “H: The test is negative”, we should have 9900 × 96%=9504 negative results from the non-carriers and four negative results from the carriers of the virus, i.e., 9508 in total negative results. Therefore, P(H) 0.958 and in this case Equation (2) gives that P(I/H) ≈ 0.1. Therefore, if the result of the test of Mr. X is negative, the probability to be a carrier is only 1%.

Assume now that Mr. X has some suspicious symptoms related to the virus and that for people having those symptoms the probability to have been infected is 80%. In that case P(I) = 0.8 and P(H/I) = 0.96. Further, 800 out of 1000 people having those symptoms are carriers of the virus and 200 are not. Therefore, we should have 800 × 96% = 768 positive results from the carriers and 200 × 4% = 8 positive results from the non-carriers, i.e., 776 in total positive results. Therefore, P(H) = 0.776 and Equation (2) gives now that P(I/H) ≈ 98.97%. Consequently, if the result of Mr. X’s test is positive, then the probability to be a carrier exceeds the accuracy of the test!

The three alternative cases of the previous example and in particular the first one support the view of many specialists currently insisting that the tests performed without any special reason by those presenting no symptoms of COVID-19 are not effective and they simply burden the healthcare systems of their countries without purpose.

Further, the first and the third example enable one to study the sensitivity of the solution of the corresponding problem, which is expressed by the value of the conditional probability P(I/H). It becomes evident that the variable which affects dramatically the solution is the value of the independent probability P(I) of a subject to be a carrier of the virus. Figure 8 represents graphically the changes of the problem’s solution P(I/H) with respect to the changes of the value of P(I).

The Bayesian process appears frequently in the scientific method (Section 3). Consider for example the events:

• H: Newton’s theory of gravity, and
• I: Velocity of Hermes around the sun.

In this case the value of the conditional probability P(H/I) will increase by replacing H with the general relativity theory.

In conclusion, the Bayesian process can distinguish science from pseudo-science more precisely than the Popper’s falsification principle [22], by assigning a degree of truth to each possible case. On the contrary, the Popper’s principle, based purely on the laws of the bivalent logic, characterizes each case only as either true or false.

6. Conclusions

The conclusions obtained by the discussion performed in this work could be summarized in the following statements:

• Induction and deduction are the two main types of human reasoning. However, despite the fact that the scientific method is based on deduction, almost all the scientific progress (with pure mathematics being possibly the unique exception) has its roots to inductive reasoning.
• FL restores the place and importance of the disdainful by the classical/bivalent logic induction as a fundamental component of the scientific reasoning.
• The success of mathematics in the natural sciences has been characterized by eminent scientists as being unreasonable (Winger’s enigma). In fact, completely theoretical topics of mathematics find frequently, in unsuspicious time, important applications to science, technology and everyday life situations.
• The scientific method is characterized by the fact that the error of inductive reasoning is transferred to deduction through its premises. Therefore, there is a need of calculating the degree of truth of both inductive and deductive arguments. In the former case, the tools available for this quantification are probability and statistics, and of course FL and its generalizations for situations characterized by imprecision. In the latter case, it has recently turned out that the basic tool is the Bayesian probabilities. All these tools can help one to make a decision about a particular study and this is actually the managerial added value of the present study.
• Eminent scientists argue nowadays that the whole of science could be characterized as a Bayesian process, that distinguishes more precisely than the Popper’s falsification principle the science from pseudo-science. A timely example, related to the validity of the viruses’ tests, was presented here illustrating the importance of the Bayesian probabilities.

It must not be considered, however, that the wide and composite subject of this treatise is integrated here. We do hope, however, that the discussion performed in the present article could be promote a wider dialogue on this philosophical topic leading to further thoughts and research on the subject.