On the Growth of Some Functions Related to z(n)

Abstract

The order of appearance $z:{\mathbb{Z}}_{>0}\to {\mathbb{Z}}_{>0}$ is an arithmetic function related to the Fibonacci sequence ${\left(F_n\right)}_n$. This function is defined as the smallest positive integer solution of the congruence $F_k\equiv 0\left(\mathrm{mod}n\right)$. In this paper, we shall provide lower and upper bounds for the functions ${\sum }_{n\le x}z\left(n\right)/n$, ${\sum }_{p\le x}z\left(p\right)$ and ${\sum }_{p^r\le x}z\left(p^r\right)$.

1. Introduction

Perhaps the most important of the binary recurrences is the Fibonacci sequence ${\left(F_n\right)}_n$. This sequence starts with $F_0=0$ and $F_1=1$ and it satisfies the 2nd order recurrence relation $F_{n+2}=F_{n+1}+F_n$ (for $n\ge 0$). A well-known, explicit, formula for the nth Fibonacci number is called the Binet-formula

$${\displaystyle F_n=\frac{{\alpha }^n-{\beta }^n}{\sqrt{5}},}$$

where $\alpha :=(1+\sqrt{5})/2$ and $\beta :=(1-\sqrt{5})/2$. It follows from this formula that the estimates ${\alpha }^{n-2}\le F_n\le {\alpha }^{n-1}$, hold for all $n\ge 1$.

The study of the divisibility properties of Fibonacci numbers has always been a popular area of research. For example, it is still an open problem to decide if there are infinitely many primes in that sequence. In order to study such kind of Diophantine problems, the arithmetic function $z:{\mathbb{Z}}_{>0}\to {\mathbb{Z}}_{>0}$ was defined by setting $z\left(n\right)=min\{k\ge 1:n\mid F_k\}$. This function is called the order of appearance in the Fibonacci sequence. For more results on $z\left(n\right)$, see [1] and references therein.

In 1878, Lucas ([2], p. 300) established that $z\left(n\right)$ is well defined and, in 1975, J. Sallé [3] proved that $z\left(n\right)\le 2n$, for all positive integers n. This is the sharpest upper bound for $z\left(n\right)$, since for example

$$z\left(n\right)=2n\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}n=6·5^k,\mathrm{for}k\ge 0.$$

(1)

However, apart from these cases this upper bound is very weak. For instance, $z\left(2255\right)=20<{10}^{-2}·2255$. In fact, Marques [4] gave sharper upper bounds for $z\left(n\right)$ for all positive integers $n\ne 6·5^k$. These upper bounds depend on the number of distinct prime factors of n, denoted by $\omega \left(n\right)$.

In the main stream of the Analytic Number Theory, we have the three following functions

$$H\left(x\right):=\sum _{n\le x}\frac{1}{n},\vartheta \left(x\right):=\sum _{p\le x}logp\mathrm{and}\psi \left(x\right):=\sum _{n\le x}\Lambda \left(n\right),$$

where $\Lambda \left(n\right)$ is the well-known von Mangoldt function defined as $logp$ if $n=p^r$, for some prime number p and $r\ge 1$, and 0 otherwise (see, e.g., [5,6]). The functions $\vartheta \left(x\right)$ and $\psi \left(x\right)$ are called the first and the second Chebyshev functions, respectively. Note that $\psi \left(x\right)$ can be rewritten as ${\sum }_{p^r\le x}logp$. Here (and in all what follows) ${\sum }_{n\le x}$, ${\sum }_{p\le x}$ and ${\sum }_{p^r\le x}$ mean that the sum is taken over all positive integers, all prime numbers and all prime powers belonging to the interval $[1,x]$, respectively.

Probably, the main importance of the functions $\psi$ and $\vartheta$ relies in the proof of the celebrated Prime Number Theorem which states that

$${\displaystyle \pi \left(x\right)\sim \frac{x}{logx},}$$

where $\pi \left(x\right)={\sum }_{p\le x}1$ is the prime counting function. Indeed, the prime number theorem and the statements $\vartheta \left(x\right)\sim x$ and $\psi \left(x\right)\sim x$ are all equivalent. Here $f\left(x\right)\sim g\left(x\right)$ (asymptotic equivalence) means that $f\left(x\right)/g\left(x\right)$ tends to 1 as $x\to \infty$ (in another way, $f\left(x\right)=g\left(x\right)+o\left(g\right(x\left)\right)$ where $o\left(g\right(x\left)\right)$ means a function $h\left(x\right)$ with ${lim}_{x\to \infty }h\left(x\right)/g\left(x\right)=0$). Actually, one has the following stronger fact

$${\displaystyle \pi \left(x\right)=\frac{x}{logx}+O\left({\displaystyle \frac{x}{{(logx)}^2}}\right).}$$

(2)

Here we shall use the Landau symbols in their usual meaning, i.e., we say that $f\left(x\right)=O\left(g\right(x\left)\right)$ (or $f\ll g$), if there exists a positive constant M such that $\left|f\right(x\left)\right|\le M\left|g\right(x\left)\right|$, for all sufficiently large x. Also, $f\asymp g$ means that $f\ll g$ and $g\ll f$.

Another function of great interest is the harmonic function $H\left(x\right)$ whose image for $x\in {\mathbb{Z}}_{>0}$ is called the xth harmonic number and denoted by $H_x$. These numbers gained much attention with their relation to the Riemann hypothesis. In fact, the Riemann hypothesis is equivalent to prove that

$$d\left(n\right)\le H_n+e^{H_n}log{H}_n,$$

for all $n\ge 1$, where $d\left(n\right)$ is the sum of the positive divisors of n (see [7]). We observe that the harmonic series, i.e., ${lim}_{x\to \infty }H\left(x\right)$ is a well-studied example of divergent series. In fact, it holds that

$$H\left(x\right)=logx+O\left(1\right),$$

which agrees with its very slow divergence.

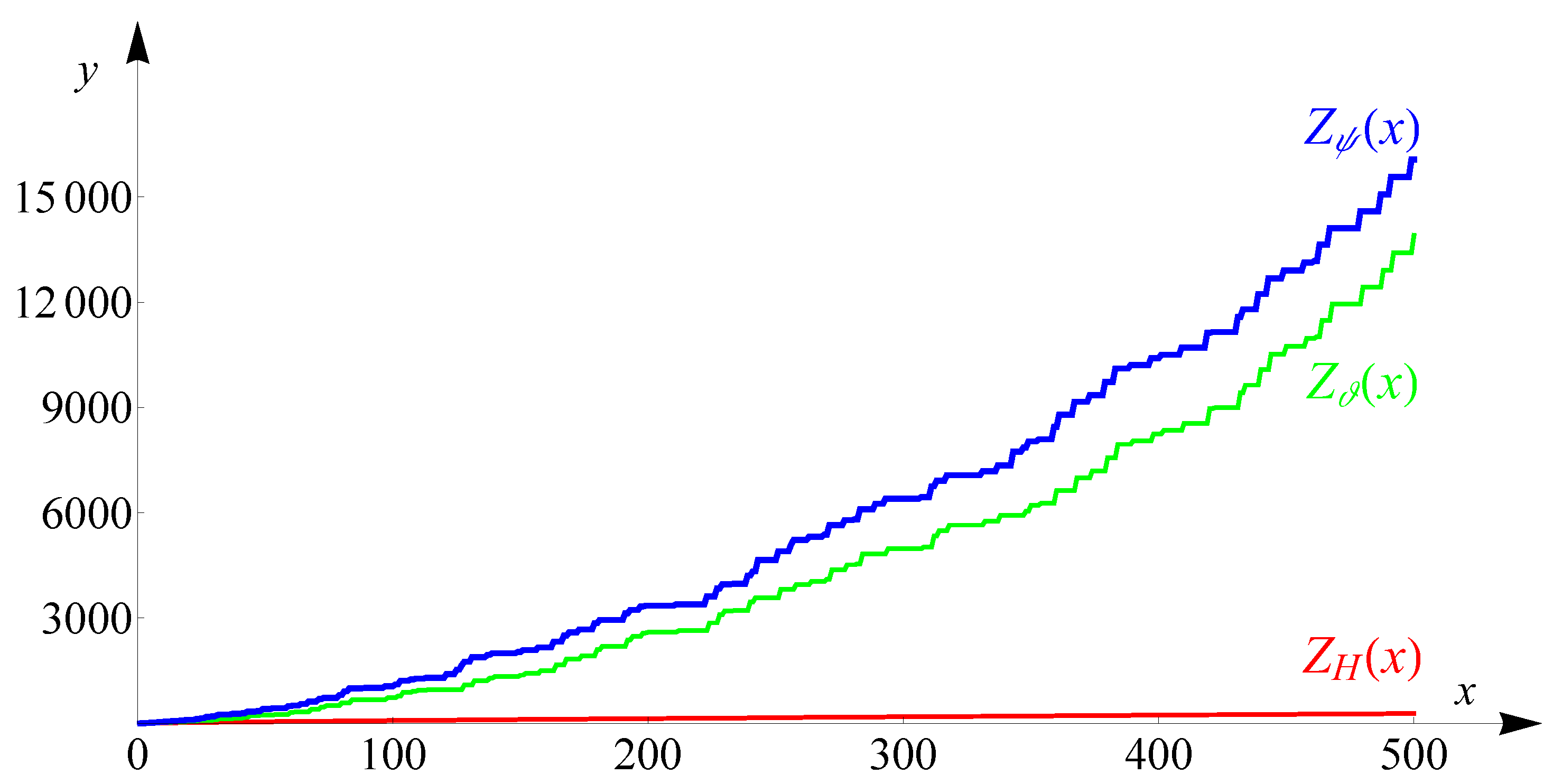
In this paper, we are interested in studying the growth of the following Fibonacci versions of $H\left(x\right)$, $\vartheta \left(x\right)$ and $\psi \left(x\right)$, thus, the functions $Z_H\left(x\right)$, $Z_{\vartheta }\left(x\right)$ and $Z_{\psi }\left(x\right)$ (see Figure 1), for a positive real x, which are defined as

$${\displaystyle Z_H\left(x\right):=\sum _{n\le x}\frac{z\left(n\right)}{n},Z_{\vartheta }\left(x\right):=\sum _{p\le x}z\left(p\right)\mathrm{and}{Z}_{\psi }\left(x\right):=\sum _{p^r\le x}z\left(p^r\right).}$$

Figure 1. The graphs of the functions $Z_H\left(x\right)$, $Z_{\vartheta }\left(x\right)$ and $Z_{\psi }\left(x\right)$ for $x\in (0,500]$.

First, observe that since $1\le z\left(n\right)\le 2n$, then the following trivial estimates hold

$${\displaystyle logx\ll H\left(x\right)\le Z_H\left(x\right)\le \sum _{n\le x}2\le 2x.}$$

However, we found the previous bounds by neglecting the contribution of $z\left(n\right)$ (which is much bigger than 1 and much smaller than $2n$, in almost all cases). In fact, by taking $z\left(n\right)$ into account, we obtain

Theorem 1.

We have that

$${\displaystyle {\left(\log x\right)}^2\ll Z_H\left(x\right)\ll \frac{x}{{(logx)}^{1/3}}.}$$

For the function $Z_{\vartheta }\left(x\right)$, if we use that $z\left(p\right)\ge 1$, we get

$${\displaystyle Z_{\vartheta }\left(x\right)\ge \sum _{p\le x}1=\pi \left(x\right)\gg \frac{x}{logx}.}$$

Again, with an extra effort, we can improve this by proving that

Theorem 2.

We have that

$${\displaystyle x\ll Z_{\vartheta }\left(x\right)\ll \frac{x^2}{logx}.}$$

Since the number of prime powers in $[1,x]$ is bigger than $\pi \left(x\right)$, a similar direct inequality (that one for $Z_{\vartheta }\left(x\right)$) could be derived for $Z_{\psi }\left(x\right)$. However, by using the behavior of $z\left(p^r\right)$, we can obtain better estimates such as

Theorem 3.

We have that

$${\displaystyle x\ll Z_{\psi }\left(x\right)\ll \frac{x^2}{logx}.}$$

Note that even with a larger number of possibilities in the sum of $Z_{\psi }\left(x\right)$, its bounds are the same (in order) than the ones for $Z_{\vartheta }\left(x\right)$ (Theorem 2). The explanation for this, follows from the fact that the contribution, i.e., the number of powers of p (for example) belonging to $[1,x]$ is $O\left(\log x\right)$ which is $o\left(x\right)$. In other words, this amount is almost negligible (compared with x, in terms of order).

In a few words, the proof of the results combine some new (sharper upper bounds for $z\left(n\right)$ due to Marques) and classical results (such as results due Abel, Sathé, Selberg) in Number Theory.

2. Auxiliary Results

In this section, we shall present some tools which will be very useful in the proofs. We start with some results due to Marques [4], which will be very helpful in our proof. Thus, we shall state his results as lemmas (in what follows, the 2-adic valuation of n is ${\nu }_2\left(n\right)=max\{k\ge 0:2^k\mid n\}$).

Lemma 1.

We have

(i) 

$z\left(2^k\right)=3·2^{k-2}$ (for $k\ge 3$), $z\left(3^k\right)=4·3^{k-1}$ (for $k\ge 1$) and $z\left(5^k\right)=5^k$ (for $k\ge 0$).

(ii) 

If $p>5$ is a prime, then

$$z\left(p^k\right)\le \left(p-\left({\displaystyle \frac{5}{p}}\right)\right)p^{k-1},fork\ge 1,$$

where, as usual, $\left(\frac{a}{q}\right)$ denotes the Legendre symbol of a with respect to a prime $q>2$.

Lemma 2.

Let n be an odd integer number with $\omega \left(n\right)\ge 2$, then

$$z\left(n\right)\le 2·{\left({\displaystyle \frac{2}{3}}\right)}^{\omega \left(n\right)-{\delta }_n}n,$$

where

$${\delta }_n=\left\{\begin{array}{cc}0,\hfill & if5\nmid n;\hfill \\ 1,\hfill & if5\mid n.\hfill \end{array}\right.$$

(3)

Lemma 3.

Let n be an even integer number with $\omega \left(n\right)\ge 2$, it holds that

(i) 

If ${\nu }_2\left(n\right)\ge 4$, then

$${\displaystyle z\left(n\right)\le \frac{3}{4}·{\left({\displaystyle \frac{2}{3}}\right)}^{\omega \left(n\right)-{\delta }_n-1}n.}$$

(ii) 

If ${\nu }_2\left(n\right)=1$, then

$$z\left(n\right)\le \left\{\begin{array}{cc}3n/2,\hfill & if\omega \left(n\right)=2and5\mid n;\hfill \\ 2n,\hfill & if\omega \left(n\right)=2and5\nmid n;\hfill \\ 3·{(2/3)}^{\omega \left(n\right)-{\delta }_n-1}n,\hfill & if\omega \left(n\right)>2.\hfill \end{array}\right.$$

(4)

(iii) 

If ${\nu }_2\left(n\right)\in \{2,3\}$, then

$$z\left(n\right)\le \left\{\begin{array}{cc}3n/2,\hfill & if\omega \left(n\right)=2and5\mid n;\hfill \\ n,\hfill & if\omega \left(n\right)=2and5\nmid n;\hfill \\ {(2/3)}^{\omega \left(n\right)-{\delta }_n-2}n,\hfill & if\omega \left(n\right)>2.\hfill \end{array}\right.$$

(5)

The next lemma is a powerful result in analytic number theory which is related to positive integers with fixed number of distinct prime factors.

Lemma 4

(Sathé–Selberg Formula). For any positive constant A, we have

$${\displaystyle \#{\mathcal{P}}_k\left(x\right):=\#\{n\le x:\omega \left(n\right)=k\}\sim G\left({\displaystyle \frac{k-1}{loglogx}}\right)\frac{x}{logx}\frac{{(loglogx)}^{k-1}}{(k-1)!},}$$

for $x\ge 3$ and $1\le k\le Aloglogx$, where

$$G\left(z\right):=\frac{1}{\Gamma (1+z)}\prod _{pprime}\left(1+\frac{z}{p}\right){\left(1-\frac{1}{p}\right)}^z.$$

In the previous statement $\Gamma \left(z\right)={\int }_0^{\infty }{x}^{z-1}{e}^{-x}dx$ (for $x>0$) is the well-known Gamma function.

The proof of Lemma 4 can be found in [8,9].

Our last tool is a very useful formula due to Abel which makes an interplay between a discrete sum and an integral (continuous sum). More precisely,

Lemma 5

(Abel’s Summation Formula). Let ${\left(a_n\right)}_n$ be a sequence of real numbers and define its partial sum $A\left(x\right):={\sum }_{n\le x}{a}_n$. For a real number $x>1$, let f be a continuously differentiable function on $[1,x]$. Then

$${\displaystyle \sum _{n\le x}{a}_{n}f\left(n\right)=A\left(x\right)f\left(x\right)-{\int }_1^{x}A\left(t\right)f^{\prime }\left(t\right)dt.}$$

Remark 1.

We remark that, throughout what follows, the implied constants in ≪ and ≫ can be made explicit. Here, we decided to use asymptotic bounds in order to leave the text more readable. However, we shall provide the explicit inequalities for convenience of the reader (they can be found in [10], for example).

(i) 

${\displaystyle \sum _{n\le x}\frac{1}{n}>log(x+1)}$;

(ii) 

$\vartheta \left(x\right)<1.000028x$, for $x>0$ and $\vartheta \left(x\right)>0.998684x$, for $x>1319007$;

(iii) 

$p_n<nlogn+nloglogn$, for $n\ge 6$;

(iv) 

${\displaystyle \frac{x}{logx}<\pi \left(x\right)<1.25506\frac{x}{logx}}$, for $x\ge 17$.

As usual, from now on we use the well-known notation $[a,b]=\{a,a+1,\dots ,b-1,b\}$, for integers $a<b$.

Now we are ready to deal with the proof of our results.

3. The Proofs

3.1. The Proof of Theorem 1

Since, by definition, $n\mid F_{z\left(n\right)}$, then $n\le F_{z\left(n\right)}\le {\alpha }^{z\left(n\right)-1}$ and so $z\left(n\right)>logn/log\alpha$. Thus

$${\displaystyle Z_H\left(x\right)=\sum _{n\le x}\frac{z\left(n\right)}{n}\gg \sum _{n\le x}\frac{logn}{n}.}$$

Now, we shall use Lemma 5 for $a_n=1/n$ and $f\left(x\right)=logx$. Then

$${\displaystyle \sum _{n\le x}\frac{logn}{n}=H\left(x\right)logx-{\int }_1^x\frac{H\left(t\right)}{t}dt.}$$

Since $H\left(x\right)=logx+O\left(1\right)$ and ${\int }_1^x\frac{logt}{t}dt={\left(\log x\right)}^2/2$, then

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{n\le x}\frac{logn}{n}}& =& {\displaystyle (logx+O\left(1\right))logx-{\int }_1^x\frac{logt+O\left(1\right)}{t}dt}\hfill \\ & =& {\displaystyle \frac{1}{2}{(logx)}^2+O(logx)\gg {(logx)}^2}\hfill \end{array}$$

and so $Z_H\left(x\right)\gg {\left(\log x\right)}^2$.

For the second part, we use Lemmas 1, 2 and 3 to derive that

$$z\left(n\right)\le 7{\left({\displaystyle \frac{2}{3}}\right)}^{\omega \left(n\right)}n,$$

for all $n>1$. First, let us write $Z_H\left(x\right)$ as

$${\displaystyle Z_H\left(x\right)=\sum _{k=1}^{h\left(x\right)}\sum _{n\in {\mathcal{P}}_k\left(x\right)}\frac{z\left(n\right)}{n},}$$

where $h\left(x\right)=max\left\{\omega \right(t):t\le x\}$. By using that $z\left(n\right)\le 7·{(2/3)}^{\omega \left(n\right)}n$, we have

$${\displaystyle Z_H\left(x\right)\ll \sum _{k=1}^{h\left(x\right)}\sum _{n\in {\mathcal{P}}_k\left(x\right)}{\left({\displaystyle \frac{2}{3}}\right)}^{\omega \left(n\right)}\ll \sum _{k=1}^{h\left(x\right)}{\left({\displaystyle \frac{2}{3}}\right)}^k\#{\mathcal{P}}_k\left(x\right)}$$

which can be written as

$${\displaystyle Z_H\left(x\right)\ll \sum _{k=1}^{\lfloor loglogx\rfloor }{\left({\displaystyle \frac{2}{3}}\right)}^k\#{\mathcal{P}}_k\left(x\right)+\sum _{k\ge \lfloor loglogx\rfloor +1}{\left({\displaystyle \frac{2}{3}}\right)}^k\#{\mathcal{P}}_k\left(x\right).}$$

(6)

Now, we shall use Lemma 4 to deal with the first sum in the right hand side above. Since $G\left(z\right)$ converges uniformly and absolutely in any bounded set, we have ${max}_{z\in [0,1]}\left\{\right|G\left(z\right)\left|\right\}\le C$, for some positive constant C. Now, by Lemma 4 for $A=1$, we get $\left|G\right(z_k\left)\right|\le C$ (for $z_k:=(k-1)/loglogx<1$) and

$$\begin{array}{ccc}\hfill {\displaystyle \sum _{k=1}^{\lfloor loglogx\rfloor }{\left({\displaystyle \frac{2}{3}}\right)}^k\#{\mathcal{P}}_k\left(x\right)}& \ll & {\displaystyle \sum _{k=1}^{\lfloor loglogx\rfloor }{\left({\displaystyle \frac{2}{3}}\right)}^{k}G\left(z_k\right)·\frac{x}{logx}\frac{{(loglogx)}^{k-1}}{(k-1)!}}\hfill \\ & \ll & {\displaystyle \frac{x}{logx}\sum _{k\ge 1}\frac{{(log{(logx)}^{2/3})}^{k-1}}{(k-1)!}}\hfill \\ & \ll & {\displaystyle \frac{x}{logx}exp(log{(logx)}^{2/3})=\frac{x}{{(logx)}^{1/3}}.}\hfill \end{array}$$

Therefore,

$${\displaystyle \sum _{k=1}^{\lfloor loglogx\rfloor }{\left({\displaystyle \frac{2}{3}}\right)}^k\#{\mathcal{P}}_k\left(x\right)\ll \frac{x}{{(logx)}^{1/3}}.}$$

(7)

For the second sum in the right hand side of (6), we use that $\#{\mathcal{P}}_k\left(x\right)\le x$ to obtain

$${\displaystyle \sum _{k\ge \lfloor loglogx\rfloor +1}{\left({\displaystyle \frac{2}{3}}\right)}^k\#{\mathcal{P}}_k\left(x\right)\ll {\left({\displaystyle \frac{2}{3}}\right)}^{loglogx}x,}$$

where we used that $\lfloor loglogx\rfloor +1>loglogx$. Since $3/2>\sqrt[3]{e}$, then

$${\left({\displaystyle \frac{3}{2}}\right)}^{loglogx}>e^{(\log logx)/3}={\left(\log x\right)}^{1/3}.$$

Thus

$${\displaystyle \sum _{k\ge \lfloor loglogx\rfloor +1}{\left({\displaystyle \frac{2}{3}}\right)}^k\#{\mathcal{P}}_k\left(x\right)\ll \frac{x}{{(logx)}^{1/3}}.}$$

(8)

By combining (6), (7) and (8), we obtain the desired result.

3.2. The Proof of Theorem 2

By the Prime Number Theorem, we have that $\vartheta \left(x\right)\sim x$. In particular, it holds that $\vartheta \left(x\right)\gg x$. Since $\vartheta \left(x\right)={\sum }_{p\le x}logp$, then

$${\displaystyle Z_{\vartheta }\left(x\right)=\sum _{p\le x}z\left(p\right)\gg \sum _{p\le x}logp=\vartheta \left(x\right)\gg x,}$$

where we used that $z\left(p\right)>logp/log\alpha$.

For the second part, since $z\left(p\right)\le p+1\le 3p/2$, then

$${\displaystyle Z_{\vartheta }\left(x\right)=\sum _{p\le x}z\left(p\right)\ll \sum _{p\le x}p\ll x\sum _{p\le x}1=x\pi \left(x\right)\ll \frac{x^2}{logx}}$$

as desired.

3.3. The Proof of Theorem 3

Note that, by Theorem 2, we have

$$Z_{\psi }\left(x\right)\ge Z_{\vartheta }\left(x\right)\gg x.$$

For the second part, since there exist exactly $\lfloor logx/logp\rfloor$ powers of p in the interval $[1,x]$, we can write $Z_{\psi }\left(x\right)$ as

$${\displaystyle Z_{\psi }\left(x\right)=\sum _{p\le x}\sum _{r\le \frac{logx}{logp}}z\left(p^r\right).}$$

By using Lemma 1 (ii), we get

$${\displaystyle Z_{\psi }\left(x\right)=\sum _{p\le x}\sum _{r\le \frac{logx}{logp}}z\left(p^r\right)\le \sum _{p\le x}\sum _{r\le \frac{logx}{logp}}(p+1)p^{r-1}\ll \sum _{p\le x}\sum _{r\le \frac{logx}{logp}}{p}^r.}$$

Note that ${\sum }_{r\le \frac{logx}{logp}}{p}^r\le (p^{\frac{logx}{logp}+1}-1)/(p-1)\ll x$. Then,

$${\displaystyle Z_{\psi }\left(x\right)\ll \sum _{p\le x}x=x\pi \left(x\right)\ll \frac{x^2}{logx},}$$

which completes the proof.

4. Conclusions

In this paper, we study some problems related to the order (of appearance) in the Fibonacci sequence, denoted by $z\left(n\right)$. This arithmetic function plays an important role in the comprehension of some Diophantine problems involving Fibonacci numbers (the most important one is the open problem about the existence of infinitely many Fibonacci prime numbers). The problems are related to the growth of Fibonacci versions of well-known number-theoretic functions (related to the Prime Number Theorem) like the first and second Chebyshev functions, $\vartheta \left(x\right)={\sum }_{p\le x}logp$ and $\psi \left(x\right)={\sum }_{p^r\le x}logp$ and the harmonic function $H\left(x\right)={\sum }_{n\le x}1/n$. These Fibonacci-like functions are defined as $Z_{\vartheta }\left(x\right)={\sum }_{p\le x}z\left(p\right),Z_{\psi }\left(x\right)={\sum }_{p^r\le x}z\left(p^r\right)$ and $Z_H\left(x\right)={\sum }_{n\le x}z\left(n\right)/n$. In particular, we shall find effective bounds for these three functions. The proofs combine elementary facts related to $z\left(n\right)$ (such as Marques’ upper bounds) together with some deep tools from Analytic Number Theory (such as Abel’s summation formula and Sathé–Selberg formula).