On Exact and Approximate Approaches for Stochastic Receptor-Ligand Competition Dynamics—An Ecological Perspective
Abstract
1. Introduction
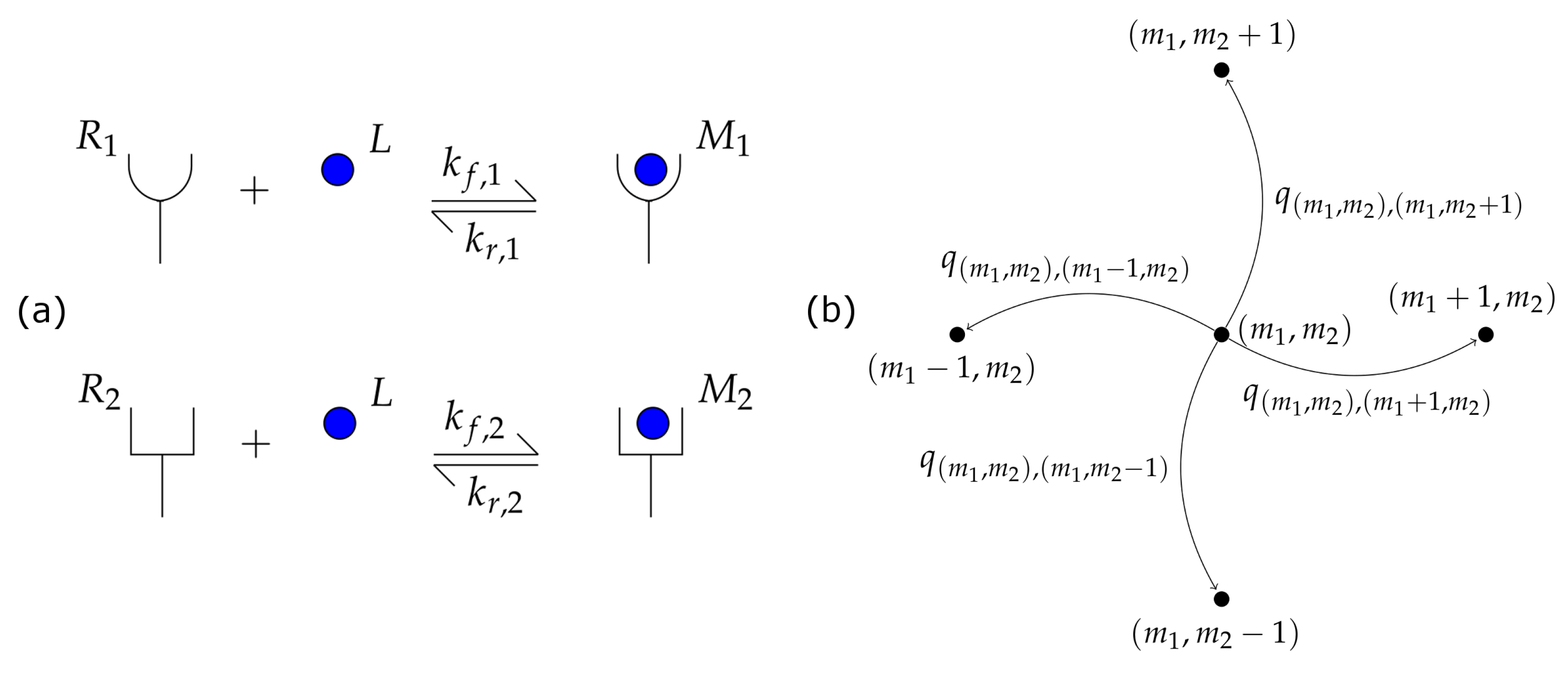
2. A Stochastic Competition Model for Receptor-Ligand Interactions
3. Summary Statistics
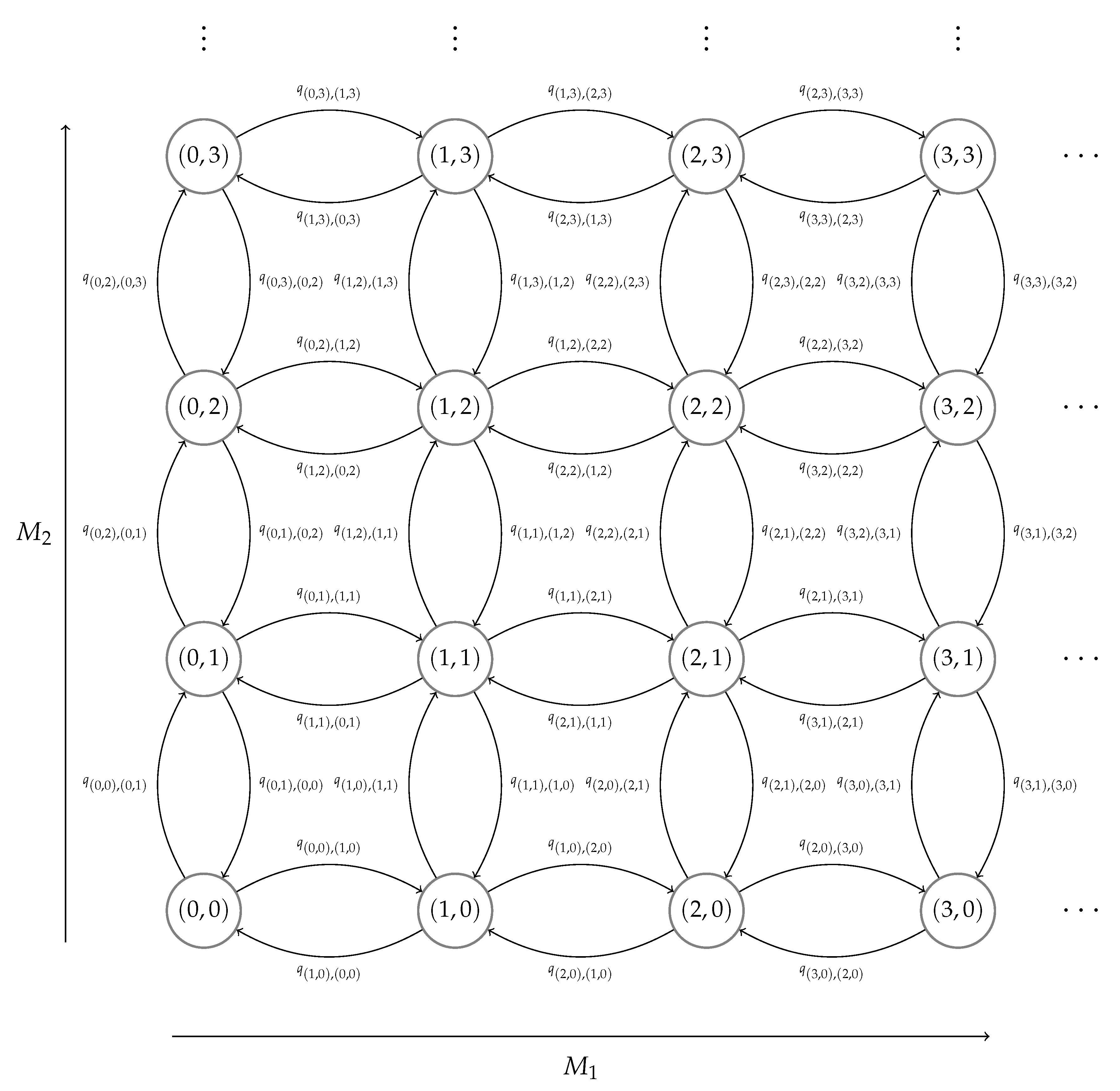
3.1. Steady-State Distribution
3.1.1. Exact Matrix-Analytic Approach (EMA)
3.1.2. No-Competition Approximation (NCA) under Excess of Ligand
3.1.3. Moderate-Competition Approximation (MCA)
| Algorithm 1 Iterative approximation for the steady-state distribution, . |
|
3.2. Timescales of Monomer Formation
3.2.1. Exact Matrix-Analytic Approach (EMA)
3.2.2. No-Competition Approximation (NCA) under Excess of Ligand
3.2.3. Moderate-Competition Approximation (MCA)
4. Results
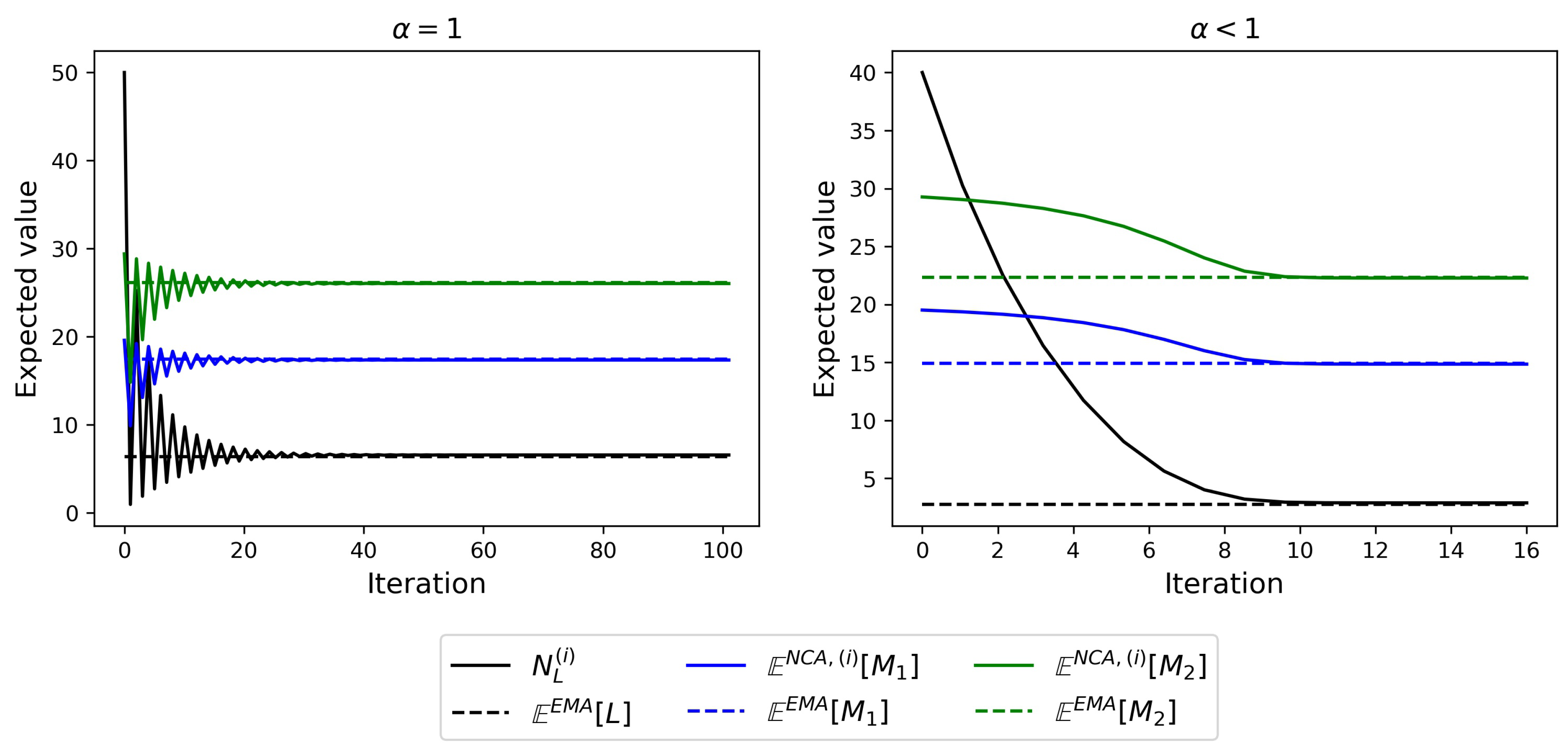
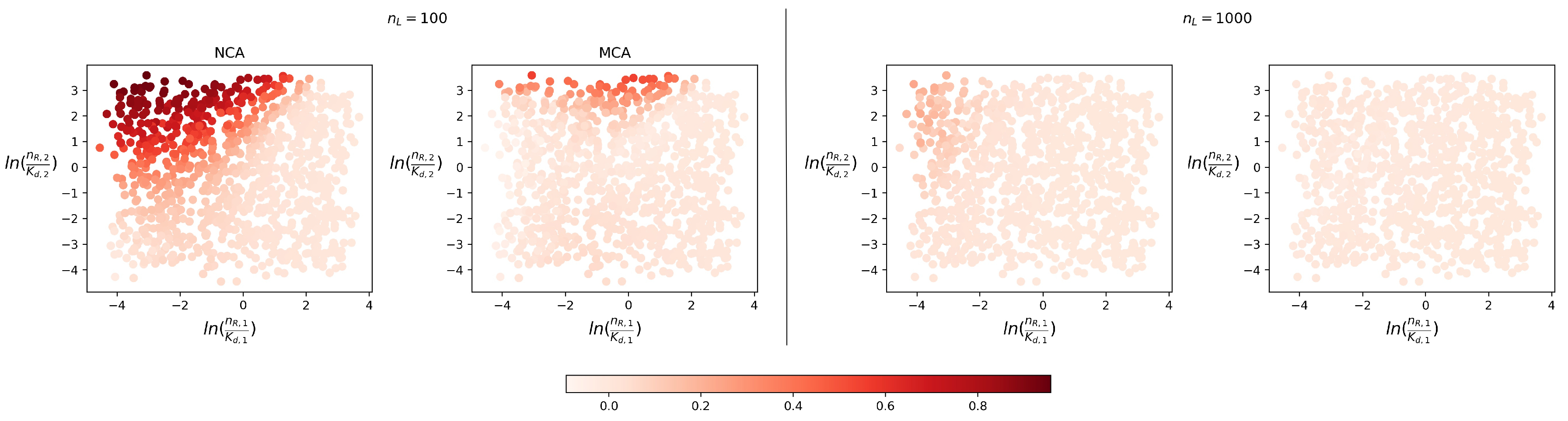
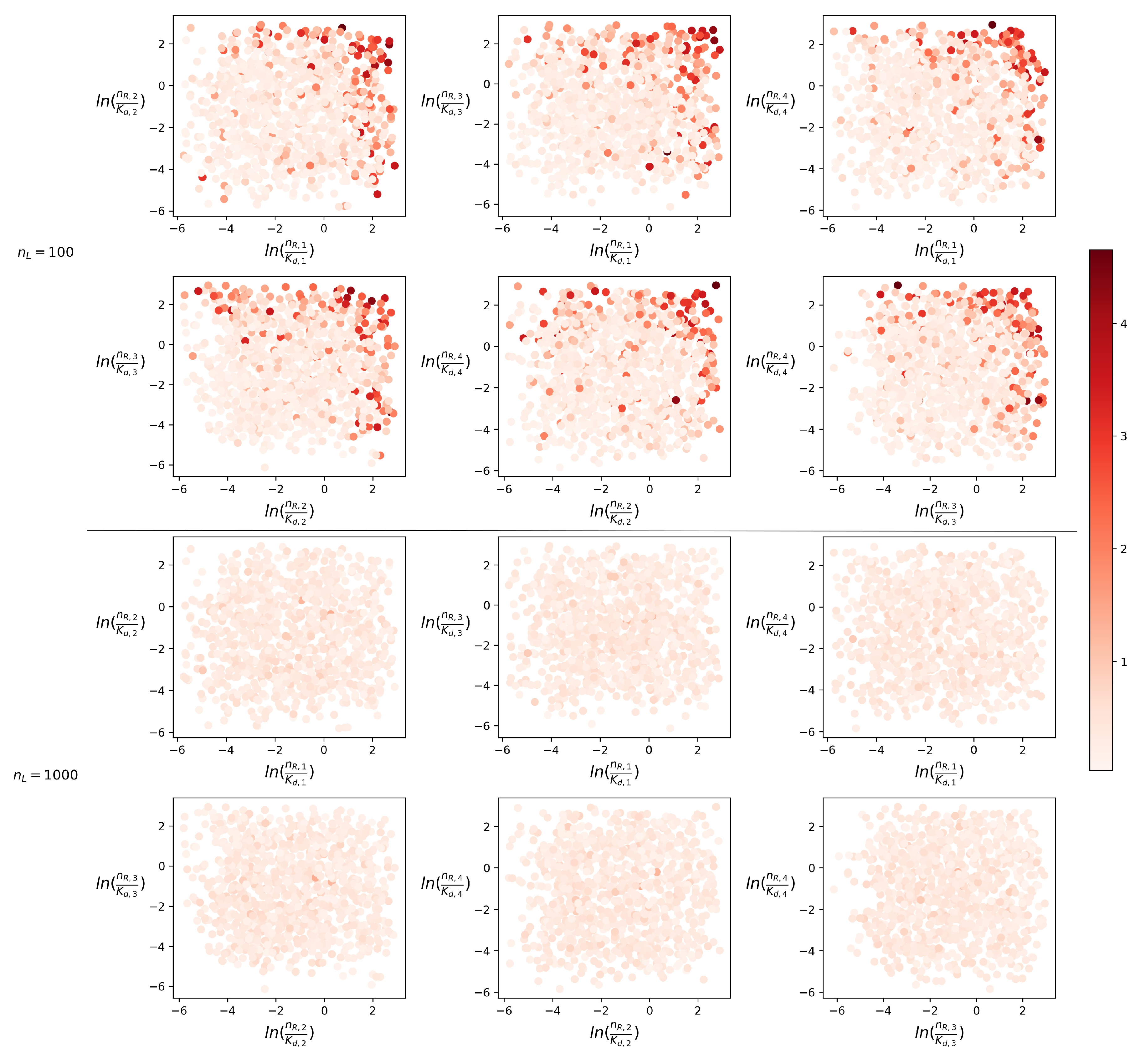
4.1. Steady-State Distribution
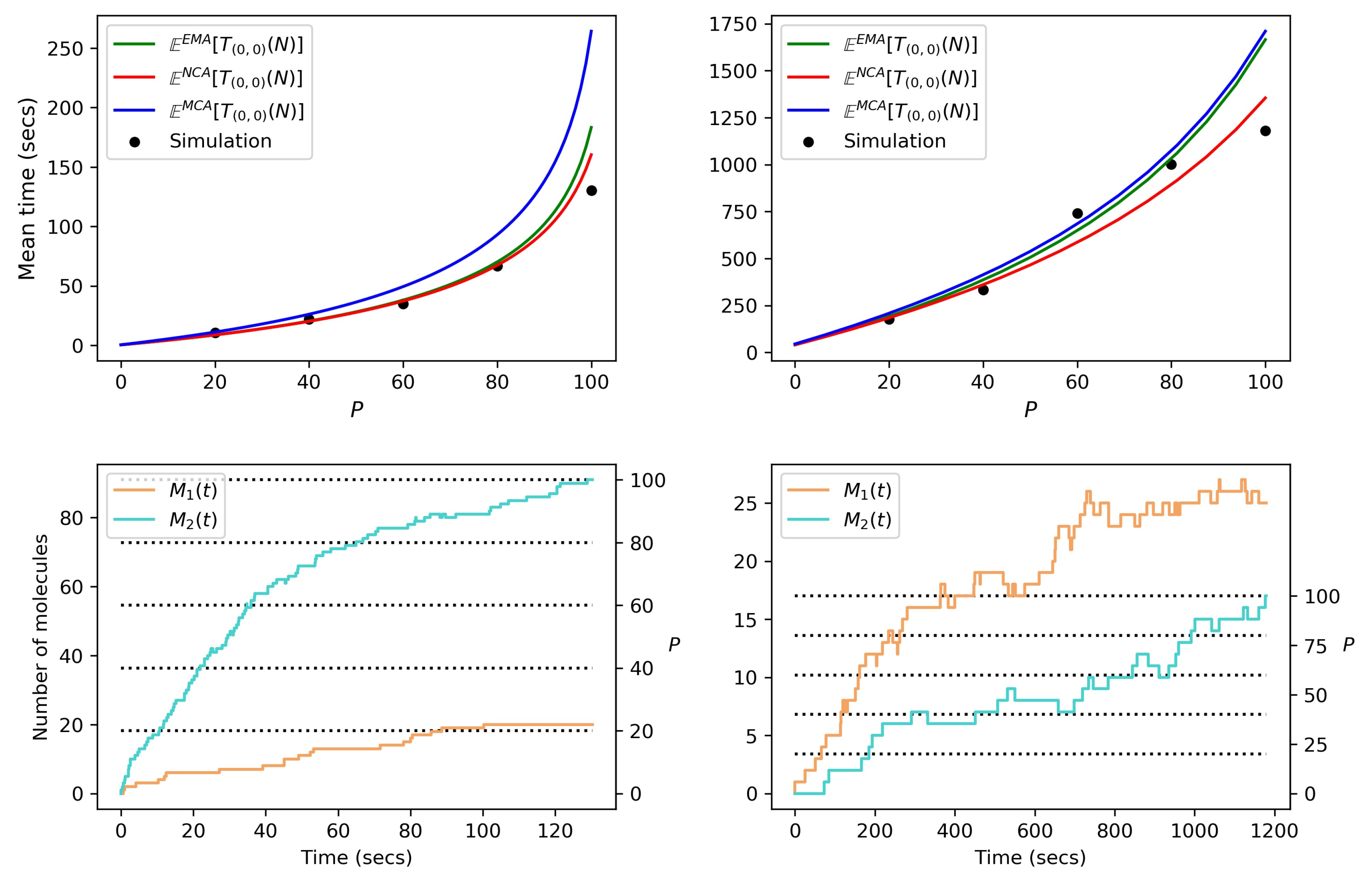
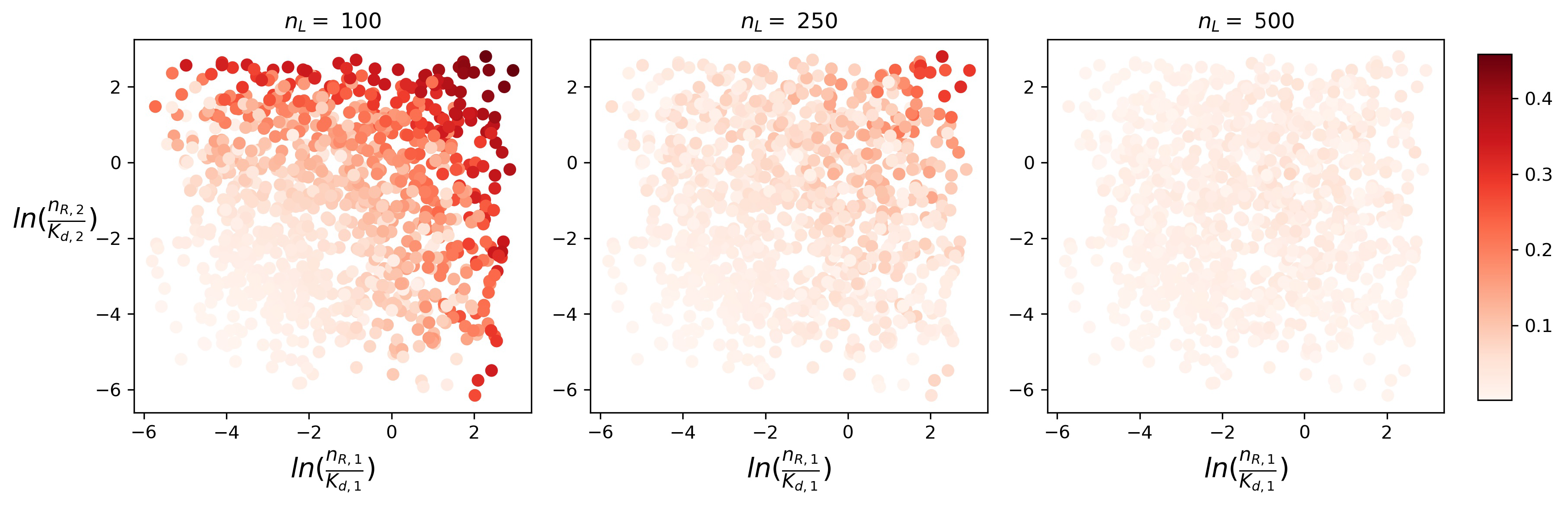
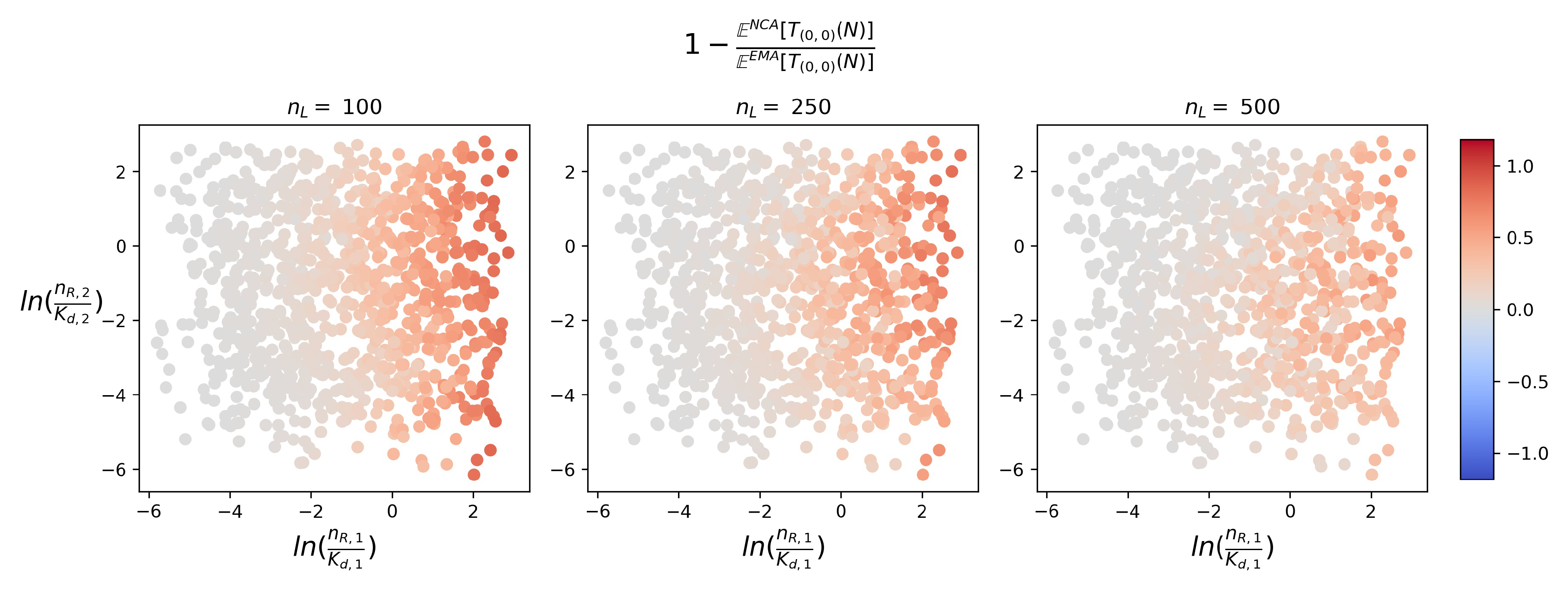
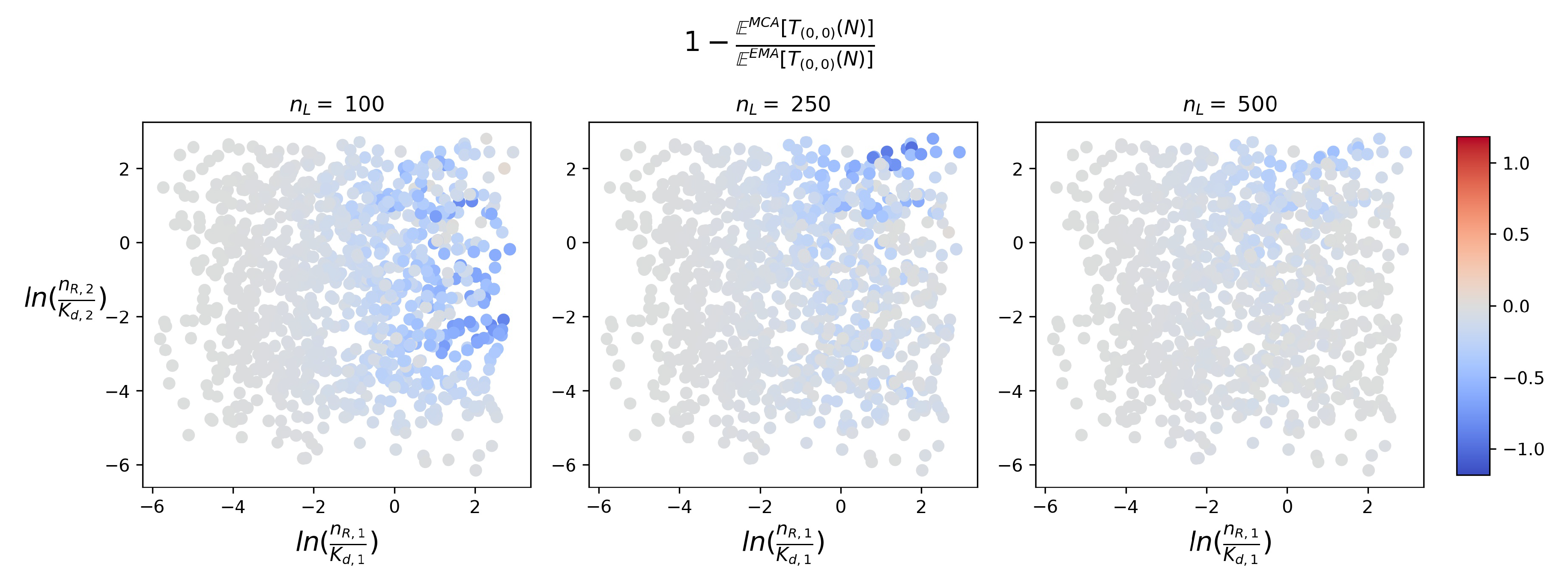
4.2. Timescales of Monomer Formation
4.3. Time to Signal Initiation: Reaching a Threshold Number of Productive Monomers
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
Abbreviations
| EMA | Exact matrix-analytic approach |
| NCA | No-competition approximation |
| MCA | Moderate-competition approximation |
Appendix A
- Forfor and .
- Forfor and .
- Forfor and .
| Algorithm A1 Computation of the steady-state distribution [47,48]. |
|
Appendix B
- Forwhere and .
- Forwhere and .
- Forwhere and .
| Algorithm A2 Moments of the random variable . |
|
Appendix C
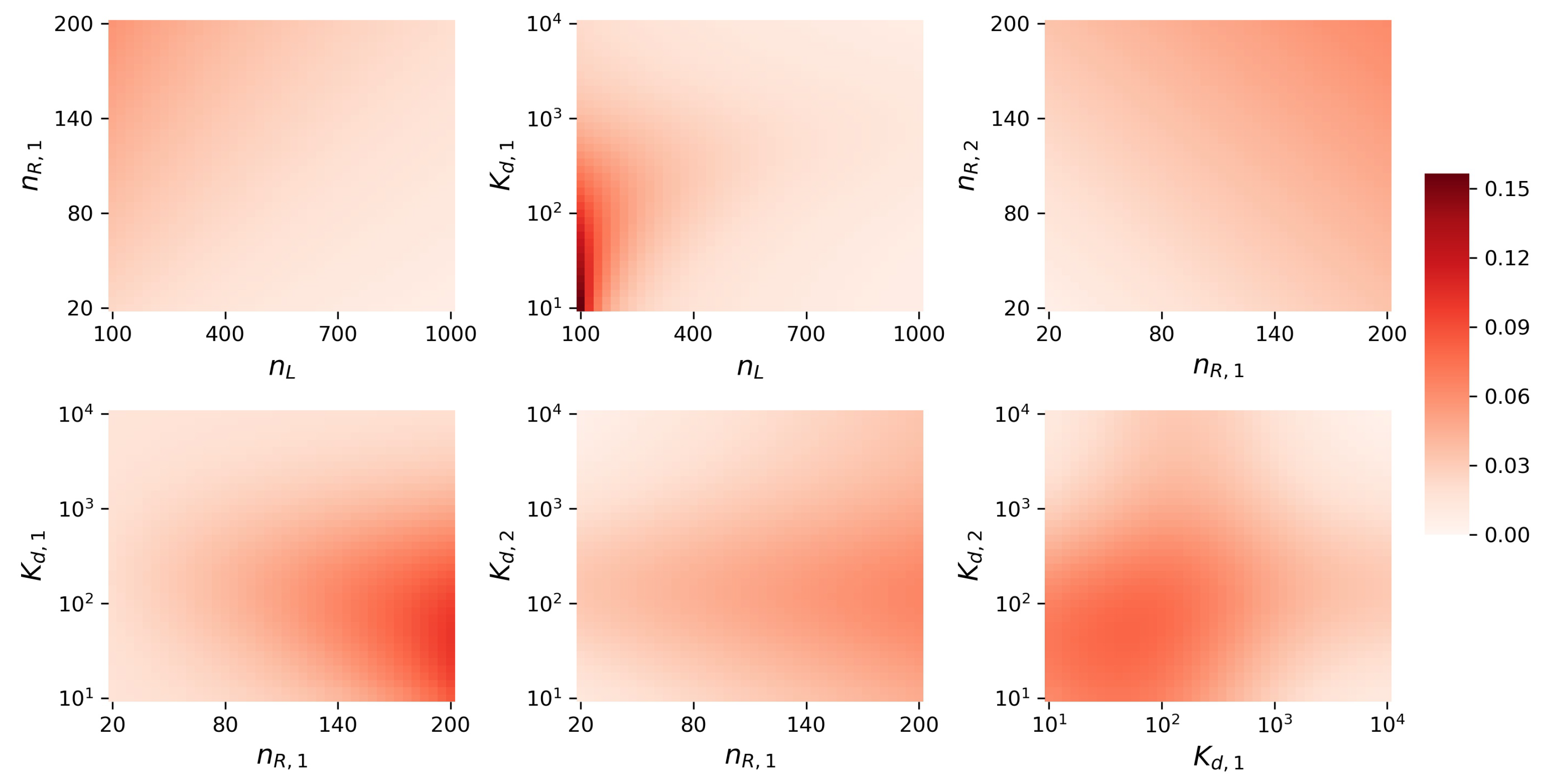

Appendix D
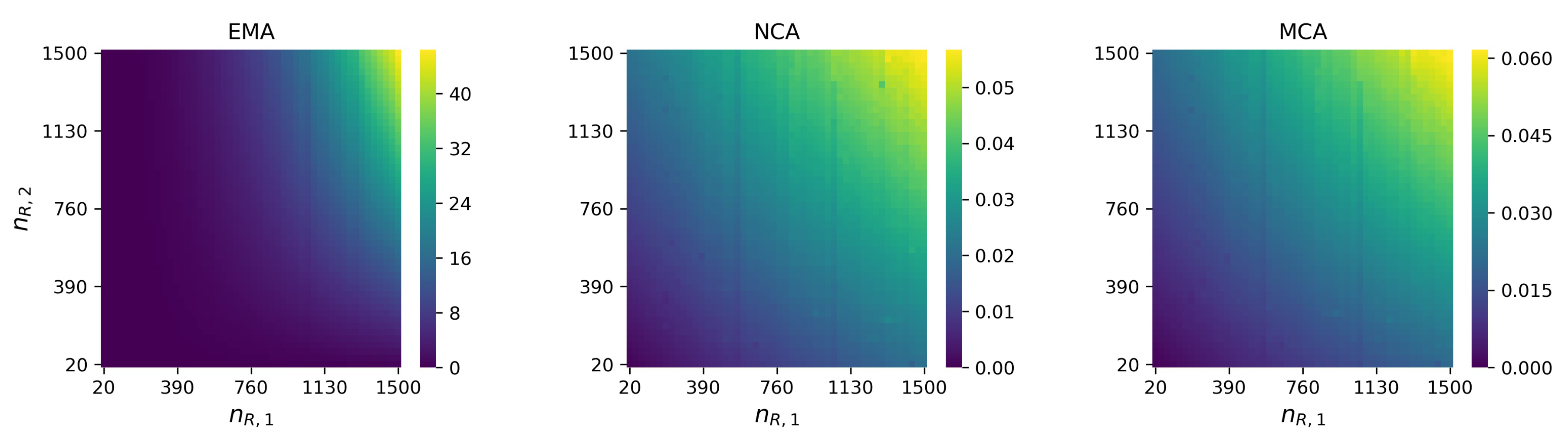
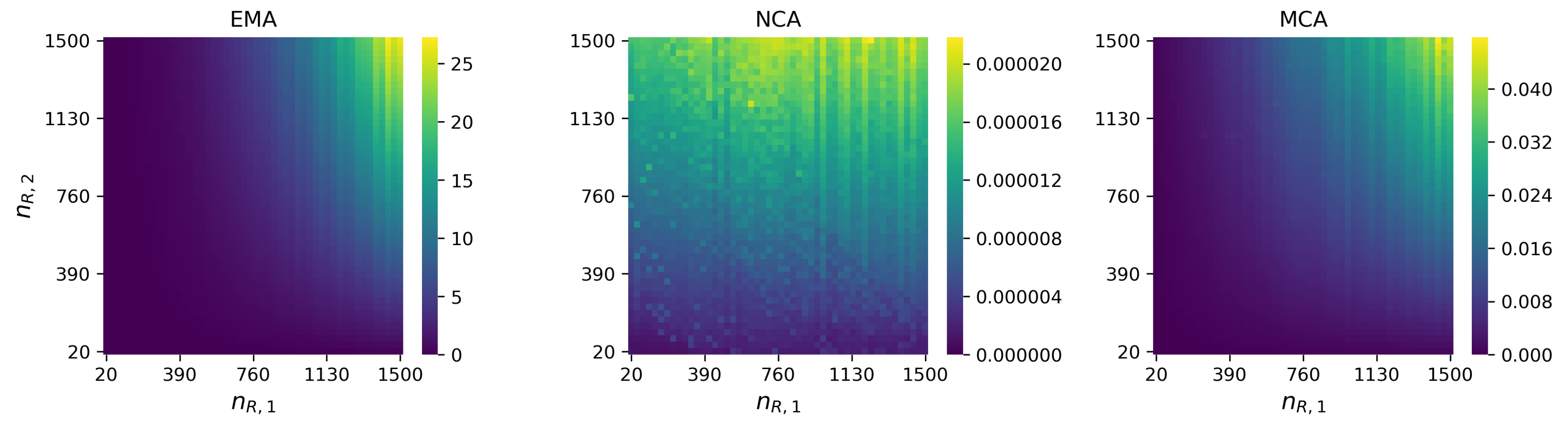

References
- Santos, S.D.; Verveer, P.J.; Bastiaens, P.I. Growth factor-induced MAPK network topology shapes Erk response determining PC-12 cell fate. Nat. Cell Biol. 2007, 9, 324. [Google Scholar] [CrossRef] [PubMed]
- Katoh, M.; Katoh, M. FGF signaling network in the gastrointestinal tract. Int. J. Oncol. 2006, 29, 163–168. [Google Scholar] [CrossRef] [PubMed]
- Ernst, M.; Jenkins, B.J. Acquiring signalling specificity from the cytokine receptor gp130. Trends Genet. 2004, 20, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Guo, X.; Imarenezor, O.; Imoukhuede, P. Quantification of VEGFRs, NRP1, and PDGFRs on endothelial cells and fibroblasts reveals serum, intra-family ligand, and cross-family ligand regulation. Cell. Mol. Bioeng. 2015, 8, 383–403. [Google Scholar] [CrossRef]
- Hackel, P.O.; Zwick, E.; Prenzel, N.; Ullrich, A. Epidermal growth factor receptors: critical mediators of multiple receptor pathways. Curr. Opin. Cell Biol. 1999, 11, 184–189. [Google Scholar] [CrossRef]
- Weddell, J.C.; Imoukhuede, P.I. Integrative meta-modeling identifies endocytic vesicles, late endosome and the nucleus as the cellular compartments primarily directing RTK signaling. Integr. Biol. 2017, 9, 464–484. [Google Scholar] [CrossRef]
- Riese, D.J.; Stern, D.F. Specificity within the EGF family/ErbB receptor family signaling network. Bioessays 1998, 20, 41–48. [Google Scholar] [CrossRef]
- López-García, M.; Nowicka, M.; Fearnley, G.W.; Ponnambalam, S.; Lythe, G.; Molina-París, C. Performance measures in stochastic processes and the matrix-analytic approach. In Quantitative Biology: Theory, Computational Methods, and Models; Springer: Cham, Switzerland, 2018; pp. 379–402. [Google Scholar]
- Starbuck, C.; Lauffenburger, D.A. Mathematical model for the effects of epidermal growth factor receptor trafficking dynamics on fibroblast proliferation responses. Biotechnol. Progress 1992, 8, 132–143. [Google Scholar] [CrossRef]
- Cross, M.J.; Dixelius, J.; Matsumoto, T.; Claesson-Welsh, L. VEGF-receptor signal transduction. Trends Biochem. Sci. 2003, 28, 488–494. [Google Scholar] [CrossRef]
- Shibuya, M. Differential roles of vascular endothelial growth factor receptor-1 and receptor-2 in angiogenesis. BMB Rep. 2006, 39, 469–478. [Google Scholar] [CrossRef]
- Dikov, M.M.; Ohm, J.E.; Ray, N.; Tchekneva, E.E.; Burlison, J.; Moghanaki, D.; Nadaf, S.; Carbone, D.P. Differential roles of vascular endothelial growth factor receptors 1 and 2 in dendritic cell differentiation. J. Immunol. 2005, 174, 215–222. [Google Scholar] [CrossRef] [PubMed]
- Kozer, N.; Barua, D.; Orchard, S.; Nice, E.C.; Burgess, A.W.; Hlavacek, W.S.; Clayton, A.H. Exploring higher-order EGFR oligomerisation and phosphorylation—A combined experimental and theoretical approach. Mol. bioSyst. 2013, 9, 1849–1863. [Google Scholar] [CrossRef] [PubMed]
- Lauffenburger, D.A.; Linderman, J.J. Receptors: Models for Binding, Trafficking, and Signaling; Oxford University Press on Demand: Oxford, UK, 1996. [Google Scholar]
- Waters, C.M.; Oberg, K.C.; Carpenter, G.; Overholser, K.A. Rate constants for binding, dissociation, and internalization of EGF: Effect of receptor occupancy and ligand concentration. Biochemistry 1990, 29, 3563–3569. [Google Scholar] [CrossRef] [PubMed]
- Klein, P.; Mattoon, D.; Lemmon, M.A.; Schlessinger, J. A structure-based model for ligand binding and dimerization of EGF receptors. Proc. Natl. Acad. Sci. USA 2004, 101, 929–934. [Google Scholar] [CrossRef]
- Blinov, M.L.; Faeder, J.R.; Goldstein, B.; Hlavacek, W.S. A network model of early events in epidermal growth factor receptor signaling that accounts for combinatorial complexity. Biosystems 2006, 83, 136–151. [Google Scholar] [CrossRef]
- Alarcón, T.; Page, K.M. Stochastic models of receptor oligomerization by bivalent ligand. J. R. Soc. Interface 2006, 3, 545–559. [Google Scholar] [CrossRef][Green Version]
- Currie, J.; Castro, M.; Lythe, G.; Palmer, E.; Molina-París, C. A stochastic T cell response criterion. J. R. Soc. Interface 2012, 9, 2856–2870. [Google Scholar] [CrossRef][Green Version]
- Castro, M.; van Santen, H.M.; Férez, M.; Alarcón, B.; Lythe, G.; Molina-París, C. Receptor pre-clustering and T cell responses: Insights into molecular mechanisms. Front. Immunol. 2014, 5, 132. [Google Scholar] [CrossRef]
- Bel, G.; Munsky, B.; Nemenman, I. The simplicity of completion time distributions for common complex biochemical processes. Phys. Biol. 2009, 7, 016003. [Google Scholar] [CrossRef]
- Resat, H.; Ewald, J.A.; Dixon, D.A.; Wiley, H.S. An integrated model of epidermal growth factor receptor trafficking and signal transduction. Biophys. J. 2003, 85, 730–743. [Google Scholar] [CrossRef]
- Gurevich, K.G.; Agutter, P.S.; Wheatley, D.N. Stochastic description of the ligand—Receptor interaction of biologically active substances at extremely low doses. Cell. Signal. 2003, 15, 447–453. [Google Scholar] [CrossRef]
- López-García, M.; Nowicka, M.; Bendtsen, C.; Lythe, G.; Ponnambalam, S.; Molina-Paris, C. Stochastic models of the binding kinetics of VEGF-A to VEGFR1 and VEGFR2 in endothelial cells. arXiv 2016, arXiv:1606.07269. [Google Scholar]
- Allen, L.J. An Introduction to Stochastic Processes with Applications to Biology; Chapman and Hall/CRC: Boca Raton, FL, USA, 2010. [Google Scholar]
- Reuter, G. Competition processes. In Proceedings of the 4th Berkeley Symposium Mathematcial Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1961; Volume 2, pp. 421–430. [Google Scholar]
- Iglehart, D.L. Multivariate competition processes. Ann. Math. Stat. 1964, 35, 350–361. [Google Scholar] [CrossRef]
- Latouche, G.; Ramaswami, V.; Kulkarni, V. Introduction to matrix analytic methods in stochastic modeling. J. Appl. Mathe. Stoch. Anal. 1999, 12, 435–436. [Google Scholar]
- López-García, M.; Nowicka, M.; Bendtsen, C.; Lythe, G.; Ponnambalam, S.; Molina-París, C. Quantifying the phosphorylation timescales of receptor–ligand complexes: A Markovian matrix-analytic approach. Open Biol. 2018, 8, 180126. [Google Scholar] [CrossRef]
- De la Higuera, L.; López-García, M.; Lythe, G.; Molina-París, C. IL-2 Stimulation of Regulatory T Cells: A Stochastic and Algorithmic Approach. In Modeling Cellular Systems; Springer: Cham, Switzerland, 2017; pp. 81–105. [Google Scholar]
- Economou, A.; Gómez-Corral, A.; López-García, M. A stochastic SIS epidemic model with heterogeneous contacts. Physica A Stat. Mech. Appl. 2015, 421, 78–97. [Google Scholar] [CrossRef]
- López-García, M. Stochastic descriptors in an SIR epidemic model for heterogeneous individuals in small networks. Math. Biosci. 2016, 271, 42–61. [Google Scholar] [CrossRef]
- Steinfeld, J.I.; Francisco, J.S.; Hase, W.L. Chemical Kinetics and Dynamics; Prentice Hall: Englewood Cliffs, NJ, USA, 1989; Volume 3. [Google Scholar]
- Gillespie, D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Stroock, D.W. An Introduction to Markov Processes; Springer Science & Business Media: Berlin, Germany, 2013; Volume 230. [Google Scholar]
- Karlin, S. A First Course in Stochastic Processes; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Weddell, J.C.; Imoukhuede, P. Quantitative characterization of cellular membrane-receptor heterogeneity through statistical and computational modeling. PLOS ONE 2014, 9, e97271. [Google Scholar] [CrossRef]
- Roepstorff, K.; Grandal, M.V.; Henriksen, L.; Knudsen, S.L.J.; Lerdrup, M.; Grøvdal, L.; Willumsen, B.M.; Van Deurs, B. Differential effects of EGFR ligands on endocytic sorting of the receptor. Traffic 2009, 10, 1115–1127. [Google Scholar] [CrossRef]
- Schmidt, A.M.; Du Yan, S.; Yan, S.F.; Stern, D.M. The biology of the receptor for advanced glycation end products and its ligands. Biochim. Biophys. Acta (BBA) Mol. Cell Res. 2000, 1498, 99–111. [Google Scholar] [CrossRef]
- Ma, B.; Shatsky, M.; Wolfson, H.J.; Nussinov, R. Multiple diverse ligands binding at a single protein site: A matter of pre-existing populations. Protein Sci. 2002, 11, 184–197. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Corral, A.; López-García, M. Extinction times and size of the surviving species in a two-species competition process. J. Math. Biol. 2012, 64, 255–289. [Google Scholar] [CrossRef]
- Gómez-Corral, A.; López-García, M. On the number of births and deaths during an extinction cycle, and the survival of a certain individual in a competition process. Comput. Math. Appl. 2012, 64, 236–259. [Google Scholar] [CrossRef]
- Gómez-Corral, A.; López-García, M. Lifetime and reproduction of a marked individual in a two-species competition process. App. Math. Compu. 2015, 264, 223–245. [Google Scholar] [CrossRef]
- Wedagedera, J.R.; Burroughs, N.J. T-cell activation: A queuing theory analysis at low agonist density. Biophys. J. 2006, 91, 1604–1618. [Google Scholar] [CrossRef]
- Wedagedara, J. Some large deviation estimates for an Erlang queue of phosphorylated T-cell receptors. J. Natl. Sci. Found. Sri Lanka 2011, 39, 03–12. [Google Scholar] [CrossRef]
- Kulkarni, V.G. Modeling and Analysis of Stochastic Systems; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
- Gaver, D.; Jacobs, P.; Latouche, G. Finite birth-and-death models in randomly changing environments. Adv. Appl. Probab. 1984, 16, 715–731. [Google Scholar] [CrossRef]
- Gómez-Corral, A.; López-García, M. Perturbation analysis in finite LD-QBD processes and applications to epidemic models. Numer. Linear Algebra Appl. 2018, 25, e2160. [Google Scholar] [CrossRef]

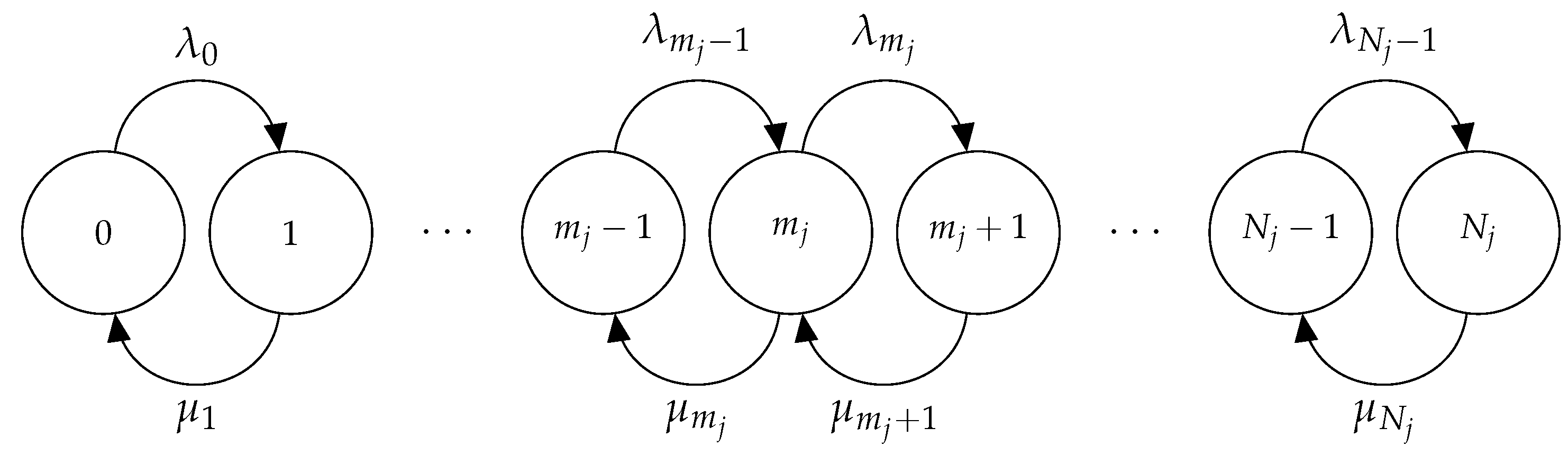


| Parameter | Range | Unit |
|---|---|---|
| molecules | ||
| molecules |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeffrey, P.-A.; López-García, M.; Castro, M.; Lythe, G.; Molina-París, C. On Exact and Approximate Approaches for Stochastic Receptor-Ligand Competition Dynamics—An Ecological Perspective. Mathematics 2020, 8, 1014. https://doi.org/10.3390/math8061014
Jeffrey P-A, López-García M, Castro M, Lythe G, Molina-París C. On Exact and Approximate Approaches for Stochastic Receptor-Ligand Competition Dynamics—An Ecological Perspective. Mathematics. 2020; 8(6):1014. https://doi.org/10.3390/math8061014
Chicago/Turabian StyleJeffrey, Polly-Anne, Martín López-García, Mario Castro, Grant Lythe, and Carmen Molina-París. 2020. "On Exact and Approximate Approaches for Stochastic Receptor-Ligand Competition Dynamics—An Ecological Perspective" Mathematics 8, no. 6: 1014. https://doi.org/10.3390/math8061014
APA StyleJeffrey, P.-A., López-García, M., Castro, M., Lythe, G., & Molina-París, C. (2020). On Exact and Approximate Approaches for Stochastic Receptor-Ligand Competition Dynamics—An Ecological Perspective. Mathematics, 8(6), 1014. https://doi.org/10.3390/math8061014






