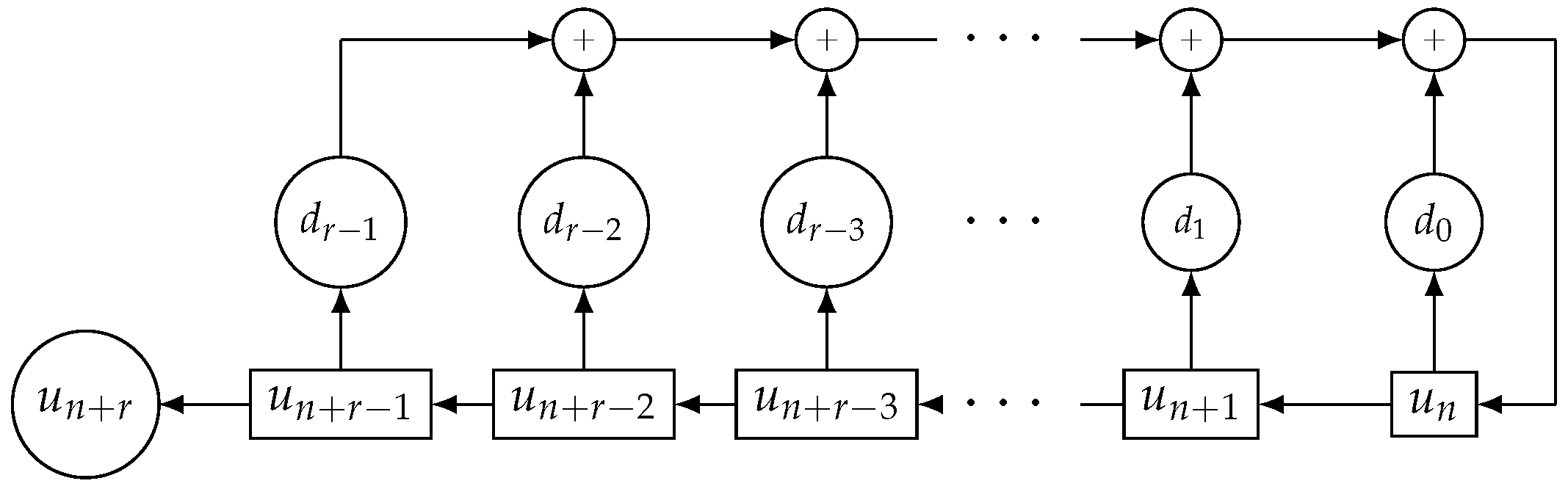
1. Introduction
Most of the devices that form part of the Internet-of-Things (IoT) require cryptographic security features to prevent users from data losses and the risks related to an improper use of passwords. Putting into effect cryptographic security is complicated. Most of the security systems are based on true random numbers, but their generation is really a difficult task [
1,
2]. Many popular random “noise” algorithms, for example, algorithms that are part of IoT devices, end up to be imperfect, showing glitches that make them predictable and vulnerable. Some weaknesses are never (publicly) found out, creating a false sense of security. The devices in which flaws are detected are those with the most flagrant errors and those most popular, for example, algorithms A5 in GSM communications cryptanalyzed in [
3,
4], the generator RC4 for encrypting Internet traffic cryptanalyzed in [
5] or the J3Gen generator for low-cost passive RFID tags cryptanalyzed in [
6]. To sum up, it is hard to build a true random number generator that can provide a strong cryptographic foundation for system security, especially for IoT devices (see [
7,
8]).
Pseudo-Random Number Generators (PRNGs) are reproducible and deterministic algorithms [
9,
10] used to generate random number sequences for cryptographic applications, such as key and nonces generation, digital signatures, and IoT security. These applications require various statistical properties, such as low autocorrelation, large period and linear complexity, rich dimensional distribution of the output sequence, and uniformity of distribution for large quantities of generated numbers (see ([
11], Chapter 2) for more details).
Binary sequences produced by maximal-length Linear Feedback Shift Registers (LFSRs), called Pseudo-Noise (PN)-sequences [
12], have been widely used in many diverse applications such as digital broadcasting, mobile wireless communications, e-commerce or cryptography (stream ciphers) [
13,
14]. In order to ensure practical cryptographic stability, it is necessary to destroy the linearity inherent to PN-sequences via different non-linear procedures.
LFSRs play an important role in the design of cryptographic PRNGs [
15,
16]. Among the most popular families of cryptographic sequence generators based on PN-sequences we can enumerate: non-linear filters with only one LFSR, combination generators that involve several LFSRs, clock-controlled registers where one LFSR controls the clock of the others or irregular decimation-based generators [
11]. We focus our attention on this latter family.
Generally speaking, the regular decimation [
17] of a sequence
by distance
d is a new sequence obtained by taking every
d-th term of
, that is,
. Nevertheless, it is the irregular decimation of PN-sequences [
18], which can be considered as a powerful PRNG, producing sequences with good cryptographic properties, such as long periods, good distribution of zeros and ones along the sequence, large linear complexity, and two-valued autocorrelation properties.
In the literature, there are three well-known irregularly decimated generators: the
shrinking generator [
19], made up of two LFSRs with different lengths, the
self-shrinking generator [
20], based on the self-decimation of one single PN-sequence, and the
generalized self-shrinking generator (GSSG) [
21], which produces a family of sequences that includes the sequence produced by the self-shrinking generator [
22]. Moreover, the modified self-shrinking generator [
23] and the t-modified self-shrinking generator [
24] are also members of such a family. These generators are fast, easy to implement and they generate good cryptographic sequences. Therefore, they seem adequate for lightweight cryptography and, in general, low-cost applications. In [
25], the authors studied the randomness of the family of sequences generated by the GSSG by means of several complete and powerful batteries of statistical tests and graphical tools. In fact, they provided a useful vision of the behavior of such sequences and proved their suitability for cryptographic applications. In [
24], the relationship among the generalized self-shrinking generator and the t-modified self-shrinking generator is deeply analyzed. Furthermore, in [
26], the authors studied the relationship between that generator and the modified self-shrinking generator. In [
27], other authors presented an extension of the self-shrinking generator to the Galois field of
elements with
p a prime integer, that is, the
p-ary Generalized Self-Shrinking Generator (
p-GSSG). Furthermore, they proved that the sequences generated by this new generator have large periods and good statistical properties.
At any rate, there exist other ways to built irregularly decimated generators, for example, irregularly decimated generators based on Feedback with Carry Shift Registers (FCSRs) instead of the traditional LFSRs [
28,
29]. These variants of the previous generators unify in a unique structure the non-linearity inherent to the FCSRs with the irregular decimation technique. An FCSR is the arithmetic or with carry analog of an LFSR. The main difference is the fact that the elementary additions are not modulo 2 additions but with the propagation of carries. FCSRs have been used in the design of stream ciphers [
30], generating pseudo-random numbers [
31], and can be efficiently implemented in parallel architectures [
32].
In modern algebra, group theory is the study of groups, which are sets of elements with an operation that satisfies certain axioms. The basic structure of groups can be found in many mathematical phenomena such as symmetry and certain types of transformations. Group theory has applications in robotics, computer vision/graphics and medical image analysis, physics, chemistry, computer science, and even puzzles like Rubik’s cube can be represented using group theory [
33,
34,
35,
36,
37]. As we show in this paper, group theory also has applications in cryptography, since the set of output sequences of the generalized self-shrinking generator has the structure of an additive group and some of the properties of this family of sequences can be deduced as a consequence of this fact.
In this work, we study in detail three different representations of the sequences produced by the GSSG: the
G-representation (introduced in [
21]), the new
p-representation and the
B-representation (introduced in [
38]). As far as we know, there are no other known representations for this kind of generators in the literature. In addition, we introduce a new way to compute the
B-representation. Such a representation relates the output sequences of our generator with shifted versions of the diagonals of the binary Sierpinski’s triangle, named binomial sequences. In terms of this representation, the structural properties of some binary sequences are easily analyzed. In brief, we give a binomial expression of these sequences, providing a relation among binomial coefficients, binary sequences and group theory.
3. Representation of Generalized Sequences
In this section, we present three different representations of the generalized self-shrunken sequences. From these representations we can obtain important information about the sequences. For instance, the binomial representation or B-representation of the generalized sequences allows us to examine the cryptographic parameters of these sequences and obtain their linear complexity; the p-representation and G-representation provide information about the shifted PN-sequences used in the decimation and allow us to define a partition of the family of generalized sequences.
It is worth saying that there exist certain advantages and disadvantages among these representations. On the one hand, the B-representation is more general and can be used for any binary sequence with a period of a power of two. On the other hand, the p-representation and the G-representation are specific representations for generalized sequences and, therefore, do not exist for other generators. However, both representations are related, being possible to get one from the other. In this section, we present some relations between the different representations.
3.1. The G-Representation of a Generalized Self-Shrunken Sequence
It is well known [
12] that a PN-sequence
generated by an LFSR with primitive polynomial
of degree
L can be represented by the trace map as follows
where
with
and
is a root of
, that is, a primitive element of
.
From now on, we consider a PN-sequence obtained from a maximal-length LFSR with characteristic polynomial of degree L.
Next theorem proves that the sequence
given in (
1) is a shifted version of the PN-sequence
.
Theorem 2. Assume that is a PN-sequence obtained from a maximal-length LFSR with characteristic polynomial of degree L. If is a nonzero vector, then the sequence obtained from Expression (1) is a shifted version of . In fact, where such thatwith being a root of . Proof. From Expressions (
1) and (
3), it follows that
□
Note that if in Expression (
1) we consider
, then
is the null sequence.
From now on, we denote by
G the decimal representation of the vector
, i.e.
Moreover, we will use indistinctly
G and
. For example
and
.
Remark 1. Since is the decimal representation of the binary number , we have thatthat is, , where denotes the Zech logarithm of 1 with basis α. Recall that the Zech logarithm of
t with a basis of the primitive element
is such that
Check [
44] for more properties of this discrete logarithm.
Example 2. Consider the LFSR in which the characteristic polynomial is . For the initial state , we obtain the PN-sequencewhich generates the family of generalized sequences shown in Table 3. The bits in bold in each sequence correspond to the positions of the ones of the PN-sequence , which appears at the bottom of the table. Furthermore, these bits are the digits of the corresponding sequence. Thus, in Table 3, the sequence corresponds to . Next, we consider some properties of this representation (G-representation) of the generalized sequences.
Theorem 3. If then is the identically 1 sequence.
Proof. Since
corresponds to the vector
, from Expression (
1) we have that
, for
, and according to the decimation rule defined in (
2), the output sequence
is the identically 1 sequence. □
Theorem 4. For , the sequences and are complementary sequences, in the sense that is the identically 1 sequence.
Proof. Since the
L-dimensional vector representations of
G and
are
and
, defined by
and
respectively, satisfy
for
. Now, from the decimation rule defined in (
2), in order to obtain the generalized sequences
and
we only consider the case when
. Therefore,
, which means that the sequences
and
are complementary. □
One can easily verify that the first 16 generalized sequences in
Table 3 are the complementary sequences of the last 16 sequences. This means that if we generate the first
generalized sequences using the above method, then the remaining sequences are just the complementary sequences of the previous ones. In this way, the computation of generalized sequences is half-reduced.
3.2. The B-Representation of a Generalized Self-Shrunken Sequence
Let
E be the shifting operator that acts on the terms of a sequence
, that is:
Let
r be a positive integer. A sequence
, of which the period is
is, in turn, a particular solution of equation:
where its characteristic polynomial is
. According to [
38,
45], the solutions of Equation (
4) can be written as:
where the coefficients
, 1 is the unique root of the polynomial
with multiplicity
and
is a binomial coefficient reduced modulo 2. Thus,
is the bit-wise XOR of
T binary sequences
weighted by
T binary coefficients
. Hence, all the solutions of the difference equation written in (
4) are sums of binomial sequences. In particular, every solution
can be written as:
with
,
, where
is the greatest value
i for which
while
for
. Expression (
5) is the
binomial representation (or
B-representation) of the sequence
.
In terms of this representation, the parameters of the sequence can be easily analyzed. Indeed, the period of is the period of the binomial sequence and the linear complexity of is the linear complexity of the binomial sequence , that is (see Theorem 1).
As a consequence we can recall the following result.
Theorem 5 ([
38], Theorem 2)
. Given the binary sequence with period , where r is a positive integer, and linear complexity , such sequence can be written as a linear combination of binomial sequences, that is, , . We will use indistinctly the notation or to denote the B-representation of the sequence . Notice that, in the B-representation, the term with the highest index is . This means that the last term provides the of the sequence. We denote by the B-representation of the null sequence.
Example 3. Consider the sequence with period . This sequence can be also written as a linear combination of the sequences :Since the binomial sequence (the term with highest index) is , then the linear complexity of will be . In the same way, its period coincides with the period of the sequence . In [
38], the authors proposed an algorithm to compute the
B-representation of any sequence with a period of the power of two. Here, our aim is to propose another method to compute the
B-representation of a generalized sequence. Next, we give a method to obtain this representation from any binary sequence of period a power of two. For this, we need to define a binary matrix called the
binomial matrix, which is similar to the construction of a binary Hadamard matrix. Consider
the binomial matrix for
, that is, a matrix of size
. We construct the binomial matrix for
as follows
which has size
. In general, we obtain the binomial matrix for
t as
where
is the binomial matrix of size
and
is the null matrix of the same size.
Let
be a binary sequence of period
. Given the binomial matrix
of size
, we construct the binary vector
The support of the vector
B, denoted by
, is the set of indices of the nonzero entries of
B, considering the first position as the 0 position. Then, we define the
B-
representation of
, denoted by
, as the sequence given by the addition of the binomial sequences
, for
, that is
Notice that, as a consequence of Expression (
6), we can only compute the
B-representation of binary sequences of period
. In particular, we can always obtain the
B-representation of any GSS-sequence since the family of generalized sequences consists of
sequences with periods power of two (see [
21]).
The following example helps us to understand this construction.
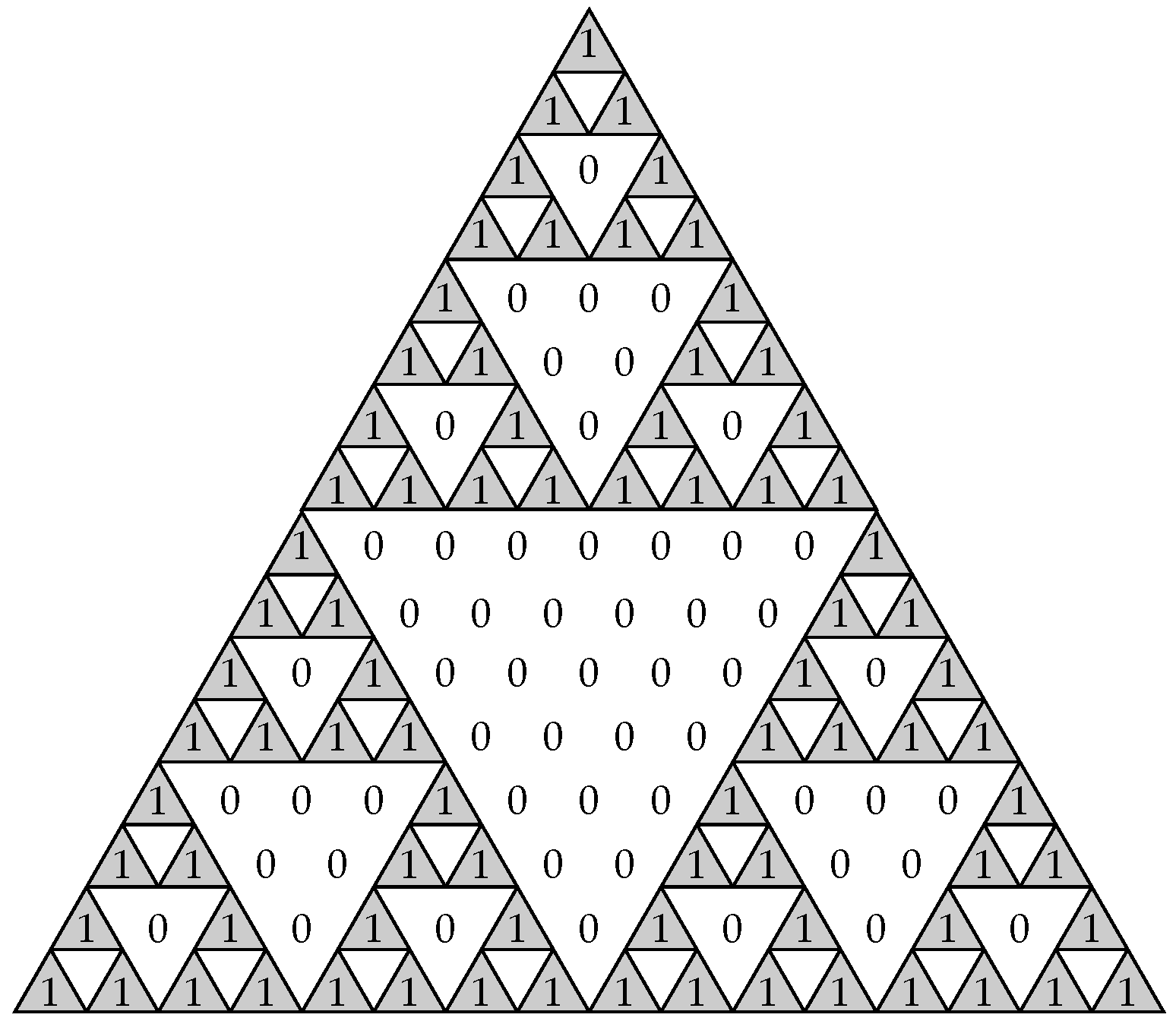
Example 4. Consider the binary sequence given in Example 3 in which the B-representation is . We check it using the method defined previously. The period of the sequence is , so we must construct the binomial matrix for , that isFrom Expression (6), we have thatand, therefore, . So, from Expression (7), we have that , as we expected. Recall that the columns of the binomial matrix (read from right to left) correspond to the successive diagonals of the Sierpinski’s triangle in
Figure 2. Thus, the binary vector
B in Expression (
6) is just the product of
by the diagonals of such a triangle.
We know that the generalized sequences have periods of the form , with . Therefore, we can express the generalized sequences as a finite sum of binomial sequences.
The following result is an immediate consequence of Theorems 4 and 3.
Theorem 6. For , the B-representations of and are equal except for the term . Furthermore, the B-representation of is exactly .
This means that if we have the B-representations of the first generalized sequences, then the B-representations of the remaining sequences are the same ones except for the term . In this way, the computation of generalized sequences is half-reduced.
Example 5. Consider again the generalized sequences obtained in Example 2. In Table 4, we can find the B-representation of each one of these generalized sequences. As we saw in Section 3.1, the last 16 generalized sequences in Table 3 are the complementary sequences of the first 16 sequences and then, from Theorem 6, the B-representation of them is the same except for the term . Furthermore, the B-representation of is , as expected. Some other properties of the family of generalized sequences can be deduced from the
B-representation. We study these properties in detail in
Section 4.
3.3. The p-Representation of a Generalized Self-Shrunken Sequence
In this subsection, we define a new representation of generalized sequences which gives us information of the shifted sequences employed in the decimation rule defined in (
2).
From Theorem 2, we have that the sequence
is a shifted version of the PN-sequence
. Therefore, instead of considering the vector
in Expression (
1) to construct
, we can simply consider the successive shifted versions of
and apply in each case the decimation rule given in (
2).
Let us consider the
p-shifted version of the PN-sequence
with
. Applying the decimation rule given in (
2), we construct the corresponding generalized sequence, which we denote by
. This new representation of a generalized sequence is called
p-representation.
One of the consequences of the group structure of is that the sum of two generalized sequences is another generalized sequence. The following theorem allows us to obtain the p-representation of the resulting generalized sequence from the p-representations of two generalized sequences given.
Theorem 7. Consider that is the PN-sequence of an LFSR with primitive characteristic polynomial of degree L and is a root of . Then, the sum of two generalized sequences obtained with shifts and is another generalized sequence with shift , i.e,where is as before the Zech logarithm with basis α. Proof. Assume that and are two generalized sequences obtained from the PN-sequence .
According to the decimation rule given in (
2), if
, then we have that
and
.
We have seen in Expression (
3) that every element of
can be expressed as
where
with
. Therefore, we have that:
Bit-wise XORing both sequences
we get:
The sequence
is the generalized sequence with shift
, that is,
□
Notice that there is not any value that represents the null binary sequence . So, we denote with the p-representation of this sequence. It is worth noticing that , where and are the G-representation and the B-representation of the null sequence, respectively.
We have introduced three different notations for generalized sequences: the
G-representation,
, introduced in
Section 3.1; the
B-representation,
given in
Section 3.2 and the
p-representation,
, given in this subsection. The next theorem, which is a direct consequence of Theorem 2, provides a relation between the
G-representation and the
p-representation. We can get a representation from the other as follows.
Theorem 8. Consider the family of generalized sequences denoted by , thenwith such that , where is a root of the primitive polynomial of the corresponding LFSR. Equivalently, . Example 6. Consider again Example 2. Applying Theorem 8 to the family of generalized sequences given in Table 3, we obtain the relation between G-representation and p-representation as depicted in Table 5. For instance, if that is , we have to compute such that . According to the results in Table 5, , therefore, from Theorem 8, . It is easy to check that . Consider now another example. For , we have . We need to find such that . According to Table 5, the value we are looking for is . Therefore , as we expected from Table 5. Corollary 1. Consider the family of generalized sequences generated by the PN-sequence of period . If , with , then and or equivalently .
Example 7. Consider again Example 2, where and . We can compute the value of p for each , where :| G | | |
| 1 | 0 | −4 mod 31 = 27 |
| 2 | 1 | −3 mod 31 = 28 |
| 4 | 2 | −2 mod 31 = 29 |
| 8 | 3 | −1 mod 31 = 30 |
| 16 | 4 | 0 mod 31 = 0 |
This result matches with the expected values for p obtained in Table 5. It is worth mentioning that the self-shrinking generator is another cryptographic sequence generator based on irregular decimation [
20]. In this case, a PN-sequence is self-decimated producing a new sequence with good cryptographic properties. In [
22], authors proved that the sequence produced by this generator can also be obtained with the generalized self-shrinking generator and the same characteristic polynomial with shift
. As a consequence of this fact and the previous theorem, we can introduce the following result.
Corollary 2. The sequence with such that is the output sequence generated by the self-shrinking generator with the same LFSR and characteristic polynomial .
Example 8. Consider again Example 2. According to the previous corollary, the sequence generated by the self-shrinking generator is with G such that . In this case, and . Therefore and which corresponds to the sequence with shift , that is, the output sequence of the self-shrinking generator, as expected.
The following lemma proves that there exists an element such that . Later, we check that the generalized sequences associated to these values, and , are the sequences with period .
Lemma 1. Let α be a primitive element in . Thenif and only if . Proof. Assume that
. Then
and therefore,
.
Conversely, assume that
. Then
Therefore, the lemma holds. □
Let the binary representation of the value of G associated to m, and its decimal representation. Next, we introduce a theorem whose proof helps us to prove Theorem 10.
Theorem 9. Let m be the integer defined in Lemma 1. Then
Proof. According to Theorem 8, we can express
m and
as:
where
and
satisfy
with
From Lemma 1 and Expression (
8) we deduce that:
Therefore,
As a consequence, the relation between
and
is
□
Theorem 10. Consider such that , where m is the value given in Lemma 1. The generalized sequences and are the sequences of period , that is, the sequences with B-representation and .
Proof. Let
be the PN-sequence used in the GSSG. Consider the corresponding shifted versions
and
, where
m is as in Lemma 1. According to the proof of Theorem 9, we know that:
Now, from Expression (
1):
As a consequence,
.
Let
be the set of indices
j such that
. Therefore
Notice that (10) implies that, when
,
As a consequence, the resulting generalized sequences,
and
, are complementary (their sum is the identically 1 sequence).
Assume that
. Let
, according to (9),
for
(i.e., the integers between
and
). Furthermore, since
is also a shifted version of
(shift
), we have
, for
. As a result, we obtain the following chain:
Therefore,
. This means that
is a shifted version of
, but they are complementary. The only option is that they are the sequences
and
. □
For example, consider
Table 5. The sequences
and
correspond to shifts
and
of the PN-sequence
. From the isomorphism defined by (
11), we have that the generalized sequence
is associated with the element
, and the generalized sequence
is associated with
. Therefore, we have
and
(see
Table 5 again), in which the difference is
as Theorem 9 indicated.
Theorem 11. Consider a primitive polynomial of degree L and let m be the positive integer defined in 1, i.e., , with α a root of . Then, given β a root of , where is the reciprocal polynomial of , we have that , with .
Proof. We know that
is a root of
. Then
and
. As a consequence, we have that
and
□
In
Table 6, we study the values of
m, such that
, for every primitive polynomial of degree 5. Consider, for instance,
. For this polynomial
. The corresponding value
for the reciprocal polynomial
is computed as
.
Remark 2. Given the value of m for a primitive polynomial , we can find the value of for without computing any logarithm.
5. Conclusions
In this work, we introduce and analyze new ways to represent the generalized sequences, from which we study different properties of the sequences. We introduce the B-representation that allows us to express such sequences by means of binomial sequences, that is, shifted versions of the diagonals of the Sierpinski’s triangle. Furthermore, this representation lets us generate binary sequences with controllable parameters such as the period and the linear complexity. We have also defined the G and p-representation, both related between them. From the p-representation we can obtain the shifted version of the corresponding input PN-sequence of the GSSG and vice versa. Using this p-representation, we can define an isomorphism between the family of generalized sequences produced by a primitive polynomial of degree L and the additive group . As a consequence, we can create a partition of the sequences into subsets of cardinal 4, known as the cosets. Moreover, the B-representations of the four generalized sequences in each coset exhibit a well defined pattern and similar characteristics. This fact might be exploited in the cryptanalysis of this generator.
We still have different open problems to solve. In
Section 4.2, we have analyzed the linear complexity of generalized sequences, but some results are just conjectures. The partition of generalized sequences into cosets of the quotient group
and the study of the linear complexity of the sequences in each coset have brought new questions to be solved. Furthermore, we want to prove that the period of any generalized sequence obtained from a primitive polynomial of degree
L, except from the sequences with period 1 and 2, is always
and that
is a lower bound on the linear complexity. Finally, another interesting future line would be to study the generalized shelf-shrinking generator based on FCSRs (or similar structures), analyze their cryptographic properties and adapt all three representations to this new model.
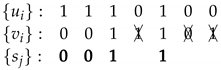 The corresponding generalized sequence is .
The corresponding generalized sequence is .