A Group Law on the Projective Plane with Applications in Public Key Cryptography ^†

Abstract

In the context of new threats to Public Key Cryptography arising from a growing computational power both in classic and in quantum worlds, we present a new group law defined on a subset of the projective plane $\mathbb{F}{P}^2$ over an arbitrary field $\mathbb{F}$, which lends itself to applications in Public Key Cryptography and turns out to be more efficient in terms of computational resources. In particular, we give explicitly the number of base field operations needed to perform the mentioned group law. Based on it, we present a Diffie-Hellman-like key agreement protocol. We analyze the computational difficulty of solving the mathematical problem underlying the proposed Abelian group law and we prove that the security of our proposal is equivalent to the discrete logarithm problem in the multiplicative group of the cubic extension of the finite field considered. We present an experimental setup in order to show real computation times along a comparison with the group operation in the group of points of an elliptic curve. Based on current state-of-the-art algorithms, we provide parameter ranges suitable for real world applications. Finally, we present a promising variant of the proposed group law, by moving from the base field $\mathbb{F}$ to the ring $\mathbb{Z}/pq\mathbb{Z}$, and we explain how the security becomes enhanced, though at the cost of a longer key length.

1. Introduction and Related Work

Neal Koblitz [1] and Victor Miller [2] presented independently but simultaneously proposals that made use of the multiplicative group of a finite field in order to implement certain asymmetric cryptosystems. Koblitz presented an implementation of Diffie-Hellman key-agreement protocol [3] based on the use of elliptic curves. On his part, Miller offered a proposal more on the theoretical side, avoiding comparisons with existing implementations. In all those cases, the security is based on the infeasibility of the discrete logarithm problem over elliptic curves (ECDLP), which is to this day considered as difficult as the integer factorization problem (IFP), upon which RSA [4] cryptosystem is based, or the discrete logarithm problem (DLP) employed in ElGamal cryptosystem [5].

Diffie-Hellman key-agreement protocol for elliptic curves (ECDH) consists essentially in mapping the operations customarily carried out in the multiplicative group ${\mathbb{Z}}_p^{\ast }$ to the set of points of an elliptic curve, endowed with an additive group operation. However, this protocol painfully succumbs in the face of a plain man-in-the-middle attack and, for this reason, Menezes, Qu, and Vanstone proposed [6] an authenticated variant, known as Elliptic Curve Menezes-Qu-Vanstone key agreement protocol (ECMQV). In general, the outcome of these key-agreement protocols is that the users eventually share a value—the key or a seed to derive the key—which was initially unknown for any of them, and cannot be inferred (more precisely: It is computationally infeasible to infer it) from the information exchanged between the parties.

Along with these key-agreement protocols, several elliptic-curve-based asymmetric cryptosystems have seen the light in these last years. The first proposals of the so-called elliptic-curve cryptosystems (ECC) were revisions adapted from existing systems, such as ElGamal’s [5], or Massey-Omura’s [7]. They were publicized by Koblitz in [1].

The problem with the elliptic-curve version of ElGamal’s and Massey-Omura’s cryptosystems is that the user needs to map each possible message to a point of the curve. This fact is an important drawback since, on the one hand, the cardinal of the curve points is finite, so the user is limited to a finite number of possible messages; and, on the other hand, the user needs some kind of “equivalence table” between messages and points in order to cipher and decipher. Therefore, these cryptosystems are limited in practice to those settings in which the set of possible messages is fixed in advance.

In order to overcome these limitations, Menezes and Vanstone proposed in [8] the Elliptic Curve Menezes-Vanstone cryptosystem (ECMV) for elliptic curves over finite fields ${\mathbb{F}}_q$. In ECMV, each message is represented by elements of the Cartesian product ${\mathbb{F}}_q^{\ast }\times {\mathbb{F}}_q^{\ast }$, not necessarily points of the elliptic curve. The protocol includes a systematic procedure to divide any message into blocks and to codify each block as an element of the Cartesian product. The downside is that ciphertext length depends entirely on plaintext length.

In spite of the efforts, ECC has abandoned the battlefield of cryptosystems in favor of key-agreement protocols as a building block for hybrid cryptosystems. In the latter, ECC permits the users to share a session (ephemeral) key, whence a symmetric key is derived to be used together with a symmetric cryptosystem, such as AES.

In this setting, Mihir Bellare and Philip Rogaway [9] published in 1997 the Discrete Logarithm Augmented Encryption Scheme (DLAES). Along with Michel Abdalla, the system was improved in 1998 by the same authors, and renamed as DHAES (Diffie-Hellman Augmented Encryption Scheme) [10]. Eventually renamed to DHIES (Diffie-Hellman Integrated Encryption Scheme) [11,12], it is an improved extension of ElGamal’s cryptosystem [5]. DHIES is really a complex protocol, much more involved than ElGamal or Koblitz’s proposal in [1], which includes public key operations, symmetric ciphering, authentication and hash function computation. While ElGamal and Koblitz directly ciphered a message, without any further use of other necessary elements for a proper integrated scheme, DHIES provides security against chosen ciphertext attacks at no extra cost in terms of number of operations or key lengths [11]. Together with other proposals, DHIES was employed in the preparation of standards [13,14].

Finally, it is worth mentioning the so-called ECIES (Elliptic Curve Integrated Encryption Scheme), which embraces several integrated ciphering schemes using DHIES-based elliptic curves and it is described in the relevant security standards, such as [13,14,15] (a comparison among different ECIES implementations may be found in [16]). Remark that, whenever ECIES is recommended (even with minor differences regarding implementations), it is to be used in a hybrid setting, where a (DH-type) session key agreement protocol is a must.

Setting aside the already mentioned cryptosystems and key-agreement protocols, it is probably in digital signature schemes that elliptic curve cryptography is mostly demanded. The ElGamal-based Elliptic Curve Digital Signature Algorithm (ECDSA) is analogous to the Digital Signature Algorithm (DSA) [17], using additive rather than multiplicative notation. ECDSA has consolidated into an internationally accepted standard [13,18].

When dealing with ECC, one of the most important aspects to keep in mind is the processes of curve generation and selection. Several standards tackle such methods and show examples of curve selection as part of the public-key generation process. Among them, it is worth mentioning X9.63 [13], IEEE 1363 [19], and FIPS 186-4 [20], issued by the National Institute of Standards and Technology (NIST) of the USA. However, in practice, such standards lack precision and clarity when it comes to selecting seeds for random generation, or prime numbers, thus limiting the ability of serving really practical purposes.

For these reasons, several initiatives have ripened, such as Brainpool [21], considered to be the first international proposal to provide clear and transparent procedures in order to generate the parameters of elliptic curves for cryptographic purposes. Under the Brainpool initiative, several elliptic curves, presented in reduced Weierstrass format, have been considered safe beyond any doubt by many experts.

Later on, researchers Daniel Bernstein and Tania Lange [22] reviewed the elliptic curve generation procedures, including those in Brainpool. In particular, they scrutinized 20 curves from several sources under a number of security requirements that they considered a must. The result was that just only Edwards and Montgomery curves [23] satisfied those requirements. In view of this outcome, the experts decided to propose a new set of curves, known as SafeCurves that really met the set of safety requirements [22]. Moreover, Baignères [24] proposed a new Edwards elliptic curve (the so-called million dollar curve) by means of a new technique that insists in the randomness of the input parameters to the generation process.

In spite of those efforts, the currently most deployed elliptic curves, both in hardware and software implementations, are those presented in the reduced Weierstrass format, whereas Edwards or Montgomery curves are seldom used, maybe because the additional security provided by them is not worth their lower computation efficiency (multiplications with scalars). A performance comparison among the three types of curves cited above can be found in [25]. In the latter, the authors resorted to the examples provided by the initiative SafeCurves, together with a Java implementation developed by them.

Koyama et al. proposed in [26] the use of elliptic curves over the ring ${\mathbb{Z}}_n$, where n is an odd composite square-free integer. In particular, n is the product of two large primes, as in the RSA cryptosystem. The security of the cryptosystem of Koyama et al.’s is based upon IFP, though the authors did not prove whether solving the IFP was equivalent to breaking their cryptosystem. Later on, Meyer and Müller proved in [27] that breaking a modified version of Koyama’s cryptosystem was indeed equivalent to factorizing n. In addition, they proposed a digital signature scheme based on elliptic curves defined over ${\mathbb{Z}}_n$.

Another interesting question is the ever growing necessity of implementing elliptic curve cryptography on ubiquitous portable devices (smartphones, smart cards, pen-drives, and the like), which gives rise to new challenges. Actually, these devices normally present severe limitations regarding storage capacity or processing power, as compared with ordinary desktop computers. Elliptic curve cryptography is amenable to these devices since key sizes are much smaller than in other cryptosystems (for example, RSA) for similar security levels.

It is very common nowadays to find elliptic curve cryptography on such devices, and hence implementations of multiplication operations. These operations, in turn, are threatened by the ever more powerful side channel and fault injection attacks. For example, Reference [28] documents recent developments on those side channel attacks to ECC implementations. It is completely necessary to implement the multiplication algorithms in such a way that they do not leak any information to possible attackers. Reference [29] describes some options to avoid such attacks when implementing scalar multiplications for elliptic curves.

It is also very well known that the advent of a universal quantum computer with sufficient computation power could break the most commonly used asymmetric cryptosystems. In fact, Shor’s algorithm [30], proposed in 1997, is known to solve IFP and DLP (or ECDLP) in polynomial time if such quantum computer does exist; however, there is no agreement as to how many qubits would be required to execute Shor’s or other quantum algorithms, but some estimations point to a number of qubits several orders of magnitude larger than the number of qubits available in currently existing quantum computers [31]. Should such number of qubits be available, IFP or DLP could be solved in a bunch of hours. For example, a personal computer needs, roughly speaking, $\mathcal{O}\left(2^{\sqrt[3]{logn}}\right)$ bit operations to factor a number n, whereas a quantum computer executing Shor’s algorithm could perform such factorization with only $\mathcal{O}\left({log}^{3}n\right)$ bit operations and using $\mathcal{O}(logn)$ bit storage.

Though it seems that a quantum computer with the required computation power will not be available any time soon, the new source of attacks coming from quantum world and the need to ensure that the information protected by current asymmetric systems continues to be accessible forced the NIST to launch an international call [32] for new cryptographic algorithms resilient to the power leveraged by quantum computation: the so-called quantum-resistant algorithms. These are expected to cover at least proposals for new asymmetric encryption schemes, digital signature schemes, and key encapsulation mechanisms (KEM). The main quantum-resistant proposals include difficult problems stemming from coding theory, lattices, hash functions, and isogenies over elliptic curves, to mention just a few. In January 2019, the NIST published the list of submitted algorithms that have passed on to the second round of the call [33]. Among them, there stands the proposal SIKE as a key encapsulation mechanism that is based on isogenies over elliptic curves.

The previous paragraphs summarize the current state of affairs regarding classic and quantum cryptography and make it clear that there is much to be done in both classic and quantum worlds. Taking that current context into account, this work presents a new group law defined on a subset of the projective plane $\mathbb{F}{P}^2$ over an arbitrary field $\mathbb{F}$, which lends itself to applications in public key cryptography. Apart from the mathematical novelty implied, this new group law presents several features worth public key cryptosystems, such as:

• a Diffie-Hellman-like key agreement, since such protocol remains a basic piece for any hybrid cryptosystem, as commented above.
• an extension to the ring ${\mathbb{Z}}_{pq}$ providing enhanced security, following the same vein as the one followed by [26,27].
• no side channel attacks known to date, given the recentness of this proposal and due to the particular group law defined.
• gives rise to new research lines, such as defining isogenies over the group structure, thus opening the path to a possibly new quantum-resistant problem.

In a nutshell, the main contribution of this paper is to propose a new group law, defined on the complement of a projective cubic plane curve, prove its properties, and consider the possibility of using it as a building block for cryptographic applications in the field of Public Key Cryptography (PKC).

The paper is organized as follows: Section 2 presents the group law and its main characteristics and properties. In particular, we define the mathematical problem associated with the considered group law, and we give the explicit formulas to compute the group operation of any two elements of the group. These formulas, which involve coefficients from the base field, are applicable to any pair of elements of the group with no exception whatsoever, which is advantageous in view of possible cryptographic applications, since this feature helps, for example, to withstand side channel attacks.

As an application of the defined group law to PKC, a cryptographic protocol, in particular, a Diffie-Hellman-like key agreement protocol, is defined in Section 3. We also analyze the computational difficulty of solving the mathematical problem underlying the defined group law, and we prove that the hardness of our problem is equivalent to that of the discrete logarithm problem on the multiplicative group of the cubic extension of the finite field considered.

In Section 4, we consider an entirely analogous system, but shifting the general base field to the ring $\mathbb{Z}/pq\mathbb{Z}$. We make it clear that this last proposal enhances the security of the system, since it now depends not only on DLP but also on the factorization problem, though at the price of doubling the key length.

The last section is devoted to the conclusions.

2. The Group Law Defined

Our purpose in this section is to search for a particular (finite) group endowed with an internal operation that makes it cyclic provided that certain conditions hold. In the latter case, we define yet another (discrete) logarithm operation, which, if found to be difficult to carry out, may give rise to cryptographic applications.

We will work with three-dimensional vector spaces and their associated two-dimensional projective spaces, defined over finite fields. We will consider certain cubic curve defined over this ambient projective space, so that the set over which we will define our new group operation is precisely the set of points of the projective space that do not belong to that cubic curve.

We will show the conditions under which the cubic curve has no points in the projective space, which means that the group embraces the the full projective space. We will provide the explicit formulas to compute the group law in the base field and the good piece of news is that these formulas are the same for any of the elements in the group, a feature much cherished in cryptographic settings.

Let $\mathbb{F}$ be a field and let us consider a linear endomorphism $A:V\to V$ of the vector space $V={\mathbb{F}}^3$. We define the polynomial $Q\left(\mathbf{x}\right)=det(x_{1}I+x_{2}A+x_3{A}^2)$, where $\mathbf{x}=(x_1,x_2,x_3)\in V$. The polynomial Q is homogeneous of degree 3, and does not depend on A, but only on the characteristic polynomial $\chi \left(X\right)$ of A.

A new group law is proposed $\oplus :V\times V\to V$. Let the multiplicative group ${\mathbb{F}}^{\ast }$ act on V by the diagonal action, i.e., $\lambda ·(x_1,x_2,x_3)=(\lambda x_1,\lambda x_2,\lambda x_3)$, and let $\mathbb{F}{P}^2$ denote the projective plane, namely $\mathbb{F}{P}^2=(V\backslash \left\{(0,0,0)\right\})/{\mathbb{F}}^{\ast }$. Then, the proposed group law induces an Abelian group law on $\mathbb{F}{P}^2\backslash Q^{-1}\left(0\right)$.

If the characteristic polynomial $\chi \left(X\right)$ is irreducible in $\mathbb{F}\left[X\right]$, then $Q^{-1}\left(0\right)=\left\{(0,0,0)\right\}$, and therefore the group law extends to the whole projective plane $\mathbb{F}{P}^2$; moreover, if the base field is a finite field ${\mathbb{F}}_q$, with characteristic different from 2 or 3, then the group $\mathbb{G}=({\mathbb{F}}_q{P}^2,\oplus )$ is proved to be cyclic.

The latter property permits us to apply the notion of discrete logarithm to the group $\mathbb{G}$. If we fix a generator $g\in {\mathbb{F}}_q{P}^2$, then any element h of the group is the addition of g with itself a finite number of times, say n, so that $h=g\oplus g\oplus \stackrel{\left(n\right)}{\cdots }\oplus g=\left[n\right]g$. The number n is the logarithm of h to the base g.

Given any element $h\in \mathbb{G}$, and a generator g of the group, the discrete logarithm problem (DLP) consists of finding the smallest integer n, such that $h=\left[n\right]g$. In this work, we prove that the DLP over $\mathbb{G}$ with a proper choice of the generator is equivalent to the DLP over the multiplicative group ${\left({\mathbb{F}}_{q^3}\right)}^{\ast }$.

Popular current cryptosystems are based on the discrete logarithm problem over different groups, such as the group of invertible elements in a finite field, or the group of points of an elliptic curve with the addition of points as group operation. Our proposal could fit perfectly well in the same niche.

As is the case for analogous public key protocols, the users of the present proposal agree to a single base field ${\mathbb{F}}_q$ and an (irreducible) polynomial:

$$\begin{array}{ccc}\hfill \chi \left(X\right)=& X^3-c_1{X}^2-c_{2}X-c_3,\hfill & c_1,c_2,c_3\in {\mathbb{F}}_q.\hfill \end{array}$$

The public system parameters include the base field ${\mathbb{F}}_q$, coefficients $c_1,c_2,c_3\in {\mathbb{F}}_q$, and a generator g.

Next, we prove that the polynomial Q does not depend on A, but only on the characteristic polynomial $\chi \left(X\right)$ of A.

Lemma 1.

Let $\mathbb{F}$ be a field and let V be the vector space ${\mathbb{F}}^3$. If $A:V\to V$ is a linear map such that the endomorphisms $I,A,A^2$ are linearly independent, then the homogeneous cubic polynomial $Q\left(\mathbf{x}\right)=det(x_{1}I+x_{2}A+x_3{A}^2)$ does not depend on the matrix A but only on the coefficients $c_1,c_2,c_3$ of its characteristic polynomial $\chi \left(X\right)=X^3-c_1{X}^2-c_{2}X-c_3$.

Proof. 

Let $\overline{\mathbb{F}}$ be the algebraic closure of $\mathbb{F}$. As the endomorphisms $I,A,A^2$ are linearly independent, the annihilator polynomial of A coincides with $\chi \left(X\right)$ by virtue of the Cayley-Hamilton theorem. Hence, there exists a basis of ${\overline{\mathbb{F}}}^3$ such that the matrix of A in this basis equals one of the following three matrices:

$$M_1=\left(\begin{array}{ccc}{\alpha }_1& 0& 0\\ 0& {\alpha }_2& 0\\ 0& 0& {\alpha }_3\end{array}\right),M_2=\left(\begin{array}{ccc}{\alpha }_1& 0& 0\\ 0& {\alpha }_2& 0\\ 0& 1& {\alpha }_2\end{array}\right),M_3=\left(\begin{array}{ccc}{\alpha }_1& 0& 0\\ 1& {\alpha }_1& 0\\ 0& 1& {\alpha }_1\end{array}\right),$$

(1)

and, from a simple calculation, we obtain

$$\begin{array}{ccc}Q\left(\mathbf{x}\right)\hfill & =\hfill & det(x_{1}I+x_2{M}_i+x_3{\left(M_i\right)}^2)\hfill \\ \hfill & =\hfill & -c_2{x}_1{\left(x_2\right)}^2+\left[{\left(c_2\right)}^2-2\left(c_1{c}_3\right)\right]x_1{\left(x_3\right)}^2+c_1{\left(x_1\right)}^2{x}_2\hfill \\ \hfill & \hfill & +\left[{\left(c_1\right)}^2+2c_2\right]{\left(x_1\right)}^2{x}_3-\left(c_2{c}_3\right)x_2{\left(x_3\right)}^2+\left(c_1{c}_3\right){\left(x_2\right)}^2{x}_3\hfill \\ \hfill & \hfill & -\left(c_1{c}_2+3c_3\right)x_1{x}_2{x}_3+{\left(x_1\right)}^3+c_3{\left(x_2\right)}^3+{\left(c_3\right)}^2{\left(x_3\right)}^3,\hfill \end{array}$$

(2)

for every $i=1,2,3$. □

Theorem 1.

Every linear map $A:V\to V$ such that the endomorphisms $I,A,A^2$ are linearly independent, induces a law of composition

$$\begin{array}{c}\oplus :V\times V\to V,\\ (\mathbf{x},\mathbf{y})\mapsto \mathbf{z}=\mathbf{x}\oplus \mathbf{y},\end{array}$$

by the following formula:

$$\begin{array}{cc}\hfill z_{1}I+z_{2}A+z_3{A}^2=& \left(x_{1}I+x_{2}A+x_3{A}^2\right)\left(y_{1}I+y_{2}A+y_3{A}^2\right),\hfill \end{array}$$

(3)

where $\mathbf{x}=(x_1,x_2,x_3)$, $\mathbf{y}=(y_1,y_2,y_3)$, $\mathbf{z}=(z_1,z_2,z_3)$.

Moreover, the set of elements $\mathbf{x}\in V$ such that $\mathbf{x}\oplus \mathbf{y}=(0,0,0)$ for some element $\mathbf{y}$ in $V\backslash \left\{\right(0,0,0\left)\right\}$ coincides with the set $Q^{-1}\left(0\right)$, and ⊕ induces a group law

$$\oplus :({\mathbb{F}}^3\backslash Q^{-1}\left(0\right))\times ({\mathbb{F}}^3\backslash Q^{-1}\left(0\right))\to ({\mathbb{F}}^3\backslash Q^{-1}\left(0\right)).$$

If C denotes the projective cubic curve defined by $Q\left(\mathbf{x}\right)=0$, then the group law ⊕ also induces a group law

$$\oplus :(\mathbb{F}{P}^2\backslash C)\times (\mathbb{F}{P}^2\backslash C)\to \mathbb{F}{P}^2\backslash C.$$

Proof. 

As $A^3=c_1{A}^2+c_{2}A+c_{3}I$, and

$$\begin{array}{cc}\hfill A^2·A^2& =A·A^3\hfill \\ \hfill & =\left(c_1{c}_3\right)I+\left(c_1{c}_2+c_3\right)A+\left[{\left(c_1\right)}^2+c_2\right]A^2,\hfill \end{array}$$

from the formula in (3), it follows:

$$\begin{array}{cc}\hfill z_1=& x_1{y}_1+c_3\left(x_2{y}_3+x_3{y}_2\right)+\left(c_1{c}_3\right)x_3{y}_3,\hfill \\ \hfill z_2=& x_1{y}_2+x_2{y}_1+c_2\left(x_2{y}_3+x_3{y}_2\right)+\left(c_1{c}_2+c_3\right)x_3{y}_3,\hfill \\ \hfill z_3=& x_2{y}_2+x_1{y}_3+x_3{y}_1+c_1\left(x_2{y}_3+x_3{y}_2\right)+\left({\left(c_1\right)}^2+c_2\right)x_3{y}_3.\hfill \end{array}$$

(4)

In matrix notation, these formulas can equivalently be written as

$$\left(\begin{array}{c}{z}_1\\ z_2\\ z_3\end{array}\right)=\left(\begin{array}{ccc}{x}_1& c_3{x}_3& c_1{c}_3{x}_3+c_3{x}_2\\ x_2& x_1+c_2{x}_3& c_2{x}_2+c_3{x}_3+c_1{c}_2{x}_3\\ x_3& x_2+c_1{x}_3& x_1+{\left(c_1\right)}^2{x}_3+c_1{x}_2+c_2{x}_3\end{array}\right)\left(\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right),$$

and as a simple computation shows, the determinant of the linear system above is equal to $Q\left(\mathbf{x}\right)$, where Q is defined by the formula (2). Hence, $\mathbf{x}\oplus \mathbf{y}=(0,0,0)$, for some $\mathbf{y}$ in $V\backslash \left\{\right(0,0,0\left)\right\}$, if and only if $Q\left(\mathbf{x}\right)=0$.

The commutativity of ⊕ is a direct consequence of the invariance of the formula (4) under the substitutions $x_i\mapsto y_i$, $y_i\mapsto x_i$, $1\le i\le 3$.

Moreover, formula (3) can also be written as follows:

$${\left(\mathbf{x}\oplus \mathbf{y}\right)}_{1}I+{\left(\mathbf{x}\oplus \mathbf{y}\right)}_{2}A+{\left(\mathbf{x}\oplus \mathbf{y}\right)}_3{A}^2=\left(x_{1}I+x_{2}A+x_3{A}^2\right)\left(y_{1}I+y_{2}A+y_3{A}^2\right).$$

From the associativity of the composition law of endomorphisms, we deduce

$$\begin{array}{c}{\left(\mathbf{x}\oplus (\mathbf{y}\oplus \mathbf{z})\right)}_{1}I+{\left(\mathbf{x}\oplus (\mathbf{y}\oplus \mathbf{z})\right)}_{2}A+{\left(\mathbf{x}\oplus (\mathbf{y}\oplus \mathbf{z})\right)}_3{A}^2\hfill \\ =\left(x_{1}I+x_{2}A+x_3{A}^2\right)·\left(\left(y_{1}I+y_{2}A+y_3{A}^2\right)·\left(z_{1}I+z_{2}A+z_3{A}^2\right)\right)\hfill \\ =\left(\left(x_{1}I+x_{2}A+x_3{A}^2\right)·\left(y_{1}I+y_{2}A+y_3{A}^2\right)\right)·\left(z_{1}I+z_{2}A+z_3{A}^2\right)\hfill \\ ={\left((\mathbf{x}\oplus \mathbf{y})\oplus \mathbf{z}\right)}_{1}I+{\left((\mathbf{x}\oplus \mathbf{y})\oplus \mathbf{z}\right)}_{2}A+{\left((\mathbf{x}\oplus \mathbf{y})\oplus \mathbf{z}\right)}_3{A}^2.\hfill \end{array}$$

Hence, $\mathbf{x}\oplus (\mathbf{y}\oplus \mathbf{z})=(\mathbf{x}\oplus \mathbf{y})\oplus \mathbf{z}$, $\forall \mathbf{x},\mathbf{y},\mathbf{z}\in V$.

From Equation (4), it follows that the unit element is the point $(1,0,0)$, which does not belong to $Q^{-1}\left(0\right)$ since $Q(1,0,0)=1$.

By taking determinants in Equation (3), we obtain

$$\begin{array}{ccc}Q(\mathbf{x}\oplus \mathbf{y})=\hfill & Q\left(\mathbf{x}\right)Q\left(\mathbf{y}\right),\hfill & \forall \mathbf{x},\mathbf{y}\in V.\hfill \end{array}$$

Therefore, the opposite element $\mathbf{y}$ of $\mathbf{x}$ exists and it is given by the following formulas:

$$\begin{array}{cc}\hfill y_1=& \frac{1}{Q\left(\mathbf{x}\right)}\left(c_1{x}_1{x}_2+\left[{\left(c_1\right)}^2+2c_2\right]x_1{x}_3-\left(c_3+c_1{c}_2\right)x_2{x}_3+{\left(x_1\right)}^2-c_2{\left(x_2\right)}^2+\left[{\left(c_2\right)}^2-c_1{c}_3\right]{\left(x_3\right)}^2\right),\hfill \\ \hfill y_2=& \frac{-1}{Q\left(\mathbf{x}\right)}\left(x_1{x}_2+{\left(c_1\right)}^2{x}_2{x}_3+c_1{\left(x_2\right)}^2-\left(c_1{c}_2+c_3\right){\left(x_3\right)}^2\right),\hfill \\ \hfill y_3=& \frac{1}{Q\left(\mathbf{x}\right)}\left(-x_1{x}_3+c_1{x}_2{x}_3+{\left(x_2\right)}^2-c_2{\left(x_3\right)}^2\right).\hfill \end{array}$$

Finally, if $\mathbf{x}$, $\mathbf{y}$ are replaced by $\lambda \mathbf{x}$, $\mu \mathbf{y}$, respectively, with $\lambda ,\mu \in {\mathbb{F}}^{\ast }$, then $\mathbf{z}$ transforms into $\lambda \mu \mathbf{z}$, thus proving that the group law projects onto $\mathbb{F}{P}^2\backslash C$. □

Remark 1.

Note that the Equations (4), allowing one to compute the ⊕ group operation in terms of the coefficients in the ground field, are applicable to any element of the group, with no exception at all.

Remark 2.

If ${\mathbf{v}}_1=(1,0,0)$, ${\mathbf{v}}_2=(0,1,0)$, ${\mathbf{v}}_3=(0,0,1)$, then, from Equation (2), we obtain $Q\left({\mathbf{v}}_2\right)=c_3$, $Q\left({\mathbf{v}}_3\right)={\left(c_3\right)}^2$. Hence, ${\mathbf{v}}_2$ and ${\mathbf{v}}_3$ belong to ${\mathbb{F}}^3\backslash Q^{-1}\left(0\right)$ if and only if $c_3\ne 0$, i.e., when A is invertible.

2.1. The Basic Cubic

Proposition 1.

Let $\chi \left(X\right)=X^3-c_1{X}^2-c_{2}X-c_3\in \mathbb{F}\left[X\right]$ be the polynomial introduced in Lemma 1 and let $\alpha =Xmod\chi$. If $N:\mathbb{F}\left[\alpha \right]\to \mathbb{F}$ is the norm of the extension $\mathbb{F}\left[\alpha \right]$ of $\mathbb{F}$, then a point $\beta ={\beta }_0+{\beta }_1\alpha +{\beta }_2{\alpha }^2$ belongs to the cubic curve C defined in Theorem 1 if and only if $N\left(\beta \right)=0$. In particular, if χ is irreducible in $\mathbb{F}\left[X\right]$, then C has no point in $\mathbb{F}{P}^2$.

Proof. 

Every $\beta \in \mathbb{F}\left[\alpha \right]$ induces an $\mathbb{F}$-linear endomorphism $E_{\beta }:\mathbb{F}\left[\alpha \right]\to \mathbb{F}\left[\alpha \right]$ given by $E_{\beta }\left(\xi \right)=\beta ·\xi$, $\forall \xi \in \mathbb{F}\left[\alpha \right]$, and, from the very definition of the norm, we have $N\left(\beta \right)=det{E}_{\beta }$. As a computation shows, we obtain $N\left(\beta \right)=Q({\beta }_0,{\beta }_1,{\beta }_2)$, thus proving the first part of the statement.

Moreover, $\chi$ is irreducible if and only if $\mathbb{F}\left[\alpha \right]$ is a field, and then the only element with norm 0 is in fact $\mathbf{0}\in \mathbb{F}\left[\alpha \right]$. To see this, assume on the contrary that $N\left(\mathbf{x}\right)=0$, with $\mathbf{x}\ne \mathbf{0}$ and $\mathbf{x}\in \mathbb{F}\left[\alpha \right]$. Since the norm is a group homomorphism, we can write

$$1=N\left(\mathbf{1}\right)=N(\mathbf{x}·{\mathbf{x}}^{-1})=N\left(\mathbf{x}\right)·N\left({\mathbf{x}}^{-1}\right)=0·N\left({\mathbf{x}}^{-1}\right)=0,$$

which is a contradiction. Consequently, the curve C has no point in $\mathbb{F}{P}^2$. □

Corollary 1.

The polynomial χ is irreducible in $\mathbb{F}\left[X\right]$ if and only if the cubic C is irreducible.

Proof. 

Actually, if $\chi$ factors in $\mathbb{F}\left[X\right]$, say $X^3-c_1{X}^2-c_{2}X-c_3=(X-h)(X^2+kX+l)$, with $h,k,l\in \mathbb{F}$, then we have

$$Q\left(\mathbf{x}\right)=[{\left(x_1\right)}^2+(k^2-2l)x_1{x}_3+l{\left(x_2\right)}^2-kl{x}_2{x}_3+l^2{\left(x_3\right)}^2-k{x}_1{x}_2][x_1+h{x}_2+h^2{x}_3].$$

Conversely, if $\chi$ is irreducible in $\mathbb{F}\left[X\right]$, then, according to the second part of Proposition 1, the only solution to the cubic equation $Q\left(\mathbf{x}\right)=0$ is $\mathbf{x}=\mathbf{0}$. Hence, Q must be irreducible, as a reducible cubic admits non-trivial solutions in the ground field. □

Corollary 2.

If the characteristic polynomial χ of A is irreducible in $\mathbb{F}\left[X\right]$, then there is no linear transformation ${\left({\lambda }_{ij}\right)}_{i,j=1}^3\in GL(\mathbb{F},3)$ reducing the polynomial Q defined in (2) to Weierstrass form.

Proof. 

Replacing $x_j$ by $X_j={\sum }_{i=1}^3{\lambda }_{ij}{x}_i$, $1\le j\le 3$, in (2), we obtain a cubic $\overline{Q}$, which is in Weierstrass form (see [34] [§2.1]) if and only if the coefficients a, b, and c of the terms ${\left(x_3\right)}^3$, ${\left(x_1\right)}^2{x}_2$, and $x_1{\left(x_2\right)}^2$, respectively, vanish. As a computation shows, we have $a=\overline{Q}({\lambda }_{31},{\lambda }_{32},{\lambda }_{33})$, and we can conclude by applying Proposition 1. □

2.2. Cyclicity

Theorem 2.

If ${\mathbb{F}}_q$ is a finite field of characteristic different from 2 or 3 and the polynomial $\chi \left(X\right)=X^3-c_1{X}^2-c_{2}X-c_3$ introduced in Lemma 1 is irreducible in ${\mathbb{F}}_q\left[X\right]$, then the group $\mathbb{G}=({\mathbb{F}}_q{P}^2,\oplus )$ is cyclic.

Proof. 

Since $char{\mathbb{F}}_q\ne 2,3$, the polynomial $\chi$ is separable and in its splitting field ${\mathbb{F}}_q^{\prime }$ we have $\chi \left(X\right)=(X-{\alpha }_1)(X-{\alpha }_2)(X-{\alpha }_3)$, the roots ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$ being pairwise distinct, and in a certain basis of ${\mathbb{F}}_q^{\prime }{\otimes }_{{\mathbb{F}}_q}V$ the matrix of A is given by the formula (1). As the Galois group $G({\mathbb{F}}_q^{\prime }/{\mathbb{F}}_q)$ acts transitively on the roots of $\chi$, there exist two automorphisms such that ${\sigma }_2\left({\alpha }_1\right)={\alpha }_2$ and ${\sigma }_3\left({\alpha }_1\right)={\alpha }_3$. If $\beta ={\beta }_1+{\beta }_2{\alpha }_1+{\beta }_3{\left({\alpha }_1\right)}^2$, ${\beta }_i\in {\mathbb{F}}_q$, $1\le i\le 3$, is an element in ${\mathbb{F}}_q\left[{\alpha }_1\right]\cong {\mathbb{F}}_{q^3}$, then, for every positive integer n, we have

$${\left({\beta }_{1}I+{\beta }_{2}A+{\beta }_3{A}^2\right)}^n=\left(\begin{array}{ccc}{\beta }^n& 0& 0\\ 0& {\sigma }_2\left({\beta }^n\right)& 0\\ 0& 0& {\sigma }_3\left({\beta }^n\right)\end{array}\right).$$

Consequently, if $\beta$ is a generator of the multiplicative group ${\left({\mathbb{F}}_{q^3}\right)}^{\ast }$, then the vector $({\beta }_1,{\beta }_2,{\beta }_3)$ generates the group $({\left({\mathbb{F}}_q\right)}^3\backslash \left\{(0,0,0)\right\},\oplus )$ and its corresponding projective point $[{\beta }_1,{\beta }_2,{\beta }_3]=({\beta }_1,{\beta }_2,{\beta }_3)mod{\mathbb{F}}_q^{\ast }$ generates the group $\mathbb{G}$, with ${\mathbb{F}}_q{P}^2=\left({\left({\mathbb{F}}_q\right)}^3\backslash \left\{(0,0,0)\right\}\right)/{\mathbb{F}}_q^{\ast }$. □

Remark 3.

It is important to keep in mind that the implication in Theorem 2 works only in the way in which it is worded. If one selects a generator of the group $\mathbb{G}$, it will in general be a generator of only a subgroup of the whole ${\left({\mathbb{F}}_{q^3}\right)}^{\ast }$ group. Consequently, when choosing a generator for $\mathbb{G}$, it is convenient to pick it from the set of generators in ${\left({\mathbb{F}}_{q^3}\right)}^{\ast }$ and, after that, project it onto ${\mathbb{F}}_q{P}^2$.

Remark 4.

As the order of the group $\mathbb{G}=({\mathbb{F}}_q{P}^2,\oplus )$ is $q^2+q+1$, the statement of Theorem 2 means that there exists an element $\beta \in \mathbb{G}$ of order $q^2+q+1$. According to the proof of Theorem 2, this is equivalent to saying that the matrix A in (1) is of order $q^2+q+1$ in the linear group $GL({\mathbb{F}}_q,3)$. A classical result (see [35] [Theorem, p. 379]) states that such a collineation always exists, but we need a direct proof of this fact to be able to apply it below in Section 3.1; see also [36] [Proposition 2.1].

Remark 5.

When the polynomial χ is reducible, experimental tests carried out in the prime field ${\mathbb{F}}_p$ show that the projective cubic curve C defined as $Q\left(\mathbf{x}\right)=0$ has a number of points from the set $\{p+2,2p+1,3p,p+1\}$ only.

Since the projective space ${\mathbb{F}}_p{P}^2$ has a total of $p^2+p+1$ points, the group $({\mathbb{F}}_p{P}^2\backslash C,\oplus )$ is left, respectively, with $\{p^2-1,p^2-p,{(p-1)}^2,p^2\}$ points.

If the number of points of C is either $p+2$ or $2p+1$, then the group $({\mathbb{F}}_p{P}^2\backslash C,\oplus )$ is still cyclic, and has the expected number of generators, namely, either $\phi (p^2-1)$ or $\phi (p^2-p)$, respectively, where φ is Euler’s totient function.

However, none of the other two possibilities give rise to a cyclic group. Rather, for the case where C has $3p$ points, there appears a number of cyclic groups, whose cardinalities are the divisors of $p-1$; it is important to remark that the total number of points left for the group is precisely ${(p-1)}^2$. Thus, the group $({\mathbb{F}}_p{P}^2\backslash C,\oplus )$ can be decomposed as a direct sum of a number of cyclic groups such that the product of their cardinalities is ${(p-1)}^2$.

As for the case when C has $p+1$ points, the group $({\mathbb{F}}_p{P}^2\backslash C,\oplus )$ is not cyclic either and can be decomposed as a direct sum of 2 cyclic groups with p points each. Remark that now the total number of points left for the group is $p^2$, so again the numbers of points of the cyclic groups of this case match the divisors of p.

Remark 6.

Hasse’s theorem states [37] [Theorem 4.1] that the number of points in an elliptic curve $E\left({\mathbb{F}}_q\right)$ verifies that $|\#E\left({\mathbb{F}}_q\right)-(q+1)|\le 2\sqrt{q}$, i.e., $\#E\left({\mathbb{F}}_q\right)=O\left(q\right)$. However, the projective space in our proposal has $O\left(q^2\right)$ points, thus rendering brute-force and known-message attacks much more difficult.

3. A Cryptographic Protocol

We have presented the group $\mathbb{G}=({\mathbb{F}}_q{P}^2,\oplus )$ and the conditions under which it is cyclic. In this section, we will show how this group can be profited as a basic building block for cryptographic applications, and we will assess its cryptographic security level.

We resort to current state-of-the-art algorithms deployed to attack the discrete logarithm problem. Among them, index-calculus algorithm stands out since it displays a subexponential expected running time.

Equipped with these tools, we will show how this group permits us to set up a basic, à la Diffie-Hellman, key-exchange protocol, and what cryptographic security is to be expected from it. Actually, we will present the range in which the protocol setup parameters should lie in order to achieve a certain security level.

We also provide an experimental setup that we have carried out in order to obtain computation times for the new group operation on a real setting, along with a comparison with computation times required to sum points on elliptic curves.

First of all, we establish the computational security of the mathematical problem defined over the cyclic group considered. Later on, as an example of cryptographic protocol, we present a Diffie-Hellman-like key agreement protocol.

3.1. Equivalence of DLP in $\mathbb{G}$ and ${\left({\mathbb{F}}_{q^3}\right)}^{\ast }$

Proposition 2.

Let ${\mathbb{F}}_q$ be a finite field of characteristic $\ne 2$ or 3. Assume the polynomial $\chi \left(X\right)=X^3-c_1{X}^2-c_{2}X-c_3$ in Lemma 1 is irreducible in ${\mathbb{F}}_q\left[X\right]$, and let $\alpha \in {\mathbb{F}}_{q^3}$ be a root of χ.

If $({\gamma }_1,{\gamma }_2,{\gamma }_3)$ is a generator of the group $({\left({\mathbb{F}}_q\right)}^3\backslash \left\{(0,0,0)\right\},\oplus )$ and $({\beta }_1,{\beta }_2,{\beta }_3)$ belongs to this group, then $n\in \mathbb{N}$ is a solution to the equation

$$\left({\beta }_1,{\beta }_2,{\beta }_3\right)=\left({\gamma }_1,{\gamma }_2,{\gamma }_3\right)\oplus \stackrel{\left(n\right)}{\dots }\oplus \left({\gamma }_1,{\gamma }_2,{\gamma }_3\right),$$

if and only if n is a solution to the equation $\beta ={\gamma }^n$ in the multiplicative group ${\left({\mathbb{F}}_{q^3}\right)}^{\ast }$, where $\beta ={\beta }_1+{\beta }_2\alpha +{\beta }_3{\alpha }^2$, and $\gamma ={\gamma }_1+{\gamma }_2\alpha +{\gamma }_3{\alpha }^2$.

Therefore, the DLP in the group $({\left({\mathbb{F}}_q\right)}^3\backslash \left\{(0,0,0)\right\},\oplus )$ is equivalent to the DLP in ${\left({\mathbb{F}}_{q^3}\right)}^{\ast }$.

Proof. 

Letting $\alpha ={\alpha }_1$, the statement follows from the matrix formula in the proof of Theorem 2 taking the very definition of the group law ⊕ by formula (3) into account. □

In the present case, Proposition 2 states the “equivalence” because the reduction of problems (see, for example, [38] [p. 5], [39] [Ch. 8]) works both ways, namely, DLP in the group $({\left({\mathbb{F}}_q\right)}^3\backslash \left\{(0,0,0)\right\},\oplus )$ reduces to the DLP in ${\left({\mathbb{F}}_{q^3}\right)}^{\ast }$ and the other way around. Hence, Proposition 2 proves that the use of the group $\mathbb{G}=({\mathbb{F}}_q{P}^2,\oplus )$ is safe for standard implementations in PKC (e.g., see [34] [§1.6]), since the security it provides is equivalent to that of DLP in ${\left({\mathbb{F}}_{q^3}\right)}^{\ast }$, as long as the caveat stated in Remark 3 is taken into account.

In terms of cryptanalysis, logarithms in $\mathbb{G}$ can be computed using “generic” algorithms, i.e., those that assume no particular structure in (or extra knowledge of) the group. The most popular ones are Pohlig-Hellman (which reduces the computation in the whole group to the computation of the logarithm in all subgroups of prime order of $\mathbb{G}$), Shank’s Baby Step/Giant Step, and Pollard’s Rho algorithm. All of them need an exponential computation time.

However, there exists the so-called index-calculus algorithm, which is much faster as it is able to compute discrete logarithms in the multiplicative group of a finite field in subexponential time (see, e.g., [40]). Since the operations in the proposed group $\mathbb{G}=({\mathbb{F}}_q{P}^2,\oplus )$ can be efficiently transferred to those in ${\left({\mathbb{F}}_{q^3}\right)}^{\ast }$, it follows that index-calculus algorithm can be applied to the multiplicative group of the latter. This fact does not render the group operation automatically useless in the face of possible cryptographic applications, as long as proper key lengths are utilized.

For general finite fields, such as the proposed one, with a multiplicative group of size N, current state-of-the-art algorithms (including index-calculus) report computation times of

$$L_N(\alpha ,c)=exp\left((c+o\left(1\right)){(logN)}^{\alpha }{(loglogN)}^{1-\alpha }\right),$$

(5)

where $\alpha$ and c are parameters in the ranges $0<\alpha <1$ and $c>0$ (sometimes c is omitted and we default to $L_N\left(\alpha \right)$). Actually, $\alpha$ drives the transition from an exponential-time algorithm (when $\alpha$ approaches 1) to a pure polynomial-time algorithm (as $\alpha$ tends to 0).

The first subexponential algorithms had complexity $L_N(1/2)$ and applied only to prime fields. Soon $L_N(1/3)$ was achieved for any finite field, with values for c ranging from ${(64/3)}^{1/3}$ for fields with high characteristic to ${(128/9)}^{1/3}$ for medium characteristic. When dealing with small characteristic fields, recent research brought down the complexity to $L_N(1/4)$ [41] and even to quasi-polynomial time [42,43]. If the group size is $N=p^n$, and we write $p=L_{p^n}\left(l_p\right)$, then the characteristic is considered “small”, “medium-sized” or “large” depending on whether $l_p\le 1/3$, $1/3<l_p<2/3$, or $l_p\ge 2/3$, respectively.

In any case, the previous results have been applied in practice and several cryptanalysis have been successfully carried out (see [44,45]), so it seems sensible to avoid using small characteristics and also extensions of moderate characteristic included in the range threatened by recent cryptanalytic techniques [42,43,46]. However, these algorithms are heuristic and are proved to work only for certain particular cases, not difficult to circumvent: for example, if one has $N=p^n$, it suffices to choose both p and n to be prime in order to thwart both [42,43]. For a detailed account of history and current status, see [47] (in particular §4.2), and [48].

Our proposal is to use a group $\mathbb{G}$ of prime order $n=q^2+q+1$, over a ground field ${\mathbb{F}}_q$. Using formula (5), we can compute how many elements in $\mathbb{G}$ provide a given security level. Since the number of elements is roughly the square of the value of q, it follows that q can be represented with only one half of the bits needed for n. This has a direct impact on the computation time of the ⊕ operation in $\mathbb{G}$, since it is performed in ${\mathbb{F}}_q$ (see Equation (4) and cost analysis in Section 3.4).

3.2. System Setup and System Parameters for a Key Agreement Protocol

The group $\mathbb{G}=({\mathbb{F}}_q{P}^2,\oplus )$ lends readily itself as a building block for standard cryptographic applications to be constructed upon it. One of such applications is a Diffie-Hellman-like key agreement protocol, which will be described in the following sections.

In the sequel, we provide the necessary steps to set up the system. Moreover, the users also need to fix some system parameters.

System Setup

To set up the system, the following steps are in order:

• Choose a ground field ${\mathbb{F}}_q$ with characteristic different from 2 or 3, such that $\ell =q^2+q+1$ is prime.
• Select elements $c_1,c_2,c_3\in {\mathbb{F}}_q$ such that the polynomial

  $$\chi \left(X\right)=X^3-c_1{X}^2-c_{2}X-c_3$$

  is irreducible in ${\mathbb{F}}_q\left[X\right]$.
• Consider ${\mathbb{F}}_{q^3}\simeq {\mathbb{F}}_q\left[X\right]/\left(\chi \left(X\right)\right)$. Select $\alpha \in {\left({\mathbb{F}}_{q^3}\right)}^{\ast }$ such that it is a generator of ${\left({\mathbb{F}}_{q^3}\right)}^{\ast }$.
• Compute the coordinates of $\alpha$ seen as a vector over ${\mathbb{F}}_q$, which will be denoted as $({\alpha }_1,{\alpha }_2,{\alpha }_3)\in {\left({\mathbb{F}}_q\right)}^3\backslash \left\{(0,0,0)\right\}$.
• Consider a projection $\pi :{\left({\mathbb{F}}_q\right)}^3\backslash \left\{(0,0,0)\right\}\to {\mathbb{F}}_q{P}^2$, such that $[{\beta }_1,{\beta }_2,{\beta }_3]=\pi ({\alpha }_1,{\alpha }_2,{\alpha }_3)$, and $Q({\beta }_1,{\beta }_2,{\beta }_3)=1$.
  Observe that $N\left(\alpha \right)=Q({\alpha }_1,{\alpha }_2,{\alpha }_3)$ (see proof of Proposition 1). If we compute $a=N{\left(\alpha \right)}^{-e}$, where $e=3^{-1}(modq-1)$, we have that $N\left(a\alpha \right)=1$. Therefore, the projection $\pi$ consists simply in computing ${\beta }_i=a{\alpha }_i$, for $1\le i\le 3$.
  Defining the projection $\pi$ in this way is convenient, since it automatically gives rise to a generator in ${\mathbb{F}}_q{P}^2$ with a unitary norm, which means that all the elements generated by it will enjoy also a unitary norm.
  Remark en passant that the previous device works only if 3 is invertible in ${\mathbb{Z}}_{q-1}$. Fortunately, this is always the case since otherwise the following implications hold: $3|(q-1)\Rightarrow q\equiv 1(mod3)\Rightarrow \ell =q^2+q+1\equiv 0(mod3)$ and the latter equation would contradict the fact that we chose ℓ as a prime.

Remark 7.

In order to save space, we can always find an irreducible χ such that $c_1=0$. Obviously, $c_3$ cannot be 0, but we may wonder whether we could in addition take $c_2=0$. However, this is not possible according to [49] (Lemma 7). The latter reference studies the number of irreducible binomials $X^t-a\in {\mathbb{F}}_q\left[X\right]$, with $a\in {\mathbb{F}}_q^{\ast }$, and concludes that the number of such irreducible binomials $N_t\left(q\right)$ is

$$N_t\left(q\right)=\left\{\begin{array}{cc}\frac{\phi \left(t\right)}{t}(q-1),\hfill & if{\mathrm{rad}}_4\left(t\right)|(q-1),\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

The largest square-free number that divides $t\ne 0$ is denoted by $\mathrm{rad}\left(t\right)$ and

$${\mathrm{rad}}_4\left(t\right)=\left\{\begin{array}{cc}\mathrm{rad}\left(t\right)\hfill & if4|/t\hfill \\ 2\mathrm{rad}\left(t\right)\hfill & otherwise.\hfill \end{array}\right.$$

For our case, $t=3$, hence ${\mathrm{rad}}_4\left(t\right)=3$. However, then $N_t\left(q\right)=0$, since we chose $\ell =q^2+q+1$ to be a prime, thus implying $3|/(q-1)$.

Accordingly, we conclude that $c_1$ and $c_2$ cannot be simultaneously taken as 0.

System Parameters

The system parameters are defined by the set $\mathcal{S}=\{{\mathbb{F}}_q,[{\beta }_1,{\beta }_2,{\beta }_3],c_1,c_2,c_3\}$, following the notation and conditions explained above.

3.3. The Key Agreement Protocol

The key agreement follows the well-known Diffie-Hellman paradigm. Any two users $A,B$, willing to agree on a common value, which remains secret, set up a system and agree on its parameters, as stated previously.

The protocol runs as follows:

• User A selects $n_A\in {\mathbb{Z}}_{\ell }$ uniformly at random, with $\ell =q^2+q+1$, computes

  $$[{\gamma }_1^A,{\gamma }_2^A,{\gamma }_3^A]={\oplus }^{n_A}[{\beta }_1,{\beta }_2,{\beta }_3]\in {\mathbb{F}}_q{P}^2$$

  and sends it to user B.
• User B selects $n_B\in {\mathbb{Z}}_{\ell }$ uniformly at random, computes

  $$[{\gamma }_1^B,{\gamma }_2^B,{\gamma }_3^B]={\oplus }^{n_B}[{\beta }_1,{\beta }_2,{\beta }_3]\in {\mathbb{F}}_q{P}^2$$

  and sends it to user A.
• User A computes $k_A={\oplus }^{n_A}[{\gamma }_1^B,{\gamma }_2^B,{\gamma }_3^B]$.
• User B computes $k_B={\oplus }^{n_B}[{\gamma }_1^A,{\gamma }_2^A,{\gamma }_3^A]$.

According to the definitions, the following equalities clearly hold:

$$\begin{array}{ccc}\hfill k_A={\oplus }^{n_A}[{\gamma }_1^B,{\gamma }_2^B,{\gamma }_3^B]& =& {\oplus }^{n_A}\left({\oplus }^{n_B}[{\beta }_1,{\beta }_2,{\beta }_3]\right)\hfill \\ & =& {\oplus }^{n_B}\left({\oplus }^{n_A}[{\beta }_1,{\beta }_2,{\beta }_3]\right)\hfill \\ & =& {\oplus }^{n_B}[{\gamma }_1^A,{\gamma }_2^A,{\gamma }_3^A]=k_B.\hfill \end{array}$$

Hence, the properties of the operation ⊕ in $\mathbb{G}$ ensure that actually $k_A=k_B$, which is the common value expected as the output of the protocol.

3.4. Cost of the ⊕ Operation in $\mathbb{G}$

Let S and P be the number of field operations in order to perform an addition and a multiplication respectively in ${\mathbb{F}}_q$. From the formula (4), it follows that the total number of operations for computing $\mathbf{x}\oplus \mathbf{y}$ is equal to $10S+15P$, once the $2S+3P$ precomputations of $c_1{c}_3$, $c_1{c}_2+c_3$, and ${\left(c_1\right)}^2+c_2$ are assumed.

3.5. A Toy Example

We provide hereafter an example of computing a discrete logarithm by brute-force search. In general, this algorithm is, of course, infeasible, but we choose very small parameters in order to illustrate the operation of the group $\mathbb{G}$.

Let us take the prime field ${\mathbb{F}}_p$, with $p=131$, for which $p^2+p+1=\mathrm{17,293}$ is also a prime. Accordingly, the group $\mathbb{G}$ is cyclic. We set the parameters $c_1=13$, $c_2=18$, $c_3=73$, since the polynomial $\chi \left(X\right)=X^3-13X^2-18X-73$ is irreducible in ${\mathbb{F}}_{131}$.

We select the element $\mathbf{x}=(126,16,1)$ as a generator in ${\left({\mathbb{F}}_q^3\right)}^{\ast }$. As explained above, it is convenient to project it onto a unitary norm point of ${\mathbb{F}}_q{P}^2$. To achieve this goal, we perform the following steps:

$$\begin{array}{ccc}\hfill N\left(\mathbf{x}\right)& =& Q(126,16,1)=90,\hfill \\ \hfill e& =& 3^{-1}(mod130)=87,\hfill \\ \hfill a& =& 1/N{\left(\mathbf{x}\right)}^e=23,\hfill \\ \hfill X& =& \pi \left(\mathbf{x}\right)=a·(126,16,1)=[16,106,23].\hfill \end{array}$$

Observe that indeed $Q(16,106,23)=1$. We choose a target point $\mathbf{y}=(86,120,1)$ and performing a similar computation we get $Y=[15,91,87]$. The problem is to find the discrete logarithm of Y to the base X, i.e., find the integer n such that $Y={\oplus }^{n}X$. Iterating the operation, we carry out an exhaustive search:

$$\begin{array}{l}[16,106,23]\to [44,78,53]\to [65,41,125]\to [40,50,43]\to \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}[35,67,125]\to [115,59,58]\to [11,95,6]\to [8,69,62]\to \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}[122,109,9]\to [15,91,87].\end{array}$$

Eventually, we come up with the target point. Since the operation has been iterated ten times, we conclude $Y={\oplus }^{10}X$ for this particular pair, so that ${log}_{X}Y=10$. Remark that, to perform each step, it suffices to follow the formula (4).

3.6. Experimental Results

We have conducted several experiments in order to assess the computation time of the ⊕ operation in $\mathbb{G}$. The basic setup consists of selecting prime fields, ${\mathbb{F}}_p$, over which the ⊕ operation will be tested. Observe that, according to formula (4), performing the operation boils down to a number of additions and multiplications over the base field; hence, the expected computation time will depend on the size of its elements; informally, size (also known as bit length) means the number of bits in the binary representation of such elements. The selected prime fields, ${\mathbb{F}}_p$, will have increasing values for the size of p, i.e., increasing bit lengths in the representation of their elements.

Taking the previous considerations into account the experiment is conducted as follows: we take increasing values of p and, for each value, we perform all the required computations to add two random points in $\mathbb{G}$, following formula (4). We repeat the experiment a large number of times for distinct points and record the mean computation time for each value of p.

In order to compare computation times, we repeated the same experiment for the point addition in elliptic curves over ${\mathbb{F}}_p$, using the same range of bit lengths. As before, the idea is selecting random points and adding them using, in particular, projective coordinates according to the formulas given in [50] [§13.2.1.b]. Repeating the computation a large number of times, we record the mean computation time for each value of p. Choosing the point addition operation in elliptic curves as the term of comparison with the ⊕ operation seems sensible since both operations share a relatively large number of basic operations (namely, additions, multiplications, and inversions) in the ground field.

We implemented the experiments using Java SE Runtime Environment version 1.8.0_171-b11 and the execution was carried out on an Intel Core i7-4790 platform (Santa Clara, CA, USA) running at $3.60$ GHz. We performed the experiment in the range 32–512 bits in steps of 32 bits.

The experiments yielded the results shown in Table 1. In each line, the first column represents the number of bits of the binary representation of the elements in ${\mathbb{F}}_p$, the ground field. The second and third columns represent the mean computation time needed to perform the addition of two points in the group $\mathbb{G}$ via the operation ⊕, and in an elliptic curve over ${\mathbb{F}}_p$, respectively. All the computation times are measured in microseconds.

Table 1. Computation time for one single operation in each setting.

Bit Length	⊕ Operation in $\mathbb{G}$ ($\mathsf{\mu }$s)	Point Addition in Elliptic Curves ($\mathsf{\mu }$s)
32	$1.10306044$	$1.07039673$
64	$1.68166612$	$1.97707724$
96	$1.97807208$	$2.55200463$
128	$2.19050201$	$2.86859037$
160	$2.52811554$	$3.35108746$
192	$2.77264771$	$3.72361810$
224	$3.15689638$	$4.29066712$
256	$3.36514379$	$4.65996446$
288	$3.77635547$	$5.34568703$
320	$4.11391404$	$5.84153419$
352	$4.60391914$	$6.43152050$
384	$4.86727126$	$6.97227992$
416	$5.41008866$	$7.75588654$
448	$5.77817335$	$8.32544612$
480	$6.31956718$	$9.02521134$
512	$6.70272949$	$9.61432718$

Having a visual idea of the results reported in Table 1 is best achieved by depicting them in a combined graph. To this end, we show in Figure 1 the graphical representation of the computation times for both operations, as reported in Table 1. Both graphs are conveniently labeled so that one of them depicts the computation time for the ⊕ operation in $\mathbb{G}$, and the other one depicts the computation time for the point addition in elliptic curves over ${\mathbb{F}}_p$. The x-axis represents the bit length of p common for both operations.

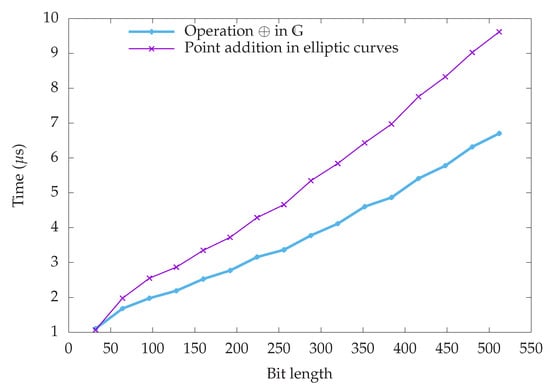
Figure 1. Comparison of average computation times for both settings.

The graph pushes to the foreground some interesting remarks:

• The computation times shown in Figure 1 for both settings show a essentially linear growth, which is convenient in view of practical applications.
• Though the point addition in elliptic curves is slightly slower than the ⊕ operation in $\mathbb{G}$ for the same bit length over the ground field, they keep a rather constant ratio between them, which is roughly equal to $0.7$.

3.7. Real World Parameters

In order to assess the size for real world parameters, we resort to the recommendations issued by NIST [51]. These recommendations are based on the knowledge of the execution time of the best algorithms solving any particular problem. We will reproduce here an excerpt of Table 2 in that reference, which summarizes the bit sizes for the relevant parameters applicable to our proposal.

Table 2. Comparable cryptographic strengths.

Security Strength	Group Order	Base Field Size
112	2048	1024
128	3072	1536
192	7680	3840
256	$\mathrm{15,360}$	7680

We explain hereafter the meaning of the columns. To begin with, Security strength represents the binary logarithm of the estimated time taken by the best known algorithm for solving the problem (which is proportional to the number of cryptographic operations), thus breaking the cryptosystem. The center column, labeled as Group order, is related to the group where the cryptosystem is defined; in our case, it is the projective space ${\mathbb{F}}_q{P}^2$ where ${\mathbb{F}}_q$ is the base field. In particular, each line in this column represents the binary logarithm of the number of elements in the projective space needed to achieve the security strength indicated in the leftmost column.

Since we propose that the number of points in the projective space is $n=q^2+q+1$, the base field size (namely, the binary logarithm of q) is half the size of n, as represented in the rightmost column. Remark that this is a nice feature, since the multiplication cost in the base field is intimately related to the size of the latter.

Finally, the public key consists of one projective point. Since we chose unitary norm for such point, it can be represented with just two elements of the base field. Therefore, public key size is twice as much as the base field size (it needs twice as many bits).

4. A More Robust System

The security of the cryptosystem proposed in the previous sections can be increased by extending the theory developed for a field to the case of a unitary commutative ring R.

Essentially, we will stick to the ring $\mathbb{Z}/m\mathbb{Z}$, where $m=pq$ is an integer, the product of two primes of similar size, p and q. We will strain ourselves in order to apply all the concepts developed in the previous sections to this new setting in an attempt to improve the security and efficiency of the proposed scheme.

We will manage to obtain the definition of a group law acting over the direct product of two projective spaces, ${\mathbb{F}}_p{P}^2\times {\mathbb{F}}_q{P}^2$. In this new setting, the security is reinforced since an attacker is forced to sequentially solve an instance of the integer factorization problem and an instance (actually two instances, but they can be parallelized) of the discrete logarithm problem.

In fact, let M be a free R-module of finite rank and let $A:M\to M$ be an R-linear map with characteristic polynomial ${\chi }_A\left(X\right)=det(XI-\mathsf{\Lambda })$, X being an indeterminate, I the identity matrix of order $r=rankM$, and $\mathsf{\Lambda }$ the matrix of A in an arbitrary basis for M. According to [52] [III, §8, 11.Proposition 20], the Cayley-Hamilton Theorem holds in this setting, namely ${\chi }_A\left(A\right)=0$.

Hence, if $M=R^3$ and ${\chi }_A\left(X\right)=X^3-c_1{X}^2-c_{2}X-c_3$, $c_1,c_2,c_3\in R$, then $A^3=c_1{A}^2+c_{2}A+c_{3}I$.

As above, we can define a degree-3 homogeneous polynomial in $R[x_1,x_2,x_3]$ by setting $Q(x_1,x_2,x_3)=det\left(x_{1}I+x_2\mathsf{\Lambda }+x_3{\mathsf{\Lambda }}^2\right)$. As a computation shows, we have

$$\begin{array}{cc}\hfill Q(x_1,x_2,x_3)& =-c_2{x}_1{\left(x_2\right)}^2+\left[{\left(c_2\right)}^2-2\left(c_1{c}_3\right)\right]x_1{\left(x_3\right)}^2+c_1{\left(x_1\right)}^2{x}_2\hfill \\ \hfill & +\left[{\left(c_1\right)}^2+2c_2\right]{\left(x_1\right)}^2{x}_3-\left(c_2{c}_3\right)x_2{\left(x_3\right)}^2+\left(c_1{c}_3\right){\left(x_2\right)}^2{x}_3\hfill \\ \hfill & -\left(c_1{c}_2+3c_3\right)x_1{x}_2{x}_3+{\left(x_1\right)}^3+c_3{\left(x_2\right)}^3+{\left(c_3\right)}^2{\left(x_3\right)}^3,\hfill \end{array}$$

thus proving that Lemma 1 still holds in this case; i.e., Q depends on ${\chi }_A$ only, but not on the matrix $\mathsf{\Lambda }$.

The projective plane over R is then defined as follows: $R{P}^2=(R^3\backslash \left\{\mathbf{0}\right\})/R^{\ast }$, where $R^{\ast }$ denotes the multiplicative group of invertible elements in R and $R^{\ast }$ acts on $R^3\backslash \left\{\mathbf{0}\right\}$ by

$$\begin{array}{cccc}\lambda ·(x_1,x_2,x_3)=\hfill & (\lambda x_1,\lambda x_2,\lambda x_3),\hfill & \forall \lambda \in R^{\ast },\hfill & \forall (x_1,x_2,x_3)\in R^3\backslash \left\{\mathbf{0}\right\}.\hfill \end{array}$$

Proceeding as in the previous sections, a composition law $\oplus :R^3\times R^3\to R^3$, $(\mathbf{x},\mathbf{y})\mapsto \mathbf{z}=\mathbf{x}\oplus \mathbf{y}$, $\mathbf{x}=(x_1,x_2,x_3)$, $\mathbf{y}=(y_1,y_2,y_3)$, $\mathbf{z}=(z_1,z_2,z_3)$, can be defined by the formula

$$\begin{array}{cc}\hfill z_{1}I+z_{2}A+z_3{A}^2=& \left(x_{1}I+x_{2}A+x_3{A}^2\right)\left(y_{1}I+y_{2}A+y_3{A}^2\right),\hfill \end{array}$$

and similarly we deduce

$$\left(\begin{array}{c}{z}_1\\ z_2\\ z_3\end{array}\right)=\left(\begin{array}{ccc}{x}_1& c_3{x}_3& c_1{c}_3{x}_3+c_3{x}_2\\ x_2& x_1+c_2{x}_3& c_2{x}_2+c_3{x}_3+c_1{c}_2{x}_3\\ x_3& x_2+c_1{x}_3& x_1+{\left(c_1\right)}^2{x}_3+c_1{x}_2+c_2{x}_3\end{array}\right)\left(\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right).$$

(6)

The determinant of the matrix of (6) is equal to $Q(x_1,x_2,x_3)$. Hence, ⊕ induces a composition law $\oplus :Q^{-1}\left(R^{\ast }\right)\times Q^{-1}\left(R^{\ast }\right)\to Q^{-1}\left(R^{\ast }\right)$. If C denotes the set of classes modulo $R^{\ast }$ of points $\mathbf{x}\in R^3$ such that $Q\left(\mathbf{x}\right)\in R\backslash R^{\ast }$, then ⊕ also induces a composition law $\oplus :P{Q}^{-1}\left(R^{\ast }\right)\times P{Q}^{-1}\left(R^{\ast }\right)\to P{Q}^{-1}\left(R^{\ast }\right)$, where $P{Q}^{-1}\left(R^{\ast }\right)=R{P}^2\backslash C$, as if $Q\left(\mathbf{x}\right)$ is invertible and $\lambda \in R^{\ast }$, then $Q\left(\lambda \mathbf{x}\right)={\lambda }^{3}Q\left(\mathbf{x}\right)$ is also invertible.

The same proof given in the case of a field shows that the composition law ⊕ is associative, commutative, and admits an identity element, which is the vector $(1,0,0)$.

If $m=pq$ with $p\ne q$ prime integers, then from Chinese Remainder Theorem there is a ring isomorphism between $\mathbb{Z}/m\mathbb{Z}$ and the product ring ${\mathbb{F}}_p\times {\mathbb{F}}_q$. Hence, each vector $\mathbf{x}\in R^3$ can be assigned a pair $({\mathbf{x}}^{\prime },{\mathbf{x}}^{″})$ in ${\left({\mathbb{F}}_p\right)}^3\times {\left({\mathbb{F}}_q\right)}^3$ and the group ${(\mathbb{Z}/m\mathbb{Z})}^{\ast }={\left({\mathbb{F}}_p\right)}^{\ast }\times {\left({\mathbb{F}}_q\right)}^{\ast }$ acts on $R^3$ in the same way as ${\left({\mathbb{F}}_p\right)}^{\ast }$ acts on ${\left({\mathbb{F}}_p\right)}^3$ and ${\left({\mathbb{F}}_q\right)}^{\ast }$ does on ${\left({\mathbb{F}}_q\right)}^3$.

Consequently, $\mathbf{x}\ne 0$ if and only if at least one of its two components ${\mathbf{x}}^{\prime },{\mathbf{x}}^{″}$ is distinct from $\mathbf{0}$, so that

$$\begin{array}{cc}\hfill R^3\backslash \left\{\mathbf{0}\right\}=& \left[\left\{\mathbf{0}\right\}\times \left({\left({\mathbb{F}}_q\right)}^3\backslash \left\{\mathbf{0}\right\}\right)\right]\bigsqcup \left[\left({\left({\mathbb{F}}_p\right)}^3\backslash \left\{\mathbf{0}\right\}\right)\times \left\{\mathbf{0}\right\}\right]\bigsqcup \hfill \\ \hfill & \multicolumn{1}{c}{\left[\left({\left({\mathbb{F}}_p\right)}^3\backslash \left\{\mathbf{0}\right\}\right)\times \left({\left({\mathbb{F}}_q\right)}^3\backslash \left\{\mathbf{0}\right\}\right)\right].}\end{array}$$

(7)

Therefore, $(\mathbb{Z}/pq\mathbb{Z})P^2={\mathbb{F}}_p{P}^2\bigsqcup {\mathbb{F}}_q{P}^2\bigsqcup \left({\mathbb{F}}_p{P}^2\times {\mathbb{F}}_q{P}^2\right)$.

Moreover, letting $\mathbf{z}=({\mathbf{z}}^{\prime },{\mathbf{z}}^{″})=\mathbf{x}\oplus \mathbf{y}$, as a computation shows, one obtains ${\mathbf{z}}^{\prime }={\mathbf{x}}^{\prime }\oplus {\mathbf{y}}^{\prime }$ and ${\mathbf{z}}^{″}={\mathbf{x}}^{″}\oplus {\mathbf{y}}^{″}$, and $Q\left(\mathbf{x}\right)$ is invertible if and only if $Q\left(\mathbf{x}\right)modp$ and $Q\left(\mathbf{x}\right)modq$ both are invertible in $\mathbb{Z}/p\mathbb{Z}$ and $\mathbb{Z}/q\mathbb{Z}$, respectively. If $\mathbf{x}\in R^3$ corresponds to $({\mathbf{x}}^{\prime },{\mathbf{x}}^{″})$ in ${\left({\mathbb{F}}_p\right)}^3\times {\left({\mathbb{F}}_q\right)}^3$, then $Q\left(\mathbf{x}\right)=(Q^{\prime }\left({\mathbf{x}}^{\prime }\right),Q^{″}\left({\mathbf{x}}^{″}\right))$, where $Q^{\prime }\left({\mathbf{x}}^{\prime }\right)=det\left(x_1^{\prime }I+x_2^{\prime }{\mathsf{\Lambda }}^{\prime }+x_3^{\prime }{{\mathsf{\Lambda }}^{\prime }}^2\right)$, $Q^{″}\left({\mathbf{x}}^{″}\right)=det\left(x_1^{″}I+x_2^{″}{\mathsf{\Lambda }}^{″}+x_3^{″}{{\mathsf{\Lambda }}^{″}}^2\right)$, and ${\mathsf{\Lambda }}^{\prime }=\mathsf{\Lambda }modp$, ${\mathsf{\Lambda }}^{″}=\mathsf{\Lambda }modq$. Hence,

$$Q^{-1}\left(R^{\ast }\right)=\left\{({\mathbf{x}}^{\prime },{\mathbf{x}}^{″})\in {\left({\mathbb{F}}_p\right)}^3\times {\left({\mathbb{F}}_q\right)}^3:Q^{\prime }\left({\mathbf{x}}^{\prime }\right)\ne 0,Q^{″}\left({\mathbf{x}}^{″}\right)\ne 0\right\}.$$

(8)

We set

$$\left.\begin{array}{cc}{\chi }^{\prime }\left(X\right)=X^3-c_1^{\prime }{X}^2-c_2^{\prime }X-c_3^{\prime }\in {\mathbb{F}}_p\left[X\right],\hfill & c_i^{\prime }=c_{i}modp\hfill \\ {\chi }^{″}\left(X\right)=X^3-c_1^{″}{X}^2-c_2^{″}X-c_3^{″}\in {\mathbb{F}}_q\left[X\right],\hfill & c_i^{″}=c_{i}modq\hfill \end{array}\right\}1\le i\le 3.$$

If both ${\chi }^{\prime }$ and ${\chi }^{″}$ are irreducible polynomials in ${\mathbb{F}}_p\left[X\right]$ and ${\mathbb{F}}_q\left[X\right]$, respectively, then, according to Proposition 1, the points of the associated curves $C^{\prime }$ and $C^{″}$ reduce to the origin; i.e., ${Q^{\prime }}^{-1}\left(0\right)=\left\{{\mathbf{0}}_p\right\}$, ${Q^{″}}^{-1}\left(0\right)=\left\{{\mathbf{0}}_q\right\}$, where ${\mathbf{0}}_p$ and ${\mathbf{0}}_q$ denote the origin in ${\left({\mathbb{F}}_p\right)}^3$ and ${\left({\mathbb{F}}_q\right)}^3$, respectively.

From (7), taking (8) into account, it follows: $P{Q}^{-1}\left(R^{\ast }\right)={\mathbb{F}}_p{P}^2\times {\mathbb{F}}_q{P}^2$. Consequently, we conclude that $P{Q}^{-1}\left(R^{\ast }\right)\cong S_p\times S_q$, where $S_p$ and $S_q$ are the subgroups given by

$$S_p=({\mathbb{F}}_p{P}^2\times \left\{(1,0,0)\right\},\oplus ),S_q=(\left\{(1,0,0)\right\}\times {\mathbb{F}}_q{P}^2,\oplus ),$$

and, from Theorem 2, we thus obtain

Proposition 3.

If the polynomials ${\chi }^{\prime }$ and ${\chi }^{″}$ are irreducible in ${\mathbb{F}}_p\left[X\right]$ and ${\mathbb{F}}_q\left[X\right]$, respectively, then the group $(P{Q}^{-1}\left(R^{\ast }\right)={\mathbb{F}}_p{P}^2\times {\mathbb{F}}_q{P}^2,\oplus )$ is isomorphic to the direct product of the cyclic groups $S_p$ and $S_q$. Hence, $(P{Q}^{-1}\left(R^{\ast }\right),\oplus )$ is cyclic if and only if $a=p^2+p+1$ and $b=q^2+q+1$ are coprimes; i.e., $gcd(a,b)=1$.

Remark 8.

If $d=gcd(a,b)$, then $a=d{a}^{\prime }$, $b=d{b}^{\prime }$, with $gcd(a^{\prime },b^{\prime })=1$. The cyclic subgroup S in $\mathbb{Z}/a\mathbb{Z}\times \mathbb{Z}/b\mathbb{Z}$ spanned by $(1moda,1modb)$ is of order $\frac{ab}{d}$. As $d<pq$ and $a=O\left(p^2\right)$, $b=O\left(q^2\right)$, it follows: $\frac{ab}{d}>\frac{O\left(p^2{q}^2\right)}{pq}=O\left(pq\right)$, which indicates that in general the group S is large enough, even if a and b are not coprimes.

Remark 9.

It is clear that the group $(P{Q}^{-1}\left(R^{\ast }\right),\oplus )$ is also amenable as a building block for a key-agreement protocol by choosing $R={\mathbb{Z}}_m$, with m composite. Observe that its security is enhanced with respect to its counterpart ${\mathbb{F}}_q$, q a prime power, since the algorithms known to be efficient to compute discrete logarithms only work in the multiplicative group of a field. This means that one is forced to factorize m in order to apply such algorithms to the present case, thus increasing the time complexity and the security of the system, though at the price of doubling the key length.

5. Conclusions

In this work, we have defined a group law, ⊕, over the set ${\mathbb{F}}_q{P}^2$, and considered the discrete logarithm problem associated with them. We have analyzed their properties and stated the security of the problem considered. Moreover, based on it, we have defined a cryptographic key agreement protocol as one possible application of this problem to public key cryptography. Finally, we shift the system to the group $(P{Q}^{-1}\left(R^{\ast }\right),\oplus )$ over the ring $\mathbb{Z}/pq\mathbb{Z}$, which turns out to be completely analogous to the previous one and offers an enhanced security, though at the cost of some extra key length.

As future work, we think that it is possible to extend this discrete logarithm problem in order to define new cryptographic protocols for encryption/decryption and digital signatures, among others, in a similar way as ElGamal or elliptic curve cryptosystems were defined from the Diffie-Hellman key agreement protocol.