Abstract
In the present paper we tested the use of Markov-switching Generalized AutoRegressive Conditional Heteroscedasticity (MS-GARCH) models and their not generalized (MS-ARCH) version. This, for active trading decisions in the coffee, cocoa, and sugar future markets. With weekly data from 7 January 2000 to 3 April 2020, we simulated the performance that a futures’ trader would have had, had she used the next trading algorithm: To invest in the security if the probability of being in a distress regime is less or equal to 50% or to invest in the U.S. three-month Treasury bill otherwise. Our results suggest that the use of t-student Markov Switching Component ARCH Model (MS-ARCH) models is appropriate for active trading in the cocoa futures and the Gaussian MS-GARCH is appropriate for sugar. For the specific case of the coffee market, we did not find evidence in favor of the use of MS-GARCH models. This is so by the fact that the trading algorithm led to inaccurate trading signs. Our results are of potential use for futures’ position traders or portfolio managers who want a quantitative trading algorithm for active trading in these commodity futures.
1. Introduction
The use of Markov-switching (MS) models [1,2,3] has spread to several applications such as the forecast of recessions [1,4,5] or distress periods in financial markets [6,7,8,9,10,11,12]. Their basic rationale is that the performance of a time series, such as the one of stock indexes or commodities, can be modelled with a stochastic process that has a number of regimes.
This rationale implies that the behavior of a given time series, , has structural breaks. It also means that it can be modelled with a probability density function (pdf) parameter set . In this set there are location (mean or ) and scale (standard deviation or ) parameters. This means, in terms of investment and trading decisions, that an analyst or investor can expect to have different levels of expected risk () or expected returns (). The values of these parameters will depend of the probability () of being in each regime at . With this in mind, MS models are useful to determine not only the level of expected risk () and return () but also the probability () of being in each regime or state of nature. A common assumption in the use of MS models is of a two-regime () stochastic process. An assumption that is held as true in the present paper. This means that it is expected that the analyst could be in a , calm or normal, regime or in a , crisis or distress, one at . Given this, she could decide whether to invest in a risky asset or not, given the probability of being in the distress regime at .
The use of MS models has spread to several applications. These have been used to characterize the two-regime performance of stock markets or socially responsible investment funds [6,13,14].
In a similar fashion, MS models have been used to characterize the time series of commodities [15,16].
From the potential uses of MS models, we are interested in their application in trading decisions as primarily suggested by Brooks and Persand [17] for U.K. stocks and bonds. This is an application later developed in other stock markets [18,19,20,21]. The rationale of this application is to determine the investment level in a security, given the probability () of being in each regime at .
For the specific case of the use of MS models for trading in agricultural soft commodity markets, little has been written. Only their use in energy futures [22] and in the corn or soy bean markets [23] has been tested. Given this, our interest was to fill the gap in the literature about active trading in the most traded soft agricultural commodities [24]: Coffee, cocoa, and sugar.
We also are interested in these three commodities by the fact that these are widely consumed around the world and are important ingredients in several end consumption products. Also, we were interested in the use of MS models with Generalized Autorregressive Conditionally Hetersokedastic standard deviation (MS-GARCH). This also for the proper commodity price hedging or future trading.
From the related benefits of soft commodity price hedging or trading with MS-GARCH models, we found the development of new environmental technologies. A good and related example of this is the impact of international oil prices. If the oil price is high, the profitability of renewable energies and cleaner oil extraction methods increases. In our specific case, the proper soft commodity price management (trading) could lead to non-dependent market decisions of several applications and sustainable projects. Examples of these are the circular consumption of soft commodities [25], the policy implementation of organic waste management in touristic places [26], or energy production with soft commodities’ waste [27]. This means that, even if our first scope is the application of MS-GARCH models in commodity price trading, there are several indirect applications to non-financial situations such as these.
Also, the proper trading or hedging of soft commodities’ prices with MS-GARCH models could be of use for the companies that produce and trade these. This, is in order to enhance their free cash flow and profitability during distress time periods in these financial markets. Finally, commodity future markets are always innovating in order to have a proper valuation of margin calls. That is, when a trader or hedger buys a future contract, she must deposit a proper goodwill margin amount. This amount will be used and paid to the future’s underwriter if she fails to honor her commitment at redemption. Given this, the proper margin estimation at the end of each trading day is of vital importance for the proper functioning of commodity future markets. Departing from this fact, we were interested in the proper use of MS-GARCH in soft commodities as a trading and hedging tool and, potentially, for future contract margin estimation.
In terms of our theoretical interests, we wanted to test the use of MS-GARCH models by the fact that these not only estimate the change in regime but also allow the intra-regime volatility to be estimated as a time-varying parameter.
As noted, our results could be important in theoretical and practical terms. We intended to extend the current literature of the use of MS models to the MS-GARCH case. Given our practical and theoretical motivations, we tested the next hypothesis:
Hypothesis 1.
A soft commodity futures’ trader could earn higher accumulated returns if she uses a MS-GARCH model in a trading decision algorithm. This is compared against a buy-and-hold (BH) investment strategy.
We believe that our results are important by the potential soft commodity future trading application. We also extend the discussion about the benefit of using MS-GARCH models in trading decisions in the commodity futures of interest.
Given this hypothesis and our theoretical applications, our paper is structured as follows: In the next section we will make a brief review of the preceding literature that we wanted to extend. There, we give a support to our research intentions and motivations. In the third section, we make a review of the mathematical rationale behind MS and MS-GARCH models. Also in that section, we will describe the simulated trading algorithm, along with a description of the input data used. In the fourth section we discuss the main results and findings and, finally, we present our conclusions and guidelines for further research.
2. Literature Review of the Use of MS-GARCH Models
The idea behind of the use of time series analysis with structural breaks or different number of regimes has been studied in several models. The threshold autoregressive (TAR) models of Tong [28] is one of the first. In this model, the analyst could split the time series of interest, according to certain threshold level () or number of levels. Then, she could perform the time series model of interest in a number of regimes’ context. Given this important step in time series analysis, this model lacks an appropriate model for the behavior of the structural breaks at . This means that this model is not useful to answer an important question: Are we going to be in a given regime at or ? This question is very important for financial and economic decisions. Given this, Hamilton [1,2,3] proposed the Markov-switching models (MS) in which the time series can be characterized in such a way that it is possible to determine which realization is made in a given regime . It also accepts the fact that the behavior of the regime at is unobservable and can be modeled as a hidden Markovian chain. A Markovian process that has its regime transition probabilities and smoothed probabilities of being in each regime at or .
After Hamilton’s proposal, several extensions to the MS models have been made. Some of the most important ones are the MS models that use time-varying generalized autoregressive conditionally heteroskedastic (GARCH) variances [29,30,31] (MS-GARCH models) and their not generalized version (MS-ARCH).
MS and MS-GARCH models were primarily used to characterize and to forecast the probability of being in recession periods [1]. One of the most used applications is the one developed by Chauvet [32], who developed a recession warning system for the U.S. This system is a MS multivariate model that estimates the probability of being in a recession and is published monthly by the Federal Reserve of Saint Louis [33].
Following this application, other previous works characterized financial time series. Klein [6], Areal, Cortez, and Silva [14], Zheng and Zuo [13], and Hauptmann et al. [19] characterized the time series of developed financial markets such as Germany, Switzerland, the U.S. and the U.K. In a similar perspective, Zhao [34], Walid et al. [35], Walid and Duc Khuong [36], Cabrera et al. [12], De la Torre, Álvarez-García, Galeana-Figueroa [37], and Rotta and Valls-Pereira [10] discuss the characterization of emerging stock market indexes. Some of these authors measure the link between the volatility of emerging countries’ stock markets and their corresponding currency pairs against the U.S. dollar. Some of these works also found a link between the stock markets of the U.S., Brazil, Russia, India, and China (BRIC) with their correspondent currencies. This is in a two or three-regime context.
In order to measure the link between stocks and credit default swaps (CDS) (a derivative contract that hedges against debt default), we mention the works of Alexander and Kaeck [38], Castellano and Scacia [39], and Ma, Deng, and Ho [40]. These works measure the spillover effect between CDS, stocks, and commodity markets. In a similar perspective in emerging CDS markets, we found the works of Ma, Deng, and Ho [40], Riedel and Sottile [41], and Riedel, Thuraisamy, and Wagner [42]. Similar to the previous authors, they found a link between emerging CDS and stock markets in normal and distress time periods.
Other papers test the spillover effect between stock and currency markets of developed and developing countries. Examples of these are the works of Mouratidis et al. [43], Miles and Vijverberg [44], Lopes and Nunes [45], Kanas [46], Álvarez-Plata and Schrooten [47], Parikakis and Merika [48], Girdzijauskas [49], Dubinskas and Stungurienė [50], Kutty [51], Ahmed et al. [52], and Sosa, Ortiz, and Cabello [11].
The influence that all the previous works have in our paper is the fact that they give proofs of the benefit of using MS or MS-GARCH models in financial markets’ time series. For the specific case of the use of MS or MS-GARCH models, we found the works of Herrera, Rodriguez, and Pino [16], Balcilar et al. [53], Uddin et al. [54], Chenghan and Nguyen [55], and Alizadeh, Nomikos, and Puliasis [56]. All these works study the characterization of commodity prices’ time series in a two- or three-regime context. From these, only the work of Alizadeh, Nomikos, and Puliasis [56] tests the use of MS models to develop a hedge ratio between the oil future and spot prices. This last case is quite related to our paper by the fact that it suggests the use of MS models for trading decisions in commodity markets.
All the previous works that we quoted in the present literature review are mainly focused in the characterization or spillover effect between financial time series in a two- or three-regime context. From all the potential uses of MS and MS-GARCH models, we were interested in their application to trading decisions. The first paper that suggests this use is the one of Brooks and Persand [17]. These authors estimated the equity/yield bond ratio (EYBR). This is a financial markets’ indicator that estimates the proportion of rate of return that an investor could have if she invests in stocks instead of bonds. The idea behind this ratio is the fact that it must be higher than 1, if the expected dividend yield in a stock index is higher than the one paid in the 10-year local Treasury bond. In their paper, these authors estimated a two-regime EYBR and estimated, in several dates, a Gaussian time-fixed MS model. This is with data of the yield paid by the Financial Times Stock Exchange (FTSE-100) index and the 10-year gilt (U.K Treasury bond). With the two smoothed probabilities of each regime in the trade date , the authors determined an investment level in stocks ( or bonds ( with the next trading rule:
This investment level vector allowed having an actively managed portfolio that dynamically invests more in stocks during normal ( periods or in bonds during distress () ones. By comparing their simulated portfolio against a buy and hold (BH) investment strategy in stocks or gilts, the authors found an over performance with their trading rule.
This paper was the most important influence to our work by the fact that we adopted a similar trading rule in the cocoa and sugar future markets and we tested the benefits of this trading rule in a two-regime, Gaussian, or t-student pdf context. The original paper of Brooks only used Gaussian time-fixed MS models. We extended that work by testing the use of time-varying symmetric variances (or standard deviations) with MS-GARCH models.
Other works that extended this paper in stock markets of developed and developing stock markets are the ones of Hauptmann et al. [19], Engel, Wahl, and Zagst [57], and De la Torre, Galeana, and Álvarez-García [20]. These authors developed the use of MS and MS-GARCH models with time-fixed or time-varying transition probabilities. These authors also found a better performance of their simulated portfolios against a BH strategy. This was in stock markets of the U.K, the U.S., Switzerland, Japan, Germany, Italy, or Mexico.
For the specific case of active trading with MS or MS-GARCH models in commodity future markets, we can mention the works of De la Torre-Torres, Galeana-Figueroa, and Álvarez-García [22] and De la Torre-Torres, Aguilasocho-Montoya, and Álvarez-García [23]. These authors tested the use of Gaussian MS and MS-GARCH models in the west Texas intermediate oil, the natural gas, the corn, and soybean markets. With weekly trading simulations, the authors found that it is preferable to use MS-GARCH or MS-ARCH models (Gaussian or t-student) in the corn and soybean markets, respectively. For the case of the natural gas and the oil markets, they found that only the Gaussian time-fixed variance MS model is useful in the West Texas Intermediate (WTI) oil futures. In a similar perspective to the previous papers and to the present one, these authors compared their simulated portfolios against a BH strategy and found a better performance with the use of MS or MS-GARCH models in their trading algorithm.
The present paper extends the work of the previous ones by the fact that we tested the benefits of MS and MS-GARCH models in three of the most traded soft agricultural commodities [24]: Coffee, cocoa, and sugar.
Given this brief literature review, we tested the performance of a U.S. dollar based (USD-based) investor who followed the next trading algorithm:
- To invest in the simulated commodity future if the investor expects to be in the low-volatility () regime at or
- To invest in the U.S. risk-free asset if the investor expects to be in the high-volatility () regime.
Once our theoretical motivations were mentioned, we presented a brief review of the rationale behind the MS-GARCH model. We did this section for introductory purposes and also to explain how we used the MS and MS-GARCH models in the investment strategy.
3. Methods and Materials
3.1. The Rationale behind MS and MS-GARCH Models, the Input Data Processing Method, and the Trading Strategy Simulation’s Parameters
MS models estimate the location (), scale (), and smoothed regime probabilities () by assuming that they come from a multimodal Gaussian or t-student pdf as follows:
In the previous expressions, and are the fixed probabilities or mixtures of each regime pdf. That is, the fixed probability or proportion that a given realization comes from the regime number .
The main rationale of MS models is the fact that , the regime at , and the location and scale parameters are unobservable for the analyst, investor, or trader. Therefore, these must be estimated as if they come from a states hidden Markovian chain. As a hidden Markovian chain, the stochastic process can transit from a given state () to another one (). This transition can be modeled with a transition probability matrix :
In order to give an example, we used the one-month, weekly historical cocoa future price. In Figure 1 we present the price time series (blue line), along with the distress periods or regime (grey areas). As we will review next, we estimated these with a time-fixed variance, Gaussian pdf MS model. As we mentioned previously, the distress time periods shown with the grey area are unobservable to the analyst. This means that their behavior must be inferred directly from the time series’ realizations.
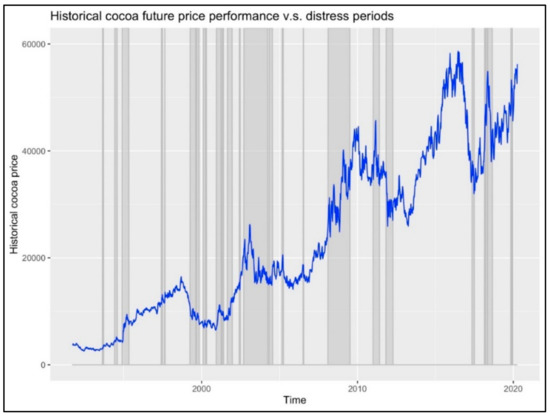
Figure 1.
The historical one-month cocoa future price and the distress regime period estimated with a two-regime, Gaussian time-fixed standard deviation MS model.
In order to model the potential regime switch, there are two possible solutions. The first comes with the threshold autoregressive (TAR) model [28]. In this model and given a user-specified threshold value (), the stochastic process can be inferred with the next indicator function:
The main drawback of this first proposal is that the analyst must have a clear value and this value cannot be known in certain securities. A good example of this situation is the potential downturn that a commodity future price could have to negative prices. If the market of a given future (such as cocoa, sugar, corn, or oil) finds that there is not enough storage for the given commodity, the future prices could fall to negative values. This could happen by the fact that future purchasers could have higher storage costs than “to pay” (with a negative price) to someone else. This could happen in order to motivate the buy of their commodity’s long position. Given this, in a single day or week, the future price could have a downturn of more than 100%. By the fact that this scenario could be seen only in extreme economic or social circumstances, a discretional threshold value would not be useful, because that does not fit to the current reality or price shortfall.
Another drawback of the TAR model in Equation (5) is the parameter estimation method. In practical terms, the TAR model is one with dummy (binary) and slope dummy regressors. As more regimes or states of nature are incorporated, the estimation process could lose degrees of freedom.
Departing from these issue, and as we previously mentioned, Hamilton proposed the use of MS models. In these, the behavior of the number of regimes is one of a regime Markovian process with a transition probability matrix such as the one in Equation (3). This Markovian process is hidden or unobserved to the analyst and must be inferred from the time series. In order to infer the parameter set of MS models, Bayesian estimation techniques are used. One of these is the quasi-maximum likelihood (QML) estimation described by Hamilton [3]. The rationale behind it is similar to the Kalman’s filter. As a first stage of the estimation process, the analyst has a prior estimate of the transition probability matrix and the parameter set (). In the second stage, the analyst filters the probability of being in each state or regime by using the prior parameter set in the regime-specific Gaussian or t-student probability density functions. This follows as, respectively:
In the previous expressions, are the prior and starting location (mean), scale (standard deviation), and t-student pdf degrees of freedom. This is in each iteration of the estimation process. Once the regime-specific probabilities were filtered from the data with Equation (6) or Equation (7), the analyst estimates the corresponding log-likelihood function (LLF), departing from Equation (2) or Equation (3):
Given the filtered regime-specific probabilities, the location and scale parameters are updated with these calculations, respectively:
With the new parameter set () in this number of iteration or step (), the analyst returns to the first stage in the estimation algorithm, as this set is the new prior. Then, she updates the filtered probabilities, Equation (6) or Equation (7), with the new parameter set, (), calculates the with Equation (8), and updates, with Equations (9) to (11), the parameter set with the new filtered probabilities. This numerical method continues until the values between the current iteration () and the previous one () have a difference lower than a threshold value ().
Once the estimation process stops, the filtered probabilities are smoothed with the method suggested by Kim [58].
As noted, this QML method suggested by Hamilton [3] is an special case of the expectation–maximization (E-M) algorithm of Dempster et al. [59]. As we will mention next, we did not use the QML method for our estimations. We used a Markov chain Monte Carlo (MCMC) method known as the Metropolis–Hastings [60] sampler. This is a Monte Carlo estimation method similar to the current one that allows a higher degree of feasibility than the QML one.
With the QML or Metropolis–Hastings estimation method described, the analyst could arrive to a result similar to the one of Figure 2. In this example, we present an estimation for the cocoa future price. In the upper left chart, we present the historical value of the continuously time percentage variation. The red lines correspond to the returns generated during the distress () regime. The blue ones are the returns generated in the normal () one. These were determined with the next indicator function, which is the criteria suggested in most of the related literature about MS models [1,2,3,17,18,19,61]:
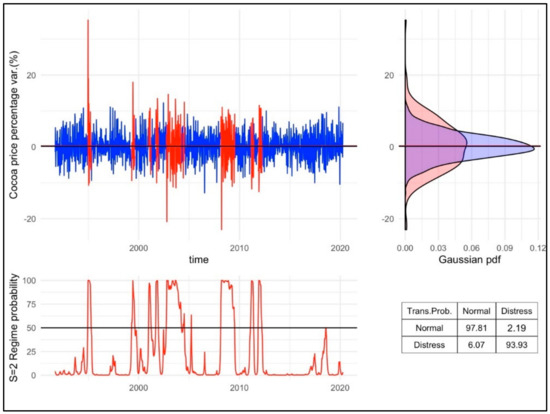
Figure 2.
The two-regime Gaussian stochastic process of the cocoa future returns.
In the upper right chart of Figure 2, we show the Gaussian kernels of the returns generated in each regime. As noted, the blue area is the narrowest one and corresponds to the Gaussian kernel of the returns generated in a normal () regime (the blue lines in the upper left chart). The red area is the kernel of the returns of the distress time periods. Given this, it is noted that the parameters of each regime, especially the scale or standard deviation, have notable differences (especially in the scale parameter).
In the lower left chart, we present the second regime’s () smoothed probability (). This was estimated with the MS model. As noted, the dates in which correspond to the dates in which the returns are marked with red in the upper chart. Finally, we also show a table with the estimated transition probability matrix. As noted in this case, the normal regime tends to be absorbing. That is, the probability of being in such a regime is notably higher and the time spent in it is also high.
Given the estimation method described previously, the parameter set of a Gaussian or t-student MS model () is useful for trading decisions. More specifically, the smoothed probability is of being in the distress regime (red line in the lower left chart), as we will mention next.
Two important assumptions in the original MS models are the fact that the transition probabilities and the scale parameters () are time-fixed. A natural extension of the MS models explained in Equations (2) to (11) is to estimate the variance through a generalized autoregressive conditionally heteroskedastic (GARCH) standard deviation [62,63]. A scale parameter estimation model with the next functional form:
This stochastic process means that the actual standard deviation is dynamic or time-varying in each regime. This leads to the time-varying standard deviation model known as the MS-GARCH [29,30,31]. Given this, and the dynamic standard deviation of the GARCH model inside the Markov-switching structure, the parameter set includes a time-varying scale parameter () for each regime:
Given the specific features of the MS-GARCH model in Equations (13) and (14), the analyst could estimate the variance by using only the lags of the residuals (). This means that she is using only the autoregressive conditionally heteroskedastic (ARCH) term. If she estimates the entire model in Equation (13), she is adding the GARCH term that is a generalization of the extra lag terms. Given the parameter set of a MS or MS-GARCH model (), a futures’ position trader or a portfolio manager could be interested in the smoothed probabilities of being in each regime. These probabilities could be used to forecast the probability of being in each regime at as follows:
With these forecasted probabilities, the trader or portfolio manager could follow a trading algorithm similar to the one of Brooks and Persand [17] or the one tested by De la Torre-Torres, Galeana-Figueroa, and Álvarez-García [20,22] or De la Torre-Torres et al. [23]:
- (1)
- To estimate the parameter set of a MS or MS-GARCH (with Gaussian or t-student pdf).
- (2)
- To forecast the smoothed probability () of being in the distress regime at with Equation (15).
- (3)
- To follow the next trading algorithm:
- If ,
- To invest in a risk-free asset (such as the three-month Treasury bill).
- Else
- To invest in the managed commodity as risky asset.
As it is expected, the estimated smoothed probability values are different if the trader or portfolio manager uses either a Gaussian or t-student pdf. The values also are different if she prefers to estimate time-fixed (MS), ARCH (MS-ARCH), or GARCH (MS-GARCH) standard deviations.
Departing from this feature, we were interested to test the performance that a futures’ position trader or a portfolio manager would have had, had she performed the previous trading algorithm each week. This was in the three soft commodities of interest.
In the next section, we will mention how we processed the input data and how we ran our back tests of the previous trading algorithm.
3.2. Data Processing
The idea behind our review is the fact that the use of a Gaussian or t-student pdf and a time-fixed, ARCH, or GARCH variance could lead to different smoothed probability () estimations. Given this difference, it is expected that the previous trading algorithm could lead to a different timing in trading decisions.
Our review was done by assuming that she traded actively in the weekly periods from 7 January 2000 to 3 April 2020 (the last available date until the writing of the present paper). In order to test the benefits of this trading rule in soft agricultural commodities, we performed our simulations in the coffee, cocoa, and sugar future prices. These three futures are the one-month to expiration ones and were used as the risky assets in the portfolio.
Also, we used as risk-free asset, a theoretical zero tracking-error fund that invests in the thee-month U.S. Treasury bill. The Refinitiv Identifier Codes (RIC), security name, and the futures’ exchange in which they are traded are summarized in Table 1.

Table 1.
The commodities used in our simulations.
The historical weekly data of the commodity futures along with the historical three-month U.S. Treasury bills’ rate were retrieved from Refinitiv Eikon-Xenith [64].
With this historical data, we simulated, week by week, the previous trading algorithm in six scenarios. Three of these had a Gaussian pdf with time-fixed (MS), ARCH (MS-ARCH), or GARCH (MS-GARCH) standard deviations. The other three used a t-student pdf.
In order to estimate the MS, MS-ARCH, or MS-GARCH models, we did not used a QML estimation method. Instead, we preferred to use Markov chain Monte Carlo (MCMC) estimation process. This was through the Metropolis–Hastings [60] sampling method, a method that is also proper of the MS-GARCH package [65] in the R programming code. R and this package were the core software in our back tests. We used the MCMC method in order to ensure the convergence in the inference of the parameters, a risk that was expected in the QML method previously described.
As an extra methodological note, we estimated the MS-ARCH or MS-GARCH with one lag in the ARCH and GARCH terms of the time-varying variance. Also, for estimation purposes of our models, we used the entire time series from 20 September 1991 to the simulated date at (from 7 January 2020 to 3 April 2020). This led to a total of 1057 back test dates. The returns were estimated with the time continuous method, given the future price at ():
By the fact that the trading commissions could be small for future position traders or institutional portfolio managers, we set aside the impact of trading costs. We did this by assuming the similar performance results observed in active trading with MS models in some stock markets [20]. This was with 0.35% and 0% of trading fee.
In order to perform our back tests, we compared the simulated performance of a USD 100,000 starting balance account against the performance of a buy-and-hold (BH) strategy. We did this by executing the next pseudocode of our trading Algorithm 1 previously described:
| Algorithm 1. The MS-GARCH based trading algorithm’s pseudocode. |
For date 1 to 1057:
End |
Before we start to review our simulation results, we tested the appropriateness of MS and MS-GARCH models in all the simulated dates. For this purpose, we estimated the deviance information criterion, or DIC, for each model. We did this in a recursive manner with data from 20 September 1991 to the back test date range (7 January 2020 to 3 April 2020). The mean DIC values of these estimations in each date are summarized in Table 2.

Table 2.
Recursive fit test of single- and two-regime stochastic process, with different standard deviation models and different probability density function (PDFs).
As noted, we compared the six MS or MS-GARCH models of interest with the single-regime DIC estimation, that is, against the case in which no MS model was used. Given these results, the MS-GARCH models with t-student pdf was the most suitable for the cocoa and the sugar future returns and the time-fixed variance, t-student MS one in the coffee. Also, and in general terms, the use of two-regime models is preferable to characterize the time series of interest during the back test periods.
Now that we described our input data processing method and our back test’s pseudocode, we will continue with the discussion of our main results.
4. Results and Discussion
As a departing and reference point, we summarized the buy-and-hold (BH) strategy in Table 3. This is for the three futures of interest and the risk-free asset. As noted, the three simulated commodities paid a higher accumulated return than the risk-free asset. Also, in the simulated commodities we found a positive Sharpe [66] ratio. This metric measures the extra return (from the risk-free asset) against the risk-free asset, given each extra 1% of risk exposure.

Table 3.
Performance summary of the simulated portfolios with the buy-and-hold strategy in the three commodities of interest (figures in %, with the exception of the Sharpe ratio).
An interesting measure that we also wanted to compare with the ones in our simulations was the lowest weekly return. This number determines the lowest downward movement that the given commodity had in a single-week period. As noted, the cocoa is the riskiest commodity because it showed a −23.05% movement in a single week.
Given our back test’s pseudocode, we show the historical performance of the six simulated portfolios in the cocoa future, in Figure 3. Contrary to fit results in Table 2, the t-student MS-ARCH is the best performer for trading decisions in this commodity. In Table 4 we summarized the results of the six simulated portfolios in this commodity. With the results of this Table and the ones of Figure 4, it is noted that the t-student MS-ARCH portfolio paid 801.24% accumulated return. This figure is notably higher than the 594.55% of the BH strategy (blue area) in Figure 3.
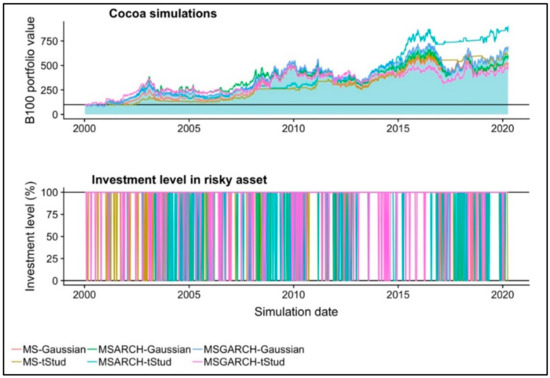
Figure 3.
The historical performance and commodity investment level in each of the six simulated portfolios in the one-month cocoa future market.

Table 4.
Performance summary of the simulated portfolios in the cocoa one-month futures’ market (figures in %, with the exception of the Sharpe ratio).
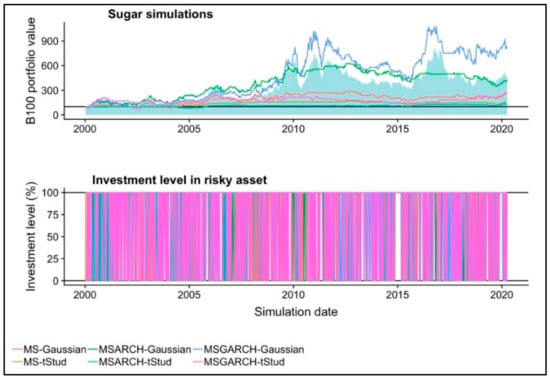
Figure 4.
The historical performance and commodity investment level in each of the six simulated portfolios in the one-month sugar future market.
Despite this, the risk profile did not improve, by the fact that the lowest weekly return in this simulated portfolio is similar to the one of the BH strategy.
As noted in Figure 3 and Table 4, only the use of Gaussian t-student MS-ARCH models led to a higher return than the BH strategy. This results was due to the fact the use of this MS-GARCH model led to a more precise trading time. As noted from Figure 3, the algorithm generated a sell trading sign, given that the smoothed forecasted probability () was higher than 50%. From all these dates, the most important or significant were the 20 March 2015 to 27 March 2015 ones. In these specific dates, the trading algorithm led to invest in the risk-free asset. This was in the same market period in which the commodity price had an important downward movement. This trade allowed protecting the loss of value in the simulated portfolio.
In a similar fashion, the 13 April 2018 to 16 May 2018 period had an important influence in the simulation’s results. This is so because, once again, the trading algorithm suggested a sell trading sign. This happened at the moment in which the commodity price fell. Finally, in all January of 2020, the simulated portfolios remained invested in the risk-free asset, given another sell trading sign from the trading algorithm. This suggested, contrary to the other MS, MS-ARCH, or MS-GARCH models summarized in Table 2, that the t-student MS-ARCH model is the most appropriate for trading purposes in the cocoa future market. That is, it is useful and accurate to determine the proper timing of trading decisions.
For the sugar future market case, we present our historical performance results in Figure 4 and the performance summary in Table 5. As noted, only the Gaussian MS-GARCH model led to a better performance than the BH strategy (blue area). This simulated portfolio paid a 710.71% accumulated return, which is higher than the observed 365.53% of the BH strategy (Table 3).

Table 5.
Performance summary of the simulated portfolios in the sugar one-month futures’ market (figures in %, with the exception of the Sharpe ratio).
Similar to the cocoa future, the lowest weekly return and the other risk metrics did not improve significantly. Despite this, the outperformance of the simulated Gaussian MS-GARCH model was due to a sensitive timing in the future sell trading sign. In the first three weeks of February 2006, the trading algorithm suggested to sell the commodity and to buy the risk-free asset. This led to the first positive difference with the BH strategy and the other simulated portfolios. This is so by the fact that the commodity future had an important price fall in that period. Also, the same situation happened during the months of June, July, and August of 2012 and 2013. In those months, several sell signs were suggested by the trading algorithm. In these periods, the commodity price had also a downward movement. Finally, in June of 2017, the simulated portfolio invested in the risk-free asset. This led to another substantial difference against the BH strategy.
For the specific case of the coffee market, we found no evidence in favor to the use of MS or MS-GARCH models for trading. As noted in Table 6, none of the simulated portfolios paid a higher accumulated return than the BH strategy presented in Table 3. Also, in Figure 5 we present the historical performance of the simulated portfolios. With the exception of the Gaussian MS-GARCH model at the beginning of the back test, most of the simulated portfolios had a similar performance to the BH strategy (blue area).

Table 6.
Performance summary of the simulated portfolios in the coffee one-month futures’ market (figures in %, with the exception of the Sharpe ratio).
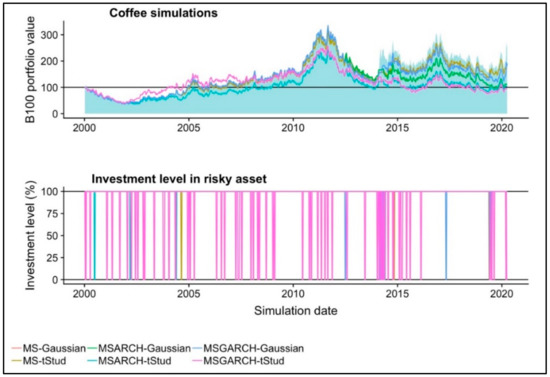
Figure 5.
The historical performance and commodity investment level in each of the six simulated portfolios in the one-month coffee future market.
An issue that we want to highlight is the fact that, at the end of the simulation period, the simulated portfolios suggested sell trading signs in the coffee position. This trading signs, contrary to the two previous commodities, did not help in the simulated performance. This is so by the fact that, given this sell sign, the BH strategy increased in value, given a coffee price increase. The simulated portfolios missed this price increase because these were invested in the risk-free asset. This situation happened in March, May, and June of 2014. Given this issue in this specific commodity, the use of active trading with MS and MS-GARCH models did not improve the performance of an actively traded futures’ position.
As noted for the three commodities of interest, the use of MS-ARCH or MS-GARCH models led to an important over performance against a buy-and-hold strategy only in the cocoa and sugar future markets, being the opposite in the coffee one.
We believe that our trading algorithm needs improvements in terms of the upward and downward price movements’ detection, during normal or distress time periods. This is an issue that we will suggest for further research.
5. Concluding Remarks
Markov-switching (MS) models with time-fixed standard deviations and with generalized autoregressive conditional heteroskedastic (MS-GARCH) ones have been a very useful time series analysis method. Several applications of these have been studied and implemented. Among the most significant, the use of these models to forecast distress time periods is the one of interest herein. This use was part of a decision-making algorithm in soft agricultural commodity futures.
The first proposal about the use of MS models for trading algorithms comes from Brooks and Persand [17]. These authors tested this use in U.K. stocks. This use was later developed by several authors [18,19,20,21] in stock markets and other commodity futures such as oil, natural gas, corn, or soybean [22,23].
Despite this, the use of MS and MS-GARCH models for trading needs more review. In the present paper we extended the current literature by testing the use of MS and MS-GARCH in the three most traded agricultural and personal consumption soft commodities [24]: Coffee, cocoa, and sugar.
From 7 January 2000 to 3 April 2020, we performed weekly simulations of the performance of a U.S. dollar-based portfolio. This, in each of the three commodities of interest. We compared our results with the ones of a buy-and-hold (BH) strategy in each commodity.
For the case of the cocoa market we found evidence in favor of the use of t-student, MS-ARCH models (the not generalized version of the MS-GARCH ones). This is so by the fact that this simulated portfolio outperformed a BH strategy.
For the specific case of the sugar market, we found strong evidence that favors the use of Gaussian MS-GARCH models for active trading.
For the specific case of these two commodities, the use of MS-ARCH or MS-GARCH models led to better performance than the BH strategy by the fact that the timing to forecast the distress regime probability at is more accurate. This led to proper sell signs in these two commodities at the moment in which the commodity price was in a distress period with significant price downward movements.
For the coffee future market case, we found the opposite. That is, the trading algorithm that we tested herein led to sell trading signs in moments in which the coffee price was in upward movements. Given this issue, the trading algorithm led to poorer performance results than the BH strategy. This is so by the fact that the simulated portfolios were invested in the risk-free asset during important upward coffee price movements.
Even if the strongest proofs of using MS-GARCH models for active trading are found only in the sugar and cocoa markets, we suggest to perform our test with other MS-GARCH models in these three commodities, as guideline for further research.
The previous recommendations mean to test the use of other types of symmetric or asymmetric likelihood functions or even the use of other GARCH estimation methods. Also, as future guidelines for research, we suggest performing the same test with the presence of trading fees, different time intervals, and also the estimation of MS models with time-varying transition probabilities.
Finally, we suggest testing the use of MS-GARCH models with a sequential estimation method, as in Hauptmann et al. [19]. These authors suggest, in order to have convergence in the estimation method and a more precise forecast of upward and downward movements, estimating the regimes by parts. That is, to estimate first the normal and distress smoothed probabilities and, later, to estimate the ones of upward and downward “regimes”. This issue, we believe, could lead to better performance results in the commodities simulated herein. More specifically, in the coffee future market.
Author Contributions
All authors contributed equally to this work. All authors wrote, reviewed, and commented on the manuscript. All authors have read and approved the final manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hamilton, J.D. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 1989, 57, 357–384. [Google Scholar] [CrossRef]
- Hamilton, J.D. Analysis of time series subject to changes in regime. J. Econom. 1990, 45, 39–70. [Google Scholar] [CrossRef]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Misas, M.; Ramírez, M.T. Depressions in the Colombian economic growth during the twentieth century: A Markov switching regime model. Appl. Econ. Lett. 2007, 14, 803–808. [Google Scholar] [CrossRef]
- Camacho, M.; Perez-Quiros, G. Commodity prices and the business cycle in latin america: Living and dying by commodities? Emerg. Mark. Financ. Trade 2014, 50, 110–137. [Google Scholar] [CrossRef]
- Klein, A.C. Time-variations in herding behavior: Evidence from a Markov switching SUR model. J. Int. Financ. Mark. Inst. Money 2013, 26, 291–304. [Google Scholar] [CrossRef]
- Ardia, D.; Kolly, J.; Trottier, D.-A. The impact of parameter and model uncertainty on market risk predictions from GARCH-type models. J. Forecast. 2017, 36, 808–823. [Google Scholar] [CrossRef]
- Ardia, D.; Hoogerheide, L.F. GARCH models for daily stock returns: Impact of estimation frequency on value-at-risk and expected shortfall forecasts. Econ. Lett. 2014, 123, 187–190. [Google Scholar] [CrossRef]
- Ye, W.; Zhu, Y.; Wu, Y.; Miao, B. Markov regime-switching quantile regression models and financial contagion detection. Insur. Math. Econ. 2016, 67, 21–26. [Google Scholar] [CrossRef]
- Rotta, P.N.; Valls Pereira, P.L. Analysis of contagion from the dynamic conditional correlation model with Markov regime switching. Appl. Econ. 2016, 48, 2367–2382. [Google Scholar] [CrossRef]
- Sosa, M.; Ortiz, E.; Cabello, A. Dynamic linkages between stock market and exchange rate in mila countries: A Markov regime switching approach (2003–2016). Análisis Económico 2018, 33, 57–74. [Google Scholar] [CrossRef]
- Cabrera, G.; Coronado, S.; Rojas, O.; Venegas-Martínez, F. Synchronization and changes in volatilities in the Latin American’s stock exchange markets. Int. J. Pure Appl. Math. 2017, 114. [Google Scholar] [CrossRef]
- Zheng, T.; Zuo, H. Reexamining the time-varying volatility spillover effects: A Markov switching causality approach. N. Am. J. Econ. Financ. 2013, 26, 643–662. [Google Scholar] [CrossRef]
- Areal, N.; Cortez, M.C.; Silva, F. The conditional performance of US mutual funds over different market regimes: Do different types of ethical screens matter? Financ. Mark. Portf. Manag. 2013, 27, 397–429. [Google Scholar] [CrossRef]
- Valera, H.G.A.; Lee, J. Do rice prices follow a random walk? Evidence from Markov switching unit root tests for Asian markets. Agric. Econ. 2016, 47, 683–695. [Google Scholar] [CrossRef]
- Herrera, R.; Rodriguez, A.; Pino, G. Modeling and forecasting extreme commodity prices: A Markov-switching based extreme value model. Energy Econ. 2017, 63, 129–143. [Google Scholar] [CrossRef]
- Brooks, C.; Persand, G. The trading profitability of forecasts of the gilt-equity yield ratio. Int. J. Forecast. 2001, 17, 11–29. [Google Scholar] [CrossRef]
- Kritzman, M.; Page, S.; Turkington, D. Regime shifts: Implications for dynamic strategies. Financ. Anal. J. 2012, 68, 22–39. [Google Scholar] [CrossRef]
- Hauptmann, J.; Hoppenkamps, A.; Min, A.; Ramsauer, F.; Zagst, R. Forecasting market turbulence using regime-switching models. Financ. Mark. Portf. Manag. 2014, 28, 139–164. [Google Scholar] [CrossRef]
- De la Torre-Torres, O.V.; Galeana-Figueroa, E.; Álvarez-García, J. Using Markov-switching models in Italian, British, US.and Mexican equity portfolios: A performance test. Electron. J. Appl. Stat. Anal. 2018, 11, 489–505. [Google Scholar] [CrossRef]
- De la Torre-Torres, O.V.; Aguilasocho-Montoya, D.; Álvarez-García, J. Active portfolio management in the Andean countries’ stock markets with Markov-switching GARCH models. Rev. Mex. Econ. Finanz. 2019, 14, 601–616. [Google Scholar] [CrossRef]
- De la Torre-Torres, O.V.; Galeana-Figueroa, E.; Álvarez-García, J. A test of using markov-switching GARCH models in oil and natural gas trading. Energies 2019, 13, 129. [Google Scholar] [CrossRef]
- De la Torre-Torres, O.V.; Aguilasocho-Montoya, D.; Álvarez-García, J.; Simonetti, B. Using Markov-switching models with Markov chain Monte Carlo inference methods in agricultural commodities trading. Soft Comput. 2020, 1–14. [Google Scholar] [CrossRef]
- US CFTC Disaggregated Futures Only Reports. Available online: https://www.cftc.gov/MarketReports/CommitmentsofTraders/HistoricalCompressed/index.htm (accessed on 22 October 2018).
- Wainaina, S.; Awasthi, M.K.; Sarsaiya, S.; Chen, H.; Singh, E.; Kumar, A.; Ravindran, B.; Awasthi, S.K.; Liu, T.; Duan, Y.; et al. Resource recovery and circular economy from organic solid waste using aerobic and anaerobic digestion technologies. Bioresour. Technol. 2020, 301, 122778. [Google Scholar] [CrossRef] [PubMed]
- Falcone, P.M. Tourism-based circular economy in Salento (South Italy): A SWOT-ANP analysis. Soc. Sci. 2019, 8, 216. [Google Scholar] [CrossRef]
- Rajesh Banu, J.; Kavitha, S.; Yukesh Kannah, R.; Dinesh Kumar, M.; Preethi; Atabani, A.E.; Kumar, G. Biorefinery of spent coffee grounds waste: Viable pathway towards circular bioeconomy. Bioresour. Technol. 2020, 302, 122821. [Google Scholar] [CrossRef]
- Tong, H. Threshold Models in Nonlinear Time Series Analysis; Springer: New York, NY, USA, 1983; Volume 21. [Google Scholar]
- Dueker, M. Markov Switching in garch processes and mean- reverting stock-market volatility. J. Bus. Econ. Stat. 1997, 15, 26–34. [Google Scholar]
- Klaassen, F. Improving GARCH volatility forecasts with regime-switching GARCH. In Advances in Markov-Switching Models; Physica-Verlag HD: Heidelberg, Germany, 2002; pp. 223–254. [Google Scholar]
- Haas, M.; Mittnik, S.; Paolella, M.S. A New approach to Markov-Switching GARCH models. J. Financ. Econom. 2004, 2, 493–530. [Google Scholar] [CrossRef]
- Chauvet, M. An econometric characterization of business cycle dynamics with factor structure and regime switching. Int. Econ. Rev. (Phila.). 2000, 10, 127–142. [Google Scholar] [CrossRef]
- Piger, J.; Max, J.; Chauvet, M. Smoothed U.S. Recession Probabilities [RECPROUSM156N]. Available online: https://fred.stlouisfed.org/series/RECPROUSM156N (accessed on 22 October 2019).
- Zhao, H. Dynamic relationship between exchange rate and stock price: Evidence from China. Res. Int. Bus. Financ. 2010, 24, 103–112. [Google Scholar] [CrossRef]
- Walid, C.; Chaker, A.; Masood, O.; Fry, J. Stock market volatility and exchange rates in emerging countries: A Markov-state switching approach. Emerg. Mark. Rev. 2011, 12, 272–292. [Google Scholar] [CrossRef]
- Walid, C.; Duc Khuong, D. Exchange rate movements and stock market returns in a regime-switching environment: Evidence for BRICS countries. Res. Int. Bus. Financ. 2014, 46–56. [Google Scholar] [CrossRef]
- De la torre-Torres, O.V.; Álvarez-García, J.; Galeana-Figueroa, E. A comparative performance review of the Venezuelan, latin-american and emerging markets stock indexes with the north-american ones using a gaussian two-regime Markov-switching model. Espacios 2018, 39, 1–10. [Google Scholar]
- Alexander, C.; Kaeck, A. Regime dependent determinants of credit default swap spreads. J. Bank. Financ. 2007, 1008–1021. [Google Scholar] [CrossRef]
- Castellano, R.; Scaccia, L. Can CDS indexes signal future turmoils in the stock market? A Markov switching perspective. CEJOR 2014, 22, 285–305. [Google Scholar] [CrossRef]
- Ma, J.; Deng, X.; Ho, K.-C.; Tsai, S.-B. Regime-switching determinants for spreads of emerging markets sovereign credit default swaps. Sustainability 2018, 10, 2730. [Google Scholar] [CrossRef]
- Sottile, P. On the political determinants of sovereign risk: Evidence from a Markov-switching vector autoregressive model for Argentina. Emerg. Mark. Rev. 2013, 160–185. [Google Scholar] [CrossRef]
- Riedel, C.; Thuraisamy, K.S.; Wagner, N. Credit cycle dependent spread determinants in emerging sovereign debt markets. Emerg. Mark. Rev. 2013, 17, 209–223. [Google Scholar] [CrossRef]
- Mouratidis, K.; Kenourgios, D.; Samitas, A.; Vougas, D. Evaluating currency crises: A multivariate Markov regime switching approach*. Manch. Sch. 2013, 81, 33–57. [Google Scholar] [CrossRef]
- Miles, W.; Vijverberg, C.-P. Formal targets, central bank independence and inflation dynamics in the UK: A Markov-switching approach. J. Macroecon. 2011, 33, 644–655. [Google Scholar] [CrossRef]
- Lopes, J.M.; Nunes, L.C. A Markov regime switching model of crises and contagion: The case of the Iberian countries in the EMS. J. Macroecon. 2012, 34, 1141–1153. [Google Scholar] [CrossRef]
- Kanas, A. Regime linkages between the Mexican currency market and emerging equity markets. Econ. Model. 2005, 22, 109–125. [Google Scholar] [CrossRef]
- Alvarez-Plata, P.; Schrooten, M. The Argentinean currency crisis: A Markov-switching model estimation. Dev. Econ. 2006, 44, 79–91. [Google Scholar] [CrossRef]
- Parikakis, G.S.; Merika, A. Evaluating volatility dynamics and the forecasting ability of Markov switching models. J. Forecast. 2009, 28, 736–744. [Google Scholar] [CrossRef]
- Girdzijauskas, S.; Štreimikienė, D.; Čepinskis, J.; Moskaliova, V.; Jurkonytė, E.; Mackevičius, R. Formation of economic bubles: Cuases and possible interventions. Technol. Econ. Dev. Econ. 2009, 15, 267–280. [Google Scholar] [CrossRef]
- Dubinskas, P.; Stungurienė, S. Alterations in the financial markets of the baltic countries and Russia in the period of Economic cownturn. Technol. Econ. Dev. Econ. 2010, 16, 502–515. [Google Scholar] [CrossRef]
- Kutty, G. The relationship between exchange rates and stock prices: The case of Mexico. N. Am. J. Financ. Bank. Res. 2010, 4, 1–12. [Google Scholar]
- Ahmed, R.R.; Vveinhardt, J.; Štreimikiene, D.; Ghauri, S.P.; Ashraf, M. Stock returns, volatility and mean reversion in emerging and developed financial markets. Technol. Econ. Dev. Econ. 2018, 24, 1149–1177. [Google Scholar] [CrossRef]
- Balcilar, M.; van Eyden, R.; Uwilingiye, J.; Gupta, R. The impact of oil price on South African GDP growth: A Bayesian Markov switching-VAR analysis. Afr. Dev. Rev. 2017, 29, 319–336. [Google Scholar] [CrossRef]
- Uddin, G.S.; Rahman, M.L.; Shahzad, S.J.H.; Rehman, M.U. Supply and demand driven oil price changes and their non-linear impact on precious metal returns: A Markov regime switching approach. Energy Econ. 2018, 73, 108–121. [Google Scholar] [CrossRef]
- Hou, C.; Nguyen, B.H. Understanding the US natural gas market: A Markov switching VAR approach. Energy Econ. 2018, 75, 42–53. [Google Scholar] [CrossRef]
- Alizadeh, A.H.; Nomikos, N.K.; Pouliasis, P.K. A Markov regime switching approach for hedging energy commodities. J. Bank. Financ. 2008, 32, 1970–1983. [Google Scholar] [CrossRef]
- Engel, J.; Wahl, M.; Zagst, R. Forecasting turbulence in the Asian and European stock market using regime-switching models. Quant. Financ. Econ. 2018, 2, 388–406. [Google Scholar] [CrossRef]
- Kim, C.-J. Dynamic linear models with Markov-switching. J. Econom. 1994, 60, 1–22. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–38. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Ang, A.; Bekaert, G. Regime switches in interest rates. J. Bus. Econ. Stat. 2002, 20, 163–182. [Google Scholar] [CrossRef]
- Engle, R. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Bollerslev, T. Moddeling the coherence in short-run nominal exchange rates: A multivariate generalized ARCH model. Rev. Econ. Stat. 1990, 72, 498–505. [Google Scholar] [CrossRef]
- Refinitiv Eikon. Available online: https://eikon.thomsonreuters.com/index.html (accessed on 3 June 2019).
- Ardia, D.; Bluteau, K.; Boudt, K.; Trottier, D. Markov–switching GARCH models in R: The MSGARCH package. J. Stat. Softw. 2019, 91, 38. [Google Scholar] [CrossRef]
- Sharpe, W. Mutual fund performance. J. Bus. 1966, 39, 119–138. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).