Exponential Stabilization of Linear Time-Varying Differential Equations with Uncertain Coefficients by Linear Stationary Feedback

Abstract

We consider a control system defined by a linear time-varying differential equation of n-th order with uncertain bounded coefficients. The problem of exponential stabilization of the system with an arbitrary given decay rate by linear static state or output feedback with constant gain coefficients is studied. We prove that every system is exponentially stabilizable with any pregiven decay rate by linear time-invariant static state feedback. The proof is based on the Levin’s theorem on sufficient conditions for absolute non-oscillatory stability of solutions to a linear differential equation. We obtain sufficient conditions of exponential stabilization with any pregiven decay rate for a linear differential equation with uncertain bounded coefficients by linear time-invariant static output feedback. Illustrative examples are considered.

1. Introduction

Consider a control system defined by an ordinary differential equation with time-varying coefficients of n-th order

$$x^{\left(n\right)}+p_1\left(t\right)x^{(n-1)}+\dots +p_n\left(t\right)x=u,$$

(1)

where $x\in \mathbb{R}$ is the state variable, $u\in \mathbb{R}$ is the control input, $t\in {\mathbb{R}}_{+}:=[0,+\infty )$. We suppose that the functions $p_i\left(t\right)$ are measurable but exact values of these functions at time moments t are unknown, we know only that the functions are bounded on ${\mathbb{R}}_{+}$ and lower and upper bounds (${\alpha }_i$ and ${\beta }_i$) are known:

$${\alpha }_i\le p_i\left(t\right)\le {\beta }_i,t\in {\mathbb{R}}_{+},i=\overline{1,n}.$$

(2)

Functions $p_i\left(t\right)$ can be arbitrary, in particular, they can vary fast or slowly. Denote $\mathbf{x}=(x,\dot{x},\dots ,x^{(n-1)})$. We consider a problem of feedback stabilization for system (1). One needs to construct a function $u(t,\mathbf{x})$, $u(t,\mathbf{0})=0$, such that, for system (1) closed-loop by $u=u(t,\mathbf{x})$, the zero solution is exponentially stable and has a given decay rate. The stated problem essentially relates to the problems of robust stabilization.

Let us assume that $p_i\left(t\right)$ are time-invariant (and hence, are known), i.e., $p_i\left(t\right)\equiv p_i(={\alpha }_i={\beta }_i)$. In that case, the stabilization problem is trivial. In fact, we construct

$$v_i=p_i-{\varphi }_i,$$

(3)

where ${\varphi }_i\in \mathbb{R}$, $i=\overline{1,n}$, are chosen such that the polynomial

$${\lambda }^n+{\varphi }_1{\lambda }^{n-1}+\dots +{\varphi }_n$$

(4)

is stable (i.e., $\mathrm{Re}{\lambda }_j<-\theta <0$ for all roots ${\lambda }_j$, $j=\overline{1,n}$, of (4)). Then system (1) closed-loop by the control

$$u\left(\mathbf{x}\right)=v_1{x}^{(n-1)}+\dots +v_{n}x$$

(5)

has the form

$$x^{\left(n\right)}+{\varphi }_1{x}^{(n-1)}+\dots +{\varphi }_{n}x=0,$$

(6)

and the zero (and hence, every) solution of (6) is exponentially stable.

Now, assume that $p_i\left(t\right)$ are time-varying. Then we can not construct the control by using (3) because $p_i\left(t\right)$ are unknown. Let the feedback control law have the form (5), where $v_i$ are constant. The closed-loop system has the form

$$x^{\left(n\right)}+(p_1\left(t\right)-v_1)x^{(n-1)}+\dots +(p_n\left(t\right)-v_n)x=0.$$

(7)

We study the following problem: construct constants $v_1,\dots ,v_n\in \mathbb{R}$ such that all solutions of (7) are exponentially stable with a given decay of rate. This problem is non-trivial due to the following reasons. For studying this problem, we need use some sufficient conditions for exponential stability of linear time-varying systems. The problem of obtaining some sufficient conditions for (asymptotic, exponential) stability of linear time-varying systems

$$\dot{x}=A\left(t\right)x,t\in {\mathbb{R}}_{+},x\in {\mathbb{R}}^n,$$

(8)

is one of the important and difficult problems in the theory of differential equations and control theory [1]. In contrast to systems with constant coefficients ($A\left(t\right)\equiv A$), the condition $\mathrm{Re}{\lambda }_j<0$, $j=\overline{1,n}$, fulfilled for the eigenvalues of the matrix of the system (8) is neither a sufficient nor a necessary condition for the asymptotic stability of the system (8) (see, e.g., [2], ([3], § 9)). Some sufficient conditions for asymptotic and exponential stability of linear time-varying systems (8) and linear time-varying differential equations

$$x^{\left(n\right)}+q_1\left(t\right)x^{(n-1)}+\dots +q_n\left(t\right)x=0$$

(9)

were obtained in [1,2,3,4,5,6,7,8,9,10,11]. The following theorem take place.

Theorem 1.

Suppose the functions $q_i\left(t\right)$ are measurable and bounded on ${\mathbb{R}}_{+}$ and the following inequalities hold:

$$0<{\sigma }_i\le q_i\left(t\right)\le {\omega }_i,t\in {\mathbb{R}}_{+},i=\overline{1,n}.$$

(10)

Let the polynomial

$$\begin{array}{c}{P}_1\left(\lambda \right)={\lambda }^n+{\omega }_1{\lambda }^{n-1}+{\sigma }_2{\lambda }^{n-2}+{\omega }_3{\lambda }^{n-3}+\dots ,\end{array}$$

(11)

$$\begin{array}{c}{P}_2\left(\lambda \right)={\lambda }^n+{\sigma }_1{\lambda }^{n-1}+{\omega }_2{\lambda }^{n-2}+{\sigma }_3{\lambda }^{n-3}+\dots \end{array}$$

(12)

have only real roots. Then all solutions of (9) are exponentially tends to 0 as $t\to +\infty$.

Theorem 1 was proved by A.Yu. Levin in [6]. Note that these roots (of the polynomials (11) and (12)) are negative necessarily due to positivity of ${\sigma }_i,{\omega }_i$, $i=\overline{1,n}$. Next, it follows from the proof of Theorem 1 [6] that every solution $x\left(t\right)$ of (9) along with its derivatives up to $(n-1)$-th order has the form $O\left(e^{-{\nu }_{n}t}\right)$ as $t\to +\infty$, where $-{\nu }_n<0$ is the largest of the roots of polynomials (11), (12).

By using standard replacement $y_1=x$, $y_2=x^{\prime }$, …, $y_n=x^{(n-1)}$, one can rewrite the control system (1), (5) in the form

$$\begin{array}{c}\dot{y}=A\left(t\right)y+Bu,\end{array}$$

(13)

$$\begin{array}{c}u=Vy.\end{array}$$

(14)

Here $A\left(t\right)$ is the companion matrix for the polynomial with the coefficients $p_i\left(t\right)$, $B=\mathrm{col}[0,\dots ,0,1]$, $V=[v_n,\dots ,v_1]$.

A large number of papers are devoted to the problems of robust asymptotic stability and stabilization for linear systems. We note here the famous works [12,13,14,15,16,17,18] and recent works [19,20,21,22]. The problems of stabilization of uncertain linear systems using linear matrix inequalities were studied in [23,24,25,26,27,28,29,30,31,32,33].

Uncertain systems (13), (14) were studied in [34,35,36,37] and in other works of A.H. Gelig and I.E. Zuber. In particular, it follows from results of [34] that system (13) is exponentially stabilizable by feedback control (14). This result is supplemented and developed in this paper. The difference between this result and the results obtained in the work is as follows. Firstly, we achieve exponential stabilization of (7) not only with some decay rate as it follows from [34] but with an arbitrary pregiven decay rate. Secondly, in contrast to [34], which uses the Second Lyapunov Method (Method of Lyapunov Function), we apply, in some sense, the First Lyapunov Method (which uses the roots of characteristic polynomial) and non-oscillation theory. Thirdly, we extend these stabilization results to systems with static output feedback control.

In this work, using Theorem 1, we prove results on exponential stabilization with any pregiven decay rate by linear stationary static state or output feedback for a control system defined by a linear time-varying differential equation of the n-th order with uncertain coefficients.

2. Preliminary Results

Theorem 2.

For any $\eta >0$ for any $n\in \mathbb{N}$ there exist polynomials

$$\begin{array}{c}f\left(\lambda \right)={\lambda }^n+{\delta }_1{\lambda }^{n-1}+{\gamma }_2{\lambda }^{n-2}+{\delta }_3{\lambda }^{n-3}+\dots ,\end{array}$$

(15)

$$\begin{array}{c}g\left(\lambda \right)={\lambda }^n+{\gamma }_1{\lambda }^{n-1}+{\delta }_2{\lambda }^{n-2}+{\gamma }_3{\lambda }^{n-3}+\dots \end{array}$$

(16)

such that the following properties hold:

$\left(i\right)$$0<{\gamma }_i\le {\delta }_i-1$, $i=1,\dots ,n$;

$\left(ii\right)$ the roots $-a_i$, $i=1,\dots ,n$, of $f\left(\lambda \right)$ and the roots $-b_i$, $i=1,\dots ,n$, of $g\left(\lambda \right)$ are real (and hence, negative);

$\left(iii\right)$ the following inequalities hold:

$$\begin{array}{c}\begin{array}{c}0>-\eta \ge -a_1>-b_1>-b_2>-a_2>-a_3>-b_3>\dots >-a_{2\ell -1}>-b_{2\ell -1}>-b_{2\ell }>-a_{2\ell }\\ \left(\mathit{if}n\mathit{is}\mathit{even}\mathit{and}n=2\ell \right);\end{array}\end{array}$$

(17)

$$\begin{array}{c}\begin{array}{c}0>-\eta \ge -b_1>-a_1>-a_2>-b_2>-b_3>-a_3>\dots >-a_{2\ell }>-b_{2\ell }>-b_{2\ell +1}>-a_{2\ell +1}\\ \left(\mathit{if}n\mathit{is}\mathit{odd}\mathit{and}n=2\ell +1\right).\end{array}\end{array}$$

(18)

Proof. 

At first, suppose that the theorem is proved for any $\eta \ge 1$. Let us construct, for $\eta =1$, the polynomials (15), (16) providing properties $\left(i\right)$, $\left(ii\right)$, $\left(iii\right)$, and denote them by $f_1\left(\lambda \right)$, $g_1\left(\lambda \right)$. Now, let $\eta \in (0,1)$. Then, let us set $f\left(\lambda \right):=f_1\left(\lambda \right)$, $g\left(\lambda \right):=g_1\left(\lambda \right)$. Hence, conditions $\left(i\right)$, $\left(ii\right)$ are satisfied. Since $-\eta >-1$, condition $\left(iii\right)$ holds as well. Thus, without loss of generality, one can assume that $\eta \ge 1$.

Let us give the proof by induction on n. The statements that we have to prove are different for odd and even numbers n: for even n, we need to ensure inequalities (17), in addition to $\left(i\right)$ and $\left(ii\right)$, and for odd n, we need to ensure inequalities (18). Therefore, the induction base as well as the induction hypothesis and the induction step should depend on whether the number n is even or odd. That is why we should check the induction base for $n=1$ and $n=2$.

Let $n=1$. For any $\eta \ge 1$, we set ${\gamma }_1:=\eta$, ${\delta }_1:=\eta +1$. Then the polynomials $f\left(\lambda \right)=\lambda +{\delta }_1$ and $g\left(\lambda \right)=\lambda +{\gamma }_1$ have the roots $-a_1=-{\delta }_1$ and $-b_1=-{\gamma }_1$ respectively. Obviously, conditions $\left(i\right)$, $\left(ii\right)$, and inequalities (18) are satisfied.

Let $n=2$. For any $\eta \ge 1$, we set

$$\begin{array}{c}{a}_1:=\eta ,a_2:=5\eta ,b_1:=2\eta ,b_2:=3\eta ,\end{array}$$

(19)

$$\begin{array}{c}f\left(\lambda \right):=(\lambda +a_1)(\lambda +a_2),g\left(\lambda \right):=(\lambda +b_1)(\lambda +b_2).\end{array}$$

(20)

Then

$${\delta }_1=6\eta ,{\gamma }_1=5\eta ,{\delta }_2=6{\eta }^2,{\gamma }_2=5{\eta }^2.$$

(21)

By (19), (20), condition $\left(ii\right)$ and inequality (17) are satisfied. By (21) and the inequality $\eta \ge 1$, condition $\left(i\right)$ is satisfied. The induction base is proved.

Let us put forward the induction hypothesis. Suppose that the assertion of the theorem is true for $n=k$. Then, let us prove that the assertion of the theorem is true for $n=k+1$. We will carry out the induction step for even and odd k separately.

By the induction hypothesis, there exist polynomials

$$\begin{array}{c}f\left(\lambda \right)={\lambda }^k+{\delta }_1{\lambda }^{k-1}+{\gamma }_2{\lambda }^{k-2}+\dots ,\end{array}$$

(22)

$$\begin{array}{c}g\left(\lambda \right)={\lambda }^k+{\gamma }_1{\lambda }^{k-1}+{\delta }_2{\lambda }^{k-2}+\dots \end{array}$$

(23)

such that

$$\begin{array}{c}0<{\gamma }_i\le {\delta }_i-1,i=\overline{1,k},\end{array}$$

(24)

$$\begin{array}{c}f\left(\lambda \right)=\prod _{i=1}^k(\lambda +a_i),g\left(\lambda \right)=\prod _{i=1}^k(\lambda +b_i),a_i,b_i\in \mathbb{R},a_i,b_i>0,i=\overline{1,k},\end{array}$$

(25)

$$\begin{array}{c}\begin{array}{c}0>-\eta \ge -a_1>-b_1>-b_2>-a_2>\dots >-a_{2\ell -1}>-b_{2\ell -1}>-b_{2\ell }>-a_{2\ell }(\mathrm{if}k=2\ell ),\end{array}\end{array}$$

(26)

$$\begin{array}{c}\begin{array}{c}0>-\eta \ge -b_1>-a_1>-a_2>-b_2>\dots >-a_{2\ell }>-b_{2\ell }>-b_{2\ell +1}>-a_{2\ell +1}(\mathrm{if}k=2\ell +1).\end{array}\end{array}$$

(27)

Let us prove that there exist polynomials

$$\begin{array}{c}F\left(\lambda \right)={\lambda }^{k+1}+{\Delta }_1{\lambda }^k+{\Gamma }_2{\lambda }^{k-1}+{\Delta }_3{\lambda }^{k-2}+\dots ,\end{array}$$

(28)

$$\begin{array}{c}G\left(\lambda \right)={\lambda }^{k+1}+{\Gamma }_1{\lambda }^k+{\Delta }_2{\lambda }^{k-1}+{\Gamma }_3{\lambda }^{k-2}+\dots \end{array}$$

(29)

such that

$$\begin{array}{c}0<{\Gamma }_i\le {\Delta }_i-1,i=\overline{1,k+1},\end{array}$$

(30)

$$\begin{array}{c}F\left(\lambda \right)=\prod _{i=1}^{k+1}(\lambda +A_i),G\left(\lambda \right)=\prod _{i=1}^{k+1}(\lambda +B_i),A_i,B_i\in \mathbb{R},A_i,B_i>0,i=\overline{1,k+1},\end{array}$$

(31)

$$\begin{array}{c}\begin{array}{c}0>-\eta \ge -B_1>-A_1>-A_2>-B_2>\dots >-A_{2\ell }>-B_{2\ell }>-B_{2\ell +1}>-A_{2\ell +1}\\ (\mathrm{if}k=2\ell ),\end{array}\end{array}$$

(32)

$$\begin{array}{c}\begin{array}{c}0>-\eta \ge -A_1>-B_1>-B_2>-A_2>\dots >-A_{2\ell +1}>-B_{2\ell +1}>-B_{2\ell +2}>-A_{2\ell +2}\\ (\mathrm{if}k=2\ell +1).\end{array}\end{array}$$

(33)

We assume that ${\delta }_0:=1$, ${\gamma }_0:=1$. Set

$$\begin{array}{c}{C}_1:={\displaystyle \underset{i=\overline{1,\ell }}{max}}\left\{{\displaystyle \frac{{\delta }_{2i-1}-{\gamma }_{2i-1}+1}{{\delta }_{2i-2}}},{\displaystyle \frac{1}{{\delta }_{2\ell }}}\right\},C_2:={\displaystyle \underset{j=\overline{1,\ell }}{max}}{\displaystyle \frac{{\delta }_{2j}-{\gamma }_{2j}+1}{{\delta }_{2j-1}}},N:={\displaystyle \underset{j=\overline{1,\ell }}{max}}{\displaystyle \frac{{\gamma }_{2j-1}}{{\delta }_{2j-1}}}\end{array}$$

(34)

for the case if $k=2\ell$, and

$$\begin{array}{c}{C}_1:={\displaystyle \underset{i=\overline{1,\ell +1}}{max}}{\displaystyle \frac{{\delta }_{2i-1}-{\gamma }_{2i-1}+1}{{\delta }_{2i-2}}},C_2:={\displaystyle \underset{j=\overline{1,\ell }}{max}}\left\{{\displaystyle \frac{{\delta }_{2j}-{\gamma }_{2j}+1}{{\delta }_{2j-1}}},{\displaystyle \frac{1}{{\delta }_{2\ell +1}}}\right\},N:={\displaystyle \underset{j=\overline{1,\ell +1}}{max}}{\displaystyle \frac{{\gamma }_{2j-1}}{{\delta }_{2j-1}}}\end{array}$$

(35)

for the case if $k=2\ell +1$. Then $C_1>0$, $C_2>0$, $0<N<1$. Consider lines

$$y=x+C_1,x=Ny+C_2.$$

(36)

They intersect at the point $M_0(x_0,y_0)$ with the coordinates $x_0={\displaystyle \frac{C_{1}N+C_2}{1-N}}>0$, $y_0={\displaystyle \frac{C_1+C_2}{1-N}}>0$. Consider the set ${\Omega }_0=\{(x,y)\in {\mathbb{R}}^2:y\ge x+C_1,x\ge Ny+C_2\}$. The set ${\Omega }_0$ is a cone, with a vertex at the point $M_0$, located in the first quadrant of the $xOy$-plane and bounded by half-lines (36) where $x\ge x_0$. The ray $m=\{(x,y)\in {\mathbb{R}}^2:x-x_0={\displaystyle \frac{1+N}{2}}(y-y_0),x\ge x_0\}$ is contained in ${\Omega }_0$. Consider the inequality system

$$\left\{\begin{array}{cc}\hfill y& \ge x+C_1,\hfill \\ \hfill x& \ge Ny+C_2,\hfill \\ \hfill x& >a_k.\hfill \end{array}\right.$$

(37)

The solution of system (37) is the set ${\Omega }_1={\Omega }_0\cap \{x>a_k\}$. The set ${\Omega }_1$ is non-empty. In particular, the point $M_1(\widehat{x},\widehat{y})$ lying on the ray m with $\widehat{x}=max\{x_0+1,a_k+1\}$ is contained in ${\Omega }_1$. Calculating $\widehat{y}$, we obtain that $\widehat{y}={\displaystyle \frac{2}{1+N}}max\{1,a_k-x_0+1\}+y_0.$

Set

$$\begin{array}{c}{A}_i:=b_i,B_i:=a_i,i=\overline{1,k},\end{array}$$

(38)

$$\begin{array}{c}{A}_{k+1}:=\widehat{y},B_{k+1}:=\widehat{x},\end{array}$$

(39)

$$\begin{array}{c}F\left(\lambda \right):=\prod _{i=1}^{k+1}(\lambda +A_i),G\left(\lambda \right):=\prod _{i=1}^{k+1}(\lambda +B_i).\end{array}$$

(40)

Then condition (31) is satisfied. Next, since $\widehat{x}>a_k$, it follows that

$$B_k<B_{k+1}.$$

(41)

Next, since $(\widehat{x},\widehat{y})$ is a solution of (37), we have

$$A_{k+1}=\widehat{y}\ge \widehat{x}+C_1>\widehat{x}=B_{k+1}.$$

(42)

Thus, it follows from inequalities (41), (42), equalities (38) and induction hypothesis (26), (27) that inequalities (32) are satisfied if $k=2\ell$, and inequalities (33) are satisfied if $k=2\ell +1$.

Let us prove inequalities (30). From the definition (40) of the polynomials $F\left(\lambda \right)$, $G\left(\lambda \right)$ and equalities (38), (25) we obtain that

$$F\left(\lambda \right)=g\left(\lambda \right)(\lambda +A_{k+1}),G\left(\lambda \right)=f\left(\lambda \right)(\lambda +B_{k+1}).$$

(43)

Substituting (22), (23) and (28), (29) into (43) and opening the brackets, we obtain equalities

$$\begin{array}{cccccc}\hfill {\Delta }_{2i-1}& =A_{k+1}{\delta }_{2i-2}+{\gamma }_{2i-1},\hfill & \hfill {\Gamma }_{2i-1}& =B_{k+1}{\gamma }_{2i-2}+{\delta }_{2i-1},\hfill & \hfill i& =\overline{1,\ell },\hfill \\ \hfill {\Delta }_{2\ell +1}& =A_{k+1}{\delta }_{2\ell },\hfill & \hfill {\Gamma }_{2\ell +1}& =B_{k+1}{\gamma }_{2\ell },\hfill & \hfill \\ \hfill {\Delta }_{2j}& =B_{k+1}{\delta }_{2j-1}+{\gamma }_{2j},\hfill & \hfill {\Gamma }_{2j}& =A_{k+1}{\gamma }_{2j-1}+{\delta }_{2j},\hfill & \hfill j& =\overline{1,\ell },\hfill \end{array}$$

for the case if $k=2\ell$, and equalities

$$\begin{array}{cccccc}\hfill {\Delta }_{2i-1}& =A_{k+1}{\delta }_{2i-2}+{\gamma }_{2i-1},\hfill & \hfill {\Gamma }_{2i-1}& =B_{k+1}{\gamma }_{2i-2}+{\delta }_{2i-1},\hfill & \hfill i& =\overline{1,\ell +1},\hfill \\ \hfill {\Delta }_{2j}& =B_{k+1}{\delta }_{2j-1}+{\gamma }_{2j},\hfill & \hfill {\Gamma }_{2j}& =A_{k+1}{\gamma }_{2j-1}+{\delta }_{2j},\hfill & \hfill j& =\overline{1,\ell },\hfill \\ \hfill {\Delta }_{2\ell +2}& =B_{k+1}{\delta }_{2\ell +1},\hfill & \hfill {\Gamma }_{2\ell +2}& =A_{k+1}{\gamma }_{2\ell +1},\hfill & \hfill \end{array}$$

for the case if $k=2\ell +1$. The inequalities ${\Gamma }_i>0$, $i=\overline{1,k+1}$, are satisfied due to inequalities (24) and the inequalities $A_{k+1}>0$, $B_{k+1}>0$. The inequalities

$${\Gamma }_i\le {\Delta }_i-1,i=\overline{1,k+1},$$

(44)

are equivalent to the inequality system

$$\left\{\begin{array}{cccc}\hfill {\gamma }_{2i-1}+A_{k+1}{\delta }_{2i-2}& \ge B_{k+1}{\gamma }_{2i-2}+{\delta }_{2i-1}+1,\hfill & \hfill i& =\overline{1,\ell },\hfill \\ \hfill A_{k+1}{\delta }_{2\ell }& \ge B_{k+1}{\gamma }_{2\ell }+1,\hfill & \hfill \\ \hfill {\gamma }_{2j}+B_{k+1}{\delta }_{2j-1}& \ge A_{k+1}{\gamma }_{2j-1}+{\delta }_{2j}+1,\hfill & \hfill j& =\overline{1,\ell },\hfill \end{array}\right.$$

(45)

for the case if $k=2\ell$, and are equivalent to the inequality system

$$\left\{\begin{array}{cccc}\hfill {\gamma }_{2i-1}+A_{k+1}{\delta }_{2i-2}& \ge B_{k+1}{\gamma }_{2i-2}+{\delta }_{2i-1}+1,\hfill & \hfill i& =\overline{1,\ell +1},\hfill \\ \hfill {\gamma }_{2j}+B_{k+1}{\delta }_{2j-1}& \ge A_{k+1}{\gamma }_{2j-1}+{\delta }_{2j}+1,\hfill & \hfill j& =\overline{1,\ell },\hfill \\ \hfill B_{k+1}{\delta }_{2\ell +1}& \ge A_{k+1}{\gamma }_{2\ell +1}+1,\hfill & \hfill \end{array}\right.$$

(46)

for the case if $k=2\ell +1$. System (45) is equivalent to the inequality system

$$\left\{\begin{array}{cccc}\hfill A_{k+1}& \ge B_{k+1}{\displaystyle \frac{{\gamma }_{2i-2}}{{\delta }_{2i-2}}}+{\displaystyle \frac{{\delta }_{2i-1}-{\gamma }_{2i-1}+1}{{\delta }_{2i-2}}},\hfill & \hfill i& =\overline{1,\ell },\hfill \\ \hfill A_{k+1}& \ge B_{k+1}{\displaystyle \frac{{\gamma }_{2\ell }}{{\delta }_{2\ell }}}+{\displaystyle \frac{1}{{\delta }_{2\ell }}},\hfill & \hfill \\ \hfill B_{k+1}& \ge A_{k+1}{\displaystyle \frac{{\gamma }_{2j-1}}{{\delta }_{2j-1}}}+{\displaystyle \frac{{\delta }_{2j}-{\gamma }_{2j}+1}{{\delta }_{2j-1}}},\hfill & \hfill j& =\overline{1,\ell }.\hfill \end{array}\right.$$

(47)

System (46) is equivalent to the inequality system

$$\left\{\begin{array}{cccc}\hfill A_{k+1}& \ge B_{k+1}{\displaystyle \frac{{\gamma }_{2i-2}}{{\delta }_{2i-2}}}+{\displaystyle \frac{{\delta }_{2i-1}-{\gamma }_{2i-1}+1}{{\delta }_{2i-2}}},\hfill & \hfill i& =\overline{1,\ell +1},\hfill \\ \hfill B_{k+1}& \ge A_{k+1}{\displaystyle \frac{{\gamma }_{2j-1}}{{\delta }_{2j-1}}}+{\displaystyle \frac{{\delta }_{2j}-{\gamma }_{2j}+1}{{\delta }_{2j-1}}},\hfill & \hfill j& =\overline{1,\ell },\hfill \\ \hfill B_{k+1}& \ge A_{k+1}{\displaystyle \frac{{\gamma }_{2\ell +1}}{{\delta }_{2\ell +1}}}+{\displaystyle \frac{1}{{\delta }_{2\ell +1}}}.\hfill & \hfill \end{array}\right.$$

(48)

For the case if $k=2\ell$, the following inequalities hold:

$${\displaystyle \frac{{\gamma }_{2i}}{{\delta }_{2i}}}\le 1,i=\overline{0,\ell };{\displaystyle \frac{{\gamma }_{2j-1}}{{\delta }_{2j-1}}}\le N,j=\overline{1,\ell }.$$

For the case if $k=2\ell +1$, the following inequalities hold:

$${\displaystyle \frac{{\gamma }_{2i}}{{\delta }_{2i}}}\le 1,i=\overline{0,\ell };{\displaystyle \frac{{\gamma }_{2j-1}}{{\delta }_{2j-1}}}\le N,j=\overline{1,\ell +1}.$$

Thus, it follows from definitions (34), (35) that to satisfy inequalities (47) (for the case if $k=2\ell$) and inequalities (48) (for the case if $k=2\ell +1$) it is sufficient to satisfy inequalities

$$\left\{\begin{array}{cc}\hfill A_{k+1}& \ge B_{k+1}+C_1\hfill \\ \hfill B_{k+1}& \ge N{A}_{k+1}+C_2.\hfill \end{array}\right.$$

(49)

By (39), inequalities (49) hold because $(\widehat{x},\widehat{y})\in {\Omega }_0$. Therefore, inequalities (44) are satisfied. Hence, (30) are satisfied. Thus, the induction step is proved. The theorem is proved.  ☐

3. Time-Invariant Stabilization by Static State Feedback

Definition 1.

We say that system (1) is exponentially stabilizable with the decay rate $\theta >0$ by linear stationary static state feedback (5) if there exist constants $v_1,\dots ,v_n\in \mathbb{R}$ such that every solution $x\left(t\right)$ of the closed-loop system (7) is exponentially stable with the decay rate θ, i.e., $x\left(t\right)$ along with its derivatives up to $(n-1)$-th order has the form $O\left(e^{-\theta t}\right)$ as $t\to +\infty$.

Theorem 3.

System (1) is exponentially stabilizable with an arbitrary pregiven decay rate $\theta >0$ by linear stationary static state feedback (5).

Proof. 

Let an arbitrary $\theta >0$ be given. Denote ${\rho }_i:={\beta }_i-{\alpha }_i$, $i=\overline{1,n}$, where ${\alpha }_i$, ${\beta }_i$ are from (2). We have ${\rho }_i\ge 0$, $i=\overline{1,n}$. We set $L:=max\{1,{\rho }_1,\sqrt{{\rho }_2},\dots ,\sqrt[n]{{\rho }_n}\}$. Then

$$L\ge 1>0,L\ge {\rho }_1,L^2\ge {\rho }_2,\dots ,L^n\ge {\rho }_n.$$

(50)

Set $\eta :=\theta /L$. Then $\eta >0$. Let us construct the polynomials (15), (16) according to Theorem 2 so that properties $\left(i\right)$, $\left(ii\right)$, $\left(iii\right)$ are satisfied. Then the roots $-a_i$ and $-b_i$ ($i=\overline{1,n}$) of the polynomials $f\left(\lambda \right)$ and $g\left(\lambda \right)$ are real and the following inequalities hold:

$$-a_i\le -\eta ,-b_i\le -\eta ,i=\overline{1,n}.$$

(51)

Let us construct the polynomials $P_1\left(\lambda \right)$, $P_2\left(\lambda \right)$ by formulas (11), (12) where ${\omega }_i={\delta }_i{L}^i$, ${\sigma }_i={\gamma }_i{L}^i$, $i=\overline{1,n}$. Then $P_1\left(\lambda \right)$ and $P_2\left(\lambda \right)$ have the roots $-c_i:=-a_{i}L$ and $-d_i:=-b_{i}L$ ($i=\overline{1,n}$) respectively. These roots are real and by virtue of (51) the following inequalities hold:

$$-c_i\le -\theta ,-d_i\le -\theta ,i=\overline{1,n}.$$

(52)

We set $v_i:={\alpha }_i-{\gamma }_i{L}^i$, $i=\overline{1,n}$, in (5) and consider the closed-loop system (7). System (7) has the form (9) where $q_i\left(t\right)=p_i\left(t\right)-v_i$, $i=\overline{1,n}$. Taking into account inequalities (2), (50) and property $\left(i\right)$, for every $i=\overline{1,n}$ for all $t\in {\mathbb{R}}_{+}$, we have

$$\begin{array}{c}0<{\sigma }_i={\gamma }_i{L}^i={\alpha }_i-{\alpha }_i+{\gamma }_i{L}^i\le p_i\left(t\right)-v_i=:q_i\left(t\right)\le \\ \le {\beta }_i-{\alpha }_i+{\gamma }_i{L}^i={\rho }_i+{\gamma }_i{L}^i\le L^i(1+{\gamma }_i)\le {\delta }_i{L}^i={\omega }_i.\end{array}$$

Thus, inequalities (10) hold. Applying Theorem 1 and inequalities (52), we obtain that the closed-loop system (7) is exponentially stable with the decay rate $\theta$. The theorem is proved.  ☐

Example 1.

Let $n=2$. Consider a control system (1):

$$x^{″}+p_1\left(t\right)x^{\prime }+p_2\left(t\right)x=u,t\in {\mathbb{R}}_{+},x\in \mathbb{R},u\in \mathbb{R}.$$

(53)

Suppose that $p_1\left(t\right),p_2\left(t\right)$ satisfy conditions ${\alpha }_1\le p_1\left(t\right)\le {\beta }_1$, ${\alpha }_2\le p_2\left(t\right)\le {\beta }_2$, $t\in {\mathbb{R}}_{+}$. Suppose, for simplicity, that ${\rho }_1:={\beta }_1-{\alpha }_1\le 1$, ${\rho }_2:={\beta }_2-{\alpha }_2\le 1$ (one can achieve this by replacing time $\tilde{x}\left(t\right)=x\left(\mu t\right))$. Let $\theta >0$ be an arbitrary number. One needs to construct the controller $u=u\left(\mathbf{x}\right)$ in (53) where

$$u\left(\mathbf{x}\right)=v_1{x}^{\prime }+v_{2}x$$

(54)

with constant numbers $v_1$, $v_2$ such that the closed-loop system

$$x^{″}+(p_1\left(t\right)-v_1)x^{\prime }+(p_2\left(t\right)-v_2)x=0$$

(55)

is exponentially stable with the decay rate θ. Without loss of generality, we suppose that $\theta \ge 1$. For constructing (54) we use the proof of Theorem 3. We have $L=1$. Set $\eta :=\theta$. Then $\eta \ge 1$. Let us construct the polynomials (15), (16) according to Theorem 2: $f\left(\lambda \right):={\lambda }^2+6\eta \lambda +5{\eta }^2$, $g\left(\lambda \right):={\lambda }^2+5\eta \lambda +6{\eta }^2$. Then ${\gamma }_1=5\eta$, ${\gamma }_2=5{\eta }^2$, ${\delta }_1=6\eta$, ${\delta }_2=6{\eta }^2$. Due to $\eta \ge 1$, condition $\left(i\right)$ holds. Next, the equalities $P_1\left(\lambda \right)=f\left(\lambda \right)$, $P_2\left(\lambda \right)=g\left(\lambda \right)$ hold. The gain coefficients constructed by Theorem 3 have the form

$$v_1={\alpha }_1-5\theta ,v_2={\alpha }_2-5{\theta }^2.$$

(56)

Let us substitute (56) into (54). The closed-loop system (55) take the form

$$x^{″}+(s_1\left(t\right)+5\theta )x^{\prime }+(s_2\left(t\right)+5{\theta }^2)x=0,t\in {\mathbb{R}}_{+}.$$

(57)

Here

$$\begin{array}{c}0\le s_1\left(t\right):=p_1\left(t\right)-{\alpha }_1\le {\beta }_1-{\alpha }_1={\rho }_1\le 1=L,\\ 0\le s_2\left(t\right):=p_2\left(t\right)-{\alpha }_2\le {\beta }_2-{\alpha }_2={\rho }_2\le 1=L^2.\end{array}$$

All solutions of (57) are exponentially stable with the decay rate θ. Let us check it.

The substitution $z_1=x$, $z_2=x^{\prime }$ reduces Equation (57) to the system

$$\begin{array}{c}\dot{z}=A\left(t\right)z,t\in {\mathbb{R}}_{+},\\ z=\left[\begin{array}{c}{z}_1\\ z_2\end{array}\right],A\left(t\right)=\left[\begin{array}{cc}0& 1\\ -(s_2\left(t\right)+5{\theta }^2)& -(s_1\left(t\right)+5\theta )\end{array}\right].\end{array}$$

(58)

Let us show that system (58) is exponentially stable with the decay rate θ. The substitution

$$z\left(t\right)=e^{-\theta t}y\left(t\right).$$

(59)

reduce system (58) to the system

$$\begin{array}{c}\dot{y}=B\left(t\right)y,t\in {\mathbb{R}}_{+},\\ y=\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right],B\left(t\right)=\left[\begin{array}{cc}\theta & 1\\ -(s_2\left(t\right)+5{\theta }^2)& -(s_1\left(t\right)+4\theta )\end{array}\right].\end{array}$$

(60)

Let us show that system (60) is Lyapunov stable. Set $S=\left[\begin{array}{cc}7{\theta }^2& 2\theta \\ 2\theta & 1\end{array}\right]$. Then $S>0$ in the sense of quadratic forms. Next, we have

$$B^T\left(t\right)S+SB\left(t\right)=\left[\begin{array}{cc}-6{\theta }^3-4\theta s_2\left(t\right)& -4{\theta }^2-2\theta s_1\left(t\right)-s_2\left(t\right)\\ -4{\theta }^2-2\theta s_1\left(t\right)-s_2\left(t\right)& -4\theta -2s_1\left(t\right)\end{array}\right].$$

(61)

Here and throughout, T is the transposition. Let us find the principal minors of (61). We obtain

$$\begin{array}{c}{\Delta }_1=-2\theta (3{\theta }^2+2s_2\left(t\right))<0,{\Delta }_2=-4\theta -2s_1\left(t\right)<0,\\ {\Delta }_{1,2}=det(B^T\left(t\right)S+SB\left(t\right))=8{\theta }^4-4{\theta }^3{s}_1\left(t\right)+8{\theta }^2{s}_2\left(t\right)-4{\theta }^2{s}_1^2\left(t\right)+4\theta s_1\left(t\right)s_2\left(t\right)-s_2^2\left(t\right).\end{array}$$

We have

$$\begin{array}{c}8{\theta }^4-4{\theta }^3{s}_1\left(t\right)-4{\theta }^2{s}_1^2\left(t\right)=4{\theta }^3(\theta -s_1\left(t\right))+4{\theta }^2({\theta }^2-s_1^2\left(t\right))\ge 0,\\ 8{\theta }^2{s}_2\left(t\right)-s_2^2\left(t\right)=s_2\left(t\right)(8{\theta }^2-s_2\left(t\right))\ge 0.\end{array}$$

Hence ${\Delta }_{1,2}\ge 0$. Thus, (61) is negative-semidefinite. Therefore, system (60) is stable. Hence, all solutions of (60) are bounded as $t\to +\infty$. Then, by (59), $\parallel z\left(t\right)\parallel =O\left(e^{-\theta t}\right)$, $t\to +\infty$, as required.

As an example of numerical simulation, consider system (53) with $p_1\left(t\right)={\displaystyle \frac{t}{1+t^2}}$, $p_2\left(t\right)=-{\displaystyle \frac{1}{1+t^2}}$:

$$x^{″}+{\displaystyle \frac{t}{1+t^2}}{x}^{\prime }-{\displaystyle \frac{1}{1+t^2}}x=u.$$

(62)

We have ${\alpha }_1:=-1/2\le p_1\left(t\right)\le 1/2=:{\beta }_1$, ${\alpha }_2:=-1\le p_1\left(t\right)\le 0=:{\beta }_2$, ${\rho }_1:={\beta }_1-{\alpha }_1=1$, ${\rho }_2:={\beta }_2-{\alpha }_2=1$. The free system (i.e., system (62) with $u=0$) has a general solution

$$x\left(t\right)=C_{1}t+C_2\sqrt{t^2+1}$$

and, obviously, is unstable. Let us set $\theta :=1$, $\eta :=\theta =1$. The gain coefficients (56) have the form

$$v_1={\alpha }_1-5\theta =-11/2,v_2={\alpha }_2-5{\theta }^2=-6.$$

The closed-loop system (57) take the form

$$x^{″}+\left({\displaystyle \frac{11}{2}}+{\displaystyle \frac{t}{1+t^2}}\right)x^{\prime }+\left(6-{\displaystyle \frac{1}{1+t^2}}\right)x=0.$$

(63)

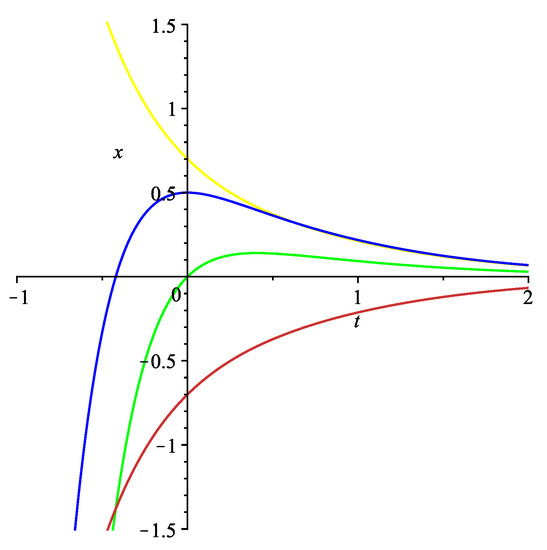
System (63) is exponentially stable with the decay rate $\theta =1$. Some graphs of the solutions to system (63) are shown in Figure 1.

Figure 1. Graphs of the solutions to (63).

4. Time-Invariant Stabilization by Static Output Feedback

Consider a linear control system defined by a linear differential equation of n-th order with time-varying uncertain coefficients satisfying (2); the input is a stationary linear combination of m variables and their derivatives of order $\le n-p$; the output is a k-dimensional vector of stationary linear combinations of the state x and its derivatives of order $\le p-1$:

$$\begin{array}{c}{x}^{\left(n\right)}+\sum _{i=1}^n{p}_i\left(t\right)x^{(n-i)}=\sum _{\tau =1}^m\sum _{l=p}^n{b}_{l\tau }{w}_{\tau }^{(n-l)},x\in \mathbb{R},b_{l\tau }\in \mathbb{R},t\in {\mathbb{R}}_{+},\end{array}$$

(64)

$$\begin{array}{c}{y}_j=\sum _{\nu =1}^p{c}_{\nu j}{x}^{(\nu -1)},j=\overline{1,k},c_{\nu j}\in \mathbb{R},\end{array}$$

(65)

$w=\mathrm{col}(w_1,\dots ,w_m)\in {\mathbb{R}}^m$ is an input vector; $y=\mathrm{col}(y_1,\dots ,y_k)\in {\mathbb{R}}^k$ is an output vector. Let the control in (64), (65) have the form of linear static output feedback

$$\begin{array}{c}w=Uy.\end{array}$$

(66)

We suppose that the gain matrix U is time-invariant. The closed-loop system has the form

$$\begin{array}{c}{x}^{\left(n\right)}+q_1\left(t\right)x^{(n-1)}+\dots +q_n\left(t\right)x=0,t\in {\mathbb{R}}_{+},\end{array}$$

(67)

where the coefficients $q_i\left(t\right)$ of (67) depends on $p_i\left(t\right)$, $b_{l\tau }$, $c_{\nu j}$, U. On the basis of system (64), (65), we construct the $n\times m$-matrix $B=\left\{b_{l\tau }\right\}$, $l=\overline{1,n}$, $\tau =\overline{1,m}$, and the $n\times k$-matrix $C=\left\{c_{\nu j}\right\}$, $\nu =\overline{1,n}$, $j=\overline{1,k}$, where $b_{l\tau }=0$ for $l<p$ and $c_{\nu j}=0$ for $\nu >p$. Denote by J the matrix whose entries of the first superdiagonal are equal to unity and whose remaining entries are zero; we set $J^0:=I$. By $\mathrm{Sp}Q$ denote the trace of a matrix Q.

Definition 2.

We say that system (64), (65) is exponentially stabilizable with the decay rate $\theta >0$ by linear stationary static output feedback (66) if there exists a constant $m\times k$-matrix U such that every solution $x\left(t\right)$ of the closed-loop system (67) is exponentially stable with the decay rate θ.

Theorem 4.

Suppose that linear stationary output feedback (66) bring system (64), (65) to the closed system (67). Then the coefficients $q_i\left(t\right)$, $i=\overline{1,n}$, of (67) satisfy the equalities

$$q_i\left(t\right)=p_i\left(t\right)-r_i,$$

where

$$r_i=\mathrm{Sp}\left(C^T{J}^{i-1}BU\right),i=\overline{1,n}.$$

(68)

The proof of Theorem 4 is identical to the proof of Theorem 1 [38].

Let us introduce the mapping $\mathrm{vec}$ that unwraps an $n\times m$-matrix $H=\left\{h_{ij}\right\}$ row-by-row into the column vector $\mathrm{vec}H=\mathrm{col}(h_{11},h_{12},\dots ,h_{1m},\dots ,h_{n1},\dots ,h_{nm})$. For any $k\times m$-matrices X, Y, the obvious equality holds:

$$\mathrm{Sp}\left(X{Y}^T\right)={\left(\mathrm{vec}X\right)}^T·\left(\mathrm{vec}Y\right).$$

(69)

Let us construct the $k\times m$-matrices

$$C^T{J}^{0}B,C^{T}JB,\dots ,C^T{J}^{n-1}B$$

(70)

and the $mk\times n$-matrix

$$P=[\mathrm{vec}\left(C^T{J}^{0}B\right),\dots ,\mathrm{vec}\left(C^T{J}^{n-1}B\right)].$$

Denote $r=\mathrm{col}(r_1,\dots ,r_n)\in {\mathbb{R}}^n$, $\psi =\mathrm{vec}\left(U^T\right)$. Equalities (68) represent a linear system of n equations with respect to the coefficients of the matrix U. Taking into account (69), one can rewrite system (68) in the form

$$P^T\psi =r.$$

(71)

Suppose that matrices (70) are linearly independent. Then $\mathrm{rank}P=n$. Hence, the system of linear equations (71) is solvable for any vector $r\in {\mathbb{R}}^n$. In particular, system (71) has the solution $\psi =P{\left(P^{T}P\right)}^{-1}r$.

By Theorem 3, for any pregiven $\theta >0$ there exists a constant vector $r=\mathrm{col}(r_1,\dots ,r_n)$ such that system (67) with $q_i\left(t\right)=p_i\left(t\right)-r_i$ is exponentially stable with the decay rate $\theta$. Resolving system (71) for that r with respect to $\psi$ and constructing U by the formula $U={\left({\mathrm{vec}}^{-1}\psi \right)}^T$, we find the gain matrix of feedback (66) exponentially stabilizing system (64), (65) with the decay rate $\theta$. Thus, the following theorem is proved.

Theorem 5.

System (64), (65) is exponentially stabilizable with an arbitrary pregiven decay rate $\theta >0$ by linear stationary static output feedback (66) if matrices (70) are linearly independent.

Example 2.

Let $n=3$. Consider a control system

$$\begin{array}{c}{x}^{″\prime }+p\left(t\right)x=w_1^{\prime }+w_1-w_2^{\prime }+w_2,t\in {\mathbb{R}}_{+},x\in \mathbb{R},w=\mathrm{col}(w_1,w_2)\in {\mathbb{R}}^2,\end{array}$$

(72)

$$\begin{array}{c}{y}_1=x-x^{\prime },y_2=x+x^{\prime },y=\mathrm{col}(y_1,y_2)\in {\mathbb{R}}^2.\end{array}$$

(73)

System (72), (73) has the form (64), (65) where $n=3$, $m=k=p=2$. Suppose that $p\left(t\right)$ is an arbitrary measurable function satisfying the condition $0\le p\left(t\right)\le 1$. Let $\theta >0$ be an arbitrary number. One needs to construct feedback control (66), where $U={\left\{u_{ij}\right\}}_{i,j=1}^2$, with constant $u_{ij}$, $i,j=1,2$, providing exponential stability of the closed-loop system with the decay rate θ. Without loss of generality, we suppose that $\theta \ge 1$. By Theorem 4, the closed-loop system has the form

$$x^{‴}-r_1{x}^{″}-r_2{x}^{\prime }+(p\left(t\right)-r_3)x=0,$$

(74)

where $r_i$ have the form (68), and

$$B=\left[\begin{array}{cc}0& 0\\ 1& -1\\ 1& 1\end{array}\right],C=\left[\begin{array}{cc}1& 1\\ -1& 1\\ 0& 0\end{array}\right].$$

At first, let us construct a constant vector $r=\mathrm{col}(r_1,r_2,r_3)$, providing exponential stability of (74). For constructing r we use the proof of Theorem 3. We have ${\alpha }_1={\beta }_1=0$, ${\alpha }_2={\beta }_2=0$, ${\alpha }_3=0$, ${\beta }_3=1$. Then ${\rho }_1=0$, ${\rho }_2=0$, ${\rho }_3=1$, $L=1$. Set $\eta :=\theta$. Using the proof of Theorem 2, we construct the polynomials (15), (16) such that properties $\left(i\right)$, $\left(ii\right)$, $\left(iii\right)$ are satisfied:

$$\begin{array}{cc}\hfill f\left(\lambda \right):=& (\lambda +2\eta )(\lambda +3\eta )(\lambda +14\eta )={\lambda }^3+19\eta {\lambda }^2+76{\eta }^2\lambda +84{\eta }^3,\hfill \\ \hfill g\left(\lambda \right):=& (\lambda +\eta )(\lambda +5\eta )(\lambda +12\eta )={\lambda }^3+18\eta {\lambda }^2+77{\eta }^2\lambda +60{\eta }^3.\hfill \end{array}$$

Then ${\gamma }_1=18\eta$, ${\gamma }_2=76{\eta }^2$, ${\gamma }_3=60{\eta }^3$, ${\delta }_1=19\eta$, ${\delta }_2=77{\eta }^2$, ${\delta }_3=84{\eta }^3$. Conditions $\left(i\right)$, $\left(ii\right)$, $\left(iii\right)$ hold. Coefficients $r_1$, $r_2$, $r_3$ have the form

$$r_1=-18\theta ,r_2=-76{\theta }^2,r_3=-60{\theta }^3.$$

(75)

Let us substitute (75) into (74). The closed-loop system (74) take the form

$$x^{‴}+18\theta x^{″}+76{\theta }^2{x}^{\prime }+(p\left(t\right)+60{\theta }^3)x=0.$$

(76)

All solutions of (76) are exponentially stable with the decay rate θ. Let us check it.

The substitution $z_1=x$, $z_2=x^{\prime }$, $z_3=x^{″}$ reduces Equation (76) to the system

$$\begin{array}{c}\dot{z}=A\left(t\right)z,t\in {\mathbb{R}}_{+},\\ z=\left[\begin{array}{c}{z}_1\\ z_2\\ z_3\end{array}\right],A\left(t\right)=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -(p\left(t\right)+60{\theta }^3)& -76{\theta }^2& -18\theta \end{array}\right].\end{array}$$

(77)

Let us show that the system (77) is exponentially stable with the decay rate θ. The substitution

$$z\left(t\right)=e^{-\theta t}y\left(t\right).$$

(78)

reduce the system (77) to the system

$$\begin{array}{c}\dot{y}=B\left(t\right)y,t\in {\mathbb{R}}_{+},\\ y=\left[\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right],B\left(t\right)=\left[\begin{array}{ccc}\theta & 1& 0\\ 0& \theta & 1\\ -(p\left(t\right)+60{\theta }^3)& -76{\theta }^2& -17\theta \end{array}\right].\end{array}$$

(79)

Let us show that system (79) is Lyapunov stable. Set $S=\left[\begin{array}{ccc}9000{\theta }^4& 2580{\theta }^3& 150{\theta }^2\\ 2580{\theta }^3& 804{\theta }^2& 46\theta \\ 150{\theta }^2& 46\theta & 3\end{array}\right]$. Let us find the successive principal minors $s_i$, $i=1,2,3$, of S. We have $s_1=9000{\theta }^4>0$, $s_2=det\left[\begin{array}{cc}9000{\theta }^4& 2580{\theta }^3\\ 2580{\theta }^3& 804{\theta }^2\end{array}\right]=579,600{\theta }^6>0$, $s_3=detS=208,800{\theta }^6>0$. Then $S>0$ in the sense of quadratic forms. Next, we have

$$B^T\left(t\right)S+SB\left(t\right)=\left[\begin{array}{ccc}-300{\theta }^{2}p\left(t\right)& -46\theta p\left(t\right)& -3p\left(t\right)\\ -46\theta p\left(t\right)& -224{\theta }^3& -10{\theta }^2\\ -3p\left(t\right)& -10{\theta }^2& -10\theta \end{array}\right].$$

(80)

Let us find the principal minors of (80). We obtain

$$\begin{array}{c}{\Delta }_1=-300{\theta }^{2}p\left(t\right)\le 0,{\Delta }_2=-224{\theta }^3<0,{\Delta }_3=-10\theta <0,\\ {\Delta }_{1,2}=67,200{\theta }^{5}p\left(t\right)-2116{\theta }^2{p}^2\left(t\right)=4{\theta }^{2}p\left(t\right)(16,800{\theta }^3-529p\left(t\right))\ge 0,\\ {\Delta }_{1,3}=3000{\theta }^{3}p\left(t\right)-9p^2\left(t\right)=3p\left(t\right)(1000{\theta }^3-3p\left(t\right))\ge 0,{\Delta }_{2,3}=2140{\theta }^4>0,\\ {\Delta }_{1,2,3}=det(B^T\left(t\right)S+SB\left(t\right))=-642,000{\theta }^{6}p\left(t\right)+20,416{\theta }^3{p}^2\left(t\right)=-16{\theta }^{3}p\left(t\right)(40,125{\theta }^3-1276p\left(t\right))\le 0.\end{array}$$

Hence, (80) is negative-semidefinite. Thus, the system (79) is stable. Hence, all solutions of (79) are bounded as $t\to +\infty$. Then, by (78), $\parallel z\left(t\right)\parallel =O\left(e^{-\theta t}\right)$, $t\to +\infty$, as required.

Next, let us construct matrices (70) and P. We obtain $P=\left[\begin{array}{ccc}-1& 0& 1\\ 1& -2& 1\\ 1& 2& 1\\ -1& 0& 1\end{array}\right]$. Obviously, $\mathrm{rank}P=3$ and matrices (70) are linearly independent. Resolving system (71) where $r_i$ has the form (75), we obtain

$$\begin{array}{c}\psi =\mathrm{col}[9\theta /2-15{\theta }^3,-9\theta /2+19{\theta }^2-15{\theta }^3,-9\theta /2-19{\theta }^2-15{\theta }^3,9\theta /2-15{\theta }^3].\end{array}$$

Thus, the gain matrix has the form

$$U=\left[\begin{array}{cc}9\theta /2-15{\theta }^3& -9\theta /2-19{\theta }^2-15{\theta }^3\\ -9\theta /2+19{\theta }^2-15{\theta }^3& 9\theta /2-15{\theta }^3\end{array}\right].$$

(81)

We obtain that feedback (66) with the matrix (81) exponentially stabilizes the system (72), (73) with the decay rate θ.

As an example of numerical simulation, consider system (72), (73) where

$$\widehat{p}\left(t\right)=\left\{\begin{array}{cc}1,\hfill & t\in [0,1),\hfill \\ 0,\hfill & t\in [1,2),\hfill \end{array}\right.p\left(t\right)=\widehat{p}(t-2k),t\in [2k,2(k+1)),k\in \mathbb{Z}.$$

We have $0\le p\left(t\right)\le 1$. The function $p\left(t\right)$ is ω-periodic with the period $\omega =2$. The free system

$$x^{‴}+p\left(t\right)x=0,x\in \mathbb{R},$$

(82)

is equivalent to the system of differential equations

$$\dot{z}=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -p\left(t\right)& 0& 0\end{array}\right]z,z\in {\mathbb{R}}^3.$$

(83)

System (83) is ω-periodic. Since system (83) is piecewise constant, the monodromy matrix $\Phi \left(\omega \right)$ for system (83) can be found explicitly. Calculating approximately eigenvalues ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$ of $\Phi \left(\omega \right)$, we obtain ${\lambda }_{1,2}\approx 0.418\pm 2.167i$, ${\lambda }_3\approx 0.205$. Hence, $|{\lambda }_1|=|{\lambda }_2|>1$. Thus, system (83) (and hence, Equation (82)) is unstable. Let us set $\theta :=1$, $\eta :=\theta =1$. The gain matrix (81) has the form

$$U=\left[\begin{array}{cc}-21/2& -77/2\\ -1/2& -21/2\end{array}\right].$$

The closed-loop system (76) take the form

$$x^{‴}+18x^{″}+76x^{\prime }+(p\left(t\right)+60)x=0.$$

(84)

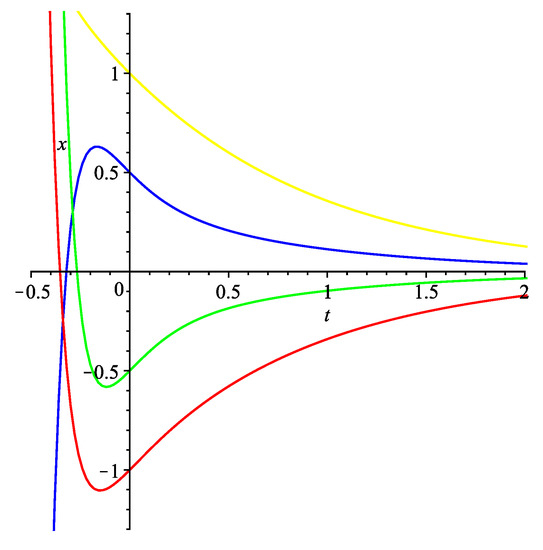
System (84) is exponentially stable with the decay rate $\theta =1$. Some graphs of the solutions to system (84) are shown in Figure 2.

Figure 2. Graphs of the solutions to (84).

5. Conclusions

We examined the problem of exponential stabilization with any pregiven decay rate for a linear time-varying differential equations with uncertain bounded coefficients by means of stationary linear static feedback. We have received sufficient conditions for the solvability of this problem by state and output feedback. For this purpose, the first Lyapunov method and the Levin theorem on non-oscillatory absolute stability were used. We plan to extend these results to systems of differential equation including systems with delays. A further development of these results may be their extension to systems (64), (65), (66), when $b_{l\tau }$ and (or) $c_{\nu j}$ depend on t. So far this question remains open.