Selecting the Low-Carbon Tourism Destination: Based on Pythagorean Fuzzy Taxonomy Method
Abstract
1. Introduction
2. Literature Review
3. Preliminaries
- a.
- if, then;
- b.
- if, then,.
- ①
- ②
- ③
- ④
- ⑤
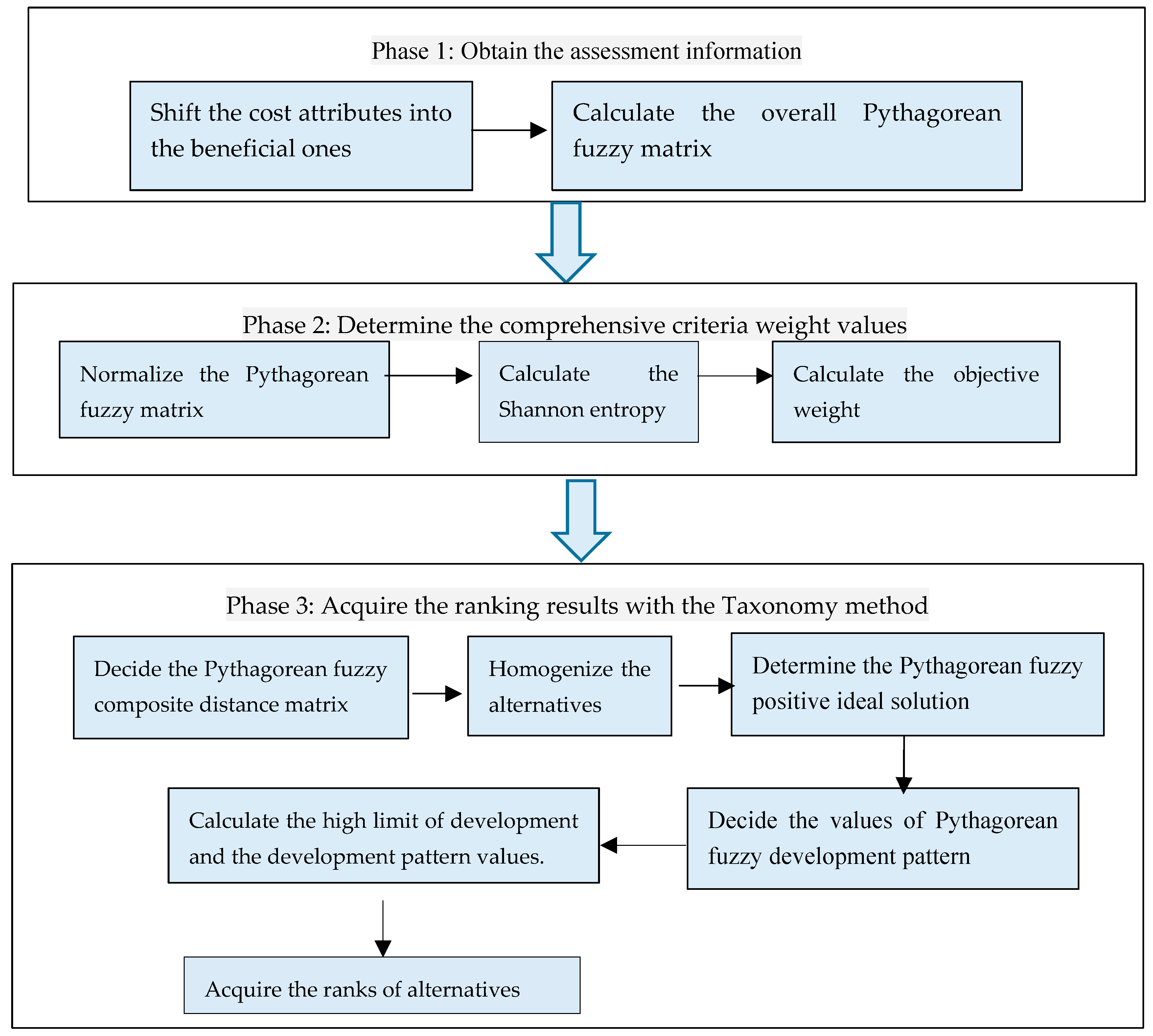
4. Taxonomy Method for Pythagorean Fuzzy MAGDM Issues with Entropy Weight
- (I)
- Phase 1: Obtain the assessment information
- Step 1.
- The cost attribute is shifted into the beneficial attribute. If the cost value is , then the corresponding beneficial value is .
- Step 2.
- Calculate the Pythagorean fuzzy overall matrix , by taking advantage of PFWA (Pythagorean fuzzy weighted average) operator and , .
- (II)
- Phase 2: Determine the comprehensive criteria weight values
- Step 3.
- Utilize the entropy to calculate the weight.
- (III)
- Phase 3: Acquire the ranking results with the taxonomy method
- Step 4.
- Calculate the Pythagorean fuzzy composite distance matrix ():
5. The Numerical Example and Comparative Analysis
5.1. The Numerical Example
5.2. Comparative Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hellwig, Z. Application of the taxonomic method to typologic distinction of countries. Przeglagd Stat. 1968, 15, 307–327. [Google Scholar]
- He, T.T.; Wei, G.W.; Lu, J.P.; Wei, C.; Lin, R. Pythagorean 2-tuple linguistic Taxonomy method for supplier selection in medical instrument industries. Int. J. Environ. Res. Public Health 2019, 16, 4875. [Google Scholar] [CrossRef]
- Atanassov, K.T. More on intuitionistic fuzzy-sets. Fuzzy Sets Syst. 1989, 33, 37–45. [Google Scholar] [CrossRef]
- Zhou, W.; Xu, Z.S. Extended intuitionistic fuzzy sets based on the hesitant fuzzy membership and their application in decision making with risk preference. Int. J. Intell. Syst. 2018, 33, 417–443. [Google Scholar] [CrossRef]
- Wu, L.P.; Wang, J.; Gao, H. Models for competiveness evaluation of tourist destination with some interval-valued intuitionistic fuzzy Hamy mean operators. J. Intell. Fuzzy Syst. 2019, 36, 5693–5709. [Google Scholar] [CrossRef]
- Wu, L.P.; Gao, H.; Wei, C. VIKOR method for financing risk assessment of rural tourism projects under interval-valued intuitionistic fuzzy environment. J. Intell. Fuzzy Syst. 2019, 37, 2001–2008. [Google Scholar] [CrossRef]
- Lu, J.P.; Wei, C. TODIM method for performance appraisal on social-integration-based rural reconstruction with interval-valued intuitionistic fuzzy information. J. Intell. Fuzzy Syst. 2019, 37, 1731–1740. [Google Scholar] [CrossRef]
- Wang, R. Research on the application of the financial investment risk appraisal models with some interval number muirhead mean operators. J. Intell. Fuzzy Syst. 2019, 37, 1741–1752. [Google Scholar] [CrossRef]
- Wei, G.W. 2-tuple intuitionistic fuzzy linguistic aggregation operators in multiple attribute decision making. Iran. J. Fuzzy Syst. 2019, 16, 159–174. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Burillo, P.; Bustince, H. Construction theorems for intuitionistic fuzzy sets. Fuzzy Sets Syst. 1996, 84, 271–281. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–356. [Google Scholar] [CrossRef]
- Hadjitodorov, S.T. An intuitionistic fuzzy version of the nearest prototype classification method, based on a moving-of-pattern procedure. Int. J. Gen. Syst. 2001, 30, 155–165. [Google Scholar] [CrossRef]
- Hung, W.L. Partial correlation coefficients of intuitionistic fuzzy sets. Int. J. Uncertain. Fuzziness Knowl. Syst. 2002, 10, 105–112. [Google Scholar] [CrossRef]
- Hung, W.L.; Yang, M.S. Similarity measures of intuitionistic fuzzy sets based on Hausdorff distance. Pattern Recognit. Lett. 2004, 25, 1603–1611. [Google Scholar] [CrossRef]
- Xu, Z.S.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Cavallaro, F.; Zavadskas, E.K.; Streimikiene, D.; Mardani, A. Assessment of concentrated solar power (CSP) technologies based on a modified intuitionistic fuzzy topsis and trigonometric entropy weights. Technol. Forecast. Soc. Chang. 2019, 140, 258–270. [Google Scholar] [CrossRef]
- Garg, H. Generalized intuitionistic fuzzy entropy-based approach for solving multi-attribute decision-making problems with unknown attribute weights. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2019, 89, 129–139. [Google Scholar] [CrossRef]
- Wu, L.P.; Wei, G.W.; Wu, J.; Wei, C. Some interval-valued intuitionistic fuzzy dombi heronian mean operators and their application for evaluating the ecological value of forest ecological tourism demonstration areas. Int. J. Environ. Res. Public Health 2020, 17, 829. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xu, Z.S. Extension of TOPSIS to multiple criteria decision making with pythagorean fuzzy sets. Int. J. Intell. Syst. 2014, 29, 1061–1078. [Google Scholar] [CrossRef]
- Gou, X.J.; Xu, Z.S.; Ren, P.J. The properties of continuous pythagorean fuzzy information. Int. J. Intell. Syst. 2016, 31, 401–424. [Google Scholar] [CrossRef]
- Peng, X.D.; Yang, Y. Some results for pythagorean fuzzy sets. Int. J. Intell. Syst. 2015, 30, 1133–1160. [Google Scholar] [CrossRef]
- Liang, D.C.; Zhang, Y.R.J.; Xu, Z.S.; Darko, A.P. Pythagorean fuzzy Bonferroni mean aggregation operator and its accelerative calculating algorithm with the multithreading. Int. J. Intell. Syst. 2018, 33, 615–633. [Google Scholar] [CrossRef]
- Liang, D.C.; Xu, Z.S.; Darko, A.P. Projection model for fusing the information of pythagorean fuzzy multicriteria group decision making based on geometric bonferroni mean. Int. J. Intell. Syst. 2017, 32, 966–987. [Google Scholar] [CrossRef]
- Ren, P.J.; Xu, Z.S.; Gou, X.J. Pythagorean fuzzy TODIM approach to multi-criteria decision making. Appl. Soft Comput. 2016, 42, 246–259. [Google Scholar] [CrossRef]
- Li, Z.X.; Lu, M. Some novel similarity and distance and measures of Pythagorean fuzzy sets and their applications. J. Intell. Fuzzy Syst. 2019, 37, 1781–1799. [Google Scholar] [CrossRef]
- Zeb, A.; Khan, M.S.A.; Ibrar, M. Approaches to multi-attribute decision making with risk preference under extended Pythagorean fuzzy environment. J. Intell. Fuzzy Syst. 2019, 36, 325–335. [Google Scholar] [CrossRef]
- Zeng, S.Z.; Peng, X.M.; Balezentis, T.; Streimikiene, D. Prioritization of low-carbon suppliers based on Pythagorean fuzzy group decision making with self-confidence level. Econ. Res.-Ekon. Istraz. 2019, 32, 1073–1087. [Google Scholar] [CrossRef]
- Gul, M.; Ak, M.F.; Guneri, A.F. Pythagorean fuzzy VIKOR-based approach for safety risk assessment in mine industry. J. Saf. Res. 2019, 69, 135–153. [Google Scholar] [CrossRef]
- Garg, H. New logarithmic operational laws and their aggregation operators for Pythagorean fuzzy set and their applications. Int. J. Intell. Syst. 2019, 34, 82–106. [Google Scholar] [CrossRef]
- Liang, D.C.; Zhang, Y.R.J.; Xu, Z.S.; Jamaldeen, A. Pythagorean fuzzy VIKOR approaches based on TODIM for evaluating internet banking website quality of Ghanaian banking industry. Appl. Soft Comput. 2019, 78, 583–594. [Google Scholar] [CrossRef]
- Thao, N.X.; Smarandache, F. A new fuzzy entropy on Pythagorean fuzzy sets. J. Intell. Fuzzy Syst. 2019, 37, 1065–1074. [Google Scholar] [CrossRef]
- Yu, L.P.; Zeng, S.Z.; Merigo, J.M.; Zhang, C.H. A new distance measure based on the weighted induced method and its application to Pythagorean fuzzy multiple attribute group decision making. Int. J. Intell. Syst. 2019, 34, 1440–1454. [Google Scholar] [CrossRef]
- Chen, T.Y. A novel PROMETHEE-based outranking approach for multiple criteria decision analysis with pythagorean fuzzy information. IEEE Access 2018, 6, 54495–54506. [Google Scholar] [CrossRef]
- Chen, T.Y. A mixed-choice-strategy-based consensus ranking method for multiple criteria decision analysis involving pythagorean fuzzy information. IEEE Access 2018, 6, 79174–79199. [Google Scholar] [CrossRef]
- Chen, T.Y. Remoteness index-based Pythagorean fuzzy VIKOR methods with a generalized distance measure for multiple criteria decision analysis. Inf. Fusion 2018, 41, 129–150. [Google Scholar] [CrossRef]
- Chen, T.Y. An effective correlation-based compromise approach for multiple criteria decision analysis with Pythagorean fuzzy information. J. Intell. Fuzzy Syst. 2018, 35, 3529–3541. [Google Scholar] [CrossRef]
- Teng, F.; Liu, Z.M.; Liu, P.D. Some power Maclaurin symmetric mean aggregation operators based on Pythagorean fuzzy linguistic numbers and their application to group decision making. Int. J. Intell. Syst. 2018, 33, 1949–1985. [Google Scholar] [CrossRef]
- Geng, Y.S.; Liu, P.D.; Teng, F.; Liu, Z.M. Pythagorean fuzzy uncertain linguistic TODIM method and their application to multiple criteria group decision making. J. Intell. Fuzzy Syst. 2017, 33, 3383–3395. [Google Scholar] [CrossRef]
- Wei, G.W.; Lu, M. Pythagorean fuzzy power aggregation operators in multiple attribute decision making. Int. J. Intell. Syst. 2018, 33, 169–186. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shao, Q.; Li, Y.J.; Ma, L.M.; Wang, J.X. Research on the evaluation of low-carbon tourism resources of Daqing wetlands. In Sustainable Development of Industry and Economy, Pts 1 and 2; Advanced Materials Research; Xu, Q., Li, H., Li, Q., Eds.; Trans Tech Publications: Stafa-Zurich, Switzerland, 2014; Volume 869–870, pp. 924–928. [Google Scholar]
- Hu, J.Q.; Lou, C.Y.; Wang, J.J. Exploration of low-carbon rural tourism in Zhejiang: A case study of lu Ci Cun, Tonglu County. In Proceedings of the 2015 International Forum on Energy, Environment Science and Materials, Shenzhen, China, 25–26 September 2015; Volume 40, pp. 1258–1261. [Google Scholar]
- Zhang, J.K. Evaluating regional low-carbon tourism strategies using the fuzzy Delphi-analytic network process approach. J. Clean. Prod. 2017, 141, 409–419. [Google Scholar] [CrossRef]
- Zha, J.P.; He, L.M.; Liu, Y.; Shao, Y.H. Evaluation on development efficiency of low-carbon tourism economy: A case study of Hubei Province, China. Socio-Econ. Plan. Sci. 2019, 66, 47–57. [Google Scholar] [CrossRef]
- Whittlesea, E.R.; Owen, A. Towards a low carbon future—The development and application of REAP Tourism, a destination footprint and scenario tool. J. Sustain. Tour. 2012, 20, 845–865. [Google Scholar] [CrossRef]
- Thongdejsri, M.; Nitivattananon, V. Assessing impacts of implementing low-carbon tourism program for sustainable tourism in a world heritage city. Tour. Rev. 2019, 74, 216–234. [Google Scholar] [CrossRef]
- Yin, P. Low-Carbon Tourism Planning Study: A Theoretical Framework. In Proceedings of International Conference on Low-carbon Transportation and Logistics, and Green Buildings; LTLGB 2012; Chen, F., Liu, Y., Hua, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1069–1075. [Google Scholar]
- Li, B.C. Research on low-carbon tourism of world heritage destinations—A case study of Nanjing Tulou, China. In Information Science and Management Engineering, Volumes 1–3; Wit Transactions on Information & Communication Technologies; Ren, P., Du, Z., Eds.; Ashurst: New Forest, UK, 2014; Volume 46, pp. 2807–2812. [Google Scholar]
- Su, J. Impact of tourism resource development based on low-carbon mode: A case study of Guizhou ethnic areas. Ecol. Process. 2019, 8. [Google Scholar] [CrossRef]
- Gao, H.; Ran, L.G.; Wei, G.W.; Wei, C.; Wu, J. VIKOR method for MAGDM based on q-rung interval-valued orthopair fuzzy information and its application to supplier selection of medical consumption products. Int. J. Environ. Res. Public Health 2020, 17, 525. [Google Scholar] [CrossRef]
- He, T.T.; Wei, G.W.; Lu, J.P.; Wei, C.; Lin, R. Pythagorean 2-tuple linguistic VIKOR method for evaluating human factors in construction project management. Mathematics 2019, 7, 1149. [Google Scholar] [CrossRef]
- Lu, J.P.; Wei, C.; Wu, J.; Wei, G.W. TOPSIS method for probabilistic linguistic MAGDM with entropy weight and its application to supplier selection of new agricultural machinery products. Entropy 2019, 21, 953. [Google Scholar] [CrossRef]
- Deng, X.M.; Gao, H. TODIM method for multiple attribute decision making with 2-tuple linguistic Pythagorean fuzzy information. J. Intell. Fuzzy Syst. 2019, 37, 1769–1780. [Google Scholar] [CrossRef]
- Gao, H.; Lu, M.; Wei, Y. Dual hesitant bipolar fuzzy hamacher aggregation operators and their applications to multiple attribute decision making. J. Intell. Fuzzy Syst. 2019, 37, 5755–5766. [Google Scholar] [CrossRef]
- Li, Z.X.; Wei, G.W.; Wang, R.; Wu, J.; Wei, C.; Wei, Y. EDAS method for multiple attribute group decision making under q-rung orthopair fuzzy environment. Technol. Econ. Dev. Econ. 2020, 26, 86–102. [Google Scholar] [CrossRef]
- Wang, P.; Wang, J.; Wei, G.W. EDAS method for multiple criteria group decision making under 2-tuple linguistic neutrosophic environment. J. Intell. Fuzzy Syst. 2019, 37, 1597–1608. [Google Scholar] [CrossRef]
- Ma, Z.M.; Xu, Z.S. Symmetric pythagorean fuzzy weighted geometric/averaging operators and their application in multicriteria decision-making problems. Int. J. Intell. Syst. 2016, 31, 1198–1219. [Google Scholar] [CrossRef]
- Wei, G.W.; Lu, M. Pythagorean fuzzy maclaurin symmetric mean operators in multiple attribute decision making. Int. J. Intell. Syst. 2018, 33, 1043–1070. [Google Scholar] [CrossRef]
- Gao, H.; Lu, M.; Wei, G.W.; Wei, Y. Some novel pythagorean fuzzy interaction aggregation operators in multiple attribute decision making. Fundam. Inform. 2018, 159, 385–428. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antucheviciene, J.; Saparauskas, J.; Turskis, Z. MCDM methods WASPAS and MULTIMOORA: Verification of robustness of methods when assessing alternative solutions. Econ. Comput. Econ. Cybern. Stud. Res. 2013, 47, 5–20. [Google Scholar]
- Lu, J.P.; Tang, X.Y.; Wei, G.W.; Wei, C.; Wei, Y. Bidirectional project method for dual hesitant Pythagorean fuzzy multiple attribute decision-making and their application to performance assessment of new rural construction. Int. J. Intell. Syst. 2019, 34, 1920–1934. [Google Scholar] [CrossRef]
- Wei, G.W.; Wei, C.; Wu, J.; Wang, H.J. Supplier selection of medical consumption products with a probabilistic linguistic MABAC method. Int. J. Environ. Res. Public Health 2019, 16, 5082. [Google Scholar] [CrossRef]
- Garg, H.; Rani, D. Some generalized complex intuitionistic fuzzy aggregation operators and their application to multicriteria decision-making process. Arab. J. Sci. Eng. 2019, 44, 2679–2698. [Google Scholar] [CrossRef]
- Garg, H.; Rani, D. Complex interval-valued intuitionistic fuzzy sets and their aggregation operators. Fundam. Inform. 2019, 164, 61–101. [Google Scholar] [CrossRef]
- Wan, S.P.; Li, D.F. Fuzzy mathematical programming approach to heterogeneous multiattribute decision-making with interval-valued intuitionistic fuzzy truth degrees. Inf. Sci. 2015, 325, 484–503. [Google Scholar] [CrossRef]
- Wei, G.W. The generalized dice similarity measures for multiple attribute decision making with hesitant fuzzy linguistic information. Econ. Res.-Ekon. Istraž. 2019, 32. [Google Scholar] [CrossRef]
- Jahan, A.; Zavadskas, E.K. ELECTRE-IDAT for design decision-making problems with interval data and target-based criteria. Soft Comput. 2019, 23, 129–143. [Google Scholar] [CrossRef]
- Wei, G.W.; Gao, H. Pythagorean 2-tuple linguistic power aggregation operators in multiple attribute decision making. Economic Research-EkonomskaIstraživanja 2020, 31, 904–933. [Google Scholar] [CrossRef]
- Wang, J.; Gao, H.; Lu, M. Approaches to strategic supplier selection under interval neutrosophic environment. J. Intell. Fuzzy Syst. 2019, 37, 1707–1730. [Google Scholar] [CrossRef]
- Wang, P.; Wang, J.; Wei, G.W.; Wu, J.; Wei, C.; Wei, Y. CODAS method for multiple attribute group decision making under 2-tuple linguistic neutrosophic environment. Informatica 2020, 31, 161–184. [Google Scholar] [CrossRef]
- Wei, G.W.; Wu, J.; Wei, C.; Wang, J.; Lu, J.P. Models for MADM with 2-tuple linguistic neutrosophic dombi bonferroni mean operators. IEEE Access 2019, 7, 108878–108905. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Wei, G.W.; Alsaadi, F.E.; Hayat, T.; Wei, C.; Zhang, Z.P. MABAC method for multiple attribute group decision making under picture 2-tuple linguistic environment. Soft Comput. 2020, 24, 5819–5829. [Google Scholar] [CrossRef]
- Wei, G.W.; Zhang, S.Q.; Lu, J.P.; Wu, J.; Wei, C. An extended bidirectional projection method for picture fuzzy MAGDM and its application to safety assessment of construction project. IEEE Access 2019, 7, 166138–166147. [Google Scholar] [CrossRef]
- Si, A.; Das, S.; Kar, S. An approach to rank picture fuzzy numbers for decision making problems. Decis. Mak. Appl. Manag. Eng. 2019, 2, 54–64. [Google Scholar] [CrossRef]
- Petrovic, I.; Kankaras, M. A hybridized IT2FS-DEMATEL-AHP-TOPSIS multicriteria decision making approach: Case study of selection and evaluation of criteria for determination of air traffic control radar position. Decis. Mak. Appl. Manag. Eng. 2020, 3, 146–164. [Google Scholar] [CrossRef]
- Wei, G.W.; Lu, J.P.; Wei, C.; Wu, J. Probabilistic linguistic GRA method for multiple attribute group decision making. J. Intell. Fuzzy Syst. 2020, 38, 4721–4732. [Google Scholar] [CrossRef]
| Alternatives | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| F1 | (0.40, 0.70) | (0.40, 0.50) | (0.30, 0.80) | (0.50, 0.70) |
| F2 | (0.60, 0.70) | (0.40, 0.60) | (0.50, 0.80) | (0.30, 0.90) |
| F3 | (0.50, 0.70) | (0.50, 0.60) | (0.40, 0.80) | (0.50, 0.80) |
| F4 | (0.40, 0.80) | (0.40, 0.80) | (0.50, 0.70) | (0.60, 0.80) |
| F5 | (0.60, 0.80) | (0.50, 0.70) | (0.60, 0.80) | (0.50, 0.70) |
| Alternatives | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| F1 | (0.50, 0.80) | (0.60, 0.30) | (0.30, 0.60) | (0.50, 0.70) |
| F2 | (0.70, 0.50) | (0.70, 0.20) | (0.70, 0.20) | (0.40, 0.50) |
| F3 | (0.60, 0.40) | (0.50, 0.70) | (0.50, 0.30) | (0.60, 0.30) |
| F4 | (0.80, 0.10) | (0.60, 0.30) | (0.30, 0.40) | (0.50, 0.60) |
| F5 | (0.60, 0.40) | (0.40, 0.80) | (0.70, 0.60) | (0.50, 0.80) |
| Alternatives | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| F1 | (0.30, 0.60) | (0.20, 0.80) | (0.10, 0.60) | (0.30, 0.50) |
| F2 | (0.50, 0.60) | (0.20, 0.80) | (0.40, 0.70) | (0.30, 0.90) |
| F3 | (0.30, 0.50) | (0.30, 0.40) | (0.20, 0.80) | (0.50, 0.70) |
| F4 | (0.20, 0.60) | (0.20, 0.70) | (0.30, 0.50) | (0.40, 0.60) |
| F5 | (0.50, 0.60) | (0.40, 0.70) | (0.40, 0.70) | (0.30, 0.50) |
| Alternatives | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| F1 | (0.40, 0.60) | (0.30, 0.50) | (0.20, 0.30) | (0.40, 0.20) |
| F2 | (0.60, 0.30) | (0.30, 0.50) | (0.50, 0.40) | (0.40, 0.60) |
| F3 | (0.40, 0.20) | (0.40, 0.80) | (0.30, 0.50) | (0.60, 0.40) |
| F4 | (0.20, 0.30) | (0.30, 0.70) | (0.40, 0.70) | (0.50, 0.30) |
| F5 | (0.60, 0.30) | (0.50, 0.60) | (0.50, 0.40) | (0.40, 0.20) |
| Alternatives | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| F1 | (0.80, 0.50) | (0.50, 0.70) | (0.70, 0.60) | (0.60, 0.80) |
| F2 | (0.60, 0.40) | (0.60, 0.50) | (0.50, 0.70) | (0.80, 0.60) |
| F3 | (0.40, 0.50) | (0.50, 0.70) | (0.60, 0.70) | (0.70, 0.50) |
| F4 | (0.80, 0.50) | (0.30, 0.80) | (0.70, 0.60) | (0.60, 0.40) |
| F5 | (0.20, 0.20) | (0.20, 0.20) | (0.20, 0.20) | (0.20, 0.20) |
| Alternatives | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| F1 | (0.40, 0.70) | (0.50, 0.40) | (0.30, 0.80) | (0.50, 0.70) |
| F2 | (0.60, 0.70) | (0.60, 0.40) | (0.50, 0.80) | (0.30, 0.90) |
| F3 | (0.50, 0.70) | (0.60, 0.50) | (0.40, 0.80) | (0.50, 0.80) |
| F4 | (0.40, 0.80) | (0.80, 0.40) | (0.50, 0.70) | (0.60, 0.80) |
| F5 | (0.60, 0.80) | (0.70, 0.50) | (0.60, 0.80) | (0.50, 0.70) |
| Alternatives | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| F1 | (0.50, 0.80) | (0.30, 0.60) | (0.30, 0.60) | (0.50, 0.70) |
| F2 | (0.70, 0.50) | (0.20, 0.70) | (0.70, 0.20) | (0.40, 0.50) |
| F3 | (0.60, 0.40) | (0.70, 0.50) | (0.50, 0.30) | (0.60, 0.30) |
| F4 | (0.80, 0.10) | (0.30, 0.60) | (0.30, 0.40) | (0.50, 0.60) |
| F5 | (0.60, 0.40) | (0.80, 0.40) | (0.70, 0.60) | (0.50, 0.80) |
| Alternatives | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| F1 | (0.30, 0.60) | (0.80, 0.20) | (0.10, 0.60) | (0.30, 0.50) |
| F2 | (0.50, 0.60) | (0.80, 0.20) | (0.40, 0.70) | (0.30, 0.90) |
| F3 | (0.30, 0.50) | (0.40, 0.30) | (0.20, 0.80) | (0.50, 0.70) |
| F4 | (0.20, 0.60) | (0.70, 0.20) | (0.30,0.50) | (0.40, 0.60) |
| F5 | (0.50, 0.60) | (0.70, 0.40) | (0.40, 0.70) | (0.30, 0.50) |
| Alternatives | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| F1 | (0.40, 0.60) | (0.50, 0.30) | (0.20, 0.30) | (0.40, 0.20) |
| F2 | (0.60, 0.30) | (0.50, 0.30) | (0.50, 0.40) | (0.40, 0.60) |
| F3 | (0.40, 0.20) | (0.80, 0.40) | (0.30, 0.50) | (0.60, 0.40) |
| F4 | (0.20, 0.30) | (0.70, 0.30) | (0.40, 0.70) | (0.50, 0.30) |
| F5 | (0.60, 0.30) | (0.60, 0.50) | (0.50, 0.40) | (0.40, 0.20) |
| Alternatives | T1 | T2 | T3 | T4 |
|---|---|---|---|---|
| F1 | (0.80, 0.50) | (0.70, 0.50) | (0.70, 0.60) | (0.60, 0.80) |
| F2 | (0.60, 0.40) | (0.50, 0.60) | (0.50, 0.70) | (0.80, 0.60) |
| F3 | (0.40, 0.50) | (0.70, 0.50) | (0.60, 0.70) | (0.70, 0.50) |
| F4 | (0.80, 0.50) | (0.80, 0.30) | (0.70, 0.60) | (0.60, 0.40) |
| F5 | (0.20, 0.20) | (0.20, 0.20) | (0.20, 0.20) | (0.20, 0.20) |
| Alternatives | T1 | T2 |
| F1 | (0.5437, 0.6320) | (0.6139, 0.3728) |
| F2 | (0.6072, 0.4789) | (0.5838, 0.3987) |
| F3 | (0.4580, 0.4258) | (0.6708, 0.4317) |
| F4 | (0.6071, 0.3728) | (0.7084, 0.3366) |
| F5 | (0.5325, 0.4095) | (0.6596, 0.3807) |
| Alternatives | T3 | T4 |
| F1 | (0.4085, 0.5533) | (0.4769, 0.5232) |
| F2 | (0.5383, 0.5004) | (0.5176, 0.6804) |
| F3 | (0.4340, 0.5827) | (0.5902, 0.5073) |
| F4 | (0.4823, 0.5674) | (0.5291, 0.5102) |
| F5 | (0.5264, 0.4852) | (0.4027, 0.4027) |
| F1 | F2 | F3 | F4 | F5 | |
|---|---|---|---|---|---|
| F1 | - | 0.0872 | 0.0776 | 0.0799 | 0.0818 |
| F2 | 0.0872 | - | 0.1017 | 0.0804 | 0.0850 |
| F3 | 0.0776 | 0.1017 | - | 0.0581 | 0.0751 |
| F4 | 0.0799 | 0.0804 | 0.0581 | - | 0.0688 |
| F5 | 0.0818 | 0.0850 | 0.0751 | 0.0688 | - |
| T1 | T2 | |
|---|---|---|
| PFPIS | (0.6072, 0.3728) | (0.7084, 0.3366) |
| T3 | T4 | |
| PFPIS | (0.5383, 0.4852) | (0.5902, 0.4072) |
| Methods | Order |
|---|---|
| PFWA operator | |
| PFWG operator | |
| SPFWA operator | |
| SPFWG operator | |
| PFWMSM operator | |
| PFIWA operator | |
| PFIWG operator | |
| PF-taxonomy method |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, G.; Tang, Y.; Zhao, M.; Lin, R.; Wu, J. Selecting the Low-Carbon Tourism Destination: Based on Pythagorean Fuzzy Taxonomy Method. Mathematics 2020, 8, 832. https://doi.org/10.3390/math8050832
Wei G, Tang Y, Zhao M, Lin R, Wu J. Selecting the Low-Carbon Tourism Destination: Based on Pythagorean Fuzzy Taxonomy Method. Mathematics. 2020; 8(5):832. https://doi.org/10.3390/math8050832
Chicago/Turabian StyleWei, Guiwu, Yanxin Tang, Mengwei Zhao, Rui Lin, and Jiang Wu. 2020. "Selecting the Low-Carbon Tourism Destination: Based on Pythagorean Fuzzy Taxonomy Method" Mathematics 8, no. 5: 832. https://doi.org/10.3390/math8050832
APA StyleWei, G., Tang, Y., Zhao, M., Lin, R., & Wu, J. (2020). Selecting the Low-Carbon Tourism Destination: Based on Pythagorean Fuzzy Taxonomy Method. Mathematics, 8(5), 832. https://doi.org/10.3390/math8050832





