Global Behavior of an Arbitrary-Order Nonlinear Difference Equation with a Nonnegative Function
Abstract
1. Introduction
2. Global Behavior
2.1. Classification of Solutions
- (i)
- eventually equals c, more precisely , which occurs when for some ;
- (ii)
- is eventually less than c, more precisely , , which occurs when for some ; or
- (iii)
- oscillates about c with at most consecutive decreasing terms greater than c and at most k consecutive increasing terms less than c.
2.2. Global Asymptotic Stability
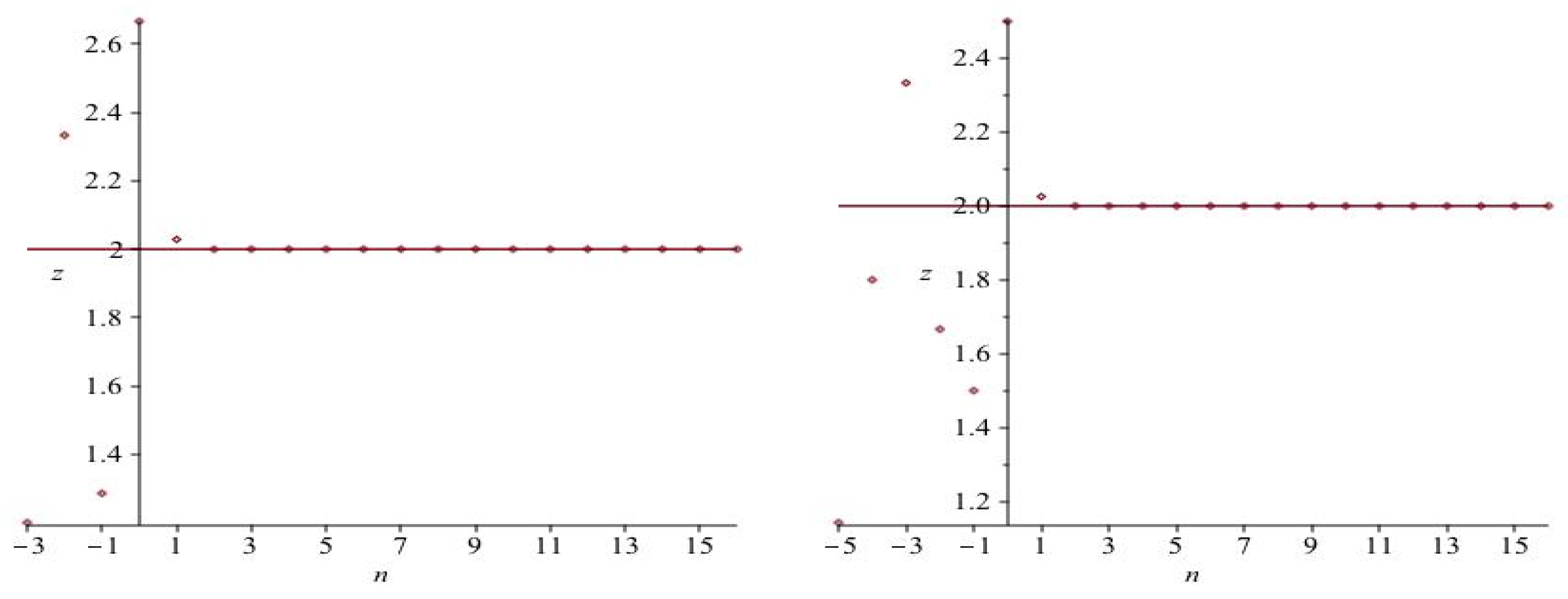
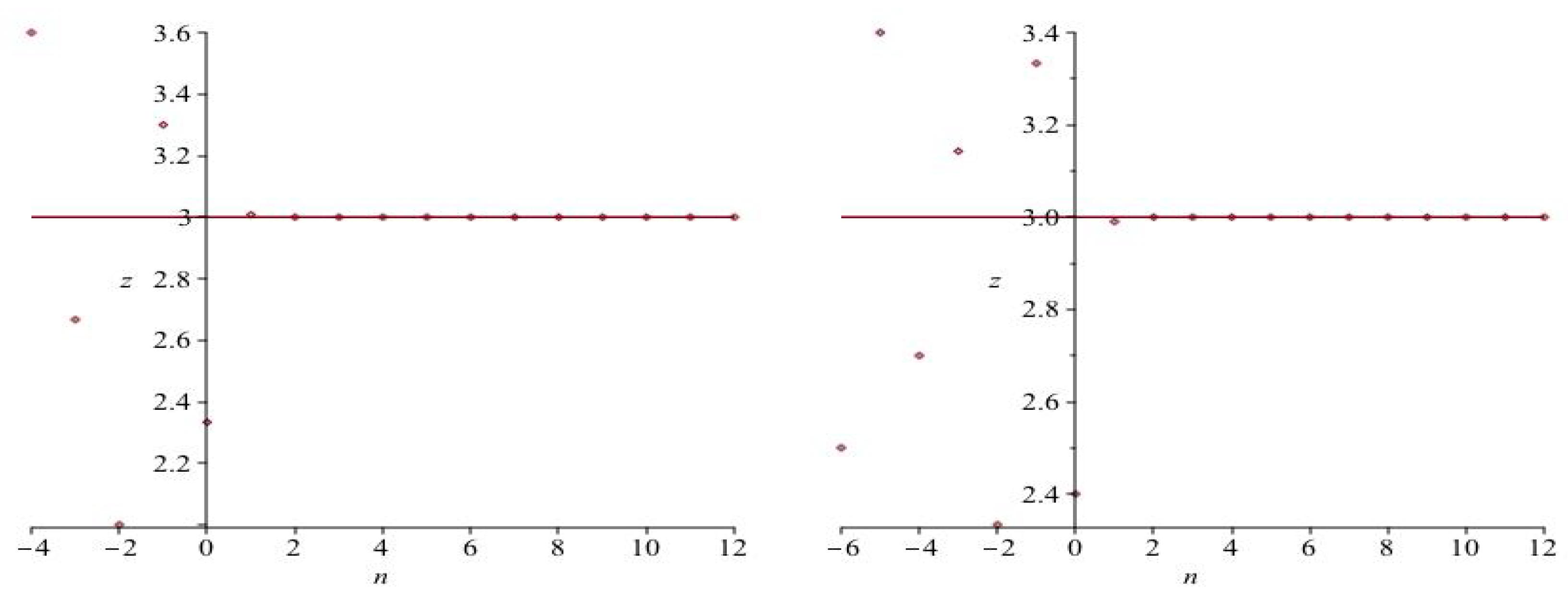
2.3. Illustrative Examples
3. Concluding Remarks
Acknowledgments
Conflicts of Interest
References
- Batchelder, P.M. An Introduction to Linear Difference Equations; Dover Publications: New York, NY, USA, 1967. [Google Scholar]
- Kocic, V.L.; Ladas, G. Global Behavior of Nonlinear Difference Equations of Higher Order with Applications; Kluwer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Ma, W.X. Trigonal curves and algebro-geometric solutions to soliton hierarchies I. Proc. Roy. Soc. A 2017, 473, 20170232. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.X. Trigonal curves and algebro-geometric solutions to soliton hierarchies II. Proc. Roy. Soc. A 2017, 473, 20170233. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.X. The inverse scattering transform and soliton solutions of a combined modified Korteweg-de Vries equation. J. Math. Anal. Appl. 2019, 471, 796–811. [Google Scholar] [CrossRef]
- Camouzis, E.; Ladas, G.; Rodrigues, I.W.; Northshield, S. The rational recursive sequence . Comput. Math. Appl. 1994, 28, 37–43. [Google Scholar] [CrossRef][Green Version]
- Li, X.; Zhu, D. Global asymptotic stability in a rational equation. J. Differ. Equ. Appl. 2003, 9, 833–839. [Google Scholar]
- Li, X.; Zhu, D. Two rational recursive sequences. Comput. Math. Appl. 2004, 47, 1487–1494. [Google Scholar] [CrossRef][Green Version]
- Rhouma, M.B.H. The Fibonacci sequence modulo π, chaos and some rational recursive equations. J. Math. Anal. Appl. 2005, 310, 506–517. [Google Scholar] [CrossRef]
- Abu-Saris, R.; Çinar, C.; Yalçinkaya, I. On the asymptotic stability of xn+1 = (a + xnxn−k)/(xn + xn−k). Comput. Math. Appl. 2008, 56, 1172–1175. [Google Scholar] [CrossRef]
- Gelişken, A.; Çinar, C.; Kurbanli, A.S. On the asymptotic behavior and periodic nature of a difference equation with maximum. Comput. Math. Appl. 2010, 59, 898–902. [Google Scholar] [CrossRef]
- Ralston, A.; Rabinowitz, P. A First Course in Numerical Analysis; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
- Sedaghat, H. The impossibility of unstable, globally attracting fixed points for continuous mappings of the line. Amer. Math. Mon. 1997, 104, 356–358. [Google Scholar] [CrossRef]
- Amleh, A.M.; Kruse, N.; Ladas, G. On a class of difference equations with strong negative feedback. J. Differ. Equ. Appl. 1999, 5, 497–515. [Google Scholar] [CrossRef]
- Kruse, N.; Nesemann, T. Global asymptotic stability in some discrete dynamical systems. J. Math. Anal. Appl. 1999, 235, 151–158. [Google Scholar] [CrossRef][Green Version]
- Li, X.; Zhu, D. Global asymptotic stability for two recursive difference equations. Appl. Math. Comput. 2004, 150, 481–492. [Google Scholar] [CrossRef]
- Gümüş, M. The global asymptotic stability of a system of difference equations. J. Differ. Equ. Appl. 2018, 24, 976–991. [Google Scholar] [CrossRef]
- Ma, W.X. Lump and interaction solutions to linear PDEs in 2 + 1 dimensions via symbolic computation. Mod. Phys. Lett. B 2019, 33, 1950457. [Google Scholar] [CrossRef]
- Ma, W.X.; Zhou, Y. Lump solutions to nonlinear partial differential equations via Hirota bilinear forms. J. Diff. Equ. 2018, 264, 2633–2659. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, W.-X. Global Behavior of an Arbitrary-Order Nonlinear Difference Equation with a Nonnegative Function. Mathematics 2020, 8, 825. https://doi.org/10.3390/math8050825
Ma W-X. Global Behavior of an Arbitrary-Order Nonlinear Difference Equation with a Nonnegative Function. Mathematics. 2020; 8(5):825. https://doi.org/10.3390/math8050825
Chicago/Turabian StyleMa, Wen-Xiu. 2020. "Global Behavior of an Arbitrary-Order Nonlinear Difference Equation with a Nonnegative Function" Mathematics 8, no. 5: 825. https://doi.org/10.3390/math8050825
APA StyleMa, W.-X. (2020). Global Behavior of an Arbitrary-Order Nonlinear Difference Equation with a Nonnegative Function. Mathematics, 8(5), 825. https://doi.org/10.3390/math8050825




