1. Introduction
The Fibonacci sequence
is presumably the most classical example of a recursion sequence. This sequence is defined by the recurrence
, for
, with initial terms
and
(see [
1,
2,
3,
4] for many surprising properties of
and some generalizations of them, e.g., in [
5,
6,
7,
8,
9]). The study of this sequence embraces a number of interesting aspects in Diophantine problems. For example, the “ingenuous” (and yet unproved) problem of the existence of infinitely many prime Fibonacci numbers is related to the powerful Zaremba’s conjecture in Diophantine approximation.
We point out that the function
(known as the order of appearance in the Fibonacci sequence) plays a pivotal role in the characterization of divisibility relations involving Fibonacci numbers. This arithmetical function is defined as
See
Table 1 for some values of
and
Figure 1 for the graphic behavior of
.
In 1878, Lucas [
10] (see p. 300) showed that
is well-defined, for all
. An immediate consequence of the Dirichlet’s Box Principle yields
. A better upper bound for
can be provided by combining the inequalities
and
, for
(this last inequality is a consequence of a result of Robin, see Théorème 2 of [
11]), where
denotes the sum of the positive divisors of
n. For a prime number
p, the better upper bound
holds. In 1975, J. Sallé [
12] found the sharpest upper bound for
. Indeed, he proved that
, for all
. His result is sharp, since we have infinitely many extremal cases (i.e., where the equality is valid):
The order of appearance in the Fibonacci sequence became an object of much interest in 1992, when Z. H. Sun and Z. W. Sun [
13] found a very close connection between the equation
and Fermat’s Last Theorem (which was an open problem in that time).
Since , one may realise the order of appearance z as a discrete dynamical system on and ask about the periodic orbits of z for some fixed periods. Recall, that n is called a periodic point of z, if , for some (Here is the jth iterate of z). The smallest positive integer k with this property is defined as the period of n (under z) and n is named as a k-period point of z (i.e., if and , for all . Here, we utilize the usual notation , for integers ). For , a 1-periodic point is usually denoted as a fixed point.
Marques [
14] and Somer and Křížek [
15] (independently) found all fixed points of
. More precisely, they proved that
Recently, two extensions of this result were proved. The first one by Trojovský [
16] (who dealt with the equation
, for
) and another by Trojovská [
17] (who studied the behavior of
“near” its sharpest upper bound, i.e., solutions of the Diophantine equation
, where
n,
k are any positive integers). We refer the reader to these two papers (and references therein) to more problems involving the
z-function.
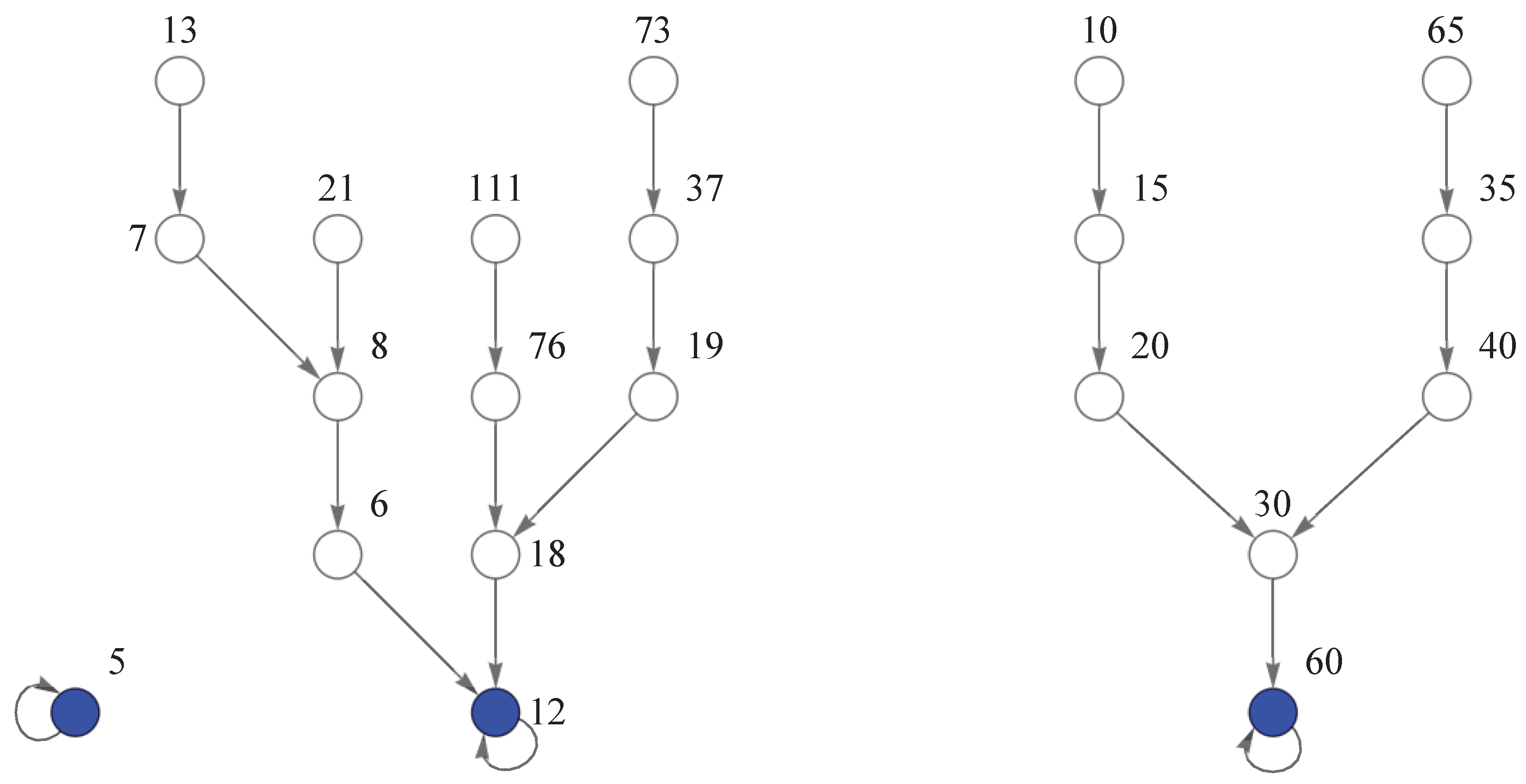
A positive integer n is called a pre-periodic point (of z) if is a periodic point. In other words, n is pre-periodic if its orbit under the order of appearance z (i.e., ) is finite. For example,
- -
;
- -
;
- -
;
- -
;
and then
and
are pre-periodic points since 12 and 60 are fixed points of
z (see
Figure 2).
With the help of Wolfram Mathematica we searched the lengths of orbits
for every
n from 1 to 50,000. This experiment showed that the maximal length of the orbit was 10 and
Table 2 summarizes how many times each length of the orbit from 1 to 10 was realized (we have included their percentage distribution in the last row).
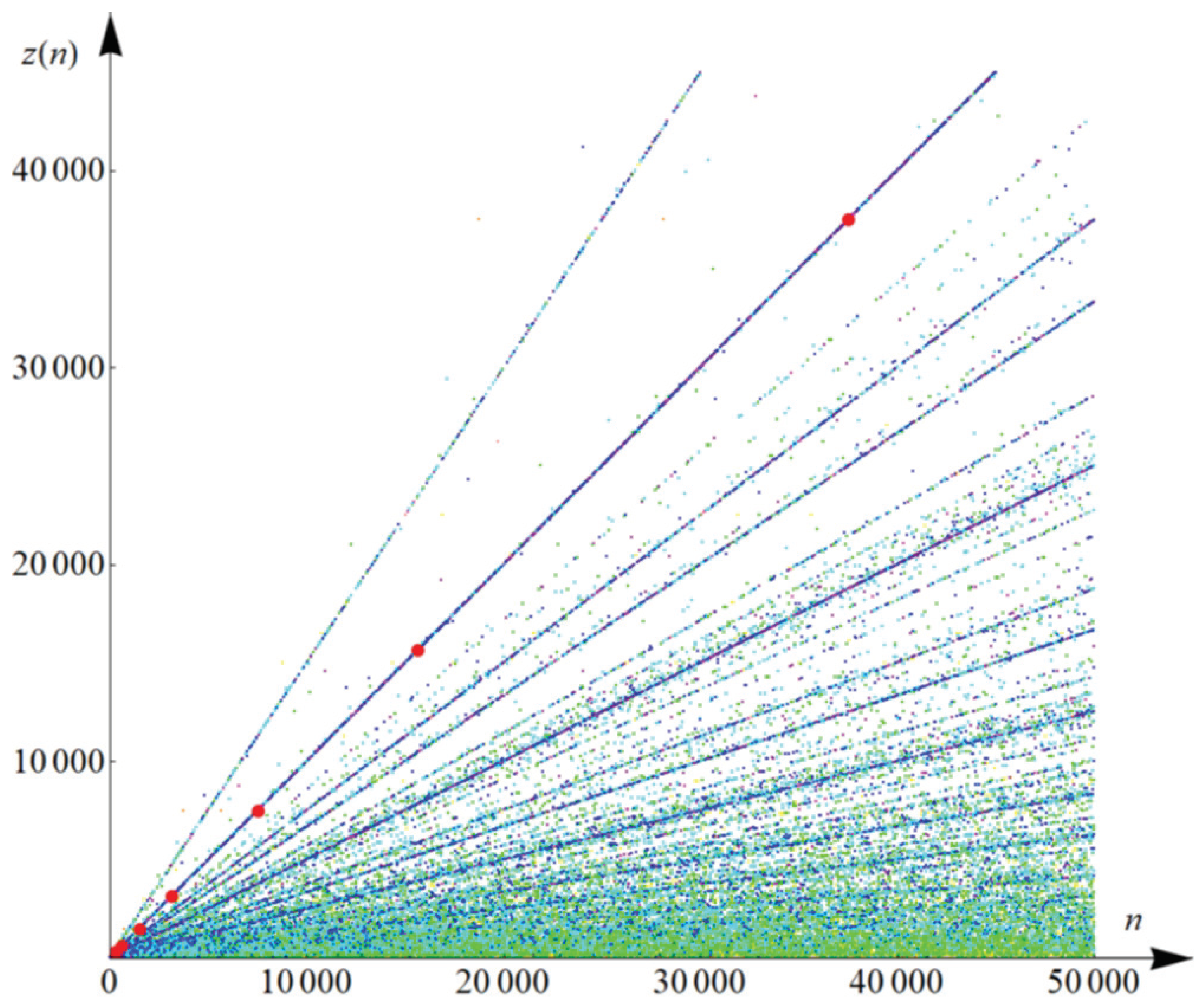
Figure 1 and
Figure 3 show graphically the relationship between
n,
and the length of the orbit
for each natural number less than or equal to 50,000. In
Figure 1 we have drawn the points of the coordinates
and to show the corresponding length of orbits we have colored these points by the colors listed in
Table 2, e.g., the red color corresponds to the length of the orbit equal to 1 (i.e., they are fixed points). In
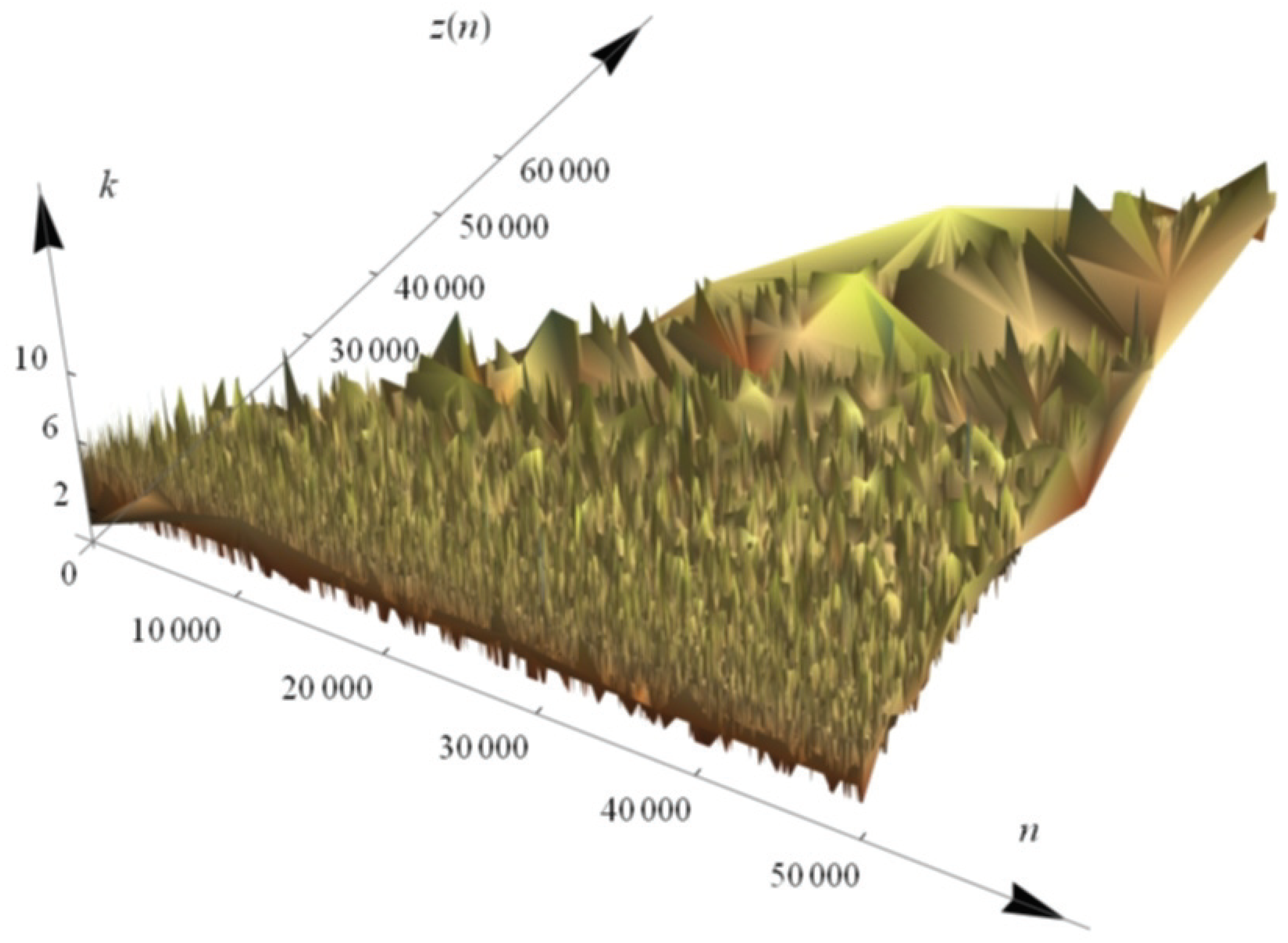
Figure 3 we plotted an analogous graph to
Figure 1, but we used a 3D-graph to plot a set of all points of coordinates
, for
n from 1 to 50,000.
Remark 1. We now turn to a brief discussion of another concept which can be helpful to the understanding of the special points (periodic and pre-periodic) in discrete dynamics. A sequence is called periodic if it satisfies , for all (for a smallest integer which is known as the period of the sequence). A sequence is called eventually periodic if it can be made periodic by deleting some finite number of terms from the beginning, i.e., if is periodic, for an . Let us denote by and the sets of the periodic and eventually periodic sequences, respectively (clearly, . Since the orbit of a point (as a multiset) may be identified as an infinite sequence, then we can say that n is a periodic point (resp., pre-periodic point) if and only if (resp., ).
Actually, Luca and Tron [
18] (see the proof of their Theorem 2.2) proved that every positive integer is a pre-periodic point of
z. Actually, they proved that for any positive integer
n, there exists a
, such that
is a fixed point of
z. Another proof for this fact is the following: if
is the Pisano period of
n (
is the smallest period of the Fibonacci sequence modulo
n), then
(see Theorem 7 of [
19]) and so,
, if
and
. Thus, by Iteration Theorem of [
20], there exists an integer
, such that
is a fixed point of
, i.e.,
, for some
(see Fixed Point Theorem] of [
20]). Since
, then
is either
or
, as desired.
Since all pre-periodic points of z close their orbit in a fixed point, the following question arises: has the function some k-periodic point, for ?
In this paper, we shall completely answer this question by proving that
Theorem 1. All periodic points of z are fixed points. In other words, if , for some , then .
Remark 2. We remark that the sets and can be written aswhere and denote, respectively, the sets of the periodic and eventually periodic sequences with period exactly p. Now, observe that (according to Remark 1) Luca and Tron result (in [18]) can be rephrased as: if , then . However, Theorem 1 is equivalent to the fact that: if , then . In brief outline, the main idea of the proof is to use a variant of the fact that (where denotes the least common multiple) together with some properties of (for a prime p). Mathematica software was very useful when performing some calculations (for remaining cases).
3. The Proof of The Theorem
First, let us make some considerations. For an integer
n with prime factorization
, we have, by Lemma 2, that
However, in view of Lemma 1 (ii) together with the fact that
divides
, we obtain
where, to simplify the notation,
denotes the Legendre symbol
.
So, let us suppose that
n is a
t-periodic point, for some
. Let us prove that
n is a fixed point of
z, i.e.,
or
, for an integer
. Since
, then there exist distinct positive integers
such that
Now, let us write the prime factorization of
as
, for all
, where we define
(also, with
). By using (
1), we have (by writing also
) that
for all
. Thus,
By multiplying all the previous relations (i.e., for all
) and after some straightforward computations, we arrive at
where
, for all
. Thus,
divides
which yields
Now the proof splits into two cases:
Case
In this case, we can write
. If
and
, then
Since for
and
, the orbits
do not return to 2 or 3, we can consider only integers in the set
. For such an integer, we have that
is a fixed point, for all
(by using some simple Mathematica routine). So, we can consider only
. However,
, for
, only if
or 12 which are fixed points. Thus, we may suppose that
and
. In this case, we have, by Lemmas 1 and 2,
and so
where we used that
and
. Note that if we proceed with this chain, we will have that
will decrease, by Lemma 1 (ii), (in the form
) if
a is large. However, since
, then, in particular, it holds that
. So, we must have
. The same is valid for
b (by using
) and so
which contradicts our assumption on
a and
b (i.e.,
and
).
Case
If
, then, by (
2), we have that
and so
. This implies that
which, by definition of the Legendre symbol, yields that
and then
. For the case in which
, we have (since
) that
(for all
) and again, by the relation in (
2), we infer that
divides
and so
(as previously deduced). In conclusion, the largest prime factor of
n is 5. Therefore, we can write
. Let us suppose that
and
. Then, by Lemmas 1 and 2, we have
and so
where we used that
and
. Observe that as before, by continuing this process, we will infer that
decreases, by Lemma 1 (ii), for large values of
a. Since
, then
which yields that
. This also holds for
b (again by applying
). So, the possible solutions are in the range
and
. Hence, the possible
k-periodic points must belong to the set
Since we are interested in iterations of z and (for all ), then it is enough to search for periodic points of z belonging to and after, multiply them by . In this case, the proof proceeds along the same lines as in the previous case. That is, only 1 and 12 are invariant. Now, by multiplying them by , we obtain that or (that is, the fixed points of z). This completes the proof of Theorem 1.