Mathematical Modeling Shows That the Response of a Solid Tumor to Antiangiogenic Therapy Depends on the Type of Growth
Abstract
1. Introduction
2. Model
2.1. Equations
2.1.1. Tumor Cells
2.1.2. Glucose and Capillaries
2.1.3. Angiogenesis and Antiangiogenic Therapy
2.2. Parameters
2.3. Numerical Solving
3. Results
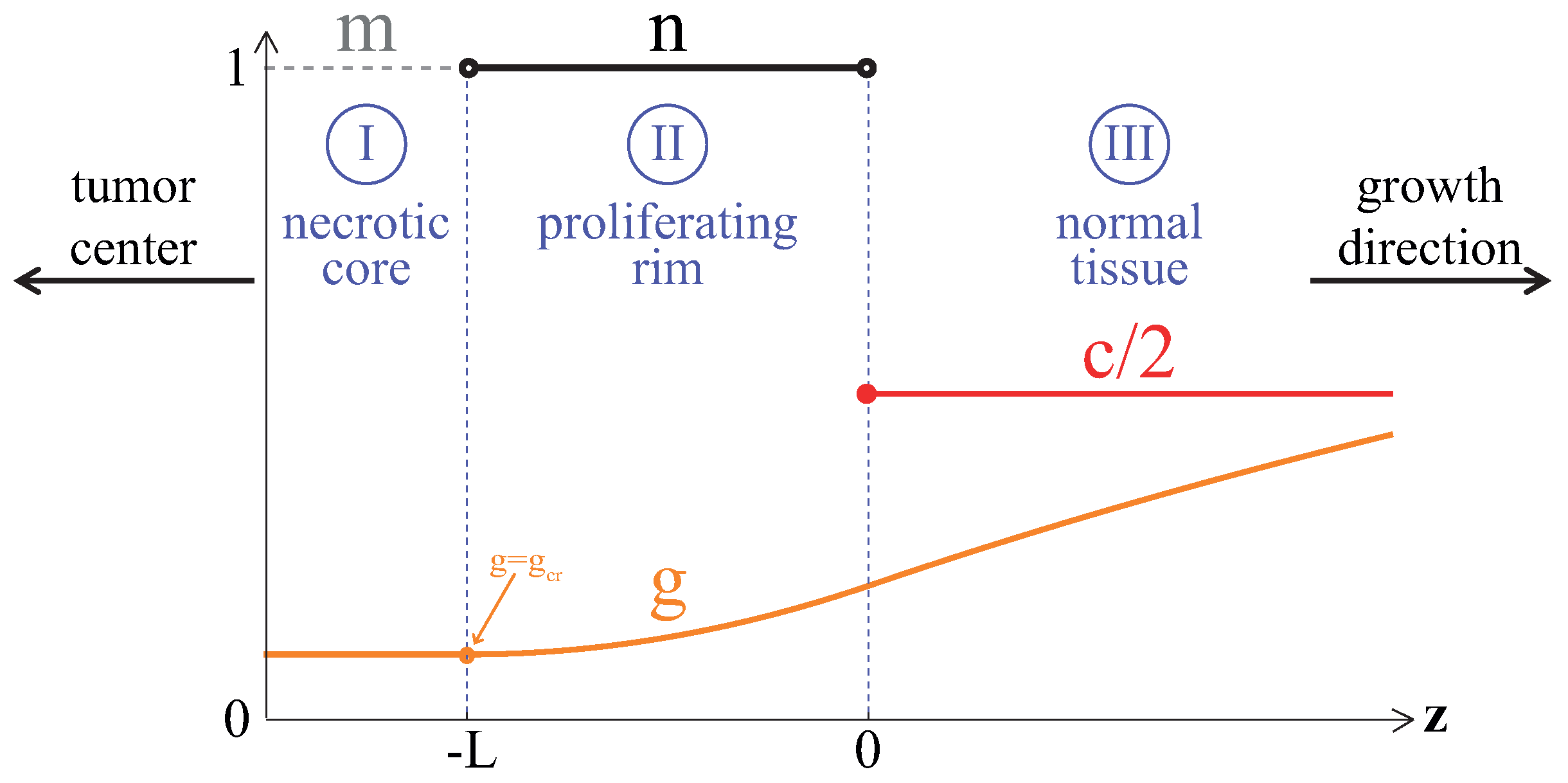
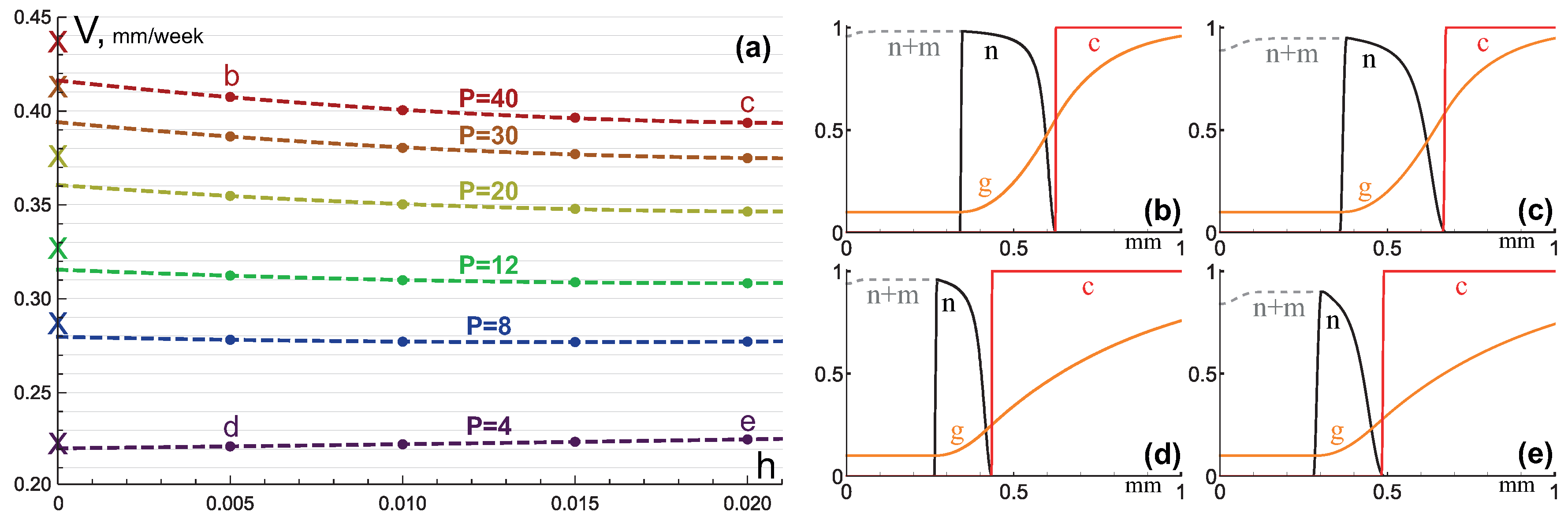
3.1. Compact Type of Growth
- , i.e., all the tumor cells either proliferate or die at a given position at a given moment;
- , i.e., tumor cells die instantaneously;
- , i.e., there are no capillaries inside the tumor.
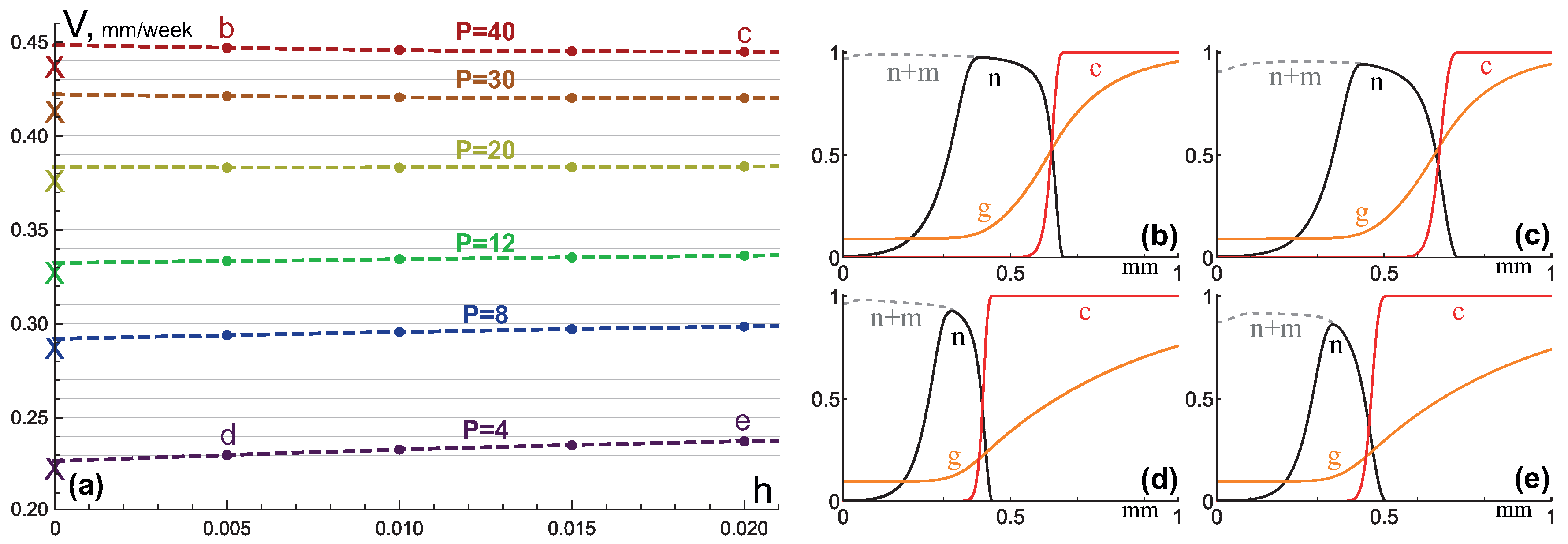
3.2. Invasive Type of Growth
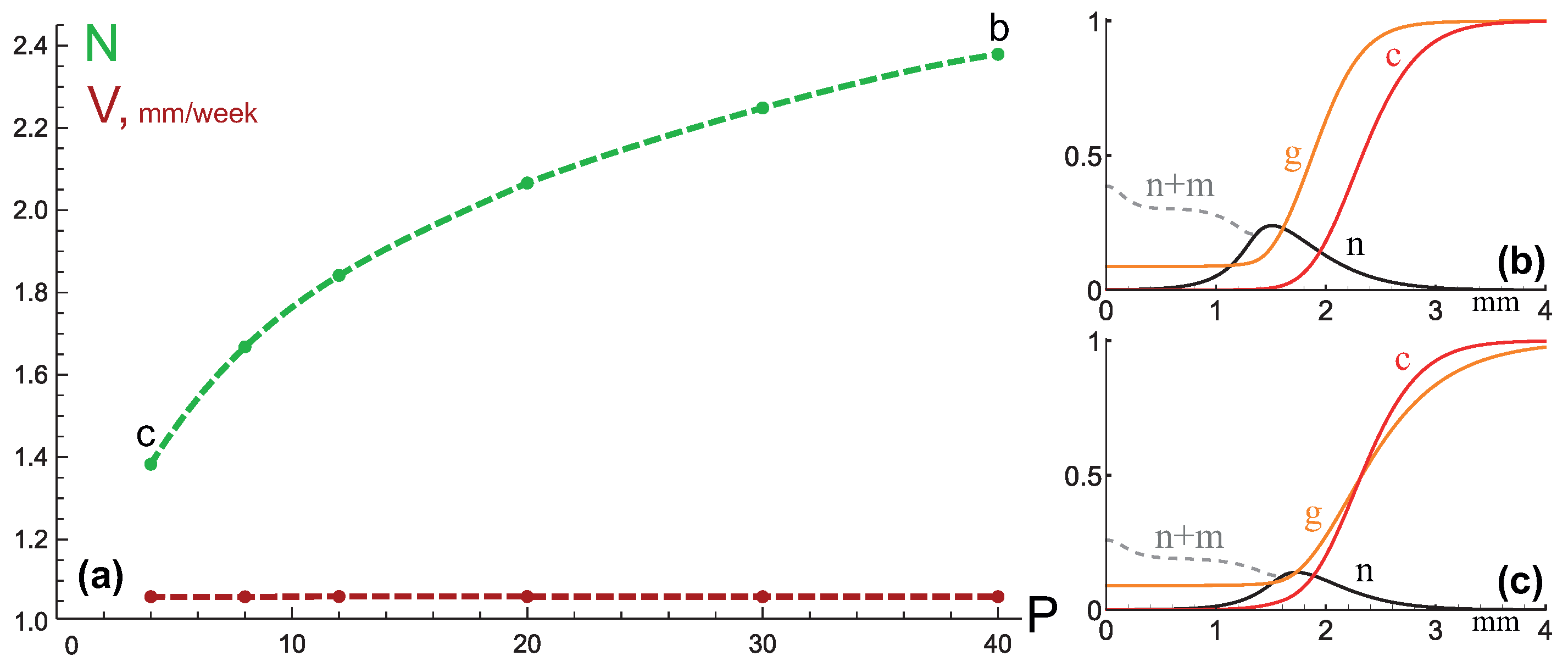
3.3. Mixed Type of Growth
4. Discussion
Supplementary Materials
Funding
Conflicts of Interest
Abbreviations
| AAT | antiangiogenic therapy |
| VEGF | vascular endothelial growth factor |
Appendix A. Analytical Estimation of Compact Tumor Growth Speed
References
- Sarker, M.S.R.; Pokojovy, M.; Kim, S. On the Performance of Variable Selection and Classification via Rank-Based Classifier. Mathematics 2019, 7, 457. [Google Scholar] [CrossRef]
- Geng, Y.; Dalhaimer, P.; Cai, S.; Tsai, R.; Tewari, M.; Minko, T.; Discher, D.E. Shape effects of filaments versus spherical particles in flow and drug delivery. Nat. Nanotechnol. 2007, 2, 249. [Google Scholar] [CrossRef] [PubMed]
- Antico, M.; Prinsen, P.; Cellini, F.; Fracassi, A.; Isola, A.A.; Cobben, D.; Fontanarosa, D. Real-time adaptive planning method for radiotherapy treatment delivery for prostate cancer patients, based on a library of plans accounting for possible anatomy configuration changes. PLoS ONE 2019, 14, e0213002. [Google Scholar] [CrossRef] [PubMed]
- Boucher, Y.; Baxter, L.; Jain, R. Interstitial pressure gradients in tissue-isolated and subcutaneous tumors: Implications for therapy. Cancer Res. 1990, 50, 4478–4484. [Google Scholar] [PubMed]
- Gatenby, R.; Gawlinski, E.; Gmitro, A.; Kaylor, B.; Gillies, R. Acid-mediated tumor invasion: A multidisciplinary study. Cancer Res. 2006, 66, 5216–5223. [Google Scholar] [CrossRef]
- Citron, M.; Berry, D.; Cirrincione, C.; Hudis, C.; Winer, E.; Gradishar, W.; Davidson, N.; Martino, S.; Livingston, R.; Ingle, J.; et al. Randomized trial of dose-dense versus conventionally scheduled and sequential versus concurrent combination chemotherapy as postoperative adjuvant treatment of node-positive primary breast cancer: First report of Intergroup Trial C9741/Cancer and Leukemia Group B Trial 9741. J. Clin. Oncol. 2003, 21, 1431–1439. [Google Scholar]
- Chmielecki, J.; Foo, J.; Oxnard, G.; Hutchinson, K.; Ohashi, K.; Somwar, R.; Wang, L.; Amato, K.; Arcila, M.; Sos, M.; et al. Optimization of dosing for EGFR-mutant non-small cell lung cancer with evolutionary cancer modeling. Sci. Transl. Med. 2011, 3, 90ra59. [Google Scholar] [CrossRef]
- Hanahan, D.; Weinberg, R.A. The hallmarks of cancer. Cell 2000, 100, 57–70. [Google Scholar] [CrossRef]
- Laird, A.K. Dynamics of tumour growth. Br. J. Cancer 1964, 18, 490. [Google Scholar] [CrossRef]
- Burton, A.C. Rate of growth of solid tumours as a problem of diffusion. Growth 1966, 30, 157–176. [Google Scholar]
- Rockne, R.; Alvord, E.; Rockhill, J.; Swanson, K. A mathematical model for brain tumor response to radiation therapy. J. Math. Biol. 2009, 58, 561. [Google Scholar] [CrossRef] [PubMed]
- Alfonso, J.; Köhn-Luque, A.; Stylianopoulos, T.; Feuerhake, F.; Deutsch, A.; Hatzikirou, H. Why one-size-fits-all vaso-modulatory interventions fail to control glioma invasion: In silico insights. Sci. Rep. 2016, 6, 37283. [Google Scholar] [CrossRef] [PubMed]
- Ward, J.P.; King, J. Mathematical modeling of avascular-tumour growth. Math. Med. Biol. J. IMA 1997, 14, 39–69. [Google Scholar] [CrossRef]
- Byrne, H.; Drasdo, D. Individual-based and continuum models of growing cell populations: A comparison. J. Math. Biol. 2009, 58, 657. [Google Scholar] [CrossRef]
- Hahnfeldt, P.; Panigrahy, D.; Folkman, J.; Hlatky, L. Tumor development under angiogenic signaling: A dynamical theory of tumor growth, treatment response, and postvascular dormancy. Cancer Res. 1999, 59, 4770–4775. [Google Scholar]
- Glick, A.; Mastroberardino, A. An Optimal Control Approach for the Treatment of Solid Tumors with Angiogenesis Inhibitors. Mathematics 2017, 5, 49. [Google Scholar] [CrossRef]
- Macklin, P.; McDougall, S.; Anderson, A.; Chaplain, M.; Cristini, V.; Lowengrub, J. Multiscale modeling and nonlinear simulation of vascular tumour growth. J. Math. Biol. 2009, 58, 765–798. [Google Scholar] [CrossRef]
- Kuznetsov, M.; Gorodnova, N.; Simakov, S.; Kolobov, A. Multiscale modeling of angiogenic tumor growth, progression, and therapy. Biophysics 2016, 61, 1042–1051. [Google Scholar] [CrossRef]
- Vasudev, N.S.; Reynolds, A.R. Anti-angiogenic therapy for cancer: Current progress, unresolved questions and future directions. Angiogenesis 2014, 17, 471–494. [Google Scholar] [CrossRef]
- Goel, S.; Wong, A.H.K.; Jain, R.K. Vascular normalization as a therapeutic strategy for malignant and nonmalignant disease. Cold Spring Harb. Perspect. Med. 2012, 2, a006486. [Google Scholar] [CrossRef]
- Ebos, J.M.; Kerbel, R.S. Antiangiogenic therapy: Impact on invasion, disease progression, and metastasis. Nat. Rev. Clin. Oncol. 2011, 8, 210. [Google Scholar] [CrossRef] [PubMed]
- Ebos, J.M.; Mastri, M.; Lee, C.R.; Tracz, A.; Hudson, J.M.; Attwood, K.; Cruz-Munoz, W.R.; Jedeszko, C.; Burns, P.; Kerbel, R.S. Neoadjuvant antiangiogenic therapy reveals contrasts in primary and metastatic tumor efficacy. EMBO Mol. Med. 2014, 6, 1561–1576. [Google Scholar] [CrossRef] [PubMed]
- Bergers, G.; Hanahan, D. Modes of resistance to anti-angiogenic therapy. Nat. Rev. Cancer 2008, 8, 592. [Google Scholar] [CrossRef] [PubMed]
- Pàez-Ribes, M.; Allen, E.; Hudock, J.; Takeda, T.; Okuyama, H.; Viñals, F.; Inoue, M.; Bergers, G.; Hanahan, D.; Casanovas, O. Antiangiogenic therapy elicits malignant progression of tumors to increased local invasion and distant metastasis. Cancer Cell 2009, 15, 220–231. [Google Scholar] [CrossRef]
- Kolobov, A.; Kuznetsov, M. Investigation of the effects of angiogenesis on tumor growth using a mathematical model. Biophysics 2015, 60, 449–456. [Google Scholar] [CrossRef]
- Kuznetsov, M.B.; Kolobov, A.V. Mathematical investigation of antiangiogenic monotherapy effect on heterogeneous tumor progression. Comput. Res. Model. 2017, 9, 487–501. [Google Scholar] [CrossRef][Green Version]
- Kuznetsov, M.B.; Gubernov, V.V.; Kolobov, A.V. Analysis of anticancer efficiency of combined fractionated radiotherapy and antiangiogenic therapy via mathematical modeling. Russ. J. Numer. Anal. Math. Model. 2018, 33, 225–242. [Google Scholar] [CrossRef]
- Patra, K.C.; Hay, N. The pentose phosphate pathway and cancer. Trends Biochem. Sci. 2014, 39, 347–354. [Google Scholar] [CrossRef]
- Levick, J.R. An Introduction to Cardiovascular Physiology; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Araujo, R.; McElwain, D. New insights into vascular collapse and growth dynamics in solid tumors. J. Theor. Biol. 2004, 228, 335–346. [Google Scholar] [CrossRef]
- Holash, J.; Maisonpierre, P.; Compton, D.; Boland, P.; Alexander, C.; Zagzag, D.; Yancopoulos, G.; Wiegand, S. Vessel cooption, regression, and growth in tumors mediated by angiopoietins and VEGF. Science 1999, 284, 1994–1998. [Google Scholar] [CrossRef]
- Swanson, K.R.; Rockne, R.C.; Claridge, J.; Chaplain, M.A.; Alvord, E.C.; Anderson, A.R. Quantifying the role of angiogenesis in malignant progression of gliomas: In silico modeling integrates imaging and histology. Cancer Res. 2011, 71, 7366–7375. [Google Scholar] [CrossRef] [PubMed]
- Szomolay, B.; Eubank, T.D.; Roberts, R.D.; Marsh, C.B.; Friedman, A. Modeling the inhibition of breast cancer growth by GM-CSF. J. Theor. Biol. 2012, 303, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, M.; Kolobov, A. Transient alleviation of tumor hypoxia during first days of antiangiogenic therapy as a result of therapy-induced alterations in nutrient supply and tumor metabolism—Analysis by mathematical modeling. J. Theor. Biol. 2018, 451, 86–100. [Google Scholar] [CrossRef] [PubMed]
- Maeda, H.; Wu, J.; Sawa, T.; Matsumura, Y.; Hori, K. Tumor vascular permeability and the EPR effect in macromolecular therapeutics: A review. J. Control. Release 2000, 65, 271–284. [Google Scholar] [CrossRef]
- Fu, B.M.; Shen, S. Structural mechanisms of acute VEGF effect on microvessel permeability. Am. J. Physiol.-Heart Circ. Physiol. 2003, 284, H2124–H2135. [Google Scholar] [CrossRef] [PubMed]
- Abdollahi, A.; Lipson, K.E.; Sckell, A.; Zieher, H.; Klenke, F.; Poerschke, D.; Roth, A.; Han, X.; Krix, M.; Bischof, M.; et al. Combined therapy with direct and indirect angiogenesis inhibition results in enhanced antiangiogenic and antitumor effects. Cancer Res. 2003, 63, 8890–8898. [Google Scholar] [PubMed]
- Dings, R.P.; Loren, M.; Heun, H.; McNiel, E.; Griffioen, A.W.; Mayo, K.H.; Griffin, R.J. Scheduling of radiation with angiogenesis inhibitors anginex and Avastin improves therapeutic outcome via vessel normalization. Clin. Cancer Res. 2007, 13, 3395–3402. [Google Scholar] [CrossRef]
- Freyer, J.; Sutherland, R. A reduction in the in situ rates of oxygen and glucose consumption of cells in EMT6/Ro spheroids during growth. J. Cell. Physiol. 1985, 124, 516–524. [Google Scholar] [CrossRef]
- Swanson, K.; Alvord, E., Jr.; Murray, J. A quantitative model for differential motility of gliomas in grey and white matter. Cell Proliferat. 2000, 33, 317–329. [Google Scholar] [CrossRef]
- Stamatelos, S.; Kim, E.; Pathak, A.; Popel, A. A bioimage informatics based reconstruction of breast tumor microvasculature with computational blood flow predictions. Microvasc. Res. 2014, 91, 8–21. [Google Scholar] [CrossRef]
- Tuchin, V.; Bashkatov, A.; Genina, E.; Sinichkin, Y.; Lakodina, N. In vivo investigation of the immersion-liquid-induced human skin clearing dynamics. Tech. Phys. Lett. 2001, 27, 489–490. [Google Scholar] [CrossRef]
- Dickson, P.V.; Hamner, J.B.; Sims, T.L.; Fraga, C.H.; Ng, C.Y.; Rajasekeran, S.; Hagedorn, N.L.; McCarville, M.B.; Stewart, C.F.; Davidoff, A.M. Bevacizumab-induced transient remodeling of the vasculature in neuroblastoma xenografts results in improved delivery and efficacy of systemically administered chemotherapy. Clin. Cancer Res. 2007, 13, 3942–3950. [Google Scholar] [CrossRef] [PubMed]
- Boris, J.P.; Book, D.L. Flux-corrected transport. I. SHASTA, a fluid transport algorithm that works. J. Comput. Phys. 1973, 11, 38–69. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Tamaskar, I.; Garcia, J.A.; Elson, P.; Wood, L.; Mekhail, T.; Dreicer, R.; Rini, B.I.; Bukowski, R.M. Antitumor effects of sunitinib or sorafenib in patients with metastatic renal cell carcinoma who received prior antiangiogenic therapy. J. Urol. 2008, 179, 81–86. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Étude de l’équation de la diffusion avec croissance de la quantité de matière et son application à un problème biologique. Bull. Univ. Moskow Ser. Intern. Sect. A 1937, 1, 1–25. [Google Scholar]
- Roose, T.; Chapman, S.J.; Maini, P.K. Mathematical models of avascular tumor growth. SIAM Rev. 2007, 49, 179–208. [Google Scholar] [CrossRef]
- Kolobov, A.; Polezhaev, A.; Solyanik, G. The role of cell motility in metastatic cell dominance phenomenon: Analysis by a mathematical model. Comput. Math. Methods Med. 2000, 3, 63–77. [Google Scholar] [CrossRef]
- Thompson, K.; Byrne, H. Modelling the internalization of labelled cells in tumour spheroids. Bull. Math. Biol. 1999, 61, 601–623. [Google Scholar] [CrossRef]
- Franks, S.; King, J. Interactions between a uniformly proliferating tumour and its surroundings: Uniform material properties. Math. Med. Biol. 2003, 20, 47–89. [Google Scholar] [CrossRef]
- Franks, S.; King, J. Interactions between a uniformly proliferating tumour and its surroundings: Stability analysis for variable material properties. Int. J. Eng. Sci. 2009, 47, 1182–1192. [Google Scholar] [CrossRef]
| Parameter | Description | Estimated Value | Model Value | Based on |
|---|---|---|---|---|
| B | tumor cells’ proliferation rate | 0.01 h | 0.01 | [39] |
| Q | tumor cells’ glucose consumption rate | mol/(cells·s) | 12 | [39] |
| glucose diffusion coefficient | cm/s | 100 | [42] | |
| P | angiogenesis parameter | cm/s | 4 | [29] |
| critical level of glucose | 0.56 mM | 0.1 | see the text | |
| tumor cells’ motility | cm/day | 0.1 | [40] | |
| M | tumor cells’ death rate | 0.05 h | 0.05 | see the text |
| R | capillaries’ degradation rate | mL/(cells·s) | 0.2 | [41] |
| tumor cells’ sensitivity to glucose level | – | 100 | see the text |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuznetsov, M. Mathematical Modeling Shows That the Response of a Solid Tumor to Antiangiogenic Therapy Depends on the Type of Growth. Mathematics 2020, 8, 760. https://doi.org/10.3390/math8050760
Kuznetsov M. Mathematical Modeling Shows That the Response of a Solid Tumor to Antiangiogenic Therapy Depends on the Type of Growth. Mathematics. 2020; 8(5):760. https://doi.org/10.3390/math8050760
Chicago/Turabian StyleKuznetsov, Maxim. 2020. "Mathematical Modeling Shows That the Response of a Solid Tumor to Antiangiogenic Therapy Depends on the Type of Growth" Mathematics 8, no. 5: 760. https://doi.org/10.3390/math8050760
APA StyleKuznetsov, M. (2020). Mathematical Modeling Shows That the Response of a Solid Tumor to Antiangiogenic Therapy Depends on the Type of Growth. Mathematics, 8(5), 760. https://doi.org/10.3390/math8050760





