Mixed Modified Recurring Rogers-Szego Polynomials Neural Network Control with Mended Grey Wolf Optimization Applied in SIM Expelling System
Abstract
1. Introduction
2. Materials and Methods
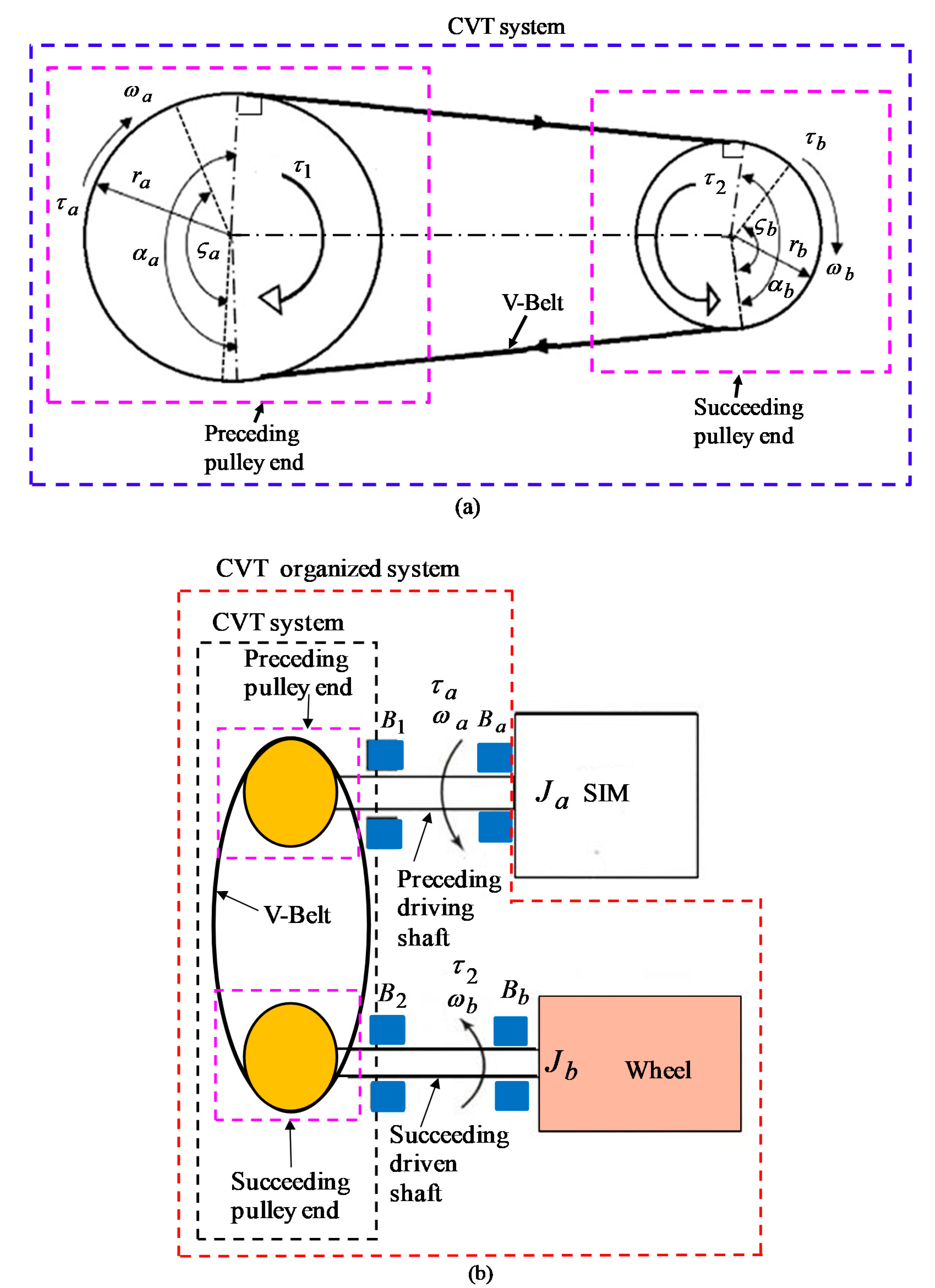
2.1. CVT Organized System and SIM Models
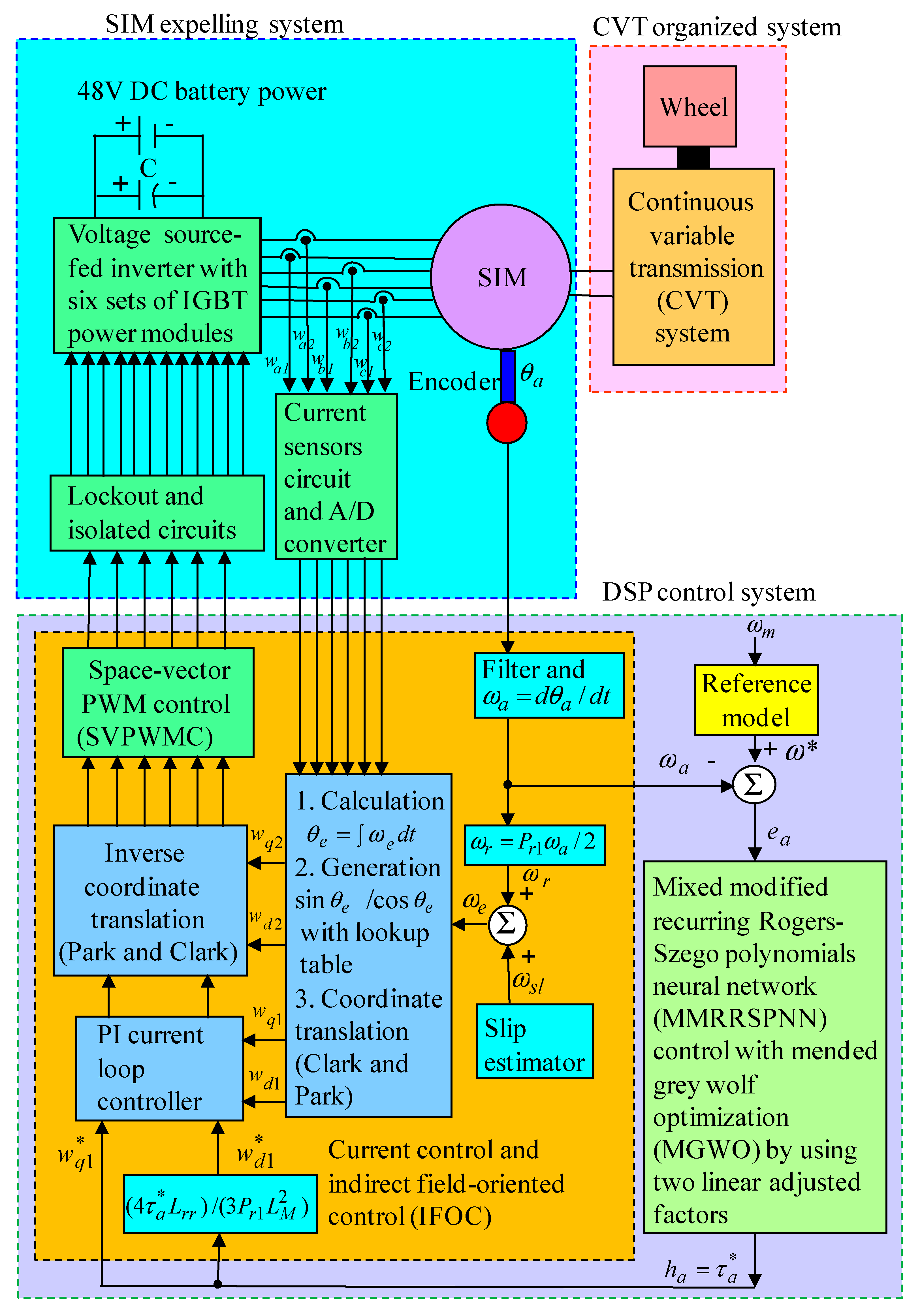
2.2. SIM Expelling CVT Organized System
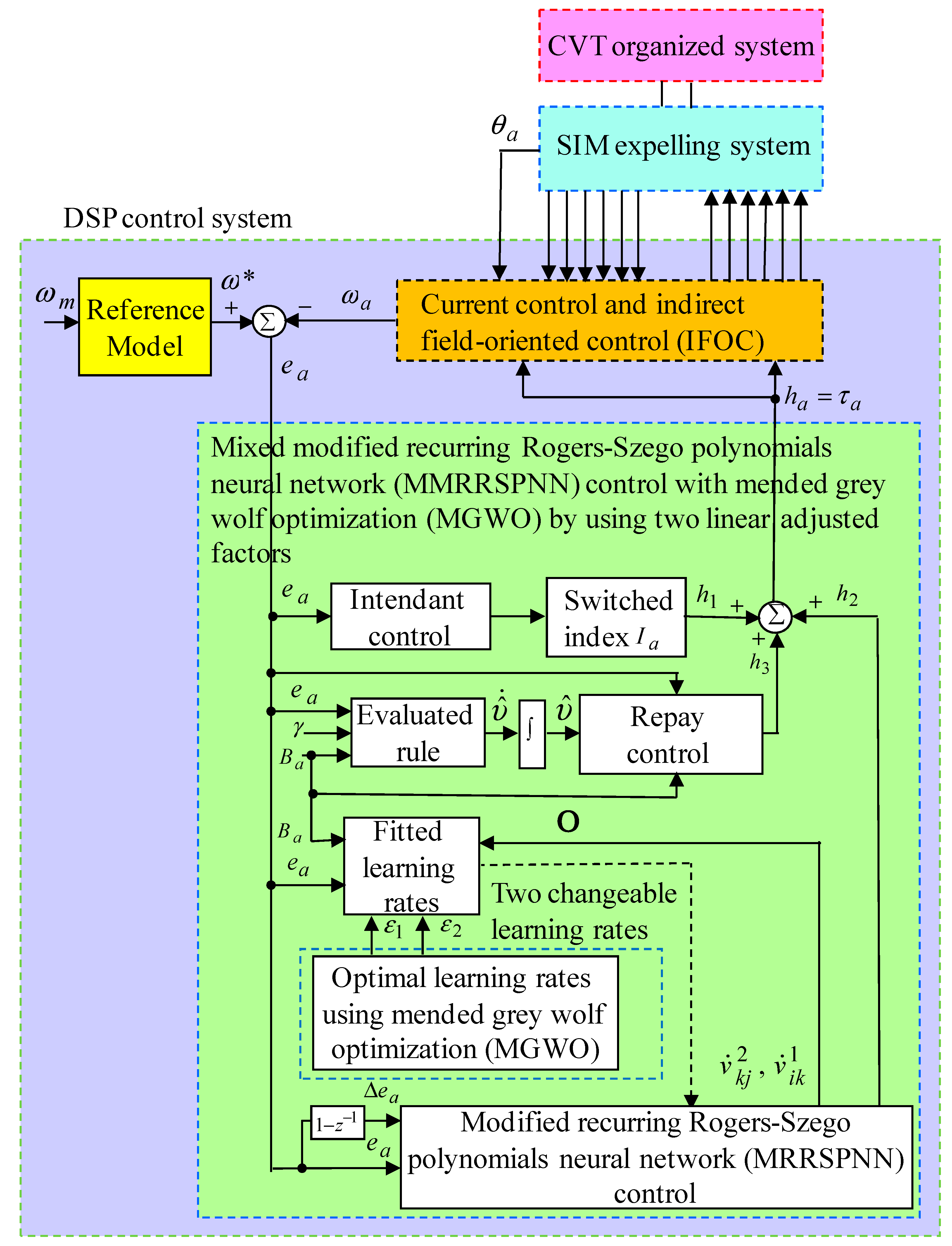
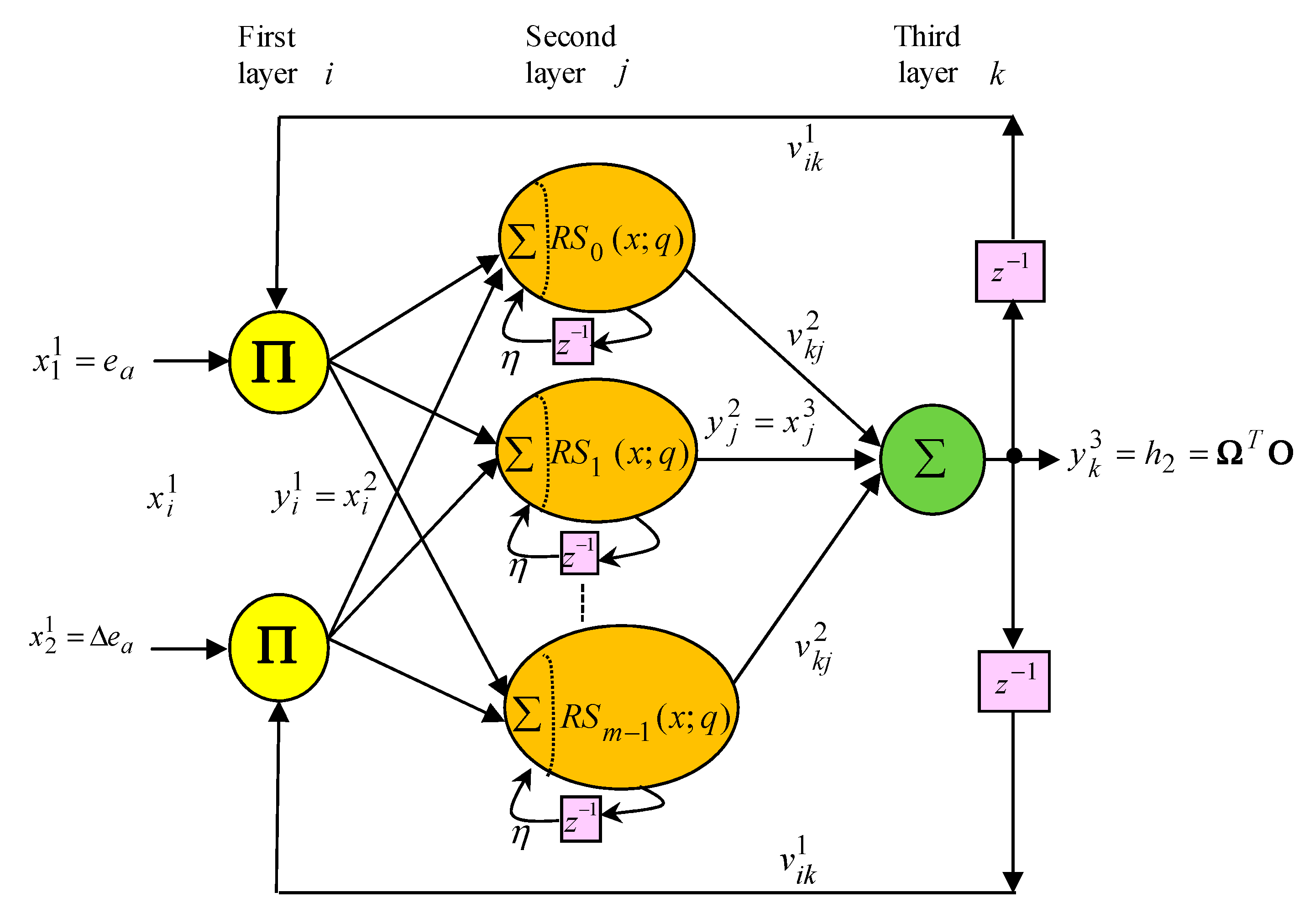
2.3. MMRRSPNN Control with MGWO by Using Two Adjusted Factors
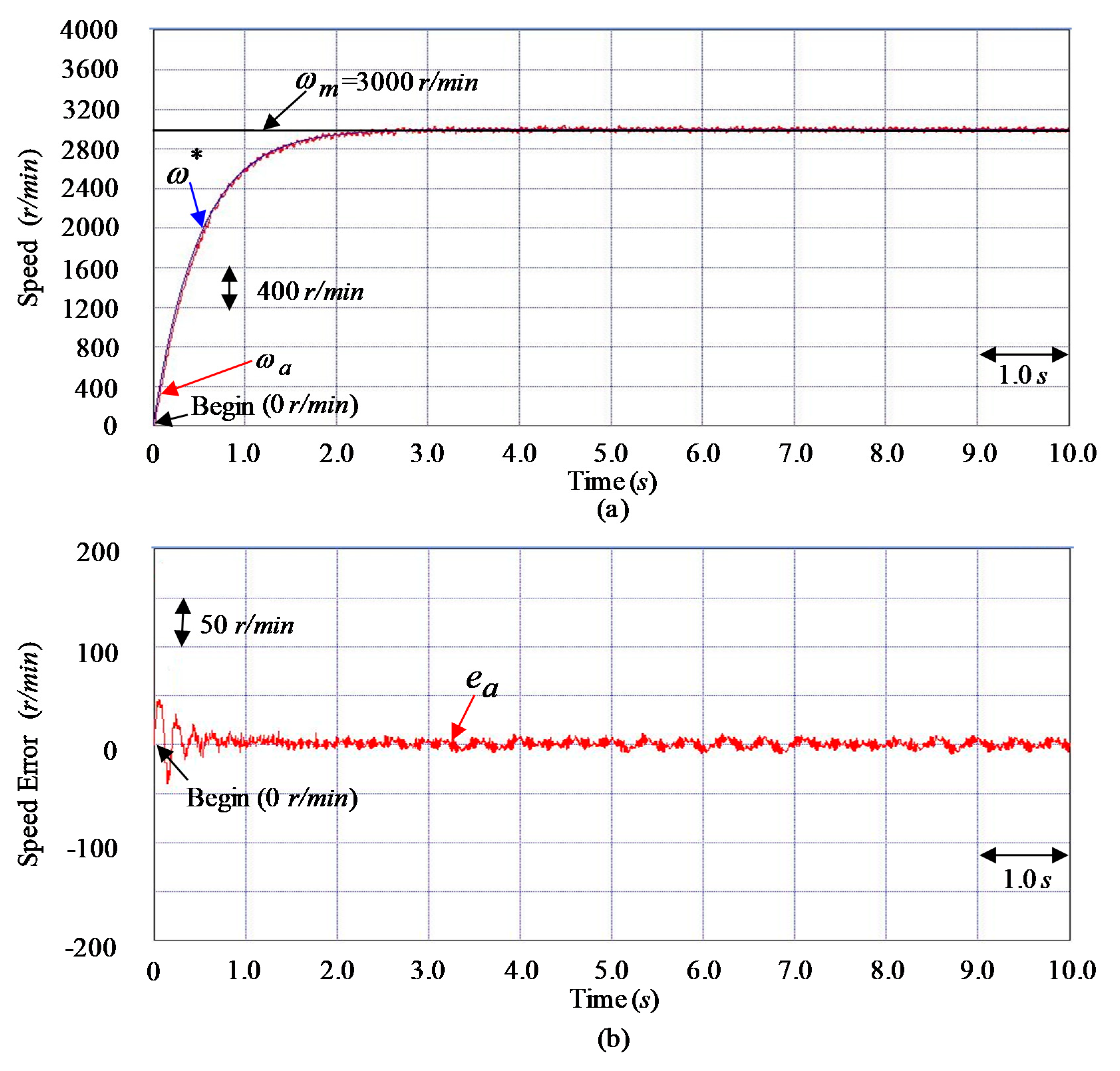
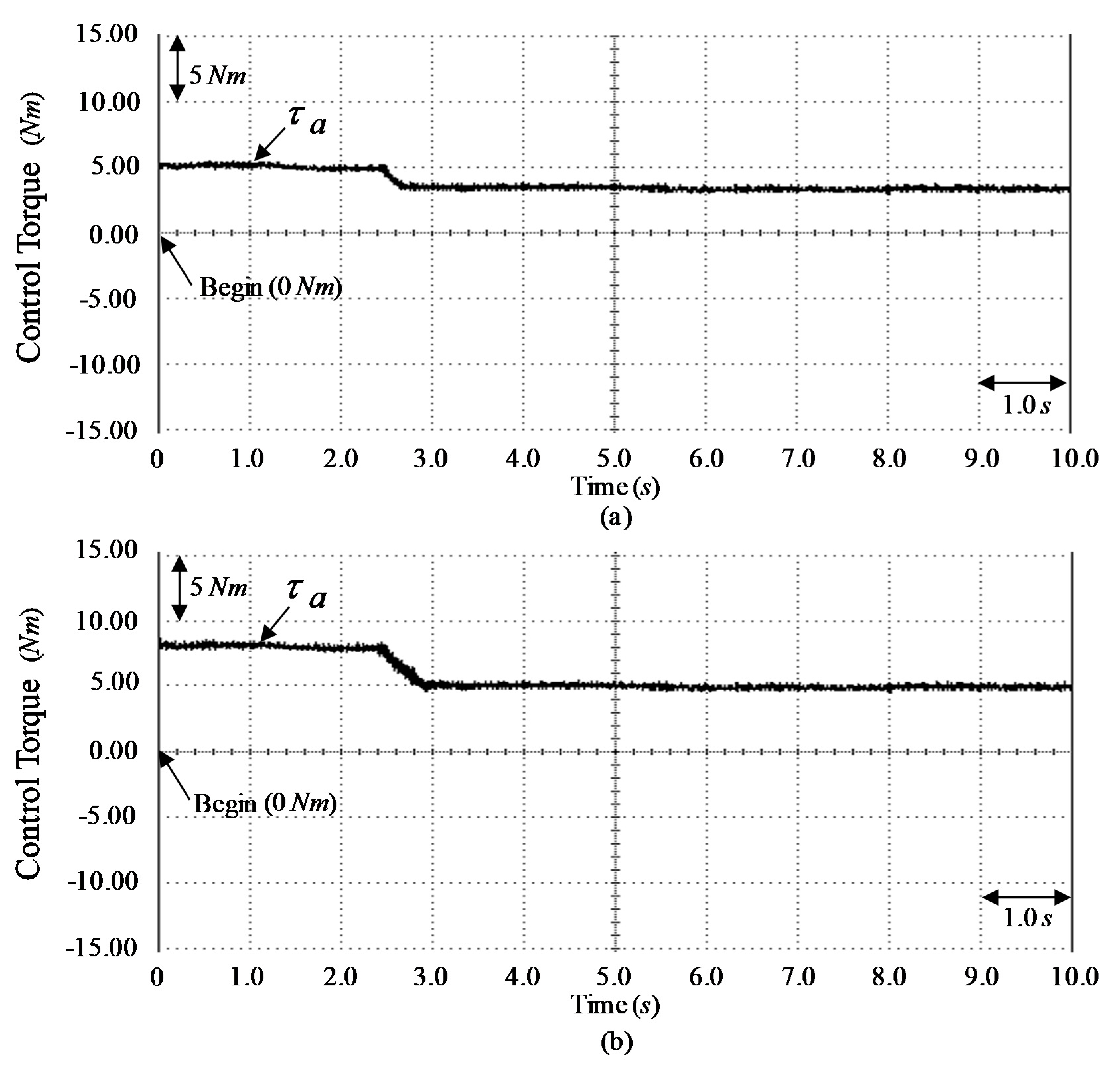
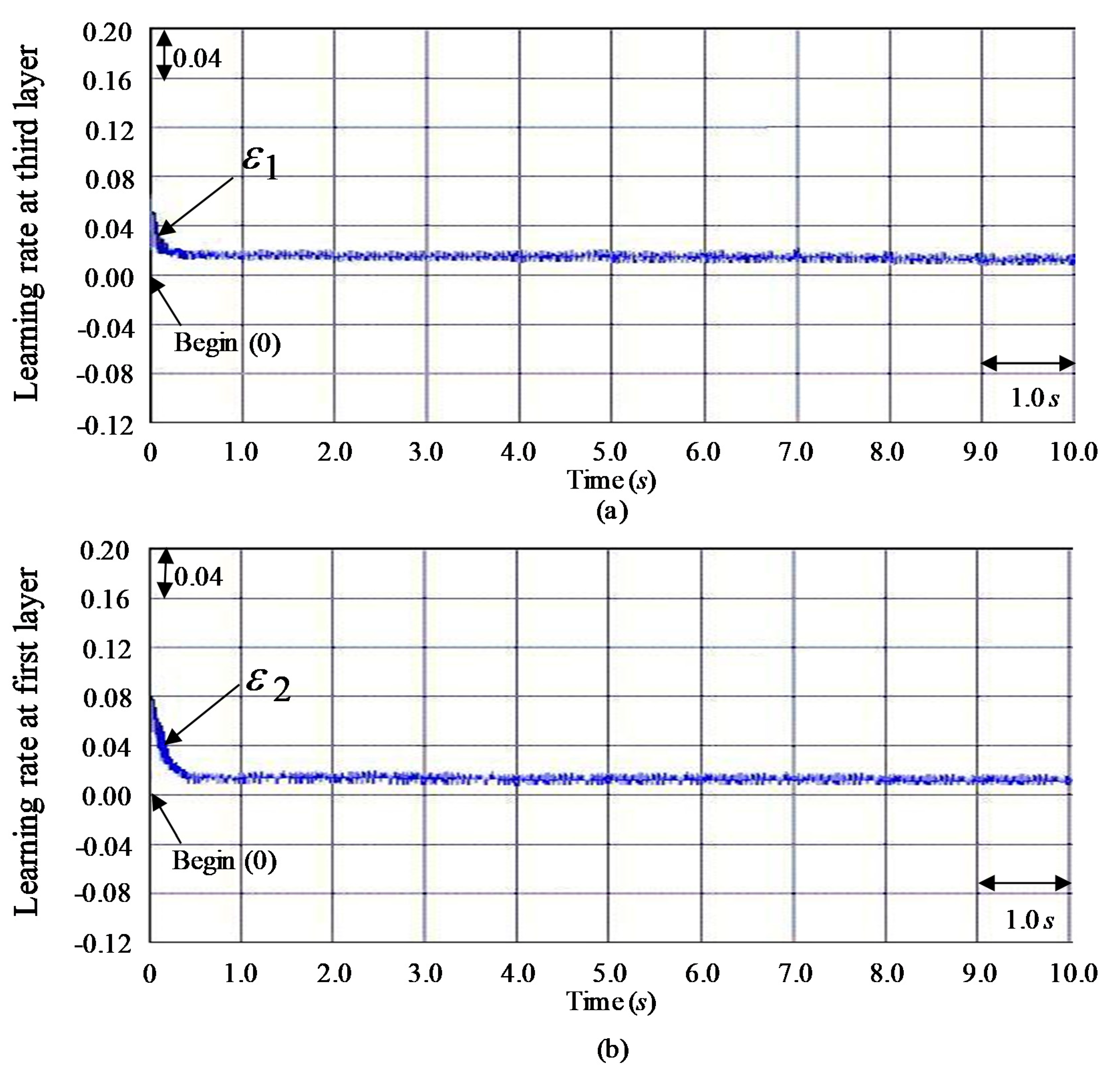
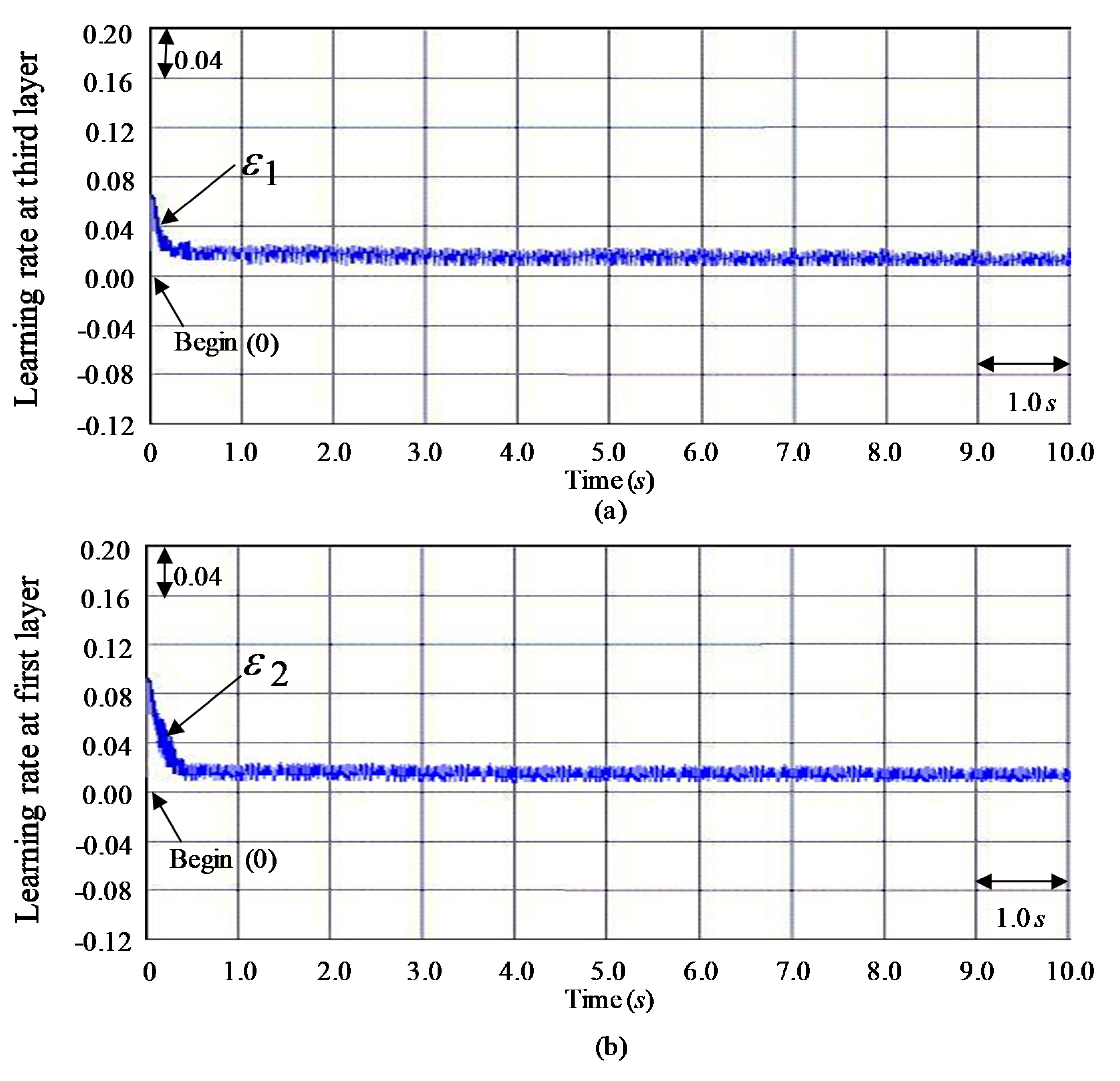
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Heydar, M.; Milad, S.; Mohammad, H.A.; Ravinder, K.; Shahaboddin, S. Modeling and efficiency optimization of steam boilers by employing neural networks and response-surface method (RSM). Mathematics 2019, 7, 629. [Google Scholar]
- Shao, Y.E.; Lin, S.C. Using a time delay neural network approach to diagnose the out-of-control signals for a multivariate normal process with variance shifts. Mathematics 2019, 7, 959. [Google Scholar] [CrossRef]
- Behzad, M.; Mahyar, G.; Mohammad, H.A.; Heydar, M.; Shahabddin, S. Moisture estimation in cabinet dryers with thin-layer relationships using a genetic algorithm and neural network. Mathematics 2019, 7, 1042. [Google Scholar]
- Shih, P.C.; Chiu, C.Y.; Chou, C.H. Using dynamic adjusting NGHS-ANN for predicting the recidivism rate of commuted prisoners. Mathematics 2019, 7, 1187. [Google Scholar] [CrossRef]
- Nagamani, G.; Ramasamy, S. Stochastic dissipativity and passivity analysis for discrete-time neural networks with probabilistic time-varying delays in the leakage term. Appl. Math. Comput. 2016, 289, 237–257. [Google Scholar] [CrossRef]
- Nagamani, G.; Ramasamy, S. Dissipativity and passivity analysis for discrete-time T–S fuzzy stochastic neural networks with leakage time-varying delays based on Abel lemma approach. J. Frankl. Inst. 2016, 353, 3313–3342. [Google Scholar] [CrossRef]
- Nagamani, G.; Ramasamy, S.; Mey-Base, A. Robust dissipativity and passivity based state estimation for discrete-time stochastic Markov jump neural networks with discrete and distributed time-varying delays. Neural Comput. Appl. 2017, 28, 717–735. [Google Scholar] [CrossRef]
- Ramasamy, S.; Nagamani, G.; Radhika, T. Further results on dissipativity criterion for markovian jump discrete-time neural networks with two delay components via discrete wirtinger inequality approach. Neural Process. Lett. 2017, 45, 939–965. [Google Scholar] [CrossRef]
- Lee, T.T.; Jeng, J.T. The Chebyshev polynomial-based unified model neural networks for functional approximation. IEEE Trans. Syst. Man Cybern. Part B 1998, 28, 925–935. [Google Scholar]
- Lin, C.H. Composite Recurring Laguerre orthogonal polynomials neural network dynamic control for continuously variable transmission system using altered particle swarm optimization. Nonlinear Dyn. 2015, 81, 1219–1245. [Google Scholar] [CrossRef]
- Lin, C.H. Comparative dynamic control for continuously variable transmission with nonlinear uncertainty using blend amend recurring Gegenbauer-functional-expansions neural network. Nonlinear Dyn. 2017, 87, 1467–1493. [Google Scholar] [CrossRef]
- Ting, J.C.; Chen, D.F. Nonlinear backstepping control of SynRM drive systems using reformed recurring Hermite polynomial neural networks with adaptive law and error estimated law. J. Power Electron. 2018, 8, 1380–1397. [Google Scholar]
- Szego, G. Beitrag zur theorie der thetafunktionen. Sitz Preuss. Akad. Wiss. Phys. Math. Ki. 1926, 19, 242–252. [Google Scholar]
- Cirovic, V.; Aleksendric, D.; Mladenovic, D. Braking torque control using recurring neural networks. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2012, 226, 754–766. [Google Scholar] [CrossRef]
- Wong, W.C.; Chee, E.; Li, J.; Wang, X. Recurring neural network-based model predictive control for continuous pharmaceutical manufacturing. Mathematics 2018, 6, 242. [Google Scholar] [CrossRef]
- Ting, J.C.; Chen, D.F. Novel mingled reformed recurring hermite polynomial neural network control system applied in continuously variable transmission system. J. Mech. Sci. Technol. 2018, 32, 4399–4412. [Google Scholar] [CrossRef]
- Lin, C.H.; Chang, K.T. Admixed recurring Gegenbauer polynomials neural network with mended particle swarm optimization control system for synchronous reluctance motor driving continuously variable transmission system. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2020, 234, 183–198. [Google Scholar]
- Liu, C.; Huang, B.; Wang, Q. Control performance assessment subject to multi-objective user- specified performance characteristics. IEEE Trans. Control Syst. Technol. 2011, 19, 682–691. [Google Scholar] [CrossRef]
- Cano-Izquierdo, J.M.; Ibarrola, J.; Kroeger, M. Control loop performance assessment with a dynamic neuro-fuzzy model (dFasArt). IEEE Trans. Autom. Sci. Eng. 2012, 9, 377–389. [Google Scholar] [CrossRef]
- Kordestani, M.; Safavi, A.A.; Sharafi, N.; Saif, M. Novel multiagent model-predictive control performance indices for monitoring of a large-scale distributed water system. IEEE Syst. J. 2018, 12, 1286–1294. [Google Scholar] [CrossRef]
- Kordestani, M.; Safavi, A.A.; Sharafi, N.; Saif, M. Fault tolerant control of Rhine-Meuse delta water system: A performance assessment based approach. In Proceedings of the International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Istanbul, Turkey, 26–27 August 2019; pp. 31–38. [Google Scholar]
- Emary, E.; Yamany, W.; Hassanien, A.E. Multi-objective gray-wolf optimization for attribute reduction. Procedia Comput. Sci. 2015, 1, 623–632. [Google Scholar] [CrossRef]
- Mosavi, M.; Khishe, M.; Ghamgosar, A. Classification of sonar data set using neural network trained by gray wolf optimization. Neural Netw. World 2016, 26, 393–415. [Google Scholar] [CrossRef]
- Khandelwal, A.; Bhargava, A.; Sharma, A.; Sharma, H. Modified grey wolf optimization algorithm for transmission network expansion planning problem. Arabian J. Sci. Eng. 2018, 43, 2899–2908. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Sultana, U.; Khairuddin, A.B.; Mokhtar, A.S. Grey wolf optimizer based placement and sizing of multiple distributed generation in the distribution system. Energy 2016, 111, 525–536. [Google Scholar] [CrossRef]
- Parsian, A.; Ramezani, M.; Ghadimi, N. A hybrid neural network-gray wolf optimization algorithm for melanoma detection. Biomed. Res. 2017, 28, 3408–3411. [Google Scholar]
- Duangjai, J.; Pongsak, P. Grey wolf algorithm with borda count for feature selection in classification. In Proceedings of the 3rd International Conference on Control and Robotics Engineering (ICCRE), Nagoya, Japan, 20–23 April 2018; pp. 238–242. [Google Scholar]
- Munoz, A.R.; Lipo, T.A. Dual stator winding induction machine drive. IEEE Trans. Ind. Appl. 2000, 36, 1369–1379. [Google Scholar] [CrossRef]
- Ojo, O.; Davidson, I.E. PWM-VSI inverter assisted stand-alone dual stator winding induction generator. IEEE Trans. Ind. Appl. 2000, 36, 1604–1611. [Google Scholar]
- Singh, G.K.; Nam, K.; Lim, S.K. A simple indirect field-oriented control scheme for multiphase induction machine. IEEE Trans. Ind. Electron. 2005, 52, 1177–1184. [Google Scholar] [CrossRef]
- Lin, C.H.; Hwang, C.C. Multiobjective optimization design for a six-phase copper rotor induction motor mounted with a scroll compressor. IEEE Trans. Magn. 2016, 52, 9401604. [Google Scholar] [CrossRef]
- Lin, C.H.; Hwang, C.C. Multi-objective optimization design using amended particle swarm optimization and Taguchi method for a six-phase copper rotor induction motor. Eng. Optim. 2017, 49, 693–708. [Google Scholar] [CrossRef]
- Lin, C.H. Modelling and control of six-phase induction motor servo-driven continuously variable transmission system using blend modified recurring Gegenbauer orthogonal polynomial neural network control system and amended artificial bee colony optimization. Int. J. Numer. Model. Electron. Netw. Devices Fields 2016, 29, 915–942. [Google Scholar] [CrossRef]
- Lin, C.H. A six-phase CRIM driving CVT using blend modified recurring Gegenbauer OPNN Control. J. Power Electron. 2016, 16, 1438–1454. [Google Scholar] [CrossRef]
- Lin, C.H. Blend modified recurring Gegenbauer orthogonal polynomial neural network control for six-phase copper rotor induction motor servo-driven continuously variable transmission system using amended artificial bee colony optimization. Trans. Inst. Meas. Control 2017, 39, 921–950. [Google Scholar] [CrossRef]
- Ting, J.C.; Chen, D.F. SynRM servo-drive CVT systems using MRRHPNN control with mend ACO. J. Power Electron. 2018, 18, 1409–1423. [Google Scholar]
- Hong, C.W.; Chen, C.C. Dynamic performance simulation of a continuously variable transmission motorcycle for fuzzy autopilot design. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 1997, 211, 477–490. [Google Scholar] [CrossRef]
- Srivastava, N.; Haque, I. Transient dynamics of metal V-belt CVT: Effects of bandpack slip and friction characteristic. Mech. Mach. Theory 2008, 43, 457–479. [Google Scholar] [CrossRef]
- Srivastava, N.; Haque, I. A review on belt and chain continuously variable transmissions (CVT): Dynamics and control. Mech. Mach. Theory 2009, 44, 19–41. [Google Scholar] [CrossRef]
- Hu, J.; Guo, Z.; Peng, H. Research on regenerative braking control strategy of plug-in hybrid electric vehicle considering CVT ratio rate of change. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 232, 1931–1943. [Google Scholar] [CrossRef]
- Xie, D.; Zhang, H.; Dong, C.; Liu, Z.; Yang, Z. Challenges of Power Engineering and Environment—A Theoretical Investigation on Experimental Model of Torsional Vibration for Turboset Shafting; Springer: Berlin/Heidelberg, Germany, 2007; pp. 568–573. [Google Scholar]
- Matyja, T.; Lazarz, B. Modeling the coupled flexural and torsional vibrations in rotating machines in transient states. J. Vibroeng. 2015, 16, 1911–1924. [Google Scholar]
- Astrom, K.J.; Hagglund, T. PID Controller: Theory, Design, and Tuning; Instrument Society of America: Research Triangle Park, NC, USA, 1995. [Google Scholar]
- Hagglund, T.; Astrom, K.J. Revisiting the Ziegler-Nichols tuning rules for PI control. Asian J. Control 2002, 4, 364–380. [Google Scholar] [CrossRef]
- Hagglund, T.; Astrom, K.J. Revisiting the Ziegler-Nichols tuning rules for PI control-part II: The frequency response method. Asian J. Control 2004, 6, 469–482. [Google Scholar] [CrossRef]
- Gasper, G.; Rahman, M. Encyclopedia of Mathematics and Its Applications, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Astrom, K.J.; Wittenmark, B. Adaptive Control; Addison-Wesley: New York, NY, USA, 1995. [Google Scholar]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Lewis, F.L.; Campos, J.; Selmic, R. Neuro-Fuzzy Control of Industrial Systems with Actuator Nonlinearities; SIAM Frontiers in Applied Mathematics: Philadelphia, PA, USA, 2012. [Google Scholar]

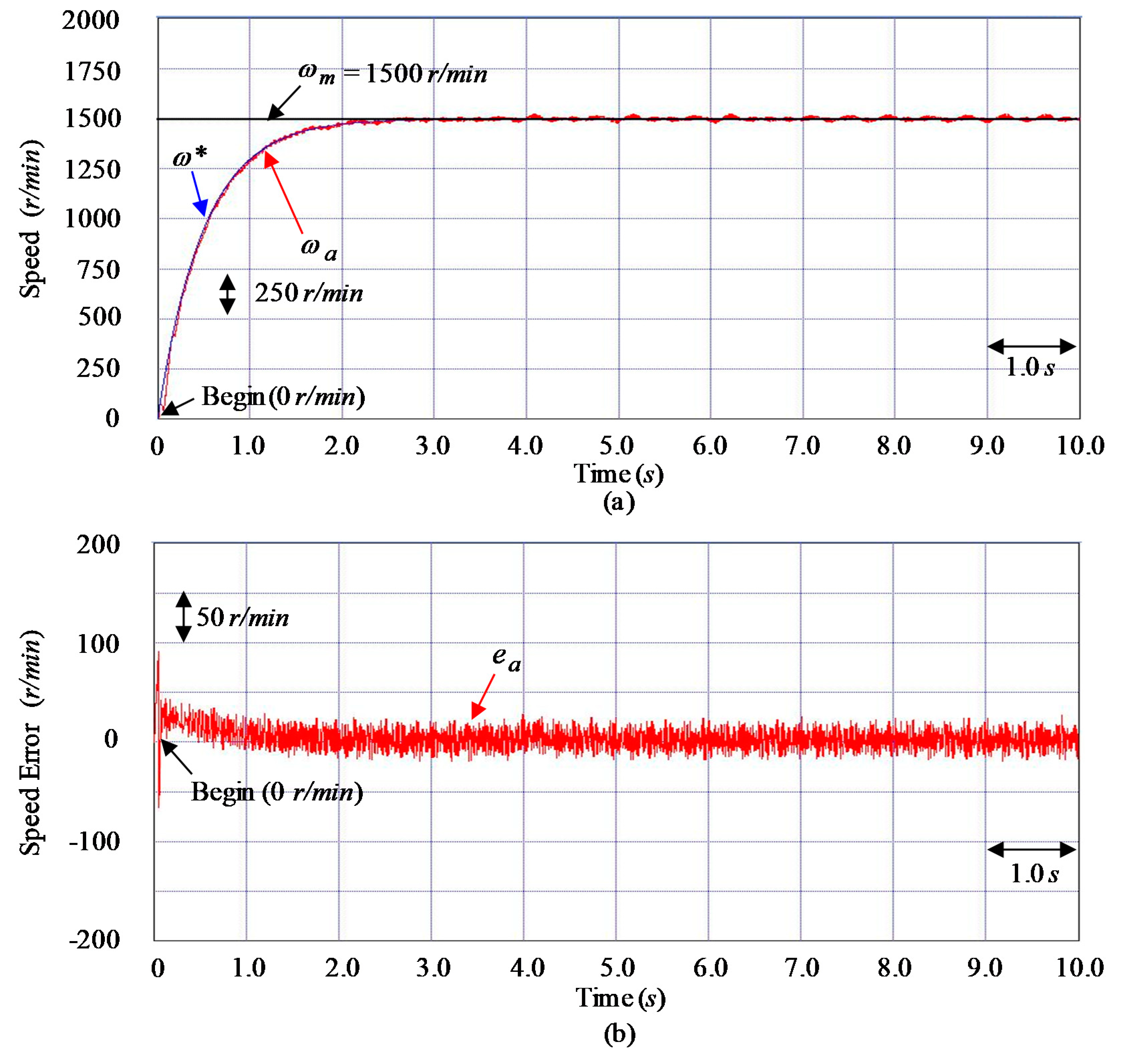

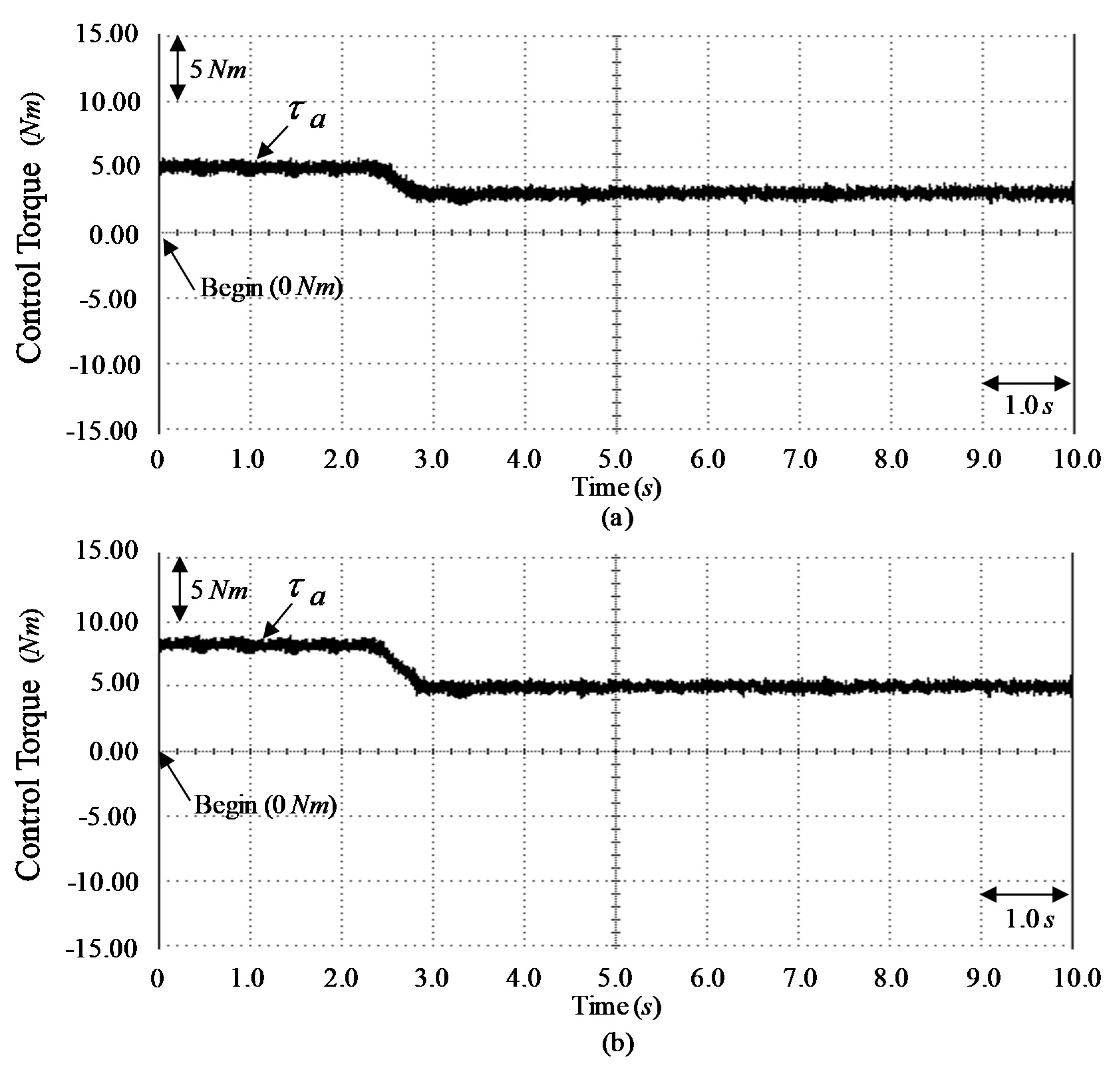
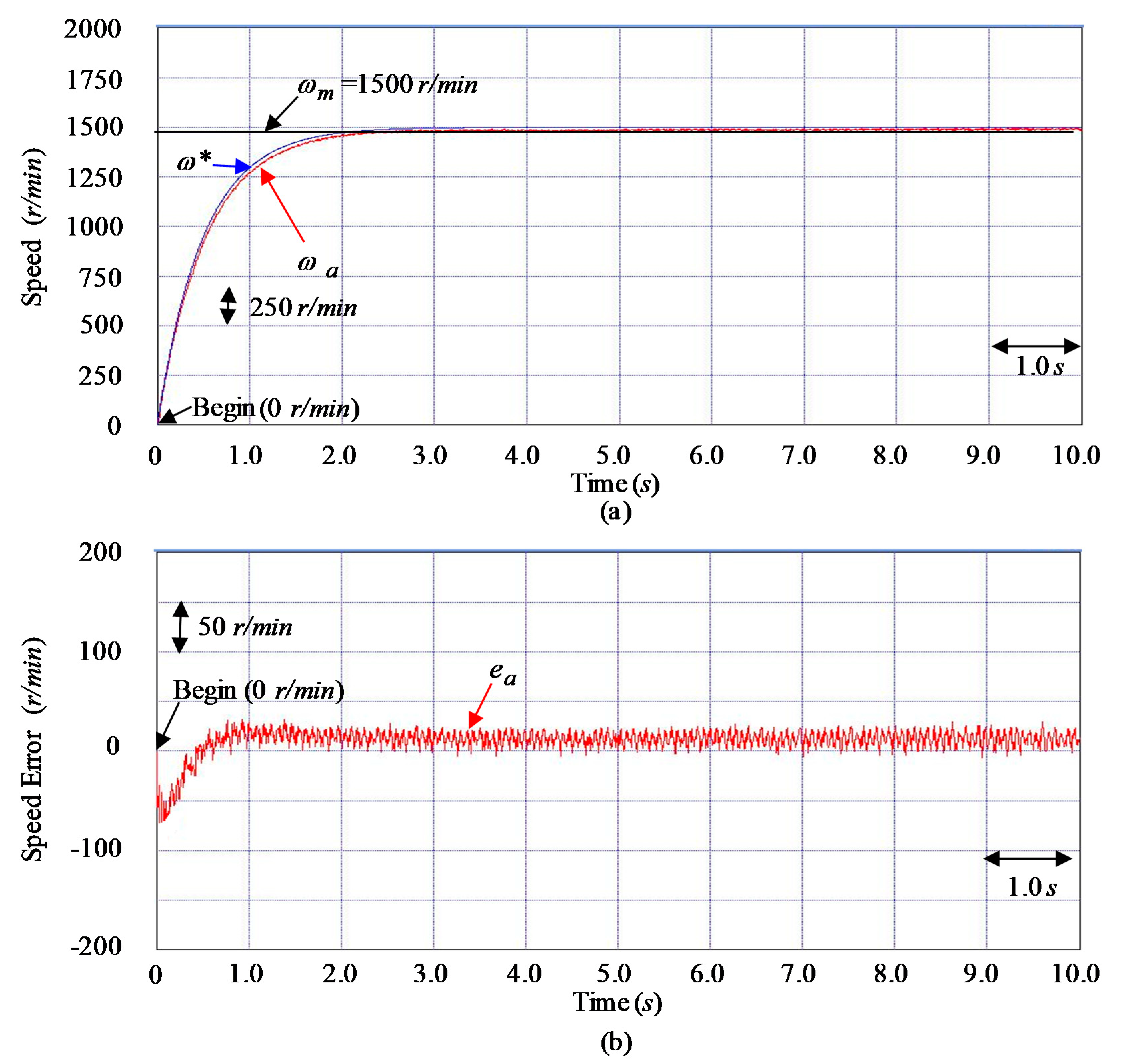
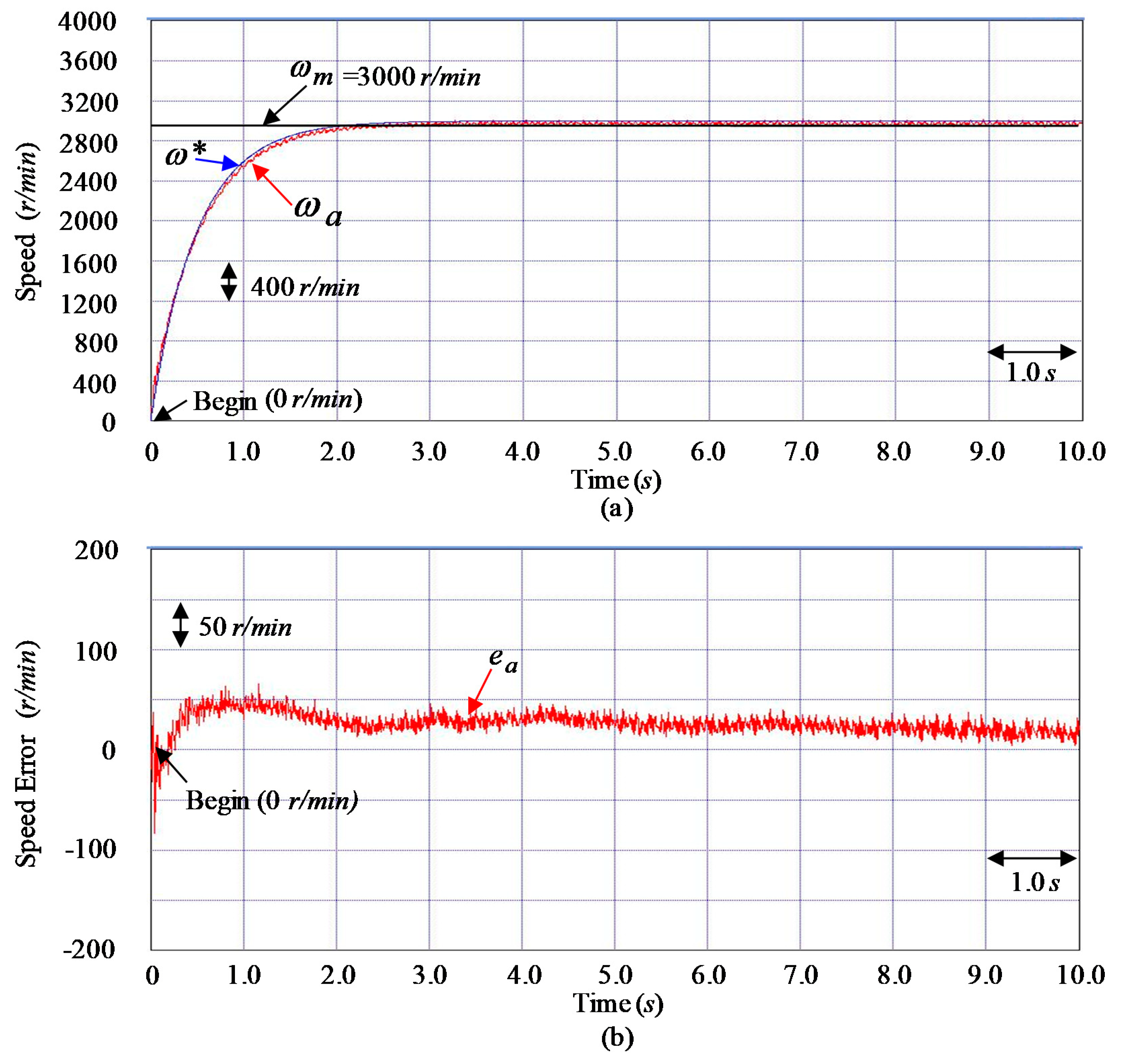


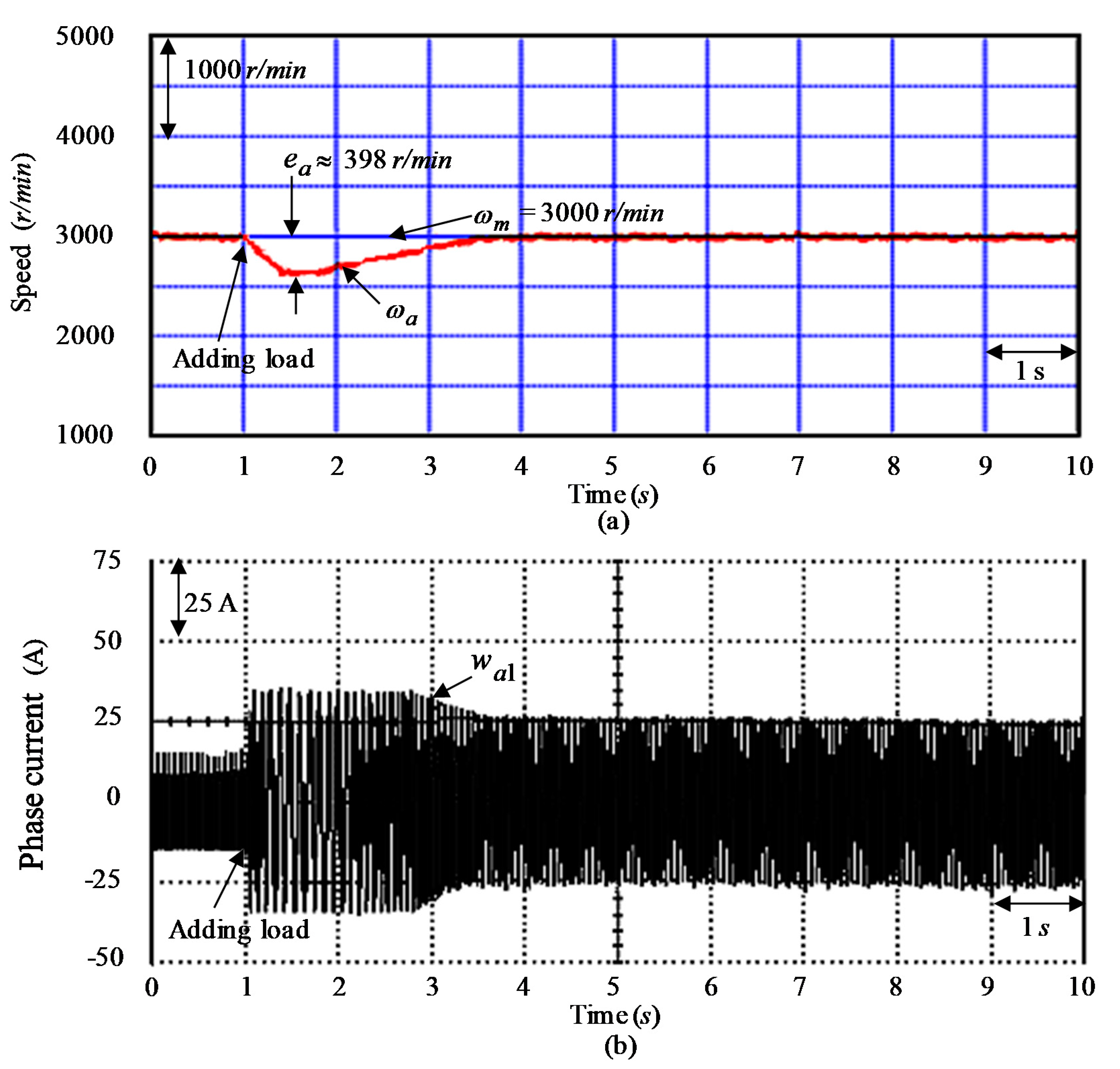
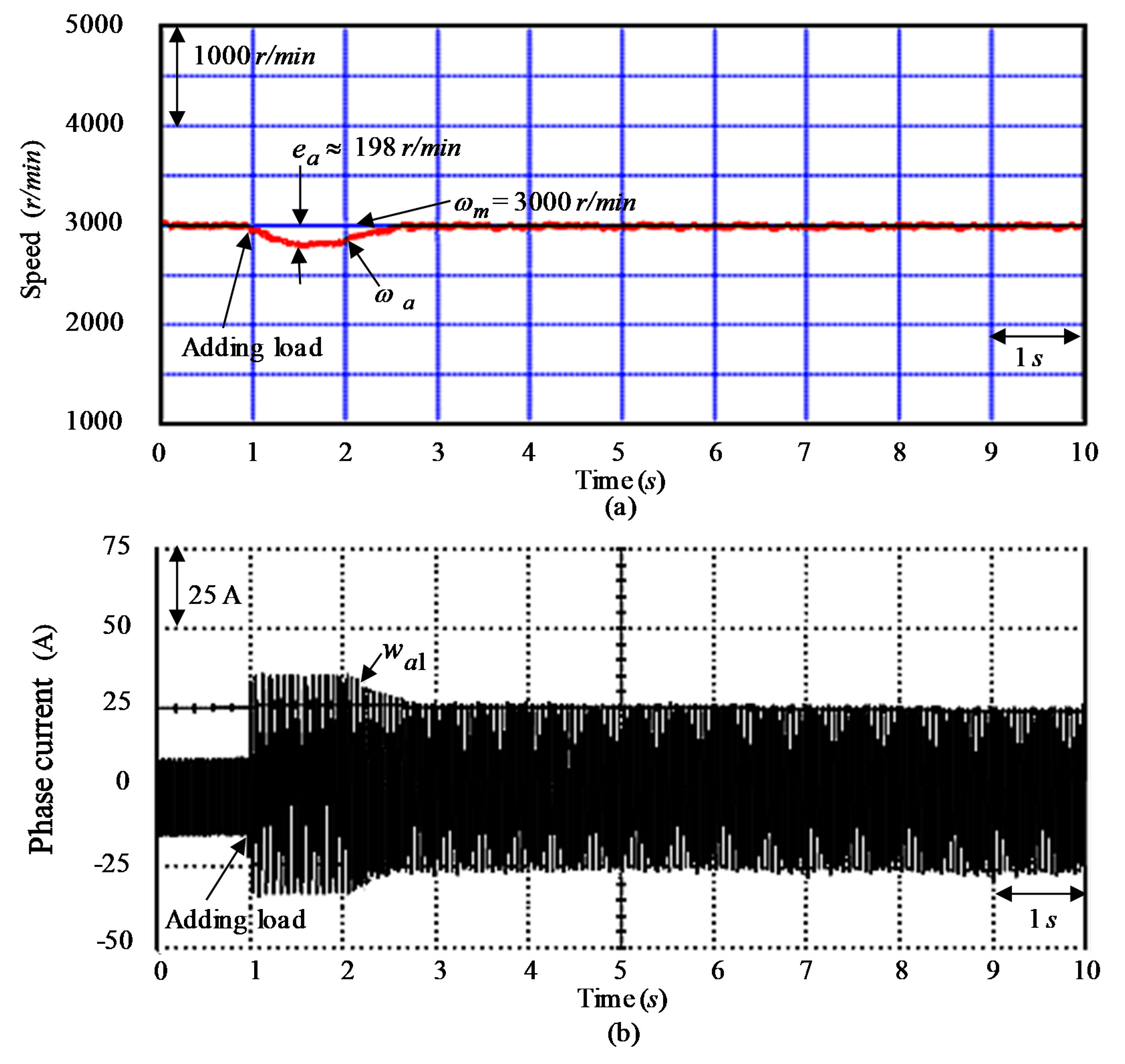
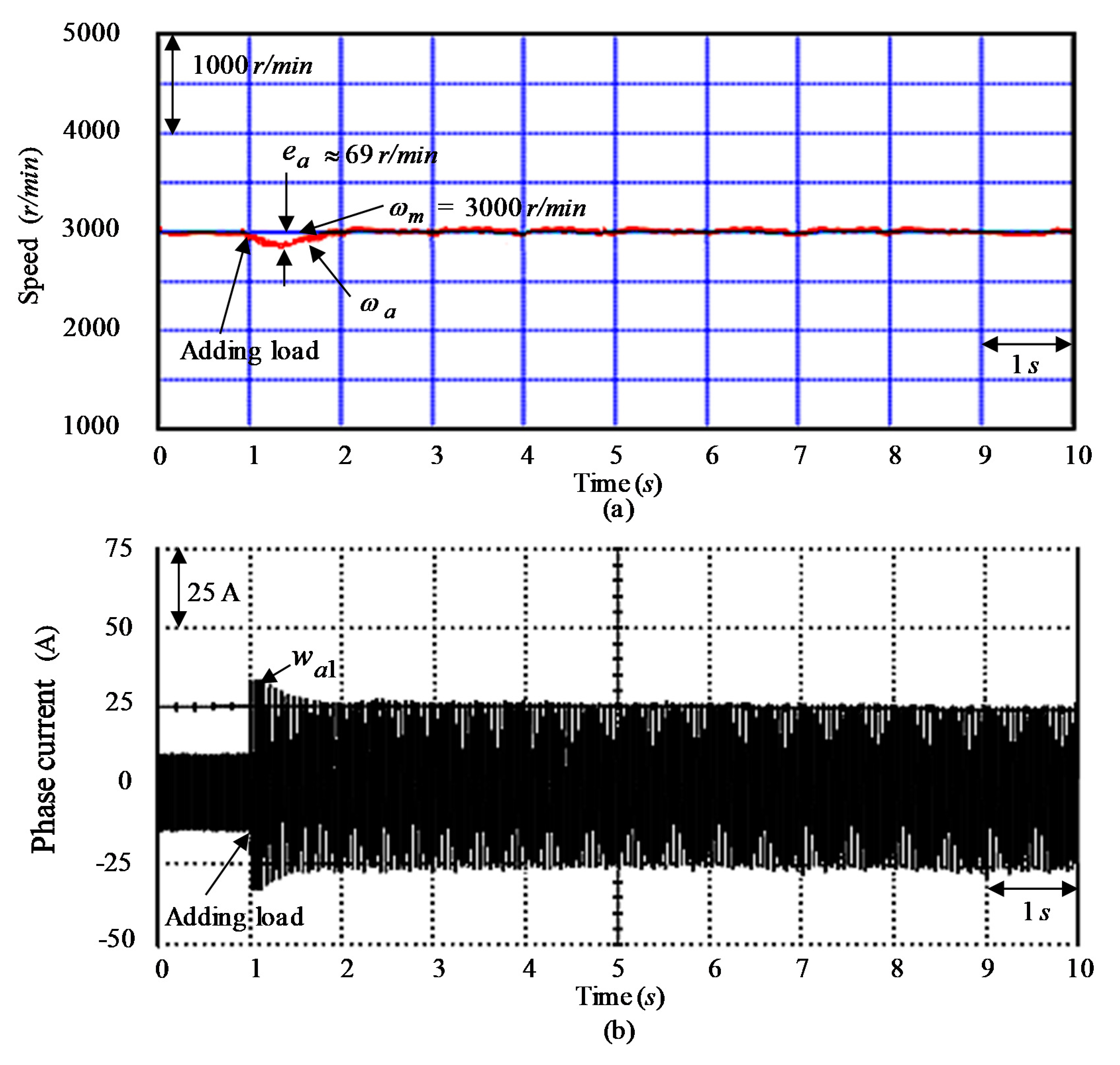
| Control System and Three Tested Cases | Controller CT1 | |||
| Performance | Tested Event E1 Case | Tested Event E2 Case | Tested Event E3 Case | |
| Maximum errors of | 88 r/min | 215 r/min | 398 r/min | |
| Root mean square errors of | 45 r/min | 60 r/min | 51 r/min | |
| Control System and Three Tested Cases | Controller CT2 | |||
| Performance | Tested Event E1 Case | Tested Event E2 Case | Tested Event E3 Case | |
| Maximum errors of | 69 r/min | 88 r/min | 198 r/min | |
| Root mean square errors of | 30 r/min | 31 r/min | 27 r/min | |
| Control System and Three Tested Cases | Controller CT3 | |||
| Performance | Tested Event E1 Case | Tested Event E2 Case | Tested Event E3 Case | |
| Maximum errors of | 40 r/min | 43 r/min | 69 r/min | |
| Root mean square errors of | 20 r/min | 22 r/min | 17 r/min | |
| Control System | Control System CT1 | Control System CT2 | Control System CT3 | |
|---|---|---|---|---|
| Characteristic Performance | ||||
| Vibration value in the control rule | Small (10% of nominal value at tested Event E2 case) | smaller (8% of nominal value at tested Event E2 case) | Smallest (6% of nominal value at tested Event E2 case) | |
| Dynamic response | Slow (rising time as 2.0 sec at tested Event E2 case) | Fast (rising time as 1.8 sec at tested Event E2 case) | Faster (rising time 1.6 sec at tested Event E2 case) | |
| Regulation capability for load torque disturbance | Poor (maximum error as 398 r/min at tested Event E3 case) | Good (maximum error as 198 r/min at tested Event E3 case) | Better (maximum error as 69 r/min at tested Event E3 case) | |
| Convergent speed | Slow (settle time as 2.5 sec at tested Event E2 case) | Fast (settle time as 2.2 sec at tested Event E2 case) | Faster (settle time as 2.0 sec at tested Event E2 case) | |
| Speed tracking error | Large (maximum error as 215 r/min at tested Event E2 case) | Middle (maximum error as 88 r/min at tested Event E2 case) | Small (maximum error as 43 r/min at tested Event E2 case) | |
| Rejection ability for parameter disturbance | Poor (maximum error as 215 r/min at tested Event E2 case) | Good (maximum error as 88 r/min at tested Event E2 case) | Better (maximum error as 43 r/min at tested Event E2 case) | |
| Two learning rates | None | Vary (two optimal learning rates) | Vary (two optimal learning rates) | |
| Torque ripple (V-belt shaking action and torsional vibration variations) | Large (12% of nominal value at tested Event E2 case) | Smaller (10% of nominal value at tested Event E2 case) | Smallest (6% of nominal value at tested Event E2 case) | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.-F.; Shih, Y.-C.; Li, S.-C.; Chen, C.-T.; Ting, J.-C. Mixed Modified Recurring Rogers-Szego Polynomials Neural Network Control with Mended Grey Wolf Optimization Applied in SIM Expelling System. Mathematics 2020, 8, 754. https://doi.org/10.3390/math8050754
Chen D-F, Shih Y-C, Li S-C, Chen C-T, Ting J-C. Mixed Modified Recurring Rogers-Szego Polynomials Neural Network Control with Mended Grey Wolf Optimization Applied in SIM Expelling System. Mathematics. 2020; 8(5):754. https://doi.org/10.3390/math8050754
Chicago/Turabian StyleChen, Der-Fa, Yi-Cheng Shih, Shih-Cheng Li, Chin-Tung Chen, and Jung-Chu Ting. 2020. "Mixed Modified Recurring Rogers-Szego Polynomials Neural Network Control with Mended Grey Wolf Optimization Applied in SIM Expelling System" Mathematics 8, no. 5: 754. https://doi.org/10.3390/math8050754
APA StyleChen, D.-F., Shih, Y.-C., Li, S.-C., Chen, C.-T., & Ting, J.-C. (2020). Mixed Modified Recurring Rogers-Szego Polynomials Neural Network Control with Mended Grey Wolf Optimization Applied in SIM Expelling System. Mathematics, 8(5), 754. https://doi.org/10.3390/math8050754




