1. Introduction
In recent years, research on complex networks has been essential since many complex systems are modelled as networks consisting of components as well as relations among these components. Some studies focused on finding properties of real networks, such as degree distribution [
1,
2], degree correlation [
3,
4,
5], and degree-based structure entropies [
6,
7]. Many significant properties of systems such as heterogeneity [
1], assortative mixing [
8,
9], and self-similarity [
10,
11,
12] are based on these statistics.
Entropy applied to graphs is one of two major approaches to measuring the complexity of relational structures. The origin of such measures goes back to Rashevsky who introduced the concept of topological information content; see [
13]. Studies of graph complexity have been performed in many areas [
8,
11,
14,
15], such as chemistry to labeled chemical structures possessing bond types and hetero-atoms; see [
16]. The aim of this paper was to review some selected entropy-based measures.
2. Definitions and Preliminaries
Here, we recall the definition of the automorphism group of a graph. It is a well-known fact that in a regular polyhedral graph such as a fullerene, the symmetry group and the automorphism group are the same; see [
17]. A permutation
π on the set of vertices of graph
G, which preserves the adjacency of vertices of
G, is called an automorphism. In other words, the permutation
π is an automorphism if
The set of all automorphisms of G, denoted by , forms a group under the composition of mappings called an automorphism group. Let the automorphism group Aut (G) act on vertex set V. This action yields an automorphism partition P = {V1, V2,..., Vk} in the which two vertices x and y are equivalent if and only if there exists g in Aut (G) such that xg = y. Each member of P is an orbit of Aut (G). The set of orbits of a graph enables us to investigate the heterogeneity of networks.
We say that Aut (G) acts transitively on the set of vertices, if for , there is an automorphism , such that In this case, we say that G is vertex-transitive. It is not difficult to see that every vertex-transitive graph has only one orbit whose size is equal to the number of vertices. For example, consider the rotation ρ = of cycle graph Cn; then, the corresponding permutation is which yields that Cn is vertex-transitive.
Measuring the heterogeneity of complex networks has been important in studies of the behaviour of complex networks. For example, existing heterogeneity measures [
6,
7] of complex networks are based on degree. Specifically, entropies in [
6,
7] are based on degree distribution [
8,
9]. As is shown in
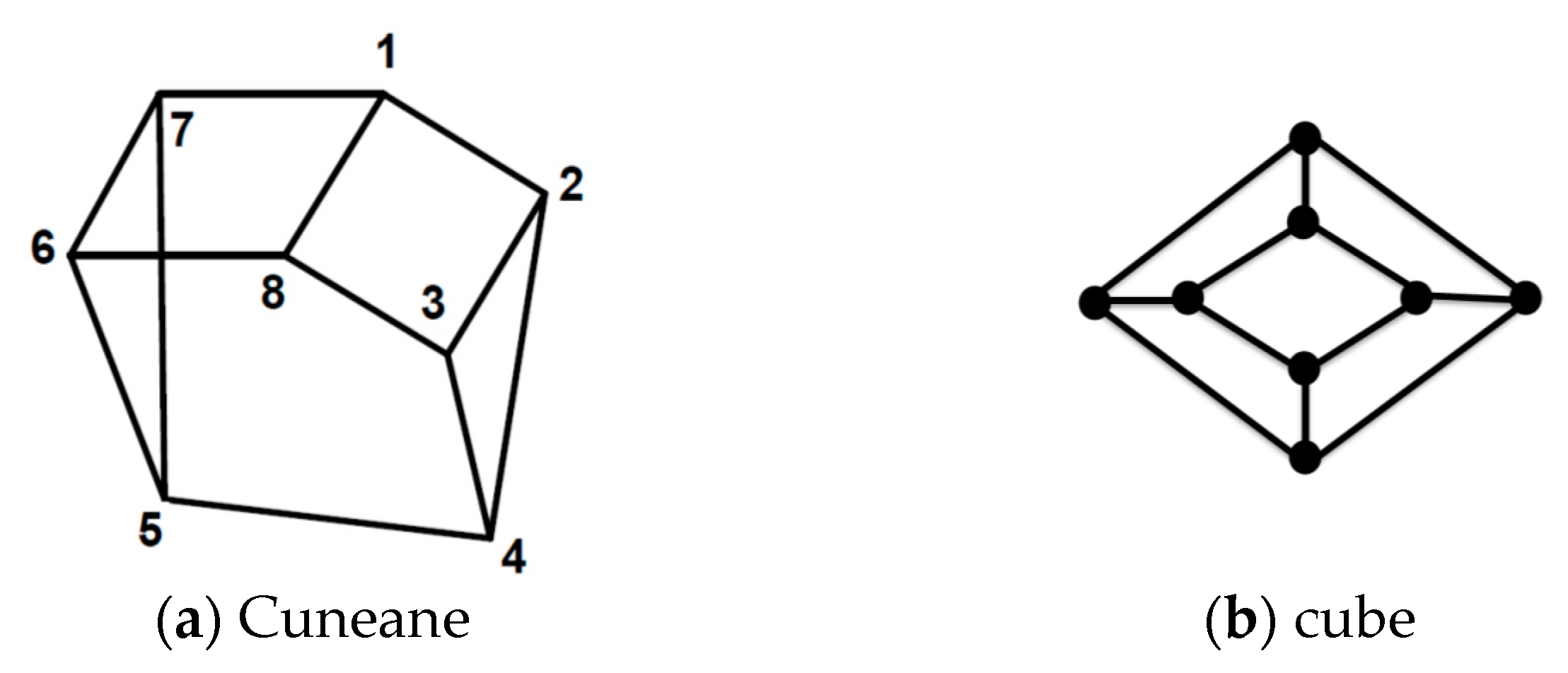
Figure 1, in a network, vertices with the same degree can be distinguished by measurement on some structural properties of particular vertex such as the number of triangles that a vertex lie on or the shortest path passing through a vertex; see
Figure 1.
The molecular graph of cuneane is depicted in
Figure 1a. This graph is not vertex-transitive. The 2-D graph of the cube graph Q
3, as depicted in
Figure 1b, indicates an example of a vertex-transitive graph. One can easily verify that the vertex partition P = {{1, 8}, {4, 5}, {2, 3, 6, 7}} in the cuneane graph is finer than the degree partition. Furthermore, we can validate that partition P is an orbit decomposition of cuneane.
For most of networks, the orbit-partition of a graph is much finer than the degree partition. The number of automorphism partitions or the number of orbits can interpret the structure of a network. For example, a graph with n vertices has exactly n orbits if and only if it is asymmetric.
3. Fullerene Graphs
In addition to the two popular forms of carbon, namely diamond and graphite, a third form of carbon called fullerene was discovered in 1985; see [
18,
19]. One of the most well-known members of this class of molecular graphs, the buckminster fullerene
C60 which contains 60 carbon atoms, 12 pentagons and 20 hexagons, is vertex-transitive.
In general, a fullerene is a cubic three-connected graph on n vertices which has n/2 - 10 hexagons and 12 pentagons.
The non-classical fullerenes are formed by a combination of triangles, quadrangles, pentagons, hexagons, etc. There are many problems concerning fullerene graphs, and many properties of them were studied by mathematicians, see [
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43,
44,
45,
46,
47,
48,
49,
50,
51,
52,
53,
54,
55,
56,
57,
58,
59,
60,
61,
62,
63,
64] as well as [
65,
66,
67,
68,
69,
70,
71,
72,
73,
74,
75]. Fullerenes are individual cases of a larger class of graphs, namely polyhedral graphs. In general, a polyhedral graph is a three-connected simple planar graph and the polyhedral graphs considered in this paper are cubic. In chemistry, a fullerene is a molecule composed of carbon atoms in the form of many shapes such as a hollow sphere, ellipsoid, tube, etc. [
51]. The non-classical fullerenes may contain hexagons and other rings.
In [
76], a method is described to obtain a fullerene graph from a zig-zag or armchair nanotubes. Here, by continuing that method, we construct some infinite classes of fullerenes. Denoted by
TZ[
m,n] means a zig-zag nanotube with
m rows and
n columns of hexagons, see
Figure 2. Combine a nanotube
TZ[5,
n − 4] with two copies of caps
B (
Figure 3), to construct a fullerene graph as shown in
Figure 4. Two caps have together 40 vertices and thus, the number of vertices of the fullerene graph is 10(
n − 4) + 40 = 10
n. This is why we did it by A
10n.
4. Entropy Measure
The concepts of entropies have been investigated extensively in [
77,
78,
79,
80,
81,
82,
83,
84] to characterize and quantify the structure of networks. Several types of them are discussed in [
1], and mathematically explored. Therefore, we omit an extensive review on graph entropies here. Studying the entropy of dendrimers, a graph class with a long-standing history in chemistry and related disciplines, is done in some references such as [
82,
83,
84] in which authors considered the individual eccentricity-based information functionals. As graph entropies, we use a specific definition due to Dehmer [
85,
86,
87,
88,
89,
90,
91,
92] as follows. Consider a probability vector
p = (
p1,…,
pn) that satisfies in two conditions 0 ≤
pi ≤ 1 and
. The Shannon’s entropy is
, where the symbol “log” is the logarithm on the basis 2. Let
where
is a tuple of none-negative integers,
, see [
90]. The entropy of tuple
is given by
There are many ways to obtain the tuple .
For a vertex
vi of graph
G, if we put
Then clearly,
and the entropy measure of
G based on
f is thus
In the literature, there are various ways to obtain the tuple (
p1,…,
pn) like the so-called magnitude-based information measures introduced by Bonchev and Trinajstić [
82], or partition—independent graph entropies, introduced by Dehmer based on information functionals; see [
91,
92,
93,
94,
95,
96] as well as [
97,
98,
99,
100,
101,
102,
103,
104,
105,
106].
A function in which for any pair of vertices of graph G such as x and y, d(x,y) is defined as the length of shortest path connecting them, indicates the distance between these vertices.
A topological index of graph
G is a numerical quantity, which is invariant under its automorphism group. The Wiener index is the first reported distance based topological index, and it defined as half sum of the distances between all the pairs of vertices in a molecular graph; see [
107]. In other words,
The Wiener (or Hosoya) polynomial of a graph [
108] is defined as
It is clear that
H(
G,1) = W(
G). For a given vertex
v, the function
is called the partial Hosoya polynomial of
G at vertex
v.
Graph entropy measures represent information—theoretic measures for characterizing networks quantitatively. The first concepts in this framework was developed in the 1950s for investigating biological and chemical systems. Seminal work on this problem was done by Rashevsky, Trucco, and Mowshowitz, [
100,
101,
102,
103,
104,
109,
110,
111,
112] who studied entropy measures for determining the structural information content of a graph. Graph entropies have been applied to various problems such as biology, computational biology, mathematical chemistry, Web mining, and knowledge engineering.
4.1. Eccentric Entropy Measure
The eccentricity of vertex
v is an information functional defined by
, see [
113,
114,
115]. Now, for a vertex
f(
vi):=
ciσ(
vi), where
ci > 0 for 1 ≤
i ≤
n. Then
Moreover, if
cis are equal, then
Theorem 1 ([
25])
. In a vertex-transitive graph, all vertices have the same eccentricity. Theorem 2. If G is a regular graph on n vertices, then In particular, if ci = cj for all, i ≠ j then Ifσ(G) = log(n).
Proof. By Theorem 1, for all , we have σ(x) = σ(y) which proves the first claim.
If
ci =
cj for all
i ≠
j then we have
□
Theorem 3. The polyhex nanotori T (Figure 5) is vertex-transitive. Proof. Suppose p and q are even. Consider two vertices uij and urs in which both integers i,r are either odd, or even, and suppose σ, π are two permutations that σ(uit) = urt, 1 ≤ t ≤ p and π(utj) = uts, 1 ≤ t ≤ q. Then, σ and π are automorphisms of T in which πσ maps uij to urs and so, they are in the same orbit. Suppose now i is odd and r is even or i is even and r is odd. Then, the permutation θ which maps uij to u(p+1−i)j is a graph automorphism which implies that uij and urs are in the same orbit of Aut(G) and we are done. □
Example 1. Consider the 2-dimensional graph of zig-zag polyhex nanotori T[p,q], as depicted in Figure 6. It can be easily seen that |V(T[p,q])|=pq. By Theorem 3, T[p,q] is vertex-transitive and if for all i≠j, ci=cj then, by Theorem 2, we have.
Let
G be an edge-transitive graph but not vertex-transitive, and
e =
xy be an arbitrary edge in
G. For an arbitrary edge
e =
uv, there exists an automorphism σ such that σ(
e) =
f. Hence,
Let
for 1 ≤
i ≤
r and
for
. As a particular case, we consider
ci =
cj for all
i≠
j. By some elementary calculations, we obtain
Hence, we proved the following theorem.
Theorem 4. Let G be edge-transitive but not vertex-transitive and let ci =
cj for all i≠
j. Then, Example 2. As usual, suppose that Sn indicates an star graph on n + 1 vertices. Suppose x is the central vertex and denotes the other vertices by. Then d(x,u1) = 1 and d(ui,uj) = 2 (1 ≤ i,j ≤ n). If ci = cj for all i≠j, then, by using Theorem 4, we infer that Theorem 5. Suppose G is a graph and V1, …, Vk are all orbits of Aut(G) on V(G). Then, Proof. For all , we have and, the proof is complete. □
Suppose for the vertex
v of graph
G,
d(
v) shows the degree of vertex
v. If
, and we put
f(
v) in Equation (1), then we achieve four new entropy-based measures as follows:
It is clear that since a fullerene is 3-regular, then
m = 3
n/2 (the number of edges) and
Moreover, the entropies of graphs based on the eccentricities of vertices are studied in [
22,
23,
24,
25,
26,
27,
28,
29,
30].
4.2. Ecc-Entropy of Fullerene Graphs
In this section, similarly to the definition of the fullerene A
10n in the last section, we present two infinite families of fullerenes namely C
24n+12 and C
12n+2 with respectively 24
n + 12 and 12
n + 2 vertices as depicted, respectively, in
Figure 7 and
Figure 8. For more details about the construction of these classes of fullerenes, see references [
25,
27].
Theorem 6. If ci’s are equal, then Equation (5) yields that for n ≥ 7 Proof. Consider the vertices of the central hexagon and other vertices of C
24n+12 as shown in
Figure 7. Consider the eccentric contribution of each vertex as reported in
Table 1. As shown in this table, there are two types of vertices. The vertices of the central and outer hexagons and the other vertices. By Equation (2) we have
□
The exceptional cases are given in
Table 2.
Theorem 7. If ci’s are equal, then the entropy of fullerene C12n+2, n ≥ 10 (see Figure 8) is Proof. Similarly, to the proof of Theorem 6 and by using the eccentricity of vertices as reported in
Table 3 and by Equation (5), we obtain
□
The exceptional cases are given in
Table 4.
4.3. Eigen—Entropy of Fullerenes
The adjacency matrix
A(
G) of graph
G with vertex set V(
G) = {
v1, v2,..., vn} is the
n ×
n symmetric matrix [
aij ] such that
aij = 1 if
vi and
vj are adjacent and 0, otherwise. The characteristic polynomial of graph
G is defined as [
116]
The roots of the characteristic polynomial are named the eigenvalues of graph G, which form the spectrum of this graph. If α is an eigenvalue of matrix A, then there exists a vector such as V, in which A.V = αV.
Let
λ1,...,
λn be the eigenvalues of
A(
G); then, the energy of
G is defined [
117,
118] as
In theoretical chemistry, the energy is a graph parameter stemming from the Hückel molecular orbital approximation for the total
π-electron energy. Thus, the graph energy has some specific chemical interests and has been extensively studied [
119,
120].
One information functional is based on absolute value of eigenvalues; see [
121,
122]. The eigen-entropy based on non-zero eigenvalues denoted by
Ifλ(
G) is defined as follows:
where
. If
cis are equal, then
Theorem 8. Let G be a connected graph with non-zero eigenvalues. Then
where
and where
s is the number of distinct eigenvalues.
Proof. It is a well-known fact that
. By using Equation (6), we have
Since logarithm is an increasing function, we have
. On the other hand,
yields
Now,
implies that
Let
. The nullity of
G is 1. By reformulating Equation (7), one can see that
□
Theorem 9. Let G be a graph whose eigenvalues are in the interval [−1,1]
. Then Proof. On the other hand,
. So
Since , thus . □
Theorem 10. Let G be a graph and m∆(G) be the ∆-th spectral moment of G. Then Proof. We have
4.4. The Hosoya Entropy of Fullerenes
Here, we introduce the Hosoya entropy based on the distance between vertices of a graph, see [
123,
124,
125]. Given a graph
G and two vertices
u and
v, the distance between them is defined as the length of the shortest path connecting them. Let
si(
u) be the number of vertices at distance
i from vertex
u. Then the sequence
dds(
v) = (
s0(
v),
s1(
v),
…, sd(
v)) is called the distance degree sequence of
v.
Two vertices
u and
v are
H-equivalent if
dds(
u) =
dds(
v) see [
126] and the class of
H -equivalent vertices constitutes the
H-partitions of a graph.
Suppose
G has
h H-equivalent classes and the cardinality of
ith
H-equivalent class is
ni (1 ≤
i ≤
h). Then,
H-entropy of
G [
127] is
where
.
Let also O
1,…, O
l be all the orbits of Aut(
G) in the set of vertices. If
li is the cardinality of the
i-th orbit for 1 ≤
i ≤
l, then the orbit entropy of
G [
116,
117,
118,
119] is given by
where
.
The value of H(G) for a graph G with n vertices is between zero and log(n). The minimum is achieved when all the vertices are H-equivalent; the maximum is reached when a non-pair of vertices are H-equivalent. Complete graphs and cycles have a H-entropy of 0.
Remark 1. In a vertex-transitive graph, all the vertices are H-equivalent and the H-entropy is zero. The converse of this fact is not true. In other words, there are many examples of non-vertex-transitive graphs with zero H-entropy.
Theorem 11. Two vertices in the same orbit are H-equivalent. In addition, the H-entropy of a vertex-transitive graph is zero [
128].
Although two similar vertices are
H-equivalent, the converse is not true. For example, in
Figure 9,
u and
v are
H-equivalent, and thus
D(
u) =
D(
v), while they are in different orbits. Moreover, two vertices
u and
v in
Figure 10 are not
H-equivalent but
D(
u) =
D(
v).
Theorem 12 ([
128])
. If G is a regular graph with diameter ρ = 2, then H(G) = 0. Theorem 13. If G is a regular graph with non-zero H-entropy, then its diameter is greater than 2.
Theorem 14 ([
128])
. If G is a connected graph on n vertices, then H(G) = n if and only if Aut(G) is trivial. Theorem 15 ([
128])
. The H-entropy of a regular graph of degree greater than n/2 is zero. Theorem 16 ([
128])
. The H-entropy of a regular graph of degree greater than or equal with n/2 is zero, if the number of vertices is an even number and G is edge-transitive. Theorem 17 ([
128])
. If G is a graph on at least five vertices which is edge-transitive but not bipartite, and each vertex has odd degree. Then, H-entropy is zero. In continuing, we compute the H-entropy of graphs with at most two orbits.
Definition 1. A graph G is called co-distance, if for each pair of vertices (u,v) their total distances are the same, namely D(u) = D(v).
Each vertex-transitive graph is co-distance, but there are examples of co-distance non-transitive graphs. The graph
G in
Figure 11 has two orbits V
1 = {1, 2, 5, 6, 8, 12} and V
2 = {3, 10, 4, 7, 11, 9}. It is not difficult to see that
d(
G) = 4 and
D(1) =
D(3) while the
H-entropy is not zero.
Theorem 18 ([
128])
. Up to isomorphism there are exactly 14 co-distance regular graphs of order at most 14 with two orbits and diameter greater than or equal with 3. Among them, only the graph G depicted in Figure 11 has non-zero H-entropy. Theorem 19 ([
128])
. Suppose the H-entropy of graph G is zero. Then nor G is a tree or a regular graph. Theorem 20 ([
128])
. Suppose G is a graph with two orbits V1 and V2 and non-zero H-entropy. Then H(G) = 1 if and only if n is even and |V1| = |V2| = n/2. Theorem 21 ([
128])
. Let G be a regular graph with two orbits and diameter less than four. If G is co-distance, then its H-entropy is zero. In the final part of this section, we compute the H-entropy of some infinite classes of fullerene graphs.
Theorem 22. The fullerene graph A12n + 4 where n ≥ 4 satisfies Proof. In
Figure 12, the vertices of ith (i = 1, 2, 3, 4, 5) layer are in the same orbit. The vertices of the layers 6, 7,…, n constitute three orbits labeled by the numbers 1, 2, and 3. Vertices with labels 2, 3 are in the same H-equivalent partition and the other vertices compose the H-equivalent partition. Finally, the vertices of the outer pentagon are H-equivalent. In other words, there are an equivalence class of size 1, nine equivalence classes of size 3, and 2n − 4 equivalence classes of size 6 which yield
□
Similarly to the structure of A
10n in last section, the fullerene graph A
12n+4 is composed of a nanotube
Tz[6,
n − 10] together with two caps
B1 and
B2, see
Figure 13,
Figure 14,
Figure 15 and
Figure 16. Thus, the vertices of A
12n+4 are labeled as given in
Figure 17. The
H-partitions and the eccentricity of vertices of caps
B1 and
B2 are given in
Table 5.
4.5. Radial Entropy and Orbit Measures
In a network, knowing, for example, the degree of vertices gives us essential information about the number of interconnections of each component. These data provide a narrow understanding of complex networks, because the vertex partition [
12] based on degree is coarser than automorphism partition. Hence, it is important to know if we substitute the degree partitions instead of orbit partitions; then, the study of complex network in the view of symmetry leads us to understand more about the structure of the regarding graph. The orbit entropy is defined as
where
Oi’s (1 ≤
i ≤
k) are orbits of
G. Regarding the orbit polynomial, the symmetry index
S(
G) is defined [
127] as follows:
Suppose
, 1 ≤
j ≤
k is the collection of all vertices with eccentricity
ij. Then, the radial entropy is defined by
Let
p1,...,
pn−10 be the
H-equivalent classes of
Tz[6,
n − 10] which contains the vertices with label
i. Then
ecc(
pi) = 2
n − i-9. Thus, the eccentricity sequence of fullerene graph A
12n+4 is
Theorem 23 ([
129])
. Consider the fullerene graph A12n+4, where n ≥ 4. If n is even, then Theorem 24 ([
129])
. The radial entropy of fullerene A12n + 4 (n ≥ 4) is Theorem 25 ([
129])
. If the ci’s are equal, the entropy of fullerene A12n + 4 (n ≥ 11) is given by
where
Theorem 26 ([
129])
. The degree-based entropy of fullerene graph A12n + 4 is