1. Introduction
Over the past year, the number of worldwide mobile App downloads from the Apple App Store and Google Play has reached 204 billion, and consumers worldwide have spent
$120 billion on Apps in 2019. Meanwhile, users spend an average of 3.7 h a day using Apps, which means that Apps have become a mainstay of people’s daily routines [
1]. The rapid development of the App industry is inseparable from the prominent role of the mobile platform as a two-sided market in connecting Apps and users [
2]. The mobile platform becomes an App retailer, and the App developer becomes an App supplier in a supply chain with a revenue-sharing contract [
3]. For example, iOS developers yield 30% of their sales revenue to the Apple Store, and 360 platform claims that App developers must pay the platform 50% of their sales revenue [
4].
The monetization of Apps mainly come from two versions: one is a free version with advertising, the other is a paid version. Paid apps can offer more functionality, better users’ experience, and fewer ads than free Apps [
5]. However, in practice, users usually experience the features and quality of the free version before deciding whether to purchase the paid version [
6]. Therefore, the goodwill generated by the quality of previous free version has become a key factor for users to buy [
7]. In addition, the degree of goodwill is also accumulated with the increase of advertising promotion [
8]. A successful advertising strategy can not only stimulate users’ demands, but also build a better image for a product, which all contribute to improving the company’s profits [
9].
Reference price, as the users’ cognitive price, is formed gradually through the users’ previous purchase experience of similar products [
10]. Note that the reference price is influenced by the past product price, product quality, advertising promotion, and many other factors [
11]. However, the decision to buy a paid App is made by comparing the reference price in users’ minds with the current selling price [
12]. For example, Apple always announces a fairly high selling price first to establish a higher reference price, and then quickly lowers the price to give users a sense of benefit, thus boosting demand [
9]. Therefore, the reference price is another factor that affects the users’ purchase.
Goodwill and reference price are both affected by the product quality and advertising promotion of the paid App, which ultimately influences the downloads. In general, product quality depends on the developers’ technical input, while promotion depends on the platform’s advertising efforts. For example, Apple Store promotes several paid Apps in specific sectors daily. Consequently, developers are willing to pay premium fees to share the advertising costs of the platform for the sake of boosting the promotion of paid Apps. For capturing the mutually beneficial interactions between the platform and the paid App, we establish the decentralized and integrated systems with the revenue-sharing contract, respectively. With goodwill and reference price as state variables and utilizing the optimal control method, we investigate the optimal decisions on the advertising effort of the platform and the product quality of the paid App. Our research yields the following main findings and management insights.
First, the steady state of the reference price is higher than the current price of the paid App. Interestingly, the higher the loyalty of the users, the higher the corresponding reference price will be, which is consistent with intuition. As for the users who lack loyalty, that is, the price gap has a great impact on the reference price of such users, then the developers and platform can consider ignoring the impact of the reference price.
Second, when the platform shares 2/3 or more of the paid App’s revenue, the paid App is no longer willing to provide any advertising subsidies to the platform, but if the platform stops sharing any revenue of the paid App, the paid App is happy to bear all the advertising costs of the platform, which is consistent with the economic intuition.
Finally, our proposed bilateral subsidy agreement can smoothly coordinate the decentralized system and achieve the optimal objective of the integrated system. Further, we demonstrate theoretically that both the platform and the paid App can benefit from the agreement under some moderate conditions. Particularly, when the effectiveness of the platform’s advertising is equal to the effectiveness of the paid App’s product quality, the platform’s revenue-sharing rate should be in the range of 40–80%, ensuring that both the platform and the paid App can get additional profits from the agreement compared to the decentralized system.
The rest of the paper is organized as follows: Literature relevant to our work is reviewed in
Section 2. In
Section 3, we establish the decision model for the platform and the paid App in the decentralized and integrated systems, respectively.
Section 4 analyzes the equilibrium results in each system. In
Section 5, we propose a bilateral subsidy agreement to coordinate the decentralized system with the integrated system. Conclusions and future research directions are discussed in
Section 6.
2. Literature Review
This paper is highly related to two streams of research: One is to study the reasonable supply chain coordination mechanism, and the other is to solve the optimal strategies of the platform and App.
2.1. Supply Chain Coordination
The literature on supply chain focuses on implementing various mechanisms to enable channel coordination, and ultimately improve the efficiency of the system. Related coordination mechanisms include the quantity discount [
13,
14,
15], revenue-sharing contract [
16,
17,
18,
19,
20], bilateral participation or cost-sharing contract [
21,
22], price discount [
23,
24,
25], and two-part tariffs [
26]. However, most of the literature is based on static model assumptions, and a few papers consider a dynamic model setting in discrete time to achieve channel coordination. Motivated by supply chain coordination, in this paper, utilizing the optimal control theory, we formulate a bilateral subsidy agreement under a continuous-time dynamic model setting to achieve channel coordination between the platform and the paid App.
Dynamic cooperative advertising program has received considerable business and academic attention in achieving supply chain coordination. A very important part of the research stream is inspired by the time-dependent demand model proposed by Nerlove and Arrow [
8]. In this model, the product goodwill will ultimately affect the demand due to the role of advertising, which stimulates a series of valuable research, including the decisions of price, quality, and the advertising in a supply chain [
27,
28], or in a horizontal competition setting [
29,
30,
31].
Only a few studies on cooperative advertising model take the reference price into account. Generally, every user has a reference price for a particular product, and when the current price of the product is lower than the reference price, the users will have a sense of gain, which promotes the sales of products, namely the reference price effect [
12,
32]. The model of reference price mainly focuses on pricing strategy [
33,
34]. Related to this paper, Zhang et al. [
35] address the issue of cooperative advertising in supply chain coordination with the reference price. However, they have not explicitly given the specific conditions in theory that both the manufacturer and the retailer can benefit from the two-way subsidy policy. Lu et al. [
9] only focus on the reference price and ignore the dynamic effect of goodwill. In addition, the model is not set up under the revenue-sharing contract, and the coordination of supply chain is not analyzed.
Inspired by the product goodwill and the reference price of users, considering the effects of the reference price and the goodwill, we develop a continuous-time dynamic model to obtain the optimal investment in the product quality of the paid App and the optimal advertising effort of the platform in promoting the paid App. Unlike [
35], our model considers the revenue-sharing contract between the platform and the paid App. Importantly, we theoretically conclude that both the platform and the paid App can benefit from the bilateral subsidy agreement under some mild conditions.
2.2. Optimal Strategies of App and Platform
With the rapid development of the mobile Internet, research on business decision-making of mobile platforms and Apps has drawn increasing attention. Sun et al. [
36] combine the sojourn and exposure effects to determine the optimal sequence of fading ads shown to the users. Xue et al. [
37] examine how the APIs provided by digital platforms affect the original Apps and App copycatting. Guo et al. [
38] conduct an economic analysis on the reward advertising mechanism of the premium content and advertising in game Apps. Nan et al. [
39] investigate the optimal protection level of the monopolistic online platform under the content and advertising model. Tao et al. [
40] explore the optimal strategies of the product pricing and delivery options for a local seller in the face of offline and App channels. However, the above literatures all start from a single perspective, ignoring the interaction between the platform and App.
To capture the interest relationship between the platform and App under the dynamic setting, Wang et al. [
4] propose a bilateral participation contract that requires the platform and App to subsidize each other’s advertising costs. Regarding the in-App advertising mode, Ji et al. [
41] introduce the rate of in-App ad impressions as a control variable. Their results show that to coordinate the system, a mixed scheme of revenue-sharing and advertising cost sharing should be adopted simultaneously. Liu and Liu [
42] extend the model to a single platform and multiple Apps, and they consider the case that Apps can deliver and display ads into each other. In addition, Wang et al. [
43] analyze the interactive relationship between the live streamers and the unions of the platform from the perspective of salary mechanism.
The business strategy decisions regarding paid Apps are well worthy of further study. Facing the different risk attitudes of App developers, Avinadav et al. [
3] study how the platform should set the optimal level of revenue-sharing and how the App developer should determine the investment in quality and the selling price of the App. Further, the above model is extended into a single common platform and multiple competitive Apps [
44]. Chen et al. [
45] develop an analytical framework for App developers, and give the conditions of providing free and paid versions. Hao et al. [
46] consider the strategies of jointly provisioning in-App ads and paid Apps to analyze the optimal advertising revenue-sharing contract. Their findings suggest that the platform owner should subsidize App developers via advertising channels, which improves both the profits of the platform and App. However, all the above researches on the paid Apps are based on the static model settings.
Our research differs from the previous literature on paid Apps. First, in the dynamic model setting, we utilize the optimal control theory to capture the interaction between the platform and the paid App. Second, considering the effects of the reference price and the goodwill of users, we obtain the optimal investment in product quality of the paid App, and the optimal advertising effort of the platform in promoting the paid App in the decentralized and integrated systems, respectively. Finally, due to the inefficiency of decentralized system in general, a bilateral subsidy agreement is proposed to achieve channel coordination and implement the optimal objective value. Further, we theoretically conclude that the platform and the paid App can simultaneously benefit from the agreement under some mild conditions. Our research may provide some guidance for establishing a reasonable strategic partnership between the paid App developers and the platform owners.
3. Model Development
This paper considers a system consisting of a paid App and a mobile platform (we refer to the paid App as ‘he’ and the mobile platform as ‘she’). In order to increase the downloads of the paid App, the App developers try their best to improve the product quality of the paid App. Additionally, the platform will use advertising to promote the paid App, with the purpose of making users willing to purchase the desired Apps. We denote the product quality of the paid App over time t as q(t) ≥ 0, and the advertising effort of the platform in promotion over time t as e(t) ≥ 0.
Facing a wide variety of Apps in the mobile App store, users’ perceptions will change over time. Specifically, every user has a reasonable price range for a certain type of paid App [
47,
48]. When users decide whether to pay to download a desired App, they will compare the current price of App with the reference price in their minds [
11,
32,
35]. Following [
11], the reference price will be affected by the users’ previous price memory of the paid App. In addition, both the product quality of the paid App and the advertising effort of the platform in promoting App have the positive effects on the reference price. Denote the reference price of the paid App over time
t as
R(
t) ≥ 0 and the current purchase price of the paid App as
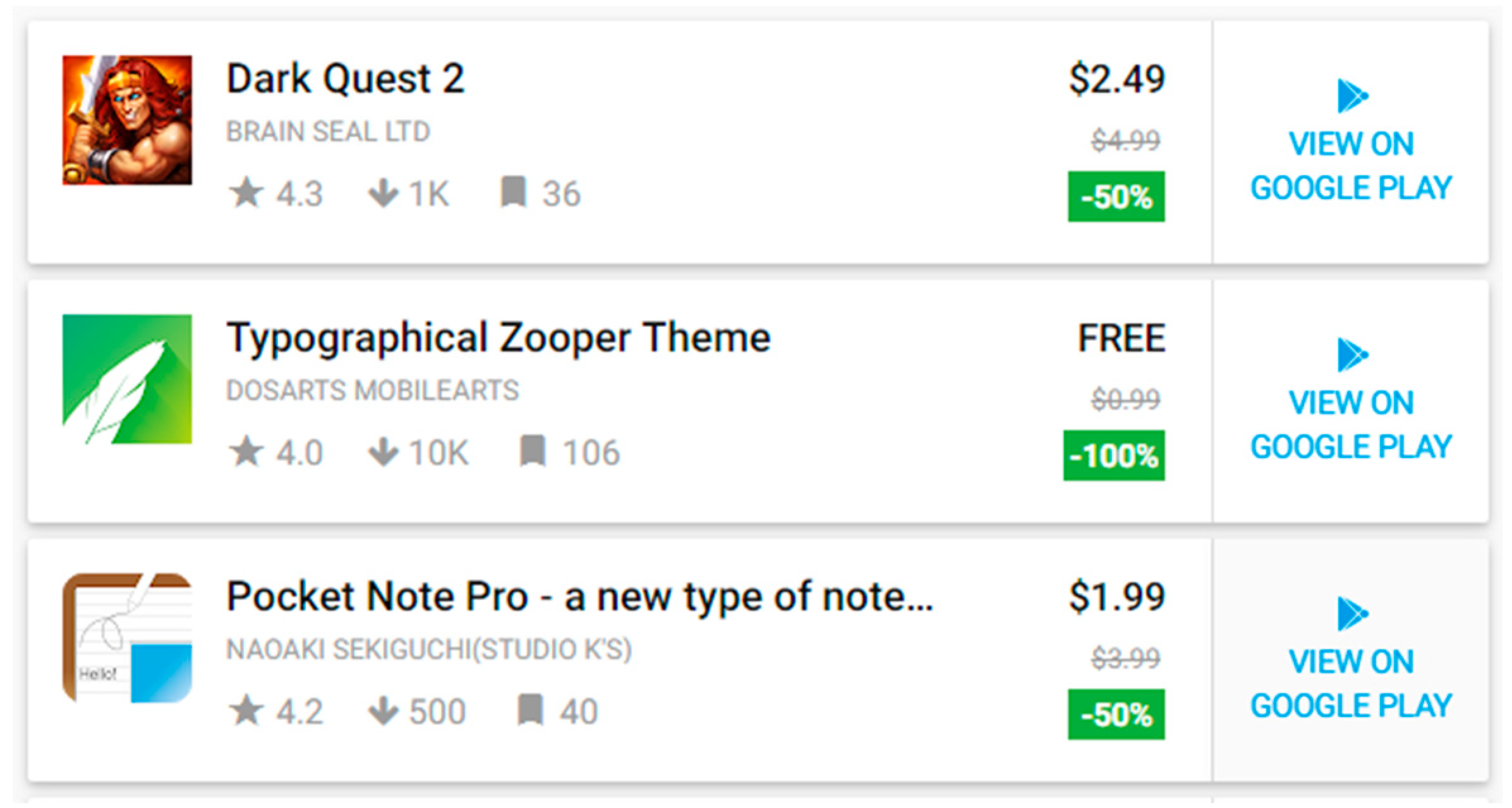
P ≥ 0. Specifically, the reference price can be formed when the users enjoy the paid Apps for free on a limited time basis, or the initial official price of the paid Apps. For instance, the initial official price of paid Apps in
Figure 1. can be considered as the reference price, while the discounted price is the current selling price of the paid Apps. According to [
11,
35], we assume that the change process of the reference price for the paid App is given by:
where
μ1 and
μ2 ≥ 0.
R′(
t) is the derivative with respect to time
t, and
R0 is the initial reference price. Parameter
β > 0 reflects the impact of the price difference on the fluctuation of the reference price of the paid App. A larger
β indicates that the reference price is greatly affected by the price gap, so this group can be seen as users who lack loyalty. In addition, when
P >
R(
t), the users will appropriately increase the reference price in their hearts, when
P <
R(
t), the reference price will be reduced accordingly, and when
P =
R(
t), this means that the reference price is the same as the current price, and the price difference has no effect. The two items
μ1q(
t) and
μ2e(
t) respectively represent the effects of the paid App’s quality and the platform’s advertising on the change process of the reference price over time. A higher product quality and a higher advertising effort can increase the reference price of the paid App. Following [
35], the official price has a certain stability over a long period of time, so we assume that the current price of the paid App,
P, is a constant.
Additionally, both the high-quality of the paid App, such as a beautiful interface, diverse functions, strong performance, few bugs, easy to operate, etc., and the effective advertising of the platform enable users to accumulate a certain degree of goodwill towards the paid App. The goodwill of the paid App contains the factors such as ratings and reviews submitted by users to the paid App on the platform. As seen in Apple’s App Store, users submit reviews and ratings to give feedback on the experience after enjoying the Apps for a while.
https://developer.apple.com/app-store/ratings-and-reviews/. We assume that the change process of the goodwill follows [
8], i.e.,:
where
G(
t) is the accumulated goodwill of the paid App, namely the purchase desire over time
t.
G′(
t) is the derivative with respect to time
t. The parameters
θ1 and
θ2 are nonnegative parameters reflecting that the paid App’s product quality and the platform’s advertising effort both have positive effects on the goodwill. Besides,
G0 is the initial goodwill. Generally, the goodwill of a paid App will fade over time. We assume that the change in goodwill over time will be negatively affected by the decay of goodwill itself. Thus,
δ > 0 is the attenuation coefficient of goodwill.
In our model setting, the downloads of the paid App are mainly affected by three aspects: (1) the product quality of the paid App, (2) the advertising effort of the platform in promoting the paid App, (3) and the reference price and the goodwill of the paid App. Thus, according to [
34,
35], the downloads of the paid App,
D(
t), is assumed to satisfy the following equation:
where
α,
η1, and
η2 are all non-negative parameters. Parameter
α reflects the influence of the price difference between the reference price and the actual price on the paid App downloads. When
R(
t) >
P means that the actual price doesn’t exceed the reference price, which has a positive effect on the paid App downloads, whereas when
R(
t) <
P, the effect will be negative. The item
G(
t) illustrates the fact that if a paid App has a high goodwill among users, then the paid App will have a large number of downloads. The other two items
η1q(
t) and
η2e(
t) reflect the positive effects of the paid App’s product quality and the platform’s advertising on the downloads.
Generally, the cost is in the form of quadratic function [
28,
35], Thus, we assume that the costs of the paid App’s product quality and the platform’s advertising effort are respectively
CA(
t) = (1/2)
q(
t)
2 and
CP(
t) = (1/2)
e(
t)
2.
Note that the platform serves as a bilateral market connecting the users and Apps, and the premise of allowing Apps to enter the platform is that a certain proportion of the download fees paid by users to purchase the paid Apps must be shared with the platform. We denote
λ ∈ [0,1] as the revenue-sharing rate set by the platform. Additionally, the platform’s advertising effort in promoting the paid App largely determines the paid App downloads. Therefore, App developer is quite willing to bear a certain proportion of the advertising costs for the platform, with the intention of motivating the platform to continuously enhance the advertising effort. We denote
s ∈ [0,1] as the advertising cost-sharing rate set by the paid App. Then, the instantaneous profit of the paid App is:
and the instantaneous profit of the platform is:
Thus, the total instantaneous profit of the whole system is:
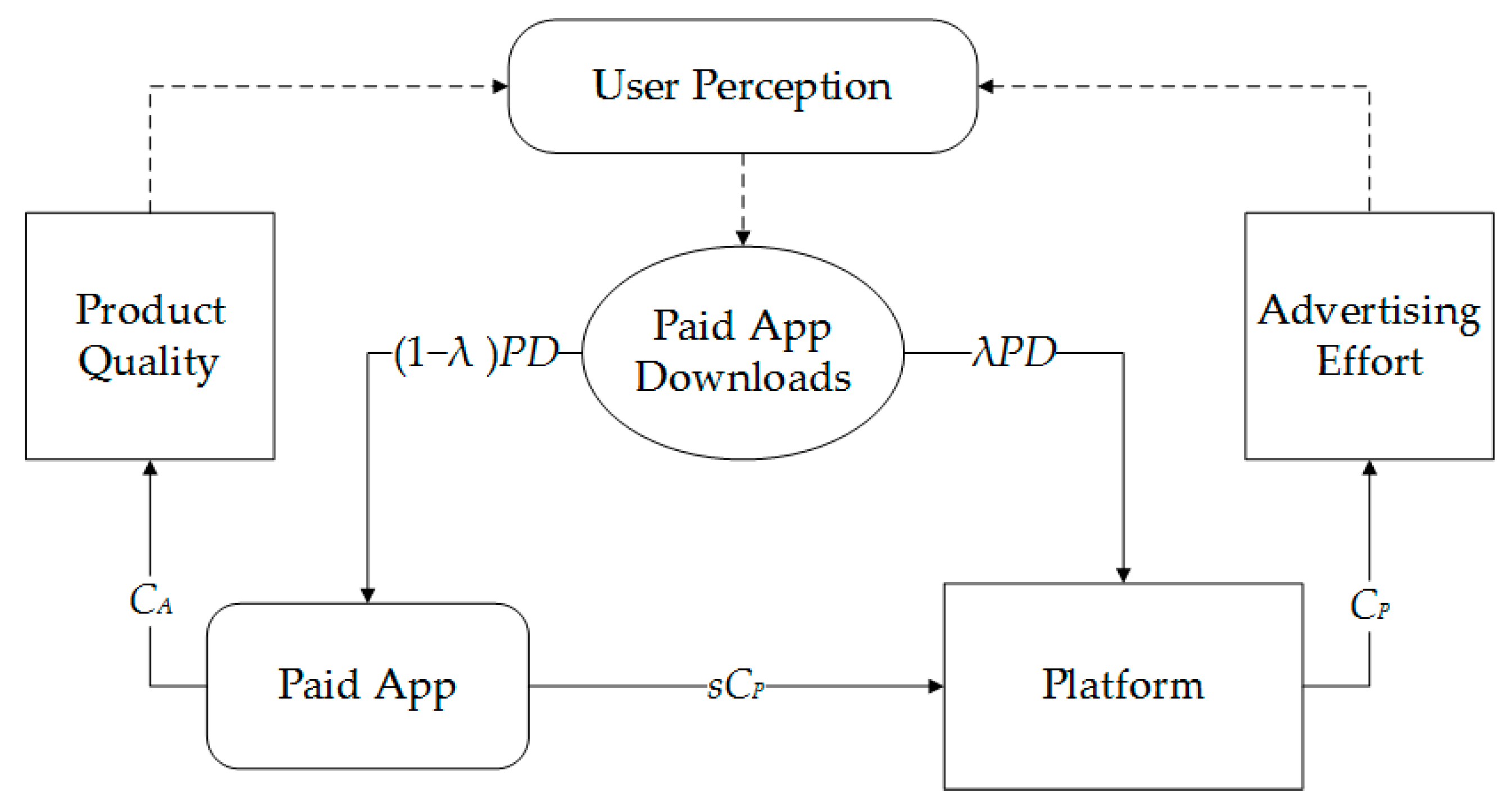
We describe the interaction between the paid App, the platform, and the users as shown in
Figure 2.
We consider an infinite horizon with a positive discount rate ρ based on the above assumptions. There are two specific systems, one is a decentralized system and the other is an integrated system. The decentralized system means that the platform and the paid App make decisions separately, which is in line with reality. And the integrated system means treating the platform and the paid App as one company. Decisions about the advertising effort and the product quality are now made jointly, which is often at odds with reality. The purpose of such design is to next compare the optimal decisions, steady states, and present value of profits of the two systems. The optimal control problems for decentralized and integrated systems are as follows:
• Decentralized system
In the decentralized system, the paid App and the platform separately maximize the present values of their own profits over [0, ∞) subject to Equations (1) and (2). We assume that the decision structure is a Stackelberg game. That means the paid App takes the lead in determining the platform’s advertising cost-sharing rate (
s). Once
s is given, the paid App will decide his own optimal product quality, and the platform will decide her own optimal advertising effort simultaneously. Thus, the optimal control problem of the paid App is:
and that of the platform is:
• Integrated system
In the integrated system, the paid App and the platform are integrated into one firm, whose objective is to determine the paid App’s optimal product quality and the platform’s optimal advertising effort by maximizing the present value of the total profits over [0, ∞) subject to Equations (1) and (2). Thus, the optimization problem of the integrated system is:
Note that the level of the paid App’s quality improvement is constrained by the App developers’ scientific and technical capabilities [
49]. Meanwhile, since the excessive advertising causes users’ annoyances [
50], the platform will not endlessly increase the advertising effort. Thus, we assume that the decision variables
q(
t) and
e(
t) both have an upper bound respectively for each system, i.e., 0 ≤
q(
t),
e(
t) ≤
M, where
M is a large enough constant.
Next,
Section 4 analyzes the results related to the two systems. Propositions 1 and 2 present the optimal decisions and steady states for the decentralized system. Proposition 3 presents the optimal decisions and steady states of the integrated system and compares them to the corresponding results of the decentralized system. Further, Proposition 4 gives the present values of profits of the decentralized and integrated systems, respectively, with a comparative analysis.
4. Two Systems
Proposition 1. In the decentralized system:
- (1)
The optimal product quality of the paid App is:and the optimal advertising effort of the platform is: - (2)
The optimal trajectories of the reference price and the goodwill of the paid App over time t are respectivelywhere:
Some conclusions can be addressed from Proposition 1 as follows:
(1) We find that the parentheses in Equations (10) and (11) have the similar structures and can be split into three parts. In Equation (10), the first part η1 reflects that the optimal product quality of the paid App (q*) positively depends on the effectiveness of the product quality on the paid App downloads. And the second and third parts, namely μ1α/(ρ+β) and θ1/(ρ+δ), reflect the influence of the users’ perceptions. Specifically, q* positively depends on the effectiveness of the product quality on the reference price and the goodwill, i.e., μ1 and θ1. Similarly, Equation (11) shows that the platform’s optimal advertising effort (e*) is positively affected by the effectiveness of e* on the paid App downloads (η2), implying that the more effective the advertising is on the downloads, the more advertising effort the platform exerts. Also, e* increases with the effects of reference price and goodwill on the downloads, i.e., μ2 and θ2. In summary, once the effects of reference price and goodwill are considered, both the optimal product quality of the paid App and the optimal advertising effort of the platform will be further strengthened.
Additionally, by Equations (10) and (11), we have ∂q*/∂α > 0 and ∂e*/∂α > 0, implying that the greater the impact of the price gap on the paid App downloads (i.e., such users have a strong price sensitivity), the higher the product quality of the paid App, and the higher the advertising effort of the platform, which is consistent with the economic intuition. Interestingly, we have ∂q*/∂β < 0 and ∂e*/∂β < 0, implying that the greater the impact of the price gap on the reference price, the lower the product quality of the paid App, and the lower the advertising effort of the platform. In particular, if the price gap has such a large impact on the reference price (such people can be considered as users who lack loyalty) that the value of μ1α/(ρ+β) is small enough to be negligible, then for the users who lack loyalty, the App developers and platform can consider to ignore the role of reference price.
(2) Due to the existence of the revenue-sharing policy set by the platform, the current price of the paid App (P) has a positive impact on both the optimal product quality of the paid App (q*) and the optimal advertising effort of the platform (e*) by Equations (10) and (11). Further, we have ∂q*/∂λ < 0, implying that the higher the revenue-sharing rate of the paid App is, the lower the optimal product quality level of the paid App will be. In addition, by Equation (11), the optimal advertising effort of the platform (e*) also increases with the platform’s advertising cost-sharing rate set by the paid App (s).
(3) Note that when
t → +∞, the reference price
R(
t) and the goodwill
G(
t), will finally reach their steady-state value, i.e.,
RDSS and
GDSS as shown in Equations (14) and (15). By Equation (14), we find that the higher the effectiveness of the paid App’s product quality or the platform’s advertising effort on the reference price (
μ1 or
μ2), the higher the steady state value of the reference price will be. Importantly, the steady state of the reference price
RDSS is higher than the current price of the paid App
P, which indicates that both the advertising promotions and the product quality can raise the reference price, which is consistent with intuition. Whereas when the effects of advertising and product quality disappear, the reference price is equal to the current price of the paid App, which leads to no sense of earning and hardly drives the users to purchase. Additionally, we have ∂
RDSS/∂
β < 0, implying that the higher the users’ loyalty (that is the smaller
β), the greater the steady state value of the reference price. Similarly, by Equation (15), the steady state of the goodwill is positively related to the effectiveness of the paid App’s product quality and the platform’s advertising effort on the goodwill (
θ1 and
θ2). Proofs of all Propositions are given in
Appendix A.
Proposition 2. In the decentralized system, the optimal platform’s advertising subsidy rate set by the paid App is: Differentiating s* with the paid App’s revenue-sharing rate set by the platform, λ, we have , implying that the more revenue the platform shares with the paid App, the less advertising subsidies the paid App provides to the platform. Note that the required condition 0 ≤ s* ≤ 1 is equivalent to 0 ≤ λ ≤ 2/3. Specifically, s* = 0 is equivalent to λ = 2/3, which means that when the proportion of the platform sharing the paid App’s revenue reaches or exceeds 2/3, the paid App will not provide any advertising subsidies for the platform (s* = 0). Additionally, s* = 1 is equivalent to λ = 0, implying that the paid App is willing to bear all advertising costs for the platform (s* = 1) if the platform no longer shares any revenue from the paid App (λ = 0), which is consistent with the business intuition.
Proposition 3. In the integrated system:
- (1)
The optimal paid App’s product quality and the optimal platform’s advertising effort are respectively: - (2)
The reference price and goodwill of the paid App over time t are respectively:where:
Comparing the optimal paid App’s product quality and the optimal platform’s advertising effort in the two systems, we find that since 0 ≤ λ ≤ 1, we have and . In essence, in the decentralized system, the platform and the paid App each maximize their own profits separately under the role of revenue-sharing contract. Instead, in the integrated system, the platform and paid App are integrated into one company, at which point the revenue-sharing contract no longer exists. That is, the decision making is not affected by the revenue-sharing rate (λ). Therefore, the optimal level of decision making in the integrated system is higher than in the decentralized system. Comparing Equation (21) with Equation (14), and comparing Equation (22) with Equation (15), since and , we find that both the steady states of the reference price and goodwill are higher in the integrated system than in the decentralized system, i.e., RISS ≥ RDSS and GISS ≥ GDSS.
Proposition 4. - (1)
In the decentralized system, the optimal present values of profits of the paid App and the platform are respectively given by:Further, the sum of VA* and VP* represented by VD*, is given by: - (2)
In the integrated system, the optimal present value of the total profits (the optimal objective value of the integrated system), is:
Comparing Equation (26) with Equation (25), we have
VI* ≥
VD*. Since
and
, we have
, which shows that the benefits of the integrated system are higher than or equal to the sum of the benefits of the platform and paid App in the decentralized system. Thus, there exists an inefficiency problem with the decentralized system compared to the integrated system. Changing the effectiveness of the price gap on the reference price (
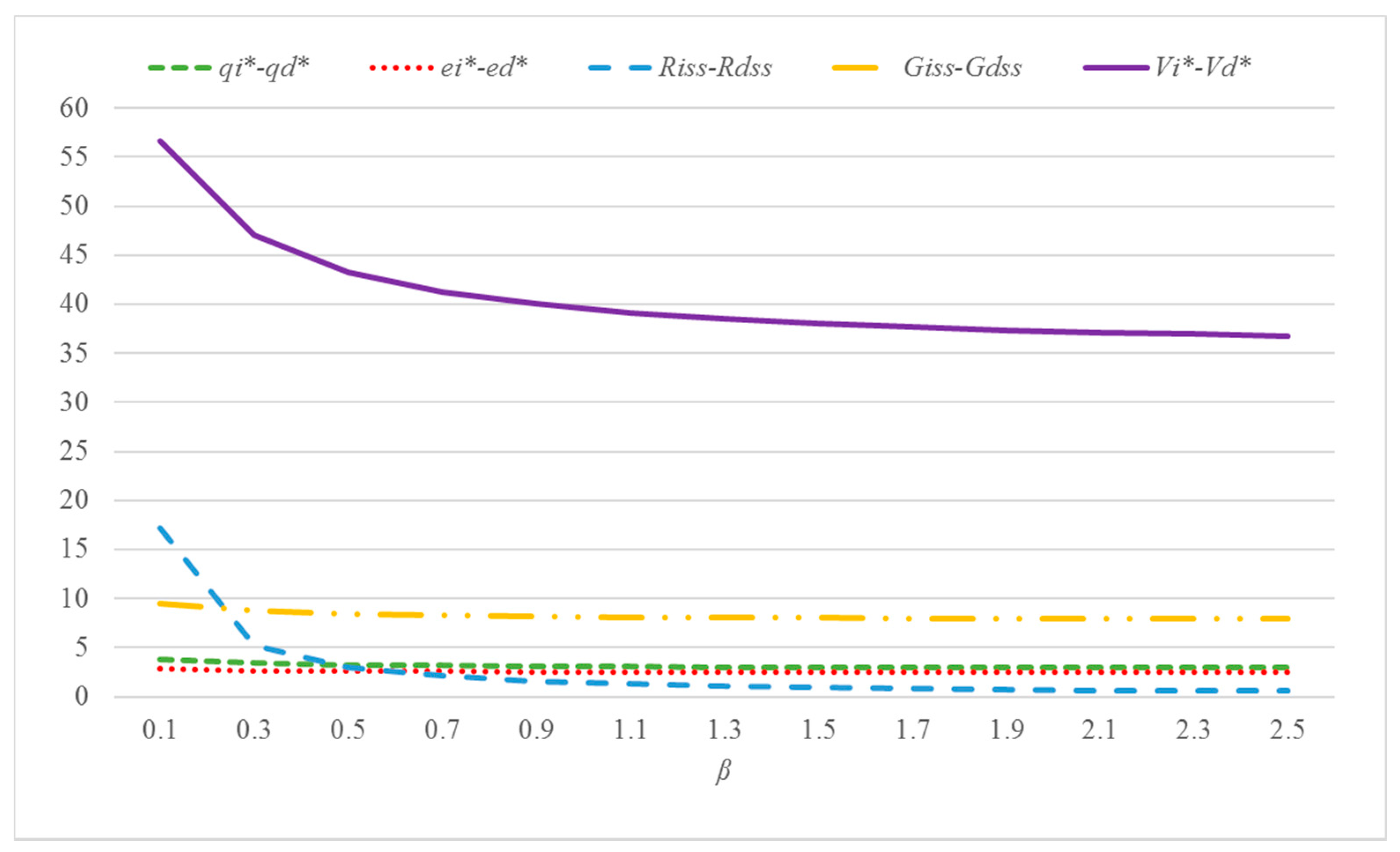
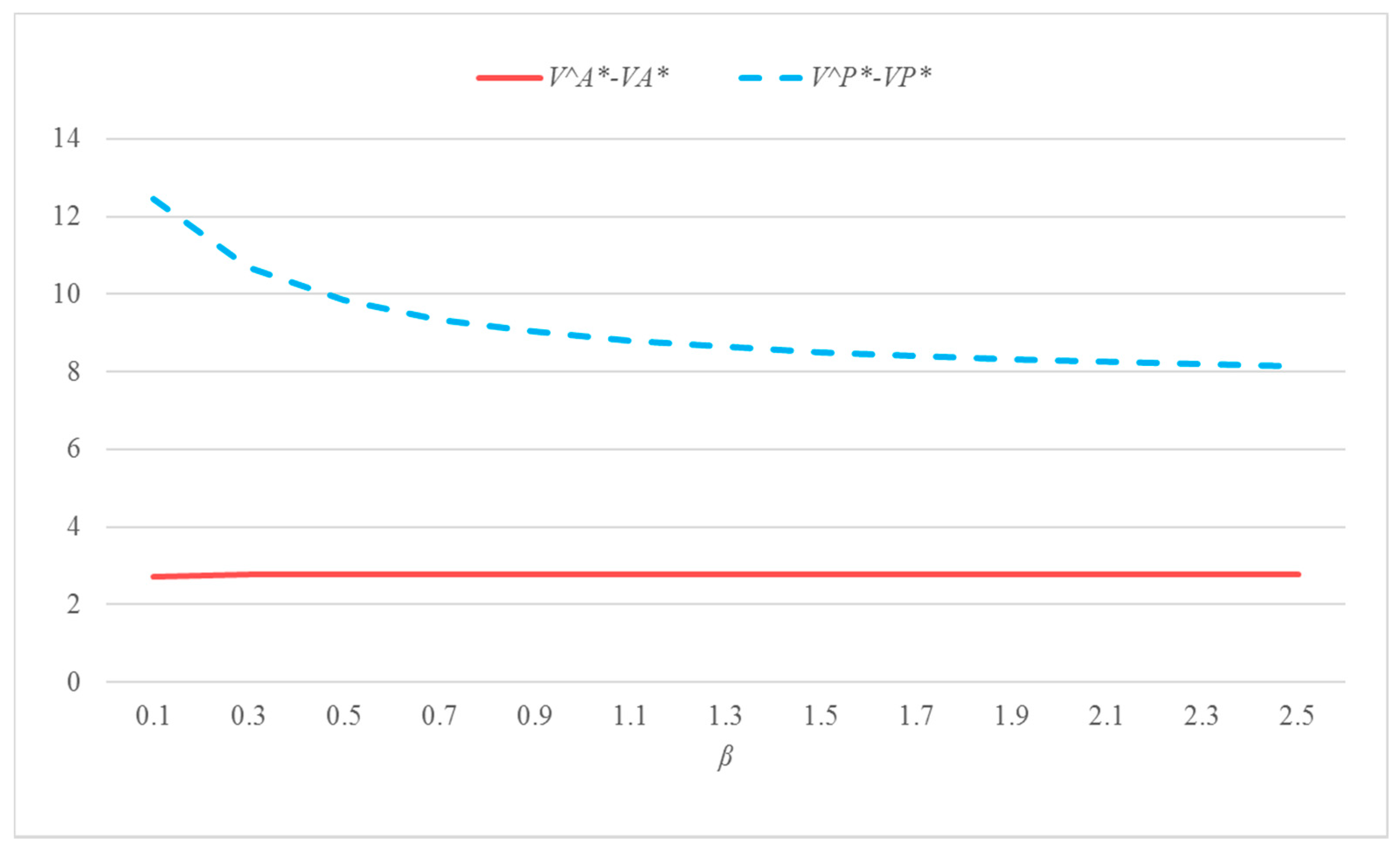
β) from 0.1 to 2.5 while keeping the other parameters fixed, we calculate the difference between the two systems regarding the optimal decision levels, the steady states, and the present values of profits. And then we draw the tendency in
Figure 3.
Figure 3 shows that the optimal decision levels and steady states of the integrated system are higher than those of the decentralized system. Further, the optimal profits of the integrated system are also higher than the sum of the optimal profits of platform and paid App in the decentralized system. Additionally, since
β is utilized to reflect the effectiveness of the price gap on the reference price, the steady state of the reference price changes more sharply than other variables. In the next section, we attempt to develop a bilateral subsidy agreement to address the inefficiencies of the decentralized system while implementing the optimal objective of the integrated system (
VI*).
5. Bilateral Subsidy Agreement
Since the decentralized system has the problem of inefficiency compared to the integrated system (see Proposition 4), we design a bilateral subsidy agreement that coordinates the decentralized system with the integrated system. Specifically, we expect to make the optimal decision levels of the decentralized system equal to the optimal decision levels of the integrated system by the agreement, and consequently the steady states of the decentralized system will be equal to the steady states of the integrated system. As a result, the sum of the present values of profits of the platform and the paid App will be equal to the present value of profits of the integrated system.
To achieve the above purpose, we propose a bilateral subsidy agreement (
k, ψ; note that the paid App’s participation rate (
k) is just the platform’s advertising subsidy rate set by the paid App (
s) in
Section 3 and
Section 4, the distinction is made to clearly compare
s* and
k*). In this agreement, 0 ≤
k ≤ 1 and 0 ≤
ψ ≤ 1 are the participation rates of the paid App and the platform respectively, which means that not only does the paid App have to share
k proportion of the cost of the platform’s advertising effort, but also the platform need to share
ψ proportion of the cost of the paid App’s product quality. Importantly, the proposed bilateral subsidy agreement can coordinate the decentralized system with the integrated system smoothly, and further achieve the optimal objective of the integrated system (
VI*).
Therefore, under the bilateral subsidy agreement (
k,
ψ), the optimization problems of the paid App and the platform are respectively become:
and:
When the participation rates k and ψ are fixed, we obtain the optimal strategies of the paid App and the platform as follows.
Proposition 5. Under the bilateral subsidy agreement, assuming the participation rates k and ψ are fixed, the optimal paid App’s product quality and the optimal platform’s advertising effort are respectively: Once there exists a particular pair (k*, ψ*) that can make the optimal paid App’s product quality and the optimal platform’s advertising effort in the bilateral subsidy agreement (Equations (29) and (30)) be equal to the corresponded ones in the integrated system (Equations (17) and (18)), i.e., and , then the decentralized system can be coordinated with the integrated system. Solving the above two equations, we obtain the following proposition.
Proposition 6. The decentralized system and integrated system can be coordinated by (k*, ψ*), where: Comparing the optimal paid App’s participation rate (k* in Equation (31)) with the optimal platform’s advertising subsidy rate set by the paid App (s* in Equation (16)), we have . That means the bilateral subsidy agreement requires the platform to participate in bearing the cost of the product quality of the paid App, which further motivates the paid App to increase the platform’s advertising subsidy rate. Additionally, we find that the optimal platform’s participation rate (ψ*) is just equal to the paid App’s revenue-sharing rate (λ), implying that the platform shares a certain proportion of the paid App’s revenue, but also need to undertake the same proportion of the paid App’s advertising cost.
Once the decentralized system has been coordinated with the integrated system, the steady states of the reference price and the goodwill in the two systems are equal. Thus, we can obtain the optimal present values of profits of the paid App and the platform respectively under the bilateral subsidy agreement.
Proposition 7. Under the unique bilateral subsidy agreement (k*, ψ*), the sum ofandis equal to the optimal present value of the total profits in the integrated system, VI*, i.e.,:where: Proposition 7 shows that as expected, under the unique bilateral subsidy agreement, the decentralized system not only coordinates with the integrated system, but also implements the optimal objective value of the integrated system, VI*. Next, we discuss whether the optimal present values of profits of the paid App and the platform can be improved simultaneously under the unique bilateral subsidy agreement.
Proposition 8. Comparing the optimal present values of profits of the paid App and the platform with and without the unique bilateral subsidy agreement, we have:
- (1)
The necessary and sufficient condition foris: - (2)
The necessary and sufficient condition foris: - (3)
The necessary and sufficient condition forandis: - (4)
The necessary and sufficient condition forandis: - (5)
The necessary and sufficient condition forandis: - (6)
anddo not hold simultaneously.
First, parts (i) and (ii) give respective conditions under which the paid App and the platform improve their present values of profits under the unique bilateral subsidy agreement. Second, parts (iii) and (iv) show that, it’s possible that under some conditions, one of the paid App and the platform will benefit from the agreement, while the other will suffer losses. Third, part (v) shows that both the optimal present values of profits of the paid App and the platform are greater in the bilateral subsidy agreement than in the original decentralized system under some conditions (i.e., Equation (40)), which means that both the paid App and the platform can obtain additional benefits from the agreement. Specifically, substituting Equations (10), (11), and (16)–(18) into Equation (40), we obtain:
If η1 = η2, μ1 = μ2, and θ1 = θ2, then the above equation becomes 2/5 ≤ λ ≤ 4/5, implying that when the effectiveness of product quality is equal to the effectiveness of advertising effort, the revenue-sharing rate should be between 40% and 80% to ensure that the paid App and the platform can simultaneously benefit from the agreement. Finally, part (vi) shows that it’s impossible that both the paid App and the platform suffer losses from the agreement, i.e., at least one of the paid App and the platform can benefit from the unique bilateral subsidy agreement.
Changing the effectiveness of the price gap on the reference price (
β) from 0.1 to 2.5 while keeping the other parameters fixed, we draw the tendency of
and
in
Figure 4,
Figure 5 and
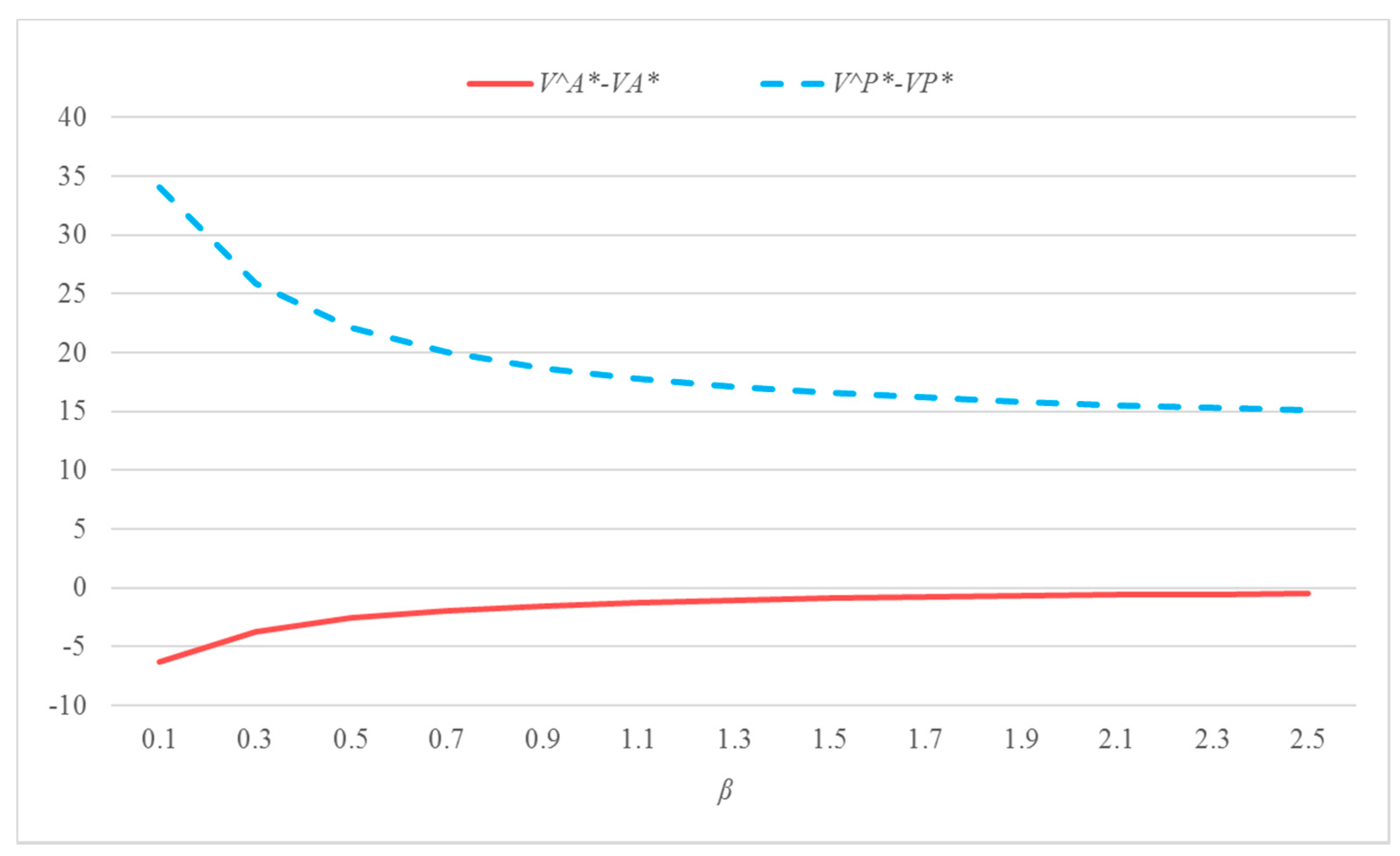
Figure 6, respectively, to show that the situations in parts (iii), (iv), and (v) can actually happen. As shown in
Figure 4 and
Figure 5, one of the paid App and the platform may have a loss in profit. Notably, both the paid App and the platform can benefit from the unique bilateral subsidy agreement under some conditions as show in
Figure 6.
6. Conclusions
Users’ perceptions have crucial reference value and guiding significance in formulating business strategies for the paid App and the platform. Taking the reference price and goodwill of the paid App as the state variables, this paper utilizes the optimal control theory to investigate the optimal product quality of the paid App and the optimal advertising effort of the platform in promoting the paid App in the decentralized and integrated systems, respectively. Due to the inefficiency of the decentralized system in general, we formulate a bilateral subsidy agreement to coordinate the decentralized system with the integrated system, which requires the paid App and the platform to share each other’s costs.
Our research obtains some findings and management insights include the following:
- (1)
Since the product quality of the paid App and the advertising effort of the platform for promotion will positively affect the reference price, the steady state of the reference price is higher than the current price of the paid App. Interestingly, the higher the loyalty of the users, the higher the corresponding reference price will be, which is consistent with intuition. As for the users who lack loyalty, that is, the price gap has a great impact on the reference price of such users, then the developers and platform can consider ignoring the impact of the reference price.
- (2)
When the platform shares 2/3 or more of the paid App’s revenue, the paid App is no longer willing to provide any advertising subsidies to the platform. Whereas when the platform stops sharing the revenue of the paid App, it makes business sense that the paid App is willing to bear full advertising costs of the platform.
- (3)
Since the optimal paid App’s product quality and the optimal platform’s advertising effort in the decentralized system is less than in the integrated system, the optimal present value of profit in the decentralized system is less than in the integrated system. Therefore, we propose a bilateral subsidy agreement that can not only smoothly achieve the channel coordination between the paid App and the platform, but also implement the optimal objective of the integrated system. Additionally, stimulated by the bilateral subsidy agreement, the advertising subsidy rate set by paid App for the platform is also higher than in the original decentralized system.
- (4)
Our proposed bilateral subsidy agreement can guarantee that at least one of the paid App and the platform can benefit more than in the original decentralized system. Further, we theoretically prove that under some mild conditions, both the paid App and the platform can benefit from the agreement. Particularly, when the effectiveness of the platform’s advertising is equal to the effectiveness of the paid App’s product quality, the paid App and the platform can both obtain additional profits from the agreement only if the revenue-sharing rate set by the platform is within the range of 40% to 80%.
Using mathematical modeling, we attempt to explain a certain economic phenomenon and hopefully provide some management insights. To better highlight the practical implications of the findings, we illustrate them in conjunction with specific examples.
Figure 7 shows the discounted prices of the three paid Apps. Here, the reference price is formed by the initial official price, while the goodwill is formed by the quantified star rating and reviews of the paid Apps. Developers can use platform’s advertising for recommending some discounted paid Apps to loyal users, which precisely increases downloads. Furthermore, our research finds that the platform’s excessive revenue-sharing rate will somewhat weaken the developers’ investment in product quality. Therefore, in such an economic process, the agreement we proposed requires the platform to provide certain subsidies to developers. For example, Apple’s Developer Program allows developers to use additional resources provided by Resource Center to better improve product quality, which will save a portion of R&D costs for developers.
https://developer.apple.com/programs/. Moreover, we theoretically propose to set a reasonable sharing rate to achieve a win-win situation for both the platform and the developers. Connecting to practice, the platform can communicate with developers about their difficulties to set a reasonable revenue-sharing rate. In addition, developers can effectively use financial metrics such as investment in advertising, R&D investment in product quality, etc. When investing in advertising, developers have the option to pay for effects, i.e., only if the users successfully complete the download via the platform’s ad link does the developer pay. In this way, developers can know exactly which downloads are attributed to the platform’s ad recommendations. Developers can also exploit users’ reviews of paid Apps to discover the product quality that should be improved. Further, through users’ return visits and feedback, we can find out the contribution of product quality to increase the downloads.
Although specific examples are used to illustrate the analytical results of the modeling, there are some limitations in the practical application. We simply assume that downloads are linearly dependent on the advertising effort, product quality, reference price, and goodwill. Furthermore, in our model, developers advertise solely through the mobile platform, ignoring the advertising effectiveness that comes from other media channels. Meanwhile, we are modeling from the perspective of the platform and the paid Apps, whereas the benefits of users are not taken into account. In addition, some critical variables, such as advertising effect and product quality, are too abstract and would be better described with concrete data. However, the relevant data are difficult for us to obtain. Utilizing empirical analysis to verify the conclusions of the theoretical model is the direction of our future research, which will have more practical application.
Some valuable future extensions of this paper include the following: Firstly, the case of multiple paid Apps with the competitive relationship is worth considering, which will make the App developers extremely complicated in formulating the strategies of price and product quality. Secondly, the competition can also exist between the multiple mobile platforms. When faced with high-potential, high-quality, and large-market Apps, how the platform owners should develop the reasonable revenue-sharing mechanism and the advertising strategies to attract the App developers is very critical. Finally, an App may be developed in a paid version and a free version in general. When facing a single platform or multiple platforms, App developers are full of challenges in the selection of App versions, the pricing of paid Apps, the adoption of advertising models for free App, and so on.