M-CFIS-R: Mamdani Complex Fuzzy Inference System with Rule Reduction Using Complex Fuzzy Measures in Granular Computing
Abstract
1. Introduction
2. Related Works
2.1. Complex Fuzzy Measures
2.2. Fuzzy Inference System in Complex Fuzzy Set
3. Preliminaries
3.1. Complex Fuzzy Set
- ,
3.2. Mamdani Complex Fuzzy Inference System (M-CFIS)
- (i)
- , with ;
- (ii)
- with and ;
- (iii)
- with and ;
- (iv)
- is a T-norm, and is the S-norm (i.e., the T-conorm) that corresponds to ;
- (v)
- Ou,v = and IFF Nu,v = ;
- (vi)
- Ou,v = or IFF Nu,v = .
3.3. Granular Computing
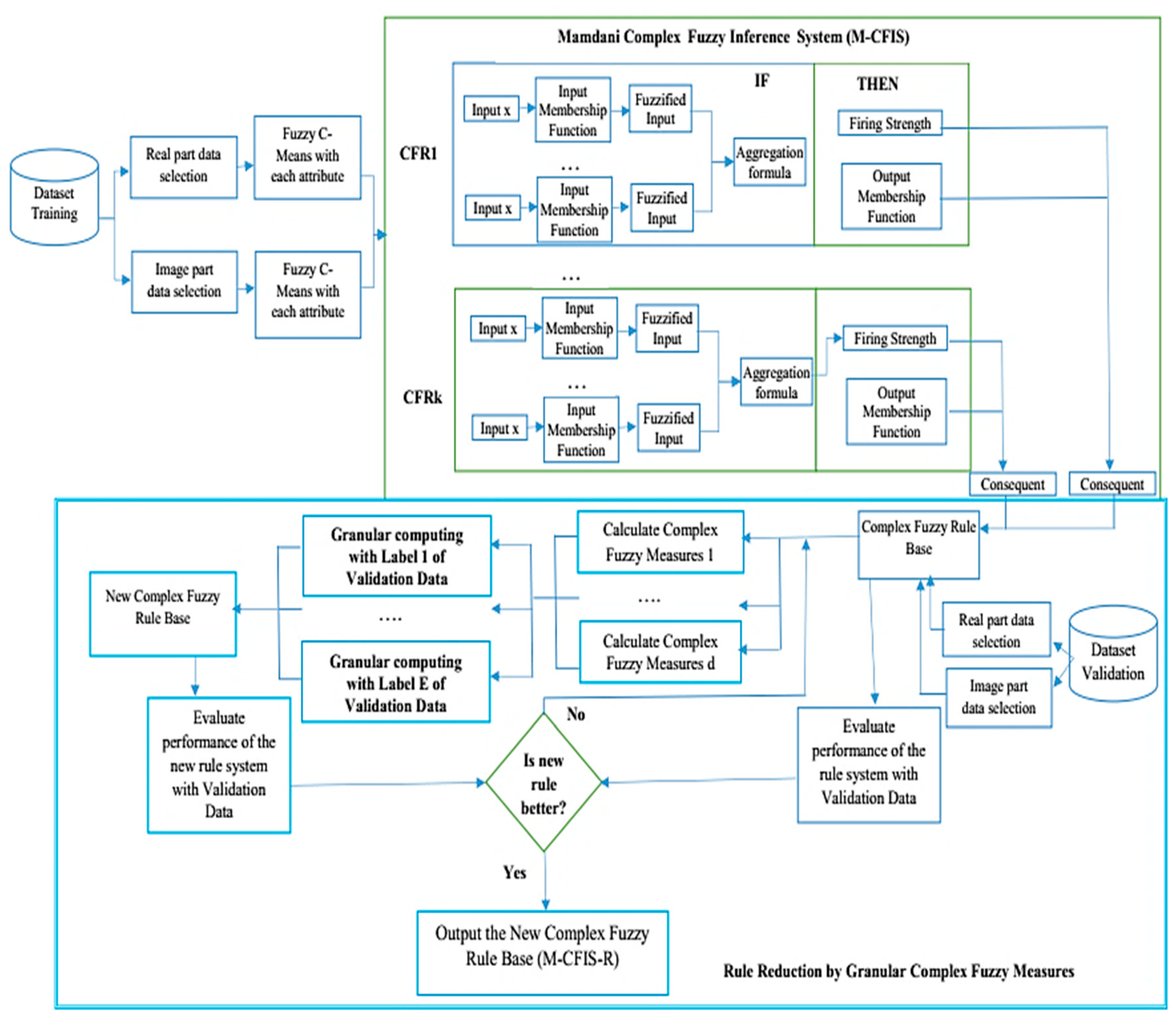
4. Proposed M-CFIS-R System
4.1. Main Ideas
4.2. Training
4.2.1. Real and Imaginary Data Selection
4.2.2. Fuzzy C-Means (FCM)
| Algorithm 1. Fuzzy C-Means algorithm. | |
| Input | Datasets X of N records; C: number of clusters; m: fuzzier; MaxStep |
| Output | Membership U and centers V |
| BEGIN | |
| 1 | Iteration t = 0 |
| 2 | Initialize ( within [0,1] and the sum constraint |
| 3 | Repeat |
| 4 | t = t + 1 |
| 5 | Compute () |
| 6 | Compute ( |
| 7 | Until or t > MaxStep |
4.2.3. Evaluating Performance of the Rule-Based System
4.2.4. Complex Fuzzy Measures
Complex Fuzzy Cosine Similarity Measure (CFCSM)
- ;
- ;
- if and only if
- If then and .
- It is correct because all positive values of cosine function are within 0 and 1.
- Trivial.
- When then obviously .If , . This implies that .
- Let and also assume that and . If , we can write that The cosine function is a decreasing function within the interval . Then, we can write and . □
Complex Fuzzy Dice Similarity Measure (CFDSM)
- ;
- ;
- if and only if ;
- If then and .
Complex Fuzzy Jaccard Similarity Measure (CFJSM)
- ;
- if and only if ;
- If then and .
4.2.5. Granular Complex Fuzzy Measures
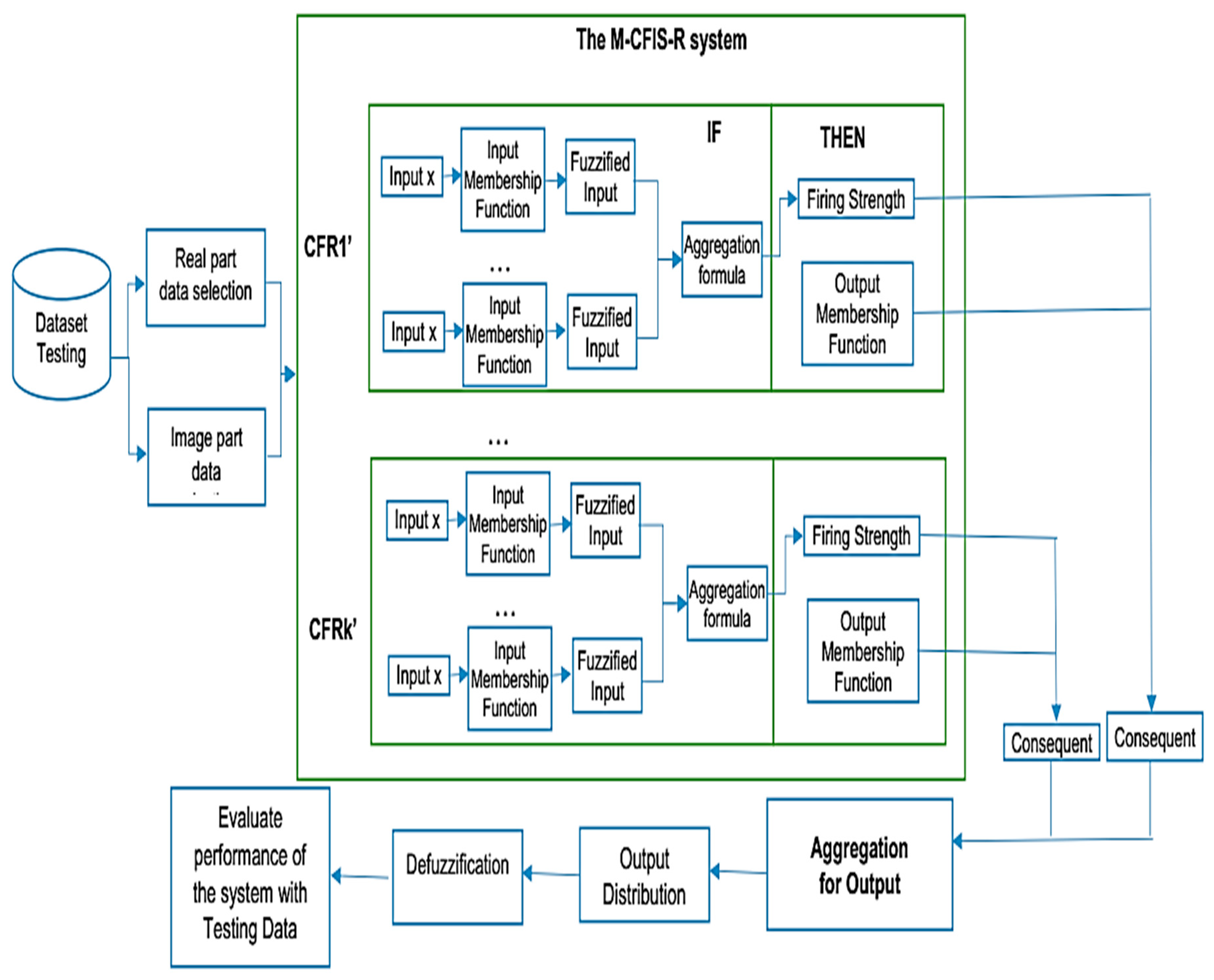
4.3. Testing
4.4. Some Notes on M-CFIS-R
5. Experiments
5.1. Experimental Environment
- (a)
- Benchmark Medical UCI Machine Learning Repository Data [49]:
- (b)
- Real Medical Datasets:
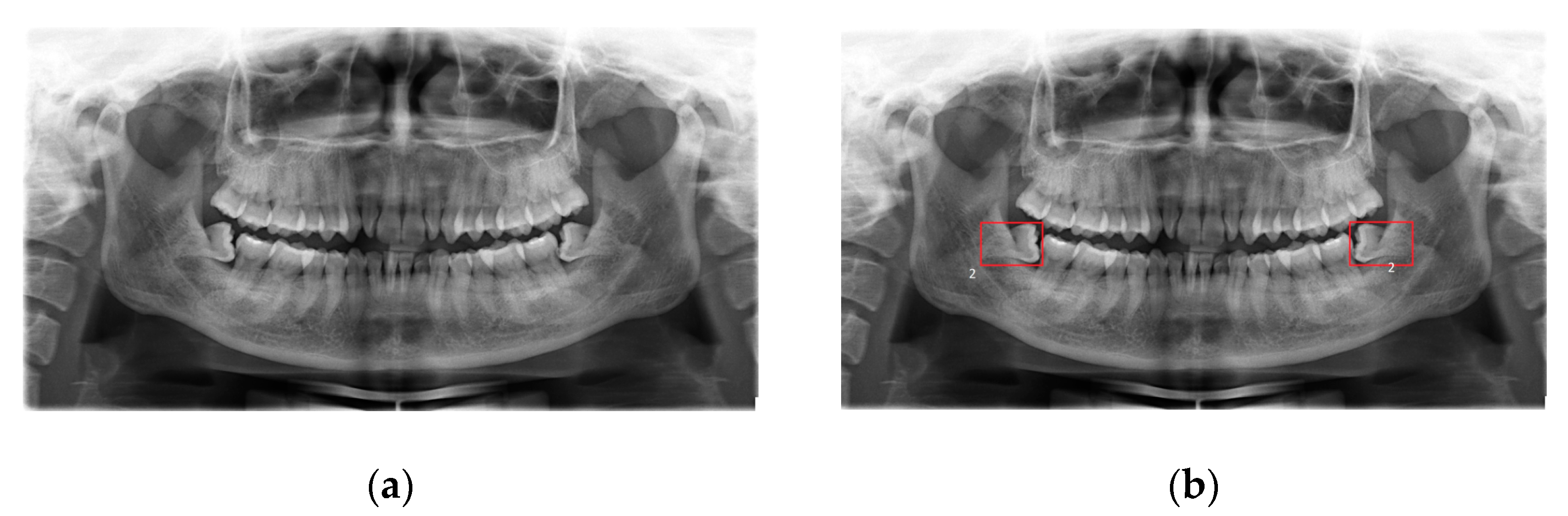
- The fourth dataset is the real dental dataset from Hanoi Medical University Hospital, Vietnam [53], in which dentists provide a properly labeled dataset that consists of 447 X-ray images with the disease of wisdom teeth deviate and 200 X-ray images without wisdom teeth deviate. The dental experts are from Hanoi Medical University and are currently working as professional dentists (Figure 3).
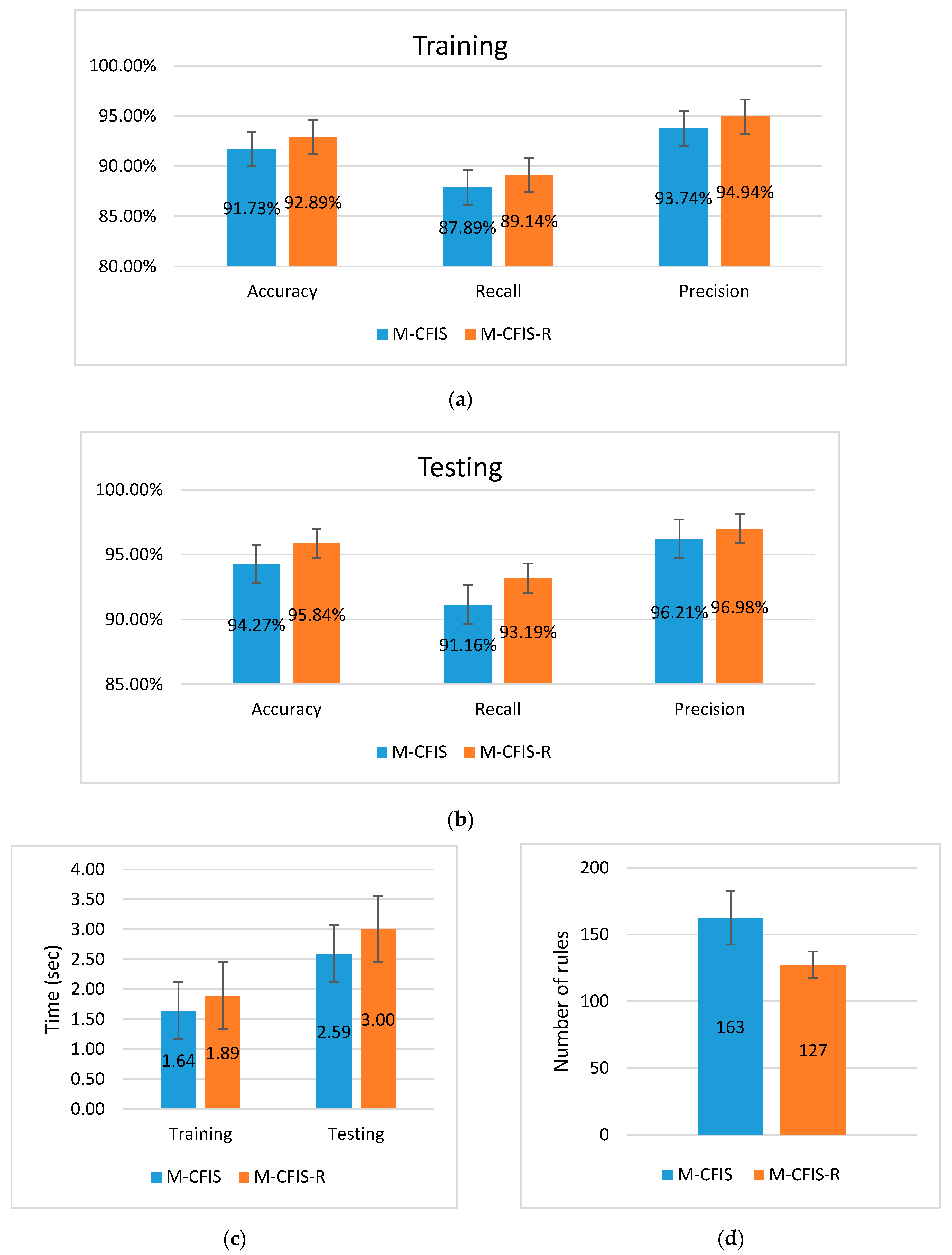
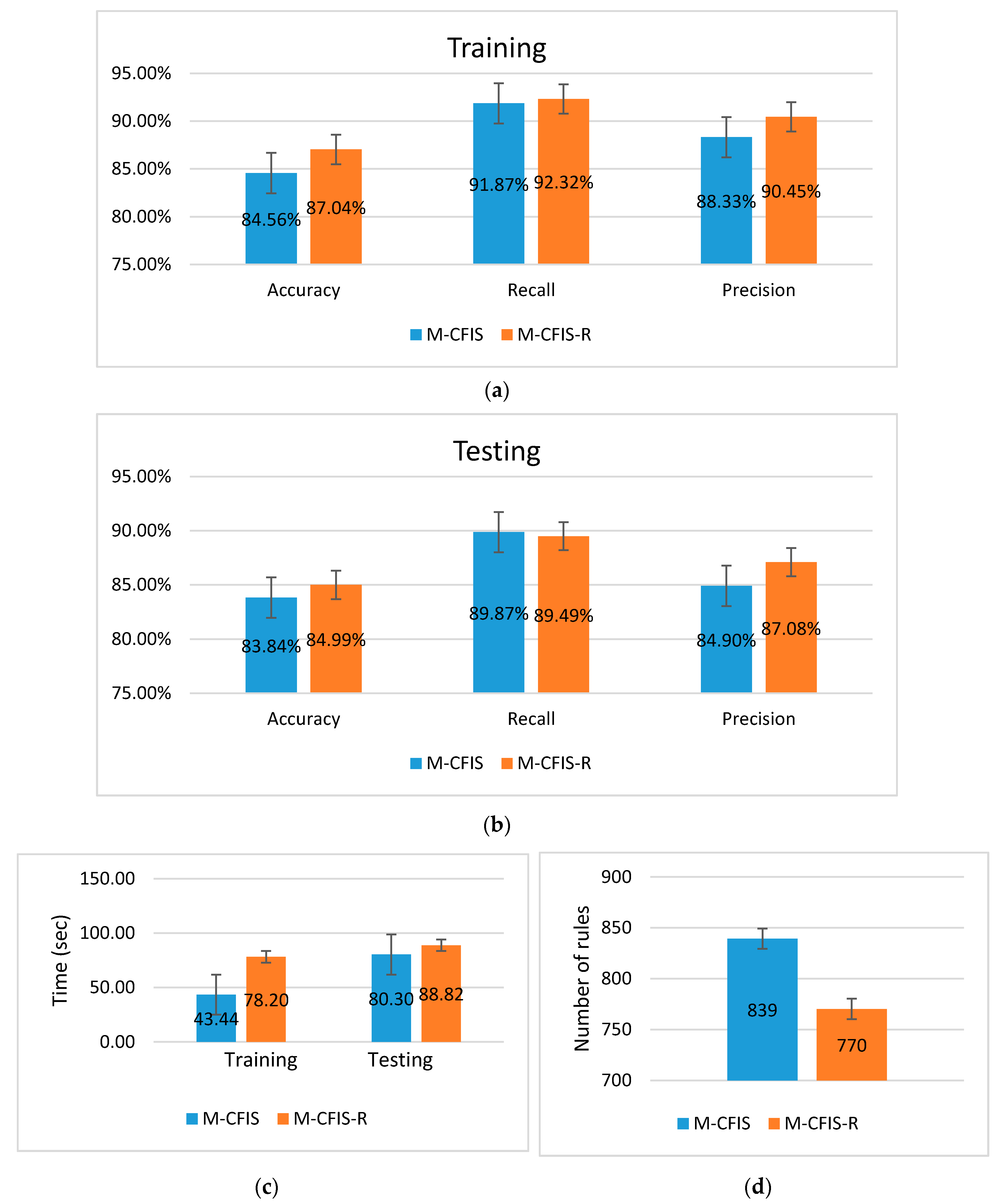
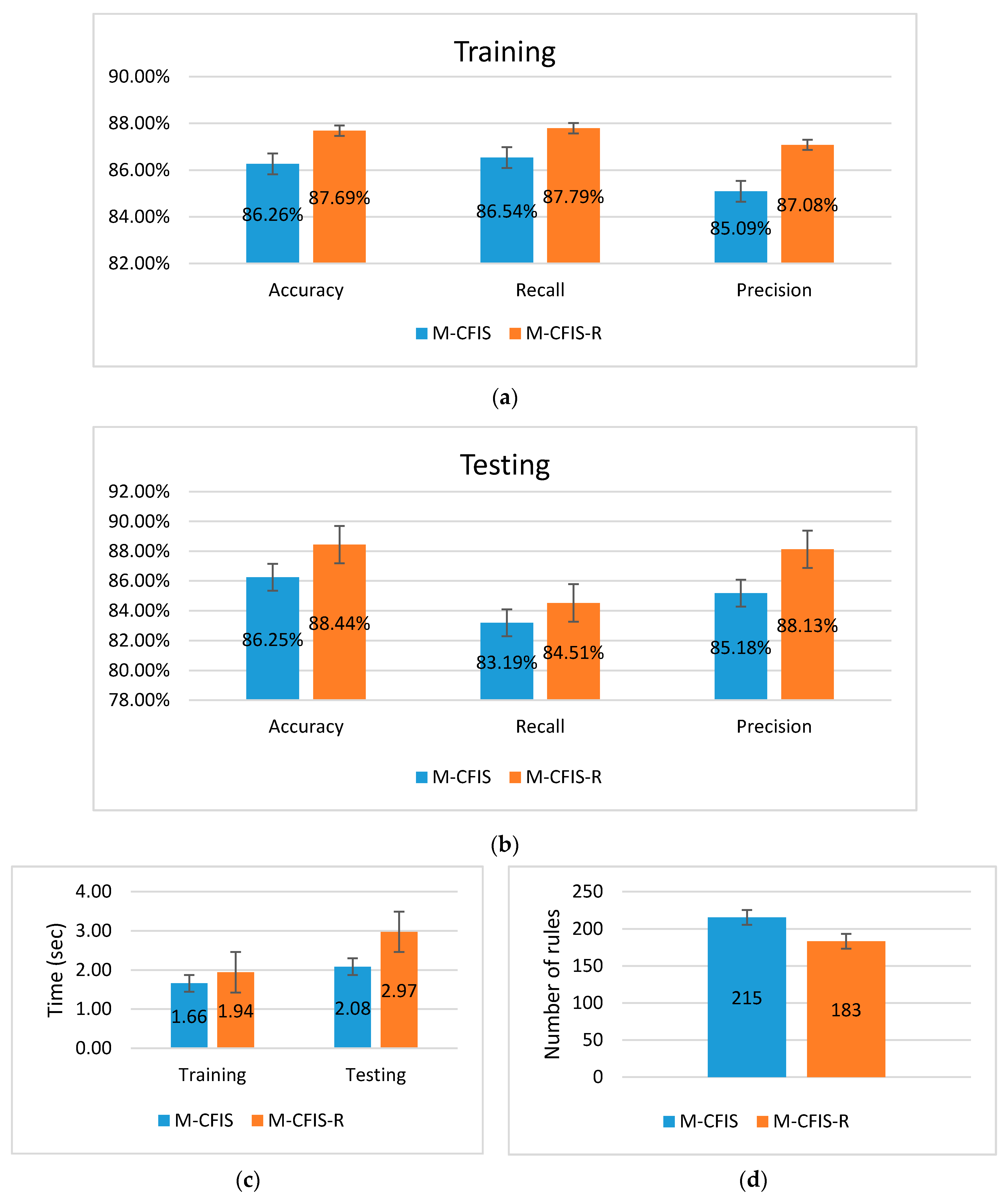
5.2. Experimental Results on the Benchmark UCI Datasets
5.3. Experimental Results on the Real Datasets
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Troussas, C.; Chrysafiadi, K.; Virvou, M. An intelligent adaptive fuzzy-based inference system for computer-assisted language learning. Expert Syst. Appl. 2019, 127, 85–96. [Google Scholar] [CrossRef]
- Tiwari, L.; Raja, R.; Sharma, V.; Miri, R. Fuzzy Inference System for Efficient Lung Cancer Detection. In Computer Vision and Machine Intelligence in Medical Image Analysis; Springer: Singapore, 2020; pp. 33–41. [Google Scholar]
- Sagir, A.M.; Sathasivam, S. A Novel Adaptive Neuro Fuzzy Inference System Based Classification Model for Heart Disease Prediction. Pertanika J. Sci. Technol. 2017, 25, 43–56. [Google Scholar]
- Afriyie Mensah, R.; Xiao, J.; Das, O.; Jiang, L.; Xu, Q.; Alhassan, M.O. Application of Adaptive Neuro-Fuzzy Inference System in Flammability Parameter Prediction. Polymers 2020, 12, 122. [Google Scholar] [CrossRef]
- Bakhshipour, A.; Zareiforoush, H.; Bagheri, I. Application of decision trees and fuzzy inference system for quality classification and modeling of black and green tea based on visual features. J. Food Meas. Charact. 2020, 1–15. [Google Scholar] [CrossRef]
- Manogaran, G.; Varatharajan, R.; Priyan, M.K. Hybrid recommendation system for heart disease diagnosis based on multiple kernel learning with adaptive neuro-fuzzy inference system. Multimed. Tools Appl. 2018, 77, 4379–4399. [Google Scholar] [CrossRef]
- Handoyo, S.; Kusdarwati, H. Implementation of Fuzzy Inference System for Classification of Dengue Fever on the villages in Malang. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 546, p. 052026. [Google Scholar]
- Shastry, K.A.; Sanjay, H.A. Adaptive Neuro-Fuzzy Inference System in Agriculture. In Fuzzy Expert Systems and Applications in Agricultural Diagnosis; IGI Global: Hershey, PA, USA, 2020; pp. 130–153. [Google Scholar]
- Abdolkarimi, E.S.; Mosavi, M.R. Wavelet-adaptive neural subtractive clustering fuzzy inference system to enhance low-cost and high-speed INS/GPS navigation system. GPS Solut. 2020, 24, 36. [Google Scholar] [CrossRef]
- Pourjavad, E.; Shahin, A. The application of Mamdani fuzzy inference system in evaluating green supply chain management performance. Int. J. Fuzzy Syst. 2018, 20, 901–912. [Google Scholar] [CrossRef]
- Lima-Junior, F.R.; Carpinetti, L.C.R. An adaptive network-based fuzzy inference system to supply chain performance evaluation based on SCOR® metrics. Comput. Ind. Eng. 2020, 139, 106191. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Azam, F.; Sharma, A.K.; Vardia, M. An Adaptive Neuro-Fuzzy Inference System-Based Intelligent Grid-Connected Photovoltaic Power Generation. In Advances in Computational Intelligence; Springer: Singapore, 2020; pp. 3–14. [Google Scholar]
- Adoko, A.C.; Yagiz, S. Fuzzy Inference System-Based for TBM Field Penetration Index Estimation in Rock Mass. Geotech. Geol. Eng. 2019, 37, 1533–1553. [Google Scholar] [CrossRef]
- Ramot, D.; Milo, R.; Friedman, M.; Kandel, A. Complex fuzzy sets. IEEE Trans. Fuzzy Syst. 2002, 10, 171–186. [Google Scholar] [CrossRef]
- Ramot, D.; Friedman, M.; Langholz, G.; Kandel, A. Complex fuzzy logic. IEEE Trans. Fuzzy Syst. 2003, 11, 450–461. [Google Scholar] [CrossRef]
- Ngan, T.T.; Lan, L.T.H.; Ali, M.; Tamir, D.; Son, L.H.; Tuan, T.M.; Rishe, N.; Kandel, A. Logic connectives of complex fuzzy sets. Rom. J. Inf. Sci. Technol. 2018, 21, 344–358. [Google Scholar]
- Ali, M.; Smarandache, F. Complex neutrosophic set. Neural Comput. Appl. 2017, 28, 1817–1834. [Google Scholar] [CrossRef]
- Ali, M.; Dat, L.Q.; Smarandache, F. Interval complex neutrosophic set: Formulation and applications in decision-making. Int. J. Fuzzy Syst. 2018, 20, 986–999. [Google Scholar] [CrossRef]
- Greenfield, S.; Chiclana, F.; Dick, S. Interval-valued complex fuzzy logic. In Proceedings of the 2016 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Vancouver, BC, Canada, 24–29 July 2016; pp. 2014–2019. [Google Scholar]
- Garg, H.; Rani, D. Some generalized complex intuitionistic fuzzy aggregation operators and their application to multicriteria decision-making process. Arabian J. Sci. Eng. 2019, 44, 2679–2698. [Google Scholar] [CrossRef]
- Man, J.Y.; Chen, Z.; Dick, S. Towards inductive learning of complex fuzzy inference systems. In Proceedings of the NAFIPS 2007-2007 Annual Meeting of the North American Fuzzy Information Processing Society, San Diego, CA, USA, 24–27 June 2007; pp. 415–420. [Google Scholar]
- Selvachandran, G.; Quek, S.G.; Lan, L.T.H.; Giang, N.L.; Ding, W.; Abdel-Basset, M.; Albuquerque, V.H.C. A New Design of Mamdani Complex Fuzzy Inference System for Multi-attribute Decision Making Problems. IEEE Trans. Fuzzy Syst. 2019. [Google Scholar] [CrossRef]
- Tu, C.H.; Li, C. Multiple Function Approximation-A New Approach Using Complex Fuzzy Inference System. In Asian Conference on Intelligent Information and Database Systems; Springer: Cham, Switzerland, 2018; pp. 243–254. [Google Scholar]
- Chen, Z.; Aghakhani, S.; Man, J.; Dick, S. ANCFIS: A neurofuzzy architecture employing complex fuzzy sets. IEEE Trans. Fuzzy Syst. 2010, 19, 305–322. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, F. An adaptive neuro-complex-fuzzy-inferential modeling mechanism for generating higher-order TSK models. Neurocomputing 2019, 365, 94–101. [Google Scholar] [CrossRef]
- Yazdanbakhsh, O.; Dick, S. FANCFIS: Fast adaptive neuro-complex fuzzy inference system. Int. J. Approx. Reason. 2019, 105, 417–430. [Google Scholar] [CrossRef]
- Alkouri, A.U.M.; Salleh, A.R. Linguistic variable, hedges and several distances on complex fuzzy sets. J. Intell. Fuzzy Syst. 2014, 26, 2527–2535. [Google Scholar] [CrossRef]
- Hu, B.; Bi, L.; Dai, S.; Li, S. Distances of complex fuzzy sets and continuity of complex fuzzy operations. J. Intell. Fuzzy Syst. 2018, 35, 2247–2255. [Google Scholar] [CrossRef]
- Dai, S.; Bi, L.; Hu, B. Distance measures between the interval-valued complex fuzzy sets. Mathematics 2019, 7, 549. [Google Scholar] [CrossRef]
- Setnes, M.; Babuska, R.; Kaymak, U.; van Nauta Lemke, H.R. Similarity measures in fuzzy rule base simplification. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1998, 28, 376–386. [Google Scholar] [CrossRef] [PubMed]
- Mondal, K.; Pramanik, S.; Giri, B.C. Some similarity measures for MADM under a complex neutrosophic set environment. In Optimization Theory Based on Neutrosophic and Plithogenic Sets; Academic Press: Cambridge, MA, USA, 2020; pp. 87–116. [Google Scholar]
- Rani, P.; Mishra, A.R.; Rezaei, G.; Liao, H.; Mardani, A. Extended Pythagorean fuzzy TOPSIS method based on similarity measure for sustainable recycling partner selection. Int. J. Fuzzy Syst. 2020, 22, 735–747. [Google Scholar] [CrossRef]
- Jang, L.C.; Kim, H.M. On Choquet integrals with respect to a fuzzy complex valued fuzzy measure of fuzzy complex valued functions. Int. J. Fuzzy Log. Intell. Syst. 2018, 10, 224–229. [Google Scholar] [CrossRef]
- Jang, L.C.; Kim, H.M. Some Properties of Choquet Integrals with Respect to a Fuzzy Complex Valued Fuzzy Measure. Int. J. Fuzzy Log. Intell. Syst. 2011, 11, 113–117. [Google Scholar] [CrossRef][Green Version]
- Ma, S.; Li, S. Complex fuzzy set-valued Complex fuzzy Measures and their properties. Sci. World J. 2014. [Google Scholar] [CrossRef]
- Ma, S.Q.; Chen, M.Q.; Zhao, Z.Q. The Complex Fuzzy Measure. In Fuzzy Information Engineering and Operations Research Management; Springer: Berlin/Heidelberg, Germany, 2014; pp. 137–145. [Google Scholar]
- Ma, S.Q.; Li, S.G. Complex Fuzzy Set-Valued Complex Fuzzy Integral and Its Convergence Theorem. In Fuzzy Systems Operations Research and Management; Springer: Cham, Switzerland, 2016; pp. 143–155. [Google Scholar]
- Garg, H.; Rani, D. Some results on information measures for complex intuitionistic fuzzy sets. Int. J. Intell. Syst. 2019, 34, 2319–2363. [Google Scholar] [CrossRef]
- Ngan, R.T.; Ali, M.; Tamir, D.E.; Rishe, N.D.; Kandel, A. Representing complex intuitionistic fuzzy set by quaternion numbers and applications to decision making. Appl. Soft Comput. 2020, 87, 105961. [Google Scholar] [CrossRef]
- Yazdanbakhsh, O.; Dick, S. Forecasting of multivariate time series via complex fuzzy logic. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2160–2171. [Google Scholar] [CrossRef]
- Tu, C.H.; Li, C. Multitarget prediction—A new approach using sphere complex fuzzy sets. Eng. Appl. Artif. Intell. 2019, 79, 45–57. [Google Scholar] [CrossRef]
- Li, C.; Tu, C.H. Complex neural fuzzy system and its application on multi-class prediction—A novel approach using complex fuzzy sets, IIM and multi-swarm learning. Appl. Soft Comput. 2019, 84, 105735. [Google Scholar] [CrossRef]
- Singh, P.K. Granular-based decomposition of complex fuzzy context and its analysis. Prog. Artif. Intell. 2019, 8, 181–193. [Google Scholar] [CrossRef]
- Zhang, G.; Dillon, T.S.; Cai, K.Y.; Ma, J.; Lu, J. Operation properties and δ-equalities of complex fuzzy sets. Int. J. Approx. Reason. 2009, 50, 1227–1249. [Google Scholar] [CrossRef]
- Bargiela, A.; Pedrycz, W. Granular computing. In Handbook on Computational Intelligence: Volume 1: Fuzzy Logic, Systems, Artificial Neural Networks, and Learning Systems; World Scientific publishing: Singapore, 2016; pp. 43–66. [Google Scholar]
- Liu, H.; Cocea, M. Granular computing-based approach of rule learning for binary classification. Granul. Comput. 2019, 4, 275–283. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Ffuzzy Objective Function Algorithms; Plenum Press: New York, NY, USA, 1981. [Google Scholar]
- The UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml/datasets.html (accessed on 9 April 2020).
- Breast Cancer. Available online: http://archive.ics.uci.edu/ml/datasets/breast+cancer+wisconsin+%28original%29 (accessed on 9 April 2020).
- Diabetes Databases. Available online: http://biostat.mc.vanderbilt.edu/wiki/Main/DataSets (accessed on 9 April 2020).
- Gangthep Hospital. Available online: http://benhviengangthep.gov.vn/ (accessed on 9 April 2020).
- Hanoi Medical University Hospital. Available online: http://benhviendaihocyhanoi.com/ (accessed on 9 April 2020).
- Ghazali, K.H.; Mustafa, M.M.; Hussain, A.; Bandar, M.E.C.; Kuantan, G. Feature Extraction technique using SIFT keypoints descriptors. In Proceedings of the The International Conference on Electrical and Engineering and Informatics Institut Technology, Institut Teknologi Bandung, Bandung, Indonesia, 17–19 June 2007; pp. 17–19. [Google Scholar]
- Ahonen, T.; Hadid, A.; Pietikainen, M. Face description with local binary patterns: Application to face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 2037–2041. [Google Scholar] [CrossRef]
- Oad, K.K.; DeZhi, X.; Butt, P.K. A Fuzzy Rule Based Approach to Predict Risk Level of Heart Disease. Glob. J. Comput. Sci. Technol. 2014, 14, 16–22. [Google Scholar]
- Lai, Y.H.; Lin, P.L. Effective segmentation for dental X-ray images using texture-based fuzzy inference system. In International Conference on Advanced Concepts for Intelligent Vision Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 936–947. [Google Scholar]
- Turabieh, H.; Mafarja, M.; Mirjalili, S. Dynamic Adaptive Network-Based Fuzzy Inference System (D-ANFIS) for the Imputation of Missing Data for Internet of Medical Things Applications. IEEE Internet Things J. 2019, 6, 9316–9325. [Google Scholar] [CrossRef]
- Ahmad, G.; Khan, M.A.; Abbas, S.; Athar, A.; Khan, B.S.; Aslam, M.S. Automated diagnosis of hepatitis b using multilayer mamdani fuzzy inference system. J. Healthc. Eng. 2019. [Google Scholar] [CrossRef]

| No. | Feature Name | Value range |
|---|---|---|
| 1 | Clump Thickness | 1–10 |
| 2 | Uniformity of Cell Size | 1–10 |
| 3 | Uniformity of Cell Shape | 1–10 |
| 4 | Marginal Adhesion | 1–10 |
| 5 | Single Epithelial Cell Size | 1–10 |
| 6 | Bare Nuclei | 1–10 |
| 7 | Bland Chromatin | 1–10 |
| 8 | Normal Nucleoli | 1–10 |
| 9 | Mitoses | 1–10 |
| 10 | Class | (2: benign, 4: malignant) |
| No | Feature Names | Value Range |
| 1 | Total Cholesterol | 78–443 |
| 2 | Stabilized Glucose | 48–385 |
| 3 | High Density Lipoprotein | 12–120 |
| 4 | Cholesterol/HDL Ratio | 1.5–19.3 |
| 5 | Glycosylated Hemoglobin | 2.68–16.11 |
| 6 | Class | (0: negative, 1: positive) |
| No. | Feature Name | Value Range |
|---|---|---|
| 1 | Age: at the exam time | 5–86 |
| 2 | Gender | (0: male; 1: female) |
| 3 | AST: aspartate transaminase | 11.4–659.76 |
| 4 | ALT: alanine aminotransferase | 78.52–647.7 |
| 5 | AST/ALT index | 0–8.5 |
| 6 | GGT: gamma glutamyl transferase | 0–3352.6 |
| 7 | Albumin | 0–58.2 |
| 8 | TB: Total bilirubin | 3–669.03 |
| 9 | DB: Direct bilirubin | 0–287.52 |
| 10 | DB/TB (%) | 0–224.8 |
| 11 | Class | (0: nondisease, 1: disease) |
| ID | Features | Value Range |
|---|---|---|
| 1 | LBP | 27.04–55.89 |
| 2 | EEI | 145.65–161.76 |
| 3 | GRA | 85.02–125.07 |
| 4 | Patch | 30.54 × 10−3–208.56 × 10−3 |
| 5 | Label | 0 or 1 |
| Authors | Model | Brief Description | Results and Limitations |
|---|---|---|---|
| Selvachandran et al. [23] | Mamdani CFIS | - Extended Mamdani FIS on complex fuzzy sets (Mamdani CFIS) together with operations on this system. - Output of Mamdani CFIS is a set of complex fuzzy rules used to solve diagnosis problems. | - Applying proposed model on six real datasets with higher accuracy than Mamdani FIS and ANFIS. - Limitation: There is redundancy in the rule base. |
| Turabieh et al. [58] | Dynamic ANFIS | - An ANFIS based model to predict missing values of incomplete samples based on complete samples. - Optimized each rule in the rule base using MSE. | - The model was validated on two medical datasets with good results in handling missing value datasets. - Limitation: Unable to deal with data that have phase or periodic interval. |
| Ahmad et al. [59] | Multilayer Mamdani FIS | - Proposed two-stage model in which Mamdani FIS is used to diagnose hepatitis B. - First layer determines hepatitis and second layer diagnoses hepatitis B. | - Experiments were done on a real dataset. The correct classification rate is high. - Limitation: This method is restricted to medical dataset of hepatitis. Does not concern periodic data. |
| This paper | M-CFIS-R | - Proposed a new rule reduction for M-CFIS [23] by using granular computing with complex similarity measures. - Theoretical proofs and theorems were provided. | - Achieved high accuracy of prediction in both the benchmark and real datasets. - Achieved the optimal number of rules. - Able to handle the limitations of rule redundancy and periodic data. - Limitation: Time-consuming. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuan, T.M.; Lan, L.T.H.; Chou, S.-Y.; Ngan, T.T.; Son, L.H.; Giang, N.L.; Ali, M. M-CFIS-R: Mamdani Complex Fuzzy Inference System with Rule Reduction Using Complex Fuzzy Measures in Granular Computing. Mathematics 2020, 8, 707. https://doi.org/10.3390/math8050707
Tuan TM, Lan LTH, Chou S-Y, Ngan TT, Son LH, Giang NL, Ali M. M-CFIS-R: Mamdani Complex Fuzzy Inference System with Rule Reduction Using Complex Fuzzy Measures in Granular Computing. Mathematics. 2020; 8(5):707. https://doi.org/10.3390/math8050707
Chicago/Turabian StyleTuan, Tran Manh, Luong Thi Hong Lan, Shuo-Yan Chou, Tran Thi Ngan, Le Hoang Son, Nguyen Long Giang, and Mumtaz Ali. 2020. "M-CFIS-R: Mamdani Complex Fuzzy Inference System with Rule Reduction Using Complex Fuzzy Measures in Granular Computing" Mathematics 8, no. 5: 707. https://doi.org/10.3390/math8050707
APA StyleTuan, T. M., Lan, L. T. H., Chou, S.-Y., Ngan, T. T., Son, L. H., Giang, N. L., & Ali, M. (2020). M-CFIS-R: Mamdani Complex Fuzzy Inference System with Rule Reduction Using Complex Fuzzy Measures in Granular Computing. Mathematics, 8(5), 707. https://doi.org/10.3390/math8050707






