Rational Transformations for Evaluating Singular Integrals by the Gauss Quadrature Rule
Abstract
1. Introduction
2. Weakly Singular Integrals
2.1. Existing Transformations
- •
- Telles polynomial transformation [15]:where with .
- •
- •
- Generalized sigmoidal transformation [16]:where , , is a sigmoidal transformation of order m(see [8,9] for the definition) with the behavior near , is a point transformed asand is the sign function whose value is 1 for and for .It is noted that both and have the following asymptotic behavior near the transformed singular point .Thus, by the change of variable or in Equations (1) and (2), the weakly singular integrals and become regular ones for m large enough because the behaviors of the integrands are transformed to and , respectively, near .For a weakly singular integral with an end-point singularity at with we introduce two famous transformations below.
- •
- •
- Semi-sigmoidal transformation [10]:Both and have the following asymptotic behavior near .
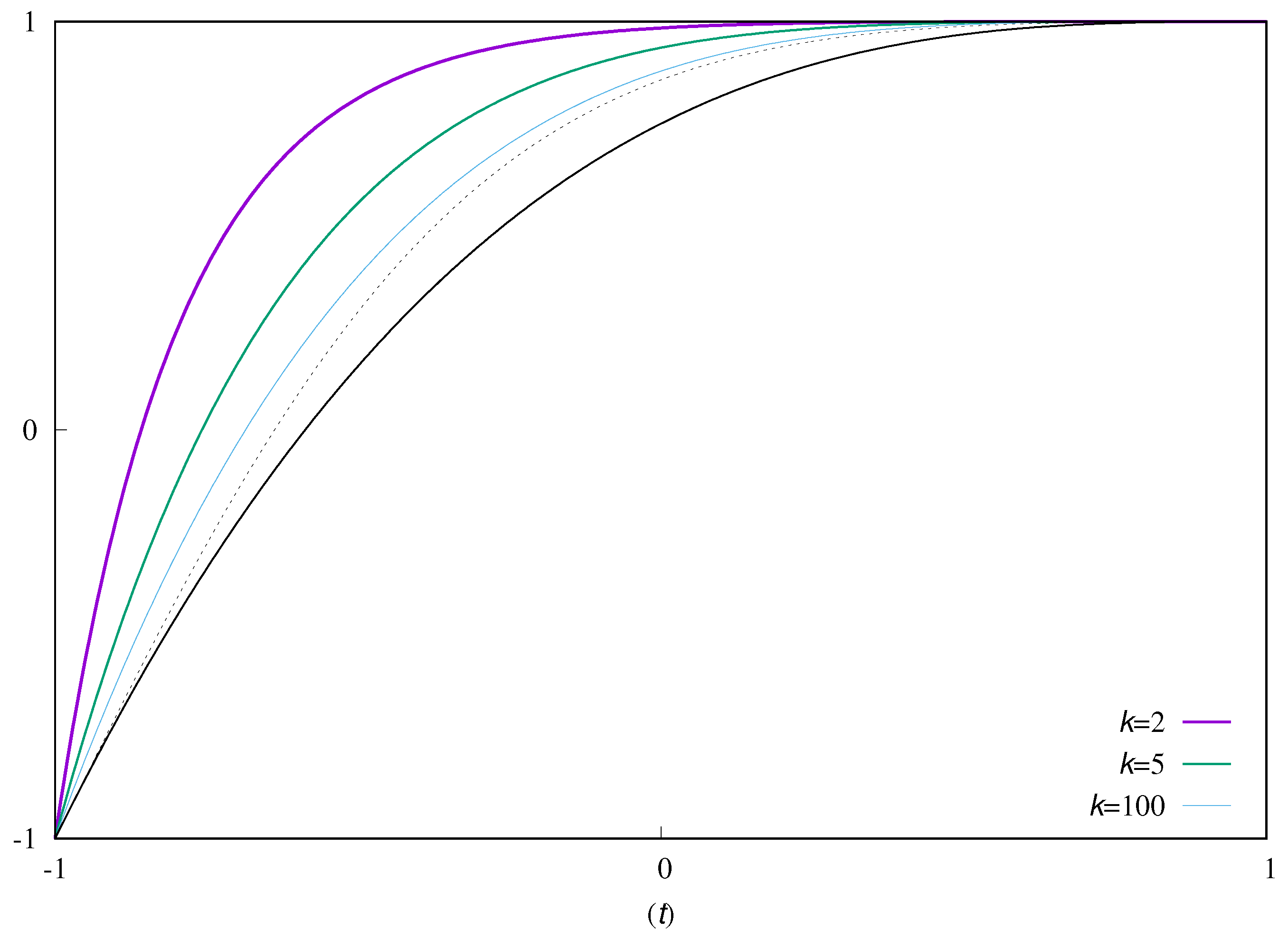
2.2. A Rational Transformation
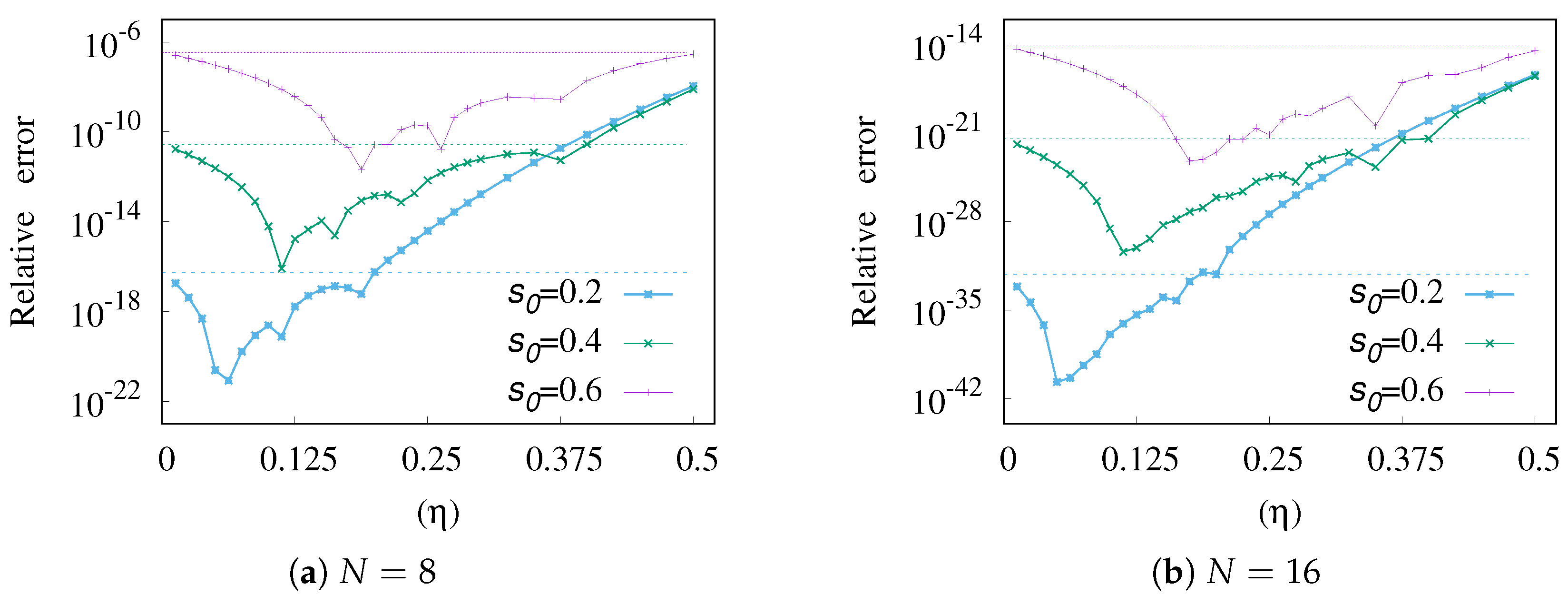
2.3. Numerical Examples
3. Cauchy Principal Value Integrals
3.1. Existing Transformations
- •
- Doblalè and Gracia transformation(DG) [6]:
- •
- Composite transformation [17]:where , , is a sigmoidal transformation of order .
3.2. A New Composite Transformation
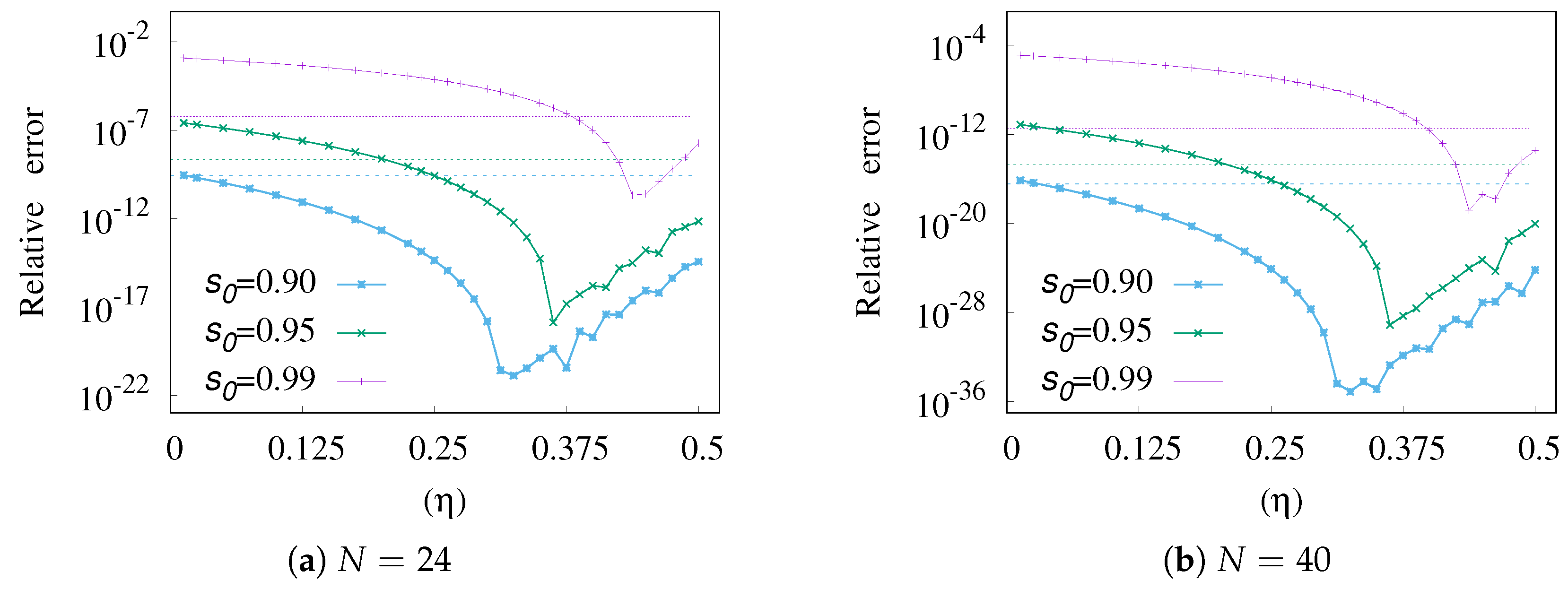
3.3. Numerical Examples
4. Conclusions
- i.
- Interior-point weakly singular integrals: The rational transformation in (11) is proposed. Numerical evaluation based on the proposed rational transformation does not require any division of the integration interval, and its numerical results are comparable to the existing transformations.
- ii.
- End-point weakly singular integrals: The rational transformation in (15) is proposed and it provides better errors than the exiting transformations when an appropriate value of k is selected.
- iii.
Funding
Conflicts of Interest
References
- Doblaré, M. Computational aspects of the boundary element methods. In Topics in Boundary Element Research; Springer: Berlin, Germany, 1987; Volume 3. [Google Scholar]
- Kythe, P.K. An Introduction to Boundary Element Method; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Ma, Y.; Huang, J. Asymptotic error expansions and splitting extrapolation algorithm for two classes of two-dimensional Cauchy principal-value integrals. Appl. Math. Comput. 2019, 357, 107–118. [Google Scholar] [CrossRef]
- Qiu, Z.H.; Wrobel, L.C.; Power, H. Numerical solution of convection-diffusion problems at high Peclét number using boundary elements. Int. J. Numer. Methods Eng. 1998, 41, 899–914. [Google Scholar] [CrossRef]
- Savruk, M.P.; Kazberuk, A. Method of Singular Integral Equations in Application to Problems of the Theory of Elasticity. In Stress Concentration at Notches; Springer: Cham, Switzerland, 2017; pp. 1–56. [Google Scholar]
- Doblaré, M.; Gracia, L. On non-linear transformations for integration of weakly-singular and Cauchy principal value integrals. Int. J. Numer. Methods Eng. 1997, 40, 3325–3358. [Google Scholar] [CrossRef]
- Elliott, D. The cruciform crack problem and sigmoidal transformations. Math. Methods Appl. Sci. 1997, 20, 121–132. [Google Scholar] [CrossRef]
- Elliott, D. The Euler Maclaurin formula revised. J. Austral. Math. Soc. Ser. B 1998, 40, E27–E76. [Google Scholar]
- Elliott, D.; Venturino, E. Sigmoidal transformations and the Euler-Maclaurin expansion for evaluating certain Hadamard finite-part integrals. Numer. Math. 1997, 77, 453–465. [Google Scholar] [CrossRef]
- Johnston, P.R. Semi-sigmoidal transformations for evaluating weakly singular boundary element integrals. Int. J. Numer. Methods Eng. 2000, 47, 1709–1730. [Google Scholar] [CrossRef]
- Johnston, P.R.; Elliott, D. Error estimation of quadrature rules for evaluating singular integrals in boundary element. Int. J. Numer. Methods Eng. 2000, 48, 949–962. [Google Scholar] [CrossRef]
- Johnston, P.R.; Elliott, D. A generalization of Telles’ method for evaluating weakly singular boundary element integrals. J. Comput. Appl. Math. 2001, 131, 223–241. [Google Scholar] [CrossRef]
- Sanz Serna, J.M.; Doblaré, M.; Alarcon, E. Remarks on methods for the computation of boundary-element integrals by co-ordinate transformation. Commun. Appl. Numer. Methods 1990, 6, 121–123. [Google Scholar] [CrossRef]
- Sato, M.; Yoshiyoka, S.; Tsukui, K.; Yuuki, R. Accurate numerical integration of singular kernels in the two-dimensional boundary element method. In Boundary Elements X; Brebbia, C.A., Ed.; Springer: Berlin, Germany, 1988; Volume 1, pp. 279–296. [Google Scholar]
- Telles, J.C.F. A self-adaptive co-ordinate transformation for efficient numerical evaluation of general boundary element integrals. Int. J. Numer. Methods Eng. 1987, 24, 959–973. [Google Scholar] [CrossRef]
- Yun, B.I. An extended sigmoidal transformation technique for evaluating weakly singular integrals without splitting the integration interval. SIAM J. Sci. Comput. 2003, 25, 284–301. [Google Scholar] [CrossRef]
- Yun, B.I. A composite transformation for numerical integration of singular integrals in the BEM. Int. J. Numer. Methods Eng. 2003, 57, 1883–1898. [Google Scholar] [CrossRef]
- Yun, B.I. A generalized non-linear transformation for evaluating singular integrals. Int. J. Numer. Methods Eng. 2006, 65, 1947–1969. [Google Scholar] [CrossRef]
- Monegato, G.; Sloan, I.H. Numerical solutions of the generalized airfoil equation for an airfoil with a flap. SIAM J. Numer. Anal. 1997, 34, 2288–2305. [Google Scholar] [CrossRef]
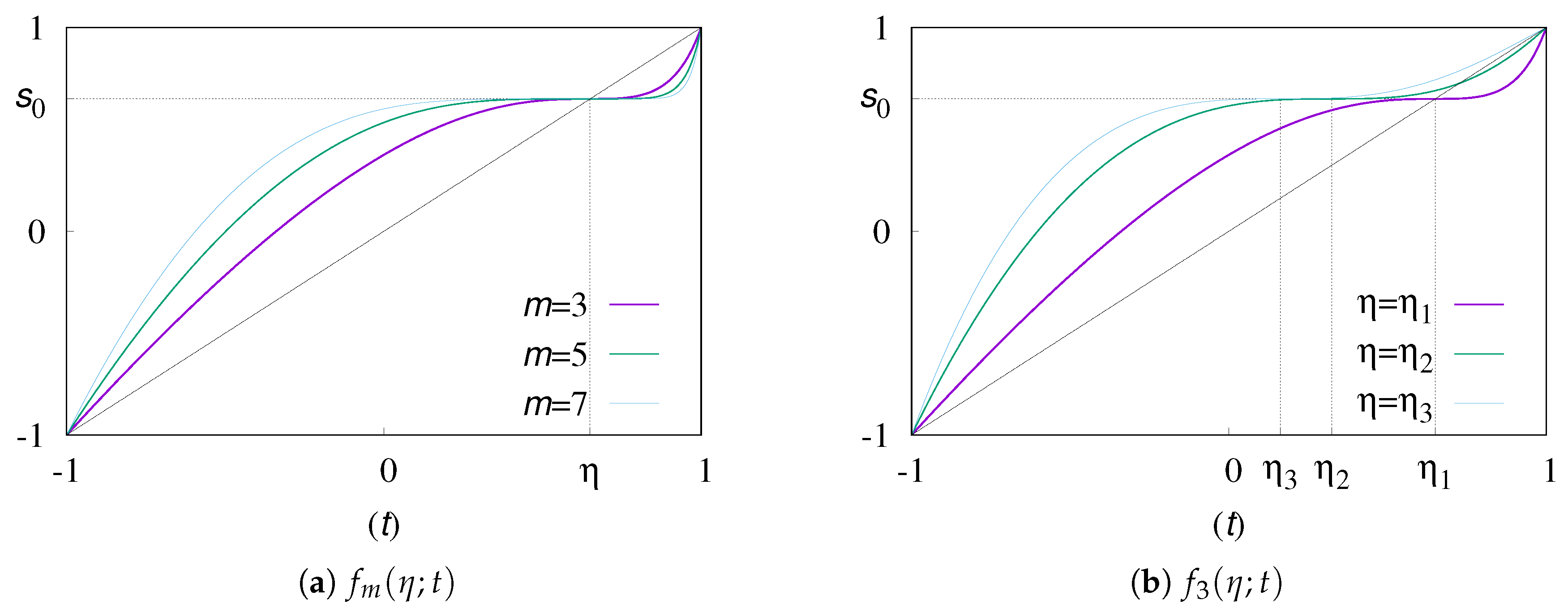
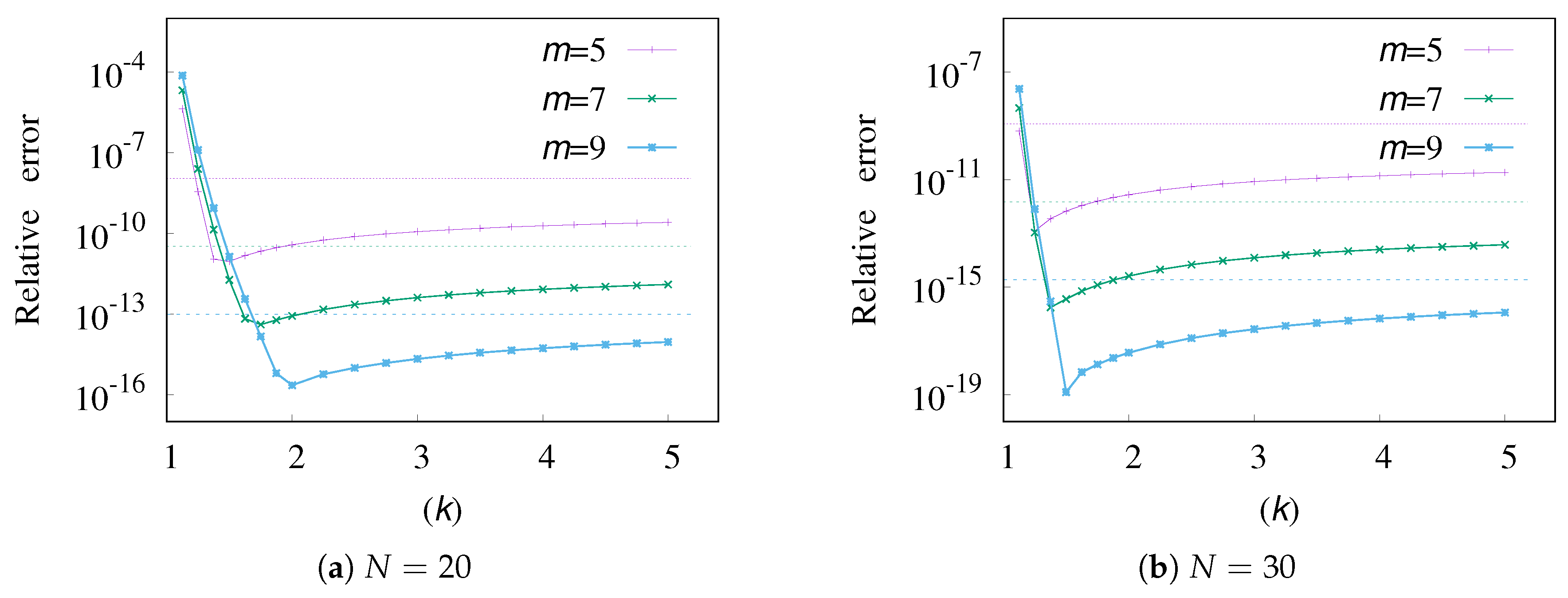

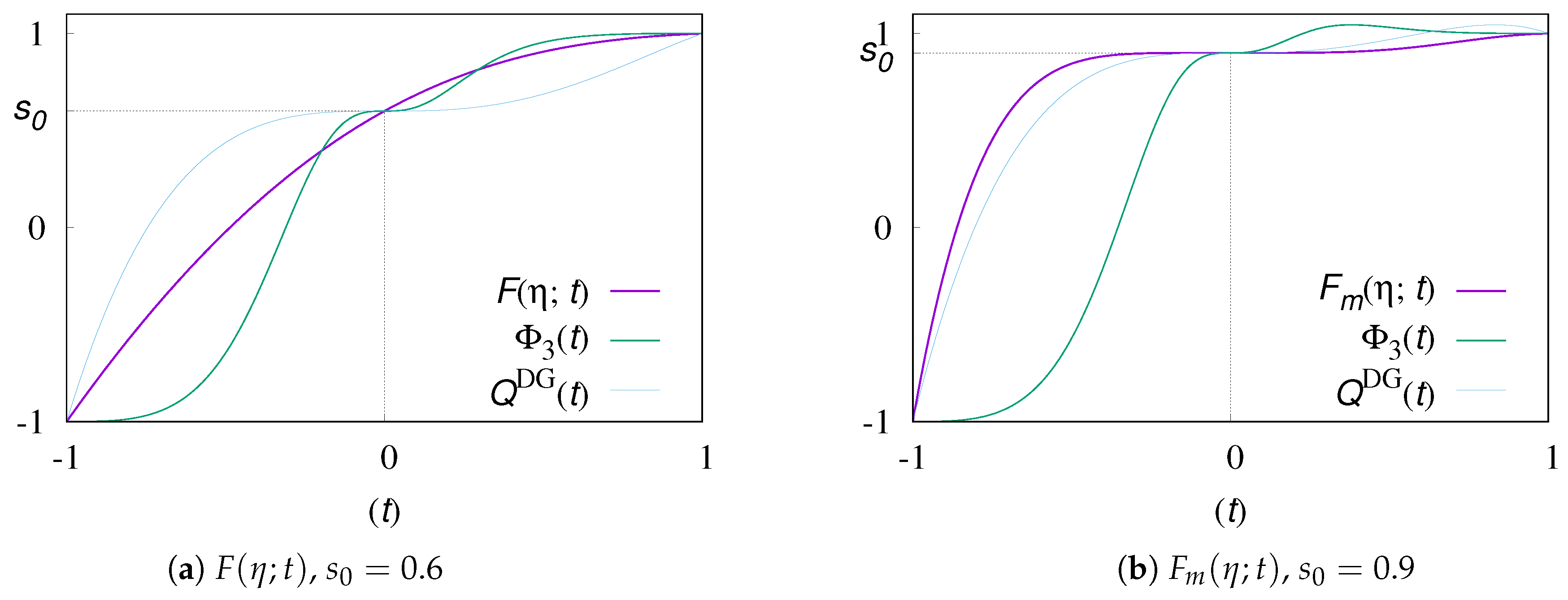
| Existing Transformations | Presented Transformation | |||||
|---|---|---|---|---|---|---|
| 7 | 10 | |||||
| 20 | ||||||
| 30 | ||||||
| 40 | ||||||
| 11 | 10 | |||||
| 20 | ||||||
| 30 | ||||||
| 40 | ||||||
| 15 | 10 | |||||
| 20 | ||||||
| 30 | ||||||
| 40 | ||||||
| Existing Transformations | Presented Transformation | |||||
|---|---|---|---|---|---|---|
| 3 | 10 | |||||
| 20 | ||||||
| 30 | ||||||
| 5 | 10 | |||||
| 20 | ||||||
| 30 | ||||||
| 7 | 10 | |||||
| 20 | ||||||
| 30 | ||||||
| 9 | 10 | |||||
| 20 | ||||||
| 30 | ||||||
| Existing Transformations | Presented Transformation | |||||
|---|---|---|---|---|---|---|
| 3 | 10 | |||||
| 20 | ||||||
| 30 | ||||||
| 5 | 10 | |||||
| 20 | ||||||
| 30 | ||||||
| 7 | 10 | |||||
| 20 | ||||||
| 30 | ||||||
| 9 | 10 | |||||
| 20 | ||||||
| 30 | ||||||
| Existing Transformation | Presented Transformation | |||||
|---|---|---|---|---|---|---|
| 0.2 | 4 | |||||
| 8 | ||||||
| 12 | ||||||
| 16 | ||||||
| 20 | ||||||
| 0.4 | 4 | |||||
| 8 | ||||||
| 12 | ||||||
| 16 | ||||||
| 20 | ||||||
| 0.6 | 4 | |||||
| 8 | ||||||
| 12 | ||||||
| 16 | ||||||
| 20 | ||||||
| Existing Transformation | Presented Transformation | |||||
|---|---|---|---|---|---|---|
| 0.90 | 16 | |||||
| 24 | ||||||
| 32 | ||||||
| 40 | ||||||
| 48 | ||||||
| 0.95 | 16 | |||||
| 24 | ||||||
| 32 | ||||||
| 40 | ||||||
| 48 | ||||||
| 0.99 | 16 | |||||
| 24 | ||||||
| 32 | ||||||
| 40 | ||||||
| 48 | ||||||
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yun, B.I. Rational Transformations for Evaluating Singular Integrals by the Gauss Quadrature Rule. Mathematics 2020, 8, 677. https://doi.org/10.3390/math8050677
Yun BI. Rational Transformations for Evaluating Singular Integrals by the Gauss Quadrature Rule. Mathematics. 2020; 8(5):677. https://doi.org/10.3390/math8050677
Chicago/Turabian StyleYun, Beong In. 2020. "Rational Transformations for Evaluating Singular Integrals by the Gauss Quadrature Rule" Mathematics 8, no. 5: 677. https://doi.org/10.3390/math8050677
APA StyleYun, B. I. (2020). Rational Transformations for Evaluating Singular Integrals by the Gauss Quadrature Rule. Mathematics, 8(5), 677. https://doi.org/10.3390/math8050677




