1. Introduction
In 2015,the United Nations adopted Agenda 2030 [
1], “
a plan of action for people, planet and prosperity”, to reach a better and more sustainable future for all through the achievement of 17 Sustainable Development Goals (SDGs) and 169 associated targets. The European Union (EU) started, at the end of 2016, a strategic approach that contains, as the most relevant actions, the integration of the SDGs into all current European policies. Furthermore, the EU intends to emphasize this strategy from 2020 onwards. While the EU stressed the need for intersectoral and multilateral coordination among member countries, the European Commission undertook to provide regular reports on the progress or setbacks related to the implementation of Agenda 2030. The involvement of the EU to achieve the SDGs seems obvious, bearing in mind that “
the EU has a strong starting position and track record, with a high level of economic development, social cohesion, democratic societies and a commitment to sustainable development, which is firmly anchored in the European Treaties” [
2]. In fact, in 2001, it introduced a first sustainable development initiative that has been maintained and updated to the Europe 2020 Strategy, based on education and innovation (smart), reducing carbon dioxide emissions and combating climate change (sustainable) and with the capacity to create employment and reduce poverty (inclusive).
In particular, the 10th SDG (reduce inequality within and among countries) is an important goal to be studied, since it has key linkages with other goals, such as no poverty (1st), good health and well-being (3rd), quality education (4th), gender equality (5th), decent work and economic growth (8th) and others. Furthermore, it is at the heart of the social and territorial cohesion policies, which are among the main objectives of the functioning of the EU [
3]. The origins of inequality and its consequences are now under intense academic and social debate which addresses either the nature of the capitalism [
4] or the origins of its crisis [
5,
6]. For these reasons, it is interesting to know how inequality evolves in Europe in order to understand its performance, avoid its expansion and propose adequate measures preventing economic and social disorders in a region so committed against inequality as the EU is.
The European Commission, in spite of the EU member states complying largely with the SDGs (all are in the top 50 and at the forefront in objectives such as ending poverty), acknowledges that there are notable differences between and within countries in the achievement of 10th SDG. However, 22.5% of the EU population is at risk of poverty or social exclusion and 6.9% of Europeans suffer severe material deprivation. Similarly, it is stated that although 2017 was the first year in which inequality declined since the onset of the financial crisis in 2007,
“income inequalities remain too large, with a continued concentration of wealth at the top. This has multiple social consequences, leading to differences in well-being and quality of life” [
7]. Then, the inequality analysis and its reduction are at the center of current European motivations since novel challenges such as globalization and technological evolution are affecting and will affect European society in the medium term, according to the context marked by the different accumulation processes of income generated by work and capital today [
8].
Taking into account the above premises, it is clear that reducing inequalities (10th SDG Agenda 2030) is a universal principle that all governments should implement in their policies and particularly, the EU has pushed their members to improve this specific SDG by the adoption and implementation of different policies. However, reducing inequality within and among countries is a complex goal that depends on different aspects. For this reason, it has been addressed from different perspectives and methods such as including additive functions about incomes [
9,
10], applying income distributions to analytical constructs [
11,
12], developing new inequality measures [
13], DEA multi-criteria decision making (MCDM) approach [
14] and using disposable data from a wide range of sources [
8]. Notwithstanding, this contribution introduces a novel approach to measure the evolution of inequalities of EU countries keeping a similar view to [
14] in which a MCDM view is used with the aim of sorting, into prior defined categories, the EU members and then show whether the goals set by the EU are being met by them. This proposal is based on a multi-criteria decision analysis, which deals with the process of taking decisions among a decision maker who evaluate different alternatives on several criteria [
15]. Classically, most of MCDM approaches have been formulated for choice and ranking problems in which it is obtained the best alternative for the decision problem or a ranking of them [
16,
17,
18,
19,
20]. Nevertheless, this contribution focuses on MCDM sorting problems, in which the alternatives are classified into several categories previously defined.
Therefore, this paper aims to evaluate the evolution of inequalities within and between different EU members since 2005 up to 2017. To achieve such goal, we define a MCDM sorting problem, in which the alternatives are represented by EU countries and evaluated by an expert according to six targets/criteria set by Agenda 2030 related to the 10th SDG. Data related to these targets for the different EU members states are periodically published by EU (
https://ec.europa.eu/eurostat/web/sdi/main-tables). Finally, the countries are classified into four different classes, according to their full, moderate, poor and null performance regarding their inequality achievements. To carry out the classification of the countries, we use an Analytic Hierarchy Process (AHP) [
21] approach for sorting MCDM problems so-called AHPSort II [
22].
3. Results
This section shows the evaluation process to classify the EU countries by means of the approach introduced in
Section 2.2.2 and a further detailed analysis of the results.
3.1. Evaluation Process
Starting from the assessments provided by the expert through the questionnaire, the relevant computations regarding AHPSort II and obtained by FLINTSTONES are:
Criteria priority importance: according to AHPSort’s 4th step, the criteria weights are derived from the pairwise comparison matrix between criteria (see
Table 3) provided by the expert by using Equation (
1).
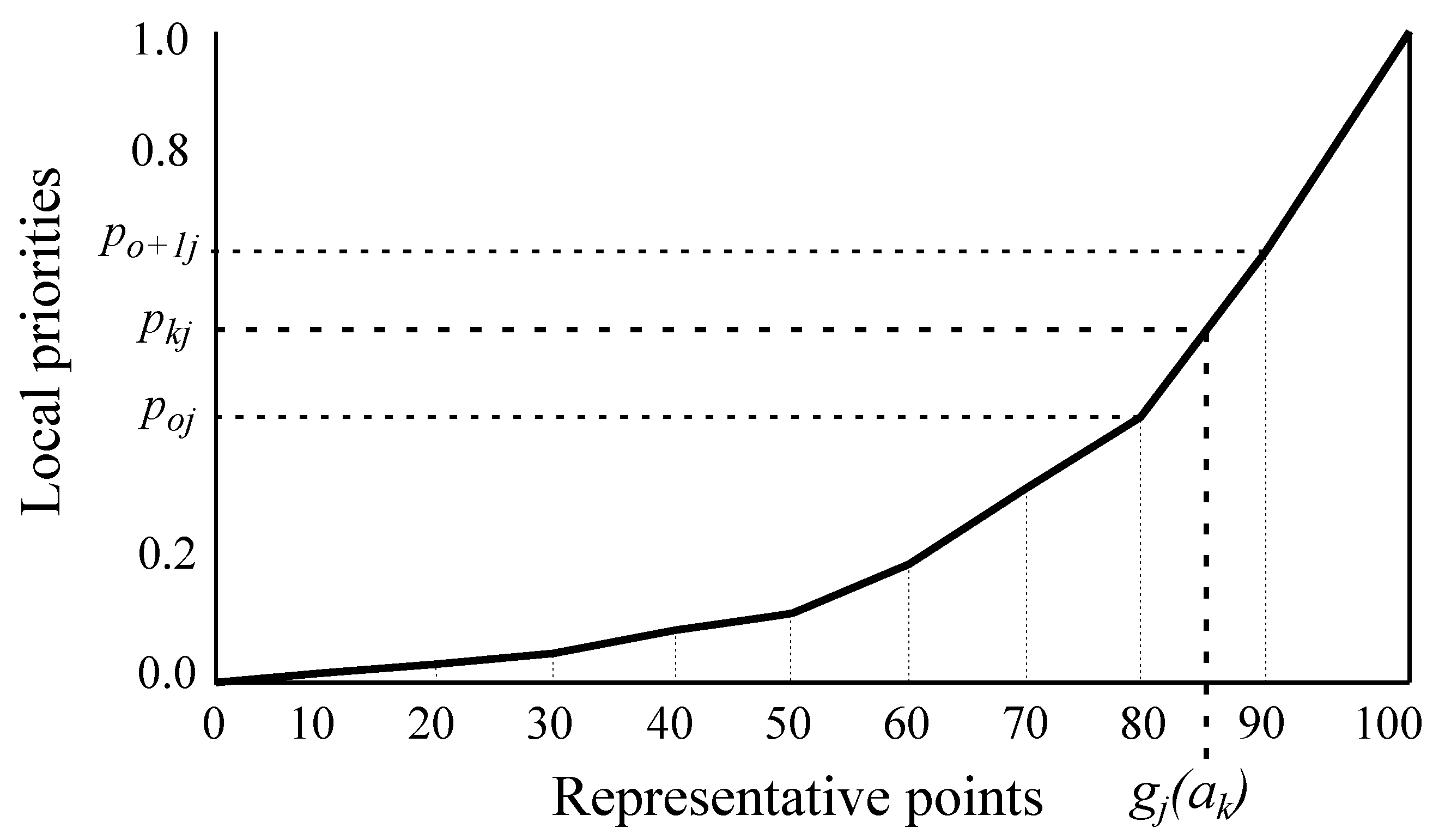
Remark 1. Note that, according to Saaty experiments [28], if the consistency ratio is less than 0.1%, then the matrix is of an acceptable consistency. Local priorities: by applying Equation (
1) to the pairwise comparison matrices between limiting profiles and RPs, the local priorities for both elements are derived. Then, the local priority functions for each criterion are built in order to derive the local priority for each alternative by means of Equation (
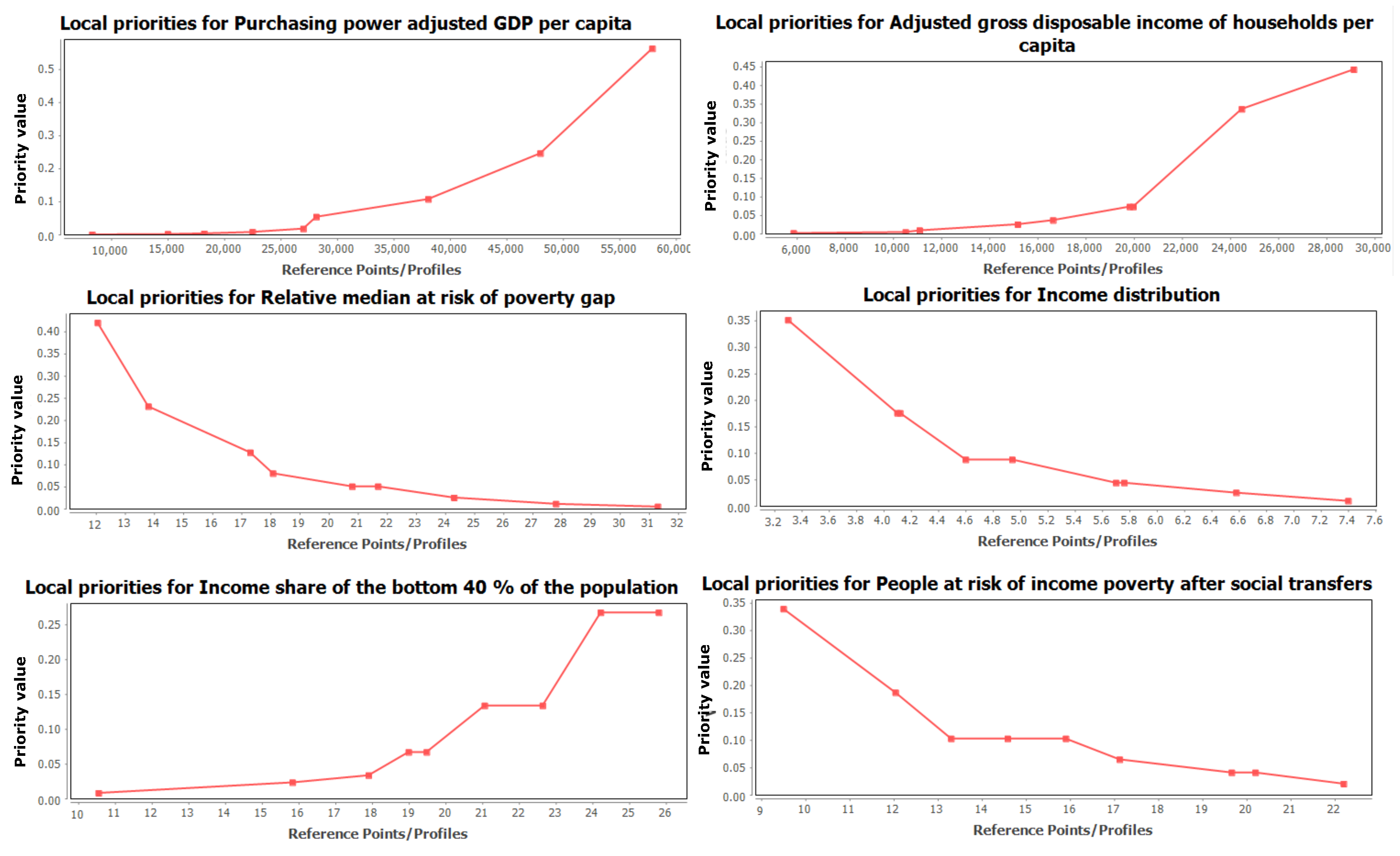
4). For the sake of clarity and taking into account that the process is exactly the same for all the years,
Figure 4 shows the local priority functions for each criterion and
Table 4 and
Table 5 the local priorities of the limiting profiles
and alternatives
for the year 2005, other years priorities are similarly computed but for reasons of clarity and avoid digression, we just show year 2005.
Global priorities: the local priorities are aggregated to obtain the global priorities for the profiles
and alternatives
by Equation (
3) and Equation (
2) respectively (see
Table 4 and
Table 5).
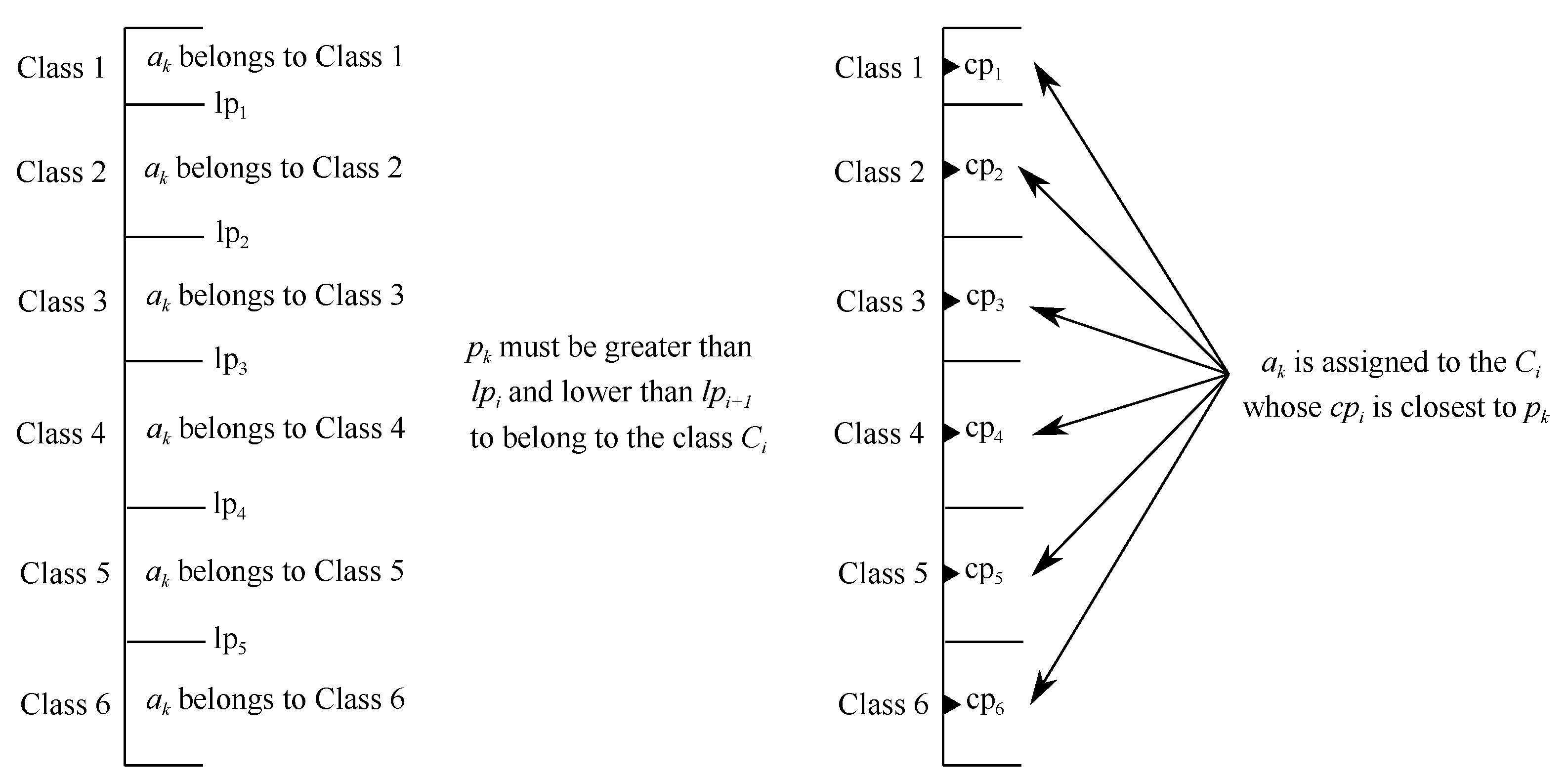
Classify countries: finally, the countries are classified by comparing the global priorities of alternatives and profiles. To show this process, for instance we are going to classify
Spain into a its corresponding class. The global priority for such a country is equal to 0.053, which is compared with the global priorities of the limiting profiles, 0.032, 0.066 and 0.152. Due to we are using limiting profiles, to classify the country in the class
, its global priority must be greater than
and lower than
. In this case, 0.032 < 0.053 < 0.066 thus, Spain is classified into the category
Poor. The rest of classifications for each year are represented in
Table 6 and
Table 7 in
Section 3.2.
3.2. Analysis of the Results
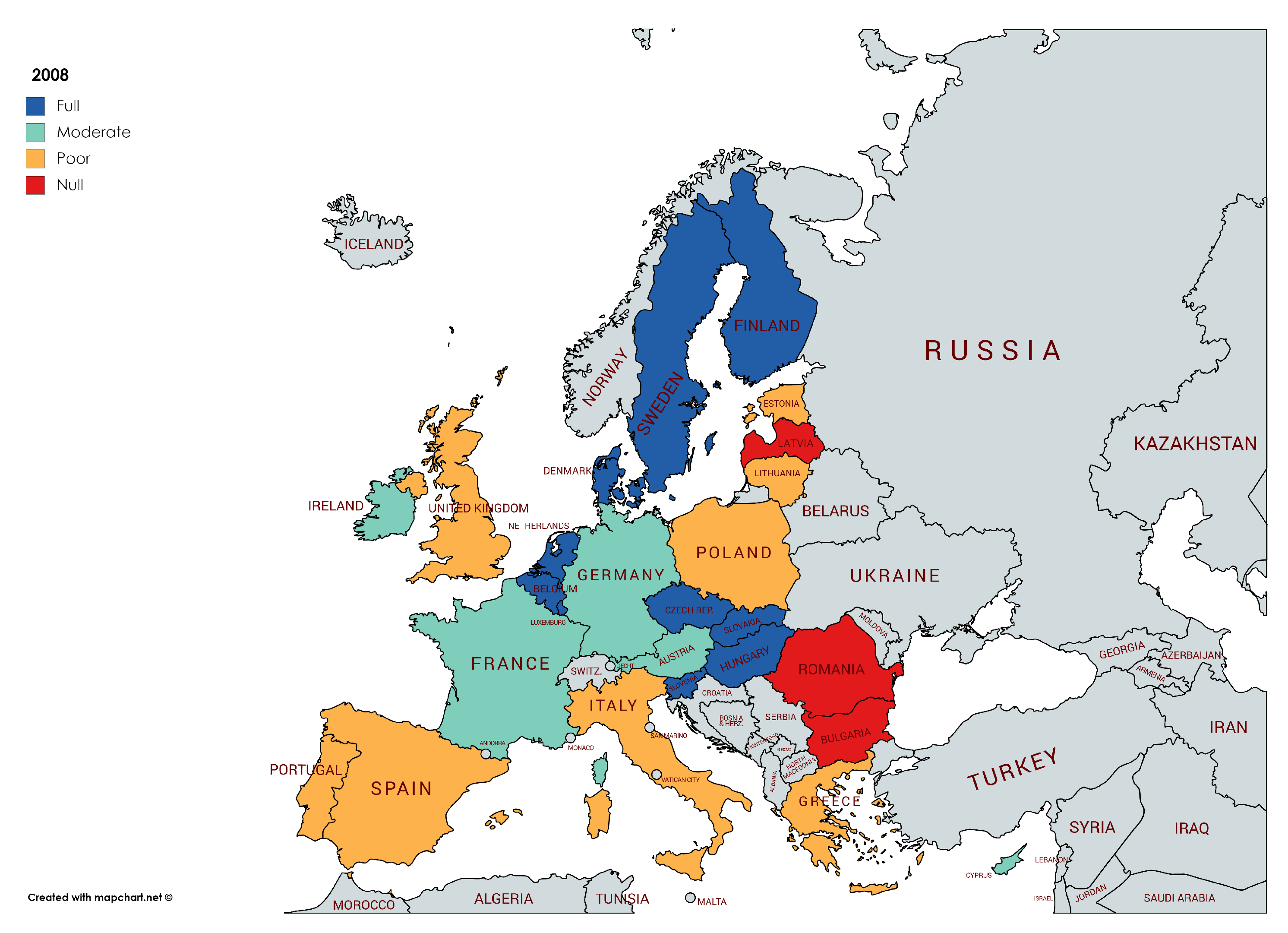
The starting point of this analysis is the year 2005 (see
Figure 5), in full phase of economic expansion. The countries that achieve the objective of reducing inequalities, according to the AHPSort II method, are shown in blue color. They are concentrated in northern and central Europe: the Nordic countries, Netherlands, France, Belgium, Germany and Austria, which have important social protection systems with a long tradition. Similarly, some of the countries that have recently joined the European Union such as Czech R., Slovakia, Hungary and Slovenia, which have benefited from their inclusion in the global production chains of large German industrial companies since the beginning of the century [
29,
30,
31], favoring the increasing complexity of their economies.
In the European periphery, the south: Spain, Italy and Greece together with the United Kingdom and Estonia present a poor reduction of inequalities. The South has great internal territorial inequalities, especially serious in the case of Italy. Noted that the liberal policies applied in the previous decade in United Kingdom have favored inequality in the expansive phase, as has also happened in Spain. Portugal and Poland, along with the Baltic republics and Romania, are the cases where the achievement of the objective of reducing inequalities is less advanced. The processes of low growth together with an inadequate institutional structure for the Portuguese case [
32], or a slow transformation towards a market economy for the Eastern European countries, justify this scarce advance, which evidences a concentration of growth in social groups that capture a greater part of the benefits that are distributed in the European project [
33].
With the exception of Ireland, Cyprus and Bulgaria, which are moderate in terms of the reduction of inequalities, we can undertake the analysis of the results from this starting situation with three large groups of countries: those that reach the objective, those that have a poor attainment and those that fail in the reduction of inequalities.
The period of expansion of the world economy ends in 2007, when the international financial crisis becomes apparent. The situation of the reduction of inequalities in Europe at that time is shown in
Figure 6.
The financial crisis is hitting the European economy harshly, especially the great industrial powers of France and Germany, which are reducing their achievements on an equal footing, as well as Austria. However, the countries of the East, such as Poland and Lithuania, improve their position because of the income distribution effect that European funds are beginning to exert. On the contrary, Bulgaria, with the recent integration into the EU, worsens its performance about reducing inequalities by increasing its exposure to the market economy.
On the other hand, Portugal and Ireland are making slight progresses (see
Table 6) in their fight against inequality. As a consequence of the effects that the economic recession has in these countries on the distribution of the income of capital owners in the case of Ireland [
34] and the improvement of the living conditions of lower-income workers because of economic expansion in Portugal [
35].
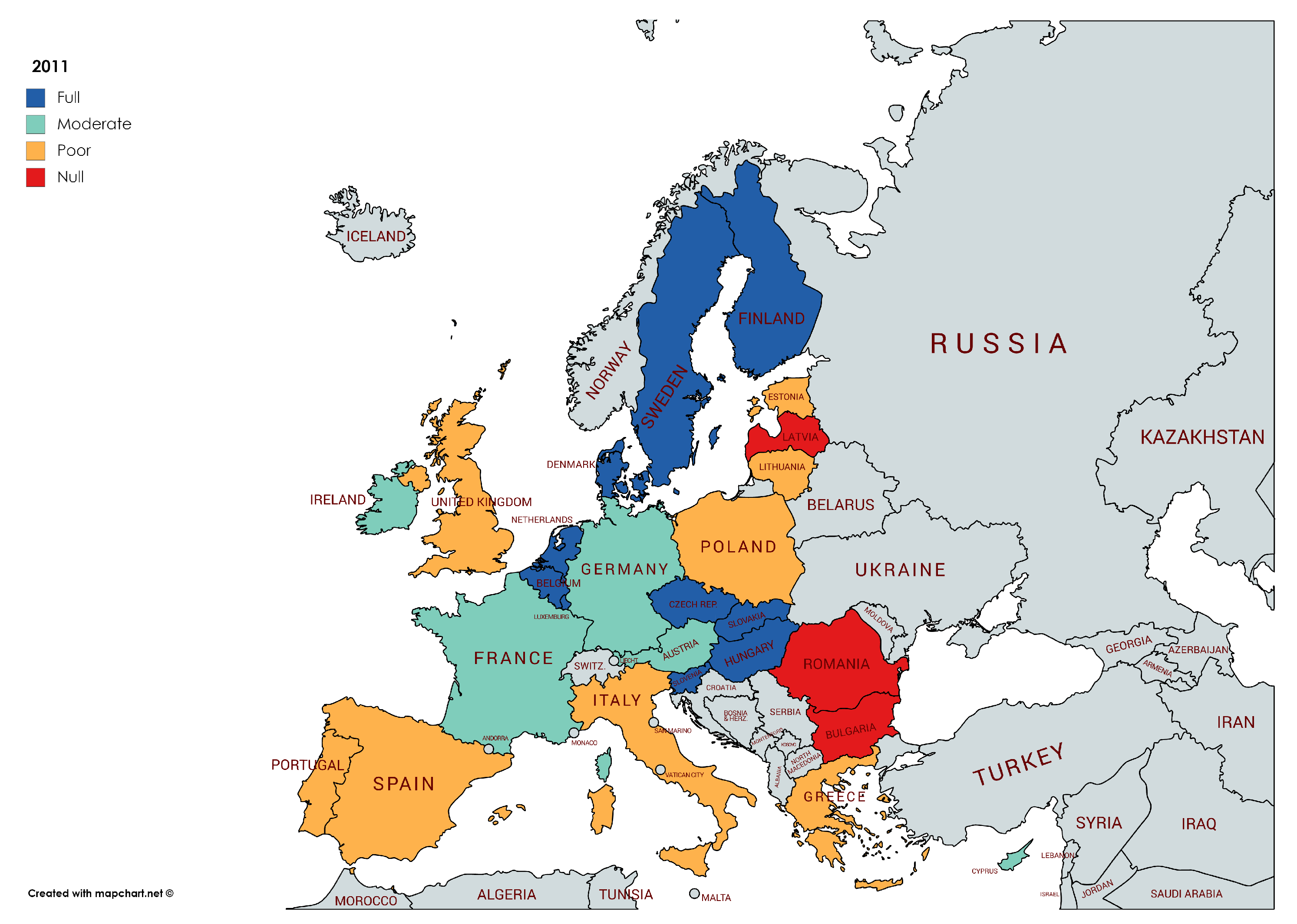
Crisis effects are more visible from 2008 on.
Figure 7 shows the situation in Europe in the hardest moment of the financial crisis, when countries were most concerned about their consequences on the very common currency project. However, despite the negative impacts on GDP in 2010, causing recession in all the countries in Europe and expanding it on Portugal and Spain till 2011 [
36], the categories for reducing inequality remain stable in 2011. This result suggests that inequality is not linked with growth in the short-term.
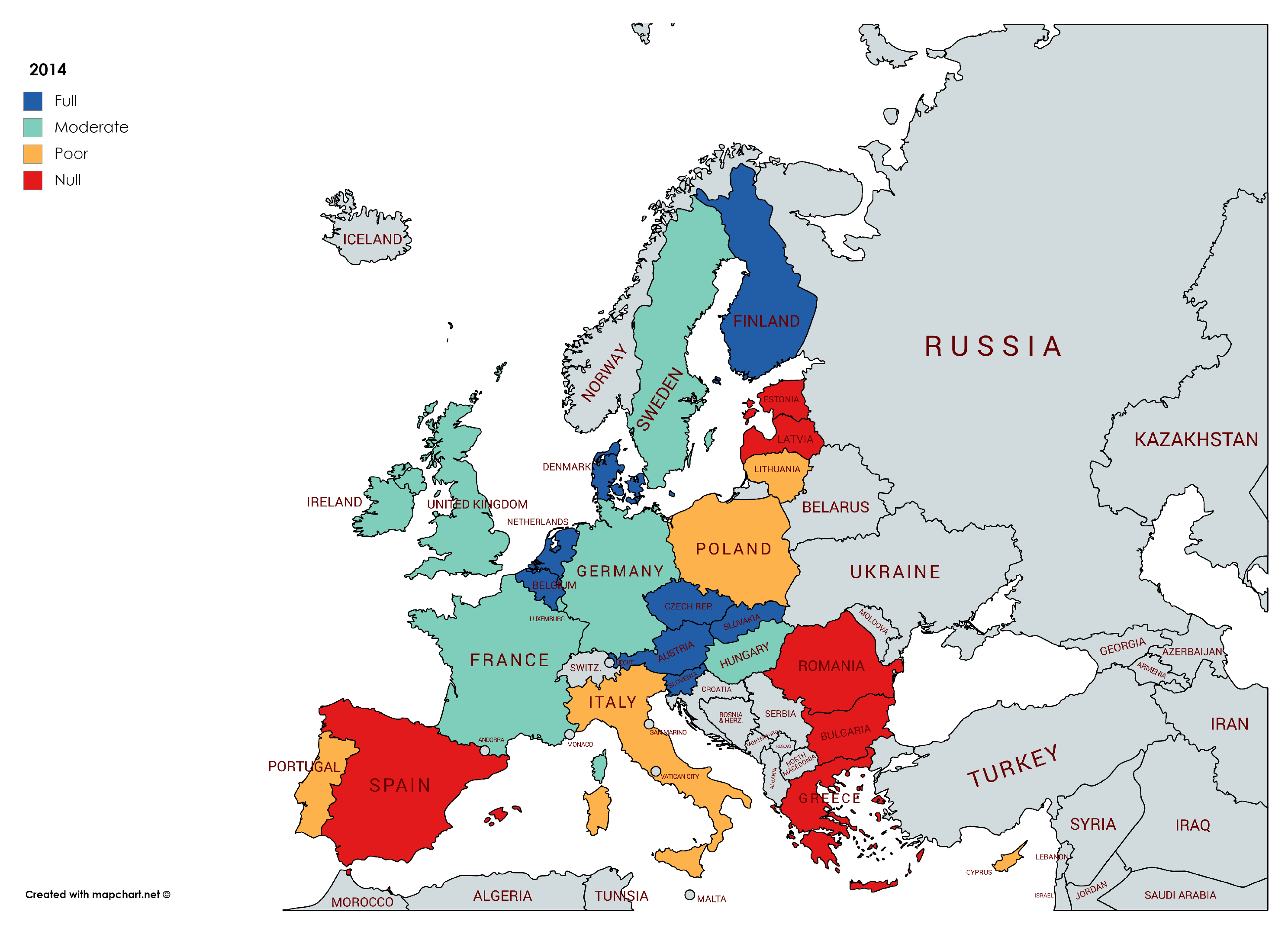
Inequality increases sharply in Europe between 2011 and 2014 due to the implementation of restrictive policies because of the idea that South countries should be more austere, committing themselves for reducing public budgets disequilibrium. However, the consequences of the austerity policies had a great impact in public employment, employment active policies and social services, producing harmful consequences on inequality across Europe [
37,
38,
39] (see
Figure 8).
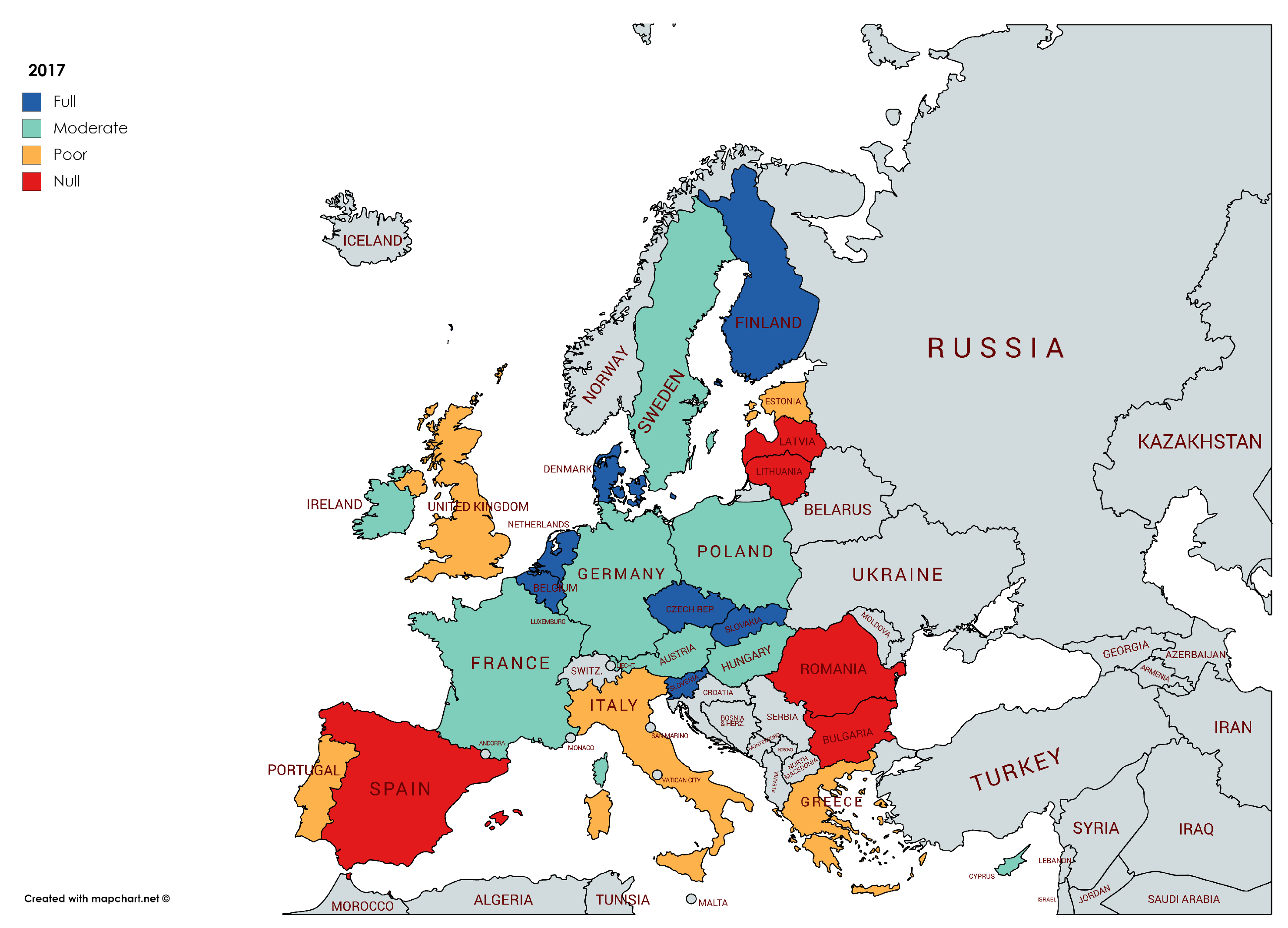
In the recovery phase, 2014–2017 the general situation in Europe does not change (see
Figure 9). Inequality has even increased in Lithuania, Austria and United Kingdom, while has been reduced in Greece, Poland and Estonia, the rest of the countries keep their level of achieving the goal. If we compare the final situation in 2017 with the initial in 2005, the progress in order to reach the SDG 10th goal is negative. Peripheries do not have achieved the goal at all or have had a poor progression, but the core of Europe, that achieved fully the goal in 2005, now presents a moderate path. Then, results (see
Table 7) show a regression for Europe in reaching reduced inequalities within and among countries.
The most successful countries in achieving 10th SDG during this period are Belgium, The Netherlands, Czech R., Slovenia, Slovakia, Denmark, and Finland. Poland is the country with a better progression in pursuing the goal. Is there something in common within these countries? Could we extract some policy recommendations for the less successful countries and Europe as a whole? These questions will be answered in discussion section.
3.3. Sensitive Analysis
This research presents a sorting MCDM approach whose results depend on the criteria weights. Therefore, a variation of such weights may affect to the results. Usually, a sensitive analysis is carried out in order to identify the possible changes in the ranking order of the alternatives when the criteria importance is modified. However, in our sorting approach, it is not so important the changes of the ranking as the changes in the countries classification, since one specific country may vary its position in the ranking but not its classification. For this reason, this section introduces a sensitive analysis in which we identify the minimum change needed in the weight of each criterion to make modifications in the ranking and we analyze if such new values provoke changes in the countries classification. The minimal changes applied to the weight of each criterion that provoke exchanges in the ranking and the resulting new weights for the rest of the criteria in the year 2005 are represented in
Table 8.
Remark 2. Note that, if and are the original weight and the new weight obtained from the minimal change for the criterion respectively, the inferred weight for the criterion is computed as .
The minimal changes obtained for each criterion are computed by FLINTSTONES by following the
most critical criterion approach [
40], which consists of modifying the current weight of a specific criterion and identifying the minimal modification of the value of such weight that provokes a change of position in the ranking of the alternatives. Therefore, to identify the minimal change, FLINTSTONES fixes a specific weight value for the analyzed criterion (from 0.001 to 1 in increments of 0.001) and computes the weights of the rest of the criteria (see Remark 2). With the new weights, FLINTSTONES derives the global priorities of the alternatives and profiles according to the AHPSort II method’s steps and obtains the new ranking and classification. To clarify this process,
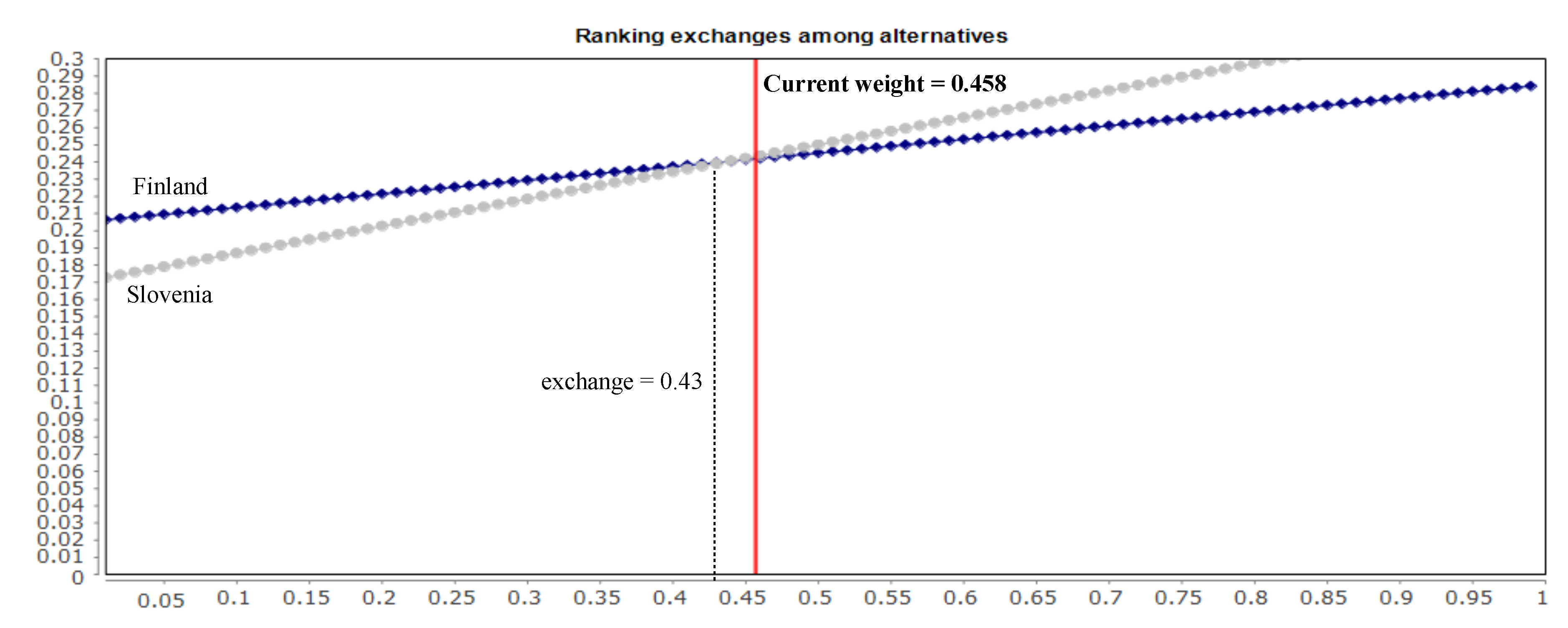
Figure 10 shows the minimal change derived from the criterion
. The X-axis in the plot represents the new weight for the analyzed criterion and the Y-axis the global priority of the alternatives regarding such weight. When the lines intersect means that there is a exchange of position among the alternatives for that weight. In
Figure 10 we can appreciate that the minimal change in
happens between the alternatives Slovenia and Finland when its weight is equal to 0.43, as it is shown in
Table 8. The minimal changes of the rest of the criteria are derived in a similar way.
Remark 3. Note that, for the sake of clarity, Figure 10 shows only the alternatives related to the minimal change for the criterion , but FLINTSTONES derives the global priorities for each new value of its weight for all the alternatives. From the minimal changes, we carry out again the classification process by using FLINTSTONES and AHPSort II in order to check if countries classification is different with the new weights.
Table 9 shows the ranking and classification of the countries in the year 2005 obtained by using the new criteria weights and we can appreciate that, despite the fact that there are changes in the ranking of the countries in terms of overall ranking and even between criteria, their classification remains the same.
Remark 4. Similar results are obtained for the years 2008, 2011, 2014 and 2017, thus they are omitted here.
4. Discussion
The most performer countries regarding to inequalities have in common some structural characteristics in their economies and institutional systems. On the one hand, all of them have a very complex economic system connected with global value chains. This framework brings about a high level of employment, high levels of women participation in the labor market and low levels of unemployment. On the other hand, their institutional system is complex and focused in permitting equal opportunities. Some of them have a very deep welfare state, which is the case of Belgium, Finland or Denmark, with a high level of protection for unemployed and people at risk of exclusion. Homogeneous societies could be a main characteristic, given the reduced size of the countries achieving the goal.
On the other side, there are countries less connected with global economy, such as Bulgaria or Romania, and the South of Europe, with a less complex production system than the North, and a not enough developed social protection system, which has provoked an intense impact of the financial crisis in the poorest. In cases such as Italy, for instance, the inequality is not due to an increase in the income of richest but a reduction in the income of poorest [
41].
Hence, we could remark two dynamics conditioning the path towards reaching the 10th SDG. The first one is in the microeconomic area: globalization process, technological change and institutional transformations in labor market affecting work flexibilization and bargaining [
42,
43,
44,
45]. The second one is macroeconomic: the push fullness of liberal ideas over social-democrat ones in Europe [
4] have brought about a reduction in fiscal progressive policies, giving rise to an increasing process of inequality in a medium and long term [
12].
Nowadays, inequality is not reduced only for the sake of growth, as the inverted U model proposed by [
46]. The economic structures of the current world have changed dramatically since then. Income inequality within a country is the result of mechanisms involving labor markets, and multinational companies exert an important influence on wage disparities, due to their territorial strategies to make the most of globalization processes [
47]. In this line, microeconomics and macroeconomics effects reinforce each other their influence on raising inequalities, since the capacity for unions to bargain has been reduced because of the dynamics of international outsourcing and offshoring.
The effects of globalization are tougher when regional and national economies are simpler. Ref. [
48] demonstrate that countries exporting more complex products tend to have lower levels of income inequality than countries exporting simple products. The microeconomics sphere matters in order to prevent inequality to rise.
However, technological change is conditioning the traditional trade-off between labor and capital in favor of the second. More importantly, in the coming years artificial intelligence could alter the structure of basic occupations, which will be an important challenge to face in order of achieving the 10th SDG.
In sum, three dynamics could be identified in the labor market contributing to inequality:
Precariousness in the access of youths to labor market [
43].
Reduced bargaining power of unions [
45].
Outsourcing of more intense labor tasks [
42] and, as a consequence, the emergence of false freelances [
44].
In the macroeconomics sphere is important to bear in mind the effects of elites in the design of economic policies. [
33] aim that some social groups push for defining policy priorities in their favor. These commitments give rise to fiscal structures seeking capture rents at expense of general interest [
49,
50,
51].
In Europe, national institutional frameworks are very different. This could be an explanation of persisting inequalities in the long term throughout Europe [
52]. As a matter of fact, besides having a strong welfare state consisting in opportunities to find good jobs and the access to good public education and health systems, three social innovation dynamics could be identified for the inequality reduction, which have been more clearly implemented in countries better achieving the goal:
Dynamics of sharing value between external firms and local societies [
53], consisting in developing strategic local linkages for multinational companies to better compete in global value chains, instead of extracting local natural resources and using low value added human resources.
Some countries with a good structure of social economy, helping small entrepreneurs to reach an international capacity to compete in a global market, are in the group with full performance [
54].
A strategic participation of workers in the decision process of big companies, which opens empowering capacities for employees to obtain better rewards for their work [
55].
The institutional disparity has contributed to reduce the offsetting effects of national policies in presence of increasing inequalities process, especially in the South of Europe, whose countries have seen how austerity policies prevented compensate the social impacts of financial crisis [
47]. Tendencies were worst because in Central European countries, in addition to a wider welfare state and the behavior of automatic stabilizers, there was a most reduced private indebtedness, all of which contributed to increase inequality among countries.
The most important problem derived from inequality is its capacity to pass on through generations, linked to the inequality of opportunities. Inclusive institutions should be developed in order to break this tendency, but political agendas, economic interests and regressive laws limit social mobility [
56]. In fact, there is a strong influence of social and family networks in the scope of education and equality of opportunities, determining social mobility processes and their consequences on inequality [
47].
Inequality is a consequence of microeconomic and macroeconomic processes, but it is also an origin of problems [
57], such as polarization of societies, putting at risk social cohesion and security, and territorial disparities, since metropolitan regions record on average higher levels of standard of living than other regions [
58,
59].
Nevertheless, a certain level of inequality could incentive economic development, such as the cases of countries achieving 10th SDG in Europe. They are not equal societies at all, but they are far from countries with null or poor performance in reducing inequalities. The idea that European policy makers should take into account is that increasing inequality above moderate levels may cut aggregate demand and thereby European economic growth, making a vicious circle of rising inequality and slower growth [
60].
5. Conclusions
The consequences of a concentration of income have been demonstrated on long-term growth [
61], and the role of institutions and technical change [
62,
63]. Therefore, it seems logical the importance of measuring the evolution of inequalities in EU countries and evaluating the achievements reached by them according to Agenda 2030. This contribution presents a new approach to achieve such aim, in which the MCDM method AHPSort II is used to classify the EU countries into different categories according to their fulfillment of 10th SDG. The classification has been carried out in different time intervals, 2005, 2008, 2011, 2014 and 2017 and it has allowed obtaining very interesting conclusions.
The EU is concerned about inequality, which is gaining momentum in the policy debate, but there is much effort to do it for achieving 10th SDG in the coming years [
64]. Social transfers are important to reduce inequality, protecting the most vulnerable and fostering economies to recover from crisis. Nevertheless, the first important idea to bear in mind is that the only relevant policy for fighting against inequality is not the redistributive one. It is necessary to act in the microeconomic sphere, since inequality has microeconomic origins too. Labor markets, innovation, education and social integration are important fields to implement new policies in order to reduce inequalities in Europe.
Labor markets policies making effective bargaining processes between workers and companies, facilitating rewarding salaries and conditions, such as minimum wages guaranteeing the standard of living in each country. Besides, social benefits in order to conciliate family and work spheres are in the core of improving microeconomic policies for reducing inequalities [
65].
Innovation policies should be in the center of a seemingly new generation of industrial policies in a new context of world competition, where countries are incorporating general discontent for globalization consequences on inequalities. For Europe, a wider place-based strategy for reducing inequality and territorial disparities should be generally implemented [
66], following the model of Germany and United Kingdom in Europe, but also Japan and USA, who have been pursuing competitive industrial policies for decades [
67].
Education policies are key tools in the long term. State investments in education may alter the supply of skilled workers changing the wage schemes in the labor market. The experience has demonstrated that countries having spent more on education tend to have not only better skilled worker but higher educational mobility as well. Actually, social mobility is one of the elements Europe needs to reduce inequality in a medium term, and education policies and mechanisms to facilitate the transitions from schools to work are fundamental pieces for reducing the risk of increasing inequalities in Europe [
68].
Austerity policies have led southern countries in Europe to a race to the bottom, which has widened social and territorial inequalities within and among countries. In order to achieve the 10th SDG a change in the policy mixed is needed to include social integration objectives. However, progressive fiscal policies face opposition of social elites who struggle for keeping their advantages for them and for their off-springs. Macroeconomic policies in tax designs should be applied to revert the inequality process in countries with a poor or null performance.
In sum, on the one hand, microeconomics actions should be attended. Developing companies’ networks, regional innovation systems, sectorial institutions and improving the level of social and economic structures are important. All this elements push territorial development processes in Europe and they are important pillars to fight against inequalities [
69]. Furthermore, the latter contribute to extend the opportunities for choosing occupations and improving skills, preventing increasing inequalities from now on.
On the other hand, the future demands policy actions in the macroeconomics sphere. In the coming years a great expansion of national budgets are going to be needed in order to attend the ageing process of European society. The needs must be matched but it is responsibility of Europe to do it in a more integrated society or in a more unequal one. Social innovation policies must be implemented with the coordination of different tiers of government if Europe wants to consolidate 10th SDG. Guaranteeing equal opportunities in the access to education, health and social protection systems is compulsory for European societies. And it is important not only for the sake of reducing inequalities but also for the sake of growth processes, since they could be burdened due to the loss of potential human resources in fostering social and technical innovation in the future Europe.