1. Introduction
In the field of Reliability Engineering, considerable research activity has been steered towards the investigation of operating features of consecutive-type structures, due to their applications in the optimization of telecommunication networks, complex infrared detecting systems, oil pipeline systems, vacuum systems in accelerators, and spacecraft relay stations.
Generally speaking, a consecutive-out-of-
n:
F system consisting of
n linearly ordered units (or components), fails if and only if at least
k consecutive ones fail (see, e.g., [
1] or [
2]). Several reliability studies related to these structures have been recently accomplished, and some generalizations and extensions have been also proposed for delivering more moldable features. As a paradigm, we mention the
r-within-consecutive
k-out-of-
n:
F system (
), which was established in [
3]. The particular structure fails if and only if there exist
k consecutive components that include among them at least
r failed components (see also [
4] or [
5]).
Furthermore, a variety of additional extensions of the traditional consecutive-
k-out-of-
n:
F system has appeared in the literature during the last three decades and studied in detail. These extended versions of the well-known consecutive-
k-out-of-
n:
F structure activate more complicated failure criteria in order to cover a larger range of applications and exhibit better performance. Among others, the interested reader is referred to the
m-consecutive-
k-out-of-
n:
F system (
) (see, e.g., [
6] or [
7]), the sparsely connected consecutive-
k systems ([
8] or [
9]), the
m-consecutive-
k-out-of-
n:F-r-S-interrupted systems ([
10]), and the
m-consecutive-
k,
l-out-of-
n systems ([
11]).
In addition, the reliability structures, which involve two common failure criteria, have attracted significant research interest in the literature. For instance, the
system established in [
12], was also studied in [
13] via a Markov chain approach, while some interesting reliability attributes and applications of it were investigated in [
14,
15]. Further extensions of
structures have been proposed; a reliability system which looks after two different failure criteria was also provided in [
16]. More precisely, the abovementioned structure combines the well-known
f-out-of-
n:
G and the classical consecutive-
k-out-of-
n:
G structure. Moreover, an innovative scheme based on a
m-consecutive
k-out-of-
n:
F and a consecutive-
-out-of-
n:
F system was proposed in [
17], the so-called constrained (
k,
d)-out-of-
n:
F system was established in [
18] (see, also [
19]), while the
structure involving
N modules with the
i-th module consisting of
ni units in parallel was introduced in [
20] (see, also [
21]). Moreover, the so-called
structure, which operates under two common failure criteria, was studied in [
22]. The particular system contains
n components and fails if and only if there exist at least
f failed components and at least
k consecutive failed components (see also [
23]).
For a detailed and up-to-date survey on the consecutive-
k-out-of-
n:
F systems and their generalizations, we suggest the detailed review papers [
24,
25] or [
26] and the well-written monographs [
27,
28]. A survey of reliability approaches in various fields of engineering and physical sciences is provided in [
29].
In this manuscript, we conduct a reliability study of the consecutive-
k1 and
k2-out-of-
n structures introduced in [
30] which operate under two common failure criteria. The consecutive-
k1 and
k2-out-of-
n structure contains
n components in a line and fails if and only if there exist at least non-overlapping consecutive
k1 failed components and consecutive
k2 failed components. The main motivation of the present paper is to deliver the generating function of the reliability for the linear consecutive
k1 and
k2-out-of-
n system. The aforementioned result has not appeared in the literature to date and is now offered by Proposition 1 of the present manuscript. It is clear that the results provided in [
30] do not overlap with the theoretical results proved in the present manuscript. To be more articulate, the outcomes given in [
30] are complementary (rather than competitive) to those established in the present manuscript.
Delivering the generating function of a structure’s reliability calls for several algebraic manipulations and consequently seems to be of some theoretical/mathematical interest. However, having at hand the generating function of the consecutive k1 and k2-out-of-n reliability system gives us the opportunity to develop recursive schemes for computing some important reliability characteristics of the underlying structure. Indeed, Propositions 2 and 3 of the present manuscript offer innovative recurrences for determining the reliability polynomial and the signature vector of the linear consecutive k1 and k2-out-of-n reliability system.
In
Section 2, we derive the generating function of the consecutive-
k1 and
k2-out-of-
n system with independent and identically distributed components ordered in a line, while recurrence relations for determining its reliability function and its signature vector are introduced and proved in
Section 3. For illustration purposes, some numerical results and figures are constructed and several concluding remarks are stated.
2. The Generating Function of the Consecutive-k1 and k2-out-of-n Systems
In this section, we study the linear consecutive-
k1 and
k2-out-of-
n structure, where
. More specifically, we employ a generating function approach in order to investigate some reliability characteristics of the linear consecutive-
k1 and
k2-out-of-
n structure. To achieve that, the Markov chain methodology established in [
31] is implemented (see, also [
32] or [
33]) and an explicit expression for determining the generating function of the reliability function of the linear consecutive-
k1 and
k2-out-of-
n structure with independent and identically distributed (
i.i.d. hereafter) components is derived.
Let us first point out the necessary methodological background, which will be proved useful for the study of the consecutive-
k1 and
k2-out-of-
n structure. We first assume that
,
corresponds to the reliability function of an imbeddable in a Markov chain structure consisting of
n components. It is evident that the general form for evaluating the reliability function
of the abovementioned system is given as
where
is the transition probability matrix related to the system and
In addition, if
corresponds to the generating function of the sequence
, then
could be expressed as
where
denotes the
element of the adjoint of matrix
. Consequently, should one be able to evaluate the last entry of the first row of the matrix
, the generating function of the reliability function of the corresponding system can be deduced after some algebraic maneuvering.
Let us next denote by
T the lifetime of a reliability system with
n components and
its components’ lifetimes. If we assume that
are independent and identically distributed, the signature of the system is defined as the probability vector
with
where
denote the respective order statistics of the random sample
. Since the system fails upon the failure of one of its components, it is clear enough that the lifetime
T coincides to the corresponding ordered lifetime of this particular fatal component. Consequently, the coordinate
depicts the probability that the system fails when its
i-th ordered component fails.
Generally speaking, the signature vector of a reliability structure has evolved as a crucial performance metric for appraising the behavior of coherent structures. Furthermore, the signature vector seems to be able to bolster the evaluation of reliability polynomial and several stochastic comparisons among systems’ lifetimes (see, e.g., [
34] or [
35]). For some recent advances on the evaluation of the signature vector of a reliability structure, one may refer to [
36], [
37] or [
38].
Applying Equation (1) and taking into account the Markov chain representation of the linear consecutive-
k1 and
k2-out-of-
n system proposed in [
30], we may determine the reliability function
,
of the consecutive-
k1 and
k2-out-of-
n structure, where
. It is evident that the outcomes given in [
30] are complementary (rather than competitive) to the ones established in the present manuscript. For example, Proposition 1 provides an explicit expression for determining the generating function
of the sequence
, while the authors in [
30] offered only the necessary blocked form of the transition probability matrix of the underlying structure.
It is worth mentioning that the below-mentioned result, which calls for several complex algebraic operations, seems to be the main theoretical outcome of the present manuscript, since it supports the proof of the remaining propositions and consequently all numerical or figurative illustrations displayed later.
Proposition 1. The generating function of the reliability function of the linear consecutive-k1 and k2-out-of-n () structure with i.i.d. components can be determined aswherecorrespond to the common reliability and unreliability of the components while Proof. Taking advantage of the blocked form of the transition probability matrix
Λ of the linear consecutive-
k1 and
k2-out-of-
n structure proposed in [
30], we may write
where
denotes the order of matrix Λ. The
element of the adjoint of the matrix
is given by
where
corresponds to the minor determinant which is deduced by deleting the last row and the first column of the square matrix
. More precisely, the determinant
takes on the following form:
We next expand the above determinant according to the elements of its first row and we repeat the same expansion
k1 times successively. We then conclude that
may we rewritten as
where
By expanding the above determinant through the items of its
column, we get
where
We then substitute the above expressions for the sub-determinants
in Equation (6) and the following ensues:
or equivalently:
Combining Equations (2), (5), and (7), the desired expression required for determining the generating function of the reliability function of the linear consecutive-k1 and k2-out-of-n () system is readily deduced. □
It is true that delivering the generating function of a structure’s reliability calls for several algebraic manipulations and consequently seems to be of some theoretical or mathematical interest. However, having at hand the generating function of the consecutive-k1 and k2-out-of-n reliability system gives us the opportunity to develop recursive schemes for computing some important reliability characteristics of the underlying structure. Indeed, Propositions 2 and 3, which appear in the next section, offer innovative recurrences for determining the reliability polynomial and the signature vector of the linear consecutive-k1 and k2-out-of-n reliability system. Based on these recursive schemes, several numerical results for specific values of the design parameters k1, k2, n could be produced for providing an illuminating impression about how the theoretical results of the manuscript could be proved useful in practice.
3. Recurrence Relations for the Reliability Function and the Signature Vector of the Consecutive-k1 and k2-out-of-n Systems
We next focus on two important performance characteristics of the linear consecutive-
k1 and
k2-out-of-
n (
) structure consisting of
i.i.d. components. More precisely, we exploit the general result proved in
Section 2 in order to establish recurrence relations not only for evaluating the reliability function of the underlying system but also for determining the coordinates of the respective signature vector.
The following proposition provides a recursive scheme in terms of the design parameter n for determining the reliability function of the linear consecutive-k1 and k2-out-of-n () structure.
Proposition 2. The reliability functionof the linear consecutive-k1 and k2-out-of-n structure ()
consisting of i.i.d. components serves the next recurrence Proof. Recalling formula (3) we may write
We next observe that the maximum power exponent on the right-hand side of the above relation equals
. Consequently, taking into account that the coefficients of
on the left-hand side should not appear for
, the above equality can be rewritten as
We next collect together the reliability terms having the same low index and the outcome we are looking for is readily deduced by applying some simple algebraic operations. □
In order to apply the recurrence for determining the reliability function of the linear consecutive-
k1 and
k2-out-of-
n structure (
) provided in Equation (8), a suitable set of initial conditions is needed. Please note that the initial conditions that follow are algebraically necessary for implying the proposed recursive scheme. However, these initial cases correspond to reliability structures without any practical interest in real applications. For example, if the total number of components is no greater than the parameter
, then we readily deduce that the resulting structure never fails. In other words, it is evident that if
, then at least one of the failure criteria of the linear consecutive-
k1 and
k2-out-of-
n structure cannot be fulfilled. This means that, given that
, the reliability function of the linear consecutive-
k1 and
k2-out-of-
n system is equal to 1. Finally, if the parameter
n equals
k2, then the underlying structure behaves actually as the traditional parallel system. One may easily deduce that the latter cases mentioned above could not be discussed as existing structures, and that we need their reliability in order to run the proposed recurrence. The sufficient group for setting forth the recursive relation in (8) is given as
Apart from the abovementioned conditions, if additional calculations are needed for running the recurrence, then these computations could be covered by the aid of the traditional definition of the signature vector of a coherent system with independent and identically distributed components (see, e.g., [
34]).
We next apply Proposition 2 in order to determine the reliability polynomial of the linear consecutive-
k1 and
k2-out-of-
n system for specific designs.
Table 1 displays the corresponding results of the linear consecutive-
k1 and
k2-out-of-
n structures for different values of their design parameters.
By casting a glance at the abovementioned results, one may deduce some interesting conclusions about the reliability function of the underlying structure. Based on
Table 1, we next construct several figures, in order to reveal the impact of the design parameters
on the reliability behavior of the linear consecutive-
k1 and
k2-out-of-
n system.
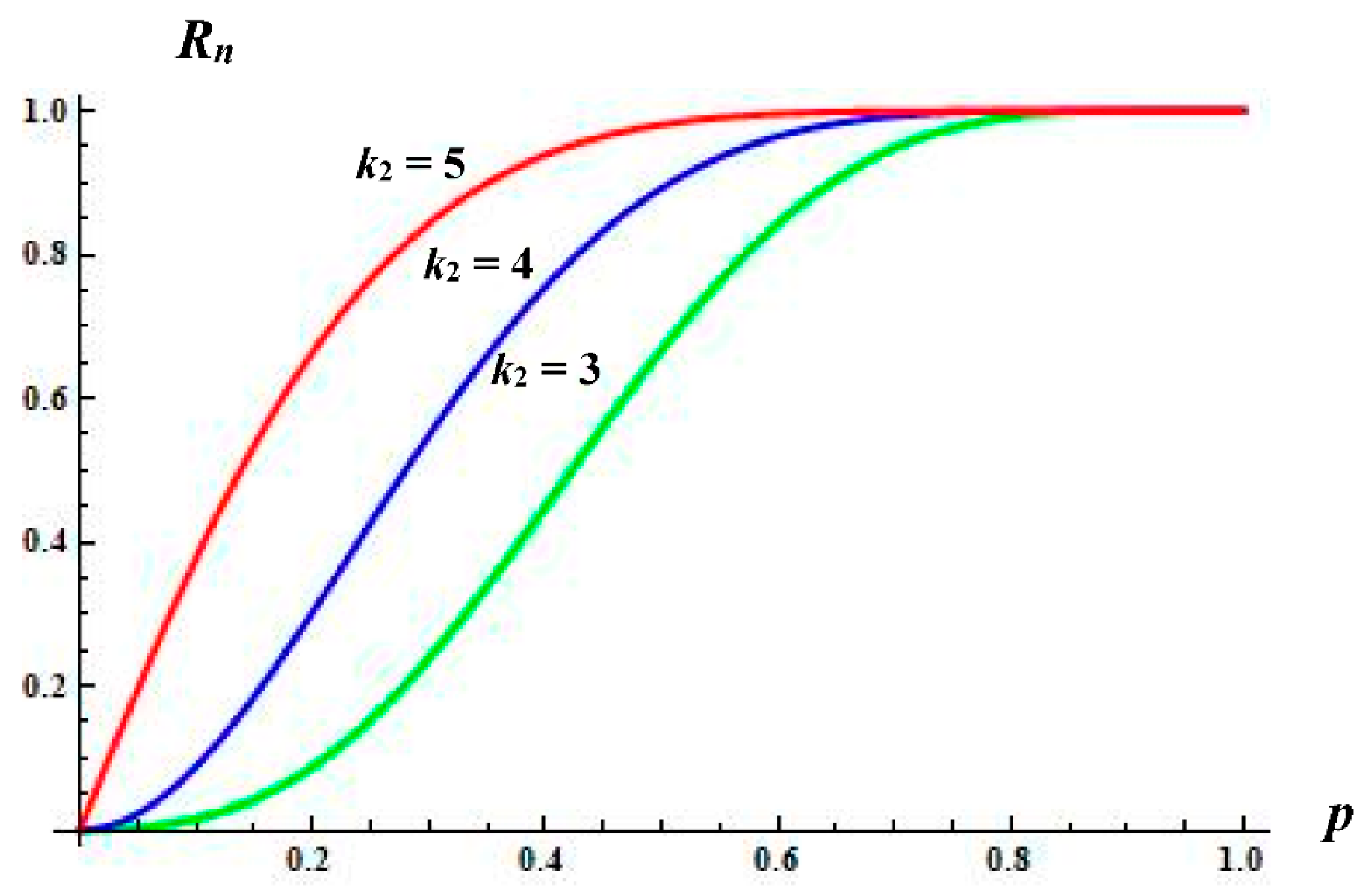
Figure 1 displays the reliability polynomial of the linear consecutive
k1 and
k2-out-of-
n systems consisting of
i.i.d. components under specified values of design parameters
n,
k1 versus the common reliability of its components. Generally speaking, as the reliability polynomial of a structure increases, its credence strengthens. Consequently, when we compare the performance of two or more systems, we look at their corresponding reliability polynomials and conclude that the frontrunner is the structure which exhibits the larger reliability values.
The above figure reveals the impact of the design parameter
k2 on the reliability of the resulting linear structure. More precisely, three different designs are depicted in
Figure 1, namely the structures under the design parameter
k2 = 3, 4, and 5 (
k2 = 3: Green,
k2 = 4: Blue,
k2 = 5: Red). It is quite clear that the reliability polynomial under the design parameter
k2 = 5 (Red color line) exceeds the remaining polynomials displayed in
Figure 1. More specifically, it seems that the polynomials under the design parameters
k2 = 4 (Blue color line) and
k2 = 3 (Green color line) lag behind. Therefore, based on the above figure, it is readily observed that the reliability of the linear consecutive-
k1 and
k2-out-of-
n system increases as the design parameter
k2 increases (given that the remaining design parameters do not change).
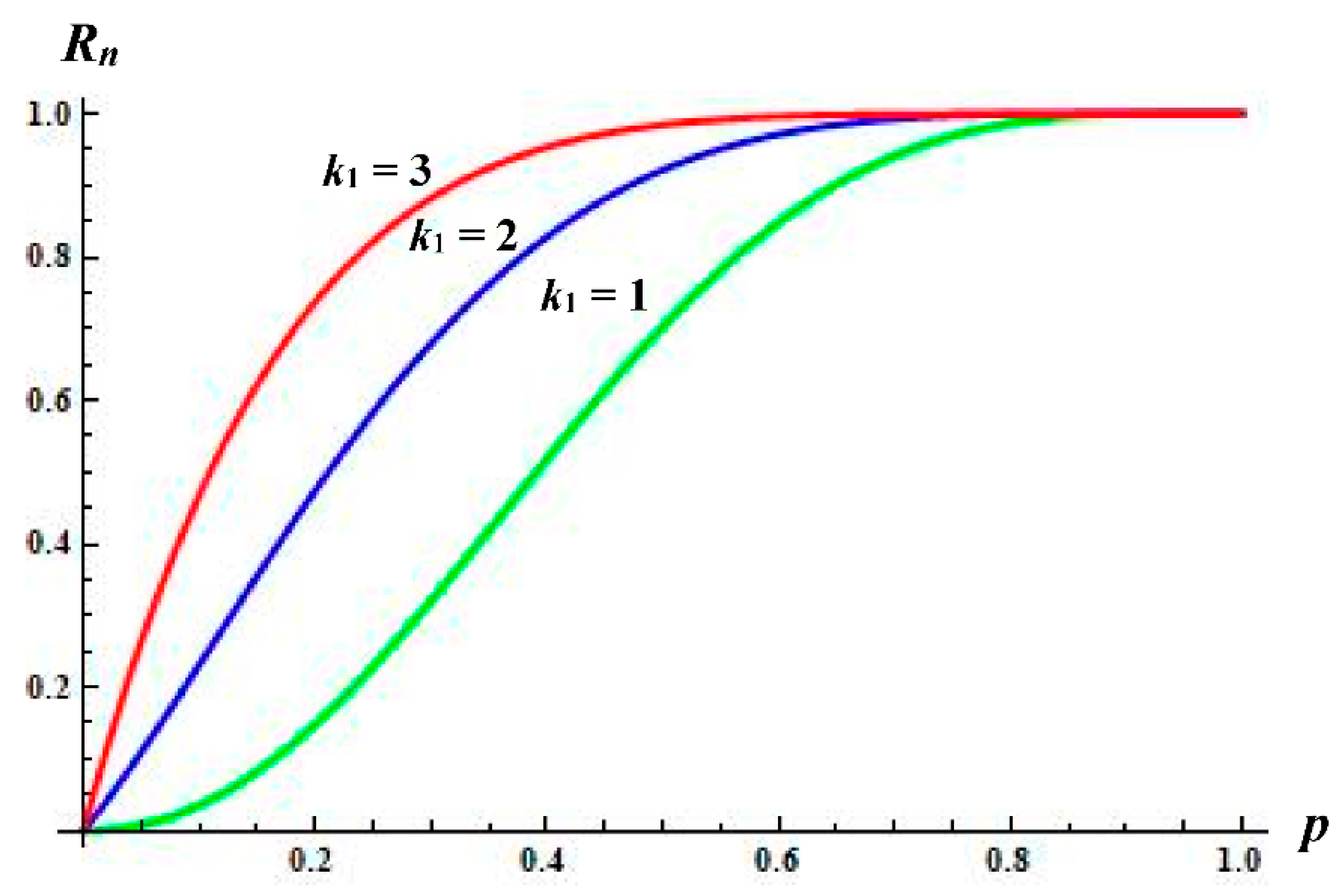
In addition, it is of some interest to investigate the impact of parameter k1 on the reliability of the consecutive-k1 and k2-out-of-n structure. For this reason, we next depict the reliability polynomial of the aforementioned system under three different designs.
More precisely, the parameters
k2 and
n are chosen to be common, namely
k2 = 3 and
n = 6, while the design parameter
k1 ranges from 1 to 3 (
k1 = 1: Green,
k1 = 2: Blue,
k1 = 3: Red). As already mentioned, larger values of the reliability polynomial indicate a more reliable structure. Having that in mind, we observe that the reliability polynomial under the design parameter
k1 = 3 (Red color line) exceeds the remaining polynomials displayed in
Figure 2. More specifically, it seems that the polynomials under the design parameters
k1 = 2 (Blue color line) and
k1 = 1 (Green color line) fall short. Consequently, based on
Figure 2, we conclude that the reliability of the linear consecutive-
k1 and
k2-out-of-
n system increases as the design parameter
k1 increases (given that the remaining design parameters do not change).
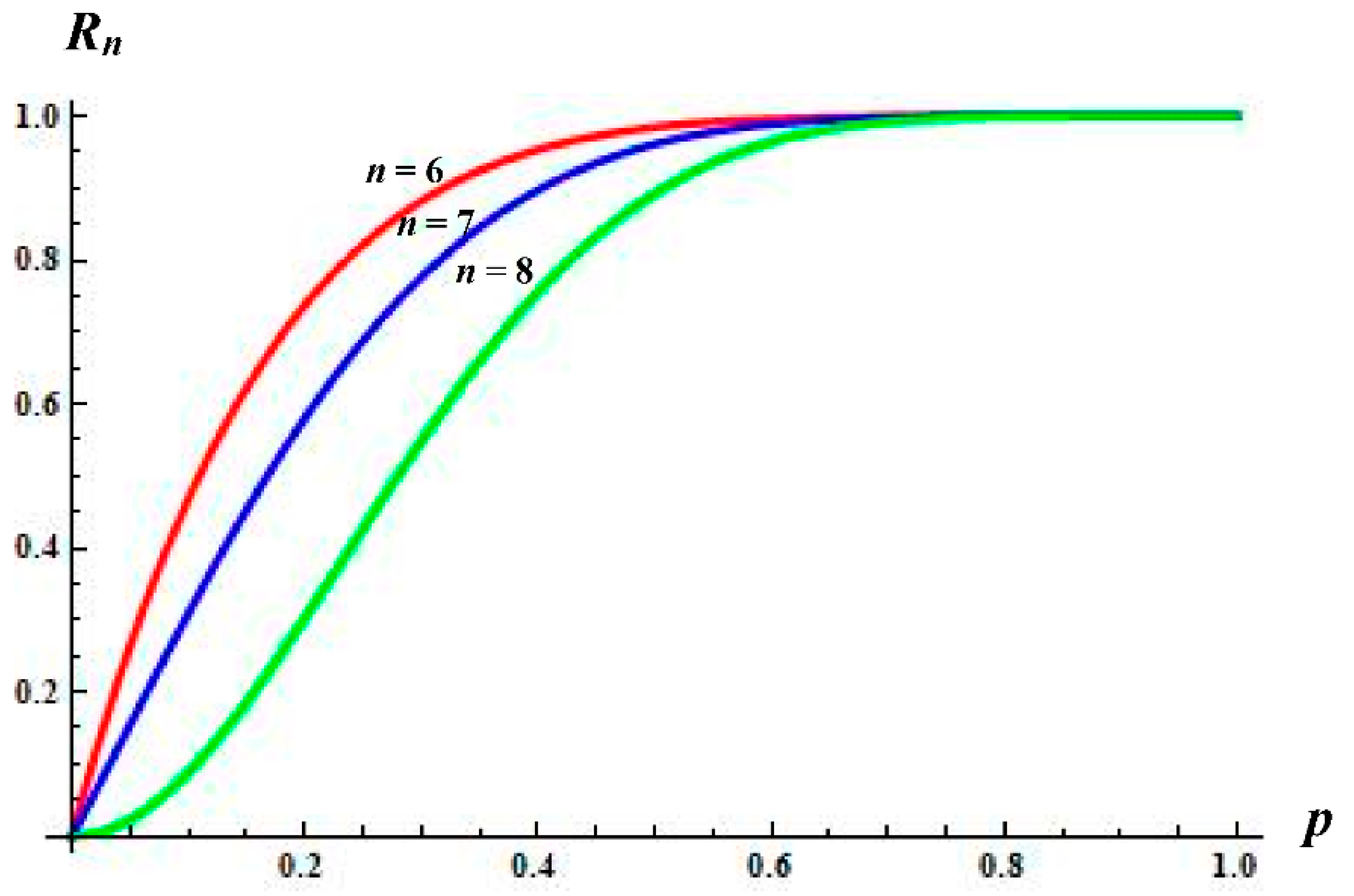
Furthermore, in order to shed light on the influence of parameter n over the reliability of the resulting system, we compare the polynomials, which correspond to structures of different order with common parameters k1 and k2.
In other words, after determining the latter parameters as
k1 = 2 and
k2 = 4, we then display the reliability function of the resulting systems of order
n = 6 (Red line), 7 (Blue line) and 8 (Green line) respectively. We then notice that the reliability polynomial of order
n = 6 (Red color line) outcompetes the remaining polynomials displayed in
Figure 3. More precisely, it seems that the polynomials of order
n = 7 (Blue color line) and
n = 8 (Green color line) give smaller reliability values in comparison with the corresponding ones of the structure with parameter
n = 6 (Red color line). Therefore, based on
Figure 3, one may readily observe that as the parameter
n increases, the reliability function decreases.
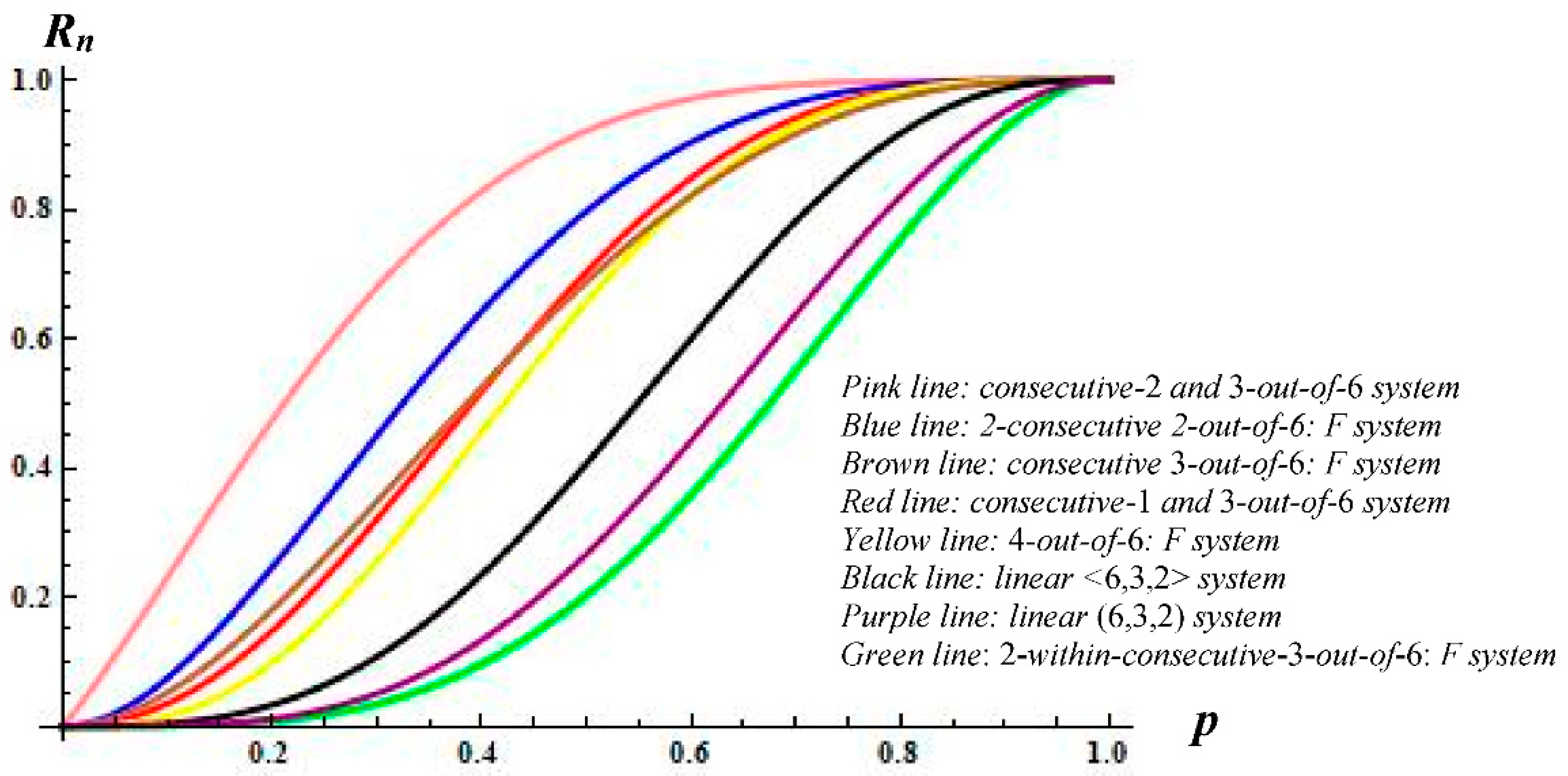
In addition,
Figure 4 depicts the reliability polynomial of several well-known consecutive-type structures. In order to accomplish some figure-based comparisons, we consider different reliability systems of order
n = 6 consisting of
i.i.d. components. More precisely, the reliability structures appearing in
Figure 4 are given as:
the linear system (Black color line)
the linear system (Purple color line)
the 4-out-of-6: F system (Yellow color line)
the consecutive 3-out-of-6: F system (Brown color line)
the 2-within-consecutive-3-out-of-6: F system (Green color line)
the 2-consecutive 2-out-of-6: F system (Blue color line)
the consecutive-1 and 3-out-of-6 system (Red color line)
the consecutive-2 and 3-out-of-6 system (Pink color line)
In order to draw conclusions referring to the abovementioned competitive structures, we recall once again that as the reliability polynomial of a system increases, its performance is appraised more favorable. Consequently, in order to examine the performance of the systems appearing in
Figure 4, we study their corresponding reliability polynomials and, based on the above figure, the following useful remarks can be stated:
the consecutive-2 and 3-out-of-6 system outperforms all competitive structures of order 6 for all cases examined;
the 2-within-consecutive-3-out-of-6: F system seems to exhibits the weakest performance in comparison with the other structures of order 6 appearing in the same figure;
the consecutive-2 and 3-out-of-6 system outperforms the linear <6,3,2> system, the linear (6,3,2) system, and the 2-within-consecutive-3-out-of-6: F structure, while it seems to be competitive with the 4-out-of-6: F system and the consecutive 3-out-of-6: F structure. However, the consecutive-2 and 3-out-of-6 system exhibits a clearly weaker performance versus the 2-consecutive 2-out-of-6: F structure and the consecutive-1 and 3-out-of-6 system.
The following proposition provides a recurrence relation in terms of the design parameter n for determining the coordinates of the signature vector of the linear consecutive-k1 and k2-out-of-n structure.
Proposition 3. The coordinatesof the signature vector of the linear consecutive k1 and k2-out-of-n () structure consisting of n i.i.d. components serves the next recursive schemewhere Proof. It is evident that the double generating function of the coordinates of the signature vector multiplied by some binomial coefficients, namely of the quantities
is related to
via the following equality [
39]:
Substituting the generating function
given by formula (3) in Equation (10) we may write
where
corresponds to the
i-th coordinate of the signature vector of the linear consecutive-
k1 and
k2-out-of-
n (
) structure consisting of
n i.i.d. components, while
We next denote
and Equation (11) takes on the following form:
or equivalently:
where
Looking carefully at the above form of
Q, we can readily observe that the coefficients of
on the left hand side of Equation (12) should vanish for
. Consequently, we may verify that
The recursive scheme we are looking for is readily deduced after several algebraic manipulations. □
Please note that in order to apply the recurrence for determining the signature vector of the linear consecutive k1 and k2-out-of-n () structure provided by the recurrence appeared in (9), a suitable set of initial conditions is needed. These values can be obtained by exploiting the same scheme and setting if , or , or in the event of deriving a negative value of . It is evident that the latter cases mentioned above (e.g., ) correspond to reliability structures without any practical interest, but we need their signature vectors in order to run the proposed recurrence.
Table 2 displays the signature vectors of linear consecutive-
k1 and
k2-out-of-
n structures for different values of their design parameters. More specifically, we next compute the signatures of the consecutive-
k1 and
k2-out-of-
n systems of order
n = 4,5,…,10 and several specified values of the remaining parameters
k1 and
k2.
By casting a glance at the abovementioned numerical results, one may deduce some interesting conclusions about the behavior of the underlying reliability structure. For example, let us focus on the special case ; namely let us assume that the underlying structure consists of n = 10 independent and identically distributed components and the system fails if and only if there exist at least and consecutive non-overlapping failed ones. As readily concluded, the aforementioned structure fails at the 8th ordered failure of its components with probability 38%, while it fails at the 9th ordered component’s failure with probability equal to 42%. Finally, the consecutive-3 and 5-out-of-10 structure manages to operate even if nine components have failed, with probability 20%. Similar conclusions could be drawn by the aid of the remaining numerical outcomes of the above table.