Abstract
A new method for the formation of parabolic curves and surfaces is proposed. It does not impose restrictions on the relative positions in space of the sequence of reference points relative to each other, meaning it compares favorably with other prototypes. The disadvantages of the Overhauser and Brever–Anderson methods are noted. The method allows one to effectively form and edit curves and surfaces when changing the coordinates of any given point. This positive effect is achieved due to the appropriate choice of local coordinate systems for the mathematical description of each parabola, which together define a composite interpolation curve or surface. The paper provides a detailed mathematical description of the method of parabolic interpolation of curves and surfaces based on the use of matrix calculations. Analytical descriptions of a composite parabolic curve and its first and second derivatives are given, and continuity analysis of these factors is carried out. For the matrix of points of the defining polyhedron, expressions are presented that describe the corresponding surfaces, as well as the unit normal at any point. The comparative table of the required number of pseudo-codes for calculating the coordinates of one point for constructing a parabolic curve for the three methods is given.
1. Introduction
In many practical CAD tasks in geometric modeling of graphic objects, the description of analytical formulas for a curve or surface is not known. However, to analyze a projected object, it is required that the curve or surface passes through the specified points, has a certain degree of smoothness, or has specific derivatives at points. To obtain analytical expressions for descriptions and to build on the basis of these expressions of curves or surfaces, a number of different mathematical interpolation methods are presented in [1,2,3,4,5,6]. Such curves are usually called splines, and depending on the formation method they are classed as cubic, parabolic, Hermite, Lagrange, or Newton-shaped splines, among others. For most splines, obtaining their mathematical description requires you to immediately determine the entire sequence of set points, and in some cases specify different additional terms. Moreover, if the view of the calculated curve or surface does not satisfy the user and the position of at least one point requires redefinition (editing), then the entire curve or surface must be recalculated, since the coordinates of each point affect the appearance of the curve or surface along their entire length. With a large number of specified points, obtaining an interpolation curve of the desired shape requires considerable time.
Sequential parabolic interpolation methods were developed by Overhauser [5,6,7] and modified by Brewer–Anderson [5,7,8]. These methods avoid these problems. The formed curves and surfaces are described by equations of the third degree and maintain continuity along their entire length. However, there is a gap between the first and second derivatives at the connection points of some segments. The curve and the surface do not require volumetric recalculations, since segments are formed sequentially as the user enters the next point, allowing their online appearance to be quickly controlled. During the subsequent editing of the set points, the recalculation must be done only within the four segments connected with the point that is being edited.
The peculiarity of the spatial parabolic curve formation method based on two flat overlapping parabolas proposed by Overhauser is that this curve is determined based on the linear interpolation operations of the corresponding vectors of two parabolic points, P(r) and Q(s). The vector P(r) is defined in the local coordinate system (LSC) based on the coordinates of the points of the first triad of four consecutive points specified in space. The second vector Q(s) is calculated in another LSC for the subsequent triad of these points. In this case, the abscissa axis of these LSCs is determined by the position of the first and third points of each triad. For the formation of parabolas with this method, it is necessary that in each LSC the second (middle) points of the triads of tasks of each individual parabola must be located within the ranges of the task of the first and third points (i.e., in the zone their abscissas are set along the r and s axes). However, this requirement cannot always be met in real conditions. In the case of assignment or editing (Figure 1a) the midpoint 1, (1′, 1″, 1‴) goes beyond the boundaries of this zone (0–2), then the parabola seems to be “turned inside out”. This leads to abrupt changes in both the shape and the adjacent parabolic curve sections (Figure 1b), which are shown by dotted and dashed lines, respectively.
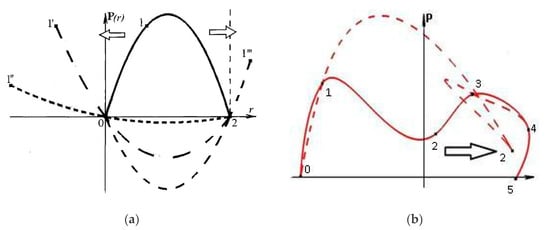
Figure 1.
Parabolic Overhauser curves: (a) curve through three points, with a changed midpoint position; (b) curves obtained with the repositioning of the second reference point.
Thus, the midpoint of a curve setting changes its location when editing. This turns out to be the extreme point of the parabola, although the order in which the points are set does not change. In this case, the part of the curve located in the area between the first and second points of the task is drawn twice (i.e., there definition in this range is ambiguous). The smoothness of the curve at the corresponding vertex (see Figure 1b, vertex 2) is also violated. The arising effect of “inversion” when the middle point of the triad goes beyond the limits of defining the extreme points, the ambiguity of the definition of the parabola, and the violation of smoothness are unexpected for the user. This fact does not allow them to intuitively feel the correctness of the construction of the curve, and this phenomenon should be considered as a significant disadvantage of the Overhauser method.
The Brever–Anderson curve is formed on the basis of matrix multiplication and is constructed much faster than the Overhauser curve. However, when the median point of the task triad deviates from a position that corresponds exactly to the middle of the task area of the triad’s extreme points for an individual parabola, the smoothness of the mixed curve is broken, which is unacceptable, particularly with the automatic development of surfaces on mechanical devices. To exclude such situations and ensure the continuity of the first derivative and the smoothness of the mixed curve, the authors provide an artificial method. They introduce special coefficients, which are calculated depending on the relative positions of the points of each triad, and provide an additional chord approximation for the resulting curve. This artificial method for ensuring the smoothness of the curve means it cannot be considered parabolic. In addition, it requires additional memory and time resources.
2. Modified Method of Forming Parabolic Curves and Surfaces
The drawbacks of these methods can be avoided with the correct choice of LSCs, in which descriptions of each individual parabola are created [9]. For this, the beginning of each LSC must be tied to the point Pm, which is located exactly in the middle between the extreme points P1 and P3 (Figure 2), rather than to the first triad point P1 in each parabola task. The axes of ordinates of such LSCs should then pass through the second P2 (middle) points of the task triad, and the abscissa axes should lie in planes, each of which is determined by the points of the corresponding triad.
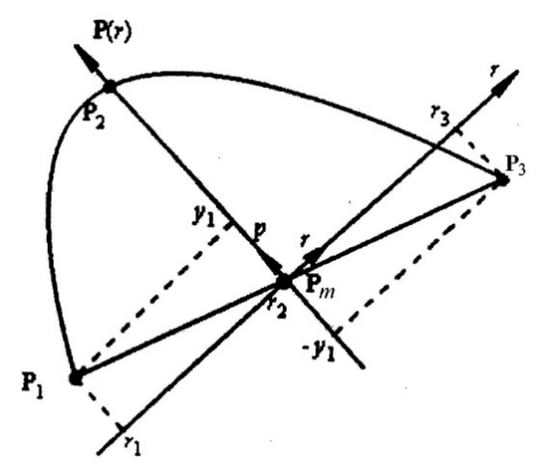
Figure 2.
A new method for specifying parabola points in a local coordinate system.
This choice of LSCs allows us to uniquely determine the parabolic curve along its entire length and ensure its smoothness without introducing any additional restrictions, since the second triad point P2 of the parabola always:
- lies between the values of the extreme points of the triad (P1 and P3) along the abscissa axis of the corresponding LSC, regardless of its location in space;
- is located exactly in the middle of the setting interval for the extreme points of the triad.
The proposed choice of LSCs means additional restrictions are imposed on the construction and editing of the curve and surface.
In this case, the parametric representation of pure parabolas passing through points P1, P2, and P3; and P2, P3, and P4, respectively, in the 3D space in the matrix form are represented as:
where [B] and [D] are matrices, whose parameters are determined from the conditions of passing parabolas through the corresponding points of the task.
In this case, the equation for the mixed parabolic curve is represented as a linear interpolation of two parabolas P (r) and Q (s)in a common interval, each of which is represented in its own LSC:
C(t) = (1 −t)P(t) + tQ(s), 0 ≤ t ≤ 1.
Given the values of parameter r corresponding to task points P1, P2, and P3, we can write:
After combining these expressions, we have:
This equation allows you to calculate the parameters of matrix [B] for Equation (1):
Substituting the obtained value of matrix [B] into Equation (1), one can form the first parabola. This value is particularly relevant for the initial segment (the segment corresponding to the “pure” parabola) of the general parabolic curve, when the r parameter changes in the range from −0.5 to 0.
Similarly, the calculation of the parameters of matrix [B] in accordance with Equation (2) is determined by the values of the elements of matrix [D]:
Substituting the obtained value of matrix [D] into Equation (2), we can form the second parabola. This value is particularly relevant for the final segment of the total parabolic curve from point Pn−1 to Pn, when the parameter s changes in the range from 0 to 0,5 (i.e., another area corresponding to a “clean” parabola).
Based on the equations of two consecutive parabolas (Equations (1) and (2)), the equation of a mixed parabola can be represented:
C(t) = (1 − t)P(t) + tQ(s) = [r2 r 1][B] (1 − t) + [ s2 s 1][D]t = [R][B](1 − t) + [S][D]t.
At the same time, the parameters for these parabolas lie within the following limits:
The relationship between the job parameters for mixed and pure parabolas is defined as:
r = 0,5t, s = 0,5(t − 1).
Substituting the values of r and s into Equation (5), depending on parameter t and the values of matrices [B] (Equation (3)) and [D] (Equation (4)), we can get the equation forthe mixed parabola in the interval between P2 and P3 when setting the parameters of the 4 points in 3D space:
where .
In this case, the parabolic spline P(m), defined by «n» points (P1, P2, …, Pn) in 3D space, can be represented as:
With the proposed interpolation, in the case of a shift of the midpoints of the parabolic curve triads beyond the boundaries defined by the extreme points of these triads will be uniquely determined on a given area and will not be distorted.
For comparison, Figure 3 shows undistorted parabolas in accordance with the changed position of the second point in each given set of triads. For each such set, its own LSC is determined, in which the parameters of this parabola are uniquely calculated. The beginnings of these LSCs lie at point Pm, located exactly in the middle of the first and third points of the assigned triad for the corresponding parabola.
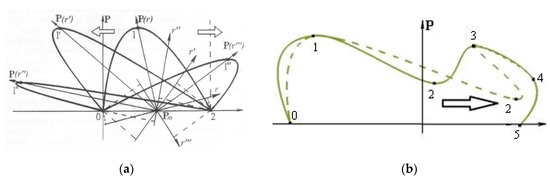
Figure 3.
Parabolic curves formed using the new method: (a) curves passing through three points with their own local coordinate systems (LSCs); (b) curves obtained by editing the position of point number 2.
It should be noted that the main drawback of such splines is the reduced but visually imperceptible degree of smoothness in the connections of the segments. For such curves, only the first derivative remains uninterrupted at the junctions of the segments of mixed parabolas. At the same time, the first derivatives undergo a break at the beginning of the parabolic curve—at the junction of the initial clean and mixed parabolas, and at the end—when moving from mixed to pure parabolas. The second derivatives undergo breaks at the conjugation points of all segments. This is easy to verify if we have the analytical expression for the spline (Equation (7)), for which it is easy to obtain an analytical expression describing the behavior of the first (Equation (8)) and second (Equation (9)) derivatives on separate segments along such a composite parabolic curve:
An analysis of these expressions (Equations (8) and (9)) confirms that at some connection points between individual segments of such a parabolic curve, a discontinuity (abrupt change) in the values and the first derivative occurs.
Therefore, the value in the proposed method changes stepwise during transitions from:
- -
- the first segment corresponding to a pure parabola (at r = 0) to the first mixed parabola (at t = 0) at point P2—from the value (−P1 + P3) to the value 0.5(−P1 + P3);
- -
- the last segment of the mixed parabola (at t = 1) to the pure parabola, completing the parabolic curve (at s = 0) (at the point Pn−1)—from the value 0.5(−Pm = n−2 + Pm = n) to value (−Pn−2 + Pn).
When passing from one segment of a mixed parabola to the next (from the m-th at t = 1 to the (m + 1)-th at t = 0), the value of the first derivative does not change, but remains equal to 0.5 (−Pm+1 + Pm+3).
The value of the second derivative changes abruptly at all points when the description changes from one segment of the parabolic curve to another.
If we have a polyhedron P(u, w):
then the family of «n» parabolic splines in the U direction with different values of the parameter «w» lying in the range from 1 to «n» is represented by:
A family of «k» parabolic splines in the W direction for different values of the parameter «u», ranging from 1 to «k», is described as:
Based on the mathematical description of the families of parabolic splines formed in the U and W directions, the equation for the parabolic surface is presented in the form:
Having the analytical equation of a parabolic surface, the values of the partial derivatives at any point P(u, w) are easily determined, and therefore the value of the unit normal at this point is:
Then, the value of the unit normal is:
As indicated earlier, in cases where it is necessary to edit the position of any point P(i, j) to specify a curve or face, recalculation should be carried out only in limited assignment ranges—from point Pi−2, j to Pi+2, j in one direction and from point Pi, j−2 to Pi, j+2 in another direction—rather than on the entire curve or surface.
One can see from Table 1, that the necessary number of pseudo-codes is determined to calculate the coordinates of only one point of the curve belonging to the corresponding segment of the parabolic curve. If we assume that the entire curve in each segment (both pure and mixed) is formed on the basis of the same number of points (for example, N) and the number of segments in the mixed parabola is K, then it is easy to calculate the total number of pseudo-codes needed for its formation. Thus, the data shown in Table 1 must be multiplied by:

Table 1.
The pseudo-code complexity analysis table for the three methods.
- -
- (N − 1) for the initial segment (pure parabola);
- -
- (N − 1) for the final segment (pure parabola);
- -
- (N − 1) × K for K segments of mixed parabola.
From the data presented in the table, it seems that the Overhauser method is faster than the rest. However, this is not true, since it is likely that a relatively long time is spent on operations with vectors and to calculate the square root of the number. The work is much slower than the other two methods. This is confirmed both by our observations and by the indication in [8] that the Brever–Anderson method works faster.
A temporary analysis of the real complexity of the presented algorithms will be presented in future studies.
3. Conclusions
The proposed parabolic approximation method, which is based on matrix calculations and local coordinate systems, the origin of which is located exactly in the middle of the first and third points and the ordinate axis, passes through the second (middle) point of the task of each parabola. The proposed method:
- eliminates the drawbacks of the Overhauser and Brever–Anderson methods associated with the possibility of generating ambiguous descriptions and with the violation of the smoothness of curves and surfaces;
- does not require the introduction of a normalized chord approximation to provide artificial smoothing of curves, which requires additional memory and time resources;
- allows one to effectively form, and if necessary, predictably edit the points of the parabolic job curves and surfaces;
- allows relatively simple determination of the normal value at each point of the surface using the presented analytical expressions when forming a realistic image of such surface.
The proposed method is supposed to be used in the development of automated tools for the formation and editing of realistic images of surfaces of objects with complex configurations, such as car bodies. It can be recommended for use in the field of construction for the representation of membrane roofing [10]. This method could be also useful for civil engineers and in the calculation of models by the finite element method. In particular, when designing cable structures, developers only need parabolic shapes traction design. This method is also useful for physicists for evaluating sound propagation contours.
Funding
This research received no external funding.
Conflicts of Interest
The author declare no conflict of interest.
References
- Stechkin, S.B.; Subbotin, Y.N. Splines in Computational Mathematics; Nauka: Moscow, Russia, 1976. (In Russian) [Google Scholar]
- Bohm, W.; Farin, G.; Kahmann, J. A Survey of Curve and Surface Methods in CAGD. Comp. Aid. Geom. Des. 1984, 1, 1–60. [Google Scholar] [CrossRef]
- Adams, J.A. A Comparison of Methods for Cubic Spline Curve Fitting. Nav. Acad. Annap. MD DIV Eng. Weapons 1973, 6, 1–9. [Google Scholar]
- Gordon, W.J.; Riesenfeld, R.F. Bernstein-Bezier Methods for the Computer Aided Design of Free-form Curves and Surfaces. J. ACM 1974, 21, 293–310. [Google Scholar] [CrossRef]
- Rogers, D.F.; Adams, J.A. Mathematical Elements for Computer Graphics, 2nd ed.; McGraw-Hill Book Company: New York, NY, USA, 1975. [Google Scholar]
- Rogers, D.F.; Adams, J.A. Mathematical Elements for Computer Graphics, 2nd ed.; McGraw-Hill Publishing Company: New York, NY, USA, 1989. [Google Scholar]
- Overhauser, A.W. Analytic Definition of Curves and Surfaces by Parabolic Blending; Ford Motor Company Scientific Laboratory: Dearborn, MI, USA, 1968. [Google Scholar]
- Brewer, J.A.; Anderson, D.C. Visual Interaction with Overhauser Curves and Surfaces. ACM SIGGRAPH Comput. Gr. 1977, 11, 132–137. [Google Scholar] [CrossRef]
- Lyachek, Y.T.; Vasil’ev, A.A.; Martinov, V.Y. New Methods of Generating Parabolic Curves of Overhauser. Izvest. SPbGETU LETI 2017, 8, 17–23. (In Russian) [Google Scholar]
- Rizzo, F.; Zazzini, P. Improving the acoustical properties of an elliptical plan space with a cable net membrane roof. Acoust. Aust. 2016, 44, 449–456. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).