Powers of the Stochastic Gompertz and Lognormal Diffusion Processes, Statistical Inference and Simulation
Abstract
1. Introduction
2. The Model and Its Basic Probabilistic Characteristics
2.1. An Overview of the Homogeneous Gompertz Stochastic Diffusion Process
2.2. The Proposed Model
2.3. Probabilistic Characteristics of the -PSGDP
3. Statistical Inference on the Model
3.1. Likelihood Parameter Estimation
3.2. Asymptotic Properties of the Parameter Drift Estimators
4. Powers of the Lognormal Diffusion Process
Estimated Trend Functions
5. Simulation and Application
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SDP | Stochastic Diffusion Processes |
| SGDP | Stochastic Gompertz Diffusion Process |
| PTDF | Probability Transition Density Function |
| SDE | Stochastic Differential Equation |
| -PSGDP | -Power of the Stochastic Gompertz Diffusion Process |
| -PSLDP | - Power of the Stochastic Lognormal Diffusion Process |
| CTF | Conditional Trend Function |
| TF | Trend Function (TF) |
| ML | Maximum Likelihood |
| SLDP | Stochastic Lognormal Diffusion Process |
| ECT | Estimated Conditional Trend |
| ET | Estimated Trend |
| SE | Standard Error |
References
- Bibby, B.M.; Sorensen, M. Martingale estimation functions for discretely observed diffusion processes. Bernoulli 1995, 1, 17–39. [Google Scholar] [CrossRef]
- Prakasa Rao, B.S.L. Statistical Inference for Diffusion Type Process; Ed. Arnold: London, UK; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Chang, J.; Chen, S.X. On the approximate maximum likelihood estimation for diffusion processes. Ann. Stat. 2011, 39, 2820–2851. [Google Scholar] [CrossRef]
- Beskos, A.; Papaspiliopoulos, O.; Roberts, G.O.; Fearnhead, P. Exact and computationally eficient likelihood-based estimation for discretely observed diffusion processes (with discussion). J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2006, 68, 333–382. [Google Scholar] [CrossRef]
- Stramer, O.; Yan, J. On the simulated likelihood of discretely observed diffusion processes and comparison to closed-form approximation. J. Comput. Graph. Stat. 2007, 16, 672–691. [Google Scholar] [CrossRef]
- Shoji, I.; Ozaki, T. Comparative study of estimation methods for continuous time stochastic processes. J. Time Ser. Anal. 1997, 18, 485–506. [Google Scholar] [CrossRef]
- Durham, G.B.; Gallant, A.R. Numerical techniques for maximum likelihood estimation of the continuous-times diffusion processes. J. Bus. Econ. Stat. 2002, 20, 297–316. [Google Scholar] [CrossRef]
- Fan, J. A selective overview of nonparametric methods in financial econometrics. Stat. Sci. 2005, 20, 317–337. [Google Scholar] [CrossRef]
- Yenkie, K.M.; Urmila, D. The “No Sampling Parameter Estimation (NSPE)” algorithm for stochastic differential equations. Chem. Eng. Res. Des. 2018, 129, 376–383. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E.; Schurz, H. Numerical Solution of SDE through Computer Experiments; Springer: Heidelberg/Berlin, Germany, 1994. [Google Scholar]
- Katsamaki, A.; Skiadas, C.H. Analytic solution and estimation of parameters on a stochastic exponential model for a technological diffusion process application. Appl. Stoch. Model. Data Anal. 1995, 11, 59–75. [Google Scholar] [CrossRef]
- Skiadas, C.H.; Giovani, A.N. A stochastic Bass innovation diffusion model for studying the growth of electricity consumption in Greece. Appl. Stoch. Model. Data Anal. 1997, 13, 85–101. [Google Scholar] [CrossRef]
- Giovanis, A.N.; Skiadas, C.H. A stochastic logistic innovation diffusion model studying the electricity consumption in Greece and the United States. Technol. Forecast. Soc. Chang. 1999, 61, 253–264. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Gutiérrez-Sánchez, R.; Nafidi, A. The stochastic Rayleigh diffusion model: Statistical inference and computational aspects. Applications to modelling of real cases. Appl. Math. Comput. 2006, 175, 628–644. [Google Scholar] [CrossRef]
- Román-Román, P.; Serrano-Pérez, J.J.; Torres-Ruiz, F. Some notes about inference for the lognormal diffusion process with exogenous factors. Mathematics 2018, 6, 85. [Google Scholar] [CrossRef]
- Ricciardi, L. Diffusion processes and related topics in biology. In Lecture Notes in Biomathematics; Springer: Berlin, Germany, 1977. [Google Scholar]
- Dennis, B.; Patil, G.B. Application in Ecology. In Lognormal Distributions: Theory and Applications; Crow, E.L., Shimizu, K., Eds.; Marcel Dekker: New York, NY, USA, 1988; pp. 310–330. [Google Scholar]
- Nafidi, A. Lognormal Diffusion Process with Exogenous Factors, Extensions from the Gompertz Diffusion Process. Ph.D. Thesis, Granada University, Granada, Spain, 1997. (In Spanish). [Google Scholar]
- Gutiérrez, R.; Nafidi, A.; Gutiérrez-Sánchez, R. Inference in the stochastic Gompertz diffusion model with continuous sampling. In Monografías del Seminario García de Galdeano; Torrens, J.J., Madaune-Tort, M., Trujillo, D., López de Silanes, M.C., Palacios, M., Sanz, G., Eds.; Prensas de la Universidad de Zaragoza: Zaragoza, Spain, 2004; Volume 31, pp. 247–253. [Google Scholar]
- Gutiérrez, R.; Nafidi, A.; Gutiérrez-Sánchez, R. Forecasting total natural-gas consumption in Spain by using the stochastic Gompertz innovation diffusion model. Appl. Energy 2005, 80, 115–124. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Gutiérrez-Sánchez, R.; Nafidi, A. Modelling and forecasting vehicle stocks using the trends of stochastic Gompertz diffusion models: The case of Spain. Appl. Stoch. Models Bus. Ind. 2009, 25, 385–405. [Google Scholar] [CrossRef]
- Ferrante, L.; Bompade, S.; Possati, L.; Leone, L. Parameter estimation in a Gompertzian stochastic-model for tumor growth. Biometrics 2000, 56, 1076–1081. [Google Scholar] [CrossRef]
- Román-Román, P.; Serrano-Pérez, J.J.; Torres-Ruiz, F. A Note on estimation of multi-sigmoidal Gompertz functions with random noise. Mathematics 2019, 7, 541. [Google Scholar] [CrossRef]
- Giorno, V.; Nobile, A.G. Restricted Gompertz-type diffusion processes with periodic regulation functions. Mathematics 2019, 7, 555. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Nafidi, A.; Gutiérrez-Sánchez, R.; Román, P.; Torres, F. Inference in Gompertz type non homogeneous stochastic systems by means of discrete sampling. Cybern. Syst. 2005, 36, 203–216. [Google Scholar]
- Gutiérrez, R.; Gutiérrez-Sánchez, R.; Nafidi, A. Electricity consumption in Morocco: Stochastic Gompertz diffusion analysis with exogenous factors. Appl. Energy 2006, 83, 1139–1151. [Google Scholar] [CrossRef]
- Rupsys, P.; Bartkevicius, E.; Petrauskas, E. A univariate stochastic Gompertz model for tree diameter modeling. Trends Appl. Sci. Res. 2011, 6, 134–153. [Google Scholar] [CrossRef][Green Version]
- Badurally Adam, N.R.; Elahee, M.K.; Dauhoo, M.Z. Forecasting of peak electricity demand in Mauritius using non-homogeneous Gompertz diffusion process. Energy 2011, 36, 6763–6769. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Gutiérrez-Sánchez, R.; Nafidi, A. A generalization of the Gompertz diffusion model: Statistical inference and application. In Monografías del Seminario García de Galdeano; Madaune-Tort, M., Trujillo, D., López de Silanes, M.C., Palacios, M., Sanz, G., Torrens, J.J., Eds.; Prensas de la Universidad de Zaragoza: Zaragoza, Spain, 2006; Volume 33, pp. 273–280. [Google Scholar]
- Ferrante, L.; Bompade, S.; Possati, L.; Leone, L.; Montanari, M.P. A stochastic formulation of the Gompertzian growth model for in vitro bactericidad kinetics: Parameter estimation and extinction probability. Biom. J. 2005, 47, 309–318. [Google Scholar] [CrossRef]
- Albano, G.; Giorno, V. A stochastic model in tumor growth. J. Theor. Biol. 2006, 242, 329–336. [Google Scholar] [CrossRef]
- Frank, T.D. Multivariate Markov processes for stochastic systems with delays: Application to the stochastic Gompertz model with delay. Phys. Rev. E 2002, 66, 011914. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Gutiérrez-Sánchez, R.; Nafidi, A. A bivariate stochastic Gompertz diffusion model: Statistical aspects and application to the joint modeling of the Gross Domestic Product and CO2 emissions in Spain. Environmetrics 2008, 19, 643–658. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Gutiérrez-Sánchez, R.; Nafidi, A. Trend analysis using nonhomogeneous stochastic diffusion processes, emission of CO2; Kyoto protocol in Spain. Stoch. Environ. Res. Risk Assess. 2008, 22, 55–66. [Google Scholar]
- Hu, G. Invariant distribution of stochastic Gompertz equation under regime switching. Math. Comput. Simul. 2014, 97, 192–206. [Google Scholar] [CrossRef]
- Zou, W.; Li, W.; Wang, K. Ergodic method on optimal harvesting for a stochastic Gompertz-type diffusion process. Appl. Math. Lett. 2013, 26, 170–174. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Gutiérrez-Sánchez, R.; Nafidi, A.; Ramos-Ábalos, E. A τ-power stochastic gamma diffusion process: Computational statistical inference and simulation aspects. A real example. Appl. Math. Comput. 2012, 219, 1576–1588. [Google Scholar]
- Zehna, P.W. Invariance of maximum likelihood estimators. Ann. Math. Stat. 1966, 37, 744–1966. [Google Scholar] [CrossRef]
- Gutiérrez-Sánchez, R.; Nafidi, A.; Pascual, A.; Ramos-Ábalos, E. Three parameter gamma-type growth curve, using a stochastic gamma diffusion model: Computational statistical aspects and simulation. Math. Comput. Simul. 2011, 82, 234–243. [Google Scholar] [CrossRef]
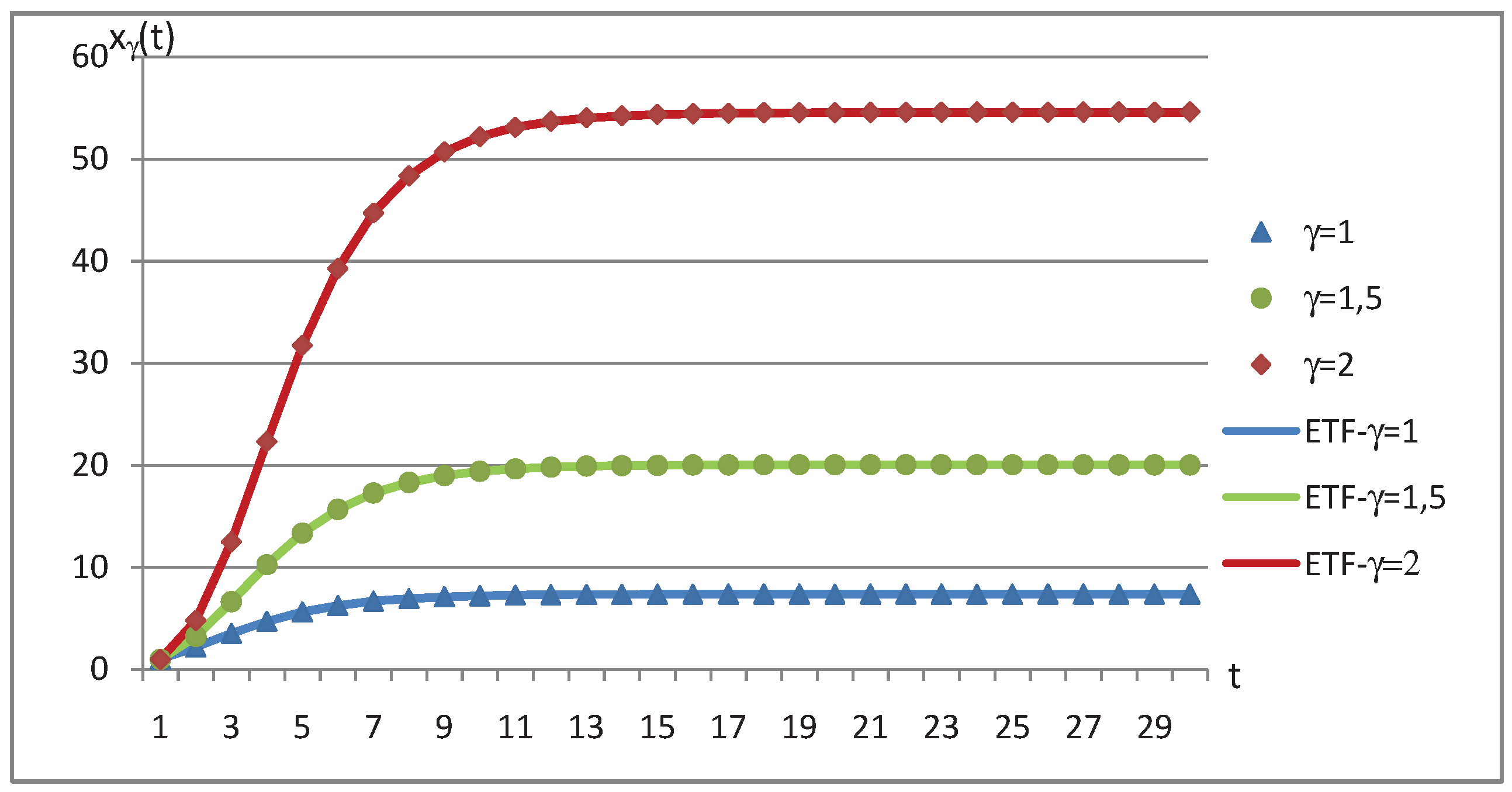
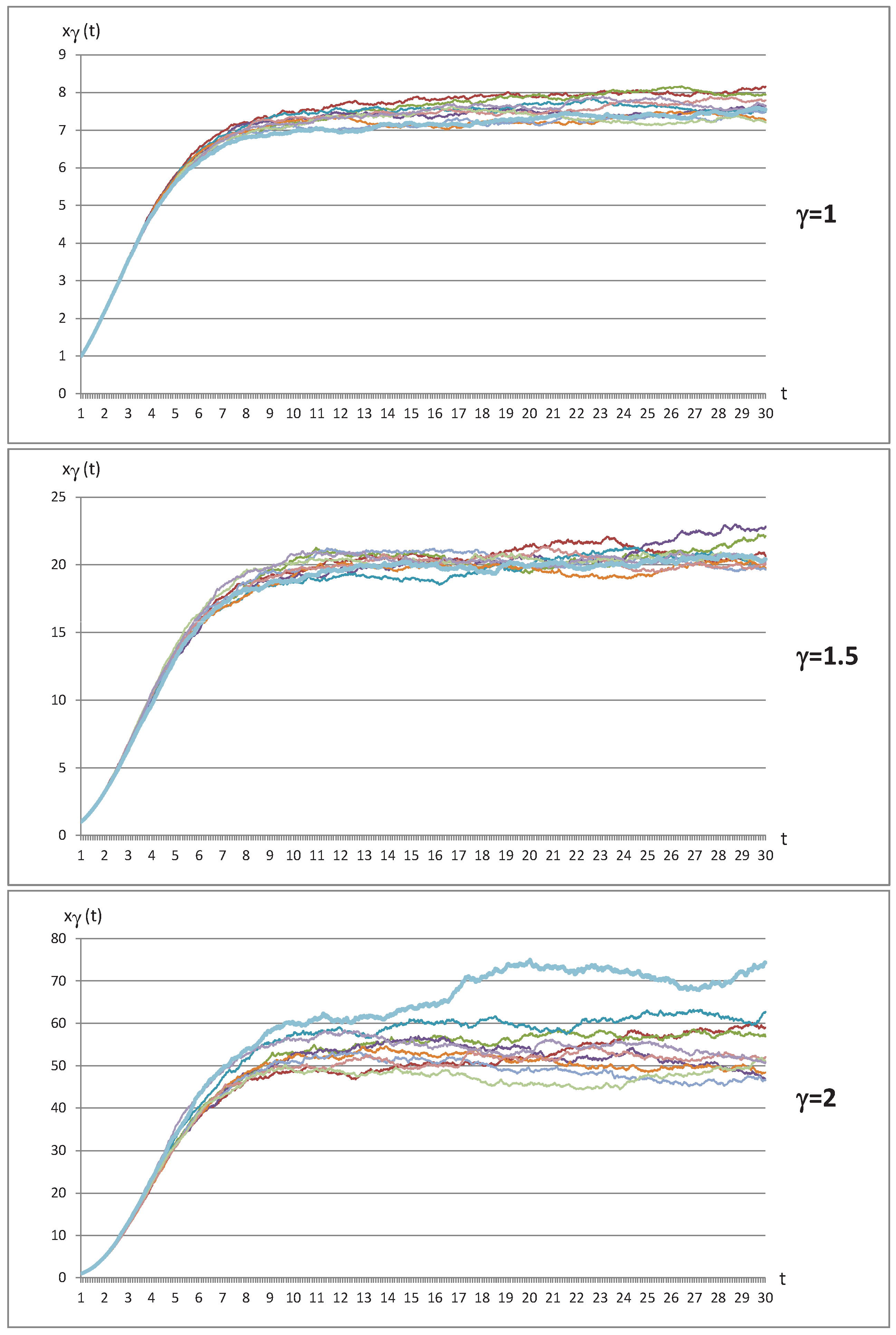
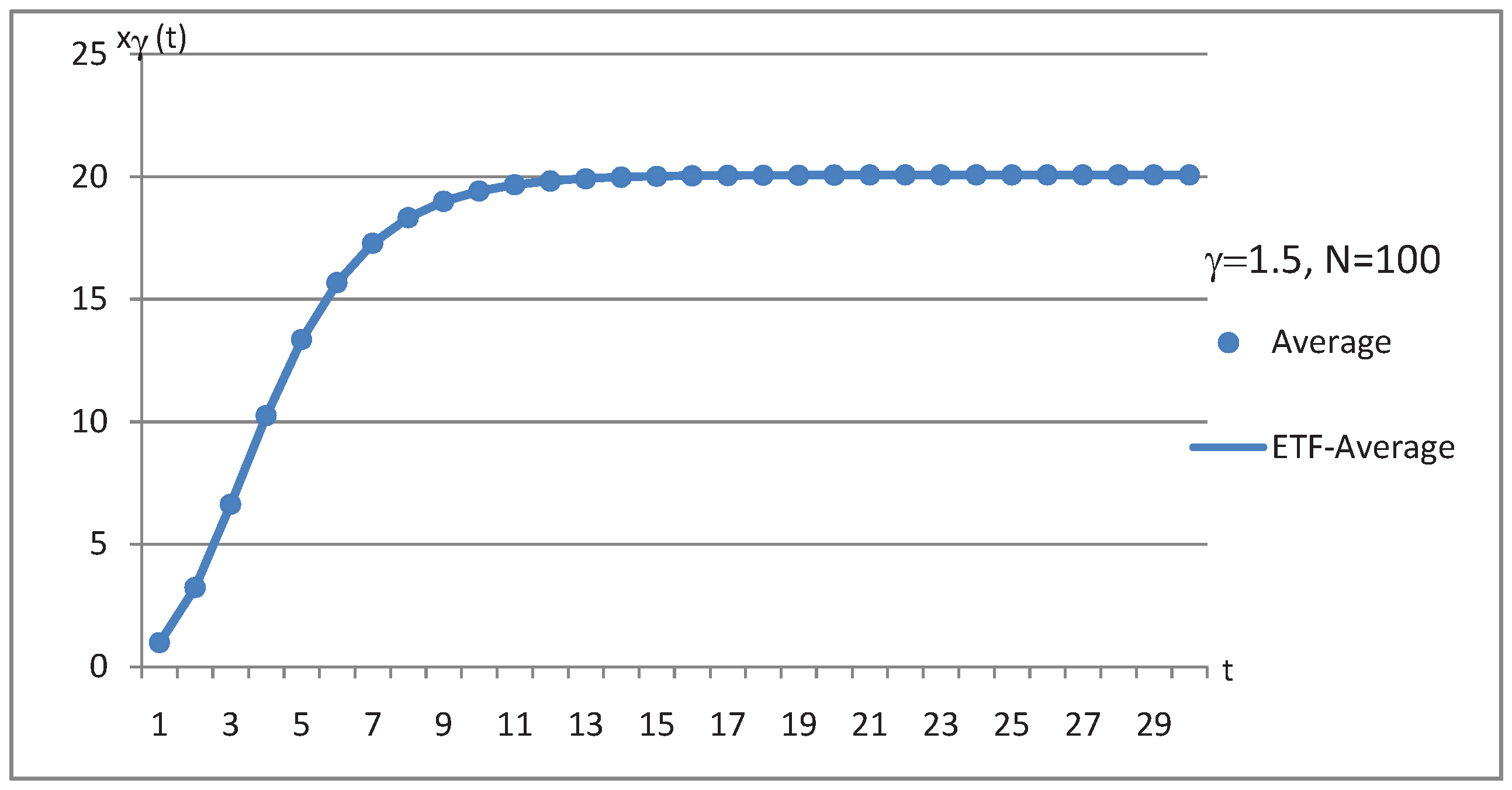
| Time | (t) | ETF- | (t) | ETF- | (t) | ETF- |
|---|---|---|---|---|---|---|
| 1 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| 2 | 2.1831 | 2.1832 | 3.2364 | 3.2369 | 4.7957 | 4.7960 |
| 3 | 3.5272 | 3.5271 | 6.6380 | 6.6385 | 12.4861 | 12.4876 |
| 4 | 4.7180 | 4.7181 | 10.2628 | 10.2613 | 22.3149 | 22.3122 |
| 5 | 5.6288 | 5.6286 | 13.3648 | 13.3620 | 31.7343 | 31.7261 |
| 6 | 6.2651 | 6.2645 | 15.6878 | 15.6818 | 39.2796 | 39.2767 |
| 7 | 6.6848 | 6.6846 | 17.2845 | 17.2802 | 44.7154 | 44.7063 |
| 8 | 6.9539 | 6.9531 | 18.3316 | 18.3276 | 48.3607 | 48.3586 |
| 9 | 7.1220 | 7.1211 | 18.9998 | 18.9933 | 50.7075 | 50.7176 |
| 10 | 7.2251 | 7.2250 | 19.4136 | 19.4087 | 52.1922 | 52.2041 |
| 11 | 7.2894 | 7.2887 | 19.6703 | 19.6649 | 53.1189 | 53.1268 |
| 12 | 7.3285 | 7.3277 | 19.8262 | 19.8219 | 53.7088 | 53.6943 |
| 13 | 7.3520 | 7.3514 | 19.9247 | 19.9177 | 54.0539 | 54.0414 |
| 14 | 7.3663 | 7.3658 | 19.9776 | 19.9761 | 54.2598 | 54.2531 |
| 15 | 7.3742 | 7.3746 | 20.0117 | 20.0115 | 54.3836 | 54.3818 |
| 16 | 7.3792 | 7.3799 | 20.0323 | 20.0330 | 54.4489 | 54.4601 |
| 17 | 7.3820 | 7.3831 | 20.0497 | 20.0461 | 54.4903 | 54.5076 |
| 18 | 7.3841 | 7.3851 | 20.0598 | 20.0540 | 54.5492 | 54.5364 |
| 19 | 7.3849 | 7.3863 | 20.0641 | 20.0588 | 54.5629 | 54.5539 |
| 20 | 7.3862 | 7.3870 | 20.0648 | 20.0617 | 54.5623 | 54.5645 |
| 21 | 7.3875 | 7.3874 | 20.0633 | 20.0635 | 54.5783 | 54.5710 |
| 22 | 7.3877 | 7.3877 | 20.0654 | 20.0645 | 54.5922 | 54.5749 |
| 23 | 7.3885 | 7.3879 | 20.0662 | 20.0652 | 54.5997 | 54.5773 |
| 24 | 7.3882 | 7.3880 | 20.0587 | 20.0656 | 54.6148 | 54.5787 |
| 25 | 7.3881 | 7.3880 | 20.0626 | 20.0658 | 54.6020 | 54.5796 |
| 26 | 7.3883 | 7.3881 | 20.0638 | 20.0660 | 54.5914 | 54.5801 |
| 27 | 7.3890 | 7.3881 | 20.0599 | 20.0661 | 54.6196 | 54.5804 |
| 28 | 7.3878 | 7.3881 | 20.0549 | 20.0661 | 54.6297 | 54.5806 |
| 29 | 7.3873 | 7.3881 | 20.0507 | 20.0661 | 54.6110 | 54.5807 |
| Prediction | ||||||
| 30 | 7.3872 | 7.3881 | 20.0473 | 20.0662 | 54.6221 | 54.5808 |
| Starting Values | 0.0001 | 1 | 0.5 |
| 1 | 0.0000852 | 0.999952 | 0.500008 |
| 1.5 | 0.0001498 | 1.00043 | 0.500377 |
| 2 | 0.0001606 | 1.00003 | 0.500052 |
| Starting values | 0.0001 | 1 | 0.5 |
| 1.5 | 0.0000106801 | 1.00006 | 0.50003 |
| h | N | Mean () | SE () | Mean () | SE () | Mean () | SE () |
|---|---|---|---|---|---|---|---|
| 0.05 | 100 | 0.025108 | 0.114736 | 1.000132 | 0.000503 | 0.500144 | 0.000439 |
| 0.05 | 500 | 0.000112 | 0.000005 | 0.999637 | 0.000839 | 0.499770 | 0.000809 |
| 0.05 | 1000 | 0.000116 | 0.000005 | 1.000181 | 0.000953 | 0.500090 | 0.000915 |
| 0.1 | 100 | 0.000106 | 0.000008 | 1.000027 | 0.000350 | 0.500007 | 0.000262 |
| 0.1 | 500 | 0.000123 | 0.000010 | 1.000020 | 0.000654 | 0.500044 | 0.000647 |
| 0.1 | 1000 | 0.000141 | 0.000016 | 0.999081 | 0.000736 | 0.499156 | 0.000672 |
| 0.5 | 100 | 0.000143 | 0.000030 | 1.000046 | 0.000253 | 0.500002 | 0.000274 |
| 0.5 | 500 | 0.000329 | 0.000069 | 0.999171 | 0.000616 | 0.499202 | 0.000570 |
| 0.5 | 1000 | 0.000491 | 0.000141 | 0.998581 | 0.000730 | 0.498779 | 0.000584 |
| 1 | 100 | 0.000230 | 0.000074 | 0.999610 | 0.000381 | 0.499638 | 0.000359 |
| 1 | 500 | 0.000584 | 0.000217 | 0.999034 | 0.000597 | 0.499092 | 0.000541 |
| 1 | 1000 | 0.000908 | 0.000318 | 0.997592 | 0.001211 | 0.498045 | 0.000923 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos-Ábalos, E.M.; Gutiérrez-Sánchez, R.; Nafidi, A. Powers of the Stochastic Gompertz and Lognormal Diffusion Processes, Statistical Inference and Simulation. Mathematics 2020, 8, 588. https://doi.org/10.3390/math8040588
Ramos-Ábalos EM, Gutiérrez-Sánchez R, Nafidi A. Powers of the Stochastic Gompertz and Lognormal Diffusion Processes, Statistical Inference and Simulation. Mathematics. 2020; 8(4):588. https://doi.org/10.3390/math8040588
Chicago/Turabian StyleRamos-Ábalos, Eva María, Ramón Gutiérrez-Sánchez, and Ahmed Nafidi. 2020. "Powers of the Stochastic Gompertz and Lognormal Diffusion Processes, Statistical Inference and Simulation" Mathematics 8, no. 4: 588. https://doi.org/10.3390/math8040588
APA StyleRamos-Ábalos, E. M., Gutiérrez-Sánchez, R., & Nafidi, A. (2020). Powers of the Stochastic Gompertz and Lognormal Diffusion Processes, Statistical Inference and Simulation. Mathematics, 8(4), 588. https://doi.org/10.3390/math8040588






