Photo-Thermal Interactions in a Semiconducting Media with a Spherical Cavity under Hyperbolic Two-Temperature Model
Abstract
1. Introduction
2. Formulation of the Problem
3. Initial and Boundary Conditions
4. Method of Solution
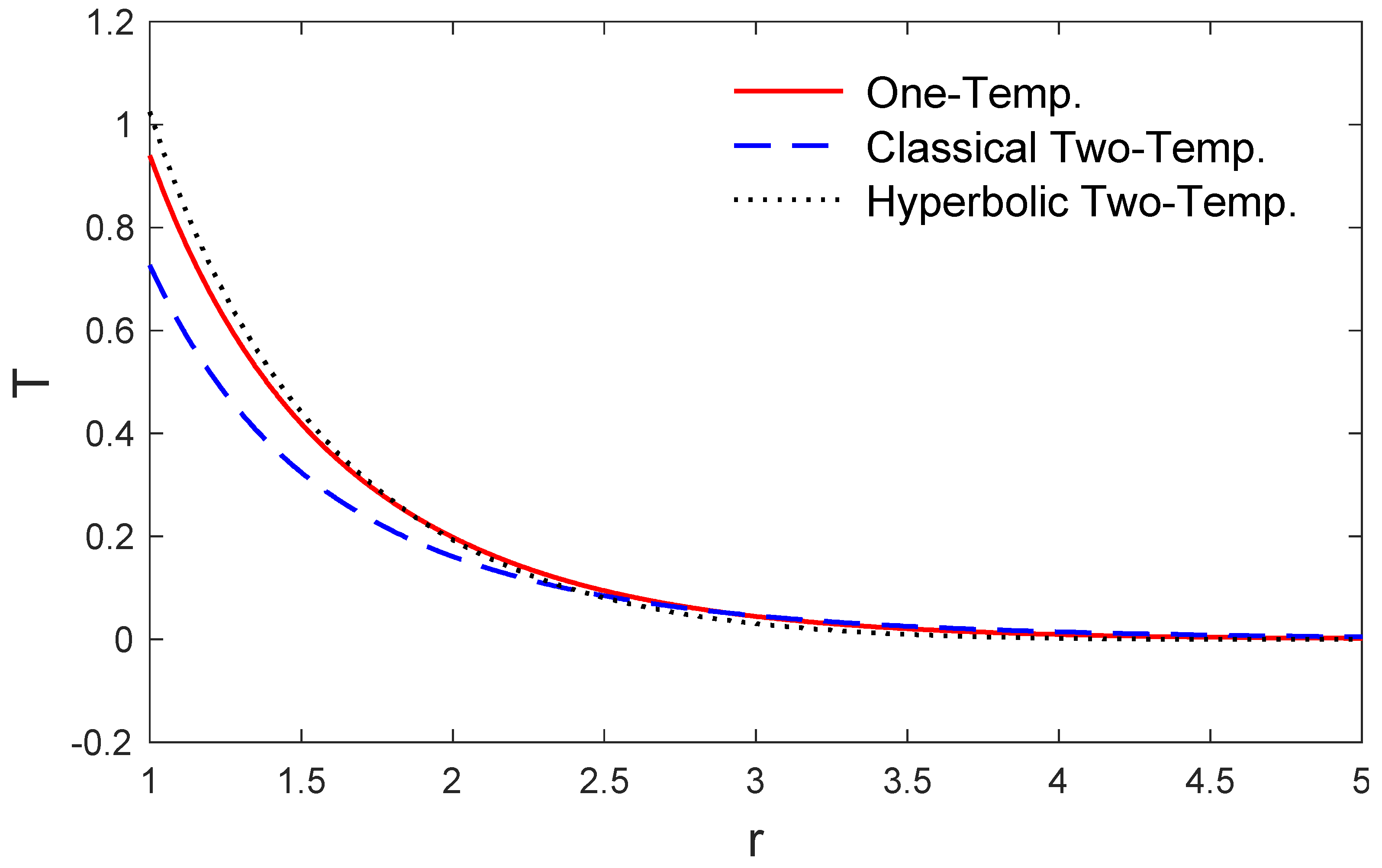
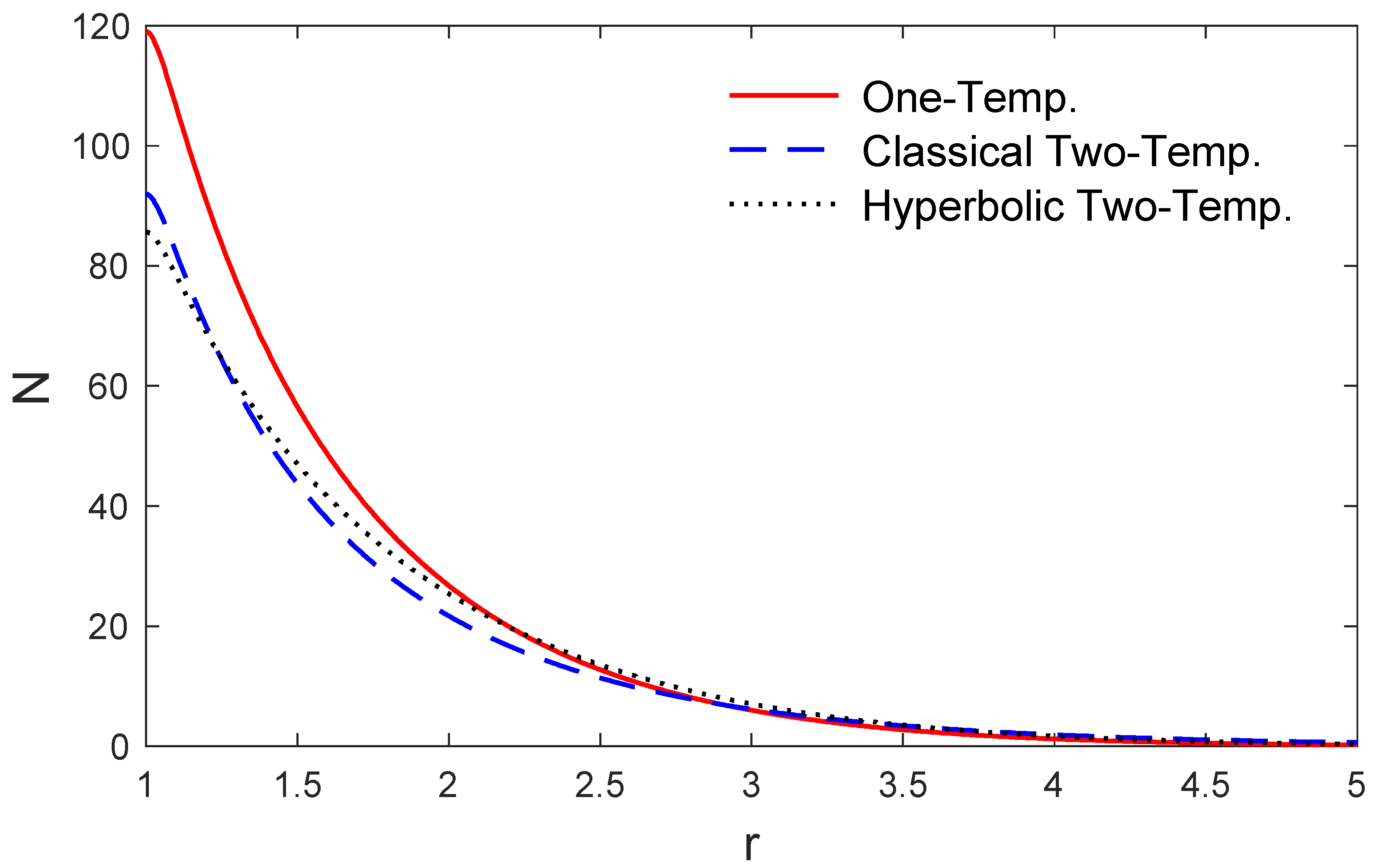
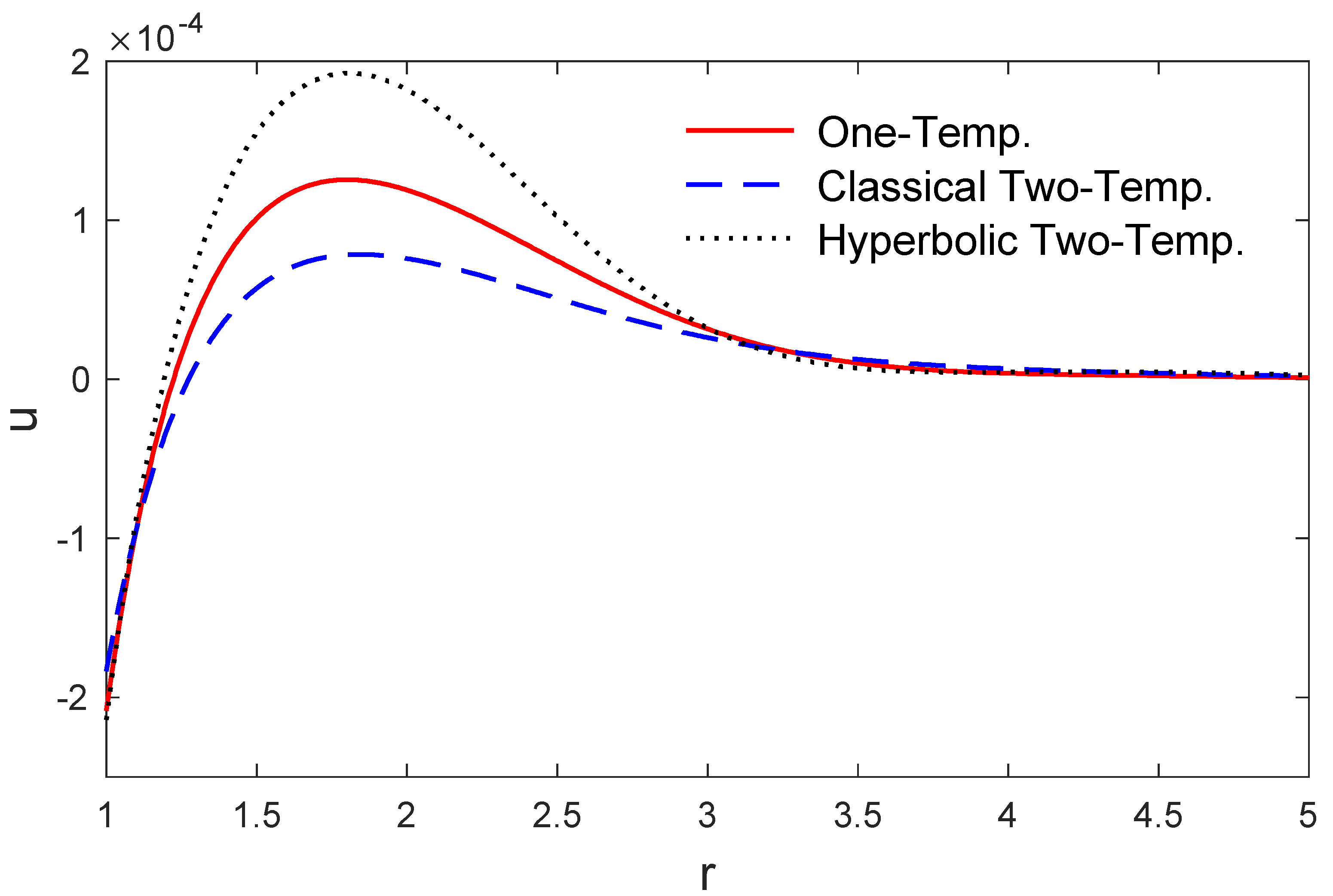
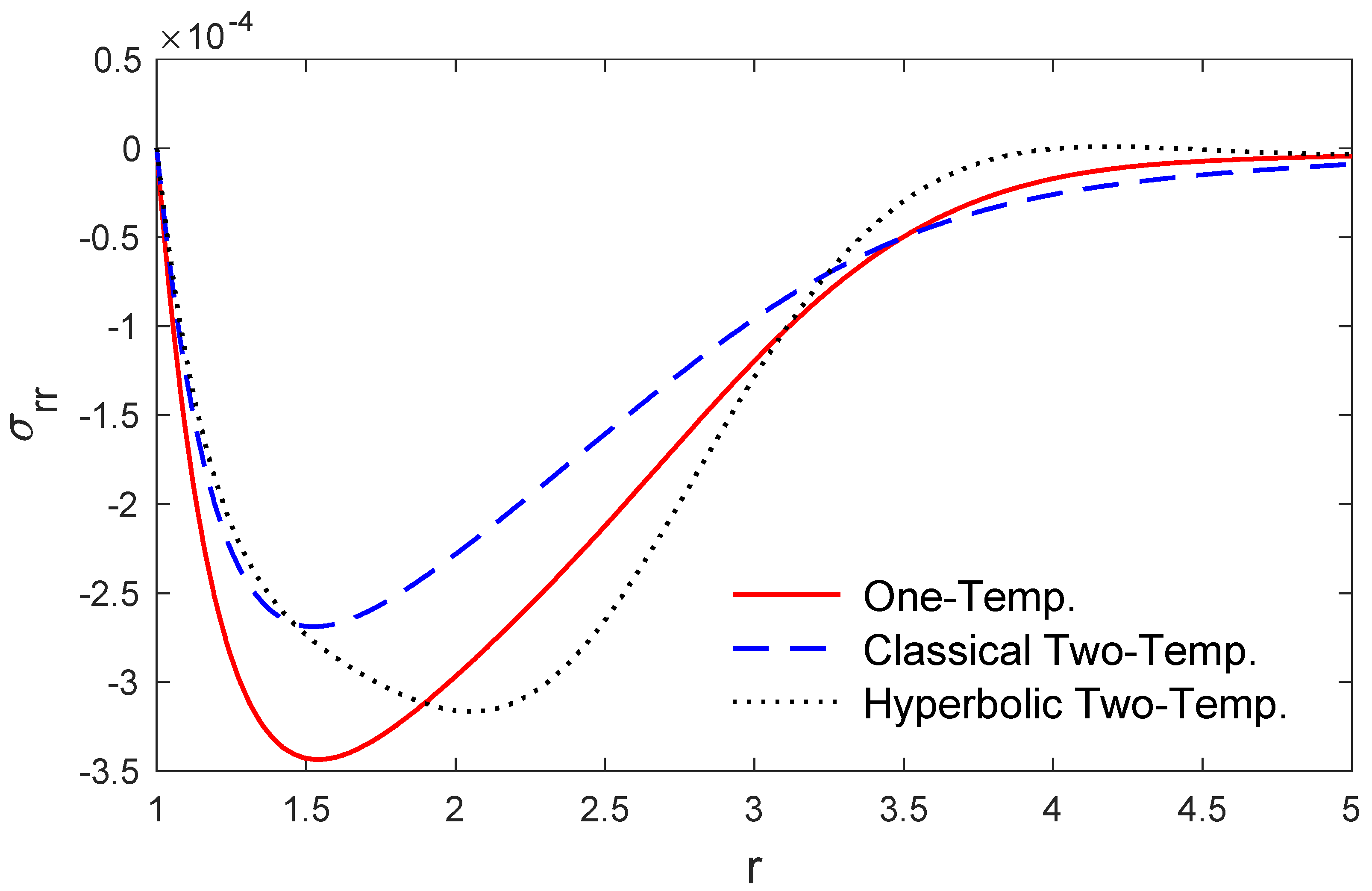
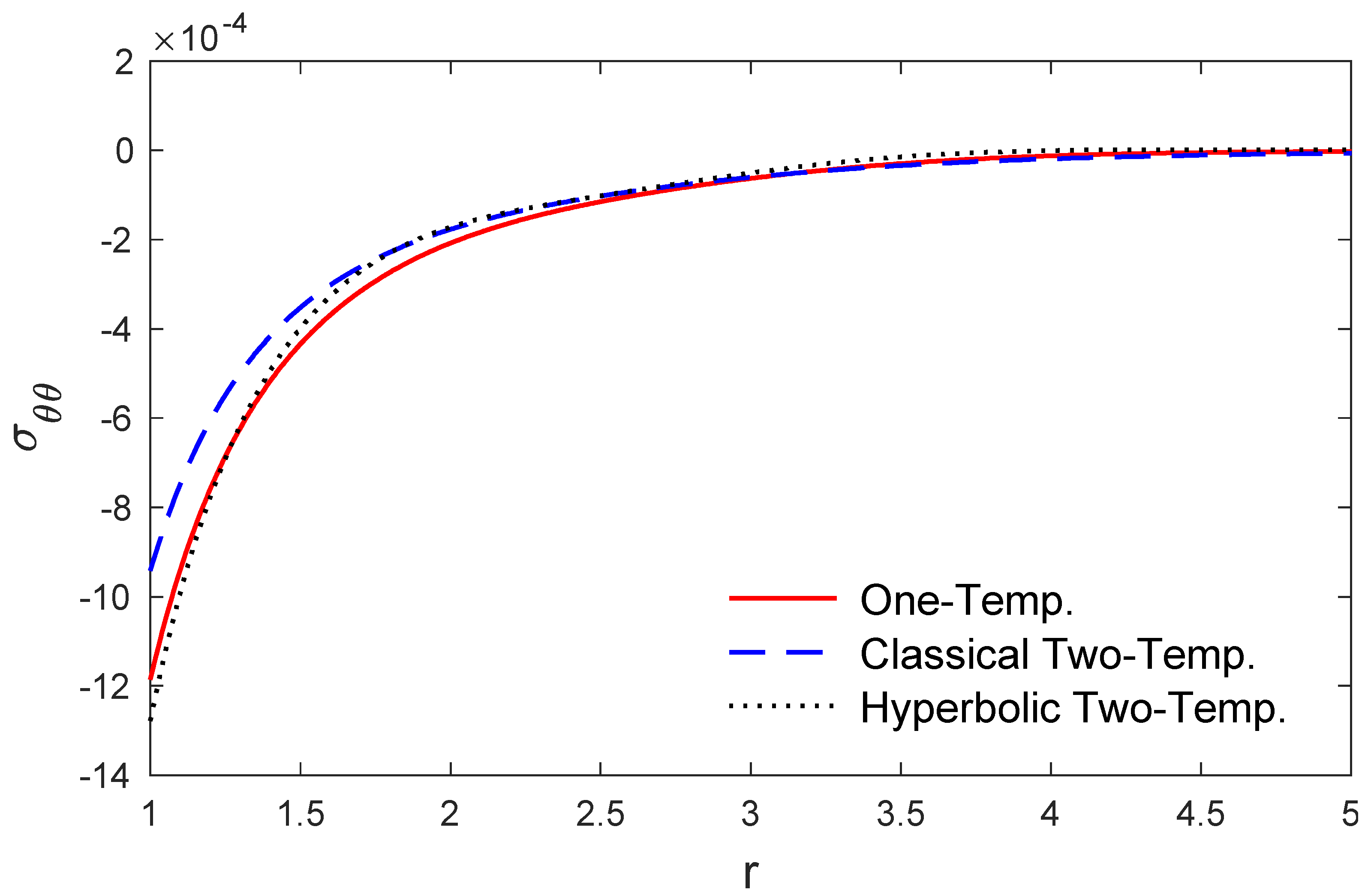
5. Numerical Results and Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gurtin, M.E.; Williams, W.O. An axiomatic foundation for continuum thermodynamics. Arch. Ration. Mech. Anal. 1967, 26, 83–117. [Google Scholar] [CrossRef]
- Chen, P.J.; Gurtin, M.E. On a theory of heat conduction involving two temperatures. Z. für Angew. Math. und Phys. 1968, 19, 614–627. [Google Scholar] [CrossRef]
- Chen, P.J.; Gurtin, M.E.; Williams, W.O. On the thermodynamics of non-simple elastic materials with two temperatures. Z. für Angew. Math. und Phys. 1969, 20, 107–112. [Google Scholar] [CrossRef]
- Ezzat, M.A.; El-Karamany, A.; Ezzat, S.M. Two-temperature theory in magneto-thermoelasticity with fractional order dual-phase-lag heat transfer. Nucl. Eng. Des. 2012, 252, 267–277. [Google Scholar] [CrossRef]
- Ezzat, M.A.; Youssef, H.M. Two-Temperature Theory in Three-Dimensional Problem for Thermoelastic Half Space Subjected to Ramp Type Heating. Mech. Adv. Mater. Struct. 2013, 21, 293–304. [Google Scholar] [CrossRef]
- Deswal, S.; Kalkal, K. Two Temperature Magneto-Thermoelasticity with Initial Stress: State Space Formulation. J. Thermodyn. 2013, 2013, 1–12. [Google Scholar] [CrossRef]
- Abbas, I.; Kumar, R.; Reen, L.S. Response of thermal source in transversely isotropic thermoelastic materials without energy dissipation and with two temperatures. Can. J. Phys. 2014, 92, 1305–1311. [Google Scholar] [CrossRef]
- Youssef, H.M.; El-Bary, A.A. Theory of hyperbolic two-temperature generalized thermoelasticity. Mater. Phys. Mech. 2018, 40, 158–171. [Google Scholar]
- Marin, M.; Vlase, S.; Ellahi, R.; Bhatti, M. On the Partition of Energies for the Backward in Time Problem of Thermoelastic Materials with a Dipolar Structure. Symmetry 2019, 11, 863. [Google Scholar] [CrossRef]
- Marin, M.; Ellahi, R.; Chirilă, A. On solutions of Saint-Venant’s problem for elastic dipolar bodies with voids. Carpathian J. Math. 2017, 33, 219–232. [Google Scholar]
- Todorović, D.M. Plasma, thermal, and elastic waves in semiconductors. Rev. Sci. Instrum. 2003, 74, 582. [Google Scholar]
- Todorović, D.M. Photothermal and electronic elastic effects in microelectromechanical structures. Rev. Sci. Instrum. 2003, 74, 578. [Google Scholar]
- Song, Y.; Todorović, D.M.; Cretin, B.; Vairac, P. Study on the generalized thermoelastic vibration of the optically excited semiconducting microcantilevers. Int. J. Solids Struct. 2010, 47, 1871–1875. [Google Scholar] [CrossRef]
- Yasein, M.; Mabrouk, N.; Lotfy, K.; El-Bary, A. The influence of variable thermal conductivity of semiconductor elastic medium during photothermal excitation subjected to thermal ramp type. Results Phys. 2019, 15, 102766. [Google Scholar] [CrossRef]
- Ailawalia, P.; Kumar, A. Ramp Type Heating in a Semiconductor Medium under Photothermal Theory. Silicon 2019, 12, 347–356. [Google Scholar] [CrossRef]
- Abbas, I.; Hobiny, A. Photo-thermal-elastic interaction in an unbounded semiconducting medium with spherical cavity due to pulse heat flux. Waves Random Complex Media 2017, 28, 1–13. [Google Scholar] [CrossRef]
- Lotfy, K.; Tantawi, R.S.; Anwer, N. Response of Semiconductor Medium of Variable Thermal Conductivity Due to Laser Pulses with Two-Temperature through Photothermal Process. Silicon 2019, 11, 2719–2730. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abbas, I.A. Nonlinear transient thermal stress analysis of temperature-dependent hollow cylinders using a finite element model. Int. J. Struct. Stab. Dy. 2014, 14, 1450025. [Google Scholar] [CrossRef]
- Mohamed, R.; Abbas, I.; Abo-Dahab, S. Finite element analysis of hydromagnetic flow and heat transfer of a heat generation fluid over a surface embedded in a non-Darcian porous medium in the presence of chemical reaction. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1385–1395. [Google Scholar] [CrossRef]
- Abbas, I.; El-Amin, M.; Salama, A.; El-Amin, M.F. Effect of thermal dispersion on free convection in a fluid saturated porous medium. Int. J. Heat Fluid Flow 2009, 30, 229–236. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abbas, I. A generalized thermoelasticity problem of an annular cylinder with temperature-dependent density and material properties. Int. J. Mech. Sci. 2014, 84, 54–60. [Google Scholar] [CrossRef]
- Abbas, I.; Zenkour, A.M. The Effect of Rotation and Initial Stress on Thermal Shock Problem for a Fiber-Reinforced Anisotropic Half-Space Using Green-Naghdi Theory. J. Comput. Theor. Nanosci. 2014, 11, 331–338. [Google Scholar] [CrossRef]
- Abbas, I.; Kumar, R. Deformation Due to Thermal Source in Micropolar Generalized Thermoelastic Half-Space by Finite Element Method. J. Comput. Theor. Nanosci. 2014, 11, 185–190. [Google Scholar] [CrossRef]
- Abbas, I. Nonlinear transient thermal stress analysis of thick-walled FGM cylinder with temperature-dependent material properties. Meccanica 2014, 49, 1697–1708. [Google Scholar] [CrossRef]
- Marin, M. Lagrange identity method for microstretch thermoelastic materials. J. Math. Anal. Appl. 2010, 363, 275–286. [Google Scholar] [CrossRef]
- Marin, M.; Nicaise, S. Existence and stability results for thermoelastic dipolar bodies with double porosity. Contin. Mech. Thermodyn. 2016, 28, 1645–1657. [Google Scholar] [CrossRef]
- Song, Y.; Bai, J.T.; Ren, Z.Y. Study on the reflection of photothermal waves in a semiconducting medium under generalized thermoelastic theory. Acta Mech. 2012, 223, 1545–1557. [Google Scholar] [CrossRef]
- Mandelis, A.; Nestoros, M.; Christofides, C. Thermoelectronic-wave coupling in laser photothermal theory of semiconductors at elevated temperatures. Opt. Eng. 1997, 36, 459. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abouelregal, A.E. Effect of temperature dependency on constrained orthotropic unbounded body with a cylindrical cavity due to pulse heat flux. J. Therm. Sci. Technol. 2015, 10, JTST0019. [Google Scholar] [CrossRef]
- Das, N.C.; Lahiri, A.; Giri, R.R. Eigenvalue approach to generalized thermoelasticity. Indian J. Pure Appl. Math. 1997, 28, 1573–1594. [Google Scholar]
- Abbas, I. Eigenvalue approach in a three-dimensional generalized thermoelastic interactions with temperature-dependent material properties. Comput. Math. Appl. 2014, 68, 2036–2056. [Google Scholar] [CrossRef]
- Abbas, I. Eigenvalue approach for an unbounded medium with a spherical cavity based upon two-temperature generalized thermoelastic theory. J. Mech. Sci. Technol. 2014, 28, 4193–4198. [Google Scholar] [CrossRef]
- Abbas, I. A Dual Phase Lag Model on Thermoelastic Interaction in an Infinite Fiber-Reinforced Anisotropic Medium with a Circular Hole. Mech. Based Des. Struct. Mach. 2015, 43, 501–513. [Google Scholar] [CrossRef]
- Abbas, I. The effects of relaxation times and a moving heat source on a two-temperature generalized thermoelastic thin slim strip. Can. J. Phys. 2015, 93, 585–590. [Google Scholar] [CrossRef]
- Song, Y.; Todorović, D.M.; Cretin, B.; Vairac, P.; Xu, J.; Bai, J. Bending of Semiconducting Cantilevers Under Photothermal Excitation. Int. J. Thermophys. 2014, 35, 305–319. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzahrani, F.S.; Abbas, I.A. Photo-Thermal Interactions in a Semiconducting Media with a Spherical Cavity under Hyperbolic Two-Temperature Model. Mathematics 2020, 8, 585. https://doi.org/10.3390/math8040585
Alzahrani FS, Abbas IA. Photo-Thermal Interactions in a Semiconducting Media with a Spherical Cavity under Hyperbolic Two-Temperature Model. Mathematics. 2020; 8(4):585. https://doi.org/10.3390/math8040585
Chicago/Turabian StyleAlzahrani, Faris S., and Ibrahim A. Abbas. 2020. "Photo-Thermal Interactions in a Semiconducting Media with a Spherical Cavity under Hyperbolic Two-Temperature Model" Mathematics 8, no. 4: 585. https://doi.org/10.3390/math8040585
APA StyleAlzahrani, F. S., & Abbas, I. A. (2020). Photo-Thermal Interactions in a Semiconducting Media with a Spherical Cavity under Hyperbolic Two-Temperature Model. Mathematics, 8(4), 585. https://doi.org/10.3390/math8040585




