Mathematical Models with Buckling and Contact Phenomena for Elastic Plates: A Review
Abstract
1. Introduction
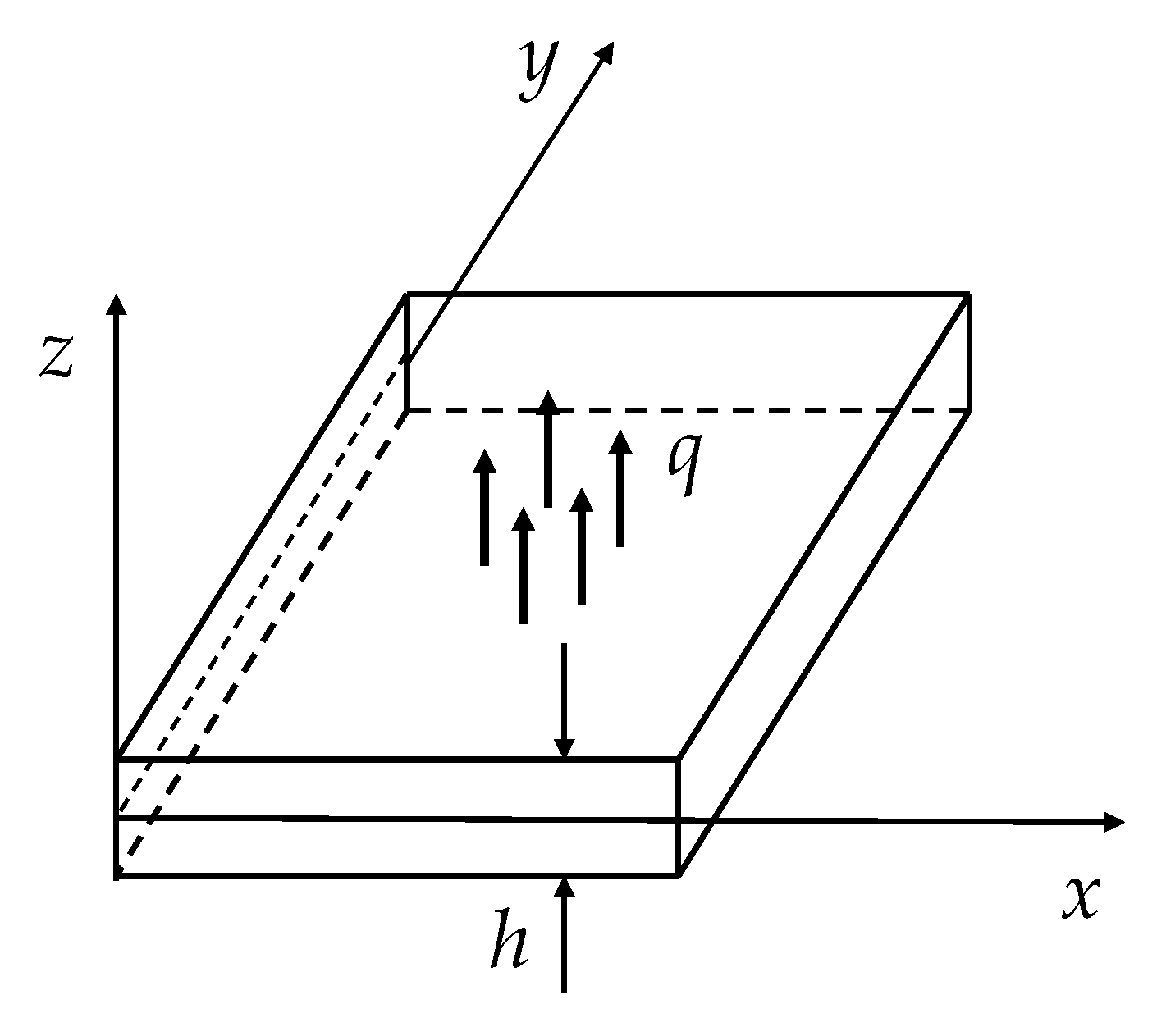
1.1. Governing Equations
- (1)
- The Airy equation for plane stress:
- (2)
- The linear plate bending Kirchhoff–Love’s model in Equation (1) (originated from Germain’s equation).
1.2. Boundary Conditions
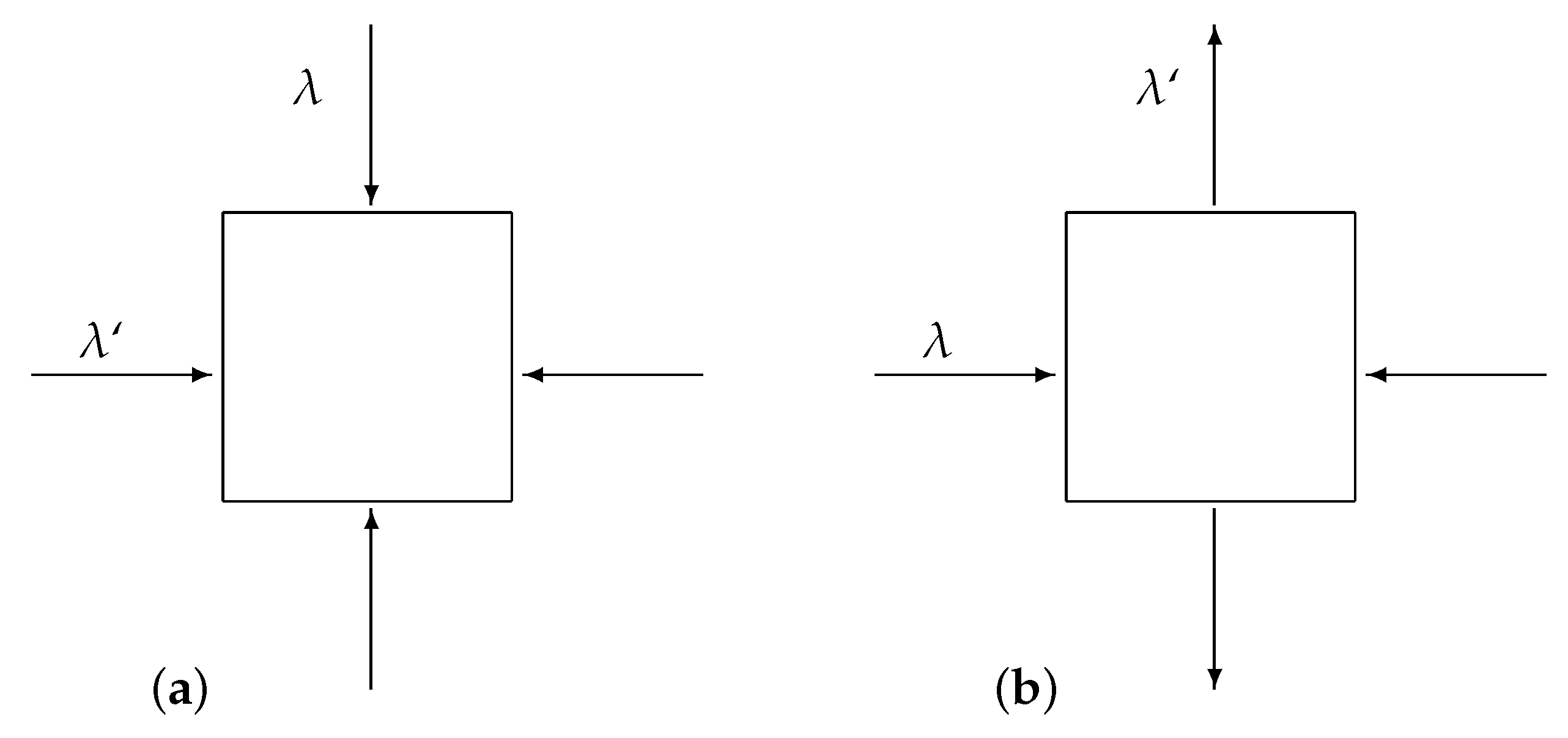
2. Buckling Phenomenon
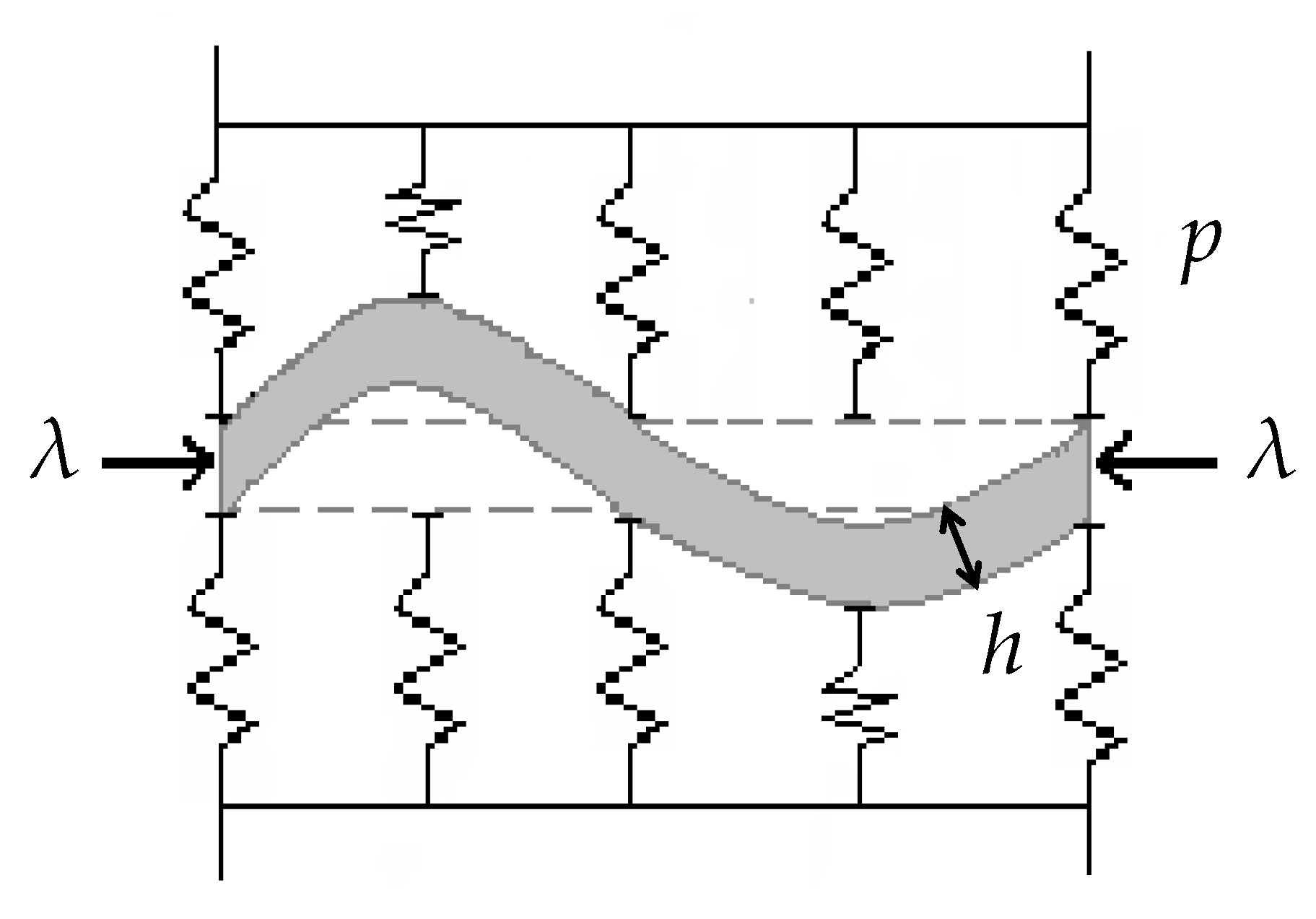
3. Contact Models with Elastic Foundations
4. Delamination of the Buckled Plate
5. Nonlinear Dynamic Equations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Duvaut, G.; Lions, G. Les Inequations en Mecaniques et en Physiques; Dunod: Paris, France, 1972. [Google Scholar]
- Ciarlet, P.G. Mathematical Elasticity: Volume II: Theory of Plates; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Ciarlet, P.G.; Rabier, P. Les équations de von Kármán; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Pergamon Press: Oxford, UK, 1970. [Google Scholar]
- Ambartsumyan, S.A. Theory of Anisotropic Plates: Strength, Stability and Vibrations; Hemisphere Publisher: New York, NY, USA, 1991. [Google Scholar]
- Panc, V. Theories of Elastic Plates Series: Mechanics of Surface Structure; Springer: Berlin/Heidelberg, Germany, 1975. [Google Scholar]
- Lekhnitskii, S.G. Theory of Elasticity of an Anisotropic Elastic Body; Mir Publishers: Moscow, Russia, 1981. [Google Scholar]
- Goldenveizer, A.L.; Kolos, A.V. On the derivation of two-dimensional equations in the theory of thin elastic plates. J. Appl. Math. Mech. 1965, 29, 151–166. [Google Scholar] [CrossRef]
- Lubliner, J. Platicity Theory; Macmillian Publishing Company: New York, NY, USA, 1990. [Google Scholar]
- Lurie, A.I. Theory of Elasticity. In Foundations of Engineering Mechanics; Springer: Berlin/Heidelberg, Germany, 2005. (In English) [Google Scholar]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Inman, D.J. Vibration with Control; Wiley: Chichester, UK, 2006. [Google Scholar]
- Vashakmadze, T.S. The Theory of Anisotropic Elastic Plates; Kluwer Academic Publishers: Alphen aan den Rijn, The Netherlands, 1999. [Google Scholar]
- Reddy, J.N. Theory and Analysis of Elastic Plates and Shells; Taylor and Francis: Abingdon, UK, 2007. [Google Scholar]
- Le van, A. Nonlinear Theory of Elastic Plates; ISTE Press-Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Maceri, A. Theory of Elasticity; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Wu, H.-C. Continuum Mechanics and Plasticity; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Szilard, R. Theories and Applications of Plate Analysis: Classical, Numerical and Engineering Methods; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Altenbach, J.; Altenbach, H.; Eremeyev, V.A. On generalized Cosserat-type theories of plates and shells: A short review and bibliography. Arch. Appl. Mech. 2010, 80, 73–92. [Google Scholar] [CrossRef]
- Ma, H.M.; Gao, X.-L.; Reddy, J.N. A non-classical Mindlin plate model based on a modified couple stress theory. Acta Mech. 2011, 220, 217–235. [Google Scholar] [CrossRef]
- Niiranen, J.; Niemi, A.H. Variational formulations and general boundary conditions for sixth order boundary value problems of gradient elastic Kirchhoff plates. Europ. J. Mech.-A/Solid 2017, 61, 164–179. [Google Scholar] [CrossRef]
- Zozulya, V.V. Higher order couple stress theory of plates and shells. ZAMM-J. Appl. Math. Mech. 2018, 98, 1834–1863. [Google Scholar] [CrossRef]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Antman, S.S. Nonlinear Problems of Elasticity; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Lagnese, J.E. Boundary Stabilization of Thin Plates; SIAM: Philadelphia, PA, USA, 1989. [Google Scholar]
- Sokolnikoff, I.S. Mathematical Theory of Elasticity; Krieger Publishing Company: Malabar, FL, USA, 1983. [Google Scholar]
- Vasiliev, V.V.; Morozov, E.V. Advanced Mechanics of Composite Materials and Structural Elements, 3rd ed.; Elsevier, ScienceDirect: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Stavroulakis, G.; Panagiotopoulos, P.D. The delamination effect in laminated von Kármán plates under unilateral boundary conditions. A variational-hemivariational inequality approach. J. Elast. 1990, 23, 69–96. [Google Scholar] [CrossRef]
- Storakers, B.; Andersson, B. Nonlinear plate theory applied to delamination in composites. J. Mech. Phys. Solids 1988, 36, 689–718. [Google Scholar] [CrossRef]
- Xue, J.; Xia, F.; Zhang, J.; Chen, S.; Xiong, Y.; Tan, Z.; Liu, R.; Yuan, H. Multiscale studies on the nonlinear vibration of delaminated composite laminates–global vibration mode with micro buckles on the interfaces. Sci. Rep. 2017, 7, 4468. [Google Scholar] [CrossRef]
- Haghani, A.; Mondali, M.; Faghidian, S.A. Linear and nonlinear flexural analysis of higher-order shear deformation laminated plates with circular delamination. Acta Mech. 2018, 229, 1631–1648. [Google Scholar] [CrossRef]
- Ohtake, K.; Oden, J.T.; Kikuchi, N. Analysis of Certain Unilateral Problems in von Kármán Plate Theory by a Penalty Method—part 1. A Variational Principle with Penalty. Comput. Meth. Appl. Mech. Eng. 1980, 24, 187–213. [Google Scholar] [CrossRef]
- Ohtake, K.; Oden, J.T.; Kikuchi, N. Analysis of Certain Unilateral Problems in von Kármán Plate Theory by a Penalty Method—part 2. A Variational Principle with Penalty. Comput. Meth. Appl. Mech. Eng. 1980, 24, 317–337. [Google Scholar] [CrossRef]
- Borisovich, A.; Dymkowska, J.; Szymczak, C. Bifurcations in von Kármán problem for rectangular, thin, elastic plate resting on elastic foundation of Winkler type. AMRX (Appl. Math. Res. eXpress) 2006, 2006, 1–24. [Google Scholar] [CrossRef]
- Malekzadeh, P.; Setoodeh, A.R. Large deformation analysis of moderately thick laminated plate on nonlinear elastic foundations by DQM. Comp. Struct. 2007, 80, 569–579. [Google Scholar] [CrossRef]
- Muradova, A.D.; Stavroulakis, G.E. A unilateral contact model with buckling in von Kármán plates. Nonlin. Anal. Real World Appl. 2007, 8, 1261–1271. [Google Scholar] [CrossRef]
- Muradova, A.D.; Stavroulakis, G.E. Postbuckling Behaviour of a Rectangular Plate Surrounded by Nonlinear Elastic Supports, Recent Advances in Contact Mechanics. In Lecture Notes in Applied and Computational Mechanics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 56, pp. 189–204. [Google Scholar]
- Muradova, A.D.; Stavroulakis, G.E. Buckling and postbuckling analysis of rectangular plates resting on elastic foundations with the use of the spectral method. Comput. Methods Appl. Mech. Eng. 2012, 205–208, 213–220. [Google Scholar] [CrossRef]
- Muradova, A.D.; Stavroulakis, G.E. Nonlinear Time Spectral Analysis for a Dynamic Contact Model with Buckling for an Elastic Plate. Key Eng. Mater. 2014, 618, 227–239. [Google Scholar] [CrossRef]
- Muradova, A.D.; Kurutz, M.; Stavroulakis, G.E. Buckling simulation of a plate, embedded in a unilaterally supported enviroment. Mech. Based Des. Struct. Mach. 2009, 37, 349–370. [Google Scholar] [CrossRef]
- Fichera, G. Boundary value problems of elasticity with unilateral constraints. In Linear Theories of Elasticity and Thermoelasticity; Springer: Berlin/Heidelberg, Germany, 1973; pp. 391–424. [Google Scholar]
- Caloz, G.; Rappaz, J. Numerical analysis for nonlinear and bifurcation problems. Handbook of Numerical Analysis; North Holland: Amsterdam, The Netherlands, 1997; pp. 487–637. [Google Scholar]
- Matkowsky, B.J.; Putnick, L.J. Multiple buckled states of rectangular plates. J. Nonlin. Mech. 1974, 9, 89–103. [Google Scholar] [CrossRef]
- Chien, C.S.; Chang, S.L.; Mei, Z. Tracing the buckling of a rectangular plate with the Block GMRES method. J. Comput. Appl. Math. 2001, 136, 199–218. [Google Scholar] [CrossRef][Green Version]
- Chien, C.S.; Gong, S.Y.; Mei, Z. Mode jumping in the von Kármán equations. SIAM J. Sci. Comput. 2000, 22, 1354–1385. [Google Scholar] [CrossRef]
- Muradova, A.D. Numerical techniques for linear and nonlinear eigenvalue problems in the theory of elasticity. ANZIAM J. 2004, 46, C426–C438. [Google Scholar] [CrossRef][Green Version]
- Muradova, A.D. The spectral method and numerical continuation algorithm for the von Kármán problem with postbuckling behaviour of solution. Adv. Comput. Math. 2008, 29, 179–206. [Google Scholar] [CrossRef]
- Muradova, A.D. A time spectral method for solving the nonlinear dynamic equations of a rectangular elastic plate. J. Eng. Math. 2015, 92, 83–101. [Google Scholar] [CrossRef]
- Dossou, K.; Pierre, R. A Newton-GMRES approach for the analysis of the postbuckling behavior of the solutions of the von Kármán equations. SIAM J. Sci. Comput. 2003, 24, 1994–2012. [Google Scholar] [CrossRef][Green Version]
- Bloom, F.; Coffin, D. Handbook of Thin Plate Buckling and Postbuckling; Chapman and Hall/CRC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Vorovich, I.I. Nonlinear theory of Shallow Shells. In Applied Mathematical Sciences; Springer: New York, NY, USA, 1999; p. 133. [Google Scholar]
- Chien, C.S.; Kuo, Y.J.; Mei, Z. Bifurcations of the von Kármán equations with Robin boundary conditions. Comput. Math. Appl. 1999, 38, 85–112. [Google Scholar] [CrossRef]
- Schaeffer, D.G.; Golubitsky, M. Boundary conditions and mode jumping in the buckling of a rectangular plate. Comm. Math. Phys. 1979, 69, 209–236. [Google Scholar] [CrossRef]
- Muradova, A.D.; Stavroulakis, G.E. The projective-iterative method and neural network estimation for buckling of elastic plates in nonlinear theory. Commun. Nonlin. Sci. Num. Sim. 2007, 12, 1068–1088. [Google Scholar] [CrossRef]
- Holder, E.J.; Schaeffer, D.G. Boundary conditions and mode jumping in the von Kármán’s equations. SIAM J. Math. Anal. 1984, 15, 446–458. [Google Scholar] [CrossRef]
- Dillard, D.A.; Mukherjee, B.; Karnal, P.; Batra, R.C.; Frechette, J. A review of Winkler’s foundation and its profound influence on adhesion and soft matter applications. Soft Matter 2018, 14, 3669–3683. [Google Scholar] [CrossRef]
- Wang, Y.H.; Tham, L.G.; Cheung, Y.K. Beams and plates on elastic foundations: A review. Progress Struct. Eng. Mater. 2005, 7, 174–182. [Google Scholar] [CrossRef]
- Wriggers, P. Computational Contact Mechanica; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Selvadurai, A.P.S. Elastic Analysis of Soil-Foundation Interaction; Elsevier: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Dumir, P.C.; Bhakar, A. Nonlinear static analysis of rectangular plates on elastic foundations by the orthogonal point collocation method. Comp. Meth. Appl. Mech. Eng. 1988, 67, 111–124. [Google Scholar] [CrossRef]
- Katsikadelis, J.T.; Yiotis, A.J. The BEM for plates of variable thickness on nonlinear biparametric elastic foundation. An analog equation solution. J. Eng. Math. 2003, 46, 313–330. [Google Scholar] [CrossRef]
- Papanikolaou, V.K.; Doudoumis, I.N. Elastic analysis and application tables of rectangular plates with unilateral contact support conditions. Comput. Struct. 2001, 79, 2559–2578. [Google Scholar] [CrossRef]
- Yu, L.H.; Wang, C.Y. Buckling of Rectangular Plates on an Elastic Foundation Using the Levy Method. AIAA J. 2008, 46, 3163–3167. [Google Scholar] [CrossRef]
- Bielski, W.R.; Telega, J.J. Existence of solutions to obstacle problems for linear and nonlinear elastic plates. Math. Comput. Model. 1998, 28, 55–66. [Google Scholar] [CrossRef]
- Shen, H.-S. Postbuckling analysis of orthotropic rectangular plates on nonlinear elastic foundations. Eng. Struct. 1995, 17, 407–412. [Google Scholar] [CrossRef]
- de Holanda, A.S.; Goncalves, P.B. Postbuckling analysis of plates resting on a tensionless elastic foundation. J. Eng. Mech.-ASCE 2003, 129, 438–448. [Google Scholar] [CrossRef]
- Shahwan, K.W.; Waas, A.M. A mechanical model for the buckling of unilaterally constrained rectangular plates. Inter. J. Solids Struct. 1994, 31, 75–87. [Google Scholar] [CrossRef]
- Shahwan, K.W.; Waas, A.M. Buckling on unilaterally constrained infinite plates. J. Eng. Mech.-ASCE 1998, 124, 127–136. [Google Scholar] [CrossRef]
- Chai, H. Contact buckling and postbuckling of thin rectangular plates. J. Mech. Phys. Solids 2001, 49, 209–230. [Google Scholar] [CrossRef]
- Ma, X.; Butterworth, J.W.; Clifton, C. Compressive buckling analysis of plates in unilateral contact. Int. J. Solids Struct. 2007, 44, 2852–2862. [Google Scholar] [CrossRef]
- Biggers, S.B.; Pageau, S.S. Shear buckling response of tailored composite plates. AIAA J. 1994, 32, 1100–1103. [Google Scholar] [CrossRef]
- Shen, H.; Li, Q.S. Postbuckling of shear deformable laminated plates resting on a tensionless elastic foundation subjected to mechanical or thermal loading. Int. J. Solids Struct. 2004, 41, 4769–4785. [Google Scholar] [CrossRef]
- Mukherjee, Y.; Xie, Z.; Ingraffea, A.R. Delamination buckling of laminated plates. Int. J. Num. Meth. Eng. 1991, 32, 1321–1337. [Google Scholar] [CrossRef]
- Uy, B.; Bradford, M.A. Elastic local buckling of steel plates in composite steel-concrete members. Eng. Struct. 1996, 18, 193–200. [Google Scholar] [CrossRef]
- Ovesy, H.-R.; Kharazi, M. Stability Analysis of Composite Plates with Through-the-Width Delamination. J. Eng. Mech. 2011, 137, 87–100. [Google Scholar] [CrossRef]
- Peck, S.O.; Springer, G.S. The Behavior of Delaminations in Composite Plates-Analytical and Experimental Results. J. Compos. Mater. 1991, 25, 907–929. [Google Scholar] [CrossRef]
- Sahoo, S.S.; Panda, S.K.; Sen, D. Effect of Delamination on Static and Dynamic Behavior of Laminated Composite Plate. AIAA J. 2016, 54, 2530–2544. [Google Scholar] [CrossRef]
- Yeh, M.-K.; Fang, L.-B.; Kao, M.-H. Bending behavior of delaminated composite plates with contact effects. Compos. Struct. 1997, 39, 347–356. [Google Scholar] [CrossRef]
- Tiwari, P.; Barman, S.K.; Maiti, D.K.; Maity, D. Free Vibration Analysis of Delaminated Composite Plate Using 3D Degenerated Element. J. Aeros. Eng. 2019, 32, 4019070. [Google Scholar] [CrossRef]
- Della, C.N.; Shu, D. Vibration of Delaminated Composite Laminates: A Review. Appl. Mech. Rev. 2007, 60, 1–20. [Google Scholar] [CrossRef]
- Obdrźálek, V.; Vrbka, J. On buckling of a plate with multiple delaminations. Eng. Mech. 2010, 17, 37–47. [Google Scholar]
- Demyanov, V.F.; Stavroulakis, G.E.; Polyakova, L.N.; Panagiotopoulos, P.D. Quasidifferentiability and Nonsmooth Modelling in Mechanics, Engineering and Economics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Chau, O.; Fernández, J.R.; Shillor, M.; Sofonea, M. Variational and numerical analysis of a quasistatic viscoelastic contact problem with adhesion. J. Comput. Appl. Math. 2003, 159, 431–465. [Google Scholar] [CrossRef]
- Lasiecka, I. Weak, classical and intermediate solutions to full von Kármán system of dynamic nonlinear elasticity. Appl. Anal. 1998, 68, 121–145. [Google Scholar]
- Matkowsky, B.J.; Putnick, L.J. Uniqueness in the nonlinear dynamic bending of elastic plates. J. Elast. 1975, 5, 167–171. [Google Scholar] [CrossRef]
- Shivamoggi, B.K. Dynamic buckling of a thin elastic plate: Non-linear theory. J. Sound Vib. 1977, 54, 75–82. [Google Scholar] [CrossRef]
- Morozov, N.F. Nonlinear vibrations of thin plates with allowance for rotational inertia. Dokl. Akad. Nauk SSSR 1967, 176, 1137–1141. [Google Scholar]
- Chia, C.-Y. Nonlinear Analysis of Plates; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Nath, Y.; Kumar, S. Chebyshev series solution to non-linear boundary value problems in rectangular domain. Comput. Methods Appl. Mech. Eng. 1995, 125, 41–52. [Google Scholar] [CrossRef]
- Gordnier, R.E.; Fithen, R. Coupling of a nonlinear finite element structural method with Navier-Stokes solver. In Proceedings of the 31st Fluid Dynamics Conference, Anaheim, CA, USA, 11–14 June 2001. [Google Scholar]
- Kirby, R.M.; Yosibash, Z. Solution of von-Karman dynamic non-linear plate equations using a pseudo-spectral method. Comput. Methods Appl. Mech. Eng. 2004, 193, 575–599. [Google Scholar] [CrossRef]
- Kanto, Y.; Yagawa, G. A dynamic contact buckling analysis by the penalty finite element method. Num. Meth. Eng. 1990, 24, 755–774. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, Q.; Qiao, P. A Critical Review on Buckling and PostBuckling Analysis of Composite Structures. Front. Aeros. Eng. 2013, 2, 157–168. [Google Scholar]
- Patil, A.; Kolhe, A.M.; Shaikh, A.S.A.W. Review of buckling in various structures like plate and shells. IJRET 2014, 3, 396–402. [Google Scholar]
- Bisagni, C.; Vescovini, R. Analytical Formulation for Local Buckling and Post-buckling Analysis of Stiffened Laminated Panels. Thin-Walled Struct. 2009, 47, 318–334. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muradova, A.D.; Stavroulakis, G.E. Mathematical Models with Buckling and Contact Phenomena for Elastic Plates: A Review. Mathematics 2020, 8, 566. https://doi.org/10.3390/math8040566
Muradova AD, Stavroulakis GE. Mathematical Models with Buckling and Contact Phenomena for Elastic Plates: A Review. Mathematics. 2020; 8(4):566. https://doi.org/10.3390/math8040566
Chicago/Turabian StyleMuradova, Aliki D., and Georgios E. Stavroulakis. 2020. "Mathematical Models with Buckling and Contact Phenomena for Elastic Plates: A Review" Mathematics 8, no. 4: 566. https://doi.org/10.3390/math8040566
APA StyleMuradova, A. D., & Stavroulakis, G. E. (2020). Mathematical Models with Buckling and Contact Phenomena for Elastic Plates: A Review. Mathematics, 8(4), 566. https://doi.org/10.3390/math8040566





