Probability-Based Wildfire Risk Measure for Decision-Making
Abstract
1. Introduction
‘How can we develop tractable models that can be used to help determine when and where to implement fuel treatments on large flammable forest and wildland landscapes?’
2. Fire Probability
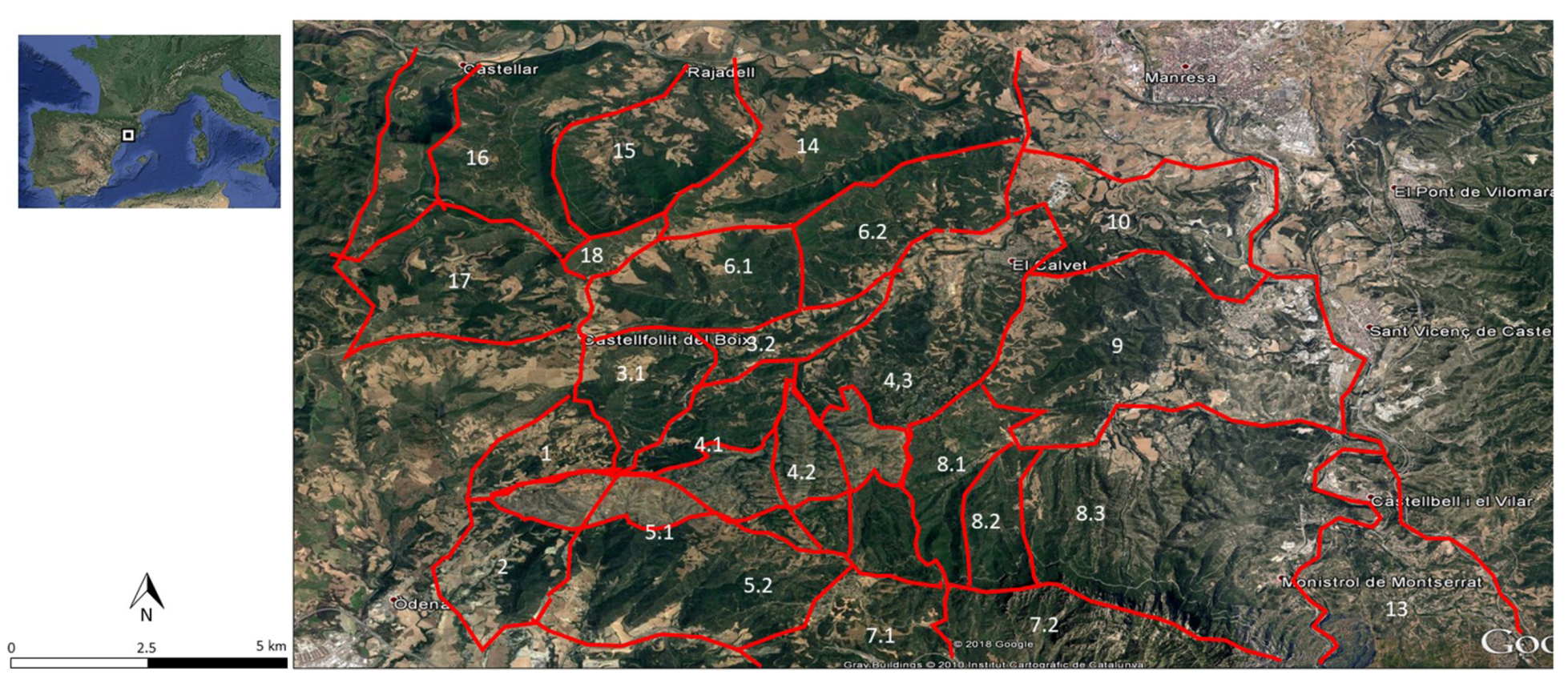
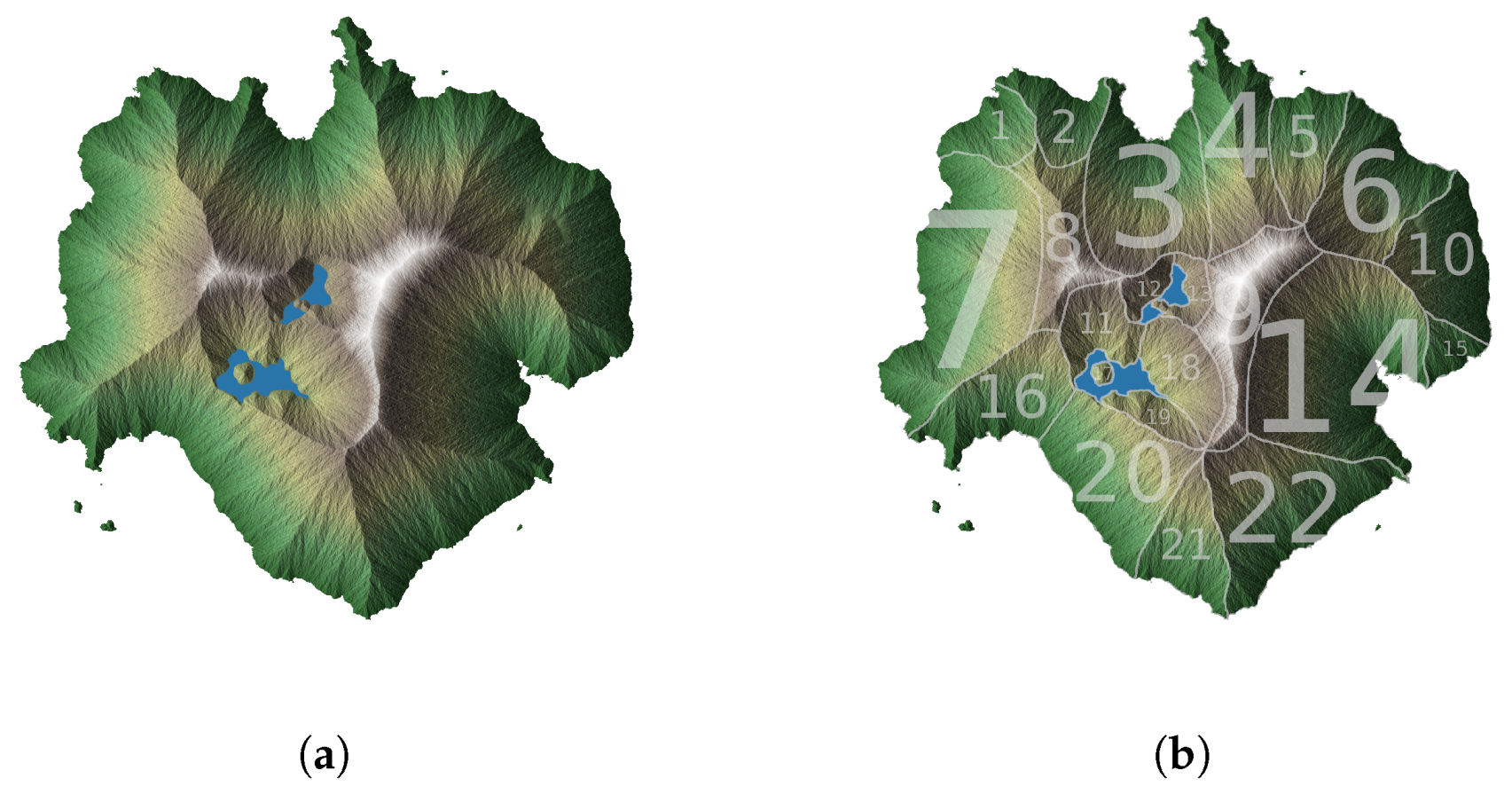
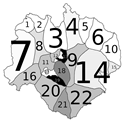
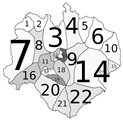
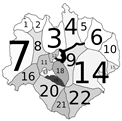
- 1st assumption: Landscape can be divided into homogeneous areas: sectors. A sector is a portion of land where in case of a fire, the only possible way of extinguishing it will be within its boundaries (Figure 1).
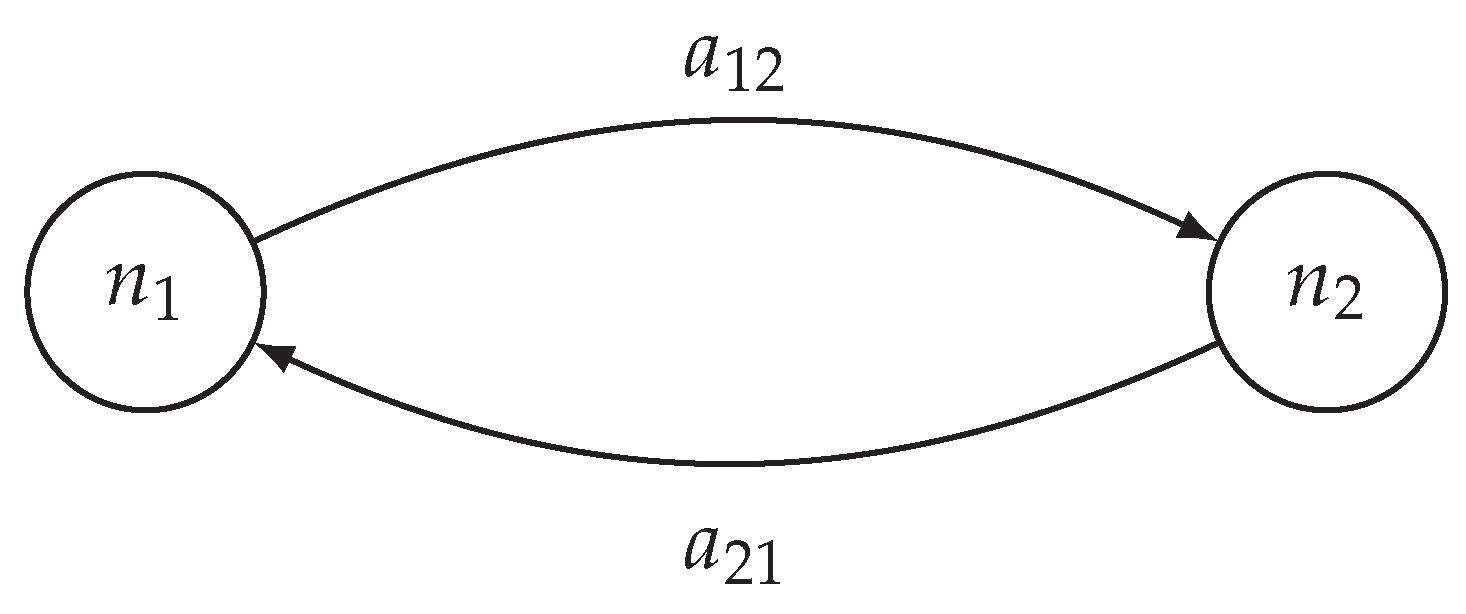
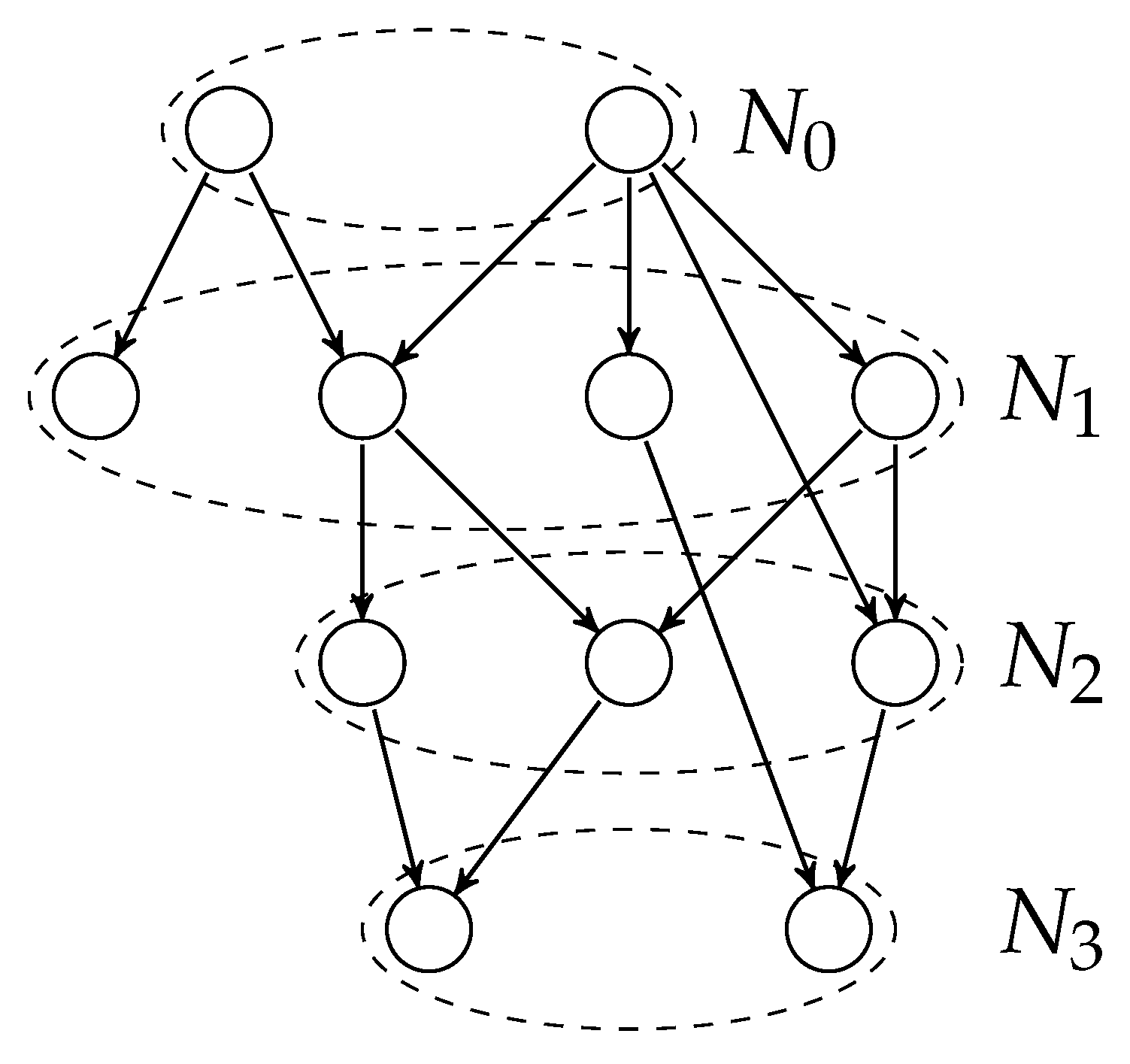
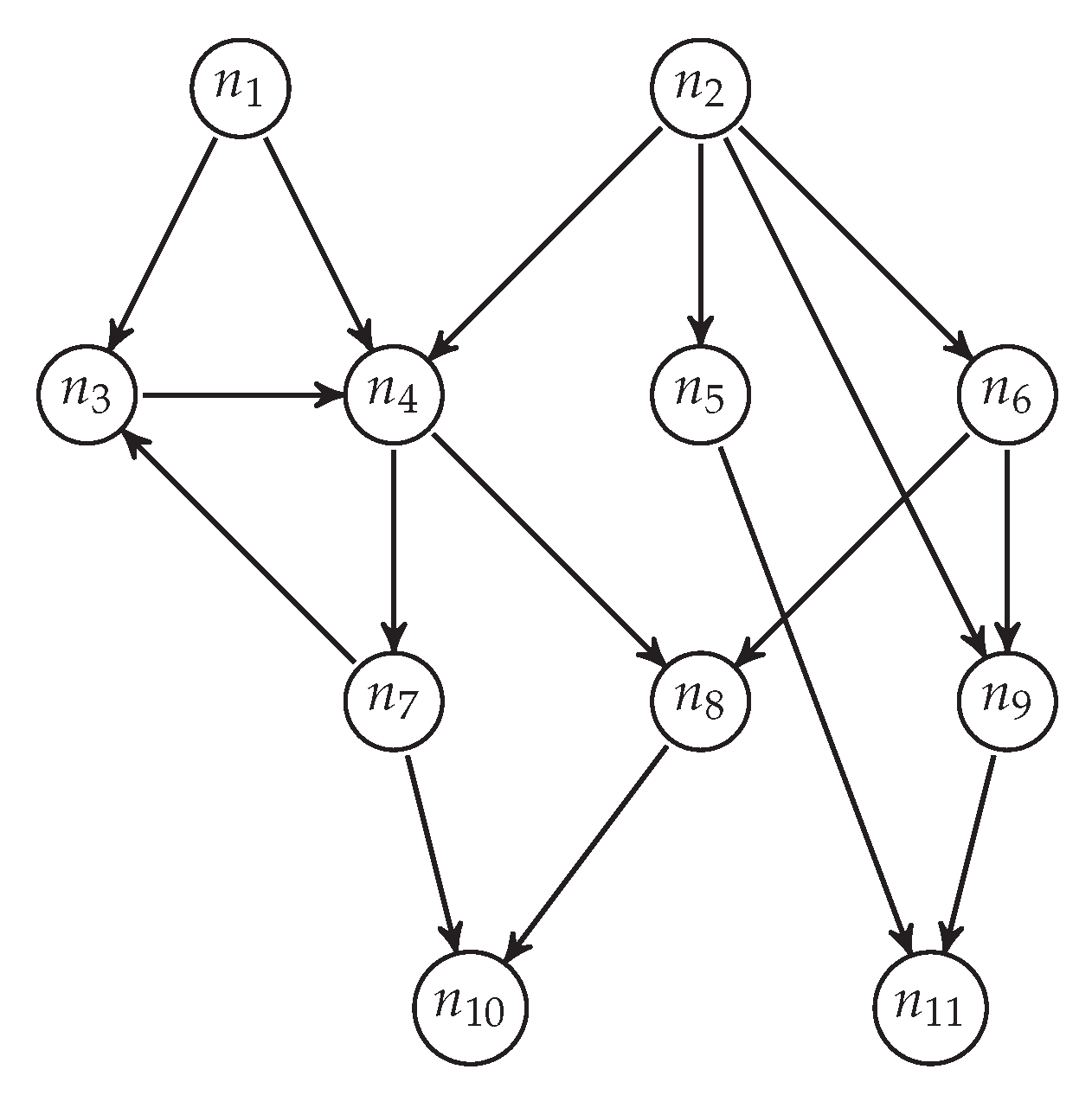
2.1. Probabilistic Network Model
- 2nd assumption: independence between nodes ignitions and arc spread capabilities.
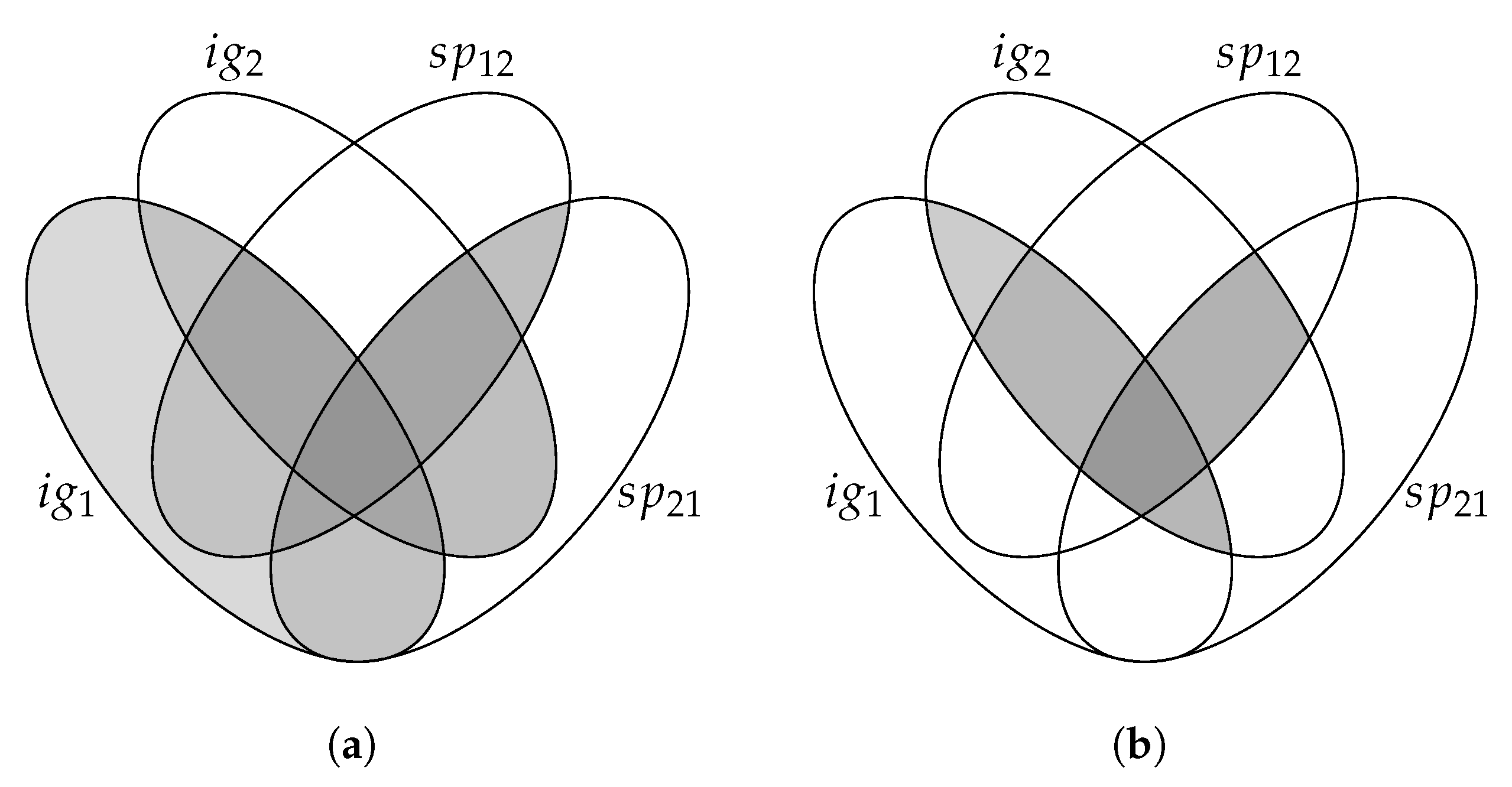
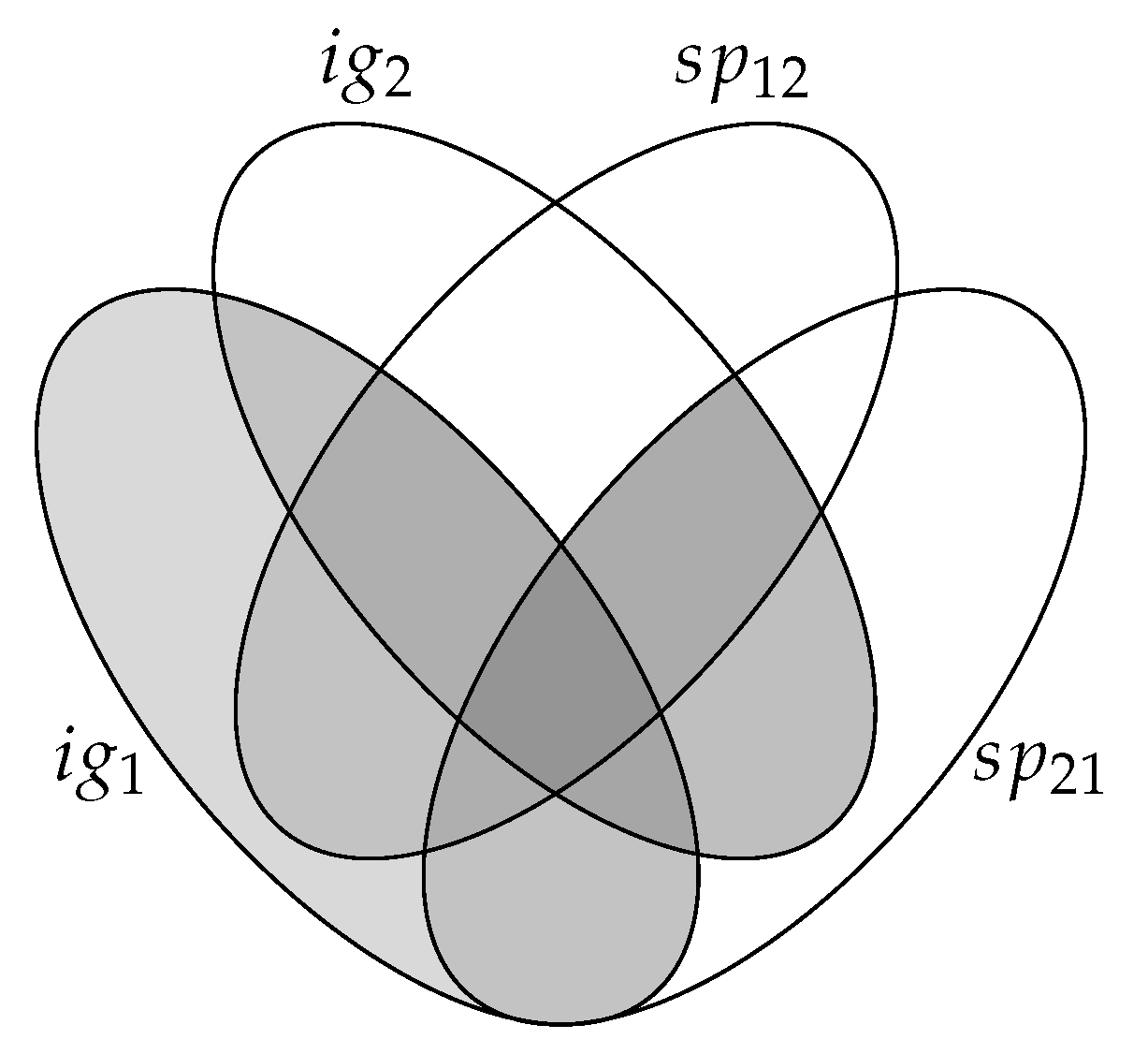
2.2. Bayesian Network
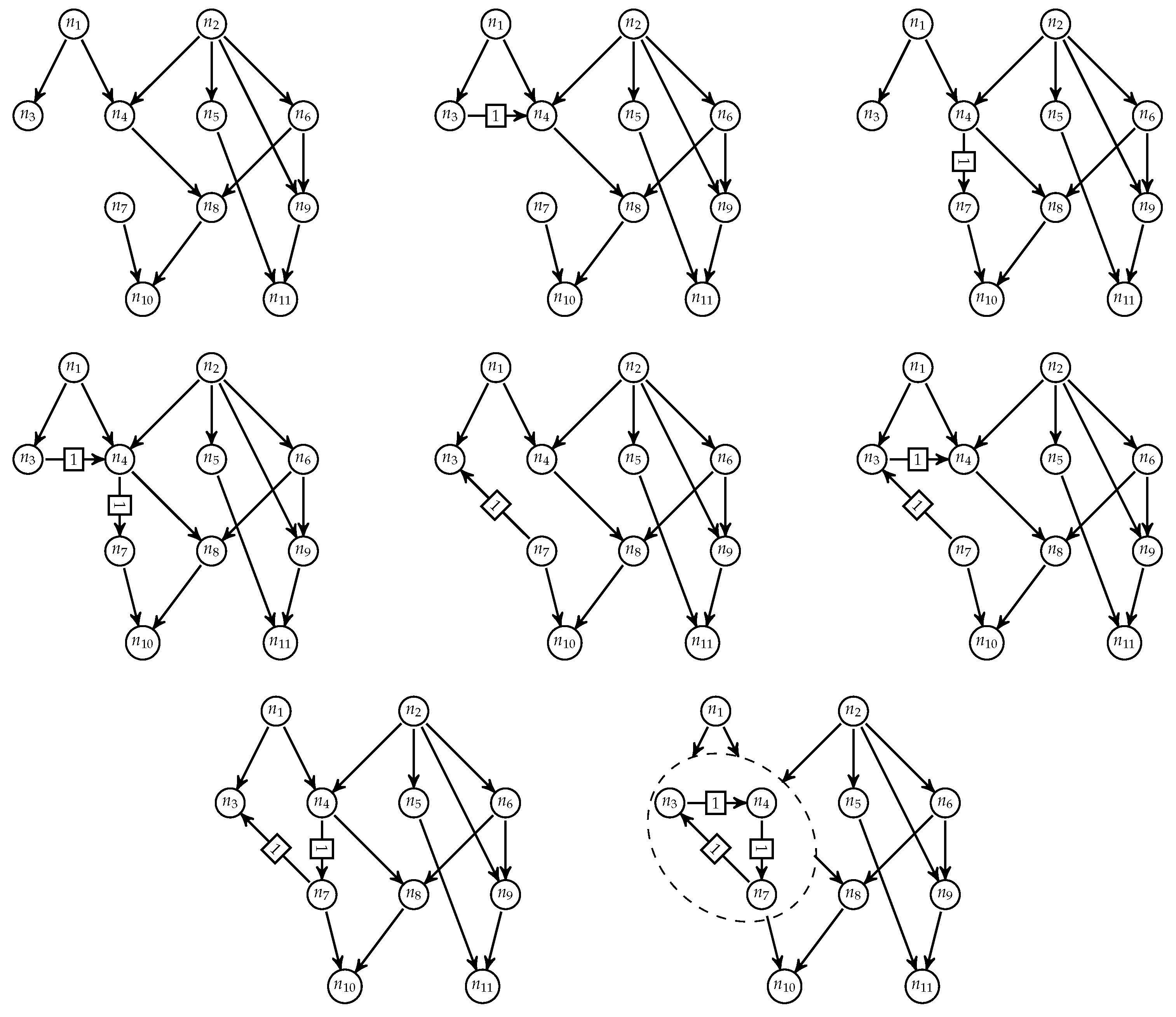
3. Risk Measure Proposed: Losses Expected Value
- 3rd assumption: A finite set of meteorological scenarios of disjoint events can be considered and, under each one of them, the network representing landscape is a DAG.
- 3rd relaxed assumption: A finite set of meteorological scenarios of disjoint events can be considered and, under each one of them, the network representing landscape is a quasi-DAG.
4. Case Example
5. Conclusions and Future Work
- 1st assumption considers that landscape can be divided in homogeneous areas. Researchers and firefighters often make this assumption when working with big scales territories. Usually watersheds are considered to section the landscape, but other methodologies may be explored.
- 2nd assumption relates to the independence between ignitions and spread capabilities. Correlations between spread and ignition events could arise mainly due to a mutual meteorological scenario affecting them. Consideration of scenarios in the analysis makes this 2nd assumption more acceptable.
- 3rd assumption, related to acyclic graphs, in its relaxed version, is accomplished considering wind direction scenarios and assuming no spread against wind direction.
Author Contributions
Funding
Conflicts of Interest
References
- Westerling, A.L.; Hidalgo, H.G.; Cayan, D.R.; Swetnam, T.W. Warming and earlier spring increase western US forest wildfire activity. Science 2006, 313, 940–943. [Google Scholar] [CrossRef]
- Alcubierre, P.C.; Ribau, M.C.; de Egileor, A.L.O.; Bover, M.M.; Kraus, P.D. Prevention of Large Wildfires Using the Fire Types Concept; Generalitat de Catalunya: Barcelona, Spain, 2011. [Google Scholar]
- Séro-Guillaume, O.; Margerit, J. Modelling forest fires. Part I: a complete set of equations derived by extended irreversible thermodynamics. Int. J. Heat Mass Transf. 2002, 45, 1705–1722. [Google Scholar] [CrossRef]
- Belval, E.J.; Wei, Y.; Bevers, M. A stochastic mixed integer program to model spatial wildfire behavior and suppression placement decisions with uncertain weather. Can. J. For. Res. 2016, 46, 234–248. [Google Scholar] [CrossRef]
- Cova, T.J.; Dennison, P.E.; Kim, T.H.; Moritz, M.A. Setting wildfire evacuation trigger points using fire spread modeling and GIS. Trans. GIS 2005, 9, 603–617. [Google Scholar] [CrossRef]
- Pultar, E.; Raubal, M.; Cova, T.J.; Goodchild, M.F. Dynamic GIS case studies: Wildfire evacuation and volunteered geographic information. Trans. GIS 2009, 13, 85–104. [Google Scholar] [CrossRef]
- McCaffrey, S.; Rhodes, A.; Stidham, M. Wildfire evacuation and its alternatives: perspectives from four United States’ communities. Int. J. Wildland Fire 2015, 24, 170–178. [Google Scholar] [CrossRef]
- Finney, M.A. Design of regular landscape fuel treatment patterns for modifying fire growth and behavior. For. Sci. 2001, 47, 219–228. [Google Scholar]
- Price, O.F.; Edwards, A.C.; Russell-Smith, J. Efficacy of permanent firebreaks and aerial prescribed burning in western Arnhem Land, Northern Territory, Australia. Int. J. Wildland Fire 2007, 16, 295–305. [Google Scholar] [CrossRef]
- Rönnqvist, M.; D’Amours, S.; Weintraub, A.; Jofre, A.; Gunn, E.; Haight, R.G.; Martell, D.; Murray, A.T.; Romero, C. Operations research challenges in forestry: 33 open problems. Ann. Oper. Res. 2015, 232, 11–40. [Google Scholar] [CrossRef]
- King, K.J.; Bradstock, R.A.; Cary, G.J.; Chapman, J.; Marsden-Smedley, J.B. The relative importance of fine-scale fuel mosaics on reducing fire risk in south-west Tasmania, Australia. Int. J. Wildland Fire 2008, 17, 421–430. [Google Scholar] [CrossRef]
- Minas, J.P.; Hearne, J.W.; Martell, D.L. A spatial optimisation model for multi-period landscape level fuel management to mitigate wildfire impacts. Eur. J. Oper. Res. 2014, 232, 412–422. [Google Scholar] [CrossRef]
- León, J.; Reijnders, V.M.; Hearne, J.W.; Ozlen, M.; Reinke, K.J. A Landscape-scale optimisation model to break the hazardous fuel continuum while maintaining habitat quality. Environ. Model. Assess. 2019, 24, 369–379. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Yepes, V. Robust Design Optimization for Low-Cost Concrete Box-Girder Bridge. Mathematics 2020, 8, 398. [Google Scholar] [CrossRef]
- Caballero, J.L. Mathematical Programming with Uncertainty and Multiple Objectives for Sustainable Development and Wildfire Management. Ph.D. Thesis, Universidad Complutense de Madrid, Madrid, Spain, 2020. [Google Scholar]
- Suffling, R.; Grant, A.; Feick, R. Modeling prescribed burns to serve as regional firebreaks to allow wildfire activity in protected areas. For. Ecol. Manag. 2008, 256, 1815–1824. [Google Scholar] [CrossRef]
- Preisler, H.K.; Brillinger, D.R.; Burgan, R.E.; Benoit, J. Probability based models for estimation of wildfire risk. Int. J. Wildland Fire 2004, 13, 133–142. [Google Scholar] [CrossRef]
- Castellnou, M.; Prat-Guitart, N.; Arilla, E.; Larrañaga, A.; Nebot, E.; Castellarnau, X.; Vendrell, J.; Pallàs, J.; Herrera, J.; Monturiol, M.; et al. Empowering strategic decision-making for wildfire management: Avoiding the fear trap and creating a resilient landscape. Fire Ecol. 2019, 15, 31. [Google Scholar] [CrossRef]
- Wei, Y.; Rideout, D.; Kirsch, A. An optimization model for locating fuel treatments across a landscape to reduce expected fire losses. Can. J. For. Res. 2008, 38, 868–877. [Google Scholar] [CrossRef]
- Cheng, H.; Hadjisophocleous, G.V. The modeling of fire spread in buildings by Bayesian network. Fire Saf. J. 2009, 44, 901–908. [Google Scholar] [CrossRef]
- Andrino, D. Three Ways of Generating Terrain with Erosion Features. 2018. Available online: https://github.com/dandrino/terrain-erosion-3-ways (accessed on 14 February 2020).
- Minas, J.; Hearne, J.; Martell, D. An integrated optimization model for fuel management and fire suppression preparedness planning. Ann. Oper. Res. 2015, 232, 201–215. [Google Scholar] [CrossRef]
- Levchenkov, V. Solution of equations in Boolean algebra. Comput. Math. Model. 2000, 11, 154–163. [Google Scholar] [CrossRef]
- Ibarrola, P.; Pardo, L.; Quesada, V. Teoría de la Probabilidad; Síntesis: Madrid, Spain, 2010. [Google Scholar]
- Russel, S.; Norvig, P. Artificial Intelligence: A Modern Approach; EUA, Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Schreiber, J. Pomegranate: Fast and flexible probabilistic modeling in python. J. Mach. Learn. Res. 2017, 18, 5992–5997. [Google Scholar]
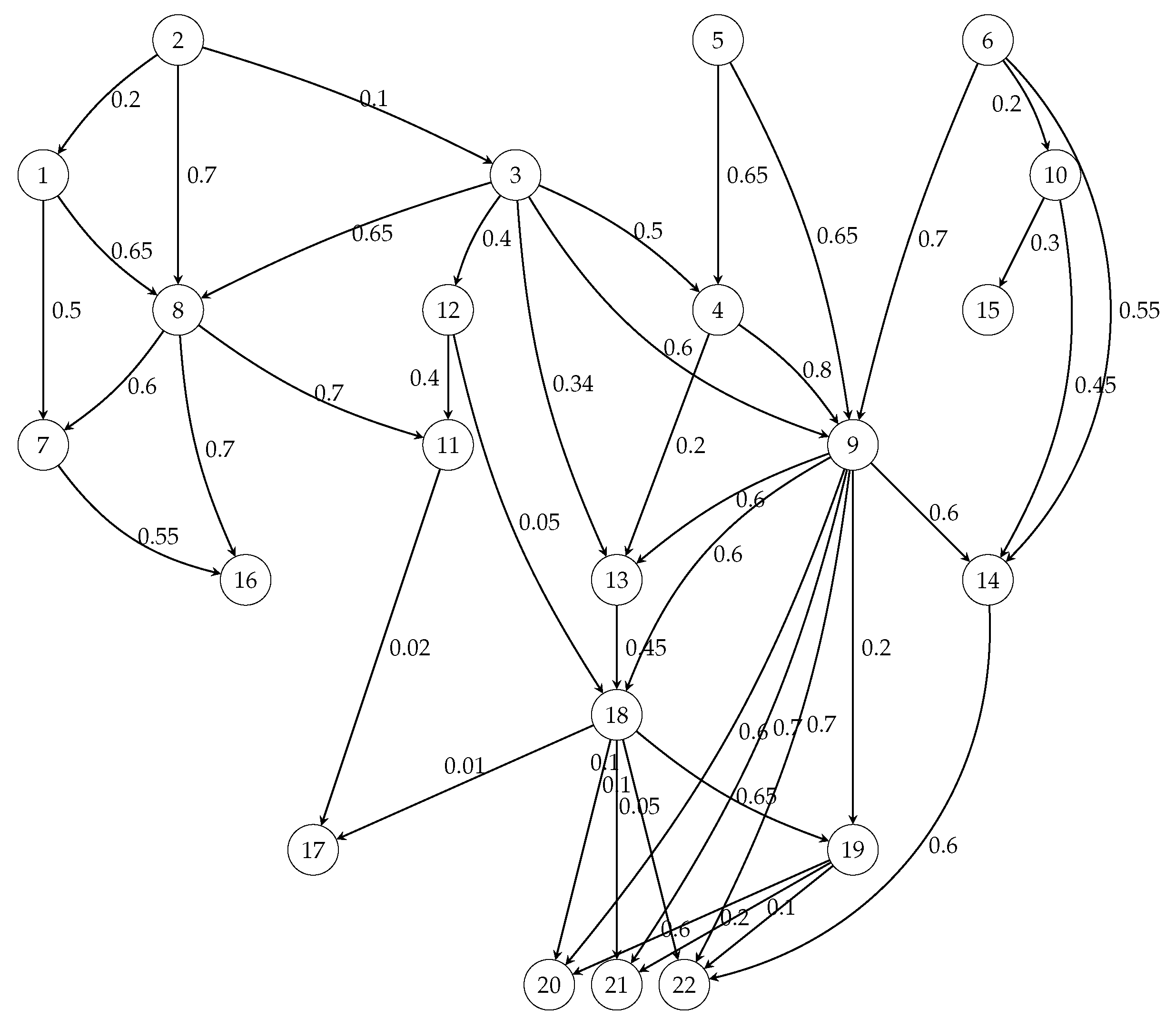
| Bayes | s | s | s | s | 410 s |
| Partition | s | s | 110 s | 500 s | − |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.483 | 1.705 | 5.239 | 4.422 | 2.172 | 4.216 | 8.166 | 2.528 | 3.433 | 3.221 | 1.623 | |
| Sector Area (ha) | 402.6 | 462.7 | 1422 | 1200 | 589.5 | 1144 | 2216 | 686.2 | 931.6 | 874.3 | 440.5 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | |
| 0.559 | 0.595 | 8.755 | 0.733 | 3.373 | 0.109 | 1.943 | 0.823 | 4.667 | 2.395 | 5.466 | |
| Sector Area (ha) | 151.6 | 161.5 | 2376 | 198.9 | 915.5 | 29.62 | 527.43 | 223.4 | 1267 | 650.0 | 1483 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FRM (MU) | 2491 | 2501 | 2412 | 2378 | 2465 | 2497 | 2671 | 2424 | 1944 | 2572 | 2520 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | |
| FRM (MU) | 2477 | 2418 | 2506 | 2491 | 2546 | 2459 | 2394 | 2384 | 2527 | 2515 | 2481 |
| FRM (MU) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 1 | 2442 | 2432 | 2420 | |||||||||||||||||||
| 2 | 2442 | 2439 | 2419 | |||||||||||||||||||
| 3 | 2439 | 2322 | 2364 | 2295 | 2446 | 2442 | ||||||||||||||||
| 4 | 2322 | 2382 | 2100 | 2443 | ||||||||||||||||||
| 5 | 2382 | 2382 | ||||||||||||||||||||
| 6 | 2299 | 2438 | 2395 | |||||||||||||||||||
| 7 | 2432 | 2339 | 2392 | |||||||||||||||||||
| 8 | 2420 | 2419 | 2364 | 2339 | 2431 | 2409 | ||||||||||||||||
| 9 | 2295 | 2100 | 2382 | 2299 | 2387 | 2195 | 2330 | 2423 | 2353 | 2391 | 2319 | |||||||||||
| 10 | 2438 | 2404 | 2451 | |||||||||||||||||||
| 11 | 2431 | 2449 | 2453 | |||||||||||||||||||
| 12 | 2446 | 2449 | 2452 | |||||||||||||||||||
| 13 | 2442 | 2443 | 2387 | 2379 | ||||||||||||||||||
| 14 | 2395 | 2195 | 2404 | 2295 | ||||||||||||||||||
| 15 | 2451 | |||||||||||||||||||||
| 16 | 2392 | 2409 | ||||||||||||||||||||
| 17 | 2453 | 2453 | ||||||||||||||||||||
| 18 | 2330 | 2452 | 2379 | 2453 | 2340 | 2436 | 2444 | 2444 | ||||||||||||||
| 19 | 2423 | 2340 | 2360 | 2438 | 2437 | |||||||||||||||||
| 20 | 2353 | 2436 | 2360 | |||||||||||||||||||
| 21 | 2391 | 2444 | 2438 | |||||||||||||||||||
| 22 | 2319 | 2295 | 2444 | 2437 |
| Scenario | No Treatment | Prescribed Burns | Firebreak |
|---|---|---|---|
 |  |  | |
 |  |  | |
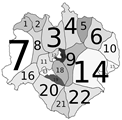 | 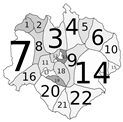 | 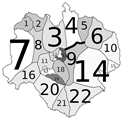 | |
| FRM | 2453 MU | 1951 MU | 2100 MU |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Martínez, A.; Vitoriano, B. Probability-Based Wildfire Risk Measure for Decision-Making. Mathematics 2020, 8, 557. https://doi.org/10.3390/math8040557
Rodríguez-Martínez A, Vitoriano B. Probability-Based Wildfire Risk Measure for Decision-Making. Mathematics. 2020; 8(4):557. https://doi.org/10.3390/math8040557
Chicago/Turabian StyleRodríguez-Martínez, Adán, and Begoña Vitoriano. 2020. "Probability-Based Wildfire Risk Measure for Decision-Making" Mathematics 8, no. 4: 557. https://doi.org/10.3390/math8040557
APA StyleRodríguez-Martínez, A., & Vitoriano, B. (2020). Probability-Based Wildfire Risk Measure for Decision-Making. Mathematics, 8(4), 557. https://doi.org/10.3390/math8040557






