When we are interested in the cases with
, we use the following error measure based on infinity norm over an interval
:
is the largest point we are interested in, i.e., we assume
in this subsection.
7.1.1. General Comparison of the NIZT Methods
For this comparison, we included the NIZT methods from the previous sections which provide the best results. Ort1 and Ort2 refer to the method presented in
Section 3.2 and [
6] (using the suggested
and
parameters), based on orthogonal functions. MB refers to the method in
Section 3.3, based on matrix pseudoinverse calculation.
Table 2 compares the error of all methods for the list of functions in
Table 1 for
and
. In the table,“∼0” means practical zero, a value smaller than
, “p.inf.” stands for practical infinity, denoting errors larger than
, while “n/a” means not applicable due to a pole of
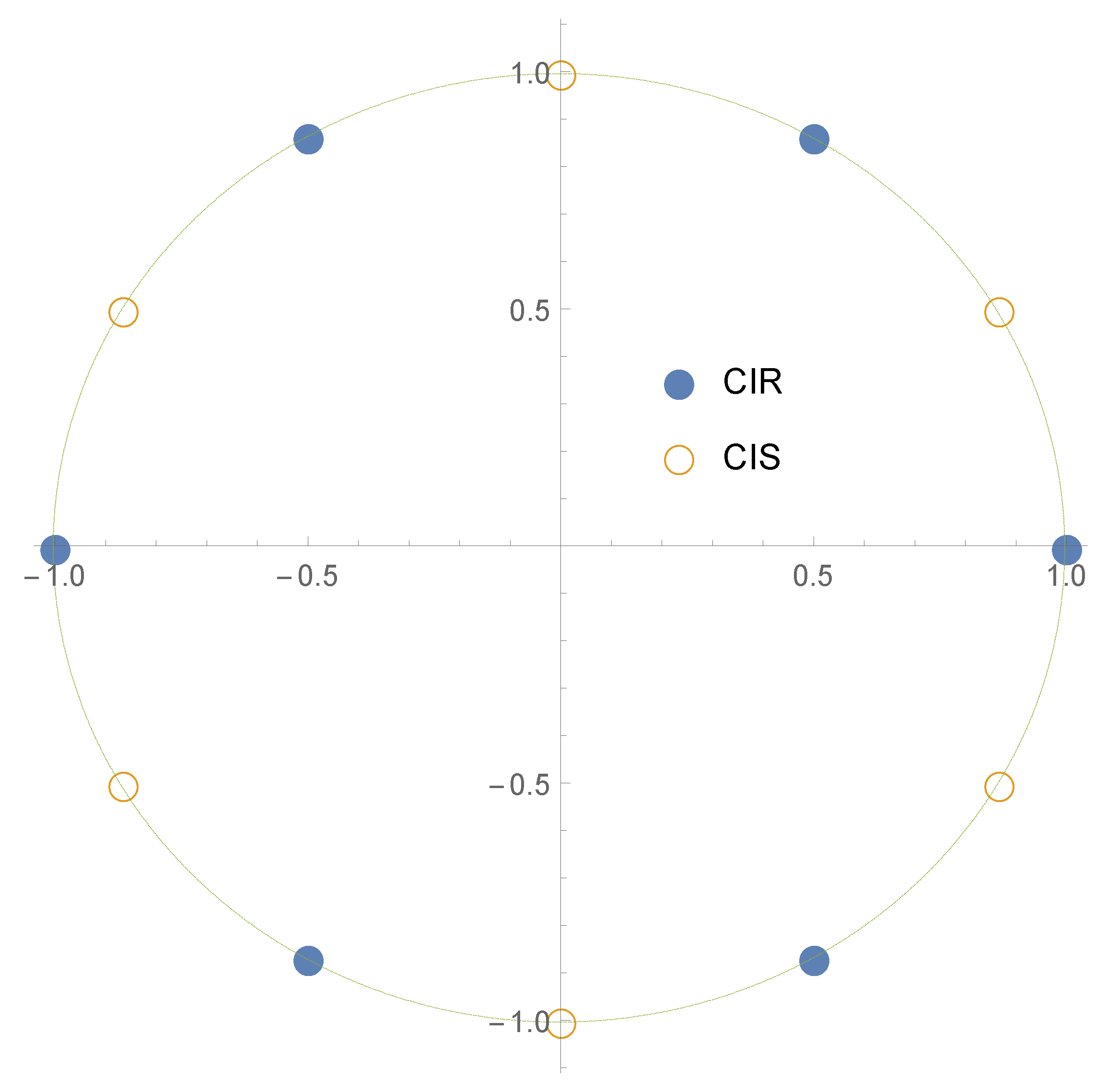
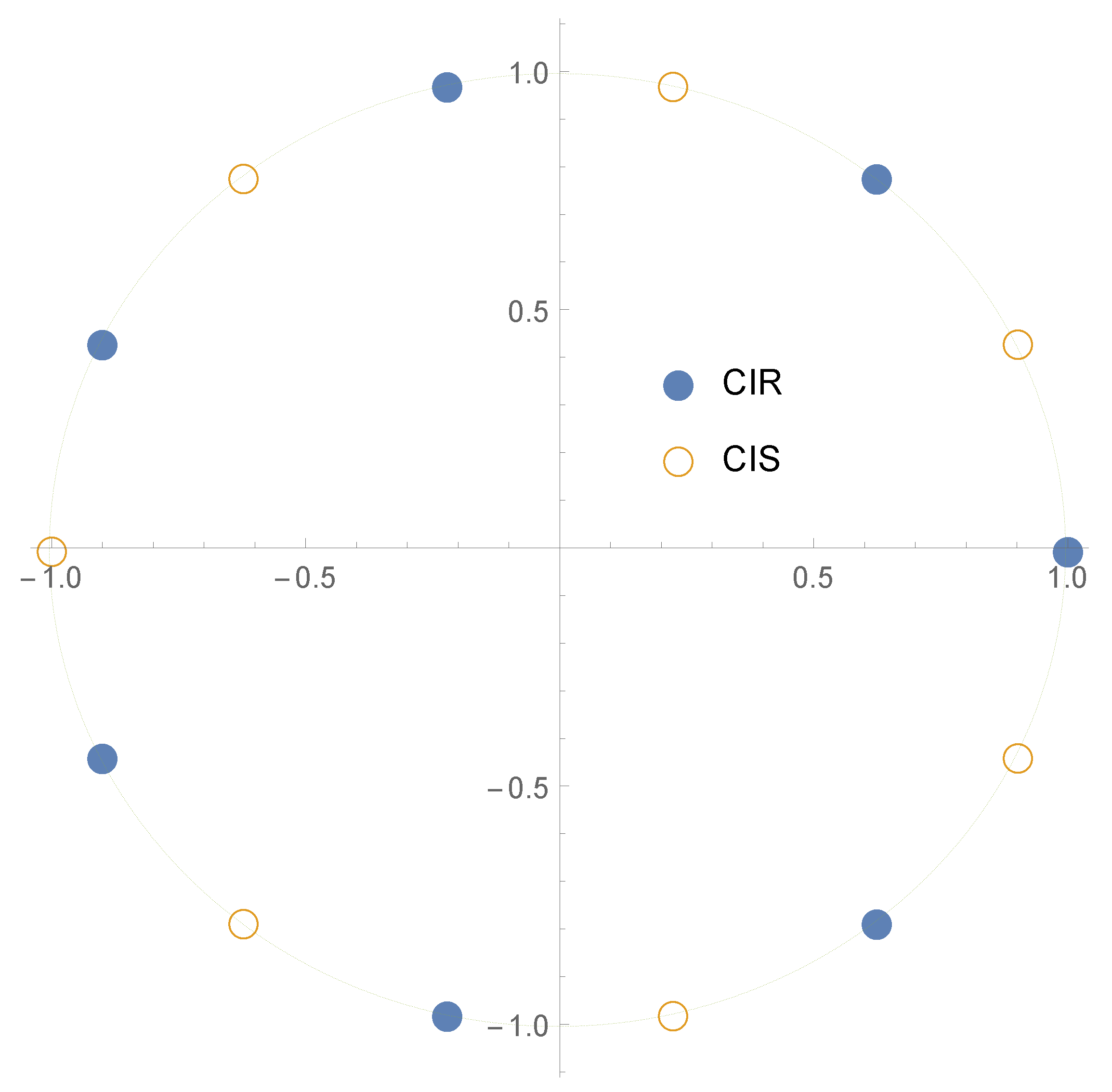
which is evaluated by the given NIZT method (e.g., the CIR method with
fails for functions with a pole at 1). All calculations related to
Table 2 were carried out using high precision (200 digits) floating point arithmetic.
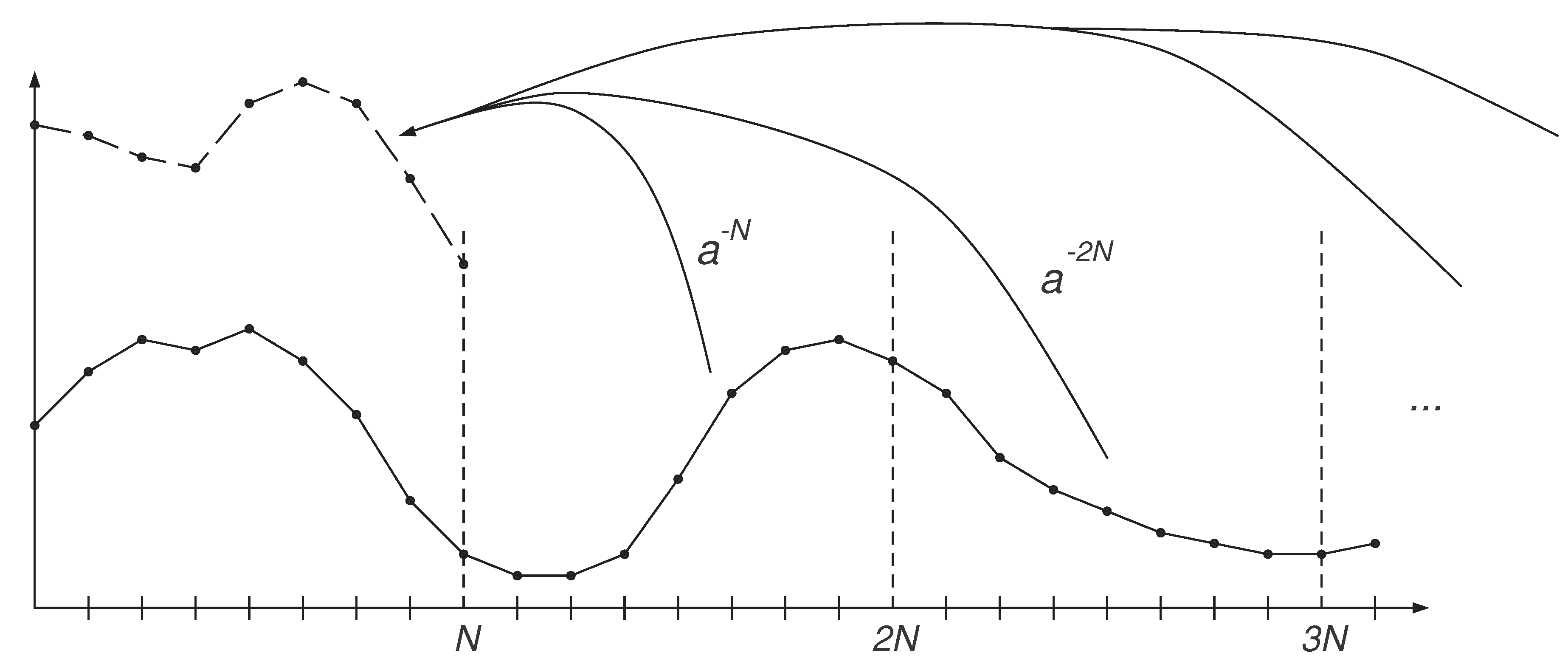
According to Remark 4 at the end of
Section 4 (and Remark 5 at the end of
Section 5), as long as
, the accuracy of the contour integral-based methods CIR and CIS improves as
a is increased, and this also helps avoiding the pole at 1 for the CIR method.
Table 3 displays this effect by setting
instead of
.
Based on
Table 2 and
Table 3, we conclude that the Ort1 method gives the most precise results, the CIR, CIS give precise results when
a is sufficiently large, the Ort2 and MB methods are unreliable, and CMG is relatively reliable for
(although the error is not as small as for CIR, CIS and Ort1), but unreliable for
. Altogether, one might have the impression that Ort1 is the best method; however, we have not yet examined other important questions like precision loss or running time. In the next subsection, precision loss is examined along with a more detailed analysis of the role of
a.
Due to their unreliability (c.f.
Table 2 and
Table 3) methods Ort2 and MB are excluded from further investigations.
7.1.2. Precision Loss and the Effect of a
For a more detailed view on the performance of the methods CIR, CIS, Ort1, and CMG, we investigate their accuracy as a function of parameter a.
Table 4 contains the error and precision loss (p.l., in digits, calculated using Wolfram Mathematica) for the Polynomial(
) function with
, and
a taking the values
.
For contour integral methods CIR and CIS, as long as
, setting
a to a larger value will diminish the error in the second term of (
14) and (
18), while the first term cancels out entirely.
For
, the approximations in
Table 4 are poor. This is because for
, the error in the tail is magnified. If
is rapidly decaying, then the error introduced by
is small, but
or
are still better choices.
For , the “n/a” values for the CIR method are due to the pole of the function at 1. This is where the CIS method has an advantage: the shifted nodes avoid the pole when , so it gives a meaningful result.
For , the error decreases rapidly for the contour integral methods CIR and CIS as the error in the tail is diminished, at the cost of increased precision loss. Interestingly, the precision loss is of similar order as the error. (This is not necessarily the case in general, but the precision loss does seem to increase rapidly with a in general.)
The error for the CIS method is slightly smaller than for the CIR due to cancellations (see Remark 6 after (
18)), but the difference is practically negligible.
The Ort1 method, while gives the lowest error, suffers from huge precision losses. Notably, for any calculations with precision smaller than 142 digits, Ort1 would give meaningless results due to precision loss. The precision loss is inherent to the Ort1 method due to the highly fluctuating orthogonal functions involved. Overall, we recommend avoiding the use of the Ort1 method due to its unpredictable high precision loss, and instead we recommend using either CIR or CIS when , with a set to as large as possible, depending on the precision loss tolerated.
Interestingly, with the Polynomial() function the CMG method works best when setting . An intuitive explanation of this property is as follows. For the CMG method, enlarges the errors that are caused by the non-zero values for and diminishes errors that are caused by the non-zero values for , and has the opposite effect. Since Polynomial() is a rather flat function the effect of enlarging the error is more dominant for both and . This property might slightly change for steeper functions, but, in general, we recommend using for the CMG method. We also note that the CMG method involves practically no loss of precision, so it can be used efficiently even with standard precision floating point arithmetic.
Table 5 investigates the error and the precision loss for various Z-transform
functions using the CIR, CIS and Ort1 methods with parameters
. We note that the CMG method fails due to
.
From
Table 5, we conclude that the precision loss heavily depends on the
function. As a result, high precision calculations with precision loss check is recommended for NIZT with the CIR, CIS and Ort1 methods. However, with high precision calculations, the precision loss remains tolerable for CIR and CIS.