An Efficient Numerical Method for Fractional SIR Epidemic Model of Infectious Disease by Using Bernstein Wavelets
Abstract
1. Introduction
2. Fractional Calculus
3. The Normalized Bernstein Wavelets and Its Properties
4. Bernstein Wavelet Operational Matrix Using Riemann–Liouville Integral Operator
5. Convergence and Error Analysis
6. Proposed Methods for Fractional SIR Epidemic Model
6.1. Bernstein Wavelets for the Numerical Solution of SIR Epidemic Model
6.2. Adams–Bashforth–Moulton (ABM) Predictor Corrector Scheme for the Numerical Solution of SIR Epidemic Model
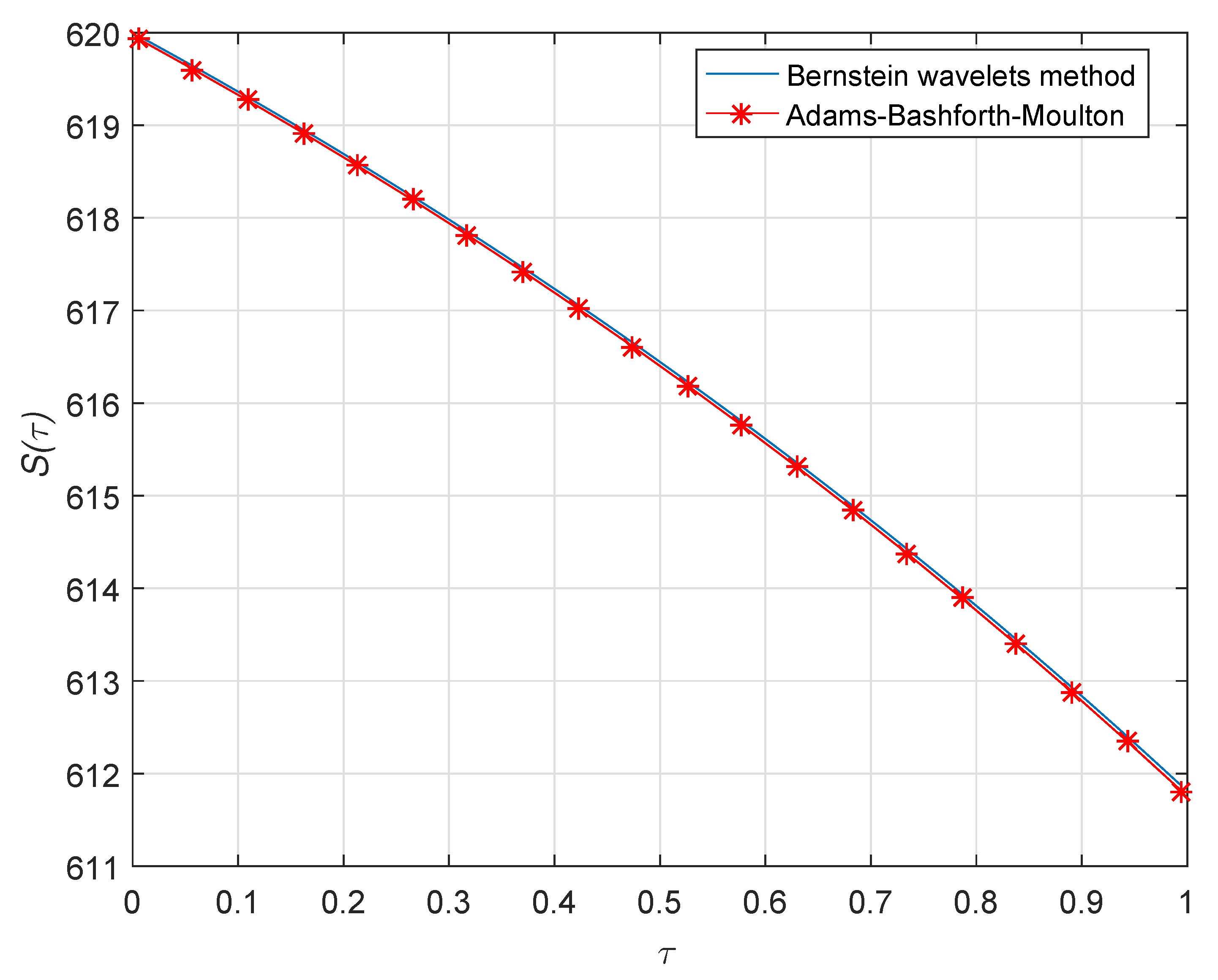
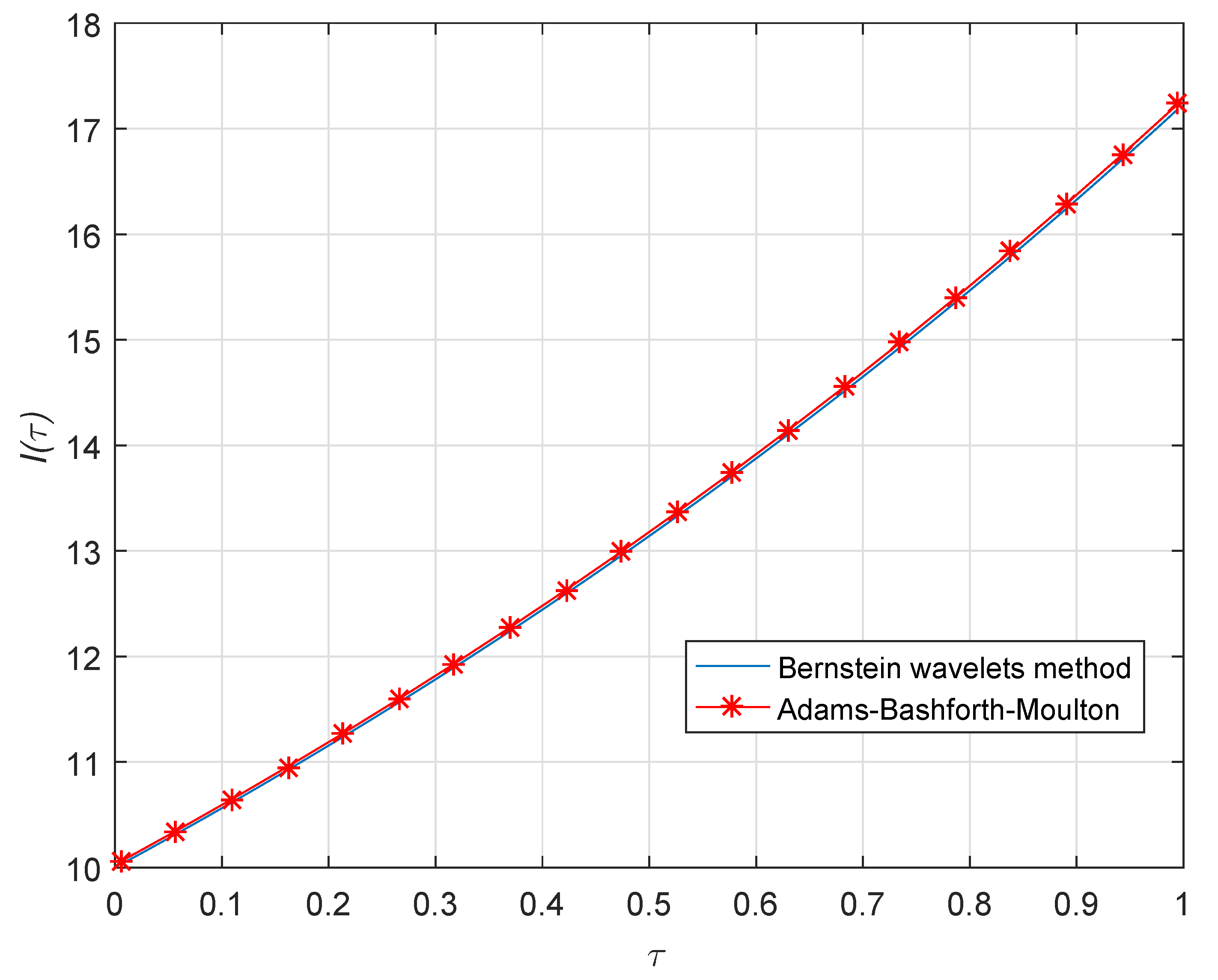
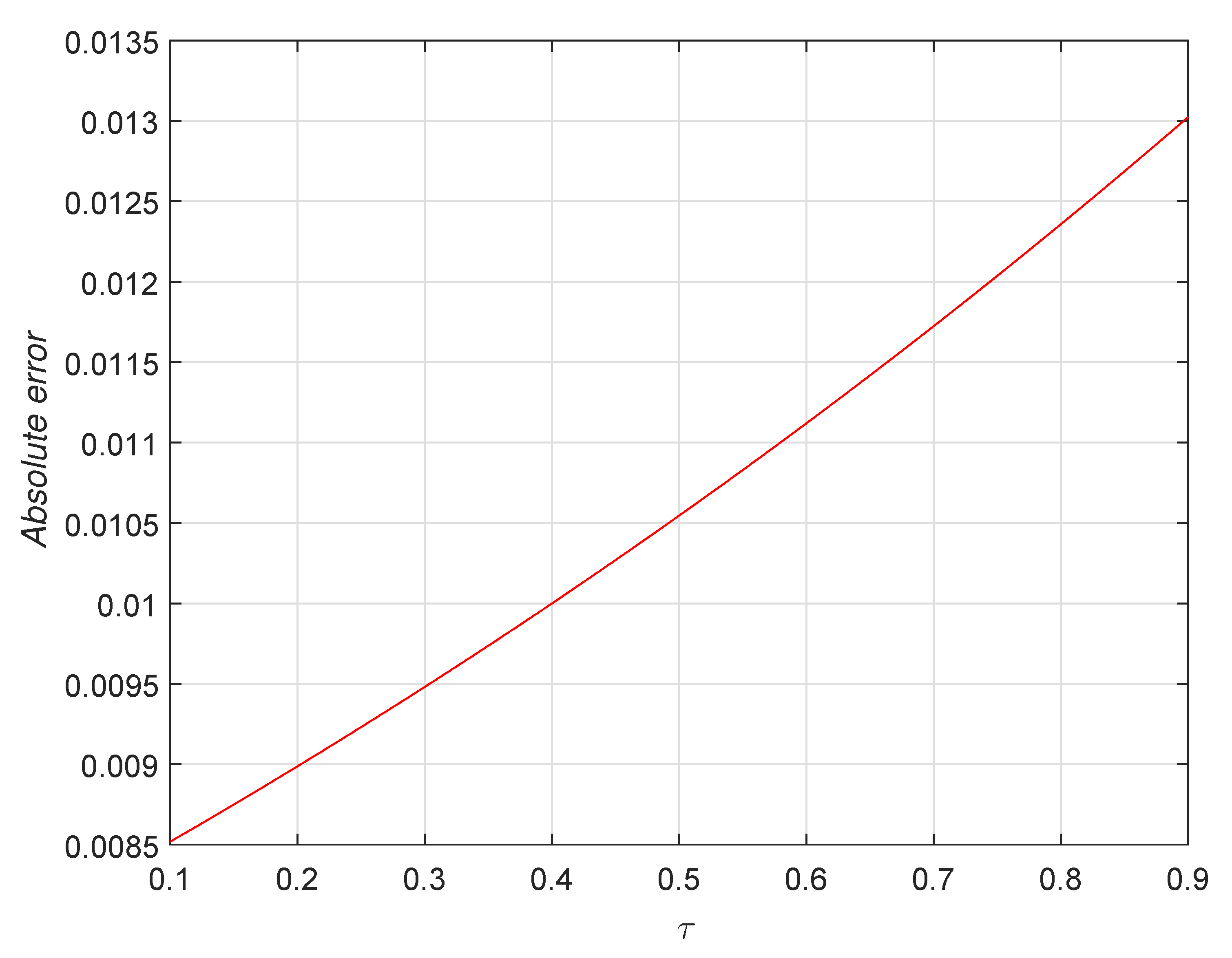
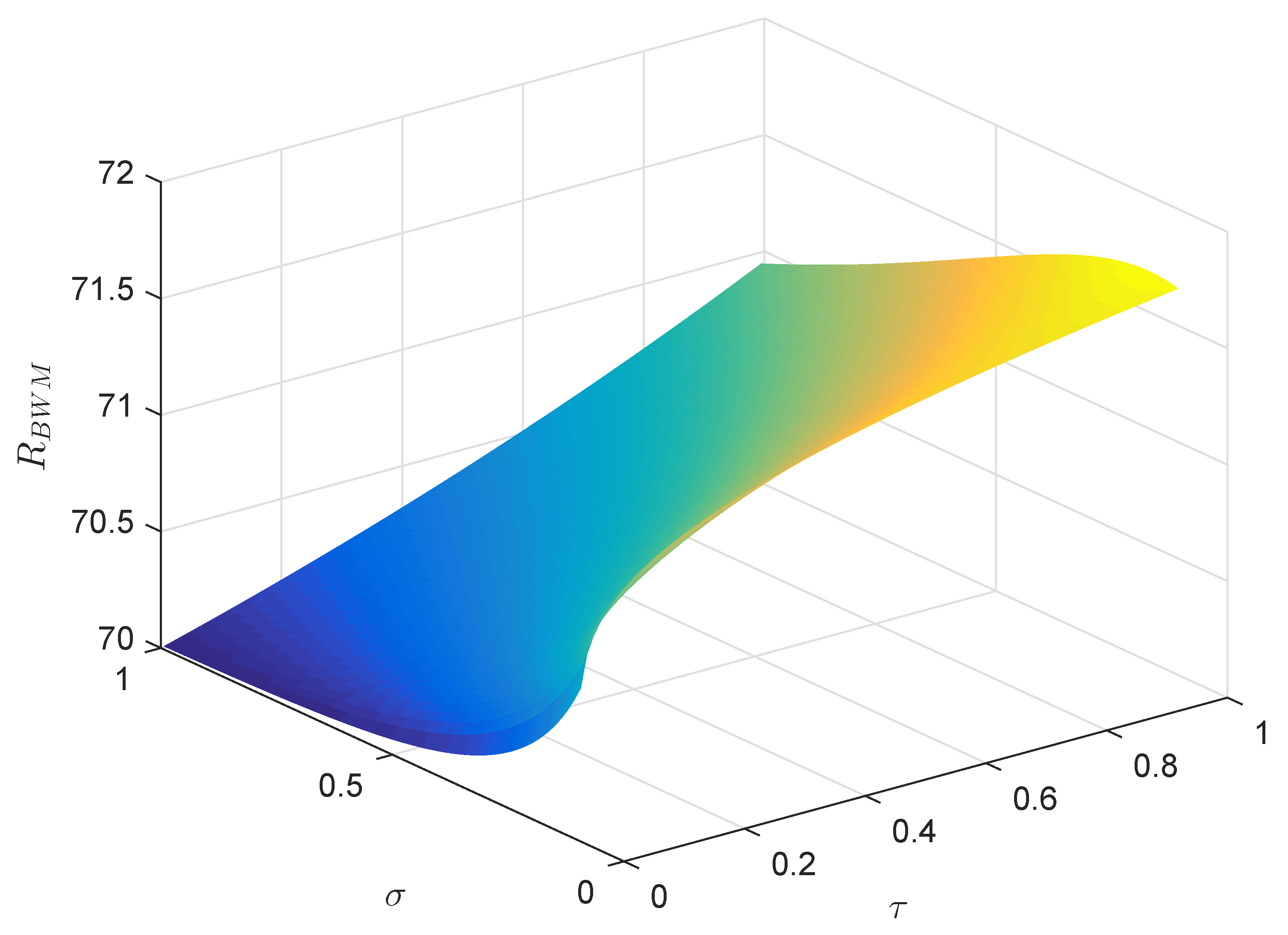
7. Numerical Results and Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar]
- Ullah, S.; Khan, M.A.; Farooq, M. A new fractional model for the dynamics of the hepatitis B virus using the Caputo-Fabrizio derivative. Eur. Phys. J. Plus 2018, 133, 237. [Google Scholar] [CrossRef]
- Cardoso, L.; Santos, F.D.; Camargo, R. Analysis of fractional-order models for hepatitis B. Comput. Appl. Math. 2018, 37, 4570–4586. [Google Scholar] [CrossRef]
- Arafa, A.; Rida, S.; Khalil, M. Solutions of fractional order model of childhood diseases with constant vaccination strategy. Math. Sci. Lett. 2012, 1, 17–23. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Khan, M.A.; Farooq, M.; Ullah, S.; Alzahrani, E.O. A fractional order model for Hepatitis B virus with treatment via Atangana–Baleanu derivative. Phys. A Stat. Mech. Its Appl. 2020, 538, 122636. [Google Scholar] [CrossRef]
- Singh, H.; Dhar, J.; Bhatti, H.S.; Chandok, S. An epidemic model of childhood disease dynamics with maturation delay and latent period of infection. Model. Earth Syst. Environ. 2016, 2, 79. [Google Scholar] [CrossRef]
- Koca, I. Analysis of rubella disease model with non-local and non-singular fractional derivatives. Int. J. Optim. Control Theor. Appl. (IJOCTA) 2017, 8, 17–25. [Google Scholar] [CrossRef]
- Rabi, F.A.; Al Zoubi, M.S.; Kasasbeh, G.A.; Salameh, D.M.; Al-Nasser, A.D. SARS-CoV-2 and Coronavirus Disease 2019: What We Know So Far. Pathogens 2020, 9, 231. [Google Scholar] [CrossRef]
- Asgari, M.; Ezzati, R. Using operational matrix of two-dimensional Bernstein polynomials for solving two-dimensional integral equations of fractional order. Appl. Math. Comput. 2017, 307, 290–298. [Google Scholar] [CrossRef]
- Mirzaee, F.; Samadyar, N. Numerical solution based on two-dimensional orthonormal Bernstein polynomials for solving some classes of two-dimensional nonlinear integral equations of fractional order. Appl. Math. Comput. 2019, 344, 191–203. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, L.; Li, B.; Sun, Y. Numerical solution for the variable order linear cable equation with Bernstein polynomials. Appl. Math. Comput. 2014, 238, 329–341. [Google Scholar] [CrossRef]
- Razzaghi, M.; Yousefi, S. The Legendre wavelets operational matrix of integration. Int. J. Syst. Sci. 2001, 32, 495–502. [Google Scholar] [CrossRef]
- Shamsi, M.; Razzaghi, M. Solution of Hallen’s integral equation using multiwavelets. Comput. Phys. Commun. 2005, 168, 187–197. [Google Scholar] [CrossRef]
- Lakestani, M.; Razzaghi, M.; Dehghan, M. Semi-orthogonal spline wavelets approximation for Fredholm integro-differential equations. Math. Probl. Eng. 2006, 2006. [Google Scholar] [CrossRef]
- Beylkin, G.; Coifman, R.; Rokhlin, V. Fast wavelet transforms and numerical algorithms i. Commun. Pure Appl. Math. 1991, 44, 141–183. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Saeed, U.; Mohyud-Din, S.T. Modified Laguerre wavelets method for delay differential equations of fractional-order. Egypt. J. Basic Appl. Sci. 2015, 2, 50–54. [Google Scholar] [CrossRef]
- Shiralashetti, S.; Kumbinarasaiah, S. Laguerre wavelets collocation method for the numerical solution of the Benjamina–Bona–Mohany equations. J. Taibah Univ. Sci. 2019, 13, 9–15. [Google Scholar] [CrossRef]
- Gümgüm, S. Laguerre wavelet method for solving Troesch equation. Balıkesir Üniversitesi Fen Bilimleri Enstitüsü Dergisi 2019, 21, 494–502. [Google Scholar] [CrossRef]
- Shiralashetti, S.; Angadi, L.; Kumbinarasaiah, S. Laguerre wavelet-Galerkin method for the numerical solution of one dimensional partial differential equations. Int. J. Math. Appl. 2018, 6, 939–949. [Google Scholar]
- Shiralashetti, S.; Kumbinarasaiah, S. Theoretical study on continuous polynomial wavelet bases through wavelet series collocation method for nonlinear Lane–Emden type equations. Appl. Math. Comput. 2017, 315, 591–602. [Google Scholar] [CrossRef]
- Wang, J.; Xu, T.-Z.; Wei, Y.-Q.; Xie, J.-Q. Numerical simulation for coupled systems of nonlinear fractional order integro-differential equations via wavelets method. Appl. Math. Comput. 2018, 324, 36–50. [Google Scholar] [CrossRef]
- Yuttanan, B.; Razzaghi, M. Legendre wavelets approach for numerical solutions of distributed order fractional differential equations. Appl. Math. Model. 2019, 70, 350–364. [Google Scholar] [CrossRef]
- Rahimkhani, P.; Ordokhani, Y. A numerical scheme based on Bernoulli wavelets and collocation method for solving fractional partial differential equations with dirichlet boundary conditions. Numer. Methods Partial Differ. Equ. 2019, 35, 34–59. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Qurashi, M.; Baleanu, D. A new fractional SIRS-SI malaria disease model with application of vaccines, anti-malarial drugs, and spraying. Adv. Differ. Equ. 2019, 2019, 278. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. On the analysis of fractional diabetes model with exponential law. Adv. Differ. Equ. 2018, 2018, 231. [Google Scholar]
- Goswami, A.; Singh, J.; Kumar, D. An efficient analytical approach for fractional equal width equations describing hydro-magnetic waves in cold plasma. Physica A 2019, 2019, 563–575. [Google Scholar] [CrossRef]
- Srivastava, M.; Agrawal, S.; Das, S. Synchronization of chaotic fractional order Lotka–Volterra system. Int. J. Nonlinear Sci. 2012, 13, 482–494. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Ghanbari, B.; Kumar, S.; Kumar, R. A study of behaviour for immune and tumor cells in immunogenetic tumour model with non-singular fractional derivative. Chaos Soliton Fractals 2020. [Google Scholar] [CrossRef]
- Kumar, S.; Nisar, K.; Kumar, R.; Cattani, C.; Samet, B. A new rabotnov fractional-exponential function based fractional derivative for diffusion equation under external force. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, R.; Singh, J.; Nisar, K.; Kumar, D. An efficient numerical scheme for fractional model of HIV-1 infection of CD4+ T-Cells with the effect of antiviral drug therapy. Alex. Eng. J. 2019. [Google Scholar] [CrossRef]
- Jleli, M.; Kumar, S.; Kumar, R.; Samet, B. Analytical approach for time fractional wave equations in the sense of Yang-Abdel-Aty-Cattani via the homotopy perturbation transform method. Alex. Eng. J. 2019. [Google Scholar] [CrossRef]
- Goufo, E.F.D.; Kumar, S.; Mugisha, S. Similarities in a fifth-order evolution equation with and with no singular kernel. Chaos Solitons Fractals 2020, 130, 109467. [Google Scholar] [CrossRef]
- El-Ajou, A.; Oqielat, M.N.; Al-Zhour, Z.; Kumar, S.; Momani, S. Solitary solutions for time-fractional nonlinear dispersive PDEs in the sense of conformable fractional derivative. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 093102. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Momani, S.; Aldhaifallah, M.; Nisar, K.S. Numerical solutions of nonlinear fractional model arising in the appearance of the stripe patterns in two-dimensional systems. Adv. Differ. Equ. 2019, 2019, 413. [Google Scholar] [CrossRef]
- Sharma, B.; Kumar, S.; Cattani, C.; Baleanu, D. Nonlinear dynamics of Cattaneo–Christov heat flux model for third-grade power-law fluid. J. Comput. Nonlinear Dyn. 2020, 15. [Google Scholar] [CrossRef]
- Kudu, M. A parameter uniform difference scheme for the parameterized singularly perturbed problem with integral boundary condition. Adv. Differ. Equ. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.; Kumar, D. An efficient technique for nonlinear time-fractional Klein–Fock–Gordon equation. Appl. Math. Comput. 2020, 364, 124637. [Google Scholar] [CrossRef]
- Bhatter, S.; Mathur, A.; Kumar, D.; Singh, J. A new analysis of fractional Drinfeld–Sokolov–Wilson model with exponential memory. Phys. A Stat. Mech. Its Appl. 2020, 537, 122578. [Google Scholar] [CrossRef]
- Choudhary, A.; Kumar, D.; Singh, J. Numerical simulation of a fractional model of temperature distribution and heat flux in the semi infinite solid. Alex. Eng. J. 2016, 55, 87–91. [Google Scholar] [CrossRef]
- Ghanbari, B.; Kumar, D. Numerical solution of predator-prey model with Beddington-DeAngelis functional response and fractional derivatives with Mittag-Leffler kernel. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 063103. [Google Scholar] [CrossRef] [PubMed]
- Hasan, S.; Al-Zoubi, A.; Freihet, A.; Al-Smadi, M.; Momani, S. Solution of fractional SIR epidemic model using residual power series method. Appl. Math. 2019, 13, 1–9. [Google Scholar] [CrossRef]

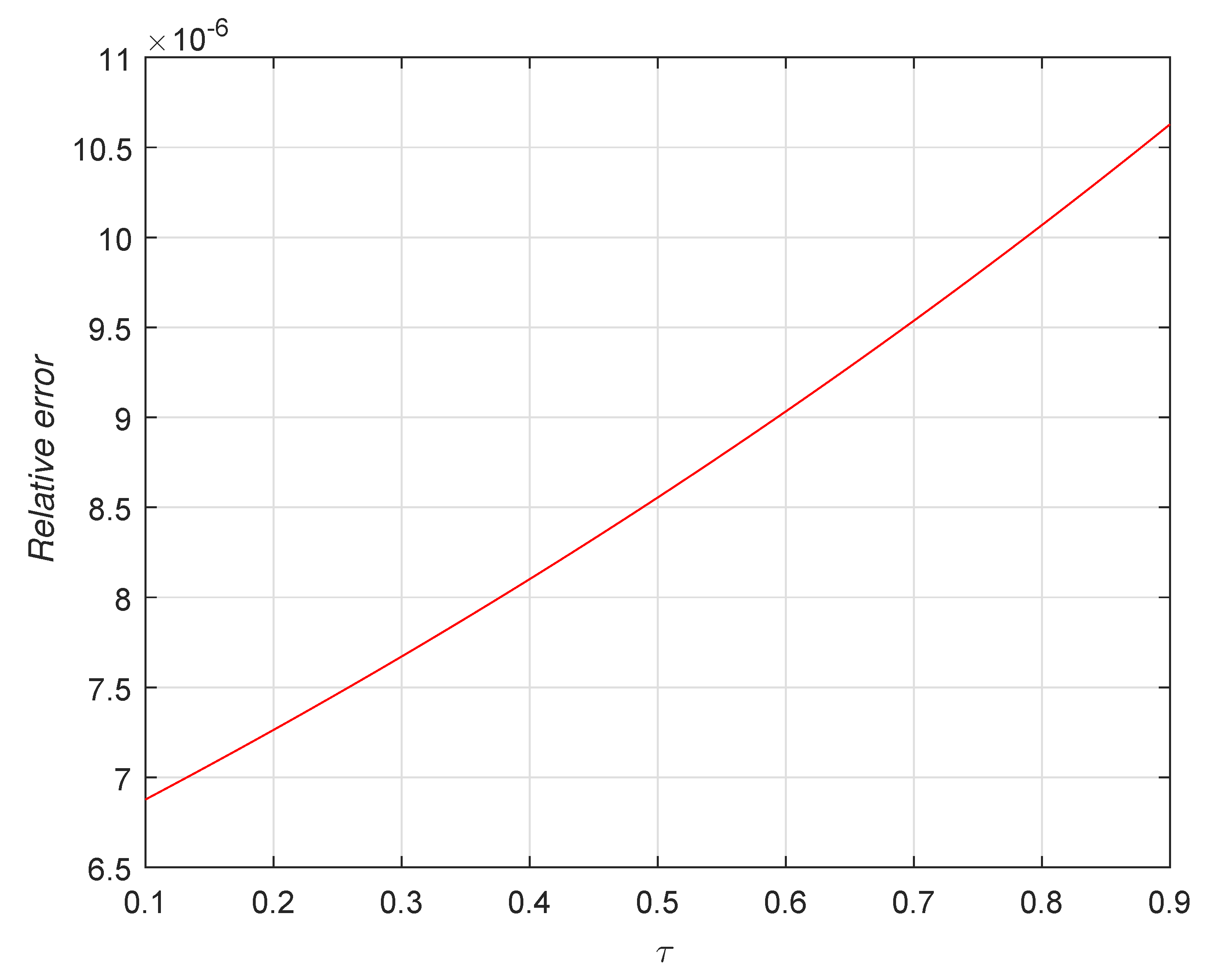
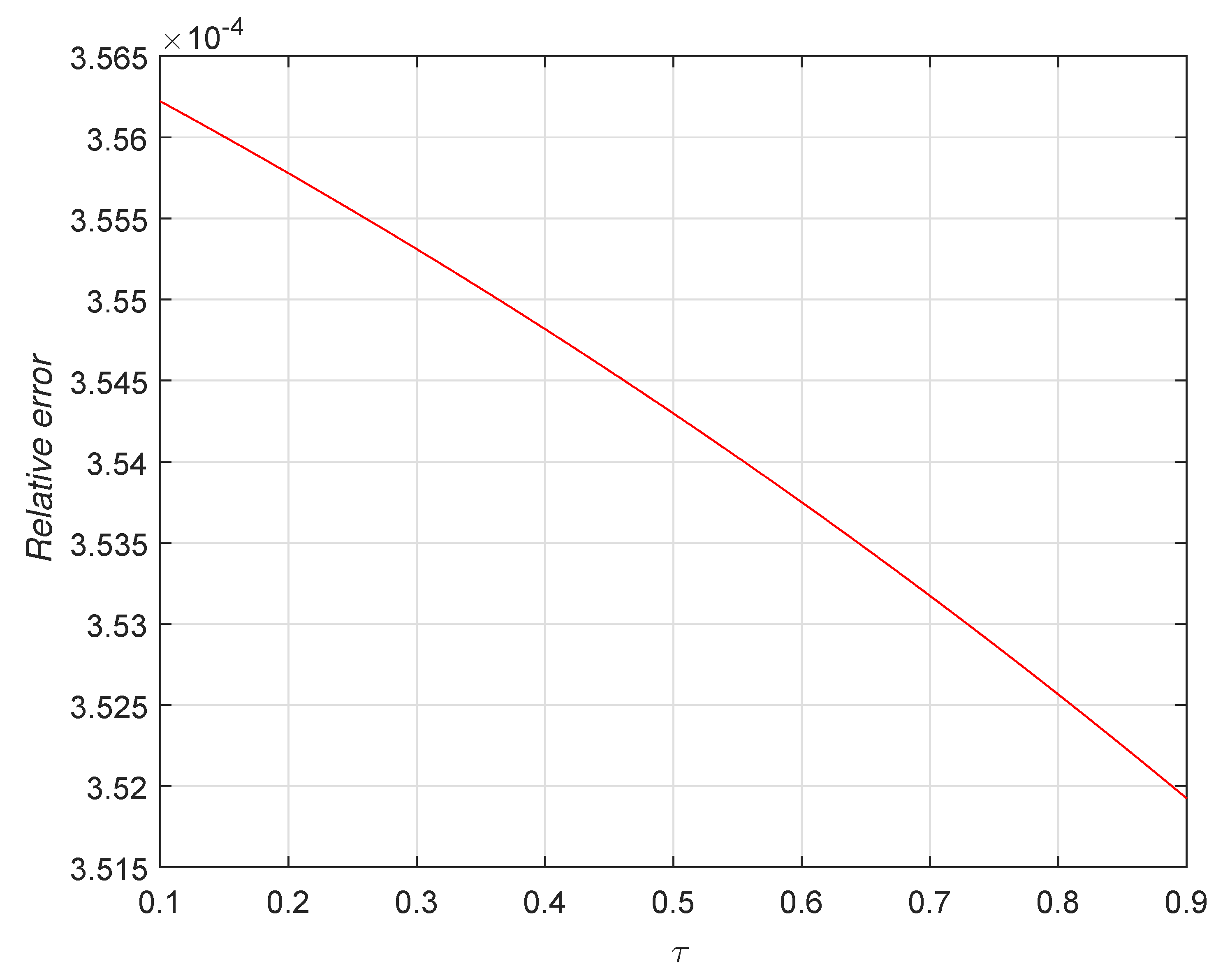
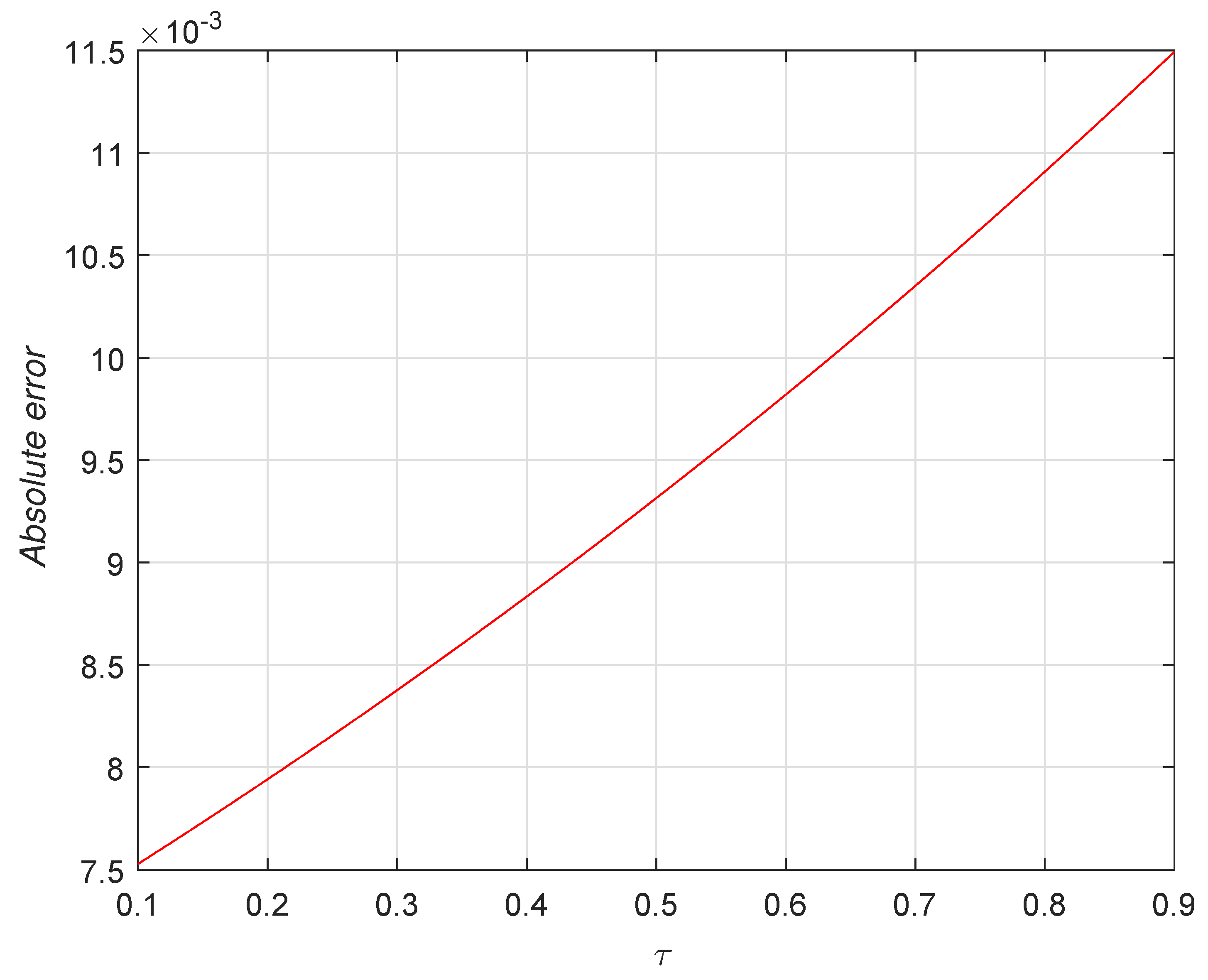
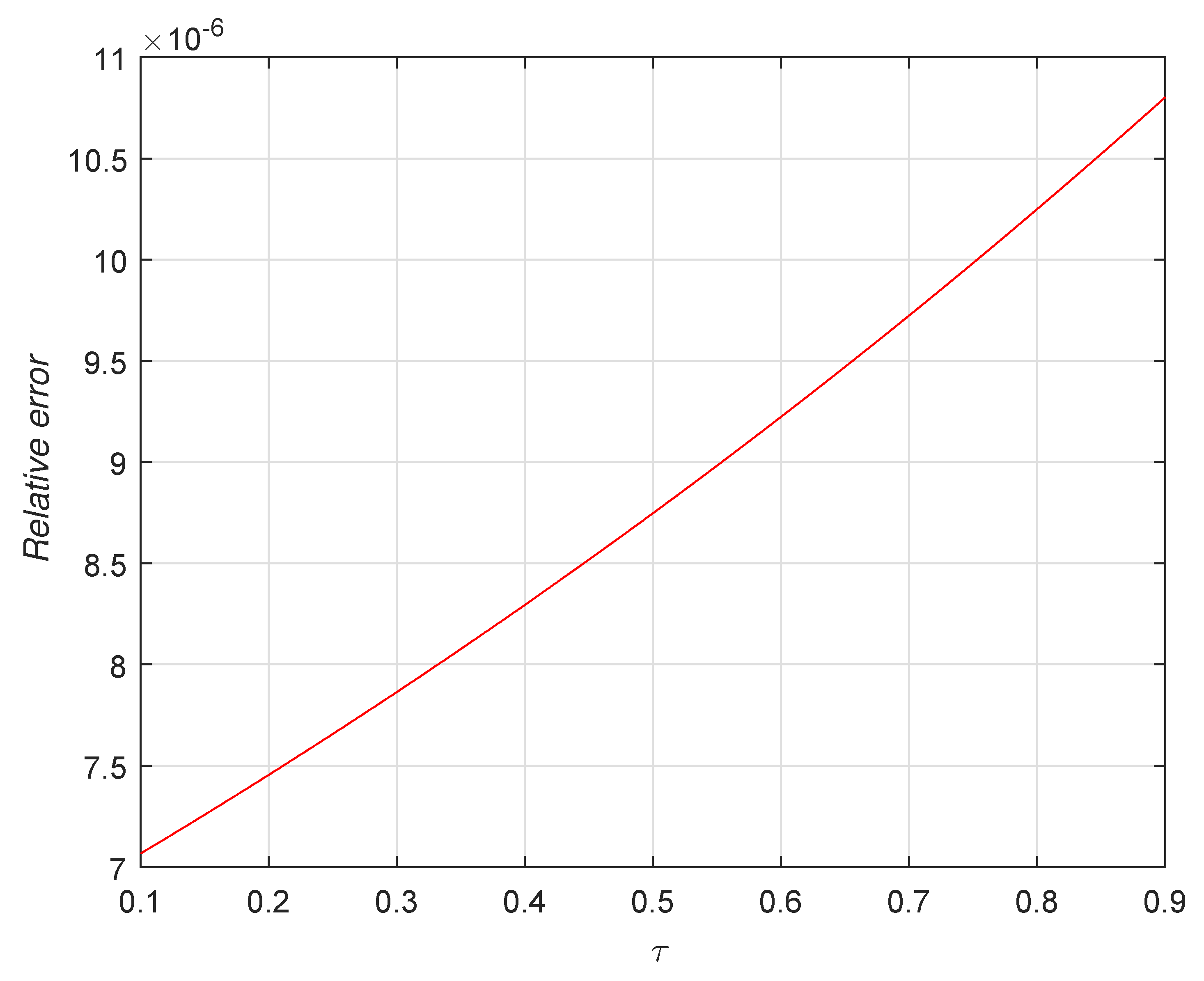
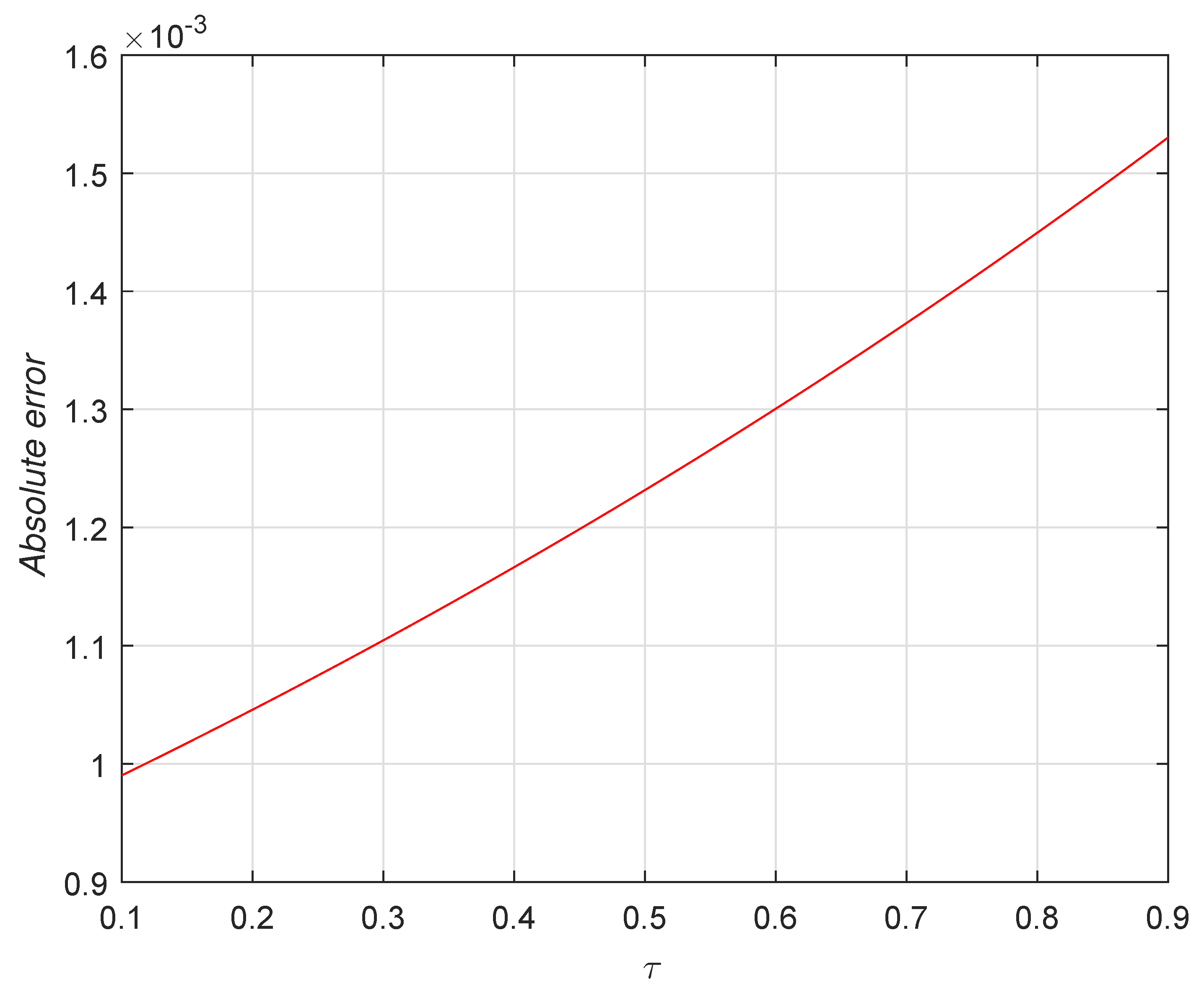
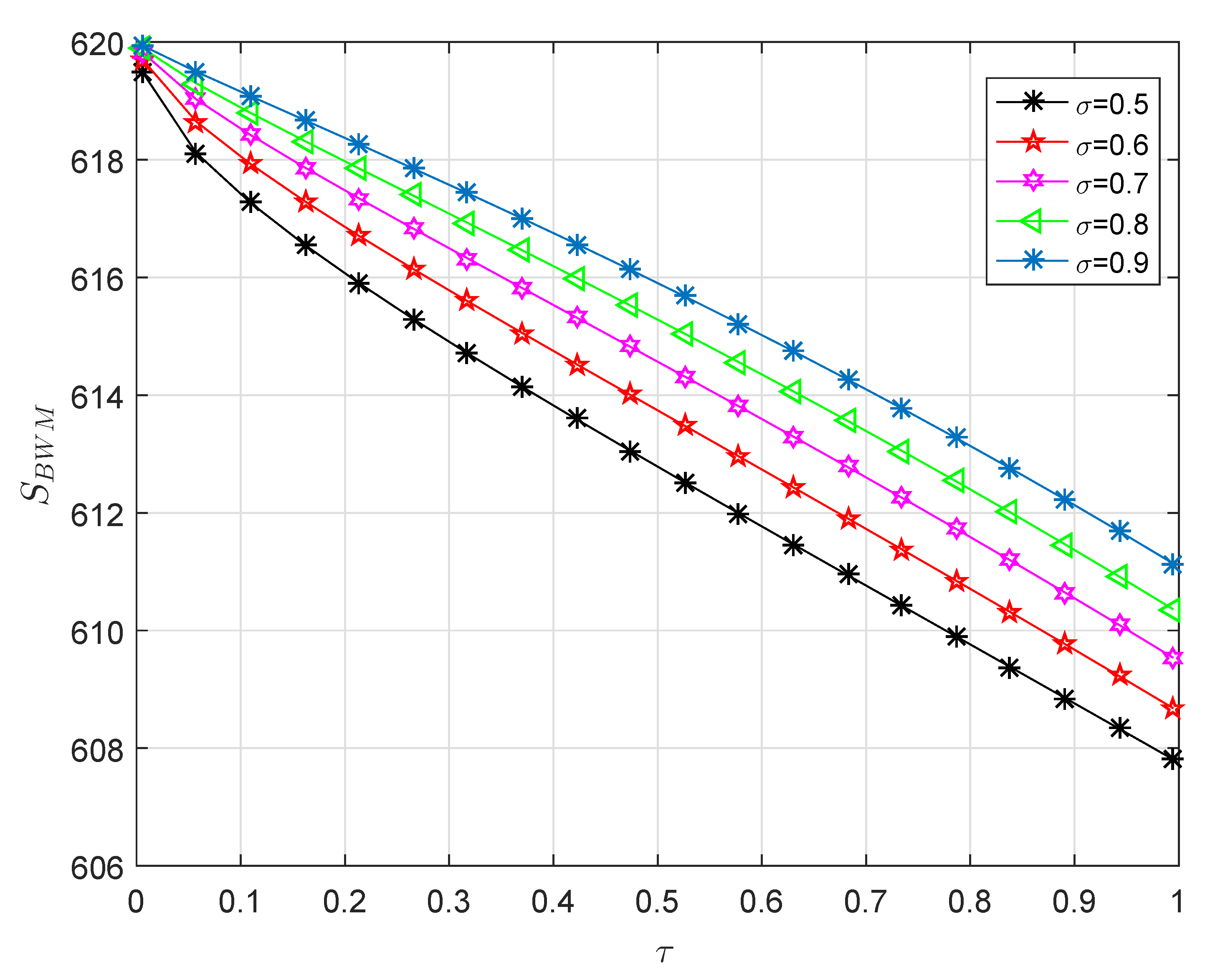

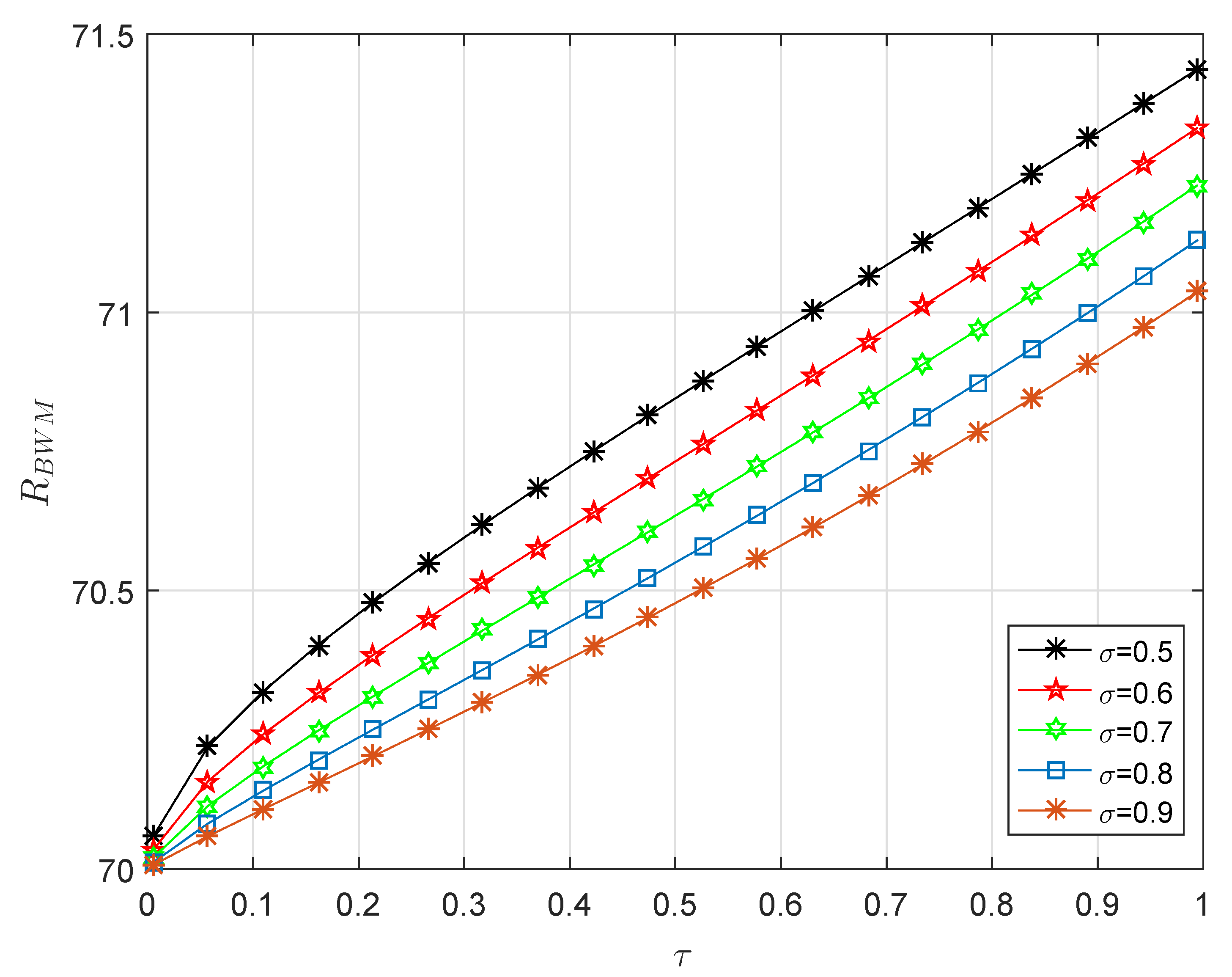
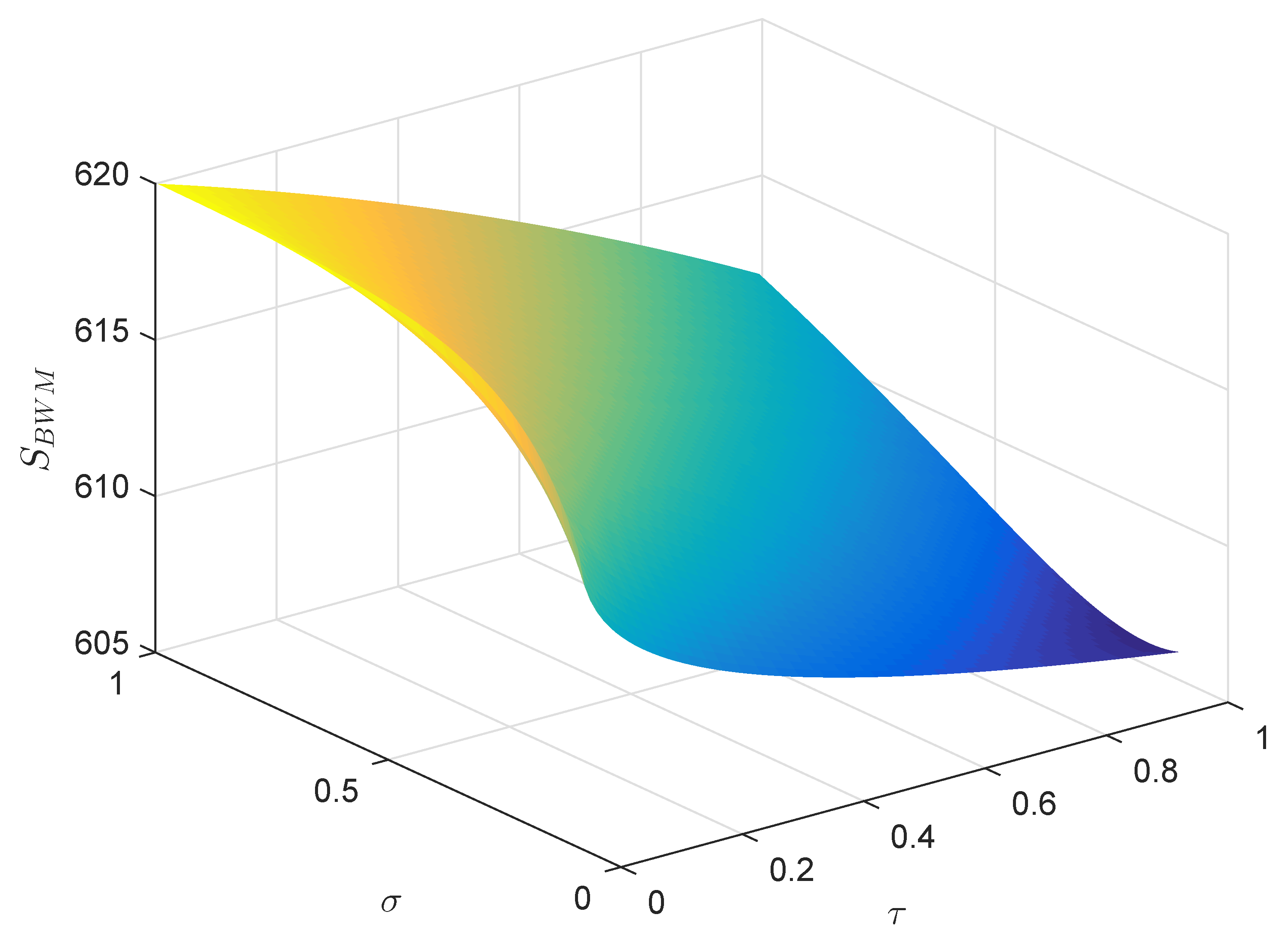
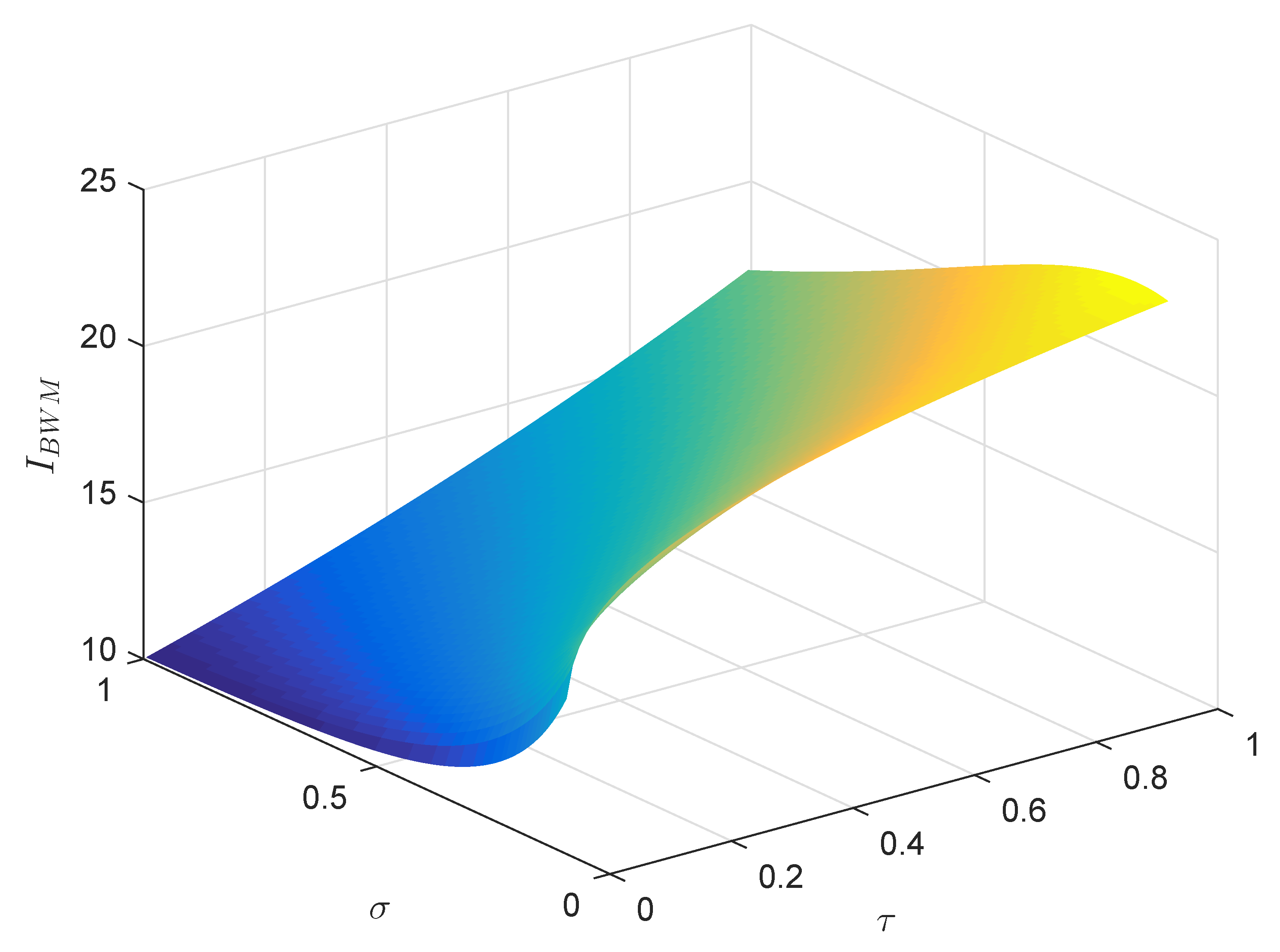
| [42] | [42] | |||
|---|---|---|---|---|
| 0.1 | 619.3630274221 | 619.3545091202 | 619.3630315796 | 619.3630315791 |
| 0.2 | 618.6909310646 | 618.6819439088 | 618.6909370609 | 618.6909370597 |
| 0.3 | 617.9818627742 | 617.9723821904 | 617.9818692109 | 617.9818692025 |
| 0.4 | 617.2338887502 | 617.2238890180 | 617.2338939798 | 617.2338939757 |
| 0.5 | 616.4449797181 | 616.4344339299 | 616.4449876950 | 616.4449876822 |
| 0.6 | 615.6130280833 | 615.6019081178 | 615.6130341588 | 615.6130341421 |
| 0.7 | 614.7358134999 | 614.7240899754 | 614.7358219653 | 614.7358219528 |
| 0.8 | 613.8110328171 | 613.7986750681 | 613.8110418712 | 613.8110418536 |
| 0.9 | 612.8362767043 | 612.8232527460 | 612.8362842538 | 612.8362842258 |
| [42] | [42] | |||
|---|---|---|---|---|
| 0.1 | 10.5629635355 | 10.5704915979 | 10.5629598705 | 10.5629598709 |
| 0.2 | 11.1568872979 | 11.1648285758 | 11.1568820133 | 11.1568820144 |
| 0.3 | 11.7833906224 | 11.7917666401 | 11.7833849513 | 11.7833849586 |
| 0.4 | 12.4441667062 | 12.4529999757 | 12.4441620994 | 12.4441621031 |
| 0.5 | 13.1409910564 | 13.1503051108 | 13.1409840323 | 13.1409840435 |
| 0.6 | 13.8757061597 | 13.8855255736 | 13.8757008108 | 13.8757008253 |
| 0.7 | 14.6502515430 | 14.6606019698 | 14.6502440931 | 14.6502441041 |
| 0.8 | 15.4666371350 | 15.4775453242 | 15.4666291698 | 15.4666291853 |
| 0.9 | 16.3269635312 | 16.3384573546 | 16.3269568911 | 16.3269569155 |
| [42] | [42] | |||
|---|---|---|---|---|
| 0.1 | 70.0740090423 | 70.0749992818 | 70.0740085497 | 70.0740085498 |
| 0.2 | 70.1521816374 | 70.1532275152 | 70.1521809256 | 70.1521809257 |
| 0.3 | 70.2347466032 | 70.2358511694 | 70.2347458376 | 70.2347458387 |
| 0.4 | 70.3219445434 | 70.3231110062 | 70.3219439206 | 70.3219439211 |
| 0.5 | 70.4140292254 | 70.4152609591 | 70.4140282725 | 70.4140282742 |
| 0.6 | 70.5112657569 | 70.5125663085 | 70.5125663085 | 70.5112650324 |
| 0.7 | 70.6139349570 | 70.6153080546 | 70.613933941 | 70.6139339429 |
| 0.8 | 70.7223300477 | 70.7237796076 | 70.7223289588 | 70.7223289610 |
| 0.9 | 70.8367597643 | 70.8382898993 | 70.8367588550 | 70.8367588586 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, S.; Ahmadian, A.; Kumar, R.; Kumar, D.; Singh, J.; Baleanu, D.; Salimi, M. An Efficient Numerical Method for Fractional SIR Epidemic Model of Infectious Disease by Using Bernstein Wavelets. Mathematics 2020, 8, 558. https://doi.org/10.3390/math8040558
Kumar S, Ahmadian A, Kumar R, Kumar D, Singh J, Baleanu D, Salimi M. An Efficient Numerical Method for Fractional SIR Epidemic Model of Infectious Disease by Using Bernstein Wavelets. Mathematics. 2020; 8(4):558. https://doi.org/10.3390/math8040558
Chicago/Turabian StyleKumar, Sunil, Ali Ahmadian, Ranbir Kumar, Devendra Kumar, Jagdev Singh, Dumitru Baleanu, and Mehdi Salimi. 2020. "An Efficient Numerical Method for Fractional SIR Epidemic Model of Infectious Disease by Using Bernstein Wavelets" Mathematics 8, no. 4: 558. https://doi.org/10.3390/math8040558
APA StyleKumar, S., Ahmadian, A., Kumar, R., Kumar, D., Singh, J., Baleanu, D., & Salimi, M. (2020). An Efficient Numerical Method for Fractional SIR Epidemic Model of Infectious Disease by Using Bernstein Wavelets. Mathematics, 8(4), 558. https://doi.org/10.3390/math8040558











