1. Introduction
Combinatorial optimization problems appear naturally in the areas of engineering and science. From the research point of view, these problems present interesting challenges in the areas of operations research, computational complexity, and algorithm theory. Examples of combinatorial problems are found in, scheduling problems [
1,
2], transport [
2], machine learning [
3], facility layout design [
4], logistics [
5], allocation resources [
6,
7], routing problems [
8,
9], robotics applications [
10], civil engineering problem [
11,
12,
13], engineering design problem [
14], fault diagnosis of machinery [
15], and social sustainability of infrastructure projects [
16], among others. Combinatorial optimization algorithms should explore the solutions space to find optimal solutions. When the space is large, this cannot be fully explored. Combinatorial optimization algorithms address this difficulty, reducing the effective space size, and exploring the search space efficiently. Among these algorithms, metaheuristics have been a good approximation to obtain adequate solutions. However, addressing large instances and requiring almost real-time solutions for some cases, motivates lines of research that strengthen the methods that address these problems.
One way to classify metaheuristics is according to the search space in which they work. In that sense, we have metaheuristics that work in continuous spaces, discrete and mixed spaces [
17]. An important line of inspiration for metaheuristic algorithms are natural phenomena, many of which develop in a continuous space. Examples of metaheuristics inspired by natural phenomena in continuous spaces are: Optimization of particle swarm [
18], black hole [
19], cuckoo search (CS) [
20], Bat algorithm [
21], Algorithm of fire fly [
22], fruit fly [
23], artificial fish swarm [
24], gravitational search algorithm [
25], among others. The design of discrete versions of these algorithms carries important challenges because they must try to preserve the intensification and diversification properties [
17].
With the aim of modifying and improving the results of a metaheuristic algorithm, the main tool available to them is tuning their control parameters. These types of modifications correspond to small modifications of the algorithm since the operating mechanism of the algorithm is not altered. However, many optimization problems cannot be efficiently addressed by an algorithm through modification of its parameters and require deep modifications that alter its mechanism of operation [
17,
26]. A strategy that has strengthened the results of metaheuristic algorithms has been the hybridization of these with techniques that come from the same and the other areas. Hybridization strategies involve deep changes to the original algorithm. The main hybridization proposals found in the literature are the following: (i) matheuristics, where mathematical programming is combined with metaheuristic techniques [
27], (ii) hybrid heuristics, hybridization between different metaheuristic methods [
28], (iii) simheuristics, that combine simulation and metaheuristics [
29], and (iv) the hybridization between machine learning and metaheuristics. The latest line of research exploring the integration between the areas of machine-learning and metaheuristic algorithms is an emerging line of research in the areas of computing, mathematics, and operational research. In developing the state-of-the-art, we find that hybridization occurs primarily for two purposes. The first, with the goal that metaheuristics help machine-learning algorithms improve their results (for example, [
30,
31]). In the second intention, machine-learning techniques are used to strengthen metaheuristic algorithms (for example, [
32,
33]). The details of the hybridization forms are specified in
Section 2.
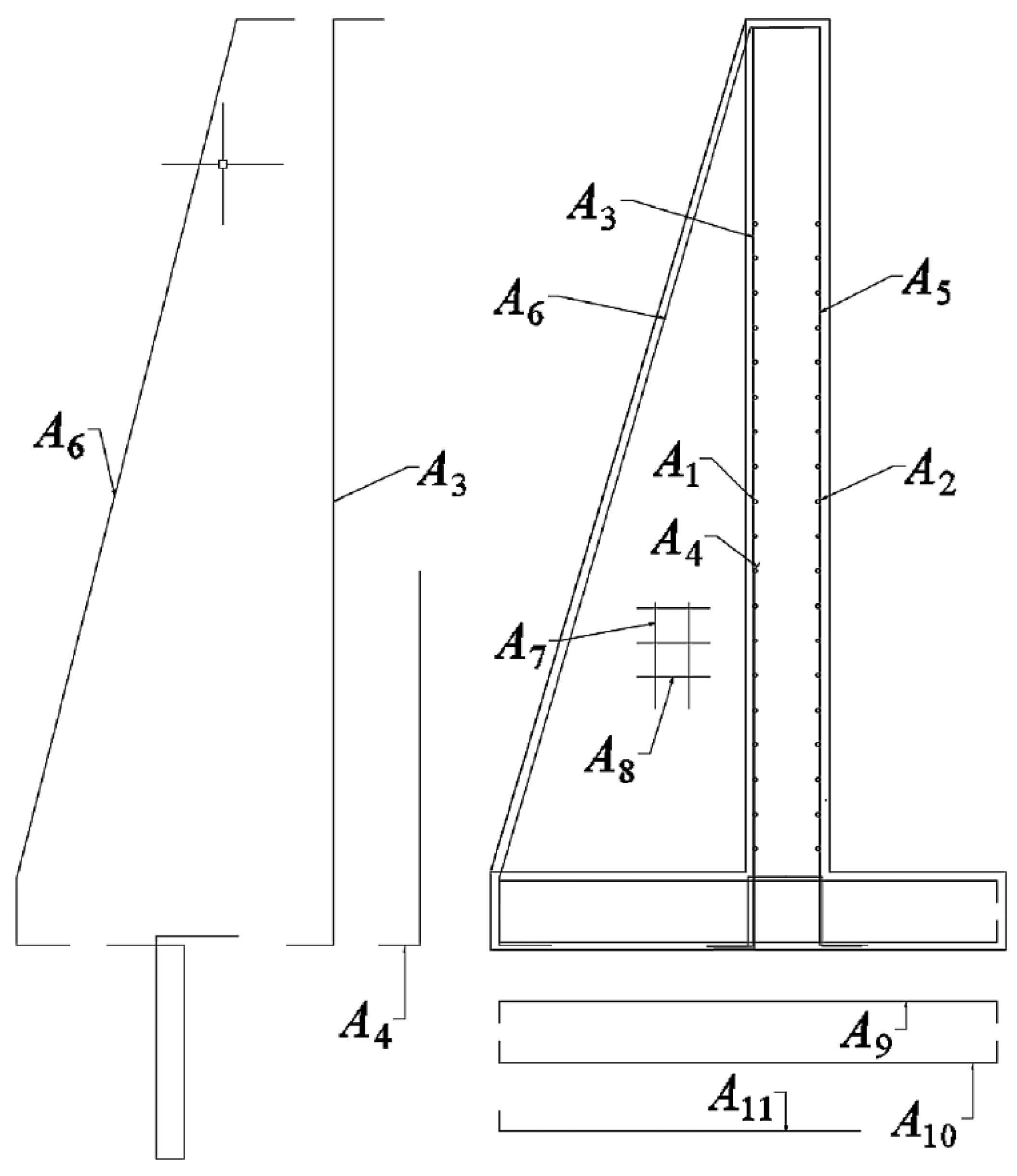
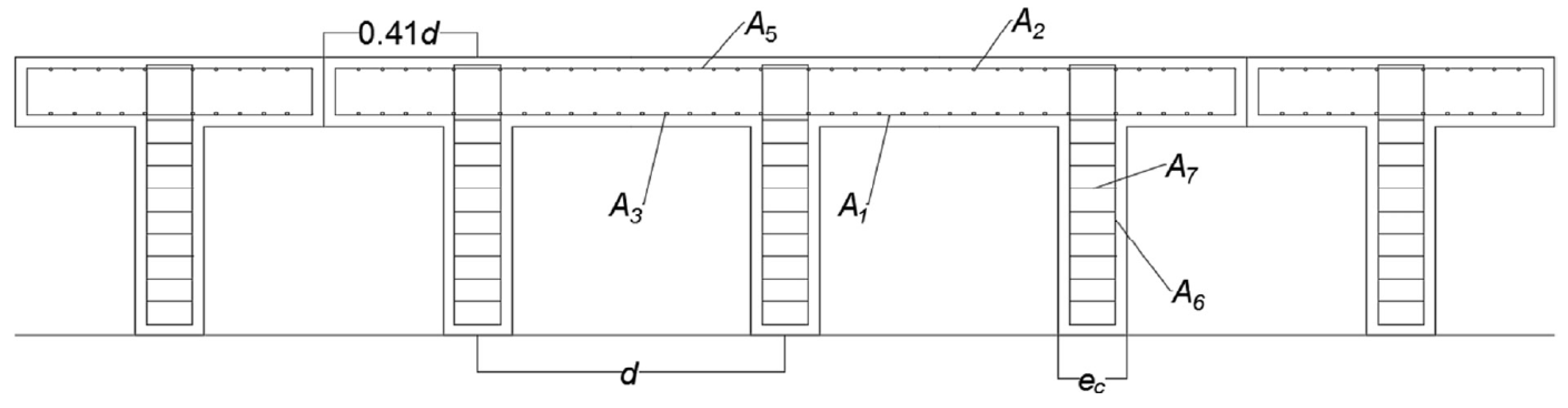
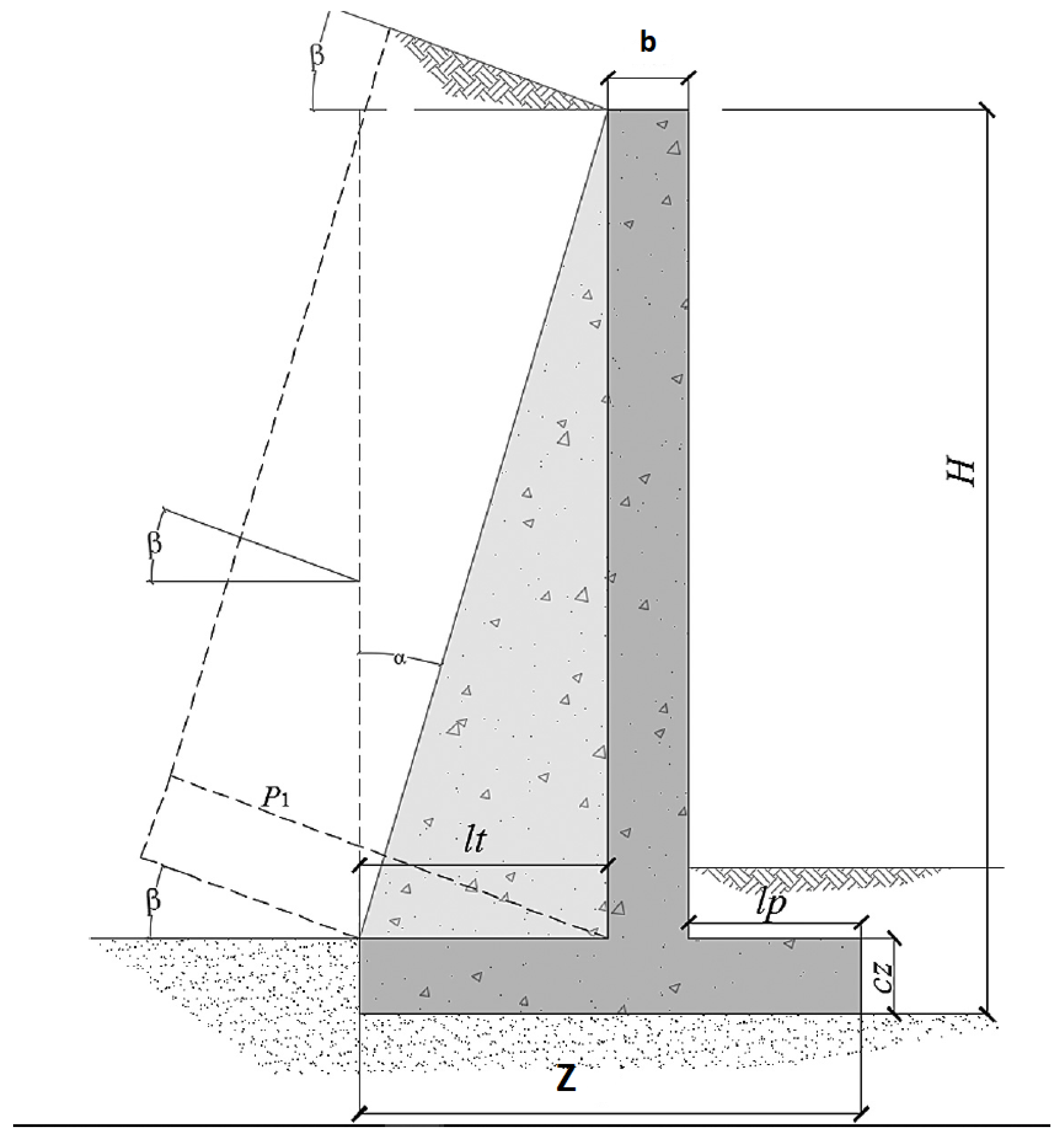
In this article, inspired by the research lines mentioned above. A hybrid algorithm is designed, which explores the application of a machine-learning algorithm in a discrete operator to allow continuous metaheuristics to address combinatorial optimization problems. We will apply our hybrid algorithm to the discrete problem of the design of counterfort retaining walls. The contributions of this work are detailed below:
The structure of the remaining of the paper is as follows: a state-of-the-art of hybridizing metaheuristics with machine learning is developed in
Section 2. In
Section 3 the optimization problem, the variables involved, and the restrictions are defined. The discrete k-means algorithm is detailed in
Section 4. The experiments and results obtained are shown in
Section 5. Finally, in
Section 6 the conclusions and new lines of research are summarized.
2. Hybridizing Metaheuristics with Machine Learning
Metaheuristics form a wide family of algorithms. These algorithms are classified as incomplete optimization techniques and are usually inspired by natural or social phenomena [
17,
35]. The main objective of these is to solve problems of high computational complexity and they own the property of not having to deeply alter their optimization mechanism when the problem to be solved is modified. On the other hand, machine-learning techniques correspond to algorithms capable of learning from a dataset [
36]. If we make a classification according to the way of learning, there are three main categories: Supervised learning, unsupervised learning, and learning by reinforcement. Usually, these algorithms are used in problems of regression, classification, transformation, dimensionality reduction, time series, anomaly detection, and computational vision, among others.
In the state-of-the-art of algorithms that integrate machine-learning techniques with metaheuristic algorithms, we have found two main approaches [
26]. In the first approach, machine-learning techniques are used in order to improve the quality of the solutions and convergence rates obtained by the metaheuristic algorithms. The second approach uses metaheuristic algorithms to improve the performance of machine-learning techniques [
26]. Usually, the metaheuristic is responsible for solving more efficiently an optimization problem related to the machine-learning technique. Adapted and extended from [
26], in
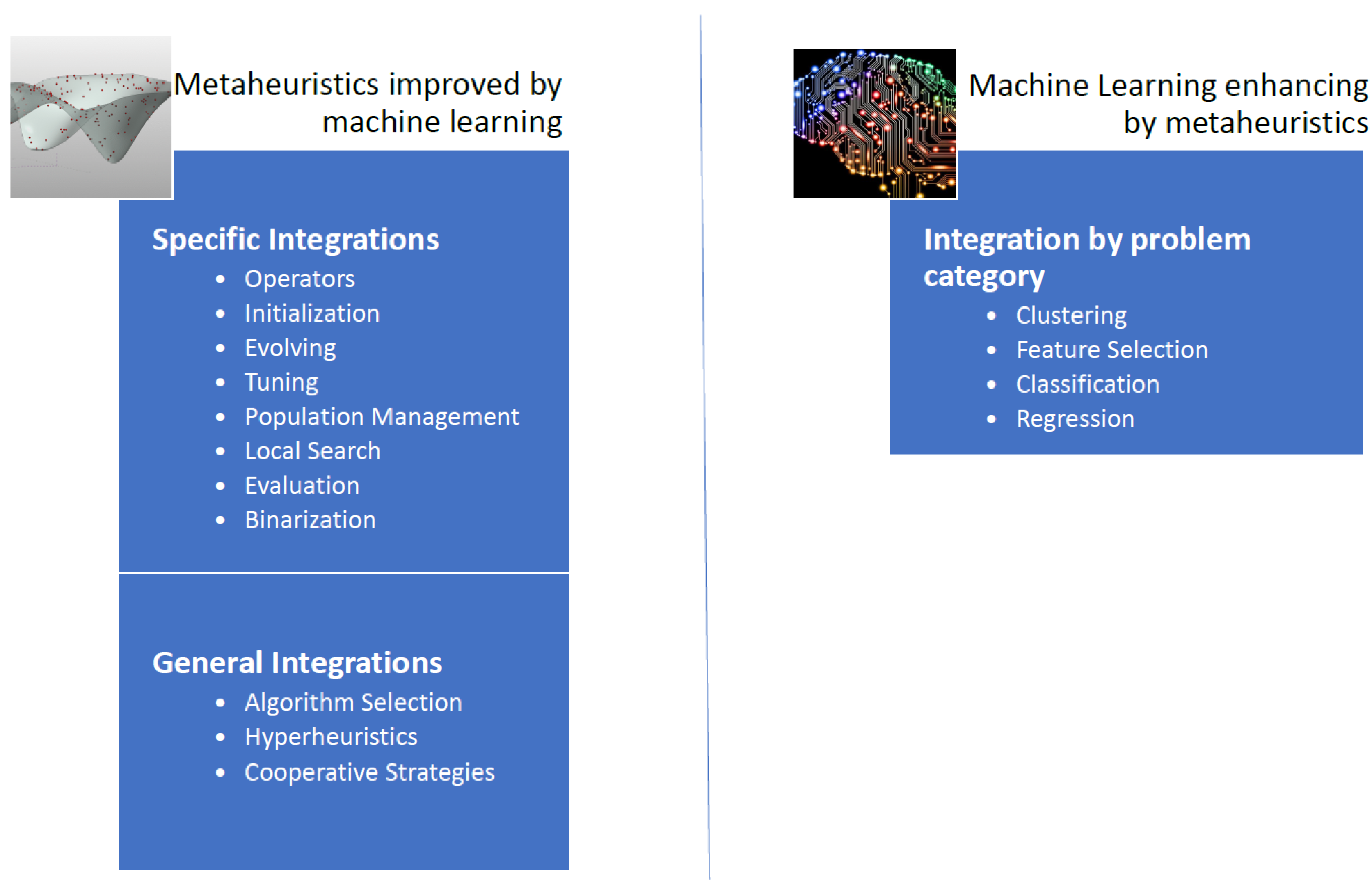
Figure 1, we have proposed a general scheme of techniques where machine learning and metaheuristics are combined.
When we analyze the integration mechanisms of the first approach, we identify two lines of research. In the first line, machine-learning techniques are used as metamodels in order to select different metaheuristics, therein choosing the most appropriate for each instance. The second line aims to use specific operators that make use of machine-learning algorithms and subsequently this specific operator is integrated into a metaheuristic [
26].
In the general integration of machine-learning algorithms on metaheuristic techniques we find three main groups: algorithm selection, hyper-heuristics, and cooperative strategies. In algorithm selection, the goal is to choose from a set of algorithms and considering the associated characteristics for each instance of the problem, an algorithm that works best for similar instances. Another way to approach the problem is to automate the design of heuristic or metaheuristic methods to tackle a wide range of problems, we call this hyperheuristic approximation. Finally, the objective of cooperative strategies is to mix algorithms in a parallel or sequential way to obtain more robust methods. The cooperation mechanism can be complete, i.e., sharing the complete solution, or partial when only part of the solution is shared. In [
32], the problem of docking scheduling in massive terminals was addressed by algorithm selection techniques. In [
37], the nurse training problem through a tensor-based hyperheuristic algorithm was addressed. Finally, a distributed framework that uses agents was proposed in [
38]. In this framework, each agent corresponds to a metaheuristic and the framework can adapt through direct cooperation. This framework was applied to the problem of permutation flow stores.
Additionally, a metaheuristic incorporates operators that allow strengthening its performance. Examples of these operators are initialization operators, solution perturbation, population management, binarization, parameter configuration, and local search operators, among others [
26]. Specific integrations explore the machine-learning application in some of these operators [
26]. In the design of binary versions of algorithms that work naturally in continuous spaces, we find binarization operators in [
2]. These binary operators use unsupervised learning techniques to perform the binarization process. In [
39], the concept of percentile was explored in the process of generating binary algorithms. In addition, in [
1], the Apache spark big data framework was applied to manage the population size of solutions to improve convergence times and the quality of results. Another interesting research line was found in the adjustment of metaheuristic parameters. In [
40], the parameter setting of a chess classification system was implemented. Based on decision trees, and using fuzzy logic, a semi-automatic parameter setting algorithm was designed in [
41]. Usually, in the initiation of solutions, a random mechanism is used. However, using machine-learning techniques, algorithms have been developed that improve the initiation stage of a solution. Applied to the problem of designing a weighted circle in [
42], a case-based reasoning technique was used to start a genetic algorithm. In [
43] Hopfield neural networks were applied to initiate solutions of a genetic algorithm. This initiation was applied to an economic dispatch problem.
To improve the quality of machine-learning algorithms, we see that metaheuristics have a broad contribution. Contributions are found in problems of feature selection, classification, clustering, extraction of characteristics, among others. In the identification of breast cancer, in [
44] a genetic algorithm was designed that improves the performance of support vector machine (SVM) when applied in image analysis. The genetic algorithm was used in the characteristic extraction stage from the images. In [
45] a multiverse algorithm was used to adjust the parameters of an SVM classifier. An improved monarch butterfly algorithm was used in [
46] with the goal to optimize the weights of a feed-forward neural network. In [
47], a geotechnical problem was addressed. In this article, a firefly algorithm was integrated with the least-squares support vector machine technique. When considering regression problems, there are again several cases where metaheuristics have contributed. For example, in predicting the strength of high-performance concrete, in [
48] a metaheuristic was used to improve the least-squares technique. In [
49], share price prediction was improved by integrating metaheuristics into a neural network. Again, in the prediction of the share price of construction companies in Taiwan, in [
30], a sliding-window metaheuristic-optimized machine-learning algorithm was designed, which integrates a metaheuristic in its learning process. Optimization of the parameters of a least-squares regression was improved, in [
50] using a firefly algorithm. We also found metaheuristic applications for unsupervised learning techniques. In particular, there are significant contributions from metaheuristics to clustering techniques. For example, in [
51], we found an algorithm application that integrates a metaheuristic with a kernel intuitionistic fuzzy c-means. This algorithm was applied to different data sets. Another integration found for clustering techniques is the search for centroids. This problem is to find the set of centroids that best group the data under a certain metric. This is an NP-hard type problem and therefore it is natural to approach it with a metaheuristic. In [
52] an algorithm was proposed that uses a bee colony to solve a problem of grouping energy efficiency data obtained from a wireless sensor network. In [
53], a metaheuristic was used to find centroids in planning the transportation of employees from an oil platform via helicopters. In the case of neural networks, metaheuristics have contributed to different types of integration. In [
54] a metaheuristic algorithm is used to automatically find the appropriate number of neurons in a feed-forward neural network. In [
55] a metaheuristic algorithm allows determining the dropout probability in convolutional neural networks. The cuckoo search and bat algorithm algorithms were used in [
56] to adjust the weights of neural networks of feed-forward type. In [
57] an algorithm was designed using metaheuristics to optimize convolutional neural networks. An application to long term short memory (LSTM) neural network training was studied in [
58]. LSTM networks were applied in healthcare analysis.
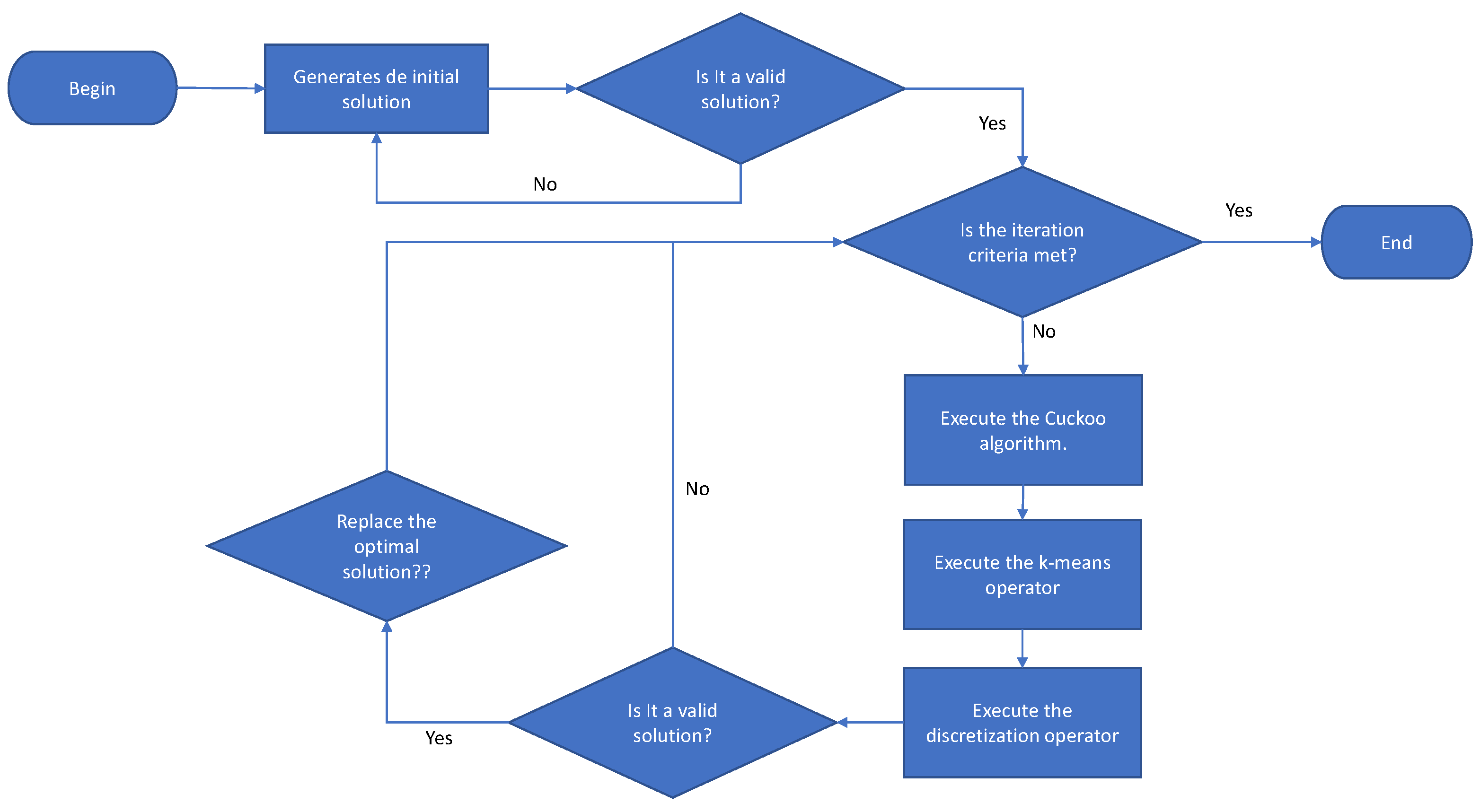
Inspired by the lines of research detailed above, this work proposes a hybrid algorithm in which the unsupervised k-means learning technique is used to obtain binary versions of the cuckoo search optimization algorithm. This hybrid algorithm was used to solve the problem of the counterfort retaining walls. The k-means technique has been widely used and in recent studies, it has been applied in [
59] to bioinformatics for detecting gene expression profile, image segmentation for pest detection [
60] in agriculture, and brain tumor identification [
61], among others. Particularly the k-means technique has been previously applied in obtaining binary versions of continuous metaheuristics and used to solve the multidimensional knapsack problem [
33] and the set covering problem [
5] which are NP-hard problems. In the case of the cuckoo search, hybrid versions of this algorithm have been applied in [
62] to numerical optimization problems in engineering. In [
63] cuckoo search was applied to benchmark functions and engineering design problems. An algorithm with reinforced learning was used in [
64] to solve a logistic distribution problem. In [
65] an improved version of the cuckoo search was applied to drone location.