Multiobjective Mixed Integer Nonlinear Model to Plan the Schedule for the Final Disposal of the Spent Nuclear Fuel in Finland

Abstract

The safe disposal of the spent nuclear fuel is the important part of the nuclear power production. In this paper, we model the geological disposal in Finland covering objectives related to the interim storage, the encapsulation facility, the disposal facility, and the costs. A notable fact is that all the fuel types used in Finland are taken into account. The resulting optimization model is of a multiobjective nonlinear mixed integer type having eight objectives. The model is solved with the interactive method utilizing the special type of the achievement scalarizing functions. From this, we obtain a disposal schedule giving amounts of canisters to encapsulate in each time period. The results obtained are analyzed from the practical point of view.

1. Introduction

In Finland, the nuclear power covers the notable share of the electricity production. However, this process also produces the spent nuclear fuel which needs to be permanently disposed of safely. In the field of the geological disposal [1], Finland is one of the pioneers by starting the geological disposal in 2020s [2]. In this paper, we aim to produce a schedule in terms of amounts of canisters disposed of periodically in order to dispose of all the spent nuclear fuel in Finland.

Most of the practical applications contain more than one aspect to be optimized, and, usually, at least some of these aspects are conflicting meaning that the problem in question is a multiobjective one. This leads us to make compromises, and the compromise solution of the multiobjective problem is called Pareto optimal. Typically, the multiobjective problem has several Pareto optimal solutions being all mathematically equally good. However, they may differ much in practice. Therefore, we are interested in finding the most desirable solution for the decision maker. This aim is succeeded in including the decision maker in the solution process. One way to do this is the utilization of interactive methods [3,4,5,6,7,8,9] such that the solution process moves from one Pareto optimal solution to another based on the decision maker’s wishes. This lets us to avoid calculating all the Pareto optimal solutions.

This paper is inspired by the study [6] where the multiobjective nonsmooth (i.e., nondifferentiable) mixed integer nonlinear programming (MINLP) problem modeling the case of the geological disposal with one fuel type is presented. In addition to the model, the multiobjective interactive method utilizing two-slope parameterized achievement scalarizing functions (MITSPA) is proposed. This method is then applied to the disposal model. In total, the model in [6] contains nine objectives related to the interim storage, the encapsulation, the area of the disposal facility, and the costs. As a result, the number of canisters to encapsulate at each time period is obtained. These schedules are then analyzed together with the objective function values.

The schedule for the final disposal of the spent nuclear fuel is studied also in [10] minimizing the total costs of the disposal in Finland with a single-objective mixed integer linear programming (MILP) and, in [11], where the area of the disposal facility is aimed to minimize with a linear transportation model. Another optimization related study to design the disposal facility is in [12] giving the multiobjective MILP problem optimizing the nuclear waste placement in the disposal facility, and in [13], the optimal initial condition for the disposal facility is investigated with multiobjective optimization. The disposal schedule can be utilized, for example, when the loading of canisters is optimized [10,14,15,16,17]. The final disposal related aspects in terms of optimization is discussed also from several other points of view, like the placement of the disposal repository [18], to route the transfer of the nuclear waste [19,20], to optimize the shut down date of the reactor [21,22], or from the safety point of view: the optimization of the nuclear safeguards [23,24] and the safety assessment of nuclear waste repositories [25].

The aim in this paper is to extend the model presented in [6] and apply it to the real world case considering all three types of the spent nuclear fuel needed to be disposed of in Finland. The new model is then solved by using MITSPA [6]. Multiobjective optimization seems to be a reasonable way to approach this problem. Even if the disposal is a notable investment economically, by minimizing only costs we may omit better solutions, for example, from the safety point of view. Furthermore, by optimizing not only the costs but also the cost factors, we may obtain more confidence for the decision-making. Compared with [6], which is designed mainly from the academic perspective, this study is carried out for the real world requirement. This is amongst the first studies using such data that the final disposal could be started based on it. Due to the real and updated data, the model in [6] has been heavily modified. For example, with the accurate data of the storage facilities, the storage of the spent fuel assemblies can be modeled more practically. Along with three fuel types, the creation of the schedule has more aspects to consider, like the disposal order of the fuel types or the possibility to have the hiatus during the disposal. Furthermore, the analysis of the results in this paper have a more practical approach.

In this paper, we present the case study of the final disposal of the spent nuclear fuel in Finland. In Section 2, we describe the final disposal process and in Section 3 this process is modeled as a multiobjective nonsmooth MINLP problem. The method used to solve the model is briefly reviewed in Section 4 and the numerical experiments are discussed in Section 5. Finally, some concluding remarks are given in Section 6.

2. Final Disposal of the Spent Nuclear Fuel in Finland

Nuclear power has a major role in the electricity production in Finland covering approximately 32% of the domestic electricity production. Indeed, in 2018, the total electricity production was 67.5 TWh from which 21.9 TWh was generated by the nuclear power [26]. At the moment, there are four nuclear reactors operating in Finland and the fifth begins the operation in the near future increasing the portion of the nuclear power of the domestic electricity production. Here, we consider the fuel assemblies irradiated in these five reactors even if there are plans for the sixth reactor in Finland. The current nuclear power plants are owned by the companies Fortum Power and Heat Oy (Fortum) and Teollisuuden Voima Oyj (TVO). In Finland, the power companies are responsible also for the final disposal of the spent nuclear fuel. In order to perform this task, Posiva Oy, owned by Fortum and TVO, was established in 1995.

Posiva needs to follow the legislation by the Ministry of Economic Affairs and Employment and the operation is controlled by the Radiation and Nuclear Safety Authority (STUK). The most important constraints for the disposal process are determined by the authorities, like the regulatory guides on nuclear safety and security by STUK [27]. For the purposes of this study, the most important safety aspects are the thermal dimensioning of the spent nuclear fuel repository, the criticality, and the radiation safety. The thermal dimensioning needs the investigation of the relation between the canister spacing and their heat powers [28] while the radiation safety can be taken into account in this context by forcing the minimum cooling time for the spent nuclear fuel [29]. It is worth noticing that in this paper no additional criticality safety analyses were established in order to simplify the analysis. Nevertheless, the criticality safety will be covered in the disposal production, for example, with the burn-up credit and loading curve criterion.

In Finland, the final disposal of the spent nuclear fuel is based on the KBS-3 (Kärnbränslesäkerhet, nuclear fuel safety) concept [30] developed by Swedish Nuclear Fuel and Waste Management Company (SKB). The concept relies on the multiple barriers isolating the spent nuclear fuel from the environment and these barriers are illustrated in Figure 1. At the beginning of the disposal process, the spent fuel assemblies are stored in Olkiluoto’s and Loviisa’s interim storages until they can be disposed of. From the interim storage, the fuel assemblies are transferred to the encapsulation facility, where they are loaded in canisters. After that, the canisters are transferred to the underground disposal facility for the final disposal. In the following, we briefly discuss the properties of the fuel assembly and follow the journey of the fuel assembly from the reactor to the bedrock.

2.1. Reactor and Spent Nuclear Fuel Types

Currently, there are two nuclear power plants in Finland, one in Olkiluoto and the other in Loviisa. In Olkiluoto, two Boiling Water Reactors (BWR) Olkiluoto 1 and Olkiluoto 2 are in operation, and the third reactor, namely Olkiluoto 3, being that a European Pressurized Water Reactor (EPR) is starting operation in the near future. In Loviisa, two Russian-type Pressurised Water Reactors (VVER-440), Loviisa 1 and Loviisa 2, are in operation. Loviisa 1 was the first reactor starting the operation on 1977, and Olkiluoto 3 is planned to be the last of these five reactors to be in operation such that it will be permanently shut down in the 2080s.

All the reactors use uranium dioxide as a fuel. However, each reactor type needs its own type of the fuel such that, for example, the geometry and the mass varies. In total, three different types of the spent nuclear fuel are produced in Finland. The spent nuclear fuel type produced by the reactors Olkiluoto 1 and 2 is referred as OL1-2, by reactors Loviisa 1 and 2 as LO1-2, and by reactor Olkiluoto 3 as OL3. In Figure 2a, the accumulated uranium mass for each fuel type is illustrated. Figure 2a contains the best estimate case i.e., uranium mass forecasts for the each, OL1-2, LO1-2, and OL3, with the total of roughly 5500 tU, whereas the licensing case is 6500 tU.

Since all the reactors in Finland use the uranium dioxide fuel matrices, the main differences for the decay heat production of different fuel types are caused by the uranium mass and the burnup (see Figure 2). The burnup tells how much energy is produced from one mass unit of the uranium, and, in Figure 2b, the average discharge burnup for each fuel type is presented. As we see, the average discharge burnup of all fuel types is increased during the time. The higher burnup, or an increase in the uranium mass, leads to the higher decay heat power of the fuel assembly, which again increases the cooling time since the decay heat power of a canister is limited. The decay heat power of a fuel assembly for each fuel type is exemplified in Figure 2c based on the representative fuel characteristics given in [32]. Note that the difference between OL3 and OL1-2 and LO1-2 is due to the larger uranium mass of the fuel assembly of OL3. These decay heat power curves have similar shape for each fuel type and also the cooling of canisters of different fuel types is similar. Indeed, in Figure 2d, how much cooling time each fuel type needs with different burnups is illustrated in order to reach their nominal canister powers.

2.2. Interim Storage

The part of the fuel assemblies in the reactor is changed annually. Once the fuel assemblies are removed from the reactor, they produce a large amount of radiation and decay heat. During the first years, this production decreases rapidly when the fuel assembly is in water absorbing radiation and cooling down the fuel together with the cooling system. Indeed, the radioactivity of the fuel assembly decreases to the level that is less than the percent from the radioactivity when the reactor is shut down. Thus, the assemblies are stored in water pools located in the reactor hall for a few years and then they are transferred to the interim storage. Before the spent fuel assemblies can be disposed of, they must be stored in the interim storage for decades. The calculation of the storage time begins when the reactor is shut down such that the fuel assembly can be removed from the reactor. Although there is the minimum storage time stated by the safety [29], the storage time of the fuel assemblies is usually longer.

The interim storages locate in the reactor facility areas such that OL1-2 and OL3 are stored in Olkiluoto and LO1-2 in Loviisa. Both storages contain several water pools. The spent fuel assemblies are placed in racks and only one type of the fuel can be stored in one pool. The storage capacity needed depends on the operating license of the reactor and the disposal pace. With the current estimated operating license [34], the interim storage in Loviisa has enough pools, but, in Olkiluoto, some additional pools might be needed. Then, a new pool with racks can be built. However, once the pool used to store OL1-2 is empty, it is possible to change the racks and store OL3 in the same pool. In the model, the racks are obtained for the whole pool at once. The interim storage is in use until the last fuel assembly is transferred to the encapsulation facility.

2.3. Encapsulation Facility

In the encapsulation facility, the fuel assemblies are loaded in canisters. Each fuel type has its own canister type, but they all have the same basic structure: the copper overpack and the iron inside. However, the dimensions, the shapes of the fuel assembly positions, and the capacity of the canister vary for each fuel type.

The fuel assemblies must be selected for a canister such that the decay heat power of the canister does not exceed the limits (see Figure 2d). The decay heat power of the canister is calculated as a sum of the decay heat powers of the fuel assemblies. In order to decrease the decay heat power of the canister, empty assembly positions can be utilized.

Only one type of the fuel can be encapsulated at one time. In the investigations of this paper, the encapsulation begins in 2025 and the order of the fuel types is fixed such that the encapsulation begins with the part of OL1-2 and continues with LO1-2. All LO1-2 must be encapsulated at once. After that, the rest of OL1-2 is encapsulated. Lastly, all OL3 is encapsulated. During the production, it is possible to have one hiatus. If a hiatus is included, it is between the second part of OL1-2 and OL3. In those years when the encapsulation is not on the hiatus, there is a minimum number of canisters that must be encapsulated. The upper bound of the yearly canister production can be exceeded by involving a two-shift work. However, the two-shift work is not allowed at the first year of the new fuel type and the upper bound for yearly canister production is lower at the first year of the encapsulation and at the first year after the hiatus.

2.4. Disposal Facility

After the canister is encapsulated, it is transferred to the disposal facility located more than 400 m under the ground. The schematic picture of the disposal facility is given in Figure 3. The canisters are placed in the vertical disposal holes on the floor of the disposal tunnel although the horizontal positioning is considered as well [30]. The disposal tunnels are connected with central tunnels. In the model, the central tunnel is built as a pair and the disposal tunnels locate on both sides of the central tunnel pair.

At each disposal tunnel, only one fuel type can be disposed of, and, in the model, each disposal tunnel has the same length. The total length of the disposal tunnels depends on the number of canisters and the canister spacing. However, the disposal tunnels need to be planned for a slightly higher number of canisters than actually needed since there might be places in the bedrock where the disposal hole cannot be drilled.

The length of the central tunnel depends on the total number of the disposal tunnels, the disposal tunnel spacing, and the length of the hiatus. Indeed, each year on the hiatus increases the length of the central tunnel such that the heat wave caused by the canisters disposed of before the hiatus can be taken into account. Furthermore, there exist brittle fault zones with varying classifications in the bedrock of Olkiluoto where disposal holes or disposal tunnels cannot be built. If the disposal facility area needs to be expanded over the brittle fault zone, the corresponding amount of the central tunnel needs to be built.

Besides the fixed minimum and maximum values, in order to define a suitable canister and disposal tunnel spacing, the surface temperature of the canisters needs to be taken into account. In [28], different canister and disposal tunnel spacings and powers of the canister are investigated such that the surface temperature of the canister stays at a suitable level (see Figure A1 in Appendix B). These calculations are utilized when the relation between the power of the canister, the distance between disposal tunnels, and the distance between canisters is approximated for each fuel type in this paper.

In order to ensure the long-term safety, the last phase of the disposal is to fill the disposal facility. The disposal tunnels are filled with bentonite and clay; meanwhile, the canisters are placed in the disposal holes. Once the disposal tunnel is filled, they are sealed with a plug. After all the disposal tunnels are sealed, the central tunnel is filled with bentonite and clay.

3. Mathematical Model

In [6], a multiobjective nonsmooth MINLP model with nine objectives for the disposal of the spent nuclear fuel is proposed. The aim there is to produce a disposal schedule in terms of the number of canisters disposed of in each time period. The model adopts the final disposal in Finland in the general level, but the limitation of the model is that it involves only one type of a fuel. In this study, the model presented in [6] is developed further to contain all three fuel types used in Finland. Due to this extension, a possibility for a hiatus is included for the new model. Additionally, the new model is adjusted to the situation in Finland taking into account, for example, the storage facilities more accurately.

The model in [6] and the model presented here have some differences also in objectives. Via more accurate information on the storage of the fuel assemblies, the objective related to the maximum storage amount is now updated to minimize the total number of new water pools in the interim storage. The total number of objectives of the new model is eight leaving the objective minimizing the maximum storage time out. This is done in order to reduce the size of the model since now we are able to omit several binary variables. However, the minimization of the average storage time is still included as the objective. The rest of the six objectives are also still included: minimize the total number of canisters, the disposal ends as early as possible, minimize the operation time of the encapsulation facility, minimize the length of the disposal tunnels and central tunnel, and minimize the total costs. All of these objectives are adjusted for the case of several fuel types.

In the following model description, the fuel type 1 refers to OL1-2, the fuel type 2 to LO1-2, and the fuel type 3 to OL3. Recall that OL1-2 and OL3 are used in Olkiluoto and LO1-2 in Loviisa. We assume that no fuel assemblies have been disposed of yet and the decay heat power of the fuel assemblies from one removal from the reactor are considered as average decay heat powers from that removal. The disposal schedule is divided in periods whose length can be adjusted. The starting time of the disposal is fixed and the last possible disposal period is given.

3.1. Parameters

We begin by introducing the parameters involved in the model. The size of the model is defined by the following three parameters:

I 

total number of removals from the reactor

J 

total number of disposal periods

Z 

length of the disposal period.

These parameters relate to the following set of indices: the set of removals from the reactor $\mathcal{I}=\{1,\dots ,I\}$ and the set of periods $\mathcal{J}=\{1,\dots ,J\}$. Furthermore, we introduce the set of fuel types $\mathcal{L}=\{1,2,3\}$.

The following set of parameters define some properties of fuel assemblies:

$M_{i,l}$ 

number of assemblies of the fuel $l\in \mathcal{L}$ belonging to the removal $i\in \mathcal{I}$

$P_{i,j,l}$ 

decay heat power of an assembly of the fuel $l\in \mathcal{L}$ belonging to the removal $i\in \mathcal{I}$ in the period $j\in \mathcal{J}$ [W]

$O_l$ 

last period when the reactor for the fuel $l\in \mathcal{L}$ is in operation

$A_{i,j,l}$ 

storage time of an assembly of the fuel $l\in \mathcal{L}$ belonging to the removal $i\in \mathcal{I}$ in the period $j\in \mathcal{J}$ [period]

R 

minimum storage time of an assembly [period]

$N_l$ 

number of removals before the first period of the fuel $l\in \mathcal{L}$.

Features of the disposal and central tunnels are denoted with the following parameters:

Q 

effective length of the disposal tunnel [m]

$Q^r$ 

coefficient taking into account the true length of the disposal tunnel

$Q^h$ 

coefficient taking care of the rejected disposal holes

$D^{ct}$ 

maximum length of the central tunnel before the brittle fault zone [m]

$D^{add}$ 

additional amount of central tunnel to transit over the brittle fault zone [m]

$D^h$ 

annual amount of the central tunnel to build during the hiatus [m]

$D^{c_{low}}$ 

lower bound for the distance between two adjacent canisters [m]

$D^{c_{up}}$ 

upper bound for the distance between two adjacent canisters [m]

$D^{{dt}_{low}}$ 

lower bound for the distance between two adjacent disposal tunnels [m]

$D^{{dt}_{up}}$ 

upper bound for the distance between two adjacent disposal tunnels [m]

M 

amount of the central tunnel available after the transition over the brittle fault zone [m].

Next, we give some parameters related to the canisters:

$U^{low}$ 

minimum number of canisters disposed of in one period

$U^{up}$ 

maximum number of canisters disposed of in one period

V 

decrease in the maximum canister capacity in the first period of the encapsulation

W 

increase in the maximum canister capacity due to the two-shift work

$K_l$ 

capacity of a canister for the fuel $l\in \mathcal{L}$

$P_l^{low}$ 

lower bound for the power of the canister for the fuel $l\in \mathcal{L}$ [W]

$P_l^{up}$ 

upper bound for the power of the canister for the fuel $l\in \mathcal{L}$ [W]

S 

the last disposal period when the encapsulation can be on the hiatus.

In order to model the water pools and racks, we need the following parameters:

$B_l^{as}$ 

capacity of the pool for the fuel $l\in \mathcal{L}\backslash \left\{2\right\}$ [assemblies]

B 

number of pools for OL1-2 at the beginning of the first period

$B^r$ 

number of pools with racks for OL1-2 at the beginning of the first period

$O^{up}$ 

maximum number of additional pools in Olkiluoto

$B_{j,l}^{up}$ 

maximum number of pools for the fuel $l\in \mathcal{L}\backslash \left\{2\right\}$ in the period $j\in \mathcal{J}$

$B_l^{up}$ 

maximum number of pools needing racks for the fuel $l\in \mathcal{L}\backslash \left\{2\right\}$.

Finally, the cost parameters are

$C_l^{{is}_{off}}$ 

maintenance cost of the interim storage for the fuel $l\in \mathcal{L}\backslash \left\{1\right\}$ when the reactor is off [€]

$C_l^{{is}_{on}}$ 

maintenance cost of the interim storage for the fuel $l\in \mathcal{L}\backslash \left\{1\right\}$ when the reactor is on [€]

$C_l^r$ 

cost to build racks for one pool for the fuel $l\in \mathcal{L}\backslash \left\{2\right\}$[€]

$C^p$ 

cost to build one pool [€]

$C_l^{st}$ 

storage cost of one assembly of the fuel $l\in \mathcal{L}$ in period [€]

$C_l^c$ 

cost of the canister for the fuel $l\in \mathcal{L}$ [€]

$C^{ef}$ 

maintenance cost of the encapsulation facility per period [€]

$C^h$ 

maintenance cost of the encapsulation facility per period during the hiatus [€]

$C^{{ef}_{ts}}$ 

portion of the encapsulation facility cost if two-shift work is in use

$C^{{ef}_{on}}$ 

cost of turning on the encapsulation facility after the hiatus [€]

$C^{{ef}_{ch}}$ 

cost of changing the fuel type in encapsulation [€]

$C_l^{dt}$ 

cost of the disposal tunnel of the fuel $l\in \mathcal{L}$ per meter [€]

$C^{ct}$ 

cost of the central tunnel per meter [€].

3.2. Continuous Variables

The model has $J(3I+11)+13$ continuous variables which all are assumed to be nonnegative. These variables are:

$x_{i,j,l}$ 

number of assemblies of the fuel $l\in \mathcal{L}$ belonging to the removal $i\in \mathcal{I}$ disposed of in the period $j\in \mathcal{J}$

$r_{j,l}$ 

equals 1 if the disposal of the fuel $l\in \mathcal{L}$ begins at the period $j\in \mathcal{J}$

$p_{j,l}$ 

summed powers of assemblies of the fuel $l\in \mathcal{L}$ disposed of in the period $j\in \mathcal{J}$

$e_j^{on}$ 

equals 1 if the encapsulation begins at the period $j\in \mathcal{J}$

$e_j^{off}$ 

equals 1 if the encapsulation ends at the period $j\in \mathcal{J}$

h 

length of the possible hiatus [period]

$q_l$ 

period when the last canister of the fuel $l\in \mathcal{L}$ is disposed of

$y_{j,l}$ 

number of canisters for the fuel $l\in \mathcal{L}$ disposed of at the period $j\in \mathcal{J}$

$p_l^{max}$ 

maximum canister power of the fuel $l\in \mathcal{L}$ [W]

$d_l^c$ 

distance between two adjacent canisters of the fuel $l\in \mathcal{L}$ in a disposal tunnel [m]

$d_l^{dt}$ 

distance between two adjacent disposal tunnels of the fuel $l\in \mathcal{L}$ [m].

Note that some of these variables, such as the number of canisters, have integer or even binary nature but they are relaxed as continuous variables to ease the computation.

3.3. Binary Variables

In the model, we have $4J+1$ binary variables given below:

$s_{j,l}$ 

fuel $l\in \mathcal{L}$ is disposed of in the period $j\in \mathcal{J}$

$w_j$ 

two-shift work in the period $j\in \mathcal{J}$

c 

transition over the brittle fault zone

3.4. Integer Variables

Besides binary variables, the model involves also $2J+3$ integer variables dedicated to model the water pools and racks. The integer variables used are:

$u_l$ 

number of pools needing racks for the fuel $l\in \mathcal{L}\backslash \left\{2\right\}$

o 

total number of additional water pools in Olkiluoto

$v_{j,l}$ 

number of pools for the fuel $l\in \mathcal{L}\backslash \left\{2\right\}$ needed in the period $j\in \mathcal{J}$

3.5. Objectives

The eight objectives of the model are:

$$mino$$

(1)

$$min\frac{{\sum }_{i\in \mathcal{I}}{\sum }_{j\in \mathcal{J}}{\sum }_{l\in \mathcal{L}}{A}_{i,j,l}{x}_{i,j,l}}{{\sum }_{i\in \mathcal{I}}{\sum }_{l\in \mathcal{L}}{M}_{i,l}}$$

(2)

$$min\sum _{j\in \mathcal{J}}\sum _{l\in \mathcal{L}}{y}_{j,l}$$

(3)

$$minmax\left\{q_l\right|l\in \mathcal{L}\}$$

(4)

$$min\sum _{j\in \mathcal{J}}\sum _{l\in \mathcal{L}}{s}_{j,l}$$

(5)

$$min{Q}^r\sum _{l\in \mathcal{L}}{Q}^h{d}_l^c\sum _{j\in \mathcal{J}}{y}_{j,l}$$

(6)

$$min\frac{1}{Q}\sum _{l\in \mathcal{L}}{d}_l^{dt}{Q}^h{d}_l^c\sum _{j\in \mathcal{J}}{y}_{j,l}+2D^{h}Zh$$

(7)

$$\begin{array}{cc}min\hfill & {\displaystyle \sum _{l=2}^3}{C}_l^{{is}_{on}}{O}_l+{\displaystyle \sum _{l=2}^3}{C}_l^{{is}_{off}}(q_l-O_l)+C^{p}o+{\displaystyle \sum _{l\in \mathcal{L}\backslash \left\{2\right\}}}{C}_l^r{u}_l+(C^{{ef}_{on}}-C^{{ef}_{ch}})({\displaystyle \sum _{j\in \mathcal{J}}}{e}_j^{on}-1)\hfill \\ \hfill +& C^{{ef}_{ch}}({\displaystyle \sum _{j\in \mathcal{J}}}{\displaystyle \sum _{l\in \mathcal{L}}}{r}_{j,l}-1)+{\displaystyle \sum _{l\in \mathcal{L}}}{C}_l^{st}\left({\displaystyle \sum _{i=1}^{N_l}}{\displaystyle \sum _{j\in \mathcal{J}}}(A_{i,j,l}+i-N_l)x_{i,j,l}+{\displaystyle \sum _{i=N_l+1}^I}{\displaystyle \sum _{j\in \mathcal{J}}}{A}_{i,j,l}{x}_{i,j,l}\right)\hfill \\ \hfill +& {\displaystyle \sum _{l\in \mathcal{L}}}{C}_l^c{\displaystyle \sum _{j\in \mathcal{J}}}{y}_{j,l}+(C^{ef}-C^h){\displaystyle \sum _{j\in \mathcal{J}}}{\displaystyle \sum _{l\in \mathcal{L}}}{s}_{j,l}+C^{h}max\left\{q_l\right|l\in \mathcal{L}\}+Q^r{\displaystyle \sum _{l\in \mathcal{L}}}{C}_l^{dt}{Q}^h{d}_l^c{\displaystyle \sum _{j\in \mathcal{J}}}{y}_{j,l}\hfill \\ \hfill +& C^{ct}(\frac{1}{Q}{\displaystyle \sum _{l\in \mathcal{L}}}{d}_l^{dt}{Q}^h{d}_l^c{\displaystyle \sum _{j\in \mathcal{J}}}{y}_{j,l}+2D^{h}Zh)+C^{ct}{D}^{add}c+C^{{ef}_{ts}}{\displaystyle \sum _{j\in \mathcal{J}}}{C}^{ef}{w}_j.\hfill \end{array}$$

(8)

Note that the objectives (4) and (6)–(8) are nonlinear and additionally the objectives (4) and (8) are nonsmooth (i.e., nondifferentiable). The first objective (1) minimizes the total number of the additional water pools in the interim storage in Olkiluoto. With the objective (2), the average storage time of the fuel assemblies in the water pools is minimized. The next three objectives focus on the encapsulation facility such that the objective (3) minimizes the total number of canisters, the objective (4) minimizes the ending time of the disposal, and the objective (5) minimizes the number of disposal periods when the encapsulation plant is in operation. The objective (6) minimizes the total length of the disposal tunnels and the objective (7) minimizes the length of the central tunnel. There is a minimum distance that must be between the central tunnel and the first canister in a disposal tunnel. This extra length of a disposal tunnel is taken into account with the coefficient $Q^r$. It is also worth noticing that, in practice, the central tunnel is built in pairs (see Figure 3), but, in the model, the variable corresponds to only one tunnel.

The last objective (8) minimizes the total costs. The first two terms specify the maintenance cost of the interim storages depending on whether the reactors are on or off in the corresponding reactor facility areas, the next two terms indicate the cost related to the water pools and the racks in there, and the next two terms take into account the cost caused by the turning on the encapsulation plant after the hiatus and the cost of changing the fuel type. The seventh term defines the storage cost of fuel assemblies followed by the canister cost. The cost related to the use of the encapsulation facility is given in the ninth and the tenth term. The building costs of disposal and central tunnels are captured in the eleventh and the twelfth terms, respectively. The last two terms in respective order are the cost of the possible transition over the brittle fault zone, and the cost of the two-shift work. All the costs are taken into account from the first period onwards.

3.6. Constraints—Interim Storage

There are $3I+5J$ linear constraints related to the interim storage:

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{j\in \mathcal{J}}}{x}_{i,j,l}=M_{i,l},i\in \mathcal{I},l\in \mathcal{L}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i=1}^{N_l+j}}(M_{i,l}+x_{i,j,l}-{\displaystyle \sum _{k=1}^j}{x}_{i,k,l})\le B_l^{as}{v}_{j,l},l\in \mathcal{L}\backslash \left\{2\right\},j=1,\dots ,I-N_l\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i\in \mathcal{I}}}(M_{i,l}+x_{i,j,l}-{\displaystyle \sum _{k=1}^j}{x}_{i,k,l})\le B_l^{as}{v}_{j,l},l\in \mathcal{L}\backslash \left\{2\right\},j=I-N_l+1,\dots ,J\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & v_{j,1}+v_{j,3}\le o+B,j\in \mathcal{J}\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & v_{j,1}\le u_1+B^r,j\in \mathcal{J}\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & v_{j,3}\le u_3,j\in \mathcal{J}.\hfill \end{array}$$

(14)

The constraint (9) ensures that all the fuel assemblies are disposed of. The constraints (10) and (11) keep track of the pools needed in Olkiluoto considering the cases before and after all the removals from the reactor are done, respectively. The amounts of additional pools in Olkiluoto are considered in the constraint (12). Additionally, (13) defines the pools needing racks for OL1-2 and (14) for OL3.

3.7. Constraints—Encapsulation Facility

In total, there are $25J+7+{\sum }_{l\in \mathcal{L}}{\sum }_{k=\widehat{k}}^I(k+R-N_l)$, where $\widehat{k}=max\{1,N_l-R+1\}$ linear constraints related to the encapsulation facility. First, we focus on constraints determining the operation times of the encapsulation facility:

$$\begin{array}{cc}\hfill & s_{1,1}=1\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{j\in \mathcal{J}}}{e}_j^{on}\le 2\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{l\in \mathcal{L}}}{s}_{1,l}=e_1^{on}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{l\in \mathcal{L}}}{s}_{j,l}-{\displaystyle \sum _{l\in \mathcal{L}}}{s}_{j-1,l}\le e_j^{on},j\in \mathcal{J}\backslash \left\{1\right\}\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{j\in \mathcal{J}}}{e}_j^{off}\le 2\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & e_1^{off}=0\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & e_J^{off}\ge {\displaystyle \sum _{l\in \mathcal{L}}}{s}_{J,l}\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{l\in \mathcal{L}}}{s}_{j-1,l}-{\displaystyle \sum _{l\in \mathcal{L}}}{s}_{j,l}\le e_j^{off},j\in \mathcal{J}\backslash \left\{1\right\}\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & j({\displaystyle \sum _{k=1}^j}{e}_k^{on}-1)+j(e_j^{on}-1)-{\displaystyle \sum _{k=1}^{j-1}}k{e}_k^{off}\le h,j\in \mathcal{J}\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & q_l\ge j·s_{j,l},j\in \mathcal{J},l\in \mathcal{L}.\hfill \end{array}$$

(24)

The constraint (15) determines that the encapsulation begins at the first disposal period with OL1-2 and the constraint (16) guarantees that the encapsulation has at most one hiatus. With the constraints (17) and (18), the variable $e_j^{on}$ determining when the encapsulation begins is defined and the constraints (19)–(22) define the variable $e_j^{off}$ considering when the encapsulation is stopped. Additionally, the constraint (23) implies the length of the hiatus and the constraint (24) captures the last period of the encapsulation.

The production related constraints are:

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{l\in \mathcal{L}}}{s}_{j,l}\le 1,j\in \mathcal{J}\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & j·e_j^{off}+J(1-e_j^{off})\ge q_l+1,j\in \mathcal{J},l\in \mathcal{L}\backslash \left\{3\right\}\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{j\in \mathcal{J}}}{r}_{j,l}\le 1,l\in \mathcal{L}\backslash \left\{1\right\}\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & s_{j,l}-s_{j-1,l}\le r_{j,l},l\in \mathcal{L},j\in \mathcal{J}\backslash \left\{1\right\}\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & s_{1,l}\le r_{1,l},l\in \mathcal{L}\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{j=1}^S}{\displaystyle \sum _{l\in \mathcal{L}}}{s}_{j,l}\le S-1.\hfill \end{array}$$

(30)

The constraint (25) controls that only one type of the fuel is encapsulated in one period. In order to encapsulate all assemblies of OL1-2 and LO1-2 before the hiatus, the constraint (26) is introduced. With the constraint (27), LO1-2 and OL3 are forced to be encapsulated continuously without the fuel type changes. With the constraints (28) and (29), the variable $r_{j,l}$ is defined. The last constraint (30) indicates that there is the hiatus in the production.

Finally, we give some constraints considering the canisters produced:

$$\begin{array}{cc}\hfill & y_{j,l}\ge \frac{1}{K_l}{\displaystyle \sum _{i\in \mathcal{I}}}{x}_{i,j,l},j\in \mathcal{J},l\in \mathcal{L}\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{l\in \mathcal{L}}}(y_{j,l}-U^{up}{s}_{j,l})+V{e}_j^{on}-W{w}_j\le 0,j\in \mathcal{J}\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{l\in \mathcal{L}}}{y}_{j,l}\ge U^{low}{\displaystyle \sum _{l\in \mathcal{L}}}{s}_{j,l},j\in \mathcal{J}\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & w_j\le {\displaystyle \sum _{l\in \mathcal{L}}}{s}_{j,l},j\in \mathcal{J}\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & w_j\le 1-{\displaystyle \sum _{l\in \mathcal{L}}}{r}_{j,l},j\in \mathcal{J}\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i\in \mathcal{I}}}{x}_{i,j,l}\le (U^{up}+W)K_l{s}_{j,l},j\in \mathcal{J},l\in \mathcal{L}\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & s_{j,l}\le {\displaystyle \sum _{i\in \mathcal{I}}}{x}_{i,j,l},j\in \mathcal{J},l\in \mathcal{L}\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill & x_{i,j,l}=0,i\ge N_l-R+1,j=1,\dots ,i+R-N_l,l\in \mathcal{L}.\hfill \end{array}$$

(38)

The constraint (31) guarantees the number of canisters to be high enough and the constraint (32) keeps track of the number of canisters staying under the maximum production capacity. On the other hand, the constraint (33) ensures that the minimum capacity is fulfilled. The constraint (34) enables the two-shift work only when the encapsulation facility is on and the constraint (35) disallows the two-shift work at the first period after the fuel change. With the constraints (36) and (37), the variable $s_{i,j}$, $i\in \mathcal{I}$ and $j\in \mathcal{J}$ is defined. The constraint (38) takes into account that fuel assemblies that do not satisfy the minimum cooling time requirement are not encapsulated.

3.8. Constraints—Disposal Facility

The $6J+4$ constraints related to the disposal facility are

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i\in \mathcal{I}}}{P}_{i,j,l}{x}_{i,j,l}\le p_{j,l},j\in \mathcal{J},l\in \mathcal{L}\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & p_{j,l}\le y_{j,l}{p}_l^{max},j\in \mathcal{J},l\in \mathcal{L}\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill & d_l^c\ge g_l(p_l^{max},d_l^{dt}),l\in \mathcal{L}\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill & \frac{1}{Q}{\displaystyle \sum _{l\in \mathcal{L}}}(d_l^{dt}{d}_l^c{Q}^h{\displaystyle \sum _{j\in \mathcal{J}}}{y}_{j,l})+2D^{h}Zh-D^{ct}\le Mc.\hfill \end{array}$$

(42)

From these constraints, $3J$ are linear and $3J+4$ and nonlinear. The constraint (39) defines the variable $p_{j,l}$, $j\in \mathcal{J}$ and $l\in \mathcal{L}$ and (40) defines the variable $p_l^{max}$, $l\in \mathcal{L}$. With the constraint (41), it is ensured that the distance between canisters is such that the temperature in the disposal facility stays in control. The function $g_l:{\mathbb{R}}^2\to \mathbb{R}$ gives a relation between the maximum canister power, the distance between canisters, and the distance between disposal tunnels, and it is approximated with the relation (A1) given in Appendix B. Finally, the constraint (42) gives a value 1 for the variable c if the brittle fault zone is met.

3.9. Constraints—Lower and Upper Bounds

We give $J(3I+7)+16$ box constraints for variables as follows:

$$\begin{array}{cc}\hfill & p_l^{max}\in [P_l^{low},P_l^{up}],l\in \mathcal{L}\hfill \\ \hfill & d_l^c\in [D^{c_{low}},D^{c_{up}}],l\in \mathcal{L}\hfill \\ \hfill & d_l^{dt}\in [D^{d{t}_{low}},D^{d{t}_{up}}],l\in \mathcal{L}\hfill \\ \hfill & x_{i,j,l}\in [0,M_{i,l}],i\in \mathcal{I},j\in \mathcal{J},l\in \mathcal{L}\hfill \\ \hfill & r_{j,l}\in [0,1],j\in \mathcal{J},l\in \mathcal{L}\hfill \\ \hfill & e_j^{on}\in [0,1],j\in \mathcal{J}\hfill \\ \hfill & e_j^{off}\in [0,1],j\in \mathcal{J}\hfill \\ \hfill & q_l\in [0,J],l\in \mathcal{L}\hfill \\ \hfill & h\in [0,0.7J]\hfill \\ \hfill & o\in [0,O^{up}]\hfill \\ \hfill & v_{j,l}\in [0,B_{j,l}^{up}],j\in \mathcal{J},l\in \mathcal{L}\backslash \left\{2\right\}\hfill \\ \hfill & u_l\in [0,B_l^{up}],l\in \mathcal{L}\backslash \left\{2\right\},\hfill \end{array}$$

and, finally, some boundaries for the variables:

$$\begin{array}{c}\hfill p_{j,l}\ge 0,y_{j,l}\ge 0,s_{j,l}\in \{0,1\},j\in \mathcal{J},l\in \mathcal{L},w_j\in \{0,1\},j\in \mathcal{J},\mathrm{and}c\in \{0,1\}.\end{array}$$

To summarize, the model has eight objectives, $J(3I+11)+13$ continuous variables, $4J+1$ binary variables, and $2J+3$ integer variables. Furthermore, the model has $3I+33J+7+{\sum }_{l\in \mathcal{L}}{\sum }_{k=\widehat{k}}^I(k+R-N_l)$, where $\widehat{k}=max\{1,N_l-R+1\}$ linear and $3J+4$ nonlinear constraints in total in addition to the $J(3I+7)+16$ box constraints. Thus, the size of the model strongly depends on the length of the disposal period. It is good to note that $x_{i,j,l}$, $y_{j,l}$, and $d_l^{dt}$ are important variables in the sense that, if the values of these are defined, then the values of the other variables can be derived. In this case, the constraints will define values for some variables (for example $s_{j,l}$) and give lower bounds to other variables (for example $d_l^c$). These lower bounds will be the final values because giving variables a higher value do not benefit any of the objectives.

3.10. Scenario without Hiatus

Since we are also interested in investigating the effect of a hiatus, we define how the model needs to be modified in order to disallow the hiatus. The constraints (16) and (19) determine that the encapsulation begins and ends no more than twice. These constraints are thus replaced respectively with the following constraints:

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{j\in \mathcal{J}}}{e}_j^{on}\le 1,\hfill \\ \hfill & {\displaystyle \sum _{j\in \mathcal{J}}}{e}_j^{off}\le 1.\hfill \end{array}$$

Furthermore, the constraint (26) ensuring that OL1-2 and LO1-2 are encapsulated before the hiatus and the constraint (30) forcing the hiatus can be omitted.

4. Methodology

In this section, we concentrate on the multiobjective MINLP problem

$$\begin{array}{c}\hfill {\displaystyle \underset{\mathit{x}\in X}{min}}\mathit{f}(\mathit{x})=\{f_1(\mathit{x}),\dots ,f_k(\mathit{x})\},\end{array}$$

(43)

where $X=\{\mathit{x}=(\mathit{y},\mathit{z})|\mathit{y}\in {\mathbb{R}}^n,\mathit{z}\in {\mathbb{Z}}^m\}\cap C$ such that C is the set of constraints, and X is the nonempty and compact set of feasible solutions. The functions $f_i:X\to \mathbb{R}$ for all $i\in I=\{1,\dots ,k\}$ are supposed to be lower semicontinuous with respect to $\mathit{y}$. In order to obtain a sensible multiobjective problem, we assume that the objectives are also at least partially conflicting. In the following, for the vectors $\mathit{p},\mathit{q}\in {\mathbb{R}}^k$, we denote by $\mathit{p}<\mathit{q}$ if $p_i<q_i$ for all $i\in I$ and $\mathit{p}\le \mathit{q}$ if $p_i\le q_i$ for all $i\in I$.

A solution of the problem (43) is Pareto optimal if any objective cannot be improved without deteriorating some other objective simultaneously. That is, a solution ${\mathit{x}}^{\ast }\in X$ is Pareto optimal if there does not exist any solution $\mathit{x}\in X$ such that $\mathit{f}(\mathit{x})\le \mathit{f}({\mathit{x}}^{\ast })$ and $f_j(\mathit{x})<f_j({\mathit{x}}^{\ast })$ for at least one index $j\in I$. Furthermore, the solution of the problem (43) ${\mathit{x}}^{\prime }\in X$ is weakly Pareto optimal if there exists no other solution $\mathit{x}\in X$ such that $\mathit{f}(\mathit{x})<\mathit{f}({\mathit{x}}^{\prime })$. Usually, the multiobjective problem has several Pareto optimal solutions and the set of these solutions is called a Pareto set. The range of the Pareto set can be approximated with an ideal ${\mathit{f}}^{id}$ and a nadir vector ${\mathit{f}}^{nad}$ as the lower and the upper bounds. The components of the ideal vector are obtained by minimizing the individual objectives while the determination of the nadir vector is much harder, and the nadir vector needs to be approximated in practice.

One acknowledged approach to solve the problem of the form (43) is the use of the achievement scalarizing functions (ASFs) (see, e.g., [4,9,35]). The idea in brief is to transfer the multiobjective problem to a single objective one such that solving the single-objective problem the result is a Pareto optimal solution for the original multiobjective problem. The single-objective problem is formed in such a way that it minimizes the distance between the Pareto set and the reference point f^R involving the decision maker’s wishes towards the solution. If ${\mathit{f}}^R\in Z+{\mathbb{R}}_{+}^k$, where Z is the image of the feasible solutions in the objective space, then the reference point is achievable and otherwise unachievable. Besides employing ASFs as such, they are also made a name as a part of interactive methods [3,4,5,7,8,9,36], where the most satisfactory solution for the decision maker is found after an active dialogue between the decision maker and the analyst.

In this paper, we utilize the interactive method using the special type of the ASFs proposed in [6] called the multiobjective interactive method utilizing the two-slope parameterized ASFs (MITSPA). The two-slope parameterized ASFs presented in [37] generalize the good properties of the parameterized ASFs [38] and the two-slope ASFs [39]. Indeed, with the two-slope parameterized ASFs, we can systematically produce different Pareto optimal solutions from the same preference information without involving any test of the achievability of the reference point.

The family of the two-slope parameterized ASFs is defined by

$$\begin{array}{c}\hfill {\displaystyle \underset{\mathit{x}\in X}{min}}{\displaystyle \underset{\begin{array}{c}{I}^q\subseteq I\\ |I^q|=q\end{array}}{max}}\left\{{\displaystyle \sum _{i\in I^q}}\left[max\{{\lambda }_i^U(f_i(\mathit{x})-f_i^R),0\}+min\{{\lambda }_i^A(f_i(\mathit{x})-f_i^R),0\}\right]\right\},\end{array}$$

(44)

where ${\mathit{\lambda }}^U$, ${\mathit{\lambda }}^A$ are positive coefficients for unachievable and achievable reference points, respectively. Additionally, $I^q\subseteq I$ is a set of q integers from the interval $[1,k]$ such that k is the number of objectives. Indeed, the maximization is taken over all the sets containing q integers from $[1,k]$. When $q=1$, the used metric is $L_{\infty }$ and if $q=k$, the linear $L_1$ metric is used. Another good property of $s_R^q(f(\mathit{x}),{\mathit{\lambda }}^U,{\mathit{\lambda }}^A)$ is that, if the objectives $f_i$, $i\in I$ and the set X are convex, $s_R^q(f(\mathit{x}),{\mathit{\lambda }}^U,{\mathit{\lambda }}^A)$ preserves the convexity (see Theorem 8 in [37]). In the case of the convex objective, the global optimality of the scalarized problem (44) is easier to guarantee.

In order to justify the use of the two-slope parameterized ASFs, we recall the following theorem from [6]. The proof of the theorem is given in Appendix A.

Theorem 1.

[6] For the scalarized problem (44), it holds that:

(i)

Any optimal solution of the scalarized problem is weakly Pareto optimal for the problem (43).

(ii)

Among optimal solutions of the scalarized problem, there exists at least one Pareto optimal solution for the problem (43).

(iii)

If${\mathit{x}}^{\ast }$is a weakly Pareto optimal solution for the problem (43), then it is a solution of the scalarized problem (44) with ${\mathit{f}}^R={\mathit{f}\mathit{x}}^{\ast })$, and the optimal value is zero.

Furthermore, the Pareto optimality of the solutions obtained can be guaranteed by adding an augmentation term [4]

$$\begin{array}{c}\hfill \rho {\displaystyle \sum _{i\in I}}{\lambda }_i(f_i(\mathit{x})-f_i^R),\rho >0,{\lambda }_i>0\mathrm{for}\mathrm{all}i\in I\end{array}$$

(45)

to the objective of the scalarized problem (44) [6,37].

The interactive framework used follows the same basic structure than many other interactive methods. First, the ranges of the Pareto set are illustrated; then, the decision maker gives some preference information and based on the preference information some problem(s) is solved. The results are then presented to the decision maker giving some new preference information based on the results. This process continues until the decision maker is satisfied with the solution. Here, the reference point is used as a tool to communicate with the decision maker. This is considered as an intuitive approach for the decision maker since the reference point and the solution vector are in the same form. Other interactive methods combining the reference point and the scalarization function are described for example in [3,4,5,7,8,9,36]. Compared with these, we gain the advantages of the two-slope parameterized ASF by using MITSPA. In the following, the outline of MITSPA is described. For further details of the method, we refer to [6].

Multiobjective interactive method utilizing the two-slope parameterized ASFs (MITSPA)

Step 0.

Illustrate the Pareto set with the ideal vector ${\mathit{f}}^{id}$ and the nadir vector ${\mathit{f}}^{nad}$.

Step 1.

Set the iteration counter $h=1$ and select the maximum number of iterations $h_{max}$. Ask the decision maker to provide the reference point ${\mathit{f}}_h^R$ and the number of solutions $s\in \{1,\dots ,k\}$ presented for each reference point.

Step 2.

Solve the problem (44) with the augmentation term (45) with the current reference point ${\mathit{f}}_h^R$.

Step 3.

Present s solutions to the decision maker and ask the decision maker to select the most preferable solution among them as the current solution f_h.

Step 4.

If $h=h_{max}$ or the decision maker is satisfied with the current solution f_h, stop with the current solution as the final solution f*. Otherwise, ask the decision maker to specify the new reference point ${\mathit{f}}_{h+1}^R$ as the current reference point, set $h=h+1$, and go to Step 2.

In Step 0 of MITSPA, the Pareto set is illustrated. In addition to the ideal and nadir vector, the solutions can be exemplified by giving some neutral solution obtained, for example, with some achievement scalarizing function using the ideal vector as the reference point or with some non-preference method (see e.g., [4,40,41,42,43,44]). By solving the scalarized problem (44) with different parameter q values, k different solutions in total can be obtained for one reference point and $s\in \{1,\dots ,k\}$ of them are presented for the decision maker. In order to aid the decision maker, it is reasonable to keep the value of s quite small. However, if the decision maker is willing to see more than s solutions with the same reference point, the rest of the k solutions can be presented between Steps 3 and 4. If even more solutions are needed, they can be calculated by varying the weighting coefficients in the scalarized problem (44). Furthermore, if the decision maker is willing to return to some previous solution, the solutions from the previous iterations can be stored. It is worth noticing that, even if the maximum number of iterations $h_{max}$ is included, it is crucial to make sure that the decision maker is willing to stop the process when the $h_{max}$ is met.

5. Numerical Experiments

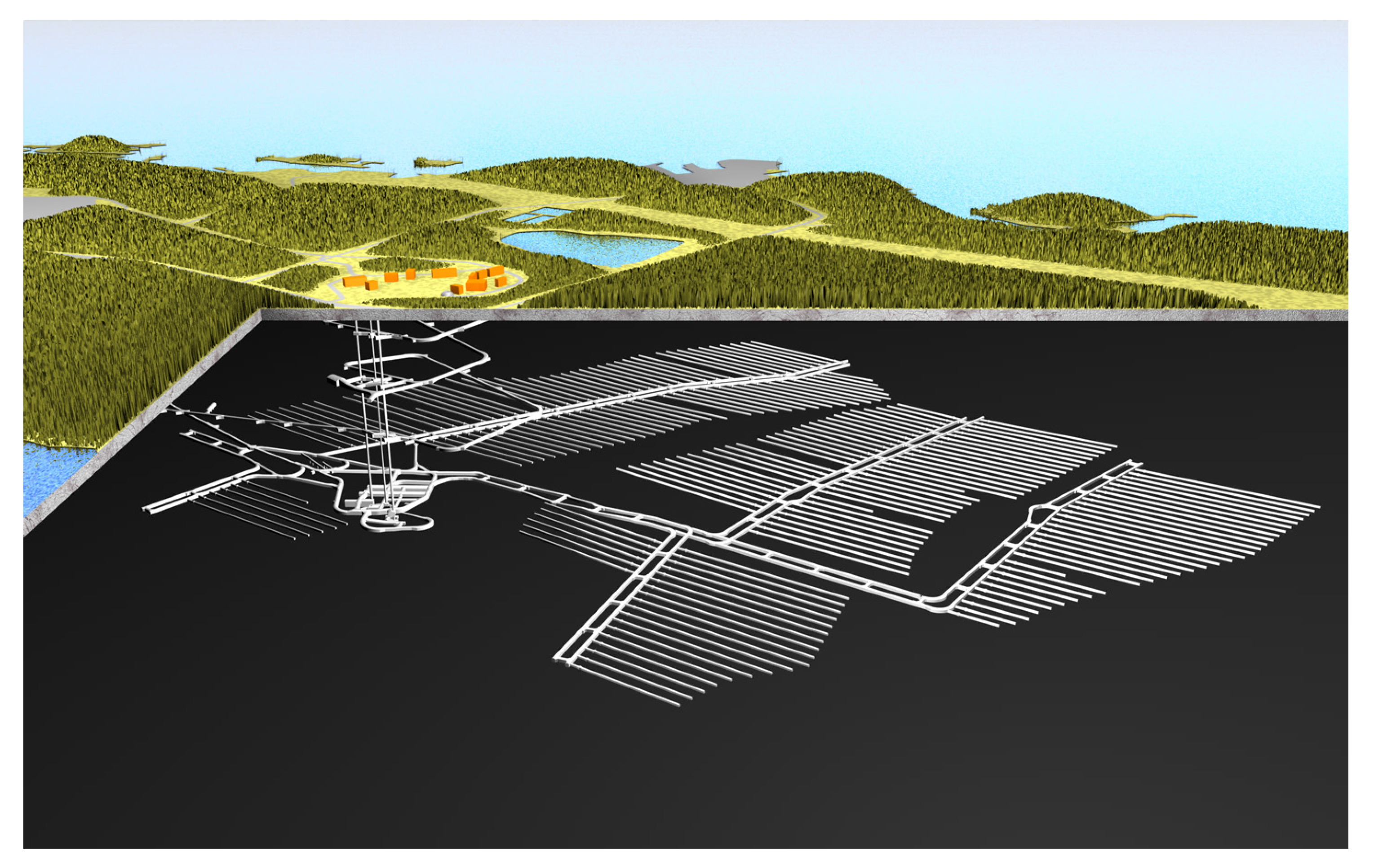
In this section, we solve the multiobjective MINLP model presented in Section 3 with the interactive approach in Section 4. In addition, we investigate the model by minimizing only the costs. Therefore, in the numerical experiments, tools for solving single- and multiobjective problems are needed. However, multiobjective problems are solved with MITSPA utilizing scalarization. Via the scalarization, multiple objectives are reformulated as a single-objective problem and by solving this problem, a Pareto optimal solution for the original problem can be obtained. Thus, we only need a solver capable of solving single-objective MINLP problems. For this purpose, we use the method employing the branch-and-bound idea called SCIP (Solving Constraint Integer Programs) [45,46,47] in GAMS [48] with SoPlex and Ipopt. The relative tolerance is set as 0.000001 and and the maximum time limit was set to 86,400 s.

5.1. Cost Minimization Results

We begin the numerical experiments by investigating the single-objective case minimizing the total costs i.e., using (8) as the only objective. The affects of the hiatus on the costs are also considered. The data used is described in Appendix A except the parameters related to the costs which are omitted due to their commercial nature. However, the repeatable single-objective example with an artificial cost data are given in Appendix B. In total, the problem has 887 linear and 61 nonlinear constraints. Furthermore, we have 963 continuous, 77 binary, and 41 integer variables. Note that the scenario without the hiatus has 39 constraints less than the base scenario. The CPU time of the single-objective base scenario having the hiatus is 579 s. For the scenario without the hiatus, the algorithm stopped after 86,439 s reaching the time limit with the 0.0005% relative gap between the dual and the primal bound.

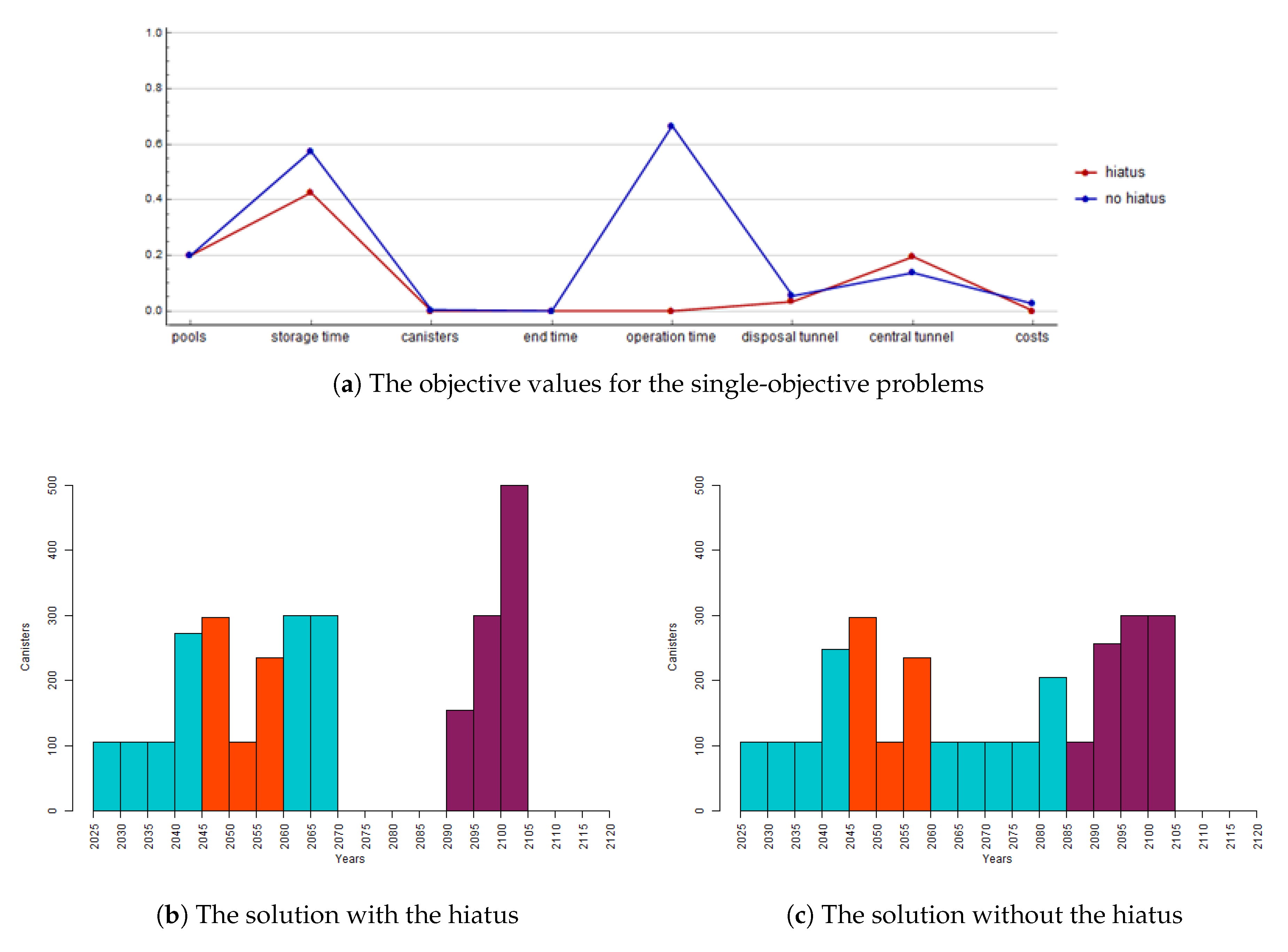
In Figure 4, the solutions for both scenarios with and without the hiatus are presented. Figure 4a illustrates the values of the objectives (1)–(8) in the interval from 0 to 1 such that 0 represents the value of the ideal vector for the corresponding objective in the base scenario and 1 represents the nadir value in the base scenario. The solution for the base scenario is given in the red line and the solution without the hiatus is given in the blue line. 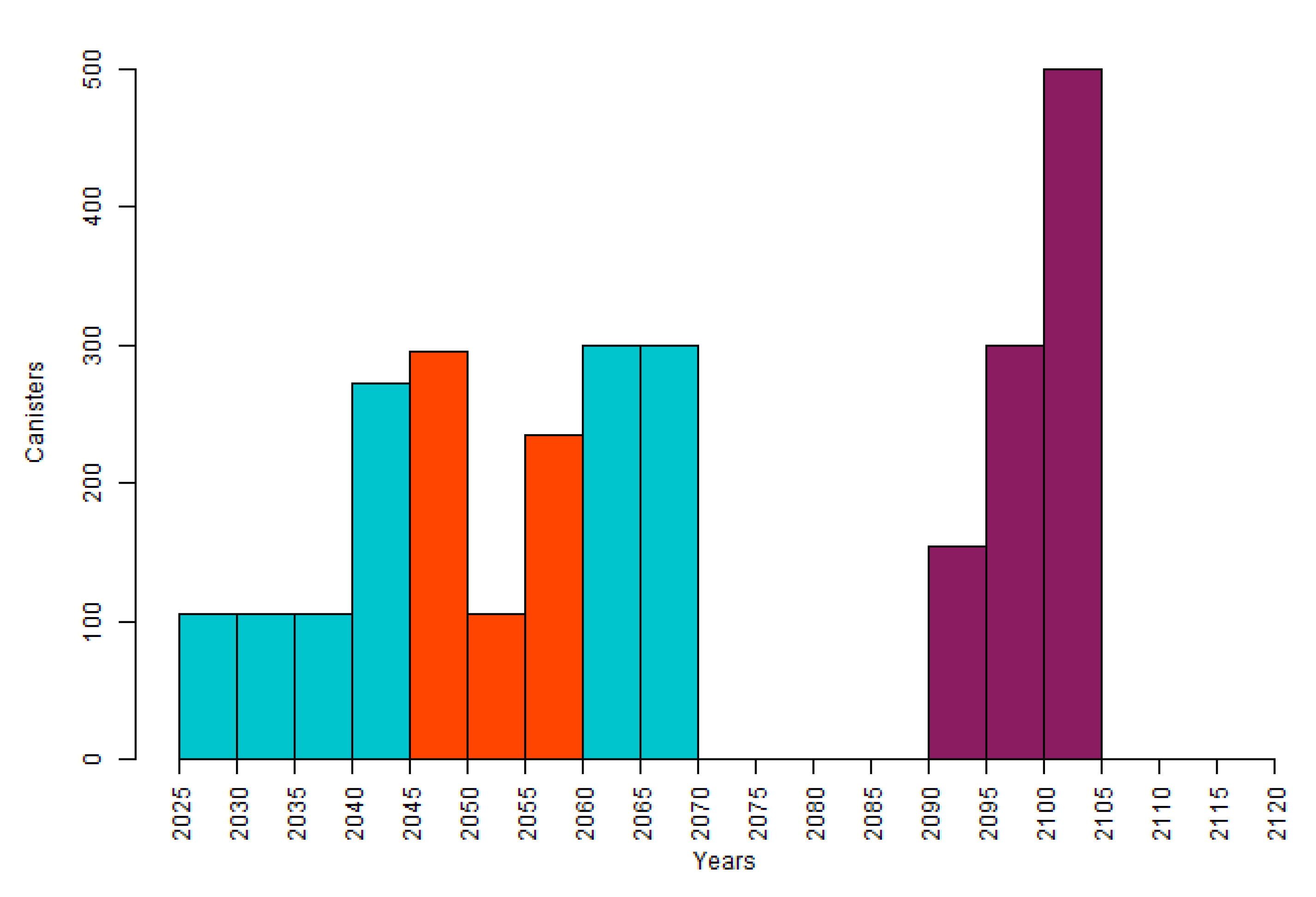Figure 4b,c shows the schedules obtained for the base scenario and the scenario without the hiatus, respectively. From these schedules, we see how many canisters are planned to be encapsulated at each period. The blue bars in Figure 4b,c refer to canisters of OL1-2, the orange refers to LO1-2, and purple refers to OL3.

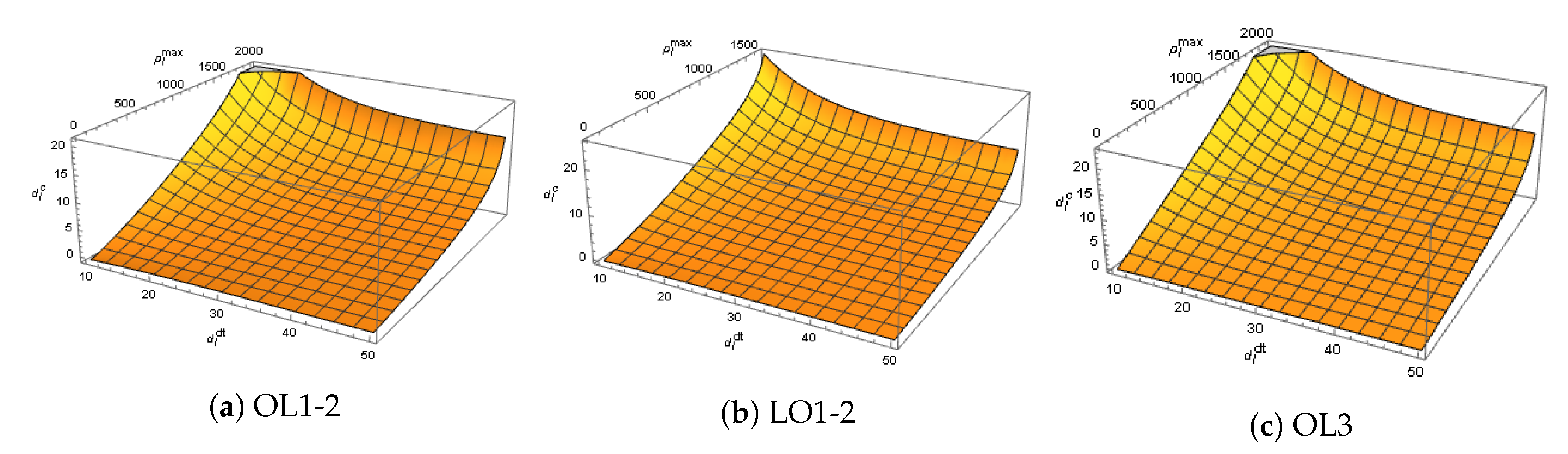
As we see, when the costs are minimized, the model gains advantage from the hiatus and the solution without the hiatus has around 1.7% higher costs than the solution of the base scenario. More significant differences of the solutions can be seen from the other objective values. For example, the scenario without the hiatus needs around 5.9% more storage time than the base scenario and, even if the both scenarios have the same ending time, the scenario without the hiatus has the encapsulation facility in operation 20 years more than the base scenario. However, the central tunnel is 11.6% longer in the base scenario than in the scenario without the hiatus.

From the schedules obtained, we see that the first three periods, or in other words 15 years, looks similar in the both scenarios. After that, one period has a minor difference and then again the next three periods are similar. Then, the rest of OL1-2 is disposed of in two periods in the base scenario and in five periods in the case without the hiatus. Finally, OL3 is disposed of and the base scenario needs one period less than the case without the hiatus, but the disposal ends at the same time in the both cases. The similar beginning in the schedules indicates that the decision about whether to have the hiatus or not does not significantly affect the disposal pace before the rest of OL1-2 will be disposed of when the costs are minimized. However, for OL1-2, the maximum canister power is higher in the base scenario than in the scenario without the hiatus. Moreover, the spacing between the disposal tunnels is larger while the canister spacing is the same being minimal.

5.2. Multiobjective Optimization Results

In the following, we solve the multiobjective model presented in Section 3 with MITSPA. First, we focus on the basic scenario with the hiatus. The data used for the parameters are given in Appendix A other than the cost related parameters which are excluded due to their commercial nature. Compared with the single-objective case, besides having eight objectives instead of one, we need some additional constraints and variables to rewrite the scalarized problem (44) as in [37]. The weighting coefficients ${\mathit{\lambda }}^U$ and ${\mathit{\lambda }}^A$ are selected as is suggested in [39] such that

$${\mathit{\lambda }}^U=\frac{1}{{\mathit{f}}^{nad}-{\mathit{f}}^R},{\mathit{\lambda }}^A=\frac{1}{{\mathit{f}}^R-{\mathit{f}}^{id}}$$

when ${\mathit{f}}^{nad}-{\mathit{f}}^R>0$ and ${\mathit{f}}^R-{\mathit{f}}^{\mathit{id}}>0$. Otherwise, the coefficient $1/({\mathit{f}}^{nad}-{\mathit{f}}^{id})$ is used. Furthermore, we set the coefficient $\rho =0.0001$.

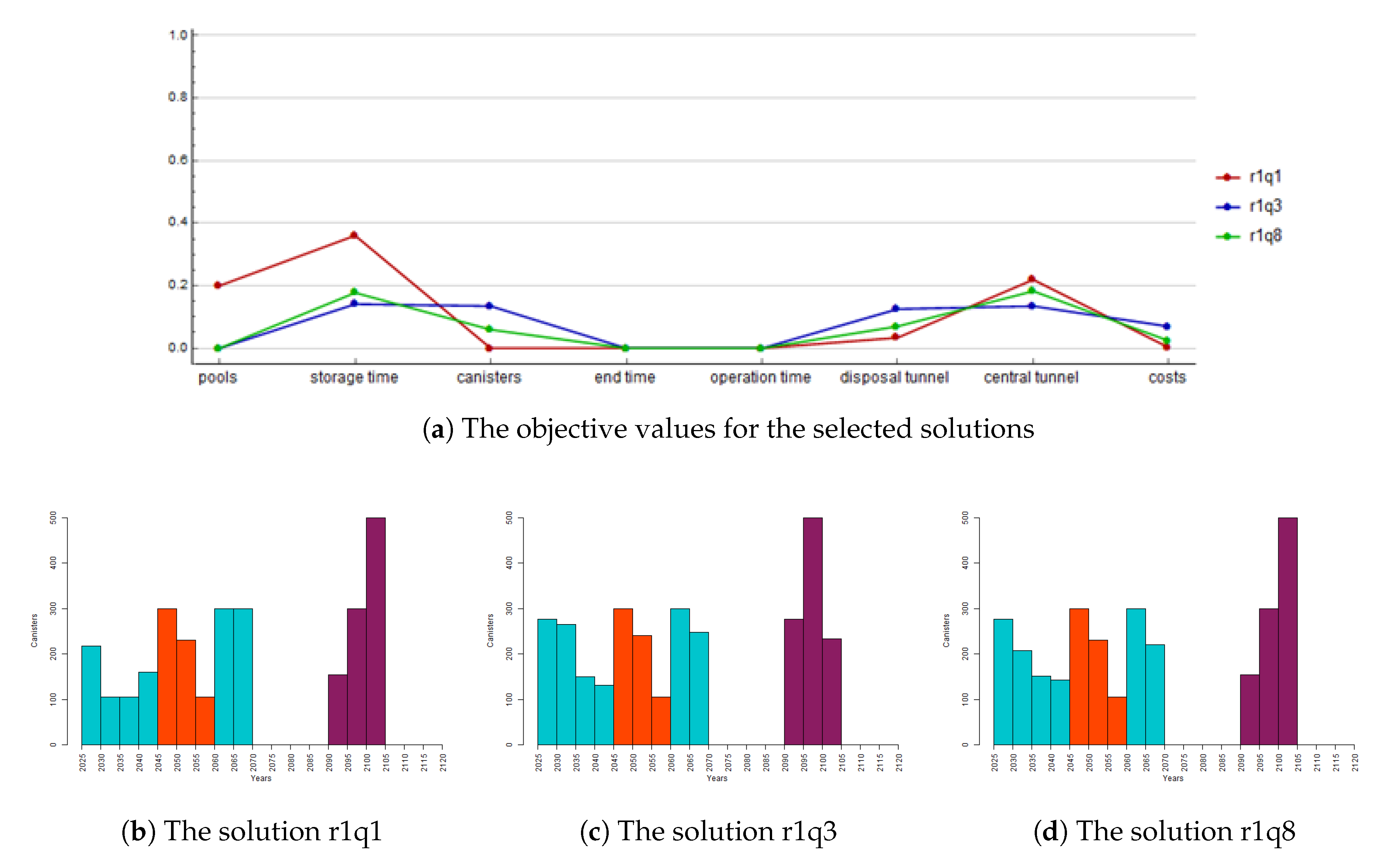
The decision maker selects the ideal vector ${\mathit{f}}^{id}$ as the first reference point ${\mathit{f}}_1^R$. Here, we present three different solutions in Step 3 of MITSPA. In Figure 5, the results for the first reference point are illustrated. Figure 5a shows the values of the objectives in the interval from 0 to 1. This interval is the same as in Section 5.1 such that 0 represents the ideal vector of the base scenario and 1 represents the nadir value. The solutions are referred to with the reference point and the value of the parameter q; for instance, the solution r1q1 is a solution obtained with the reference point 1 when $q=1$. Figure 5b–d presents the disposal schedules for the solutions r1q1, r1q3, and r1q8, respectively. In those figures, blue refers to OL1-2, orange to LO1-2, and purple to OL3.

Based on the objective function values illustrated in Figure 5a, the length of the central tunnel and the total costs seem to be conflicting objectives. In addition, the smaller number of canisters yields to the longer central tunnel. Nevertheless, this sounds reasonable since, with fewer canisters, the power of the canister may be larger, which leads to the larger spacings between canisters. This in its turn lengthens the central tunnel. Furthermore, the lengths of the disposal and central tunnels are also conflicting objectives. Indeed, if the canister heat powers are equal, we may increase the canister spacing or the disposal tunnel spacing to control the temperature on the surface of canisters in the disposal facility. The increase in the canister spacing will increase the disposal and central tunnel lengths. However, the increase in the disposal tunnel spacing will increase only the central tunnel length, but the increase is typically much larger. The schedules in Figure 5b–d propose the same ending time and the place for the hiatus.

From the first iteration, the decision maker selects the solution r1q8 as the current solution f₁ since it is a good compromise between the solutions presented. It minimizes the additional water pools, and the total costs are still at the reasonable level. The next reference point ${\mathit{f}}_2^R$ adapts the solution r1q8 expect that the number of canisters is selected to be minimal and the ending and the operation time are increased. These changes aim to minimize the canisters needed while keeping the costs reasonable and trying to avoid the additional water pools.

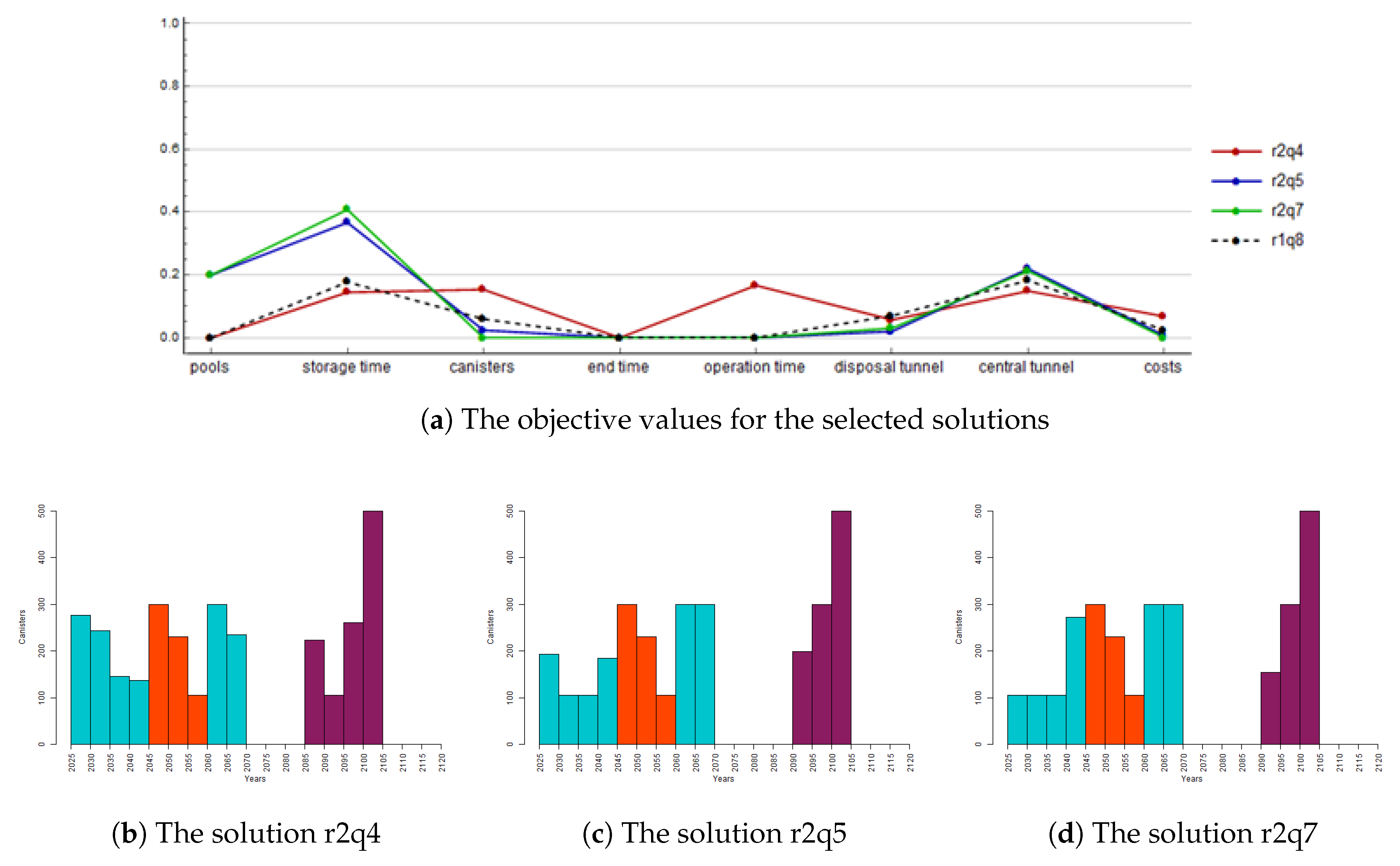
The results of the second iteration are illustrated in Figure 6. From Figure 6a, we see that the solutions r2q5 and r2q7 are quite similar, and the solution r2q4 is clearly a different kind. Both solutions r2q5 and r2q7 need less canisters than the current solution f₁, but one additional pool is needed and the storage time is increased. On the other hand, the solution r2q4 lengthens the operation time as was suggested by the reference point ${\mathit{f}}_2^R$, but also the number of canisters is increased. However, the central tunnel is shorter than in the current solution. In schedules given in Figure 6b–d, we see that, in the solution r2q4 in Figure 6b, the hiatus is one period shorter than in other schedules.

The decision maker selects the solution r2q7 as the current solution f₂. This is selected since the number of canister is the lowest and also the costs are low. Furthermore, the schedule in Figure 6d looks most feasible from the practical point of view due to the calm beginning. The reference point ${\mathit{f}}_3^R$ adjusts this solution such that the central and disposal tunnels are set to the minimum and the storage, ending, and operation time are deteriorated.

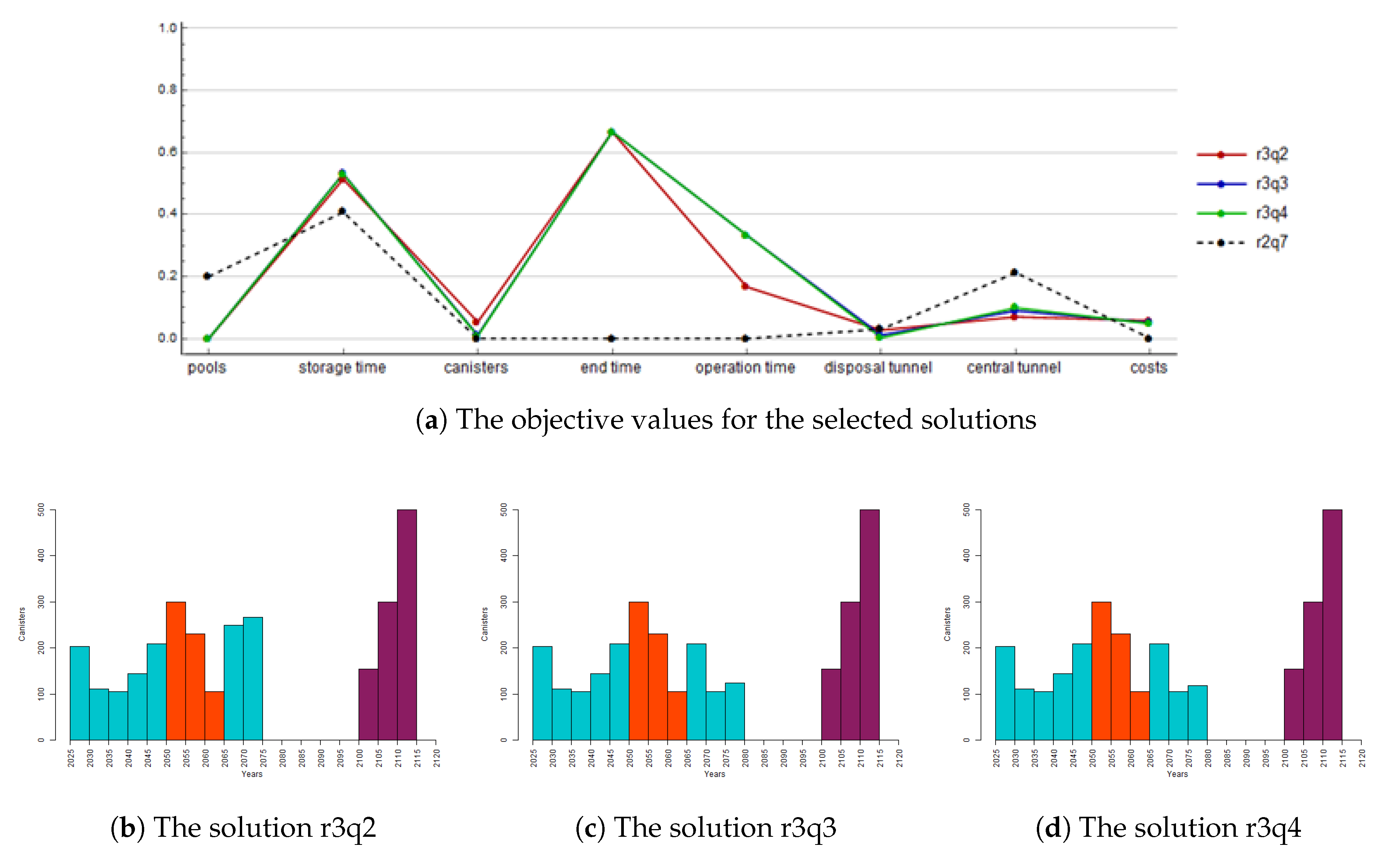
The solutions of the third iteration all have longer storage, ending, and operation time than the current solution f₂ as is seen in Figure 6a. Additionally, the total costs are increased. Furthermore, the total length of the central and disposal tunnels are shorter in all the solutions, and no additional water pools are needed. In this iteration, the solutions have less variety. Indeed, the differences of the solutions r3q3 and r3q4 are hard to see from Figure 6a. However, the solution r3q3 has a bit longer storage time, few extra canisters, longer disposal tunnel, and it is a slightly more expensive than the solution r3q4. However, the central tunnel in the solution r3q3 is shorter than in the solution r3q4. The schedules in Figure 7b–d show that the biggest differences between the solutions can be seen in the second part of OL1-2. However, the solution r3q3 has a few extra canisters in the last period of LO1-2 compared to the solution r3q4. By considering all the schedules presented, the two-shift work is utilized only when OL3 is encapsulated.

The decision maker selects the solution r3q4 as the final solution ${\mathit{f}}^{\ast }={\mathit{f}}_3$. Both solutions r3q3 and r3q4 would be good alternatives, but the solution r3q4 is selected due to the smaller number of canisters and the shorter disposal tunnel. During the interactive process, we learned that the model suggests schedules with heavy starting which will decrease in later periods. The behavior of this kind is very hard to employ in practice, and, thus, we investigate what happens, if the reference point is the solution r3q4, or, in other words ${\mathit{f}}_4^R={\mathit{f}}_3$, and we add the following constraint:

$${\displaystyle \sum _{l\in \mathcal{L}}}{y}_{j-1,l}\le {\displaystyle \sum _{l\in \mathcal{L}}}{y}_{j,l}+(W+U^{up})·(1-{\displaystyle \sum _{l\in \mathcal{L}}}{s}_{j,l}),j\in \mathcal{J}\backslash \left\{1\right\}.$$

This constraint guarantees that, at every period, the hiatus is not applied and the number of canisters to be encapsulated needs to be at least as many as in the previous period.

Here, we observe only one solution, namely r4q5. As we see from Figure 8a, the additional constraint increases the number of the canisters needed together with the length of the disposal tunnel and the costs. On the other hand, the storage, ending, and operation times get shorter. From the schedule point of view in Figure 8b, the encapsulation before the hiatus is very even except the last period when the two-shift work is needed. Compared to the solution r3q4, the solution r4q5 has a longer hiatus taking 25 years, and the disposal ends one period earlier.

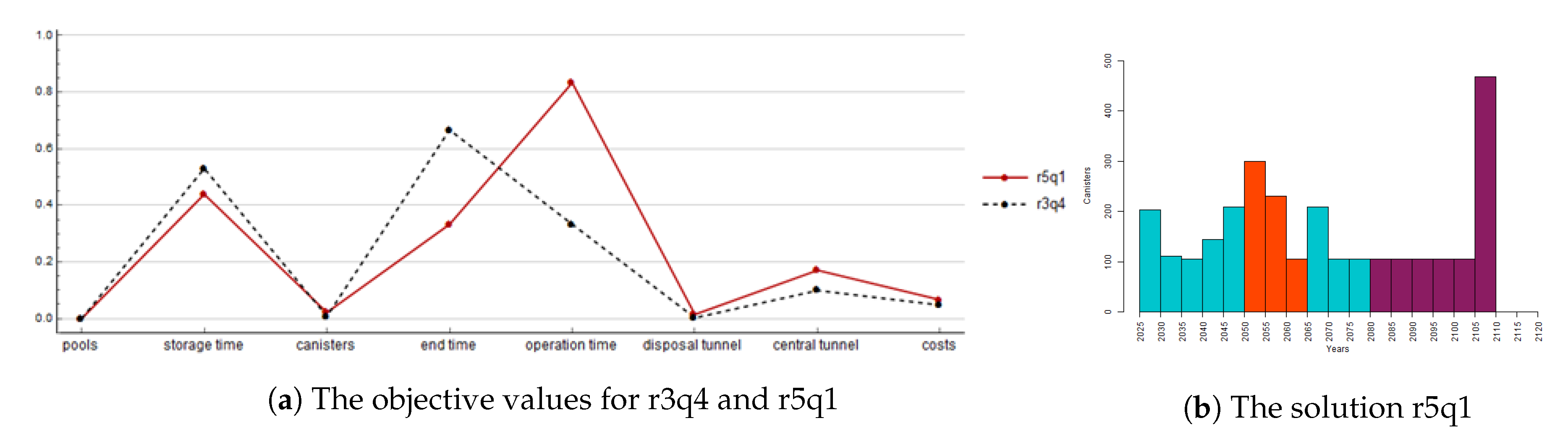
All the results obtained during the interactive process suggest a hiatus between 15 to 25 years. This indicates that the model gains advantage from the hiatus since only a 5-year hiatus is forced. Unfortunately, the hiatus has its own risks. Therefore, we test how well we can achieve the objective values of the solution f^* with the scenario without the hiatus. Thus, we set ${\mathit{f}}_5^R={\mathit{f}}_4^R$ and the result is shown in Figure 9.

By omitting the hiatus, the objective values for the operation time and the central tunnel increase as well as the number of canisters, the disposal tunnel, and the costs but only 1.2%. However, the objective values for the ending and storage time decrease. The schedule of the solution r5q1 in Figure 9b is similar to the solution r3q4 for the first nine periods. After that, the minimal amount of canisters are encapsulated until the last period when as many canisters as possible are encapsulated by using the two-shift work, and the final disposal ends one period sooner than in the solution r3q4. Again, the similar beginning in the schedules of the base scenario and the scenario without hiatus can be observed as in the single-objective case minimizing costs. However, in this case, the differences in the maximum canister power and the disposal tunnel spacing are less significant.

The CPU times of solving each scalarized problem (44) with the augmentation term in the base scenario reported here varies from 645 s to 6008 s while the average CPU time is 3101 s and the median CPU time is 1898 s. The CPU time of the solution r4q5 is 7265 s and of the solution r5q1 3943 s making both alternative scenarios more time-consuming than the average problem of the base scenario. In general, it seems that the scalarized problems with the smaller value of the parameter q (i.e., closer to the $L_{\infty }$ metric) are computationally harder than the scalarized problems with the higher value of q (i.e., closer to the $L_1$ metric). Similar behavior is also observed in [37].

6. Conclusions

In this paper, we have proposed a new model for the final disposal of the spent nuclear fuel in Finland. The model involves all the spent nuclear fuel produced in Finland by the current estimates. As a result, we obtain a schedule giving the number of canisters encapsulated periodically. Note that the schedule obtained gives only guidelines, and it does not consider how the individual canisters are loaded. Moreover, the model does not give any complex layout of the disposal facility. The model is a multiobjective MINLP problem having eight objectives. This is solved with the interactive method called MITSPA. The multiobjective results are presented and commented also from the practical point of view. Furthermore, the solutions minimizing only the total costs are given. Indeed, by comparing these solutions, by increasing the costs around 3.33%, the additional water pool can be omitted and the lengths of the central and disposal tunnels can be decreased.

In the numerical experiments, only 5-year disposal periods are considered. As the numerical experiments have shown, the CPU times of the 5-year model are moderate. However, 5 years is a bit long of a disposal period, and the properties of the spent nuclear fuel are taken conservatively into account yielding the overestimation of the heat power. Therefore, we have tested also more practical 2- and 1-year disposal periods. These tests indicate the similar nature of the solutions than solutions obtained with a 5-year disposal period length. Unfortunately, the size of the problem grows a lot: the number of variables increase around fivefold and 18-fold, and the number of constraints increase around threefold and ninefold for 2-year and 1-year period length, respectively. These combined with the integer variables, the computational efforts grow as well, and the optimum cannot be guaranteed in the most of the cases. Nevertheless, the number of the objectives is so high that the several metrics are available for the two-slope parameterized ASF and, in most of the cases, at least some metric provides an optimal solution in the 2-year case.

Another issue concerning the properties of the several metrics of the two-slope parameterized ASF is the role of the parameter q. In [6], the solutions were clearly divided into two groups based on the value of the q. Thus, if only one metric would have been used, the other type of solutions would have been omitted. In these experiments, the separation of this kind was not observed. However, by systematically producing different Pareto optimal solutions, we obtain a reasonably distributed sample of the Pareto set. Furthermore, we do not have to test the achievability of the reference point. Even though all the reference points utilized here are unachievable, especially in the beginning of the solution process, the decision maker may have realistic and cautious expectations towards the solutions yielding more achievable reference points.

For the further studies, different scenarios could be investigated, for example, by changing the order of the fuel types. In the future, the model needs to be resolved once the data become more accurate along with the further investigations, for instance, related to the estimations of the thermal conductivity. It would also be interesting to consider more accurate time resolution such that schedules for transporting the fuels could be included. However, it is worth noticing that it is impossible to know the fuel transportations for the whole production beforehand. In addition, the schedule obtained with the current model could be utilized when the loading of the canister is considered.