Gene-Similarity Normalization in a Genetic Algorithm for the Maximum k-Coverage Problem
Abstract
1. Introduction
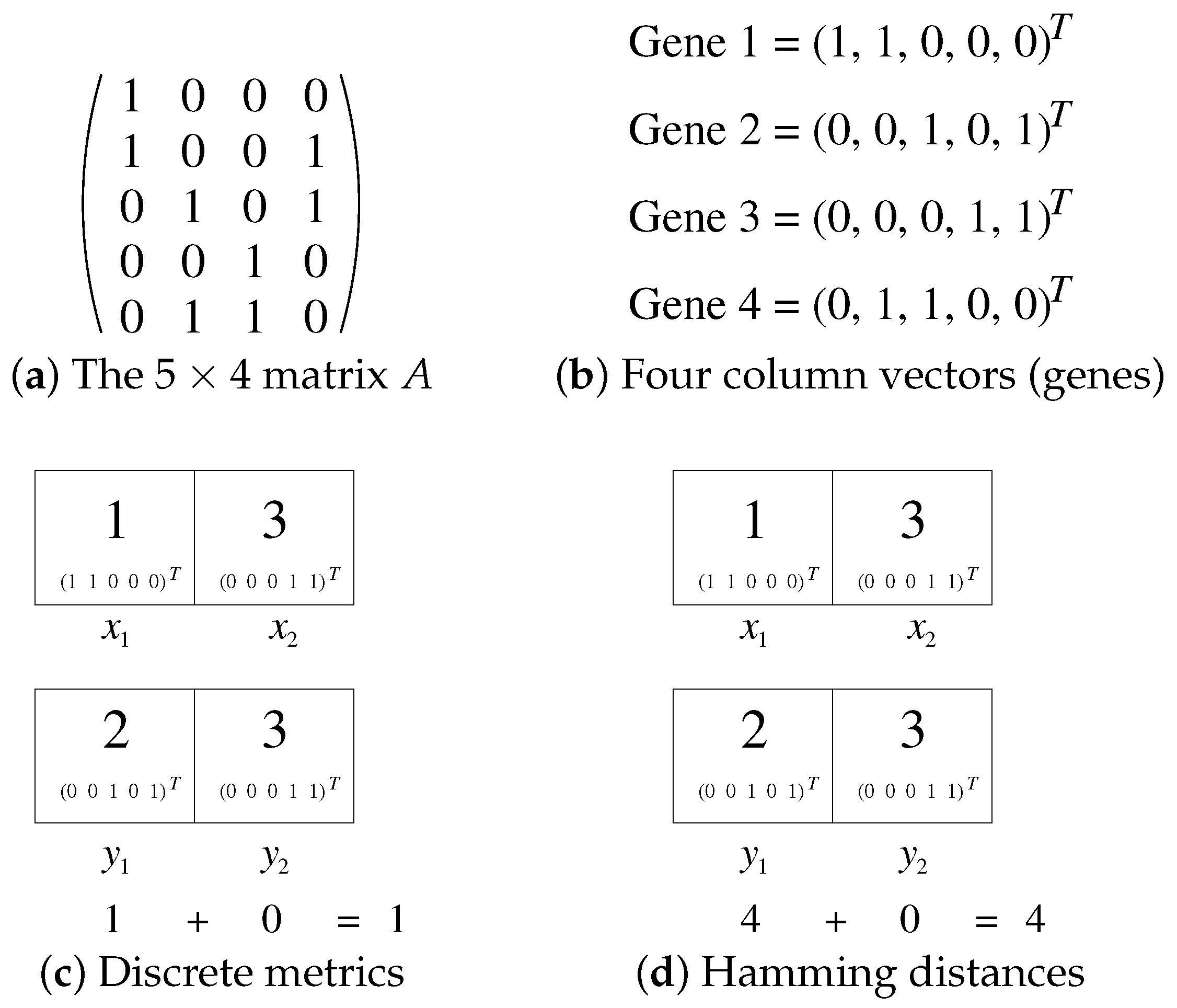
2. Representation and Space of Solution to MKCP
3. Normalization in MKCP
3.1. Preserving Feasibility
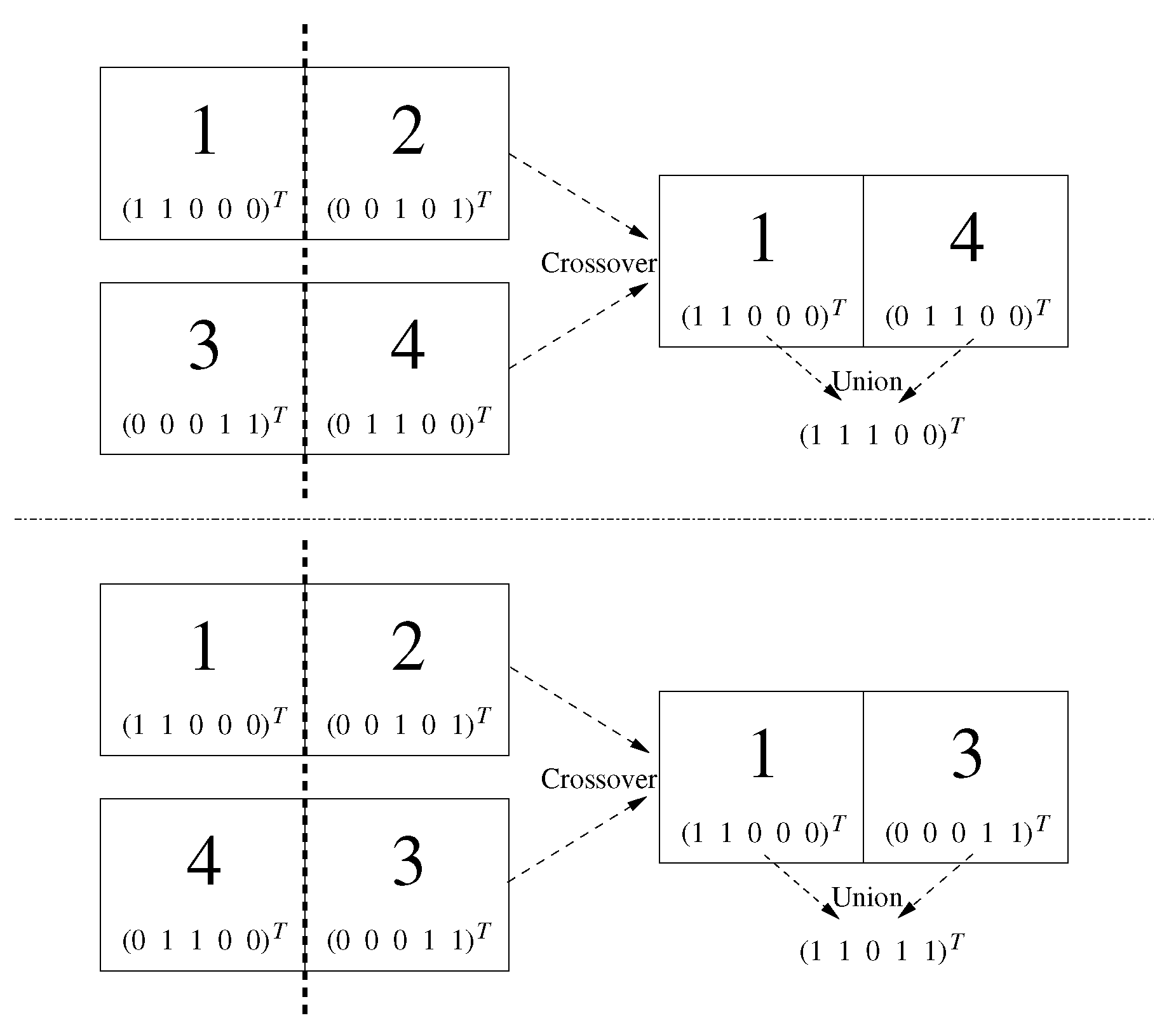
3.2. Normalization for Improving Solution Quality
4. Experiments
4.1. Test Sets and Test Environments
4.2. Effect of Normalization on a Crossover
- REPAIR: The second parent is not rearranged before the crossover, but infeasible offspring are repaired to restore feasibility after the crossover.
- FP: The second parent is rearranged to produce only feasible offspring using the normalization in Figure 3.
- (1)
- N parent chromosomes were randomly generated. (N was set to 100.)
- (2)
- The chromosomes were randomly paired, making couples.
- (3)
- The second parent in each pair was rearranged using the methods described above.
- (4)
- A uniform crossover was applied to each couple.
- (5)
- We computed the mean and the standard deviation for the coverage of each of the offspring.
4.3. Performance of GAs with Normalization Methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Disclosure
References
- Hochbaum, D.S.; Pathria, A. Analysis of the greedy approach in problems of maximum k-coverage. Nav. Res. Logist. 1998, 45, 615–627. [Google Scholar] [CrossRef]
- Caprara, A.; Fischetti, M.; Toth, P.; Vigo, D.; Guida, P.L. Algorithms for railway crew management. Math. Program. 1997, 79, 125–141. [Google Scholar] [CrossRef]
- Indyk, P.; Mahabadi, S.; Mahdian, M.; Mirrokni, V.S. Composable Core-sets for Diversity and Coverage Maximization. In Proceedings of the 33rd ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems, Snowbird, UT, USA, 22–27 June 2014; pp. 100–108. [Google Scholar]
- Indyk, P.; Vakilian, A. Tight Trade-offs for the Maximum k-Coverage Problem in the General Streaming Model. In Proceedings of the 38th ACM SIGMOD-SIGACT-SIGAI Symposium on Principles of Database Systems, Amsterdam, The Netherlands, 30 June–5 July 2019; pp. 200–217. [Google Scholar]
- Saha, B.; Getoor, L. On Maximum Coverage in the Streaming Model & Application to Multi-topic Blog-Watch. In Proceedings of the the SIAM International Conference on Data Mining, Sparks, NV, USA, 30 April–2 May 2009; pp. 697–708. [Google Scholar]
- Zheng, S.; Dmitriev, P.; Giles, C.L. Graph Based Crawler Seed Selection. In Proceedings of the 18th International Conference on World Wide Web, WWW ’09, Madrid, Spain, 20–24 April 2009; pp. 1089–1090. [Google Scholar]
- Chierichetti, F.; Kumar, R.; Tomkins, A. Max-cover in Map-reduce. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; pp. 231–240. [Google Scholar]
- Li, F.H.; Li, C.T.; Shan, M.K. Labeled Influence Maximization in Social Networks for Target Marketing. In Proceedings of the IEEE International Conference on Privacy, Security, Risk, and Trust, and IEEE International Conference on Social Computing, Boston, MA, USA, 9–11 October 2011; pp. 560–563. [Google Scholar]
- Hammar, M.; Karlsson, R.; Nilsson, B.J. Using Maximum Coverage to Optimize Recommendation Systems in e-Commerce. In Proceedings of the 7th ACM Conference on Recommender Systems, Hong Kong, China, 12–16 October 2013; pp. 265–272. [Google Scholar]
- Yoon, Y.; Kim, Y.H. An Efficient Genetic Algorithm for Maximum Coverage Deployment in Wireless Sensor Networks. IEEE Trans. Cybern. 2013, 43, 1473–1483. [Google Scholar] [CrossRef] [PubMed]
- Yaghini, M.; Karimi, M.; Rahbar, M. A set covering approach for multi-depot train driver scheduling. J. Comb. Optim. 2015, 29, 636–654. [Google Scholar] [CrossRef]
- Liu, Q.; Cai, W.; Shen, J.; Fu, Z.; Liu, X.; Linge, N. A speculative approach to spatial-temporal efficiency with multi-objective optimization in a heterogeneous cloud environment. Secur. Commun. Netw. 2016, 9, 4002–4012. [Google Scholar] [CrossRef]
- Máximo, V.R.; Nascimento, M.C.V.; Carvalho, A.C.P.L.F. Intelligent-guided adaptive search for the maximum covering location problem. Comput. Oper. Res. 2017, 78, 129–137. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Thanou, A.; Papavassiliou, S. Quality of Experience-based museum touring: A human in the loop approach. Soc. Netw. Anal. Min. 2017, 7, 33. [Google Scholar] [CrossRef]
- Sikeridis, D.; Tsiropoulou, E.E.; Devetsikiotis, M.; Papavassiliou, S. Socio-spatial resource management in wireless powered public safety networks. In Proceedings of the IEEE Military Communications Conference (MILCOM), Los Angeles, CA, USA, 29–31 October 2018; pp. 810–815. [Google Scholar]
- Fragkos, G.; Tsiropoulou, E.E.; Papavassiliou, S. Disaster Management and Information Transmission Decision-Making in Public Safety Systems. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Garey, M.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; Freeman: San Francisco, CA, USA, 1979. [Google Scholar]
- Caserta, M.; Doerner, K.F. Tabu search-based metaheuristic algorithm for the large-scale set covering problem. In Metaheuristics: Progress in Complex Systems Optimization; Springer: New York, NY, USA, 2007; pp. 43–63. [Google Scholar]
- Aickelin, U. An indirect genetic algorithm for set covering problems. J. Oper. Res. Soc. 2002, 53, 1118–1126. [Google Scholar] [CrossRef]
- Beasley, J.E.; Chu, P.C. A Genetic Algorithm for the Set Covering Problem. Eur. J. Oper. Res. 1996, 94, 392–404. [Google Scholar] [CrossRef]
- Balaji, S.; Revathi, N. A new approach for solving set covering problem using jumping particle swarm optimization method. Nat. Comput. 2016, 15, 503–517. [Google Scholar] [CrossRef]
- Al-Shihabi, S.; Arafeh, M.; Barghash, M. An improved hybrid algorithm for the set covering problem. Comput. Ind. Eng. 2015, 85, 328–334. [Google Scholar] [CrossRef]
- Ausiello, G.; Boria, N.; Giannakos, A.; Lucarelli, G.; Paschos, V. Online maximum k-coverage. Discret. Appl. Math. 2012, 160, 1901–1913. [Google Scholar] [CrossRef]
- Yu, H.; Yuan, D. Set coverage problems in a one-pass data stream. In Proceedings of the the SIAM International Conference on Data Mining, Austin, TX, USA, 2–4 May 2013; pp. 758–766. [Google Scholar]
- Chandu, D.P. Big Step Greedy Heuristic for Maximum Coverage Problem. Int. J. Comput. Appl. 2015, 125, 19–24. [Google Scholar]
- Wang, Y.; Ouyang, D.; Yin, M.; Zhang, L.; Zhang, Y. A restart local search algorithm for solving maximum set k-covering problem. Neural Comput. Appl. 2018, 29, 755–765. [Google Scholar] [CrossRef]
- Lin, G.; Guan, J. Solving maximum set k-covering problem by an adaptive binary particle swarm optimization method. Knowl.-Based Syst. 2018, 142, 95–107. [Google Scholar] [CrossRef]
- Yoon, Y.; Kim, Y.H.; Moon, B.R. Feasibility-Preserving Crossover for Maximum k-Coverage Problem. In Proceedings of the Genetic and Evolutionary Computation Conference, Atlanta, GA, USA, 12–16 July 2008; pp. 593–598. [Google Scholar]
- Fraleigh, J.B. A First Course in Abstract Algebra, 7th ed.; Addison Wesley: Boston, MA, USA, 2002. [Google Scholar]
- Burago, D.; Burago, Y.; Ivanov, S.; Burago, I.D. A Course in Metric Geometry; American Mathematical Society: Providence, RI, USA, 2001. [Google Scholar]
- Yoon, Y.; Kim, Y.H.; Moraglio, A.; Moon, B.R. Quotient geometric crossovers and redundant encodings. Theor. Comput. Sci. 2012, 425, 4–16. [Google Scholar] [CrossRef]
- Choi, S.S.; Moon, B.R. Normalization in Genetic Algorithms. In Proceedings of the Genetic and Evolutionary Computation Conference, Chicago, IL, USA, 12–16 July 2003; pp. 862–873. [Google Scholar]
- Dorne, R.; Hao, J.K. A New Genetic Local Search Algorithm for Graph Coloring. In Proceedings of the Fifth Conference on Parallel Problem Solving from Nature, Amsterdam, The Netherlands, 27–30 September 1998; pp. 745–754. [Google Scholar]
- Laszewski, G. Intelligent Structural Operators for the k-way Graph Partitioning Problem. In Proceedings of the Fourth International Conference on Genetic Algorithms, San Diego, CA, USA, 13–16 July 1991; pp. 45–52. [Google Scholar]
- Mühlenbein, H. Parallel genetic algorithms in combinatorial optimization. In Computer Science and Operations Research: New Developments in Their Interfaces; Pergamon: Oxford, MS, USA, 1992; pp. 441–456. [Google Scholar]
- Van Hoyweghen, C.; Naudts, B.; Goldberg, D.E. Spin-flip symmetry and synchronization. Evol. Comput. 2002, 10, 317–344. [Google Scholar] [CrossRef]
- Kang, S.J.; Moon, B.R. A Hybrid Genetic Algorithm for Multiway Graph Partitioning. In Proceedings of the Genetic and Evolutionary Computation Conference, Las Vegas, NV, USA, 8–12 July 2000; pp. 159–166. [Google Scholar]
- Moraglio, A.; Kim, Y.H.; Yoon, Y.; Moon, B.R. Geometric Crossovers for Multiway Graph Partitioning. Evol. Comput. 2007, 15, 445–474. [Google Scholar] [CrossRef]
- Choi, S.S.; Moon, B.R. Normalization for Genetic Algorithms with Nonsynonymously Redundant Encodings. IEEE Trans. Evol. Comput. 2008, 12, 604–616. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian Method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Papadimitriou, C.H.; Steiglitz, K. Combinatorial Optimization: Algorithms and Complexity; Prentice-Hall: Englewood Cliffs, NJ, USA, 1955. [Google Scholar]
- Avis, D. A survey of heuristics for the weighted matching problem. Networks 1983, 13, 475–493. [Google Scholar] [CrossRef]
- Beasley, J.E. OR-Library: Distributing test problems by electronic mail. J. Oper. Res. Soc. 1990, 41, 1069–1072. [Google Scholar] [CrossRef]
- Eshelman, L.J. The CHC adaptive search algorithm: How to have safe search when engaging in nontraditional genetic recombination. In Foundations of Genetic Algorithms; Morgan Kaufmann: Burlington, MA, USA, 1991; pp. 265–283. [Google Scholar]
- Alba, E.; Luque, G.; Araujo, L. Natural language tagging with genetic algorithms. Inf. Process. Lett. 2006, 100, 173–182. [Google Scholar] [CrossRef]
- Cordón, O.; Damasb, S.; Santamaría, J. Feature-based image registration by means of the CHC evolutionary algorithm. Image Vis. Comput. 2006, 24, 525–533. [Google Scholar] [CrossRef]
- Guerra-Salcedo, C.; Whitley, D. Genetic Search for Feature Subset Selection: A Comparison Between CHC and GENESIS. In Proceedings of the Third Annual Conference on Genetic Programming; Morgan Kaufmann: Burlington, MA, USA, 1998; pp. 504–509. [Google Scholar]
- Nebro, A.J.; Alba, E.; Molina, G.; Chicano, F.; Luna, F.; Durillo, J.J. Optimal antenna placement using a new multi-objective CHC algorithm. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation, London, UK, 7–11 July 2007; pp. 876–883. [Google Scholar]
- Tsutsui, S.; Goldberg, D.E. Search space boundary extension method in real-coded genetic algorithms. Inf. Sci. 2001, 133, 229–247. [Google Scholar] [CrossRef]
- Yoon, Y.; Kim, Y.H.; Moraglio, A.; Moon, B.R. A Theoretical and Empirical Study on Unbiased Boundary-extended Crossover for Real-valued Representation. Inf. Sci. 2012, 183, 48–65. [Google Scholar] [CrossRef]
- Pinch, R.G.E. The distance of a permutation from a subgroup of Sn. arXiv 2005, arXiv:math/0511501. [Google Scholar]
- Kim, Y.H.; Moraglio, A.; Kattan, A.; Yoon, Y. Geometric generalisation of surrogate model-based optimisation to combinatorial and program spaces. Math. Probl. Eng. 2014, 2014, 184540. [Google Scholar] [CrossRef]
- Nam, Y.W.; Kim, Y.H. Automatic jazz melody composition through a learning-based genetic algorithm. In Proceedings of the 8th International Conference on Computational Intelligence in Music, Sound, Art and Design (EvoMUSART), Leipzig, Germany, 24–26 April 2019; Lecture Notes in Computer Science. Springer: Berlin, Germany; Volume 11453, pp. 217–233. [Google Scholar]
- Lee, J.; Kim, Y.H. Epistasis-based basis estimation method for simplifying the problem space of an evolutionary search in binary representation. Complexity 2019, 2019, 2095167. [Google Scholar] [CrossRef]


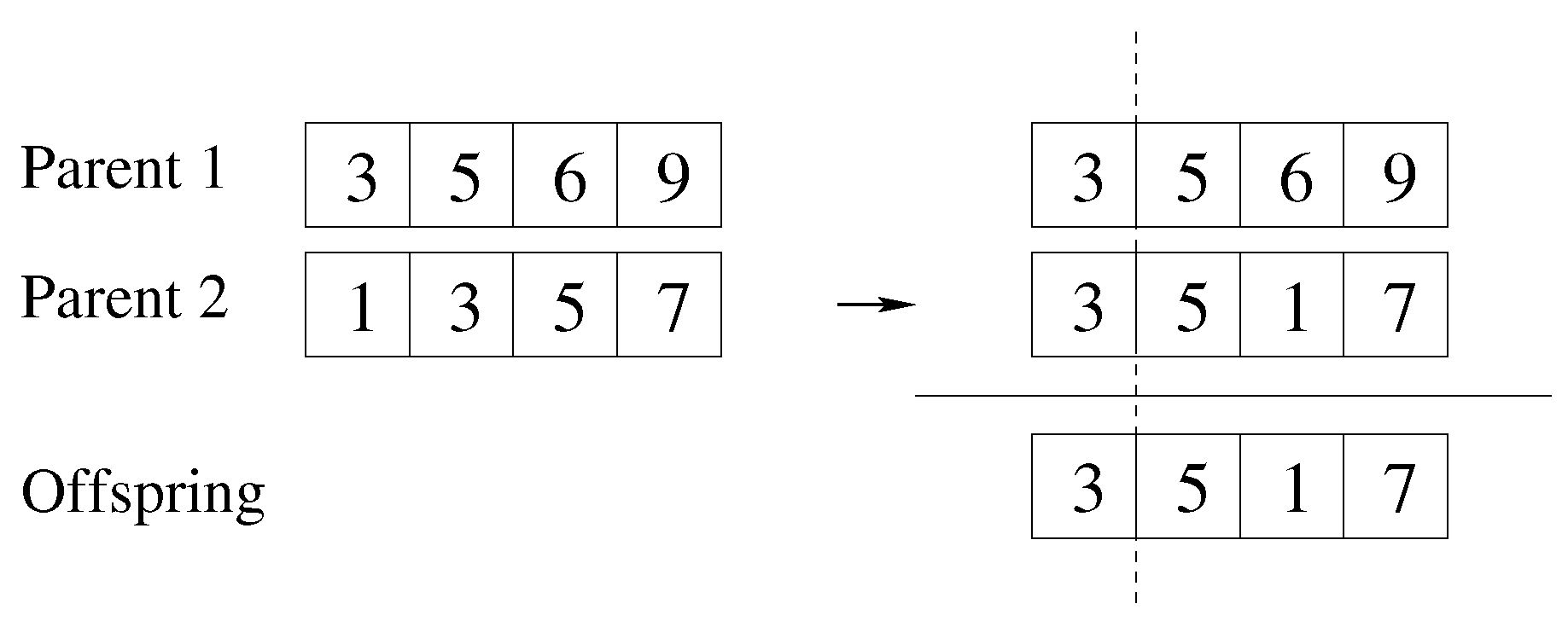
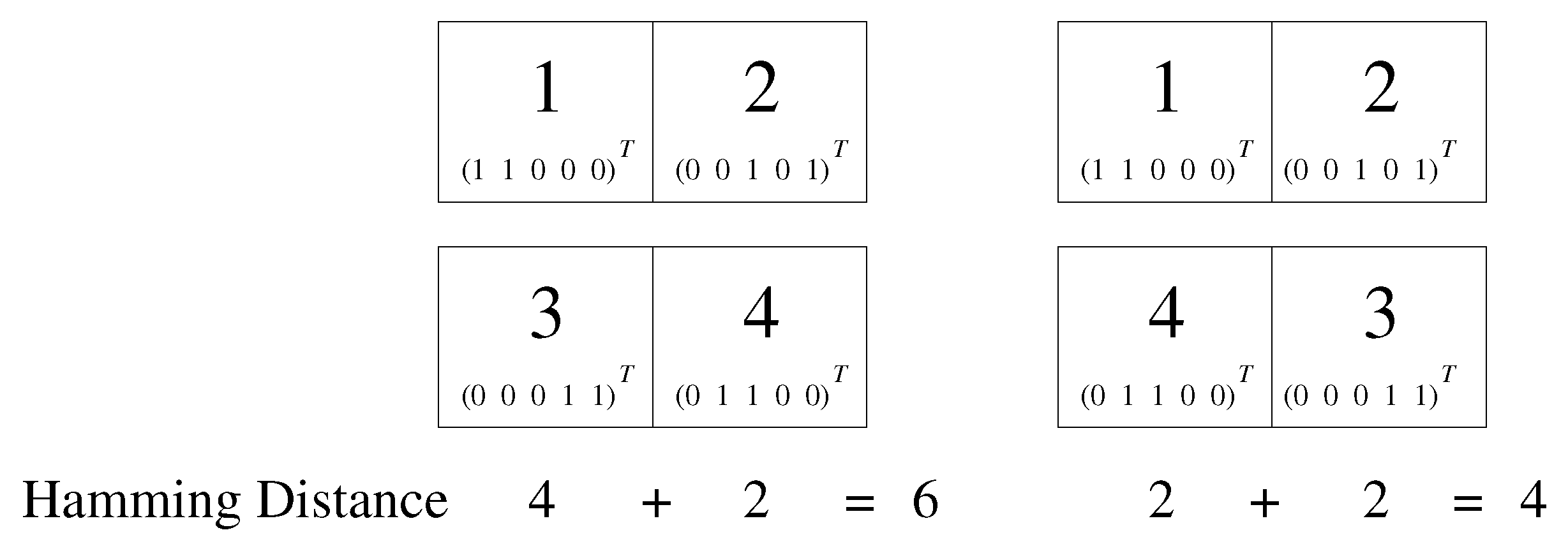


| Problem | m | n | Density | #Instances |
|---|---|---|---|---|
| Set | Tested | |||
| I-4 | 200 | 1000 | 2% | 10 |
| I-5 | 200 | 2000 | 2% | 10 |
| I-6 | 200 | 1000 | 5% | 5 |
| I-A | 300 | 3000 | 2% | 5 |
| I-B | 300 | 3000 | 5% | 5 |
| I-C | 400 | 4000 | 2% | 5 |
| I-D | 400 | 4000 | 5% | 5 |
| I-E | 500 | 5000 | 10% | 5 |
| I-F | 500 | 5000 | 20% | 5 |
| I-G | 1000 | 10,000 | 2% | 5 |
| I-H | 1000 | 10,000 | 5% | 5 |
| Tightness | Parents | REPAIR | FP | OPT | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | Instance | k | Ave | SD | Ave | SD | Ave | SD | Ave | SD |
| scp41 | 40 | 110.27 | 6.33 | 110.30 | 5.89 | 110.00 | 5.46 | 113.80 | 6.12 | |
| scp51 | 40 | 110.72 | 6.62 | 110.00 | 6.95 | 111.82 | 6.90 | 115.02 | 6.77 | |
| scp61 | 16 | 111.33 | 6.43 | 111.24 | 6.64 | 111.20 | 6.73 | 114.20 | 6.24 | |
| scpa1 | 40 | 167.69 | 7.76 | 166.80 | 7.83 | 167.68 | 8.47 | 173.66 | 8.93 | |
| scpb1 | 16 | 168.31 | 9.27 | 170.80 | 9.79 | 168.90 | 9.11 | 171.36 | 9.25 | |
| 0.8 | scpc1 | 40 | 220.40 | 10.53 | 221.04 | 10.83 | 220.42 | 9.76 | 225.84 | 9.91 |
| scpd1 | 16 | 223.74 | 9.22 | 222.34 | 10.15 | 224.36 | 8.69 | 228.56 | 9.48 | |
| scpnre1 | 8 | 284.43 | 10.23 | 285.08 | 10.93 | 285.76 | 11.08 | 287.14 | 9.27 | |
| scpnrf1 | 4 | 295.44 | 10.76 | 294.94 | 9.94 | 294.44 | 9.50 | 297.34 | 9.75 | |
| scpnrg1 | 40 | 553.30 | 14.49 | 553.96 | 14.56 | 553.82 | 16.10 | 561.28 | 12.16 | |
| scpnrh1 | 16 | 560.94 | 14.49 | 562.12 | 16.57 | 563.14 | 16.24 | 567.46 | 17.09 | |
| scp41 | 30 | 90.40 | 6.41 | 90.80 | 6.34 | 89.98 | 4.82 | 95.34 | 6.14 | |
| scp51 | 30 | 90.77 | 6.74 | 91.92 | 6.92 | 91.44 | 6.50 | 94.20 | 6.64 | |
| scp61 | 12 | 90.96 | 6.54 | 90.56 | 6.17 | 90.94 | 5.86 | 91.88 | 7.75 | |
| scpa1 | 30 | 137.54 | 8.09 | 136.74 | 8.95 | 137.60 | 7.63 | 143.74 | 8.01 | |
| scpb1 | 12 | 138.05 | 8.31 | 138.44 | 8.36 | 139.68 | 9.08 | 141.68 | 8.28 | |
| 0.6 | scpc1 | 30 | 181.59 | 10.64 | 178.52 | 10.55 | 180.24 | 11.30 | 186.06 | 10.09 |
| scpd1 | 12 | 185.27 | 9.08 | 184.80 | 9.06 | 185.34 | 9.01 | 188.30 | 7.72 | |
| scpnre1 | 6 | 233.02 | 11.34 | 231.60 | 12.83 | 234.04 | 12.41 | 234.12 | 11.04 | |
| scpnrf1 | 3 | 244.40 | 11.37 | 245.04 | 10.48 | 244.24 | 10.28 | 245.68 | 9.57 | |
| scpnrg1 | 30 | 452.91 | 14.48 | 452.70 | 14.52 | 452.58 | 14.07 | 461.34 | 13.42 | |
| scpnrh1 | 12 | 461.87 | 13.66 | 460.80 | 16.68 | 462.22 | 16.58 | 462.40 | 15.61 | |
| scp41 | 20 | 66.44 | 5.52 | 66.84 | 5.59 | 67.30 | 6.09 | 68.06 | 5.19 | |
| scp51 | 20 | 66.41 | 5.54 | 67.44 | 6.61 | 66.84 | 6.44 | 68.98 | 6.71 | |
| scp61 | 8 | 66.55 | 6.80 | 67.68 | 6.05 | 66.72 | 5.91 | 67.74 | 5.71 | |
| scpa1 | 20 | 100.82 | 8.40 | 99.80 | 7.62 | 100.00 | 7.63 | 103.54 | 6.80 | |
| scpb1 | 8 | 101.25 | 7.43 | 101.74 | 8.91 | 101.06 | 7.38 | 104.06 | 8.43 | |
| 0.4 | scpc1 | 20 | 132.47 | 10.42 | 131.68 | 8.78 | 133.14 | 9.07 | 136.14 | 9.92 |
| scpd1 | 8 | 135.48 | 10.49 | 136.32 | 8.49 | 134.72 | 9.46 | 136.94 | 9.96 | |
| scpnre1 | 4 | 171.43 | 10.32 | 172.04 | 10.14 | 172.94 | 12.05 | 173.16 | 11.10 | |
| scpnrf1 | 2 | 179.95 | 10.83 | 180.04 | 9.85 | 179.94 | 11.46 | 182.90 | 11.22 | |
| scpnrg1 | 20 | 331.51 | 13.57 | 332.10 | 13.64 | 330.52 | 14.89 | 337.30 | 14.60 | |
| scpnrh1 | 8 | 338.58 | 14.59 | 336.84 | 14.80 | 337.30 | 14.42 | 343.44 | 13.90 | |
| t-test p-value * | - | |||||||||
| Tightness | Instance | Multi-Start | RR-GA | t-Test | FP-GA | t-Test | OPT-GA | t-Test | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | Set | k | %-Gap | Ave | %-Gap | Ave | p-Value | %-Gap | Ave | p-Value | %-Gap | Ave | p-Value |
| I-4 | 40 | 28.17 | 141.35 | 7.08 | 182.86 | 3.36 | 190.19 | 1.96 | 192.95 | ||||
| I-5 | 40 | 28.67 | 141.52 | 6.84 | 184.82 | 3.95 | 190.57 | 1.64 | 195.14 | ||||
| I-6 | 16 | 20.56 | 143.77 | 4.22 | 173.35 | 4.21 | 173.37 | 2.53 | 176.42 | ||||
| I-A | 40 | 27.62 | 207.57 | 6.16 | 269.13 | 4.29 | 274.49 | 1.81 | 281.61 | ||||
| I-B | 16 | 20.56 | 208.93 | 4.52 | 251.10 | 4.73 | 250.54 | 2.68 | 255.94 | ||||
| 0.8 | I-C | 40 | 26.81 | 269.33 | 6.12 | 345.48 | 4.85 | 350.16 | 2.10 | 360.28 | |||
| I-D | 16 | 18.78 | 271.43 | 3.91 | 321.14 | 4.15 | 320.31 | 1.90 | 327.84 | ||||
| I-E | 8 | 12.65 | 336.81 | 3.63 | 371.60 | 4.04 | 369.99 | 2.65 | 375.37 | ||||
| I-F | 4 | 6.23 | 346.58 | 2.25 | 361.27 | 2.42 | 360.66 | 1.83 | 362.82 | ||||
| I-G | 40 | 21.61 | 630.13 | 4.73 | 765.78 | 3.82 | 773.12 | 1.64 | 790.58 | ||||
| I-H | 16 | 14.79 | 634.61 | 3.31 | 720.14 | 3.75 | 716.83 | 1.93 | 730.41 | ||||
| I-4 | 30 | 31.62 | 121.57 | 6.72 | 165.85 | 4.75 | 169.35 | 2.69 | 173.01 | ||||
| I-5 | 30 | 32.71 | 121.79 | 6.76 | 168.76 | 5.69 | 170.70 | 2.53 | 176.42 | ||||
| I-6 | 12 | 21.51 | 124.00 | 4.35 | 151.12 | 4.21 | 151.35 | 2.56 | 153.95 | ||||
| I-A | 30 | 31.03 | 178.49 | 6.12 | 242.97 | 5.30 | 245.09 | 2.36 | 252.70 | ||||
| I-B | 12 | 22.15 | 179.34 | 4.83 | 219.27 | 5.22 | 218.36 | 3.00 | 223.47 | ||||
| 0.6 | I-C | 30 | 29.54 | 230.25 | 5.89 | 307.54 | 5.19 | 309.85 | 2.63 | 318.20 | |||
| I-D | 12 | 20.18 | 232.11 | 4.28 | 278.34 | 4.73 | 277.03 | 2.71 | 282.91 | ||||
| I-E | 6 | 11.82 | 287.65 | 3.12 | 316.02 | 3.48 | 314.85 | 2.25 | 318.84 | ||||
| I-F | 3 | 4.29 | 296.71 | 1.43 | 305.56 | 1.91 | 304.09 | 1.13 | 306.50 | ||||
| I-G | 30 | 24.17 | 531.23 | 5.18 | 664.26 | 5.00 | 665.56 | 2.42 | 683.65 | ||||
| I-H | 12 | 15.06 | 535.09 | 2.95 | 611.43 | 3.34 | 608.92 | 1.80 | 618.66 | ||||
| I-4 | 20 | 32.30 | 95.98 | 5.56 | 133.91 | 4.54 | 135.36 | 2.40 | 138.39 | ||||
| I-5 | 20 | 34.33 | 96.27 | 6.20 | 137.51 | 6.12 | 137.62 | 2.76 | 142.55 | ||||
| I-6 | 8 | 19.63 | 98.21 | 3.14 | 118.37 | 3.38 | 118.08 | 2.08 | 119.66 | ||||
| I-A | 20 | 32.95 | 140.65 | 5.88 | 197.46 | 6.12 | 196.95 | 2.92 | 203.66 | ||||
| I-B | 8 | 21.41 | 141.44 | 4.02 | 172.76 | 4.84 | 171.27 | 2.48 | 175.53 | ||||
| 0.4 | I-C | 20 | 31.50 | 179.73 | 5.50 | 247.96 | 5.77 | 247.24 | 2.66 | 255.41 | |||
| I-D | 8 | 19.61 | 180.87 | 3.74 | 216.59 | 4.48 | 214.91 | 2.56 | 219.23 | ||||
| I-E | 4 | 9.00 | 222.76 | 2.14 | 239.55 | 2.64 | 238.34 | 1.64 | 240.78 | ||||
| I-F | 2 | 1.87 | 229.63 | 1.72 | 229.97 | 1.97 | 229.39 | 1.55 | 230.37 | ||||
| I-G | 20 | 25.35 | 405.93 | 4.45 | 519.61 | 4.65 | 518.51 | 2.32 | 531.16 | ||||
| I-H | 8 | 14.64 | 408.88 | 3.15 | 463.92 | 3.52 | 462.16 | 1.87 | 470.06 | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, Y.; Kim, Y.-H. Gene-Similarity Normalization in a Genetic Algorithm for the Maximum k-Coverage Problem. Mathematics 2020, 8, 513. https://doi.org/10.3390/math8040513
Yoon Y, Kim Y-H. Gene-Similarity Normalization in a Genetic Algorithm for the Maximum k-Coverage Problem. Mathematics. 2020; 8(4):513. https://doi.org/10.3390/math8040513
Chicago/Turabian StyleYoon, Yourim, and Yong-Hyuk Kim. 2020. "Gene-Similarity Normalization in a Genetic Algorithm for the Maximum k-Coverage Problem" Mathematics 8, no. 4: 513. https://doi.org/10.3390/math8040513
APA StyleYoon, Y., & Kim, Y.-H. (2020). Gene-Similarity Normalization in a Genetic Algorithm for the Maximum k-Coverage Problem. Mathematics, 8(4), 513. https://doi.org/10.3390/math8040513






