Abstract
Dilation and erosion are two elementary operations from mathematical morphology, a non-linear lattice computing methodology widely used for image processing and analysis. The dilation-erosion perceptron (DEP) is a morphological neural network obtained by a convex combination of a dilation and an erosion followed by the application of a hard-limiter function for binary classification tasks. A DEP classifier can be trained using a convex-concave procedure along with the minimization of the hinge loss function. As a lattice computing model, the DEP classifier assumes the feature and class spaces are partially ordered sets. In many practical situations, however, there is no natural ordering for the feature patterns. Using concepts from multi-valued mathematical morphology, this paper introduces the reduced dilation-erosion (r-DEP) classifier. An r-DEP classifier is obtained by endowing the feature space with an appropriate reduced ordering. Such reduced ordering can be determined using two approaches: one based on an ensemble of support vector classifiers (SVCs) with different kernels and the other based on a bagging of similar SVCs trained using different samples of the training set. Using several binary classification datasets from the OpenML repository, the ensemble and bagging r-DEP classifiers yielded mean higher balanced accuracy scores than the linear, polynomial, and radial basis function (RBF) SVCs as well as their ensemble and a bagging of RBF SVCs.
1. Introduction
Cyber-physical systems (CPS) is a broad interdisciplinary area which combines computational and physical devices in an integrated manner [1,2,3,4]. Internet of things (IoT), for instance, can be viewed as an important class of CPS where physical objects are interconnected in a network with identified address [5]. Besides Industry 4.0 and related technologies [6], applications of CPS include social robots for educational purposes [7], medical services and healthcare [8], and many other fields.
Although modeling a CPS comprises both physical and computational process [4], this paper focuses only on the latter. Specifically, we model the computational process using lattice computing paradigm. Lattice computing (LC) comprises the many techniques and mathematical modeling methodologies based on lattice theory [9,10]. Lattice theory is concerned with a mathematical structure obtained by enriching a non-empty set with an ordering scheme with well defined extrema operations. Specifically, a lattice is a partially ordered set in which any finite set has both an infimum and a supremum [11]. One of the main advantages of LC is its capability to process ordered data which include logic values, sets and more generally fuzzy sets, images, graphs, and many other types of information granules [9,10,12,13]. Mathematical morphology and morphological neural networks are examples of well succeeded LC modeling methodologies. Let us briefly address these two LC methodologies in the following paragraphs.
Mathematical morphology (MM) is a non-linear theory widely used for image processing and analysis [14,15,16,17]. MM was originally conceived for processing binary images in the 1960s. Subsequently, it has been extended to gray-scale images using the notions of umbra, level sets, and fuzzy set theory [18,19,20]. Complete lattice is one key concept to extend MM from binary to more general contexts [21,22]. Specifically, MM is a theory mainly concerned with mappings between complete lattices [23,24]. Dilations and erosions, which are defined algebraically as mappings that commute respectively with the supremum and infimum operations, are elementary operations of MM. Many other operators from MM are defined by combining dilations and erosions [17,23,25]. Although complete lattice provides an appropriate mathematical background for binary and gray-scale MMs, defining morphological operators for multi-valued images is not straightforward because there is no universal ordering for vector-valued spaces [26,27]. In fact, the development of appropriate ordering scheme for multi-valued MM is an active area of research [28,29,30,31,32]. In this paper, we make use of the suprevised reduced ordering proposed by Velasco-Forero and Angulo [33]. In a few words, a supervised reduced ordering is defined using a training set of negative (or background) and positive (or foreground) values. As a consequence, the resulting multi-valued morphological operators can be interpreted in terms of positive and negative training values. One contribution of this paper is the definition of morphological neural networks based on supervised reduced orderings (see Section 4).
Morphological neural networks (MNNs) refer to the broad class of neural networks whose processing units perform an operation from MM, possibly followed by the application of an activation function [34]. The single-layer morphological perceptron, introduced by Ritter and Sussner in the middle 1990s, is one of the earliest MNNs along with the morphological associative memories [35]. Briefly, the morphological perceptron performs either a dilation or an erosion from gray-scale MM followed by a hard-limiter activation function. The original morphological perceptron has been subsequently investigated and generalized by many prominent researchers [34,36,37,38]. For example, Sussner addressed the multilayer morphological perceptron and introduced a supervised learning algorithm for binary classification problems [36]. In a few words, the learning algorithm proposed by Sussner is an incremental algorithm which adds hidden morphological neurons until all the training set is correctly classified. By taking into account the relevance of dendrites in biological neurons, Ritter and Urcid proposed a morphological neuron with dendritic structure [37]. Apart from the biological motivation, the morphological perceptron with dendritic structure is similar to the multilayer morphological perceptron investigated by Sussner. In fact, like the learning algorithm of the multilayer morphological perceptron, the morphological perceptron with dendritic structure grows as it learns until there are no mis-classified training samples. Furthermore, the decision surface of both multilayer perceptron and the morphological perceptron with dentritic structure depends on the order in which the training samples are presented to the network. The morphological perceptron with competitive layer (MPC) introduced by Sussner and Esmi does not depend on the order in which the training samples are presented to the network [34]. Like the previous models, however, training morphological perceptron with competitive layer finishes only when all training patterns are correctly classified. Thus, it is possible to the network to end up overfitting the training data.
In contrast to the greedy methods described in the previous paragraph, many researchers formulated the training of MNNs and hybrid models as an optimization problem. For example, Pessoa and Maragos used pulse functions to circumvent the non-differentiability of lattice-based operations on a steepest descent method designed for training a hybrid morphological/rank/linear network [39]. Based on the ideas of Pessoa and Maragos, Araújo proposed a hybrid morphological/linear network called dilation-erosion perceptron (DEP), which is trained using a steepest descent method [40]. Steepest descent methods are also used by Hernández et al. for training hybrid two-layer neural networks, where one layer is morphological and the other is linear [41]. In a similar fashion, Mondal et al. proposed a hybrid morphological/linear model, called a dense morphological network, which was trained using stochastic gradient descent method such as adam optimization [42]. Apparently unaware of the aforementioned works on MNNs, Franchi et al. recently integrated morphological operators with a deep learning framework to introduce the so-called deep morphological network, which was also trained using a steepest descent algorithm [43]. In contrast to steepest descent methods, Arce et al. trained MNNs using differential evolution [44]. Moreover, Sussner and Campiotti proposed a hybrid morphological/linear extreme learning machine which hads a hidden-layer of morphological units and a linear output layer that was trained by regularized least-squares [45]. Recently, Charisopoulos and Maragos formulated the training of a single morphological perceptron as the solution of a convex-concave optimization problem [46,47]. Apart from the elegant formulation, the convex-concave procedure outperformed gradient descent methods in terms of accuracy and robustness on some computational experiments.
In this paper, we investigate the convex-concave procedure for training the DEP classifier. As a lattice-based model, DEP requires a partial ordering on both feature and class label spaces. Furthermore, the traditional approach assumes the feature space is equipped with the component-wise ordering induced by the natural ordering of real numbers. The component-wise ordering, however, may be inappropriate in the feature space. Based on ideas from multi-valued MM, we make use of supervised reduced orderings for the feature space of the DEP model. The resulting model is referred to as reduced dilation-erosion perceptron (r-DEP). The performance of the new r-DEP model is evaluated by considering 30 binary classification problems from the OpenML repository [48,49], most of which are also available at the well-known UCI Machine Learning Repository [50].
The paper is organized as follows. The next section presents a brief review on the basic concepts from lattice theory and MM, including the supervised reduced ordering-based approach to multi-valued MM. Traditional MNNs, including the DEP classifier and the convex-concave procedure, are discussed in Section 3. Section 4 presents the main contribution of this paper: the reduced DEP classifier. In Section 5, we compare the performance of the r-DEP classifier with other traditional machine learning approaches from the literature. The paper finishes with some concluding remarks in Section 6.
2. Basic Concepts from Lattice Theory and Mathematical Morphology
Let us begin by recalling some basic concepts from lattice theory and mathematical morphology (MM). Precisely, we shall only present the necessary concepts for understanding of morphological perceptron models. Furthermore, we will focus on elementary concepts without going deep into these rich theories. The reader interested on lattice theory is invited to consult [11]. Detailed account on MM and its applications can be found in [14,17,23,25]. The reader familiar with lattice theory and MM may skip Section 2.1.
2.1. Lattice Theory and Mathematical Morphology
First of all, a non-empty set equipped with a binary relation "≤" is a partially ordered set (poset) if the following conditions hold true:
- P1:
- For all , we have . (Reflexive)
- P2:
- If and , then . (Transitivity)
- P3:
- If and , then . (Antisymmetry)
In this case, the binary relation “≤” is called a partial order. We speak of a pre-ordered set if is equipped with a binary relation which satisfies the properties P1 and P2.
A partially ordered set is a complete lattice if any subset has a supremum (least upper bound) and an infimum (greatest lower bound) denoted respectively by and . When is finite, we write and .
Example 1.
The extended real numbers with the natural ordering is an example of a complete lattice. The Cartesian product of the extended real numbers is also a complete lattice with the partial order defined as follows in a component-wise manner:
In this case, the infimum and the supremum of a set is also determined in a component-wise manner by
where is the set of the ith component of all the vectors in X, for .
Mathematical morphology is a non-linear theory widely used for image processing and analysis [24,25]. From the mathematical point of view, MM can be viewed as a theory of mappings between complete lattices. In fact, the elementary operations of MM are mappings that distribute over either infimum or supremum operations. Precisely, two elementary operations of MM are defined as follows [15,23]:
Definition 1
(Erosion and Dilation). Let and be complete lattices. A mapping is an erosion and a mapping is a dilation if the following identities hold true for any :
From Theorem 3 on [34], we have the following example of dilations and erosions:
Example 2.
Consider real-valued vectors and . The operators and given by
for all are respectively an erosion and a dilation.
Remark 1.
The mappings and given by (4) can be extended for by appropriately dealing with indeterminacy such as [34]. In this paper, however, we only consider finite-valued vectors .
Definition 2
(Increasing Operators). Let and be two complete lattices. An operator is isotone or increasing if implies .
Proposition 1
(Lemma 2.1 from [51]). Erosions and dilations are increasing operators.
Despite the rich theory on morphological operators and their many successful applications, the concepts presented above are sufficient for this paper. Let us now turn our attention to some concepts from multi-valued MM.
2.2. Multi-valued Mathematical Morphology
Although MM can be very well defined on complete lattices (see Definition 1), there is no unambiguous ordering for vector-valued sets. For example, although equipped with the component- wise ordering is a complete lattice, the partial order given by (1) does not take into account possible relationship between the vector components. Furthermore, the component-wise order given by (1) results the so-called “false color” problem in multi-valued MM [52]. As a consequence, a great deal of effort has been devoted to finding appropriate ordering schemes for vector-valued data [26,27,29,31,53]. Among the many approaches to multi-valued MM, those based on reduced orderings are particularly interesting and computationally cheap [32,33,53].
In a reduced ordering, also referred to as an r-ordering, the elements of a vector-valued non-empty set are ranked according to a surjective mapping , where is a complete lattice. Precisely, an r-ordering is defined as follows using the mapping :
In analogy to Definition 2, r-increasing operators are defined as follows using r-orderings:
Definition 3
(r-Increasing Operator). Let and be surjective mappings from non-empty sets and to complete lattices and . An operator is r-increasing if implies .
Although been reflexive and transitive, an r-ordering is in principle a pre-ordering because it may fails to be anti-symmetric. Notwithstanding, morphological operators can be defined as follows using reduced orderings [53]:
Definition 4
(r-Increasing Morphological Operator). Let and be non-empty sets, and be complete lattices, and and be surjective mappings. A mapping is an r-increasing morphological operator if there exists an increasing morphological operator such that , that is,
In words, the mapping applied on an r-increasing morphological operator corresponds to the morphological operator applied on the output of the mapping . For example, an operator is an r-increasing erosion, or simply an r-erosion, if there exists an erosion such that . Dually, a mapping is an r-increasing dilation, or simply an r-dilation, if there exists a dilation such that .
Remark 2.
Definition 4, which is motivated by Proposition 2.5 in [53], generalizes of the notions of r-erosion and r-dilation as well as r-opening and r-closing from Goutsias et al. Precisely, if and , then one can consider , where is a surjective mapping. Thus, an operator is an r-erosion if and only if there exists an erosion such that , which is exactly the definition of r-erosion introduced by Goutsias et al. (shortly after Proposition 2.11 in [53]).
Example 3.
A general approach to multi-valued MM based on supervised reduced ordering have been proposed by Velasco-Forero and Angulo [33]. Briefly, in a supervised reduced ordering the sobrejective mapping is determined using training sets and of positive (foreground) and negative (background) values, respectively. Furthermore, the mapping ρ is expected to satisfy
where and denote respectively the largest (top) and the least (bottom) elements of . As a consequence, a supervised r-ordering is interpretable with respect to the training sets and [32]. Assuming and , Velasco-Forero and Angulo proposed to determine ρ using a support vector machine [54,55,56]. As usual, let us first combine the positive and negative sets into a single training set such that if and if . Given a suitable kernel function κ, the supervised reduced ordering mapping ρ corresponds to the decision function of a support vector classifier (SVC) given by
where is the solution of the quadratic programming problem
where is a user specified parameter which controls the trade-off between minimizing the training error and maximizing the separation margin [55,56]. Examples of kernels include
- Linear kernel:
- Gaussian kernel:The Gaussian kernel yields a radial-basis function (RBF) SVC.
- Polynomial kernel:The polynomial kernel yields a polynomial SVC.
We would like to point out that the intercept term is not relevant for a reduced ordering scheme and, thus, we refrained from including it on (8). In addition, we would like to remark that the decision function ρ maps the multi-valued set to a totally ordered subset of , which allows for efficient implementation of multi-valued morphological operators using look-up table and the usual gray-scale operators (see Algorithm 1 in [32] for details).
3. Morphological Perceptron and the Convex-Concave Procedure
Morphological neural network (MNN) refer to the broad class of neural networks whose neurons (processing units) perform an operation from MM possibly followed by the application of an activation function [34]. Examples of MNNs include (fuzzy) morphological associative memories [57,58,59,60,61,62] and morphological perceptrons [34,35,36,38,46]. In this paper, we focus on the dilation-erosion perceptron trained using the recent convex-concave procedure and applied as a binary classifier [40,46,47].
Recall that a classifier is a mapping , where and are respectively the sets of features and classes. In a binary classification problem, the set of classes can be identified with by means of a one-to-one mapping . In this paper, we say that the elements of associated with the class labels and belong respectively to the negative and positive classes. In a supervised binary classification task, the classifier is determined from a finite set of samples referred to as the training set.
3.1. Morphological and Dilation-Erosion Perceptron Models
Morphological perceptron has been introduced by Ritter and Sussner in the mid-1990s for binary classification problems [35]. In analogy to Rosenblatt’s perceptron, Ritter and Sussner define a morphological perceptron by either one of the two equations
where f denotes a hard limiter activation function. To simplify the exposition, we consider in this paper with the convention . By adopting the signal function, the morphological perceptrons given by (14) can be used for binary classification whose labels are and .
Note that a morphological perceptron is given by either the composition or the composition , where and denote respectively the dilation and the erosion given by (4) for . Therefore, we refer to the models in (14) as erosion-based and dilation-based morphological perceptrons, respectively. Furthermore, and are respectively the decision functions of the erosion-based and dilation-based morphological perceptron.
Let us now briefly address the geometry of the morphological perceptrons with . Given a weight vector , let
be the set of all points such that . Since if and only if for all , we conclude that is equivalently given by
The decision boundary of an erosion-based morphological perceptron corresponds to the boundary of the set : The class label is assigned to all patterns in while the class label is given to all patterns outside . In view of this remark, we may say that an erosion-based morphological perceptron focuses on the positive class, whose label is . Dually, a dilation-based morphological perceptron focuses on the negative class, whose label is . Specifically, given a weight vector , the set of all points such that satisfies
The decision boundary of a dilation-based morphological perceptron corresponds to the boundary of , that is, patterns inside are classified as negative while patterns outside are classified as . For illustrative purposes, Figure 1 shows the sets (yellow region) and (purple region), obtained by considering respectively and . Figure 1 also shows the decision boundary of the dilation-erosion perceptron described below.
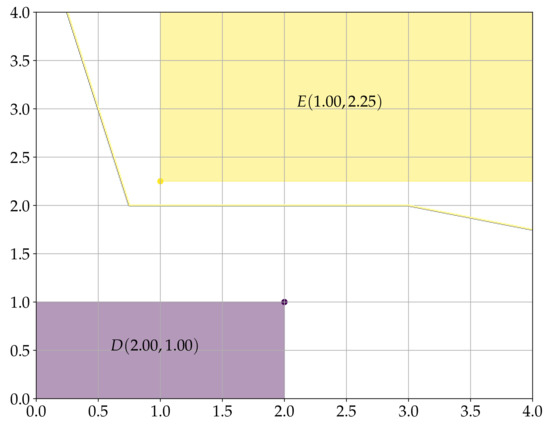
Figure 1.
The purple and the yellow regions corresponds respectively to the sets and . The piece-wise linear curve corresponds to the decision boundary of the DEP classifier with .
In the previous paragraph, we pointed out that erosion-based and dilation-based morphological perceptrons focus respectively on the positive and the negative classes. The dilation-erosion perceptron (DEP) proposed by Araújo allows a graceful balance between the two classes [40]. The dilation-erosion perceptron is simply a convex combination of an erosion-based and a dilation-based morphological perceptron. In mathematical terms, given and , the decision function of a DEP classifier is defined by
The binary DEP classifier is defined by the composition
In other words, given and , the class of an unknown pattern is determined by evaluating .
Note that given by (18) corresponds respectively to and when and . More generally, the parameter controls the trade off between the dilation-based and the erosion-based morphological perceptrons, which focus on negative and positive classes, respectively. For illustrative purposes, the decision boundary of a DEP classifier obtained by considering , and is depicted in Figure 1. In this case, the decision boundary of the DEP classifier is closer to the decision boundary of than that of . We address a good choice of the parameter of a DEP classifier in the following subsection. In the following subsection we also review the elegant convex-concave procedure proposed recently by Charisopoulus and Maragos to train the morphological perceptrons and [46].
3.2. Convex-Concave Procedure for Training Morphological Perceptron
In analogy to the soft-margin support vector classifier, the weights of a morphological perceptron can be determined by solving a convex-concave optimization problem [46,47]. Precisely, consider a training set , where is a training pattern and is its binary class label for . To simplify the exposition, let and denote respectively the sets of negative and positive training patterns, that is,
In addition, let be the decision function of either an erosion-based or a dilation-based morphological perceptron. In other words, let with or with . The vector of either or is defined as the solution of the following convex-concave optimization problem:
where C is a regularization parameter, is a reference value for , and are slack variable and and are their penalty weights. As usual, and denote the cardinality of and , respectively. Different from the procedure proposed by Charisopoulos and Maragos [46], the convex-concave optimization problem proposed in this paper includes the regularization term in the objective function.
The slack variables and measure the classification error of negative and positive training patterns weighted by and , respectively. Indeed, the objective function is minimized when all slack variables are non-positive, that is, and for all index i. On the one hand, a negative training pattern is mis-classified if . From (22), however, we have and, therefore, the objective function is not minimized. On the other hand, if a positive training pattern is mis-classified then . Equivalently, and, again, the objective is not minimized.
The slack variable penalty weights ’s have been introduced to deal with the presence of outliers. The following presents a simple weighting scheme proposed by Charisopoulus and Maragos to penalizes training patterns with greater chances of being outliers [46]. Let and be the mean of the negative and positive training patterns, that is,
In addition, let and be the reciprocal of the distance between and either the mean or . In mathematical terms, define
Finally, the slack variable weights and are obtained by scaling and to the interval as follows for all indexed i:
As to the reference, we recommend respectively and for the synaptic weights and . In this case, and classify correctly the largest possible number of negative and positive training patterns, respectively. In addition, we recommend a small regularization parameter C so that the objective is dominated by the classification error measured by the slack variables. Although in our computational implementation we adopted , we recommend to fine tune this hyper-parameter using, for example, exhaustive search or a randomized parameter optimization strategy [63].
Finally, we propose to train a DEP classifier using a greedy algorithm. Intuitively, the greedy algorithm first finds the best erosion-based and the best dilation-based morphological perceptrons and then it seeks for their best convex combination. Formally, we first solve two independent convex-concave optimization problems formulated using (21)–(23), one to determine the synaptic weight of the erosion-based morphological perceptron and the other to compute of the dilation-based morphological perceptron . Subsequently, we determine the parameter by minimizing the average hinge loss. In mathematical terms, is obtained by solving the constrained convex problem:
Remark 3.
In our computational experiments, we solved the optimization problem (21)–(23) using CVXOPT python package with the DCCP extension for convex-concave programing [47] and the MOSEK solver. Further information on the MOSEK software package can be obtained on www.mosek.com. The source-code of the DEP classifier, trained using convex-concave programming and compatible with the scikit-learn API, is available at https://github.com/mevalle/r-DEP-Classifier.
Example 4
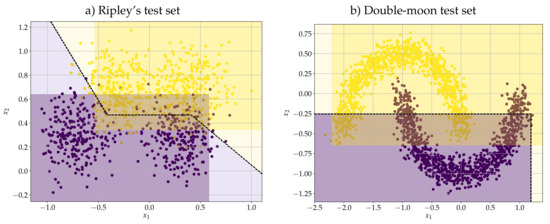
(Ripley Dataset). To illustrate how the DEP classifier works, let us consider the synthetic two-class dataset of Ripley, which is already split into training and test sets [64]. We would like to recall that each class of Ripley’s synthetic dataset has a known bimodal distribution and the best accuracy score is approximately 0.92. Using the training set with 250 samples, the convex-concave procedure yielded the synaptic weight vectors and for and , respectively. Moreover, the convex optimization problem given by (27) yielded the parameter . The accuracy score on the training and test set was respectively and . Figure 2a) shows the scatter plot of the test set along with the decision boundary of the DEP classifier. This figure also depicts the regions and for the erosion-based and dilation-based morphological perceptrons.

Figure 2.
Performance of the dilation-erosion perceptron (DEP) classifier on Ripley’s and double-moon datasets described on Examples 4 and 5. Scatter plot of test data and the decision boundary of DEP classifier. The purple and the yellow regions corresponds respectively to the sets and .
Example 5
(Double-Moon). In analogy to Haykin’s dooble-moon classification problem, this problem consists of two interleaving half circles which resembles a pair of “moons” facing each other [56]. Using the command make_moons from python’s scikit-learn API, we generated training and test sets with 1000 and 2000 pairs of data, respectively. Furthermore, we corrupted both training and test data with Gaussian noise with standard variation . Figure 2b) shows the test data together with the decision boundary of the DEP classifier and the regions and given respectively by (17) and (16). In this example, the convex-concave procedure yielded the synaptic weight vectors and . In addition, the convex optimization problem (27) yielded , which means that the DEP classifier coincides with the dilation-based morphological perceptron . The DEP classifier yielded an accuracy score of and for training and test sets, respectively.
Despite the DEP classifier yielding satisfactory accuracy scores in test sets from the two previous examples, this classifier has a serious drawback: As a lattice-based classifier, the DEP classifier presupposes a partial ordering on the feature space as well as on the set of classes. From (14), the component-wise ordering given by (1) is adopted in the feature space while the usual total ordering of real-numbers is used to rank the class labels. Most importantly, the DEP classifier defined by the composition (19) is an increasing operator because both sgn and are increasing operators. Note that is increasing because it is the convex combination of increasing operators and .
As a consequence, the patterns from the positive class must be in general greater than the patterns from the negative class. In many practical situations, however, the component-wise ordering of the feature space is not in agreement with the natural ordering of the class labels. For example, if we invert the class labels on the synthetic dataset of Ripley, the accuracy score of the DEP classifier decreases to and for the training and test data, respectively. Similarly, the accuracy score of the DEP classifier decreases respectively to and on training and test set if we invert the class labels in the double-moon classification problem. Fortunately, we can circumvent this drawback through the use of dendrite computations [37], morphological competitive units [34], or hybrid morphological/linear neural networks [41,45]. Alternatively, we can avoid the inconsistency between the partial orderings of the feature and class spaces by making use of multi-valued mathematical morphology.
4. Reduced Dilation-Erosion Perceptron
As pointed out in the previous section, the DEP classifier is an increasing operator , where the feature space is equipped with the component-wise ordering given by (1) while the set of classes inherits the natural ordering of real-numbers. In many practical situations, however, the component-wise ordering is not appropriate for the feature space. Motivated by the developments on multi-valued MM, we propose to circumvent this drawback using reduced orderings. Precisely, we introduce the so-called reduced dilation-erosion perceptron (r-DEP) which is a reduced morphological operator derived from (19).
Formally, let us assume the feature space is a vector-valued nonempty set and let be the set of classes. In practice, the feature space is usually a subset of , but we may consider more abstract feature sets. In addition, let and be complete lattices with the component-wise ordering and the natural ordering of real numbers, respectively. Consider the DEP classifier defined by (19) for some and . Given a one-to-one mapping and a surjective mapping , from Definition 4, the mapping given by
is an r-increasing morphological operator because is increasing and the identity . holds true. Most importantly, (28) defines a binary classifier called reduced dilation-erosion perceptron (r-DEP). The decision function of the r-DEP classifier is the mapping given by
Note that the r-DEP classifier is obtained from its decision function by means of the identity .
Simply put, the decision function of an r-DEP is obtained by composing the surjective mapping and the decision function of a DEP, that is, . In other words, is obtained by applying sequentially the transformation and . Thus, given a training set , we simply train a DEP classifier using the transformed training data
Then, the classification of an unknown pattern is achieved by computing .
The major challenge for the design of a successful r-DEP classifier is how to determine the surjective mapping . Intuitively, the mapping performs a kind of dimensionality reduction which takes into account the lattice structure of patterns and labels. In this paper, we propose to determine in a supervised manner. Specifically, based on the successful supervised reduced orderings proposed by Velasco-Forero and Angulo [33], we define using the decision function of support vector classifiers.
Formally, consider a training set , where and . The mapping is obtained by setting and . The mapping is defined in a component-wise manner by means of the equation , where are the decision functions of distinct support vector classifiers. Recall that the decision function of a support vector classifier is given by (8). Moreover, the distinct support vector classifiers can be determined using either one of the following approaches referred to as ensemble and bagging:
- Ensemble: The support vector classifiers are determined using the whole training set but they have different kernels.
- Bagging: The support vector classifiers have the same kernel and parameters but they are trained using different samples of the training set .
The following examples, based on Ripley’s and double-moon datasets, illustrate the transformation provided by these two approaches. The following examples also address the performance of the r-DEP classifier.
Example 6
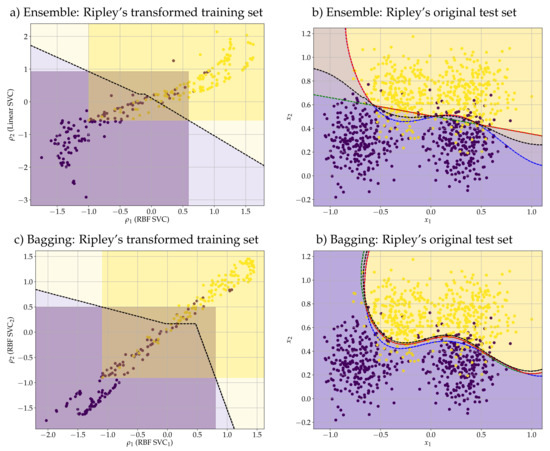

(Ripley’s Dataset). Consider the synthetic dataset of Ripley [64]. Using the Gaussian radial basis function (RBF SVC) and the linear SVC (Linear SVC), both with the default parameters of python’s scikit-learn API, we determined the reduced mapping ρ from the training data. Figure 3a) shows the scatter plot of the transformed training set given by (30). Figure 3a) also shows the regions and and the decision boundary (black-dashed-line) of the DEP classifier on the transformed space. In this example, the convex-concave optimization problem given by (21)–(23) and the minimization of the hinge loss (27) yielded , , and . Figure 3b) shows the decision boundary of the ensemble r-DEP classifier (black) on the original space together with the scatter plot of the original test set. For comparison purposes, Figure 3b) also shows the decision boundary of the RBF-SVC (blue), linear SVC (green), and the hard-voting classifier (red) obtained using the RBF and linear SVCs. Table 1 contains the accuracy score (between 0 and 1) of each of the classifiers on both training and test sets. Note that the greatest accuracy scores on the test set have been achieved by the r-DEP and the RBF-SVC classifiers. In particular, the r-DEP classifier outperformed the hard-voting ensemble classifier in this example.

Figure 3.
Performance of ensemble and bagging reduced dilation-erosion (r-DEP) classifiers on Ripley’s dataset (see Example 6). (a) and (c) show the scatter plot of transformed training data, the regions and , and the decision boundary of the DEP classifier. (b) and (d
) depict the scatter plot of the original test data and the decision boundary of r-DEP (black) and other binary classifiers.

Table 1.
Accuracy score of the classifiers considered in Example 6 on Ripley’s dataset.
Similarly, we determined the mapping ρ using a bagging of two distinct RBF SVCs trained with different samplings of the original training set. Precisely, we used the default parameters of a bagging classifier (BaggingClassifier) of the scikit-learn but with only two esmitamtors (n_estimators=2) for a visual interpretation of the transformed data. Figure 3c) shows the scatter plot of the training data along with the regions and . In this example, the optimization problem (27) yielded . Figure 3d) shows the scatter plot of the original data and the decision boundaries of the classifiers: bagging r-DEP (black), RBF SVC (blue), RBF SVC (green), and the bagging of the two RBF SVCs (red). Table 1 contains the accuracy score of these four classifiers on both training and test data. Although the RBF SVC yielded the greatest accuracy score in the test set, the bagging r-DEP produced the largest accuracy on the training set. In general, however, the four classifiers are competitive.
Example 7
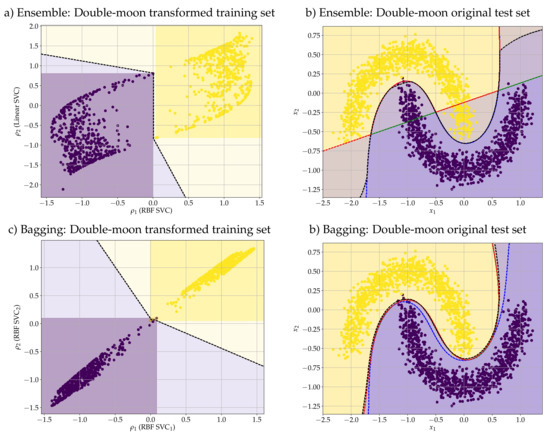

(Double-Moon). In analogy to the previous example, we also evaluated the performance of the r-DEP classifier on the double-moon problem presented in Example 5. Figure 4a,c) show the transformed training set obtained from the mappings determined using the ensemble and bagging strategies, respectively. We considered again a Gaussian RBF and a linear SVC in the ensemble strategy and two Gaussian RBF SVCs for the bagging. In addition, we adopted the default parameters of python’s scikit-learn API except for the number of estimators in the bagging strategy which we set to two (n_estimators = 2) for a visual interpretation of the transformed data. Figure 4b) shows the scatter plot of the original test set with the decision boundaries of the ensemble r-DEP (black), RBF SVC (blue), linear SVC (green), and the hard-voting ensemble classifier (red). Similarly, Figure 4d) shows the test data with the decision boundary of the bagging r-DEP (black), RBF SVC (blue), RBF SVC (green), and the bagging classifier (red). Table 2 lists the accuracy score (between 0 and 1) of all the classifiers on both training and test sets of the double-moon problem. As expected, the linear SVC yielded the worst perforamnce. The largest scores have been achieved by both ensemble and bagging r-DEP as well as the Gaussian RBF SVCs and their bagging.

Figure 4.
Performance of the ensemble r-DEP classifier on double-moon datasets described on Example 7. (a) and (c) show the scatter plot of transformed training data, the regions and , and the decision boundary of the DEP classifier. (b) and (d) depict the scatter plot of the original test data and the decision boundary of r-DEP (black) and other binary classifiers.

Table 2.
Accuracy score of the classifiers considered in Example 7 on double-moon problem.
We would like to point out that, in contrast to the original DEP classifier, the perforamance of the r-DEP model remains high if we change the pattern labels. In the following section we provide more conclusive computational experiments concerning the performance of r-DEP for binary classification.
5. Computational Experiments
Let us now provide extensive computational experiments to evaluate the performance of the ensemble and bagging r-DEP classifiers. In the ensemble strategy, the mapping is obtained by considering a RBF SVC, a linear SVC, and a polynomial SVC. The bagging strategy consists of 10 RBF SVCs where each base estimator has been trained using a sampling of the original training set with replacement. Let us also compare the new r-DEP classifiers with the original DEP classifier, linear SVC, RBF SVC, the polynomial SVC (poly SVC) as well as an ensemble of the three SVCs and a bagging of RBF SVCs. We would like to point out that we used the default parameters of the python’s scikit-learn API in our computational experiments [65,66].
We considered a total of 30 binary classification problems from the OpenML repository available at https://www.openml.org/ [48]. We would like to point out that most datasets we considered are also available at the well-known UCI machine learning repository [50]. We used the OpenML repository because all the datasets can be accessed by means of the command fetch_openml from python’s scikit-learn [65]. Moreover, we handled missing data using the SimpleImputer command, also from scikit-learn. Table 3 lists the 30 datasets considered. Table 3 also include the number of instances (#instances), the number of features (#features), the percentage of the negative and positive patterns, denoted by the pair , and the OpenML name/version.

Table 3.
Informations on the considered datasets.
Note that the number of samples ranges from 200 (Arsene) to 14,980 (Egg-Eye-State) while the number of features varies from 2 (Banana) to 10,000 (Arsene). Furthermore, some datasets such as the Sick and Toracic Surgery are extremely unbalanced. Therefore, we used the balanced accuracy score, which ranges from 0 to 1, to measure the performance of a classifier [67]. Table 4 contain the mean and standard deviation of the balanced accuracy score obtained using a stratified 10-fold cross-validation. The largest mean score for each dataset have been typed using boldface.

Table 4.
Average and standard deviation of the balanced accuracy scores obtained from the classifiers using stratified 10-fold cross-validation. The largest average score for each dataset have been typed using boldface.
We would like to point out that, to avoid biases, we used the same training and test partition for all the classifiers. In addition, we pre-processed the data using the command StandardScaler from scikit-learn, that is, we computed the mean and the standard deviation of each feature on the training set and normalized both training and test sets using the obtained values. The StandardScaler transformation has also been applied on the output of the mapping. The source-code of the computational experiment is available at https://github.com/mevalle/r-DEP-Classifier.
From Table 4, the largest average of the balanced accuracy scores have been achieved by the ensemble and bagging r-DEP classifiers. Using paired Student’s t-test with confidence level at 99%, we confirmed that the ensemble and bagging r-DEP, in general, performed better than the other classifiers. In fact, Figure 5 shows the Hasse diagram of the outcome of paired hypothesis tests [68,69]. Specifically, an edge in this diagram means that the hypothesis test discarded the null hypothesis that the classifier on the top yielded balanced accuracy score less than or equal to the classifier on the bottom. For example, Student’s t-test discarded the null hypothesis that the ensemble r-DEP classifier performs as well as or worst than the hard-voting ensemble of SVCs. In other words, the ensemble r-DEP statistically outperformed the ensemble of SVCs. Concluding, in Figure 5, the method on the top of an edge statistically outperformed the method on the bottom.
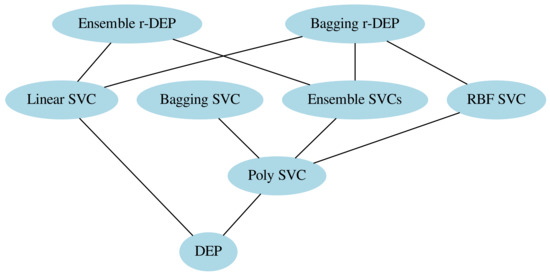
Figure 5.
Hasse diagram of paired Student’s t-test with confidence level at 99%.
The outcome of the computational experiment is also summarized on the boxplot shown on Figure 6. The boxplot confirms that the ensemble and bagging r-DEP classifiers yielded, in general, the largest balanced accuracy scores. This boxplot also reveals the poor performance of the DEP classifier which presupposes the positive samples are, in general, greater than or equal to the negative samples according to the component-wise ordering. In particular, the three points above the box of the DEP classifier corresponds to the average balanced accuracy score values 0.90, 0.88, and 0.77 obtained from the datasets Ionosphere, Breast Cancer Wisconsin, and Internet Advertisement, respectively. It turns out, however, that the ensemble and bagging r-DEP classifiers outperformed the original DEP model even in these three datasets. This remark confirms the important role of the transformations and for successful applications of increasing lattice-based models.
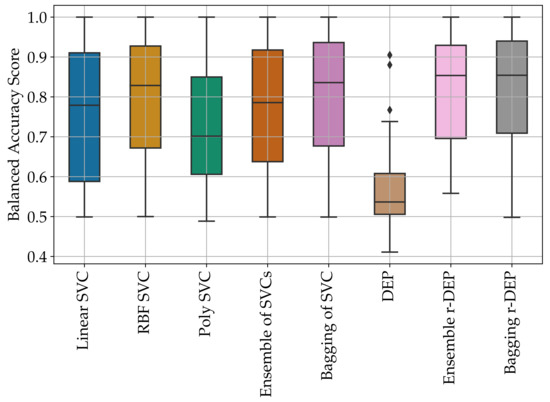
Figure 6.
Boxplot summarizing the average balanced accuracy scores provided on Table 4. In general, the ensemble and bagging r-DEP classifiers yielded largest balanced accuracy scores.
6. Concluding Remarks
In analogy to Rosemblatt’s perceptron, the morphological perceptron introduced by Ritter and Sussner can be applied for binary classification [35]. In contrast to the traditional perceptron, however, the usual algebra is replaced by lattice-based operations in the morphological perceptron models. Specifically, the erosion-based and the dilation-based morphological perceptrons compute respectively an erosion and a dilation given by (3) followed by the application of the sign function. The erosion-based and dilation-based morfological perceptrons focus respectively on the positive and negative classes. A graceful balance between the two morphological perceptrons is provided by the dilation-erosion perceptron (DEP) classifier whose decision function given by (18) is nothing but a linear combination of the an erosion and a dilation [40].
In this paper, we propose to train a DEP classifier in two steps. First, based on the works of Charisopoulus and Maragos [46], the synaptic weights and of and are determined by solving two independent convex-concave optimization problems given by (21)–(23) [47]. Subsequently, the parameter is determined by minimizing the hinge loss given by (27).
Despite its elegant formulation, as a lattice-based model the DEP classifier presupposes that both feature and class spaces are partially ordered sets. The feature patterns, in particular, are ranked according to the component-wise ordering given by (1). Furthermore, the DEP classifier is an increasing operator. Therefore, it implicitly assumes a relationship between the orderings of features and classes. In many practical situations, however, the component-wise ordering is not appropriate for ranking features. Using results from multi-valued mathematical mophology, in this paper we introduced the reduced dilation-erosion perceptron (r-DEP) classifier. The r-DEP classifier corresponds to the r-increasing morphological operator derived from the DEP classifier by means of (28) using a one-to-one correspondence between the set of classes and and a surjective mapping from the feature space to . Finding appropriate transformation mapping is the major challenge on the design of an r-DEP classifier.
Inspired by the supervised reduced ordering proposed by Velasco-Forero and Angulo [33], we defined the transformation mapping using the decision functions of either an ensemble of SVCs with different kernels or a bagging of a base SVC trained using different samples of the original traning set. The source-codes of the ensemble and bagging r-DEP classifiers are available at https://github.com/mevalle/r-DEP-Classifier. Both ensemble and bagging r-DEP classifiers yielded the highest average of the balanced accuracy score among SVCs, their ensemble, and bagging of RBF SVCs, on 30 binary classification problems from the OpenML repository. Furthermore, paired Student’s t-test with significance level at confirmed that the bagging r-DEP classifier outperformed the individual SVCs as well as their ensemble in our computational experiment. The outcome of the computational experiment shows the potential application of the ensemble and bagging r-DEP classifier on practical pattern recognition problems including—but not limited to—credit card fraud detection or medical diagnosis. Moreover, although we only focused on binary classification, multi-class problems can be addressed using one-against-one or one-against-all strategies available, for instance, in the scikit-learn API.
In the future, we plan to investigate further the approaches used to determine the mapping . We also intent to study in details the optimization problem used to train a r-DEP classifier.
Funding
This research was funded by the São Paulo Research Foundation (FAPESP) under grant number 2019/02278-2 and the National Council for Scientific and Technological Development (CNPq) under grant number 310118/2017-4.
Conflicts of Interest
The author declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Lee, E.A. Cyber Physical Systems: Design Challenges. In Proceedings of the 2008 11th IEEE International Symposium on Object and Component-Oriented Real-Time Distributed Computing (ISORC), Orlando, FL, USA, 5–7 May 2008; pp. 363–369. [Google Scholar]
- Rajkumar, R.; Lee, I.; Sha, L.; Stankovic, J. Cyber-physical systems: The next computing revolution. In Proceedings of the Design Automation Conference, Anaheim, CA, USA, 13–18 June 2010; pp. 731–736. [Google Scholar]
- Shi, J.; Wan, J.; Yan, H.; Suo, H. A survey of Cyber-Physical Systems. In Proceedings of the 2011 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 9–11 November 2011; pp. 1–6. [Google Scholar]
- Derler, P.; Lee, E.A.; Sangiovanni Vincentelli, A. Modeling Cyber–Physical Systems. Proc. IEEE 2012, 100, 13–28. [Google Scholar] [CrossRef]
- Stojmenovic, I.; Zhang, F. Inaugural issue of ‘cyber-physical systems’. Cyber-Phys. Syst. 2015, 1, 1–4. [Google Scholar] [CrossRef][Green Version]
- Oztemel, E.; Gursev, S. Literature review of Industry 4.0 and related technologies. J. Intell. Manuf. 2020, 31, 127–182. [Google Scholar] [CrossRef]
- Pachidis, T.; Vrochidou, E.; Kaburlasos, V.G.; Kostova, S.; Bonković, M.; Papić, V. Social Robotics in Education: State-of-the-Art and Directions. In Advances in Service and Industrial Robotics; Aspragathos, N.A., Koustoumpardis, P.N., Moulianitis, V.C., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; Volume 67, pp. 689–700. [Google Scholar]
- Zhang, Y.; Qiu, M.; Tsai, C.; Hassan, M.M.; Alamri, A. Health-CPS: Healthcare Cyber-Physical System Assisted by Cloud and Big Data. IEEE Syst. J. 2017, 11, 88–95. [Google Scholar] [CrossRef]
- Kaburlasos, V.G. Towards a Unified Modeling and Knowledge-Representation Based on Lattice Theory; Computational Intelligence and Soft Computing Applications Series (Studies in Computational Intelligence); Springer: Secaucus, NJ, USA, 2006; Volume 27. [Google Scholar]
- Kaburlasos, V.; Ritter, G. (Eds.) Computational Intelligence Based on Lattice Theory; Springer: Heidelberg, Germany, 2007. [Google Scholar]
- Birkhoff, G. Lattice Theory, 3rd ed.; American Mathematical Society: Providence, RI, USA, 1993. [Google Scholar]
- Skowron, A.; Stepaniuk, J. Information granules: Towards foundations of granular computing. Int. J. Intell. Syst. 2001, 16, 57–85. [Google Scholar] [CrossRef]
- Yao, J.T.; Vasilakos, A.V.; Pedrycz, W. Granular Computing: Perspectives and Challenges. IEEE Trans. Cybern. 2013, 43, 1977–1989. [Google Scholar] [CrossRef] [PubMed]
- Serra, J. Image Analysis and Mathematical Morphology; Academic Press: London, UK, 1982. [Google Scholar]
- Serra, J. Image Analysis and Mathematical Morphology, Volume 2: Theoretical Advances; Academic Press: New York, NY, USA, 1988. [Google Scholar]
- Soille, P. Morphological Image Analysis; Springer: Berlin, Germany, 1999. [Google Scholar]
- Najman, L.; Talbot, H. (Eds.) Mathematical Morphology: From Theory to Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Sternberg, S. Grayscale Morphology. Comput. Vis. Graph. Image Process. 1986, 35, 333–355. [Google Scholar] [CrossRef]
- Nachtegael, M.; Kerre, E.E. Connections between binary, gray-scale and fuzzy mathematical morphologies. Fuzzy Sets Syst. 2001, 124, 73–85. [Google Scholar] [CrossRef]
- Sussner, P.; Valle, M.E. Classification of Fuzzy Mathematical Morphologies Based on Concepts of Inclusion Measure and Duality. J. Math. Imaging Vis. 2008, 32, 139–159. [Google Scholar] [CrossRef]
- Ronse, C. Why Mathematical Morphology Needs Complete Lattices. Signal Process. 1990, 21, 129–154. [Google Scholar] [CrossRef]
- Nachtegael, M.; Sussner, P.; Mélange, T.; Kerre, E. On the role of complete lattices in mathematical morphology: From tool to uncertainty model. Inf. Sci. 2011, 181, 1971–1988. [Google Scholar] [CrossRef]
- Heijmans, H. Morphological Image Operators; Academic Press: New York, NY, USA, 1994. [Google Scholar]
- Heijmans, H.J.A.M. Mathematical Morphology: A Modern Approach in Image Processing Based on Algebra and Geometry. SIAM Rev. 1995, 37, 1–36. [Google Scholar] [CrossRef]
- Soille, P.; Beucher, S.; Rivest, J.F. Morphological gradients. J. Electron. Imaging 1993, 2, 326–336. [Google Scholar] [CrossRef]
- Angulo, J. Morphological colour operators in totally ordered lattices based on distances: Application to image filtering, enhancement and analysis. Comput. Vis. Image Underst. 2007, 107, 56–73. [Google Scholar] [CrossRef]
- Aptoula, E.; Lefèvre, S. A Comparative Study on Multivariate Mathematical Morphology. Pattern Recognit. 2007, 40, 2914–2929. [Google Scholar] [CrossRef]
- Burgeth, B.; Kleefeld, A. An approach to color-morphology based on Einstein addition and Loewner order. Pattern Recognit. Lett. 2014, 47, 29–39. [Google Scholar] [CrossRef]
- Burgeth, B.; Didas, S.; Kleefeld, A. A Unified Approach to the Processing of Hyperspectral Images. In Mathematical Morphology and Its Applications to Signal and Image Processing; Burgeth, B., Kleefeld, A., Naegel, B., Passat, N., Perret, B., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 202–214. [Google Scholar]
- Lézoray, O. Complete lattice learning for multivariate mathematical morphology. J. Vis. Commun. Image Represent. 2016, 35, 220–235. [Google Scholar] [CrossRef]
- Sangalli, M.; Valle, M.E. Approaches to Multivalued Mathematical Morphology Based on Uncertain Reduced Orderings. Mathematical Morphology and Its Applications to Signal and Image Processing; Burgeth, B., Kleefeld, A., Naegel, B., Passat, N., Perret, B., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 228–240. [Google Scholar]
- Velasco-Forero, S.; Angulo, J. Vector Ordering and Multispectral Morphological Image Processing. Advances in Low-Level Color Image Processing; Celebi, M.E., Smolka, B., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 223–239. [Google Scholar]
- Velasco-Forero, S.; Angulo, J. Supervised Ordering in Rp: Application to Morphological Processing of Hyperspectral Images. IEEE Trans. Image Process. 2011, 20, 3301–3308. [Google Scholar] [CrossRef]
- Sussner, P.; Esmi, E.L. Morphological Perceptrons with Competitive Learning: Lattice-Theoretical Framework and Constructive Learning Algorithm. Inf. Sci. 2011, 181, 1929–1950. [Google Scholar] [CrossRef]
- Ritter, G.X.; Sussner, P. An Introduction to Morphological Neural Networks. In Proceedings of the 13th International Conference on Pattern Recognition, Vienna, Austria, 25–29 August 1996; pp. 709–717. [Google Scholar]
- Sussner, P. Kernels for Morphological Associative Memories. In Proceedings of the International ICSA/IFAC Symposium on Neural Computation, Vienna, Austria, 23–25 September 1998; pp. 79–85. [Google Scholar]
- Ritter, G.X.; Urcid, G. Lattice Algebra Approach to Single-Neuron Computation. IEEE Trans. Neural Netw. 2003, 14, 282–295. [Google Scholar] [CrossRef]
- Sussner, P.; Esmi, E.L. Introduction to Morphological Perceptrons with Competitive Learning. In Proceedings of the International Joint Conference on Neural Networks 2009, Atlanta, GA, USA, 14–19 June 2009; pp. 3024–3031. [Google Scholar]
- Pessoa, L.; Maragos, P. Neural networks with hybrid morphological/rank/linear nodes: a unifying framework with applications to handwritten character recognition. Pattern Recognit. 2000, 33, 945–960. [Google Scholar] [CrossRef]
- Araújo, R.D.A. A class of hybrid morphological perceptrons with application in time series forecasting. Knowl.-Based Syst. 2011, 24, 513–529. [Google Scholar]
- Hernández, G.; Zamora, E.; Sossa, H.; Téllez, G.; Furlán, F. Hybrid neural networks for big data classification. Neurocomputing 2019. [Google Scholar] [CrossRef]
- Mondal, R.; Santra, S.; Chanda, B. Dense Morphological Network: An Universal Function Approximator. arXiv, 2019; arXiv:1901.00109. [Google Scholar]
- Franchi, G.; Fehri, A.; Yao, A. Deep morphological networks. Pattern Recognit. 2020, 102, 107246. [Google Scholar] [CrossRef]
- Arce, F.; Zamora, E.; Sossa, H.; Barrón, R. Differential evolution training algorithm for dendrite morphological neural networks. Appl. Soft Comput. 2018, 68, 303–313. [Google Scholar] [CrossRef]
- Sussner, P.; Campiotti, I. Extreme learning machine for a new hybrid morphological/linear perceptron. Neural Netw. 2020, 123, 288–298. [Google Scholar] [CrossRef]
- Charisopoulos, V.; Maragos, P. Morphological Perceptrons: Geometry and Training Algorithms. In Mathematical Morphology and Its Applications to Signal and Image Processing; Angulo, J., Velasco-Forero, S., Meyer, F., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 3–15. [Google Scholar]
- Shen, X.; Diamond, S.; Gu, Y.; Boyd, S. Disciplined convex-concave programming. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 1009–1014. [Google Scholar]
- Vanschoren, J.; van Rijn, J.N.; Bischl, B.; Torgo, L. OpenML: Networked Science in Machine Learning. SIGKDD Explor. 2013, 15, 49–60. [Google Scholar] [CrossRef]
- Feurer, M.; van Rijn, J.N.; Kadra, A.; Gijsbers, P.; Mallik, N.; Ravi, S.; Müller, A.; Vanschoren, J.; Hutter, F. OpenML-Python: An extensible Python API for OpenML. arXiv, 2019; arXiv:1911.02490. [Google Scholar]
- UCI Repository of Machine Learning Databases. Available online: https://archive.ics.uci.edu/ (accessed on 31 March 2020).
- Heijmans, H.J.A.M.; Ronse, C. The algebraic basis of mathematical morphology I. Dilations and erosions. Comput. Vis. Graph. Image Process. 1990, 50, 245–295. [Google Scholar] [CrossRef]
- Serra, J. The “False Colour” Problem. In Mathematical Morphology and Its Application to Signal and Image Processing; Wilkinson, M.H., Roerdink, J.B., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5720, pp. 13–23. [Google Scholar]
- Goutsias, J.; Heijmans, H.J.A.M.; Sivakumar, K. Morphological Operators for Image Sequences. Comput. Vis. Image Underst. 1995, 62, 326–346. [Google Scholar] [CrossRef]
- Vapnik, V.N. Statistical Learning Theory; John Wiley and Sons: New York, NY, USA, 1998. [Google Scholar]
- Schölkopf, B.; Smola, A. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Ritter, G.X.; Sussner, P.; de Leon, J.L.D. Morphological Associative Memories. IEEE Trans. Neural Netw. 1998, 9, 281–293. [Google Scholar] [CrossRef] [PubMed]
- Ritter, G.X.; de Leon, J.L.D.; Sussner, P. Morphological Bidirectional Associative Memories. Neural Netw. 1999, 6, 851–867. [Google Scholar] [CrossRef]
- Sussner, P.; Valle, M.E. Grayscale Morphological Associative Memories. IEEE Trans. Neural Netw. 2006, 17, 559–570. [Google Scholar] [CrossRef] [PubMed]
- Valle, M.E.; Sussner, P. A General Framework for Fuzzy Morphological Associative Memories. Fuzzy Sets Syst. 2008, 159, 747–768. [Google Scholar] [CrossRef]
- Valle, M.E.; Sussner, P. Storage and Recall Capabilities of Fuzzy Morphological Associative Memories with Adjunction-Based Learning. Neural Netw. 2011, 24, 75–90. [Google Scholar] [CrossRef]
- Santos, A.S.; Valle, M.E. Max-plus and min-plus projection autoassociative morphological memories and their compositions for pattern classification. Neural Netw. 2018, 100, 84–94. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API design for machine learning software: experiences from the scikit-learn project. In Proceedings of the ECML PKDD Workshop: Languages for Data Mining and Machine Learning, Prague, Czech Republic, 23 September 2013; pp. 108–122. [Google Scholar]
- Brodersen, K.H.; Ong, C.S.; Stephan, K.E.; Buhmann, J.M. The Balanced Accuracy and Its Posterior Distribution. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 3121–3124. [Google Scholar]
- Burda, M. paircompviz: An R Package for Visualization of Multiple Pairwise Comparison Test Results. 2013. Available online: https://www.bioconductor.org/packages/release/bioc/html/paircompviz.html (accessed on 30 March 2020).
- Weise, T.; Chiong, R. An alternative way of presenting statistical test results when evaluating the performance of stochastic approaches. Neurocomputing 2015, 147, 235–238. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).