Hybridization of Multi-Objective Deterministic Particle Swarm with Derivative-Free Local Searches
Abstract
1. Introduction
2. Multi-Objective Optimization Problem Formulation and Definitions
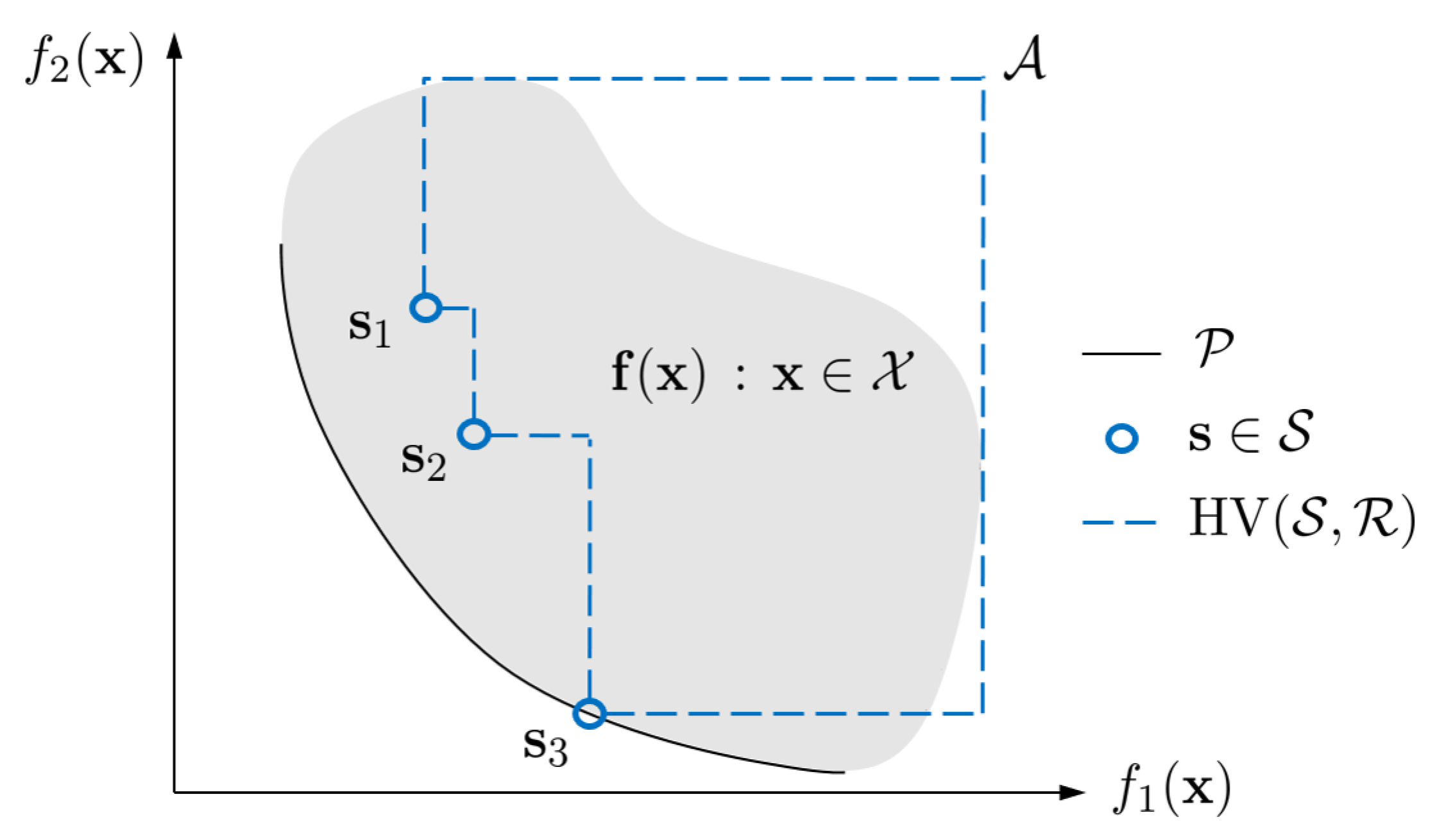
Performance Metrics
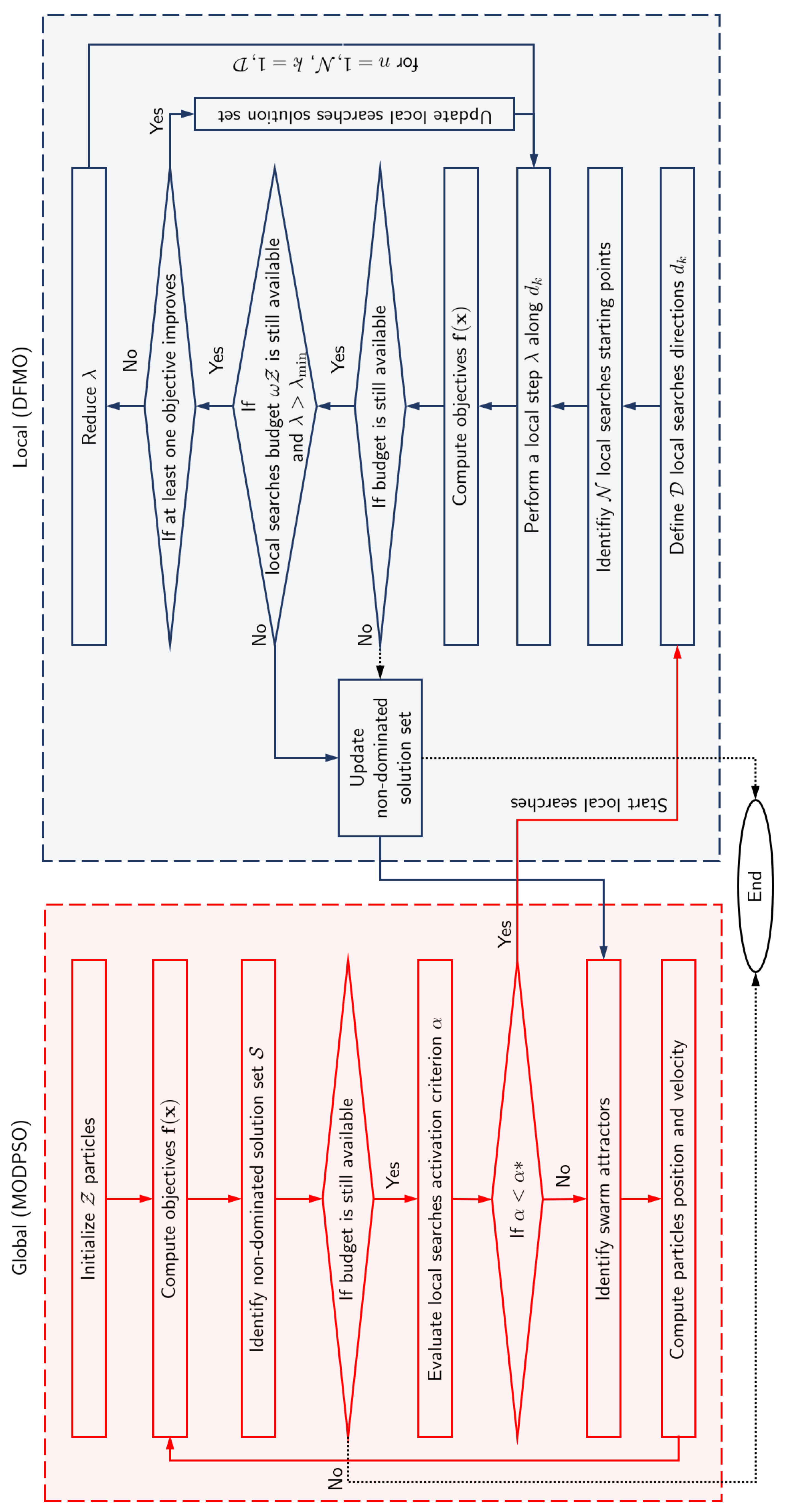
3. Multi-Objective Deterministic Hybrid Algorithm: MODHA
3.1. Multi-Objective Deterministic Particle Swarm Optimization (MODPSO)
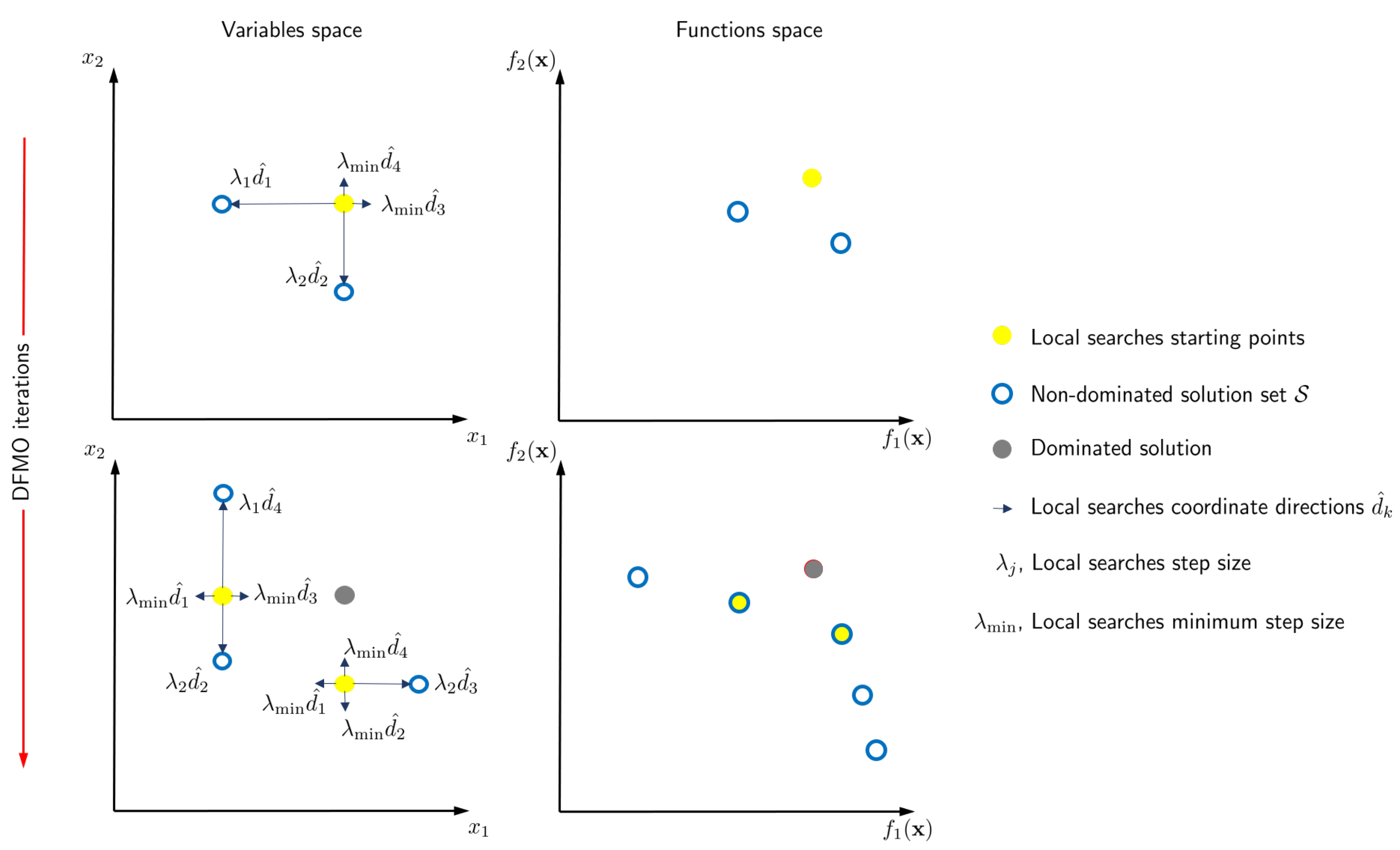
3.2. Derivative-Free Multi-Objective Local Searches (DFMO)
3.3. Hybridization Scheme
| Algorithm 1 MODHA pseudo-code. |
|
4. Analytical Test Problems
5. Simulation-Based Design Optimization Problems
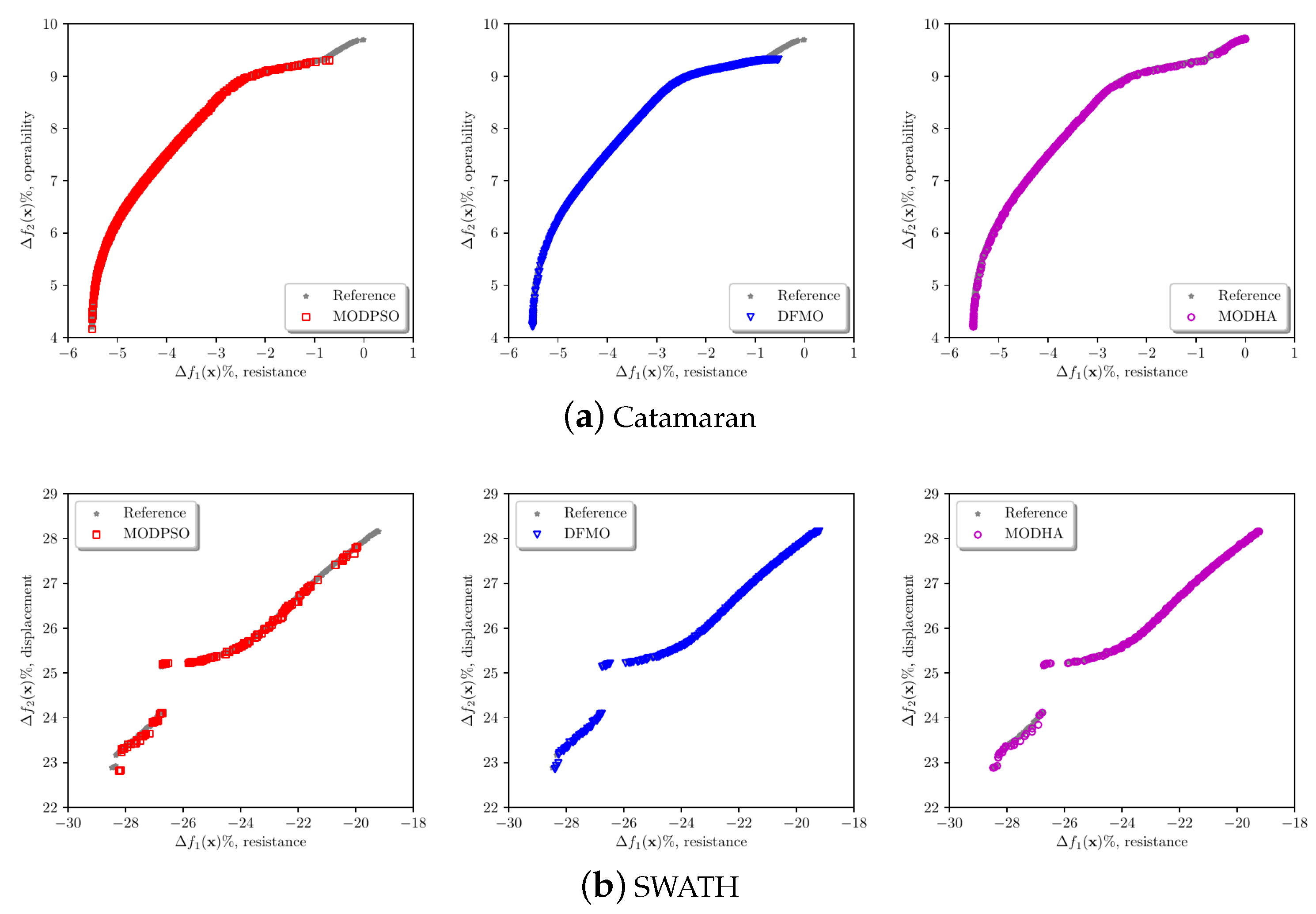
5.1. Catamaran Problem
5.2. SWATH Problem
6. Numerical Results
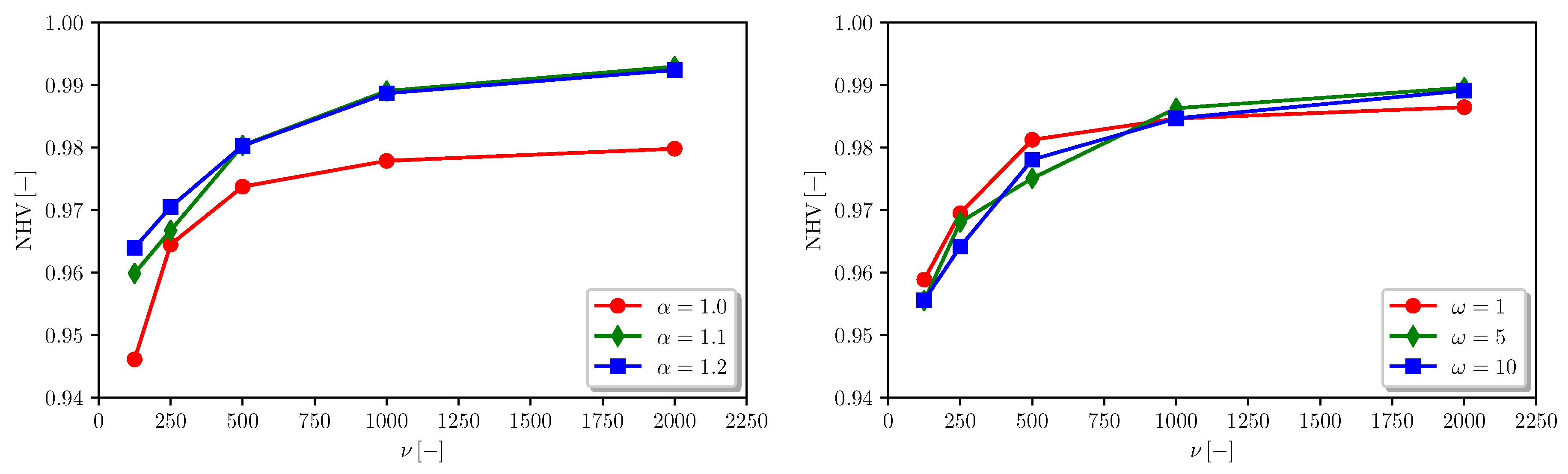
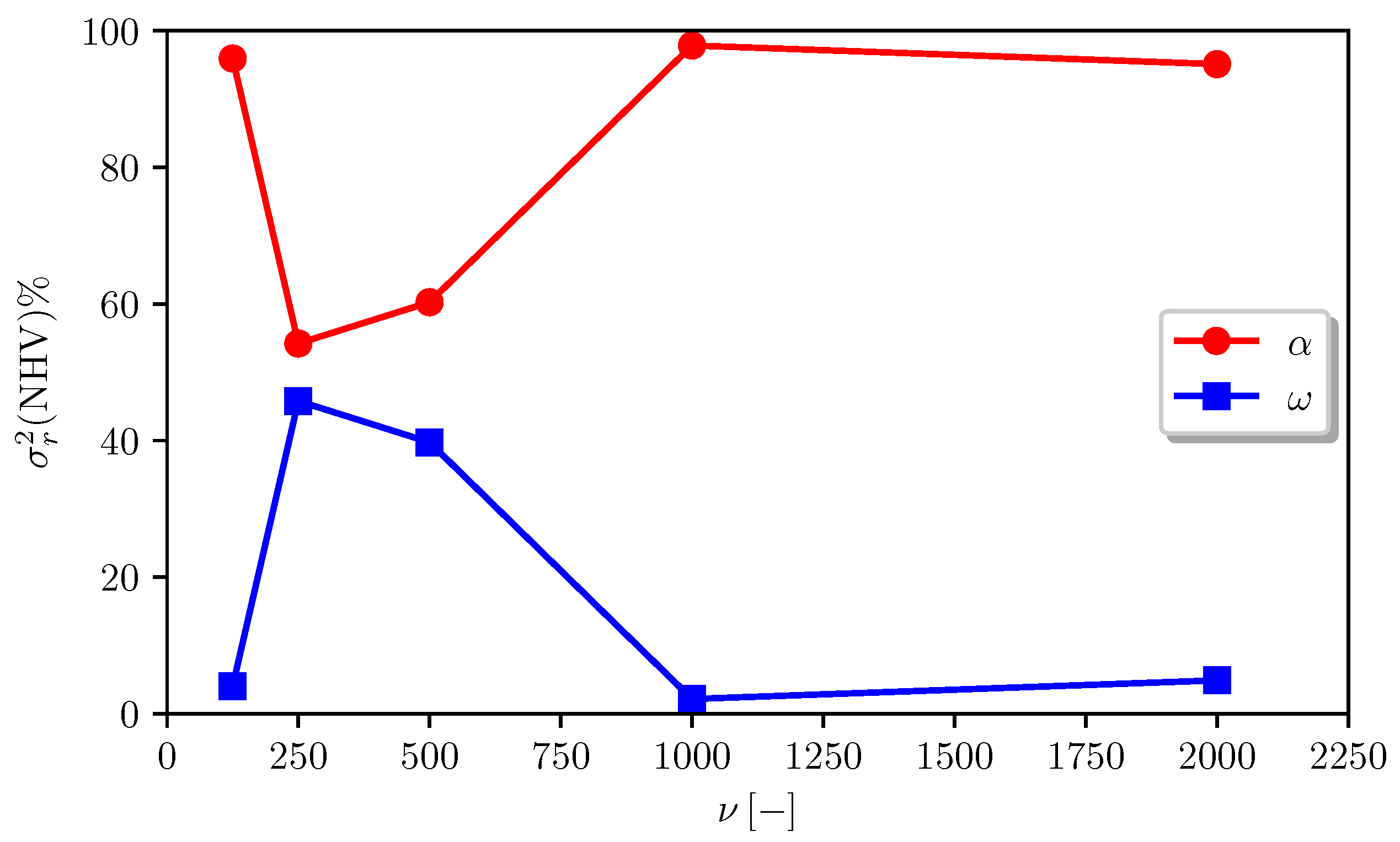
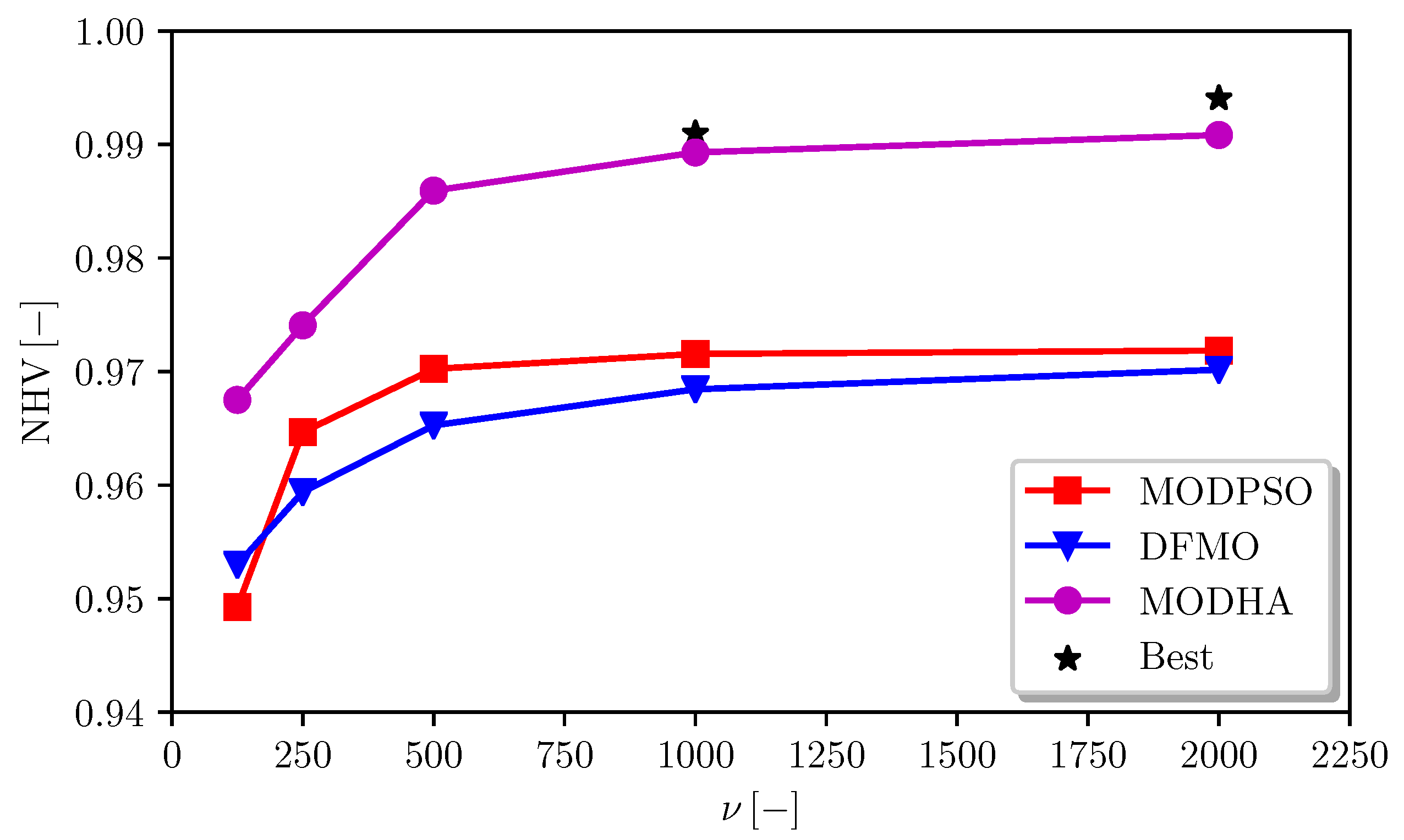
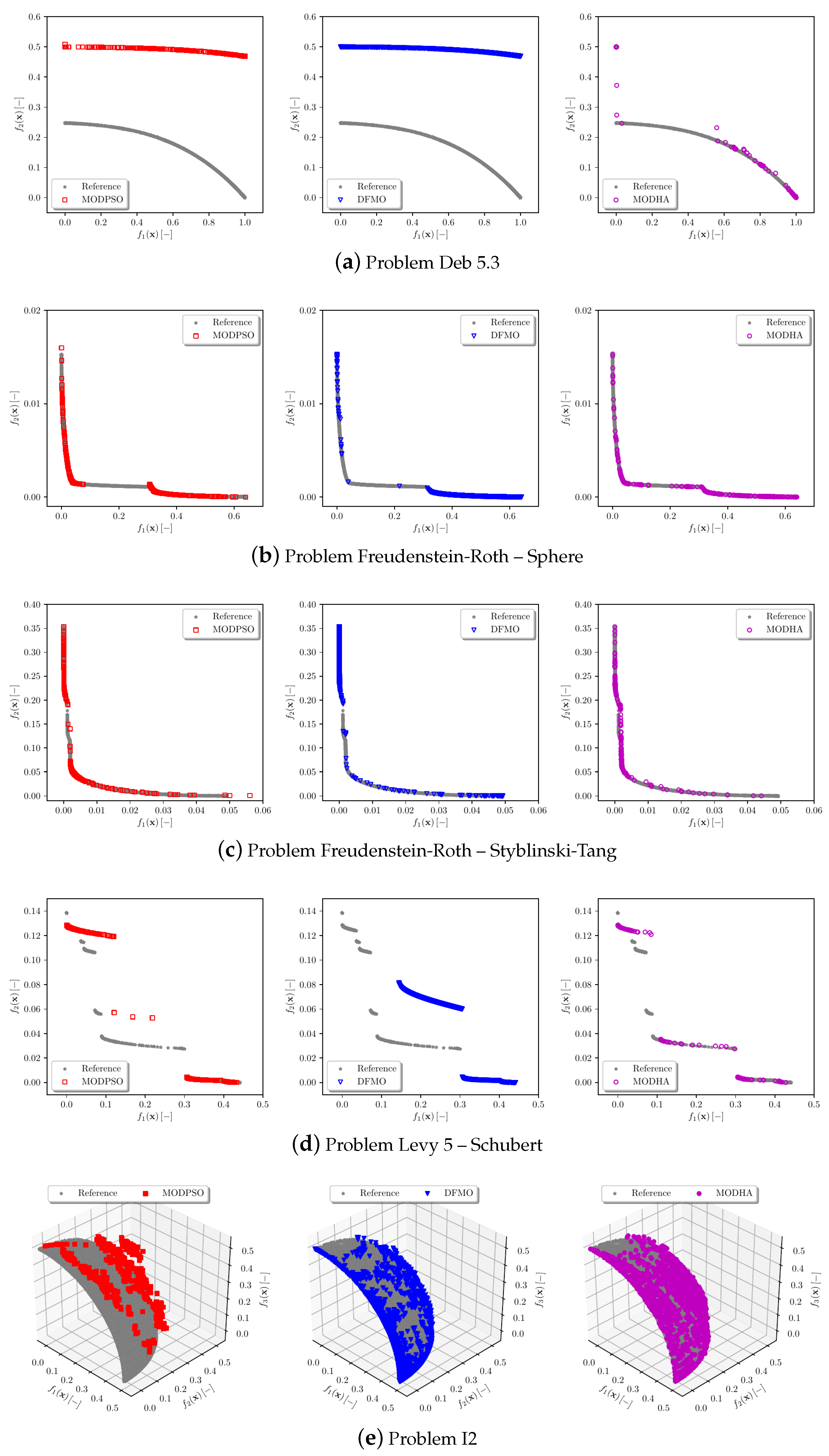
6.1. Analytical Benchmark Problems
6.2. Simulation-Based Design Optimization Problems
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Diez, M.; Campana, E.F.; Stern, F. Stochastic optimization methods for ship resistance and operational efficiency via CFD. Struct. Multidiscip. Optim. 2018, 57, 735–758. [Google Scholar] [CrossRef]
- Martins, J.R.R.A.; Lambe, A.B. Multidisciplinary design optimization: A survey of architectures. AIAA J. 2013, 51, 2049–2075. [Google Scholar] [CrossRef]
- Ehrgott, M. Multicriteria Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; Volume 491. [Google Scholar]
- Zhang, J.; Xing, L. A Survey of Multiobjective Evolutionary Algorithms. In Proceedings of the 2017 IEEE International Conference on Computational Science and Engineering (CSE) and IEEE International Conference on Embedded and Ubiquitous Computing (EUC), Guangzhou, China, 21–24 July 2017; Volume 1, pp. 93–100. [Google Scholar]
- Evtushenko, Y.G.; Posypkin, M. A deterministic algorithm for global multi-objective optimization. Optim. Methods Softw. 2014, 29, 1005–1019. [Google Scholar] [CrossRef]
- Pellegrini, R.; Serani, A.; Leotardi, C.; Iemma, U.; Campana, E.F.; Diez, M. Formulation and parameter selection of multi-objective deterministic particle swarm for simulation-based optimization. Appl. Soft Comput. 2017, 58, 714–731. [Google Scholar] [CrossRef]
- Campana, E.F.; Diez, M.; Liuzzi, G.; Lucidi, S.; Pellegrini, R.; Piccialli, V.; Rinaldi, F.; Serani, A. A multi-objective DIRECT algorithm for ship hull optimization. Comput. Optim. Appl. 2018, 71, 53–72. [Google Scholar] [CrossRef]
- Larson, J.; Menickelly, M.; Wild, S.M. Derivative-free optimization methods. Acta Numer. 2019, 28, 287–404. [Google Scholar] [CrossRef]
- Serani, A.; Fasano, G.; Liuzzi, G.; Lucidi, S.; Iemma, U.; Campana, E.F.; Stern, F.; Diez, M. Ship hydrodynamic optimization by local hybridization of deterministic derivative-free global algorithms. Appl. Ocean Res. 2016, 59, 115–128. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Połap, D.; Woźniak, M. Polar bear optimization algorithm: Meta-heuristic with fast population movement and dynamic birth and death mechanism. Symmetry 2017, 9, 203. [Google Scholar] [CrossRef]
- Serani, A.; Diez, M. Dolphin Pod Optimization: A Nature-Inspired Deterministic Algorithm for Simulation-Based Design. In Machine Learning, Optimization, and Big Data: Second International Workshop, MOD 2017, Volterra, Italy, 14–17 September 2017; Lecture Notes in Computer Science; Nicosia, G., Pardalos, P., Giuffrida, G., Umeton, R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 10710. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the Fourth IEEE Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Serani, A.; Leotardi, C.; Iemma, U.; Campana, E.F.; Fasano, G.; Diez, M. Parameter selection in synchronous and asynchronous deterministic particle swarm optimization for ship hydrodynamics problems. Appl. Soft Comput. 2016, 49, 313–334. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Hart, W.E.; Krasnogor, N.; Smith, J.E. Memetic evolutionary algorithms. In Recent Advances in Memetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2005; pp. 3–27. [Google Scholar]
- Serani, A.; Diez, M.; Campana, E.F.; Fasano, G.; Peri, D.; Iemma, U. Globally Convergent Hybridization of Particle Swarm Optimization Using Line Search-Based Derivative-Free Techniques. In Recent Advances in Swarm Intelligence and Evolutionary Computation; Yang, X.S., Ed.; Studies in Computational Intelligence; Springer International Publishing: Cham, Switzerland, 2015; Volume 585, pp. 25–47. [Google Scholar]
- Santana-Quintero, L.V.; Ramírez, N.; Coello, C.C. A multi-objective particle swarm optimizer hybridized with scatter search. In Proceedings of the Mexican International Conference on Artificial Intelligence, Apizaco, Mexico, 13–17 November 2006; pp. 294–304. [Google Scholar]
- Liu, D.; Tan, K.C.; Goh, C.K.; Ho, W.K. A multiobjective memetic algorithm based on particle swarm optimization. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2007, 37, 42–50. [Google Scholar] [CrossRef]
- Izui, K.; Nishiwaki, S.; Yoshimura, M.; Nakamura, M.; Renaud, J.E. Enhanced multiobjective particle swarm optimization in combination with adaptive weighted gradient-based searching. Eng. Optim. 2008, 40, 789–804. [Google Scholar] [CrossRef]
- Kaveh, A.; Laknejadi, K. A novel hybrid charge system search and particle swarm optimization method for multi-objective optimization. Expert Syst. Appl. 2011, 38, 15475–15488. [Google Scholar] [CrossRef]
- Mousa, A.; El-Shorbagy, M.; Abd-El-Wahed, W. Local search based hybrid particle swarm optimization algorithm for multiobjective optimization. Swarm Evol. Comput. 2012, 3, 1–14. [Google Scholar] [CrossRef]
- Xu, G.; Yang, Y.Q.; Liu, B.B.; Xu, Y.H.; Wu, A.J. An efficient hybrid multi-objective particle swarm optimization with a multi-objective dichotomy line search. J. Comput. Appl. Math. 2015, 280, 310–326. [Google Scholar] [CrossRef]
- Cheng, S.; Zhan, H.; Shu, Z. An innovative hybrid multi-objective particle swarm optimization with or without constraints handling. Appl. Soft Comput. 2016, 47, 370–388. [Google Scholar] [CrossRef]
- Qian, C.; Yu, Y.; Zhou, Z.H. Pareto Ensemble Pruning. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, AAAI’15, Austin, TX, USA, 25–30 January 2015; pp. 2935–2941. [Google Scholar]
- Qian, C.; Tang, K.; Zhou, Z.H. Selection Hyper-heuristics Can Provably Be Helpful in Evolutionary Multi-objective Optimization. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Edinburgh, UK, 17–21 September 2016; pp. 835–846. [Google Scholar]
- Pellegrini, R.; Serani, A.; Liuzzi, G.; Rinaldi, F.; Lucidi, S.; Campana, E.F.; Iemma, U.; Diez, M. Hybrid global/local derivative-free multi-objective optimization via deterministic particle swarm with local linesearch. In Machine Learning, Optimization, and Big Data: Second International Workshop, MOD 2017, Volterra, Italy, 14–17 September 2017; Nicosia, G., Pardalos, P., Giuffrida, G., Umeton, R., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2018; Volume 10710, pp. 198–209. [Google Scholar]
- Liuzzi, G.; Lucidi, S.; Rinaldi, F. A Derivative-Free Approach to Constrained Multiobjective Nonsmooth Optimization. SIAM J. Optim. 2016, 26, 2744–2774. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective optimization using evolutionary algorithms - a comparative case study. In Proceedings of the 5th Parallel Problem Solving from Nature, Amsterdam, The Netherlands, 27–30 September 1998; pp. 292–301. [Google Scholar]
- Audet, C.; Bigeon, J.; Cartier, D.; Le Digabel, S.; Salomon, L. Performance Indicators in Multiobjective Optimization. Optim. Online. 2018. Available online: http://www.optimization-online.org/DB_FILE/2018/10/6887.pdf (accessed on 7 April 2020).
- Haftka, R.T. Requirements for papers focusing on new or improved global optimization algorithms. Struct. Multidiscip. Optim. 2016, 54. [Google Scholar] [CrossRef]
- Jiang, S.; Ong, Y.S.; Zhang, J.; Feng, L. Consistencies and contradictions of performance metrics in multiobjective optimization. Cybern. IEEE Trans. 2014, 44, 2391–2404. [Google Scholar] [CrossRef] [PubMed]
- Campana, E.F.; Diez, M.; Iemma, U.; Liuzzi, G.; Lucidi, S.; Rinaldi, F.; Serani, A. Derivative-free global ship design optimization using global/local hybridization of the DIRECT algorithm. Optim. Eng. 2015, 17, 127–156. [Google Scholar] [CrossRef]
- Pinto, A.; Peri, D.; Campana, E.F. Global optimization algorithms in naval hydrodynamics. Ship Technol. Res. 2004, 51, 123–133. [Google Scholar] [CrossRef]
- Serani, A.; Diez, M. Are Random Coefficients Needed in Particle Swarm Optimization for Simulation-Based Ship Design? In Proceedings of the 7th International Conference on Computational Methods in Marine Engineering (Marine 2017), Nantes, France, 15–17 May 2017. [Google Scholar]
- Pinto, A.; Peri, D.; Campana, E.F. Multiobjective optimization of a containership using deterministic particle swarm optimization. J. Ship Res. 2007, 51, 217–228. [Google Scholar]
- Kolda, T.G.; Lewis, R.M.; Torczon, V. Optimization by direct search: New perspectives on some classical and modern methods. SIAM Rev. 2003, 45, 385–482. [Google Scholar] [CrossRef]
- Custódio, A.L.; Madeira, J.F.A.; Vaz, A.I.F.; Vicente, L.N. Direct Multisearch for Multiobjective Optimization. SIAM J. Optim. 2011, 21, 1109–1140. [Google Scholar] [CrossRef]
- Huband, S.; Hingston, P.; Barone, L.; While, L. A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans. Evol. Comput. 2006, 10, 477–506. [Google Scholar] [CrossRef]
- Fonseca, C.M.; Paquete, L.; Lòpez-Ibà nez, M. An improved dimension-sweep algorithm for the hypervolume indicator. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC’06), Vancouver, BC, Canada, 16–21 July 2006; pp. 1157–1163. [Google Scholar]
- Deb, K. Multi-objective Genetic Algorithms: Problem Difficulties and Construction of Test Problems. Evol. Comput. 1999, 7, 205–230. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable multi-objective optimization test problems. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02, Honolulu, HI, USA, 12–17 May 2002; Volume 1, pp. 825–830. [Google Scholar]
- Jin, Y.; Olhofer, M.; Sendhoff, B. Dynamic weighted aggregation for evolutionary multi-objective optimization: Why does it work and how? In Proceedings of the 3rd Annual Conference on Genetic and Evolutionary Computation, San Francisco, CA, USA, 7–11 July 2001; pp. 1042–1049. [Google Scholar]
- Lovison, A. A synthetic approach to multiobjective optimization. arXiv 2010, arXiv:1002.0093. [Google Scholar]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of Multiobjective Evolutionary Algorithms: Empirical Results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef]
- Volpi, S.; Diez, M.; Gaul, N.; Song, H.; Iemma, U.; Choi, K.K.; Campana, E.F.; Stern, F. Development and validation of a dynamic metamodel based on stochastic radial basis functions and uncertainty quantification. Struct. Multidiscip. Optim. 2015, 51, 347–368. [Google Scholar] [CrossRef]
- Huang, J.; Carrica, P.M.; Stern, F. Semi-coupled air/water immersed boundary approach for curvilinear dynamic overset grids with application to ship hydrodynamics. Int. J. Numer. Methods Fluids 2008, 58, 591–624. [Google Scholar] [CrossRef]
- Diez, M.; Campana, E.F.; Stern, F. Design-space dimensionality reduction in shape optimization by Karhunen–Loève expansion. Comput. Methods Appl. Mech. Eng. 2015, 283, 1525–1544. [Google Scholar] [CrossRef]
- He, W.; Diez, M.; Zou, Z.; Campana, E.F.; Stern, F. URANS study of Delft catamaran total/added resistance, motions and slamming loads in head sea including irregular wave and uncertainty quantification for variable regular wave and geometry. Ocean Eng. 2013, 74, 189–217. [Google Scholar] [CrossRef]
- Pellegrini, R.; Serani, A.; Broglia, R.; Diez, M.; Harries, S. Resistance and Payload Optimization of a Sea Vehicle by Adaptive Multi-Fidelity Metamodeling. In Proceedings of the 56th AIAA Aerospace Sciences Meeting, SciTech 2018, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Serani, A.; Pellegrini, R.; Wackers, J.; Jeanson, C.E.; Queutey, P.; Visonneau, M.; Diez, M. Adaptive multi-fidelity sampling for CFD-based optimisation via radial basis function metamodels. Int. J. Comput. Fluid Dyn. 2019, 33, 237–255. [Google Scholar] [CrossRef]
- Broglia, R.; Durante, D. Accurate prediction of complex free surface flow around a high speed craft using a single-phase level set method. Comput. Mech. 2018, 62, 421–437. [Google Scholar] [CrossRef]
- Bassanini, P.; Bulgarelli, U.; Campana, E.F.; Lalli, F. The wave resistance problem in a boundary integral formulation. Surv. Math. Ind. 1994, 4, 151–194. [Google Scholar]
- Pellegrini, R.; Serani, A.; Liuzzi, G.; Lucidi, S.; Rinaldi, F.; Campana, E.F.; Diez, M. Hull-form optimization via hybrid global/local multi-objective derivative-free algorithms. In Proceedings of the 21st Conference of the International Federation of Operational Research Societies, Québec City, QC, Canada, 17–21 July 2017. [Google Scholar]
- Wong, T.T.; Luk, W.S.; Heng, P.A. Sampling with Hammersley and Halton Points. J. Graph. Tools 1997, 2, 9–24. [Google Scholar] [CrossRef]
- Clerc, M. Stagnation Analysis in Particle Swarm Optimization or What Happens When Nothing Happens. Technical Report; hal-00122031. 2006. Available online: https://www.researchgate.net/publication/247636881_Stagnation_Analysis_in_Particle_Swarm_Optimisation_or_What_Happens_When_Nothing_Happens (accessed on 7 April 2020).
- Raquel, C.R.; Naval, P.C., Jr. An effective use of crowding distance in multiobjective particle swarm optimization. In Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation, Washington, DC, USA, 25–29 June 2005; pp. 257–264. [Google Scholar]

| Problem q | Name | Reference | N | M |
|---|---|---|---|---|
| 1 | Deb 4.1 | [42] | 2 | 2 |
| 2 | Deb 5.3 | [42] | 2 | 2 |
| 3 | Deb 5.1.3 | [42] | 2 | 2 |
| 4 | DTLZ1 | [43] | 7 | 3 |
| 5 | DTLZ3 | [43] | 12 | 3 |
| 6 | DTLZ3n2 | [43] | 2 | 2 |
| 7 | DTLZ5 | [43] | 12 | 3 |
| 8 | F2 | [44] | 2 | 2 |
| 9 | Far1 | [40] | 2 | 2 |
| 10 | FES2 | [40] | 10 | 3 |
| 11 | I2 | [40] | 8 | 3 |
| 12 | I5 | [40] | 8 | 3 |
| 13 | IKK1 | [40] | 2 | 3 |
| 14 | IM1 | [40] | 2 | 2 |
| 15 | lovison4 | [45] | 2 | 2 |
| 16 | lovison5 | [45] | 3 | 3 |
| 17 | lovison6 | [45] | 3 | 3 |
| 18 | MOP3 | [40] | 2 | 2 |
| 19 | MOP4 | [40] | 3 | 2 |
| 20 | MOP6 | [40] | 2 | 2 |
| 21 | Sch1 | [40] | 1 | 2 |
| 22 | TKLY1 | [40] | 4 | 2 |
| 23 | VU2 | [40] | 2 | 2 |
| 24 | WFG4 | [40] | 8 | 3 |
| 25 | ZDT6 | [46] | 10 | 2 |
| 26 | Freudenstein-Roth—Multi Modal | [34] | 2 | 2 |
| 27 | Freudenstein-Roth—Sphere | [34] | 2 | 2 |
| 28 | Freudenstein-Roth—Styblinski-Tang | [34] | 2 | 2 |
| 29 | Freudenstein-Roth—Three-Hump Camel Back | [34] | 2 | 2 |
| 30 | Levy 5 —Schubert | [34] | 2 | 2 |
| 31 | Levy 10—Griewank | [34] | 2 | 2 |
| 32 | Levy 15—Ackley | [34] | 2 | 2 |
| 33 | Schubert P1—Matyas | [34] | 2 | 2 |
| 34 | Schubert P2—Exponential | [34] | 2 | 2 |
| 35 | Sphere—Booth | [34] | 2 | 2 |
| 36 | Sphere—Schubert P1 | [34] | 2 | 2 |
| 37 | Sphere—Six-Hump Camel Back | [34] | 2 | 2 |
| 38 | Test Tube Holder—Ackley | [34] | 2 | 2 |
| 39 | Test Tube Holder—Schubert | [34] | 2 | 2 |
| 40 | Test Tube Holder—Schubert P1 | [34] | 2 | 2 |
| MODHA | Computational Budget Coefficient | |||||
|---|---|---|---|---|---|---|
| Parameters | 125 | 250 | 500 | 1000 | 2000 | Average |
| , | 0.9458 | 0.9641 | 0.9725 | 0.9751 | 0.9770 | 0.9669 |
| (9.0934 × 10) | (7.7112 × 10) | (7.3252 × 10) | (7.0314 × 10) | (6.8226 × 10) | (7.5968 × 10) | |
| , | 0.9464 | 0.9651 | 0.9745 | 0.9788 | 0.9808 | 0.9691 |
| (9.2159 × 10) | (7.7439 × 10) | (7.1709 × 10) | (6.8668 × 10) | (6.6934 × 10) | (7.5382 × 10) | |
| , | 0.9462 | 0.9643 | 0.9743 | 0.9797 | 0.9817 | 0.9692 |
| (9.4873 × 10) | (7.6855 × 10) | (7.1750 × 10) | (6.7123 × 10) | (6.5631 × 10) | (7.5246 × 10) | |
| , | 0.9634 | 0.9704 | 0.9854 | 0.9896 | 0.9915 | 0.9800 |
| (5.8652 × 10) | (5.0271 × 10) | (3.1711 × 10) | (2.3128 × 10) | (1.5723 × 10) | (3.5897 × 10) | |
| , | 0.9580 | 0.9682 | 0.9742 | 0.9891 | 0.9941 | 0.9767 |
| (7.0017 × 10) | (6.6010 × 10) | (5.6875 × 10) | (2.4307 × 10) | (1.4171 × 10) | (4.6276 × 10) | |
| , | 0.9583 | 0.9617 | 0.9815 | 0.9885 | 0.9933 | 0.9767 |
| (7.1280 × 10) | (6.9339 × 10) | (3.8687 × 10) | (2.3486 × 10) | (1.7157 × 10) | (4.3989 × 10) | |
| , | 0.9675 | 0.9741 | 0.9859 | 0.9893 | 0.9910 | 0.9815 |
| (5.5413 × 10) | (4.6050 × 10) | (3.1321 × 10) | (2.6102 × 10) | (1.9876 × 10) | (3.5798 × 10) | |
| , | 0.9621 | 0.9710 | 0.9765 | 0.9910 | 0.9939 | 0.9789 |
| (6.6240 × 10) | (6.0512 × 10) | (5.1914 × 10) | (2.3339 × 10) | (1.5871 × 10) | (4.3575 × 10) | |
| , | 0.9623 | 0.9664 | 0.9785 | 0.9858 | 0.9924 | 0.9771 |
| (6.4324 × 10) | (6.1208 × 10) | (4.3171 × 10) | (2.9605 × 10) | (2.2869 × 10) | (4.4235 × 10) | |
| MODSPO | 0.9493 | 0.9647 | 0.9702 | 0.9715 | 0.9725 | 0.9659 |
| (8.6609 × 10) | (7.6035 × 10) | (7.4521 × 10) | (7.4430 × 10) | (7.3635 × 10) | (7.6978 × 10) | |
| DFMO | 0.9530 | 0.9594 | 0.9653 | 0.9684 | 0.9708 | 0.9641 |
| (9.0301 × 10) | (8.6761 × 10) | (8.2138 × 10) | (8.0448 × 10) | (7.9084 × 10) | (8.3362 × 10) | |
| Problem | N | M | MODPSO | DFMO | MODHA |
|---|---|---|---|---|---|
| Catamaran | 4 | 2 | 0.9871 | 0.9895 | 0.9935 |
| (915) | (998) | (1774) | |||
| SWATH | 4 | 2 | 0.9732 | 0.9947 | 0.9900 |
| (210) | (367) | (341) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pellegrini, R.; Serani, A.; Liuzzi, G.; Rinaldi, F.; Lucidi, S.; Diez, M. Hybridization of Multi-Objective Deterministic Particle Swarm with Derivative-Free Local Searches. Mathematics 2020, 8, 546. https://doi.org/10.3390/math8040546
Pellegrini R, Serani A, Liuzzi G, Rinaldi F, Lucidi S, Diez M. Hybridization of Multi-Objective Deterministic Particle Swarm with Derivative-Free Local Searches. Mathematics. 2020; 8(4):546. https://doi.org/10.3390/math8040546
Chicago/Turabian StylePellegrini, Riccardo, Andrea Serani, Giampaolo Liuzzi, Francesco Rinaldi, Stefano Lucidi, and Matteo Diez. 2020. "Hybridization of Multi-Objective Deterministic Particle Swarm with Derivative-Free Local Searches" Mathematics 8, no. 4: 546. https://doi.org/10.3390/math8040546
APA StylePellegrini, R., Serani, A., Liuzzi, G., Rinaldi, F., Lucidi, S., & Diez, M. (2020). Hybridization of Multi-Objective Deterministic Particle Swarm with Derivative-Free Local Searches. Mathematics, 8(4), 546. https://doi.org/10.3390/math8040546






