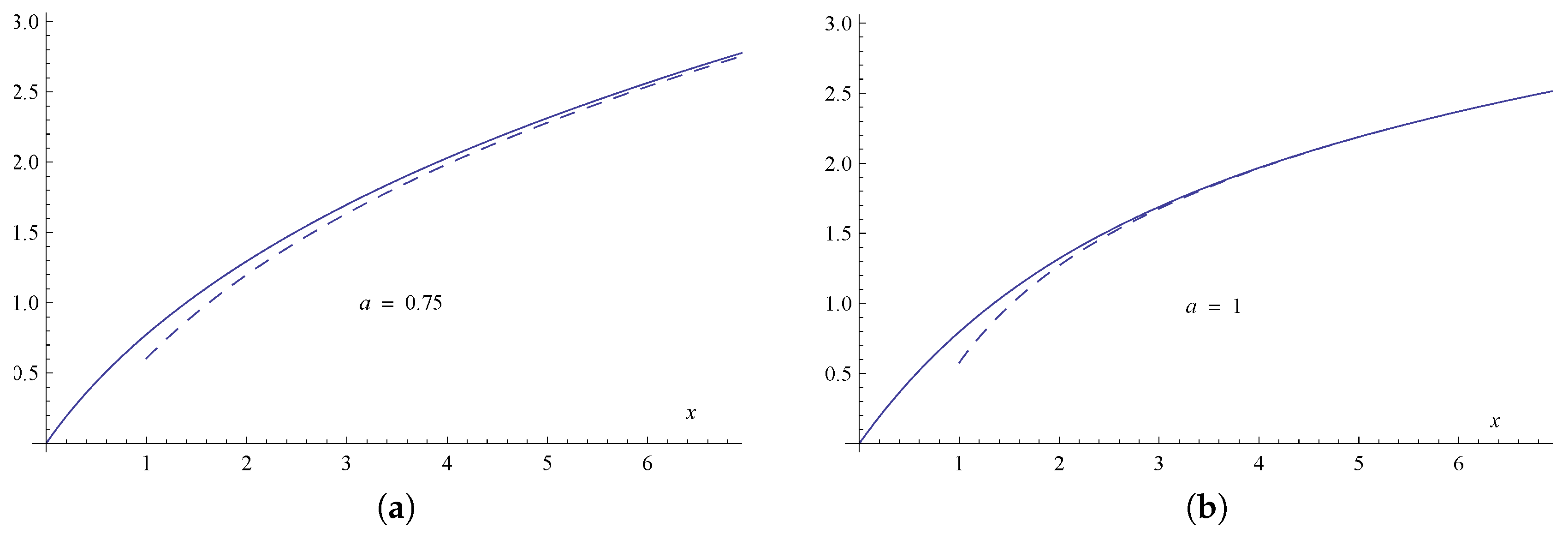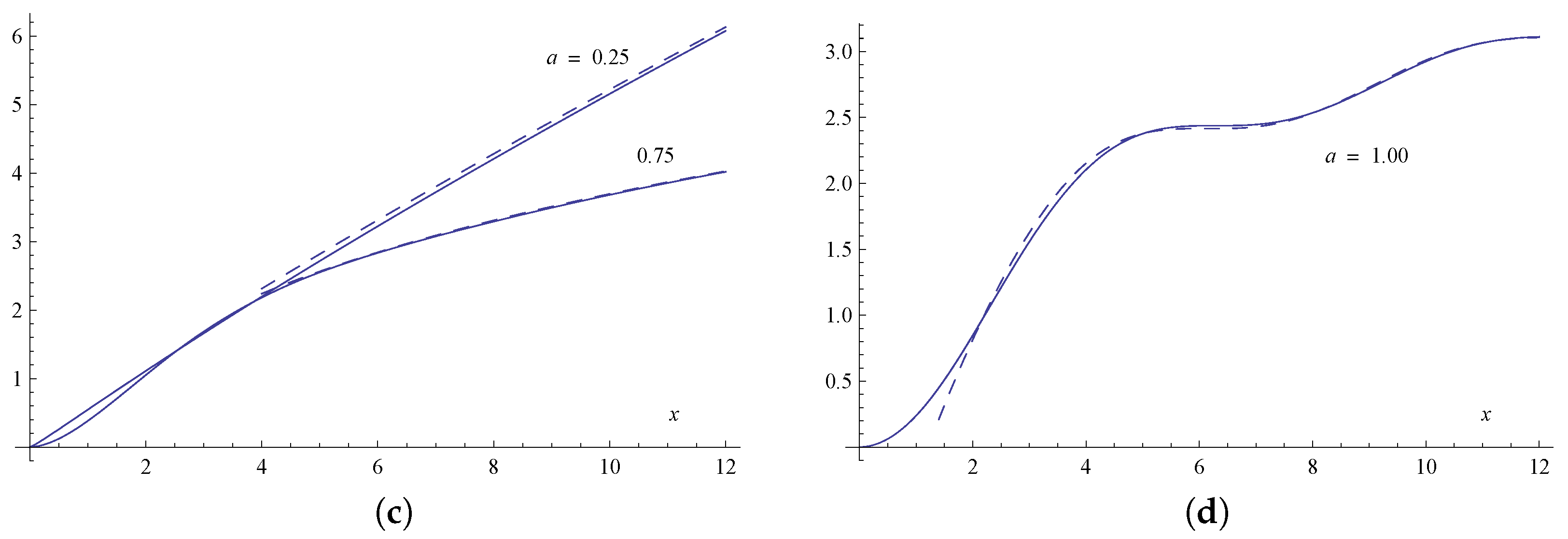1. Introduction
The complementary exponential integral
is defined by
and is an entire function. Its connection with the classical exponential integral
, valid in the cut plane
, is [
1], p. 150.
where
is the Euler-Mascheroni constant.
In a recent paper, Mainardi and Masina [
2] proposed an extension of
by replacing the exponential function in (
1) by the one-parameter Mittag-Leffler function
which generalises the exponential function
. They introduced the function for any
in the cut plane
which when
reduces to the function
. A physical application of this function for
arises in the study of the creep features of a linear viscoelastic model; see Reference [
3] for details. An analogous extension of the generalised sine and cosine integrals was also considered in Reference [
2]. Plots of all these functions for
were given.
Here we consider a slightly more general version of (
3) based on the two-parameter Mittag-Leffler function given by
where
will be taken to be real. Then the extended complementary exponential integral we shall consider is
upon replacement of
by
n in the last summation. When
this reduces to (
3) so that
.
The asymptotic expansion of this function will be obtained for large complex
z with the parameters
,
held fixed. We achieve this by consideration of the asymptotics of a related function using the theory developed for integral functions of hypergeometric type as discussed, for example, in Reference [
4], §2.3. An interesting feature of the expansion of
for
when
is the appearance of a logarithmic term whenever
. Similar expansions are obtained for the extended sine and cosine integrals in
Section 4. The paper concludes with the presentation of some numerical results that demonstrate the accuracy of the different expansions obtained.
2. The Asymptotic Expansion of a Related Function for
To determine the asymptotic expansion of
for large complex
z with the parameters
and
held fixed, we shall find it convenient to consider the related function defined by
where
It is readily seen that, when
,
The parameter
, but will be chosen to have two specific values in
Section 3 and
Section 4; namely,
and
. It will be shown that the asymptotic expansion of
consists of an algebraic and an exponential expansion valid in different sectors of the complex
-plane.
The function
in (
5) is a case of the Fox-Wright function
corresponding to
. In (
6) the parameters
and
are real and positive and
and
are arbitrary complex numbers. We also assume that the
and
are subject to the restriction
so that no gamma function in the numerator in (
6) is singular. We introduce the following parameters associated (empty sums and products are to be interpreted as zero and unity, respectively) with
which play a key role in the analysis of its asymptotic behaviour. are given by
The asymptotic expansion of
is discussed in detail in Reference [
5] Section 12, and is summarised in [
4,
6]. The algebraic expansion of
is obtained from the Mellin-Barnes integral representation [
4], p. 56.
where, with
, the integration path lies to the left of the poles of
at
but to the right of the poles at
and
,
. The upper or lower sign is taken according as
or
, respectively. It is seen that when
,
the pole at
is double and its residue must be evaluated accordingly. Displacement of the integration path to the left when
and evaluation of the residues then produces the algebraic expansion
, where
and
denotes the logarithmic derivative of the gamma function.
The exponential expansion associated with
is given by [
6] p. 299, [
4] p. 57.
where the coefficients
are those appearing in the inverse factorial expansion
with
. Here
M is a positive integer and
for
in
. The constant
is specified by
The coefficients
are independent of
s and depend only on the parameters
p,
q,
,
,
and
.
For the function
, we have
We are in the fortunate position that the normalised coefficients
in this case can be determined explicitly as
. This follows from the well-known (convergent) expansion given in Reference [
4,
7], p. 41.
to which, in the case of
, the ratio of gamma functions appearing on the left-hand side of (
10) reduces. Then, with
we have from (
9) the exponential expansion associated with
given by
From Reference [
4] pp. 57–58, we then obtain the asymptotic expansion for
when
and, when
,
The upper and lower signs are chosen according as
or
, respectively. It may be noted that the expansions
in (
14) only become significant in the neighbourhood of
. When
, the expansion of
is exponentially large for all values of
(see Reference [
4], p. 58) and accordingly we omit this case as it is unlikely to be of physical interest.
Remark 1. The exponential expansion in (13) continues to hold beyond the sector , where it becomes exponentially small in the sectors when . The rays are Stokes lines, where is maximally subdominant relative to the algebraic expansion . On these rays, undergoes a Stokes phenomenon, where the exponentially small expansion “switches off” in a smooth manner as increases [1], §2.11(iv), with its value to leading order given by ; see Reference [8] for a more detailed discussion of this point in the context of the confluent hypergeometric functions. We do not consider exponentially small contributions to here, except to briefly mention in Section 3 the situation pertaining to the case . 3. The Asymptotic Expansion of for
The asymptotic expansion of
defined in (
4) can now be constructed from that of
with the parameter
. It is sufficient, for real
,
, to consider
, since the expansion when
is given by the conjugate value. With
, the exponentially large sector
becomes
; that is
On the boundaries of this sector the exponential expansion is of an oscillatory character. When
, we note that the exponentially large sector (
15) lies outside the sector of interest
.
We define the algebraic and exponential asymptotic expansions
where
, and
where we recall that
. Then the following result holds:
Theorem 1. Let m be a positive integer, with and β real and . Then the following expansions hold for when , andwhen . Finally, when we haveand it is therefore sufficient to consider . Then, from (14), we obtain the expansion when We note from Theorem 1 that when the value of is, in general, complex-valued.
In the case of main physical interest, when is a real variable, we have the following expansion:
Theorem 2. When we have from Theorem 1 the expansionsfor , and from (17) and (20) when as . It is worth noting that a logarithmic term is present in the asymptotic expansion of whenever .
The Case
The special case
deserves further consideration. From (
16) and (
21) we obtain the expansion
If
, the asymptotic sum in (
23) vanishes and
for large
x. But we have the exact evaluation (compare (
2))
by Reference [
1], (6.12.1). The additional asymptotic sum appearing in (
25) is exponentially small as
and is consequently not accounted for in the result (
24).
From Remark 1, it is seen that there are Stokes lines at
, which coalesce on the positive real axis when
. In the sense of increasing
in the neighbourhood of the positive real axis, the exponential expansion
is in the process of
switching on across
and
(where the bar denotes the complex conjugate) is in the process of
switching off across
. When
, this produces the exponential contribution
for large
x. Thus, the more accurate version of (
23) should read
as
. When
, this correctly reduces to (
25).
When
, we have [
9]
This can be seen also to agree with (
26) after a little rearrangement.
4. The Generalised Sine and Cosine Integrals
The sine and cosine integrals are defined by [
1], §6.2,
Mainardi and Masina [
2] generalised these definitions by replacing the trigonometric functions by
with
to produce
Here we extend the definitions (
27) by including the additional parameter
in the Mittag-Leffler functions and consider the functions
The asymptotics of
and
can be deduced from the results in
Section 2. However, here we restrict ourselves to determining the asymptotic expansion of these functions for large
in a sector enclosing the positive real
z-axis, where for
they only have an algebraic-type expansion. We observe in passing that
Comparison of the series expansion for
with
in
Section 2, with the substitutions
,
and
(or from the above identity combined with Theorems 1 and 2), produces the following expansion:
Theorem 3. For and we have the algebraic expansionsas in the sector . A similar treatment for shows that with the substitutions , and we obtain the following expansion:
Theorem 4. For and we have the algebraic expansionsas in the sector . The expansions of and as when follow immediately from Theorems 3 and 4.
As
when
, the exponentially oscillatory contribution to
can be obtained directly from (
22) together with (
29). In the case of
, we obtain from (
9) with
,
,
,
and
the exponential expansion
with the coefficients
. Then the exponential contribution to
is
Collecting together these results we finally obtain the following theorem.
Theorem 5. When and β is real the following expansions hold:
and
as . When , it is seen that approaches the constant value whereas grows logarithmically like as .
5. Numerical Results
In this section we present numerical results confirming the accuracy of the various expansions obtained in this paper. In all cases we have employed optimal truncation (that is truncation at, or near, the least term in modulus) of the algebraic and (when appropriate) the exponential expansions. The numerical values of
were computed from (
4) using high-precision evaluation of the terms in the suitably truncated sum.
We first present results in the physically interesting case of
and
considered in Reference [
2].
Table 1 shows the values (In the tables we write the values as
instead of
.) of the absolute relative error in the computation of
from the asymptotic expansions in Theorem 2 for several values of
x and different
in the extended range
. The expansion for
is given by the algebraic expansion in (
21); this contains a logarithmic term for the values
. The progressive loss of accuracy when
can be attributed to the presence of the approaching exponentially large sector, whose lower boundary is, from (
15), given by
. In the final case
, the accuracy is seen to suddenly increase considerably. This is due to the inclusion of the (oscillatory) exponential contribution, which from (
22), takes the form
In
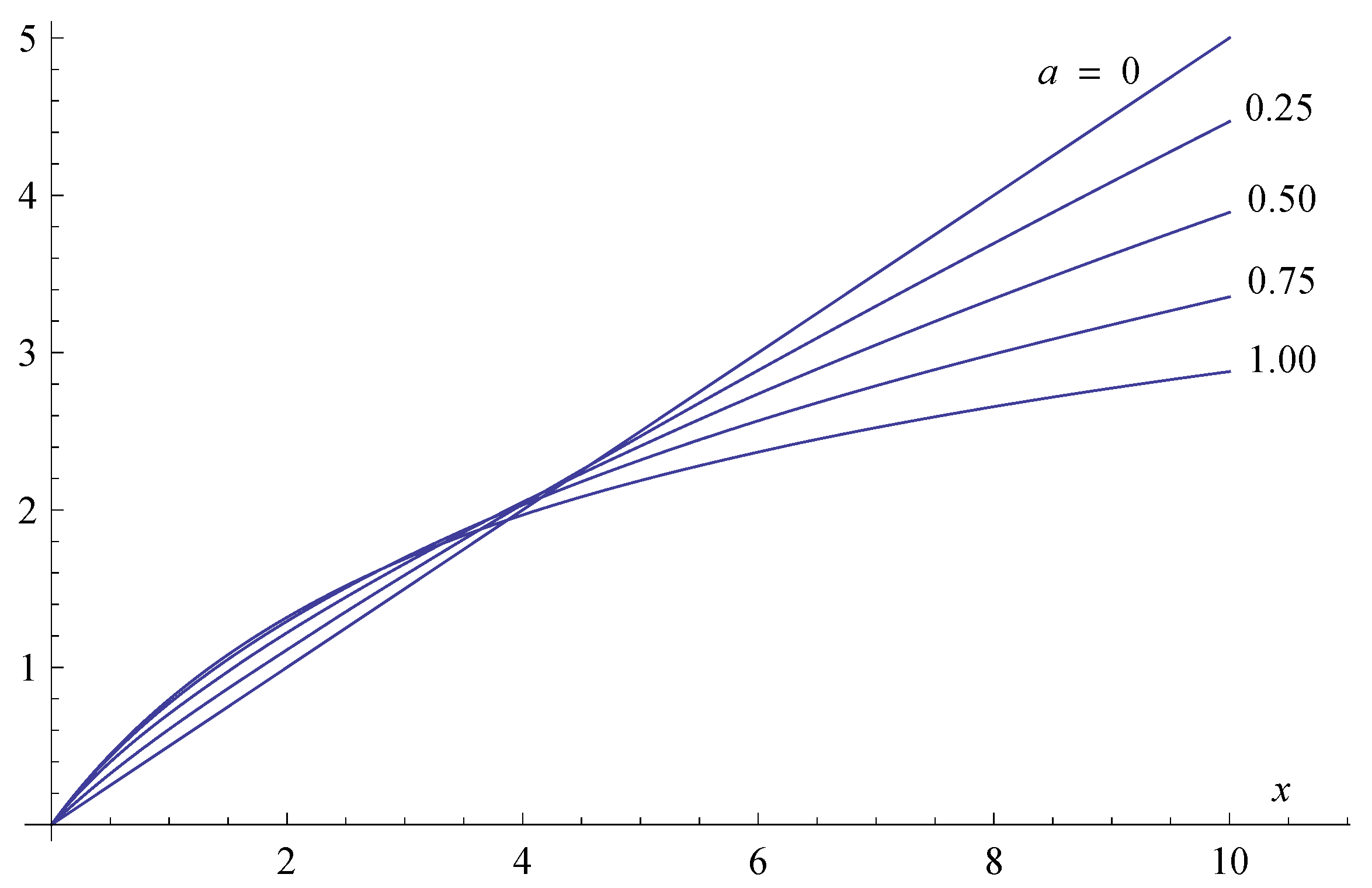
Figure 1 we show some plots of
for values of
in the range
. In
Figure 2 the asymptotic approximations for two values of
are shown compared with the corresponding curves of
.
Table 2 shows the values of the absolute relative error in the computation of
from the asymptotic expansions in Theorem 1 for complex
z for values of
in the range
. It will noticed that there is a sudden reduction in the error when
and
. In this case, the value of
and a more accurate treatment would include the exponentially small contribution
. When this term is included we find the absolute relative error equal to
.
Finally, in
Table 3 we present the error associated with the expansions of the generalised sine and cosine integrals
and
as
given in Theorems 3–5. For
, the logarithmic expansion in (
30) arises for
and
; for
the logarithmic expansion in (
31) arises for
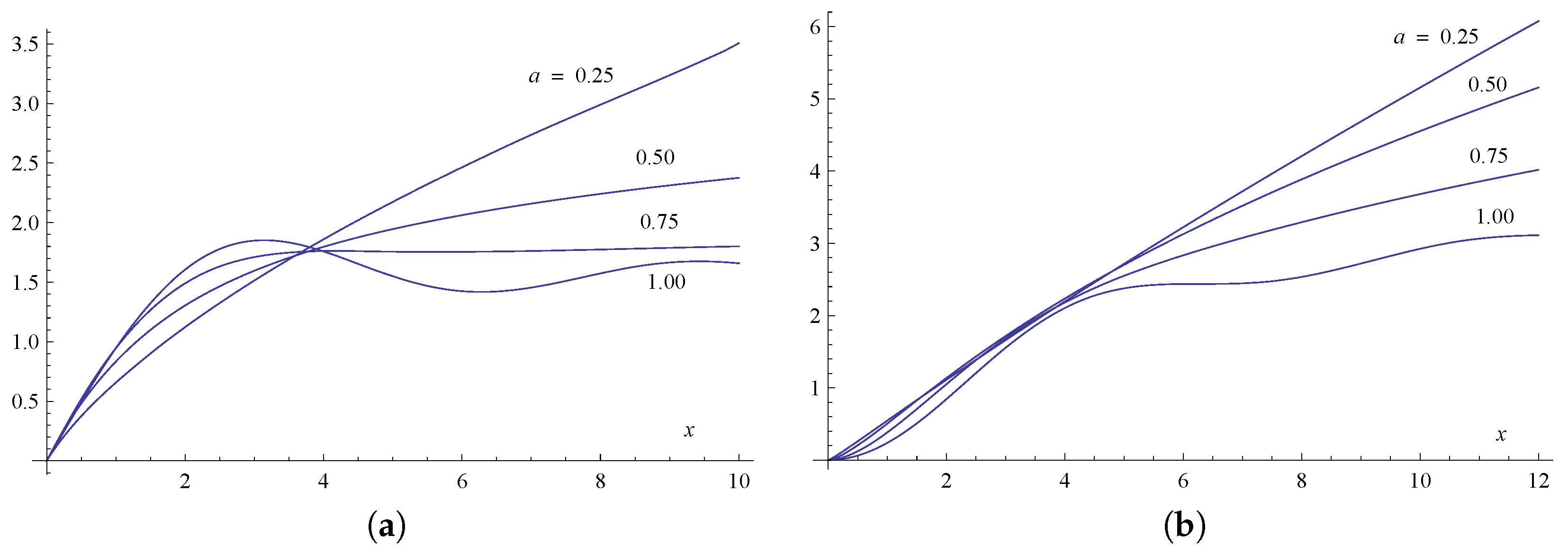
. In
Figure 3 are shown plots (We remark that the plot of
in
Figure 3b differs from that shown in
Figure 4 of Reference [
2].) of
and
for different
and in
Figure 4 the leading asymptotic approximations from the expansions in Theorem 5 are compared with the corresponding plots of these functions.
In conclusion, it is worth mentioning that the function
, and also the generalised sine and cosine integrals, can be extended by using the three-parameter Mittag-Leffler function (or Prabhakar function) defined by
A comprehensive discussion of this function and its applications can be found in Reference [
10]; see also Reference [
6] Section 5.1, for details of its large-
z asymptotic expansion.