Digital k-Contractibility of an n-Times Iterated Connected Sum of Simple Closed k-Surfaces and Almost Fixed Point Property

Abstract

The paper firstly establishes the so-called n-times iterated connected sum of a simple closed k-surface in ${\mathbb{Z}}^3$, denoted by ${\mathcal{C}}_k^n$, $k\in \{6,18,26\}$. Secondly, for a simple closed 18-surface $MS{S}_{18}$, we prove that there are only two types of connected sums of it up to 18-isomorphism. Besides, given a simple closed 6-surface $MS{S}_6$, we prove that only one type of $MS{S}_6♯MS{S}_6$ exists up to 6-isomorphism, where ♯ means the digital connected sum operator. Thirdly, we prove the digital k-contractibility of ${\mathcal{C}}_k^n:=\stackrel{\mathrm{n}-\mathrm{times}}{\overbrace{MS{S}_k♯\cdots ♯MS{S}_k}},k\in \{18,26\}$, which leads to the simply k-connectedness of ${\mathcal{C}}_k^n$, $k\in \{18,26\}$, $n\in \mathbb{N}$. Fourthly, we prove that ${\mathcal{C}}_6^2$ and ${\mathcal{C}}_k^n$ do not have the almost fixed point property (AFPP, for short), $k\in \{18,26\}$. Finally, assume a closed k-surface $S_k(\subset {\mathbb{Z}}^3)$ which is $(k,\overline{k})$-isomorphic to $(X,k)$ in the picture $({\mathbb{Z}}^3,k,\overline{k},X)$ and the set X is symmetric according to each of $xy$-, $yz$-, and $xz$-planes of ${\mathbb{R}}^3$. Then we prove that $S_k$ does not have the AFPP. In this paper given a digital image $(X,k)$ is assumed to be k-connected and its cardinality $\left|X\right|\ge 2$.

1. Introduction

In ${\mathbb{Z}}^3$, the concept of closed k-surface was introduced in [1,2,3] and its digital topological characterizations were also studied in many papers including [4,5,6,7,8,9,10]. Many explorations of various properties of closed k-surfaces have been proceeded from the viewpoints of digital topology, digital geometry, and fixed point theory [1,2,4,5,6,9,10,11,12,13,14,15,16]. Despite the studies of the earlier works [5,6,7,17,18], given (digital) closed k-surfaces, we need to further study both the digital k-contractibility of n-times iterated connected sums of closed k-surfaces and the non-almost fixed point property of them. Besides, we need to find a condition determining if a digital image $(X,k)$ in ${\mathbb{Z}}^n$ has the AFPP. This approach facilitates the studies of digital geometry and fixed point theory.

So far, there were several kinds of approaches to establish a digital k-surface [3,5,6,7,9]. In the present paper we will often use the symbol “$:=$” to define a new term, and given a digital image $(X,k)$ is assumed to be k-connected and its cardinality $\left|X\right|\ge 2$. Since the digital surface theory is related to computer science, the present paper mainly deals with digital k-surfaces X in ${\mathbb{Z}}^3$. Hence, we need to consider a binary digital image structure $(X,k,\overline{k})$ in ${\mathbb{Z}}^3$, denoted by $P:=({\mathbb{Z}}^3,k,\overline{k},X)$, where the $\overline{k}$-adjacency is concerned with the set ${\mathbb{Z}}^3\backslash X$. To be precise, in the case of the study of a closed k-surface $X\subset {\mathbb{Z}}^3$, we should assume X in the binary digital picture P. For instance,

$$P\in \left\{({\mathbb{Z}}^3,k,\overline{k},X)\right|(k,\overline{k})\in \{(6,26),(18,6),(26,6)\}\}.$$

(1)

Let us now study a (digital) closed k-surface X with one of the above frames P of (1).

Given two closed k-surfaces $S_k$ and $S_k^{\prime }$ in ${\mathbb{Z}}^n$, the concept of digital connected sum of them was firstly introduced in [5,7] by using several types of simple closed k-curves in ${\mathbb{Z}}^2,k\in \{4,8\}$ (see Section 4). Hereafter, we denote by $S_k$ a (simple) closed k-surface in ${\mathbb{Z}}^3$ (for the details, see Definition 5). Indeed, when studying various properties of closed k-surfaces, some digital k-homotopic features of $S_k$ such as the k-contractibility are very important in digital surface theory.

For convenience, let $MS{S}_6$ (resp. $MS{S}_{18}$) be the minimal simple closed 6-surface (resp. the minimal simple closed 18-surface) [6]. The present paper deals with the following queries.

• (Q1) We may ask if it is possible to propose the simple closed 6-surface $MS{S}_6$ in the picture $({\mathbb{Z}}^3,6,18,MS{S}_6)$ instead of $({\mathbb{Z}}^3,6,26,MS{S}_6)$.
  Hereafter, the operator “$♯$” means the digital connected sum (see Section 4 for the details).
  (Q2) How many types of $MS{S}_6♯MS{S}_6$ exist ?
  Let ${\mathcal{C}}_6^n:=\stackrel{n-\mathrm{times}}{\overbrace{MS{S}_6♯\cdots ♯MS{S}_6}}$. Then we have the following queries:
  (Q3) How can we formulate ${\mathcal{C}}_6^n,n\in \mathbb{N}\backslash \left\{1\right\}$ ?
  Given an $MS{S}_{18}$, we may raise the following query.
  (Q4) How many types of $MS{S}_{18}♯MS{S}_{18}$ exist ?
  Let ${\mathcal{C}}_{18}^n:=\stackrel{n-\mathrm{times}}{\overbrace{MS{S}_{18}♯\cdots ♯MS{S}_{18}}}$. Then we have the following questions:
  (Q5) How can we formulate ${\mathcal{C}}_{18}^n,n\in \mathbb{N}\backslash \left\{1\right\}$?
  (Q6) How about the almost fixed point property (AFPP for short) of ${\mathcal{C}}_6^n,n\in \mathbb{N}$?
  (Q7) How about the AFPP of ${\mathcal{C}}_{18}^n,n\in \mathbb{N}$?
  (Q8) What are some properties relating to the AFPP of a closed k-surface in ${\mathbb{Z}}^3$.

The rest of the paper is organized as follows: Section 2 refers to some notions involving a digital k-surface and a connected sum of two digital k-surfaces. Section 3 stresses some utilities of the minimal simple closed surfaces $MS{S}_6$, $MS{S}_{18}$, $MS{S}_{18}^{\prime }$, and $MS{S}_{26}^{\prime }$ from the viewpoints of digital curve and digital surface theory. Section 4 shows several types of n-times iterated connected sums of the minimal simple closed 6-surfaces, e.g., ${\mathcal{C}}_6^3:=MS{S}_6♯MS{S}_6♯MS{S}_6$. Section 5 proves that there are only two types of connected sums $MS{S}_{18}♯MS{S}_{18}$ up to 18-isomorphism. Besides, in the case of $MS{S}_{18}♯MS{S}_{18}\ne MS{S}_{18}$, we prove that only one type of ${\mathcal{C}}_{18}^3:=MS{S}_{18}♯MS{S}_{18}♯MS{S}_{18}$ exists up to 18-isomorphism. Section 6 intensively explores the 18-contractibility of an n-times iterated connected sum of simple closed 18-surfaces ${\mathcal{C}}_{18}^n:=\stackrel{n-\mathrm{times}}{\overbrace{MS{S}_{18}♯\cdots ♯MS{S}_{18}}}$. Section 7 proves that both ${\mathcal{C}}_6^2$ and ${\mathcal{C}}_k^n$ do not have the almost fixed point property, $k\in \{18,26\}$, $n\in \mathbb{N}$. Thus, these approaches play important roles in digital topology, digital geometry, fixed point theory, and so on. Section 8 concludes the paper with some remarks.

2. Basic Notions Involving Digital k-Surfaces and Connected Sums of Closed k-Surfaces

Let us now recall some terminology from digital curve and digital surface theories. Let $\mathbb{N}$ and $\mathbb{Z}$ represent the sets of natural numbers and integers, respectively.

We call a set $X(\subset {\mathbb{Z}}^n)$ with a k-adjacency a digital image, denoted by $(X,k)$ [4,5,7,9,10]. In particular, in digital surface theory, we are absolutely required to consider a closed k-surface $(X,k)$ with a k-adjacency in a binary digital picture $({\mathbb{Z}}^n,k,\overline{k},X)$ [19,20], where $n\in \mathbb{N}$ and the $\overline{k}$-adjacency is concerned with the set ${\mathbb{Z}}^n\backslash X$. In order to study $(X,k)$ in ${\mathbb{Z}}^n,n\ge 1$, we need the k-adjacency relations of ${\mathbb{Z}}^n$ which are generalizations of the commonly used k-adjacency of ${\mathbb{Z}}^2$, $k\in \{4,8\}$, and k-adjacency of ${\mathbb{Z}}^3$, $k\in \{6,18,26\}$. As a generalization of this approach into those of ${\mathbb{Z}}^n$, a paper [17] firstly established the digital k-connectivity of ${\mathbb{Z}}^n$, as follows: We say that distinct points $p,q\in {\mathbb{Z}}^n$ are k-(or $k(t,n)$-)adjacent if they satisfy the following property [17] (for the details, see also [21,22]).

For a natural number t, $1\le t\le n$, we say that distinct points

$$\begin{gathered} p=(p_1,p_2,\cdots ,p_n)\mathrm{and}q=(q_1,q_2,\cdots ,q_n)\in {\mathbb{Z}}^n, \\ \mathrm{are}k(t,n)-(k-,\mathrm{for}\mathrm{short})\mathrm{adjacent}\mathrm{if} \\ \mathrm{at}\mathrm{most}t\mathrm{of}\mathrm{their}\mathrm{coordinates}\mathrm{differs}\mathrm{by}\pm 1,\mathrm{and}\mathrm{all}\mathrm{the}\mathrm{others}\mathrm{coincide}. \end{gathered}$$

(2)

These $k(t,n)$-adjacency relations of ${\mathbb{Z}}^n$ are determined according to the number $t\in \mathbb{N}$ [17] (see also [21,22]). Using the statement of (2), the k-adjacency relations of ${\mathbb{Z}}^n$ are obtained [17] (see also [21,22]), as follows

$$k:=k(t,n)=\sum _{i=1}^t{2}^i{C}_i^n,\mathrm{where}{C}_i^n=\frac{n!}{(n-i)!i!}.$$

(3)

For instance, [7,22]

$$(n,t,k)\in \left\{\begin{array}{c}(3,1,6),(3,2,18),(3,3,26);\hfill \\ (4,1,8),(4,2,32),(4,3,64),(4,4,80);\hfill \\ (5,1,10),(5,2,50),(5,3,130),(5,4,210),(5,5,242).\hfill \end{array}\right\}$$

A digital image $(X,k)$ in ${\mathbb{Z}}^n$ can indeed be considered to be a set $X(\subset {\mathbb{Z}}^n)$ with one of the k-adjacency relations of (3). Using the k-adjacency relations of ${\mathbb{Z}}^n$ of (3), we say that a digital k-neighborhood of p in ${\mathbb{Z}}^n$ is the set [20]

$$N_k\left(p\right):=\left\{q\right|p\mathrm{is}k-\mathrm{adjacent}\mathrm{to}q\}\cup \left\{p\right\}.$$

Furthermore, we often use the notation [19]

$$N_k^{*}\left(p\right):=N_k\left(p\right)\backslash \left\{p\right\}.$$

For $a,b\in \mathbb{Z}$ with $a⪇b$, the set ${[a,b]}_{\mathbb{Z}}=\{n\in \mathbb{Z}|a\le n\le b\}$ with 2-adjacency is called a digital interval [19]. Let us now recall some terminology and notions [17,19] which are used in this paper.

• It is natural to say that a digital image $(X,k)$ is k-disconnected if there are nonempty sets $X_1,X_2\subset X$ such that $X=X_1\cup X_2$, $X_1\cap X_2=\varnothing$ and further, there are no points $x_1\in X_1$ and $x_2\in X_2$ such that $x_1$ and $x_2$ are k-adjacent.
• We say that a digital image $(X,k)$ is k-connected (or k-path connected) if it is not k-disconnected. Owing to this approach, we see that a singleton subset of $(X,k)$ is obviously k-connected.
• Given a k-connected digital image $(X,k)$ whose cardinality is greater than 1, the so-called k-path with $l+1$ elements in ${\mathbb{Z}}^n$ is assumed to be a finite sequence ${\left(x_i\right)}_{i\in {[0,l]}_{\mathbb{Z}}}\subset {\mathbb{Z}}^n$ such that $x_i$ and $x_j$ are k-adjacent if $|i-j|=1$ [19]. Eventually, in the case that a digital image $(X,k)$ is k-connected, for any distinct points such as $x,y$ in $(X,k)$, we see that there is a k-path ${\left(x_i\right)}_{i\in {[0,l]}_{\mathbb{Z}}}\subset X$ such that $x=x_0$ and $y=x_l$.
• For a digital image $(X,k)$, the k-component of $x\in X$ is defined to be the maximal k-connected subset of $(X,k)$ containing the point x [19].
• We say that a simple k-path means a finite set ${\left(x_i\right)}_{i\in {[0,m]}_{\mathbb{Z}}}\subset {\mathbb{Z}}^n$ such that $x_i$ and $x_j$ are k-adjacent if and only if $|i-j|=1$ [19]. In the case of $x_0=x$ and $x_m=y$, we denote the length of the simple k-path with $l_k(x,y):=m$.
• A simple closed k-curve (or simple k-cycle) with l elements in ${\mathbb{Z}}^n$, denoted by $S{C}_k^{n,l}$ [17,19], $l\ge 4,l\in {\mathbb{N}}_0\backslash \left\{2\right\}$, ${\mathbb{N}}_0$ is the set of even natural numbers, means the finite set ${\left(x_i\right)}_{i\in {[0,l-1]}_{\mathbb{Z}}}\subset {\mathbb{Z}}^n$ such that $x_i$ and $x_j$ are k-adjacent if and only if $|i-j|=\pm 1\left(modl\right)$.
• For a digital image $(X,k)$, a digital k-neighborhood of $x_0\in X$ with radius $\epsilon$ is defined in X as the following subset [17] of X

  $$N_k(x_0,\epsilon ):=\{x\in X|l_k(x_0,x)\le \epsilon \}\cup \left\{x_0\right\},$$

  (4)

  where $l_k(x_0,x)$ is the length of a shortest simple k-path from $x_0$ to x and $\epsilon \in \mathbb{N}$. For instance, for $X\subset {\mathbb{Z}}^n$, we obtain [17]

  $$N_k(x,1)=N_k\left(x\right)\cap X.$$

  (5)

For a digital image $(X,k)$, since X is a subset of ${\mathbb{Z}}^n$, if it is assumed as a subspace of the typical n-dimensional Euclidean topological space, it can naturally be a discrete topological subspace. However, as mentioned above, since a digital image $(X,k)$ with the digital k-connectivity (see (3)) is a kind of a digital graph in ${\mathbb{Z}}^n$, the paper [17] already established another metric for $(X,k)$. Eventually, the sets of (4) and (5) can be represented by using this metric on X derived from $(X,k)$. The important thing is that this metric is different from the typical Euclidean metric. Indeed, a paper [17] firstly established the metric using the “length of a shortest simple k-path from $x_0$ to x” for two points $x_0,x$ in $(X,k)$. Owing to the length of a shortest k-path in (4), we prove that a k-connected digital image $(X,k)$ can be considered to be a metric space, as follows:

Let us consider the map $d_k$ on a k-connected (or k-path connected) digital image $(X,k)$ defined by

$$d_k:(X,k)\times (X,k)\to \mathbb{N}\cup \left\{0\right\}$$

such that

$$d_k(x,x^{\prime }):=\left\{\begin{array}{c}{l}_k(x,x^{\prime }),\mathrm{if}x\ne x^{\prime };\hfill \\ 0,\mathrm{if}x=x^{\prime }.\hfill \end{array}\right\}$$

(6)

Owing to (6), we can see that $d_k(x,x^{\prime })\ge 1$ if $x\ne x^{\prime }$ and further, we obviously see that the function $d_k$ satisfies the metric axioms. Thus, we can represent the set $N_k(x_0,\epsilon )$ of (4) in the following way

$$N_k(x_0,\epsilon )=\{x\in X|d_k(x_0,x)\le \epsilon \}.$$

(7)

Consequently, we can represent the set of (5), as follows:

$$N_k(x_0,1)=\{x\in X|d_k(x_0,x)\le 1\}.$$

(8)

Rosenfeld [23] defined the notion of digital continuity of a map $f:(X,k_0)\to (Y,k_1)$ by saying that f maps every $k_0$-connected subset of $(X,k_0)$ into a $k_1$-connected subset of $(Y,k_1)$.

Motivated by this approach, using the set of (5) or (8), we can represent the digital continuity of a map between digital images by using a digital k-neighborhood (see Proposition 1 below). Due to this approach, we have strong advantages of calculating digital fundamental groups of digital images $(X,k)$ in terms of the unique digital lifting theorem [17], the digital homotopy lifting theorem [24], a radius 2-$(k_0,k_1)$-isomorphism and its applications [24], the study of multiplicative properties for a digital fundamental group [25,26], a Cartesian product of the covering spaces [26], and so on, as follows:

Proposition 1.

[17,18] Let $(X,k_0)$ and $(Y,k_1)$ be digital images in ${\mathbb{Z}}^{n_0}$ and ${\mathbb{Z}}^{n_1}$, respectively. A function $f:(X,k_0)\to (Y,k_1)$ is (digitally) $(k_0,k_1)$-continuous if and only if for every $x\in X$$f\left(N_{k_0}(x,1)\right)\subset N_{k_1}(f\left(x\right),1)$.

In Proposition 1, in the case $n_0=n_1$ and $k:=k_0=k_1$, the map f is called a ‘k-continuous’ map. Since an n-dimensional digital image $(X,k)$ is considered to be a set X in ${\mathbb{Z}}^n$ with one of the k-adjacency relations of (3) (or a digital k-graph [27]), regarding a classification of n-dimensional digital images, we prefer the term a $(k_0,k_1)$-isomorphism (or k-isomorphism) as in [27] (see also [18]) to a $(k_0,k_1)$-homeomorphism (or k-homeomorphism) as in [28].

Definition 1.

[27] (see also a $(k_0,k_1)$-homeomorphism in [28]) Consider two digital images $(X,k_0)$ and $(Y,k_1)$ in ${\mathbb{Z}}^{n_0}$ and ${\mathbb{Z}}^{n_1}$, respectively. Then a map $h:X\to Y$ is called a $(k_0,k_1)$-isomorphism if h is a $(k_0,k_1)$-continuous bijection and further, $h^{-1}:Y\to X$ is $(k_1,k_0)$-continuous. Then we use the notation $X{\approx }_{(k_0,k_1)}Y$. Besides, in the case $k:=k_0=k_1$, we use the notation $X{\approx }_{k}Y$.

The following notion of interior is often used in establishing a digital connected sum of digital closed k-surfaces.

Definition 2.

[5] Let $c^{*}:=(x_0,x_1,\cdots ,x_n)$ be a closed k-curve in $({\mathbb{Z}}^2,k,\overline{k},c^{*})$. A point x of $\overline{c^{*}}$, the complement of $c^{*}$ in ${\mathbb{Z}}^2$, is said to be interior to $c^{*}$ if it belongs to the bounded $\overline{k}$-connected component of $\overline{c^{*}}$.

The following digital images $MS{C}_8^{*}$, $MS{C}_4^{*}$, and $MS{C}_8^{\prime *}$ in ${\mathbb{Z}}^2$ [5,6,17] have essentially been used in establishing a connected sum and studying the digital fundamental group of a digital connected sum of closed k-surfaces. Thus we now recall them.

• $(\star )$$MS{C}_8^{*}:=MS{C}_8\cup Int\left(MS{C}_8\right)$ [6], where $MS{C}_8$ is a digital image 8-isomorphic to the digital image, $MS{C}_8:=S{C}_8^{2,6}:=\{c_0=(0,0),c_1=(1,1),c_2=(1,2),c_3=(0,3),c_4=(-1,2),c_5=(-1,1)\}$.
  $(\star )$$MS{C}_4^{*}:=MS{C}_4\cup Int\left(MS{C}_4\right)$ [6], where $MS{C}_4$ is a digital image 4-isomorphic to the digital image, $MS{C}_4:=S{C}_4^{2,8}:=\{v_0=(0,0),v_1=(1,0),v_2=(2,0),v_3=(2,1),v_4=(2,2),v_5=(1,2),v_6=(0,2),v_7=(0,1)\}$.
  $(\star )$$MS{C_8^{\prime }}^{*}:=MS{C}_8^{\prime }\cup Int\left(MS{C}_8^{\prime }\right)$ [6], where $MS{C}_8^{\prime }$ is a digital image 8-isomorphic to the digital image, $MS{C}_8^{\prime }:=S{C}_8^{2,4}:=\{w_0=(0,0),w_1=(1,1),w_2=(0,2),w_3=(-1,1)\}$.

Based on the pointed digital homotopy in [29] (see also [28]), the following notion of k-homotopy relative to a subset $A\subset X$ is often used in studying k-homotopic properties of digital images $(X,k)$ in ${\mathbb{Z}}^n$. For a digital image $(X,k)$ and $A\subset X$, we often call $\left(\right(X,A),k)$ a digital image pair.

Definition 3.

[17,24,28] Let $((X,A),k_0)$ and $(Y,k_1)$ be a digital image pair and a digital image in ${\mathbb{Z}}^{n_0}$ and ${\mathbb{Z}}^{n_1}$, respectively. Let $f,g:X\to Y$ be $(k_0,k_1)$-continuous functions. Suppose there exist $m\in \mathbb{N}$ and a function $H:X\times {[0,m]}_{\mathbb{Z}}\to Y$ such that

• for all $x\in X,H(x,0)=f\left(x\right)$ and $H(x,m)=g\left(x\right)$;
• for all $x\in X$, the induced function $H_x:{[0,m]}_{\mathbb{Z}}\to Y$ given by
  $H_x\left(t\right)=H(x,t)$ for all $t\in {[0,m]}_{\mathbb{Z}}$ is $(2,k_1)$-continuous;
• for all $t\in {[0,m]}_{\mathbb{Z}}$, the induced function $H_t:X\to Y$ given by $H_t\left(x\right)=H(x,t)$ for all $x\in X$ is $(k_0,k_1)$-continuous.
  Then we say that H is a $(k_0,k_1)$-homotopy between f and g [28].
• Furthermore, for all $t\in {[0,m]}_{\mathbb{Z}}$, assume that the induced map $H_t$ on A is a constant which follows the prescribed function from A to Y [17] (see also [5]). To be precise, $H_t\left(x\right)=f\left(x\right)=g\left(x\right)$ for all $x\in A$ and for all $t\in {[0,m]}_{\mathbb{Z}}$.

Then we call H a $(k_0,k_1)$-homotopy relative to A between f and g, and we say that f and g are $(k_0,k_1)$-homotopic relative to A in Y, $f{\simeq }_{(k_0,k_1)rel.A}g$ in symbols [17].

In Definition 3, if a k-continuous map $f:X\to X$ is k-homotopic to a certain constant map $c_{\left\{x_0\right\}},x_0\in X$, then we say that f is (pointed) k-null homotopic in $(X,k)$ [28]. In Definition 3, if $A=\left\{x_0\right\}\subset X$, then we say that F is a pointed $(k_0,k_1)$-homotopy at $\left\{x_0\right\}$ [28]. When f and g are pointed $(k_0,k_1)$-homotopic in Y, we use the notation $f{\simeq }_{(k_0,k_1)}g$. In the case $k:=k_0=k_1$ and $n_0=n_1$, f and g are said to be pointed k-homotopic in Y and we use the notation $f{\simeq }_{k}g$ and $f\in \left[g\right]$ which denotes the k-homotopy class of g. If, for some $x_0\in X$, $1_X$ is k-homotopic to the constant map in the space X relative to $\left\{x_0\right\}$, then we say that $(X,x_0)$ is pointed k-contractible [28]. Indeed, motivated by this approach, the notion of strong k-deformation retract was developed in [30].

Based on this k-homotopy, the notion of digital homotopy equivalence was firstly introduced in [31] (see also [32]), as follows:

Definition 4.

[31] (see also [32]) For two digital images $(X,k)$ and $(Y,k)$ in ${\mathbb{Z}}^n$, if there are k-continuous maps $h:X\to Y$ and $l:Y\to X$ such that the composite $l\circ h$ is k-homotopic to $1_X$ and the composite $h\circ l$ is k-homotopic to $1_Y$, then the map $h:X\to Y$ is called a k-homotopy equivalence and is denoted by $X{\simeq }_{k·h·e}Y$. Besides, we say that $(X,k)$ is k-homotopy equivalent to $(Y,k)$. In the case that the identity map $1_X$ is k-homotopy equivalent to a certain constant map $c_{\left\{x_0\right\}},x_0\in X$, we say that $(X,k)$ is k-contractible.

In Definition 4, in the case $X{\simeq }_{k·h·e}Y$, we say that $(X,k)$ is the same k-homotopy type as $(Y,k)$. In view of Definitions 3 and 4, we obviously see that the pointed k-contractibility implies the k-contractibility, the converse does not hold. Let $(X,k)$ be k-contractible. Then it is obvious that any k-loop in $(X,k)$ is k-null homotopic in $(X,k)$.

The digital k-fundamental group is induced from the pointed k-homotopy [28]. For a given digital image $(X,k)$, by using several notions such as digital k-homotopy class [29], Khalimsky operation of two k-homotopy classes [29], trivial extension [28], the paper [28] defined the digital k-fundamental group, denoted by ${\pi }^k(X,x_0),x_0\in X$. Indeed, in digital topology there are several kinds of digital fundamental groups [33]. In addition, we have the following: If X is pointed k-contractible, then ${\pi }^k(X,x_0)$ is a trivial group [28]. Hereafter, we shall assume that each digital image $(X,k)$ is k-connected.

Using the unique digital lifting theorem [17] and the homotopy lifting theorem [24] in digital covering theory [4,17,18,25,26], for a non-k-contractible space $S{C}_k^{n,l}$, we obtain the following:

Theorem 1.

[17] For a non-k-contractible $S{C}_k^{n,l}$, ${\pi }_1^k\left(S{C}_k^{n,l}\right)$ is an infinite cyclic group.

Namely, for an $S{C}_k^{n,l},l\ge 6$, it turns out that ${\pi }_1^k\left(S{C}_k^{n,l}\right)$ is an infinite cyclic group. Regarding Theorem 1, we see that $S{C}_{3^n-1}^{n,4}$ has the trivial group, $n\ge 2$ [24,28] and further, $S{C}_4^{2,4}$ also has the trivial group because $S{C}_4^{2,4}$ is 4-contractible (see a certain idea from Example 1 below).

The following are proven in [5,7,17,18,28].

• $MS{C}_8:=S{C}_8^{2,6}$ is not 8-contractible and $MS{C}_4:=S{C}_4^{2,8}$ is not 4-contractible either [5,17].
• $MS{C}_8^{\prime }$ are 8-contractible [5,7,28].
• Due to Theorem 1, it turns out that $S{C}_k^{n,l}$ is not k-contractible if $l\ge 6$.

In particular, both the non-8-contractibility of $MS{C}_8$ and the non-4-contractibility of $MS{C}_4$ play important roles in formulating a connected sum of two closed k-surfaces (see Section 4 for the details).

Whereas $S{C}_6^{3,6}$ itself is not 6-contractible (see Theorem 1), identity map $1_{S{C}_6^{3,6}}$ is 6-null homotopic in $(I^3,6)$, where $S{C}_6^{3,6}\subset I^3$. To be precise, we obtain the following:

Example 1.

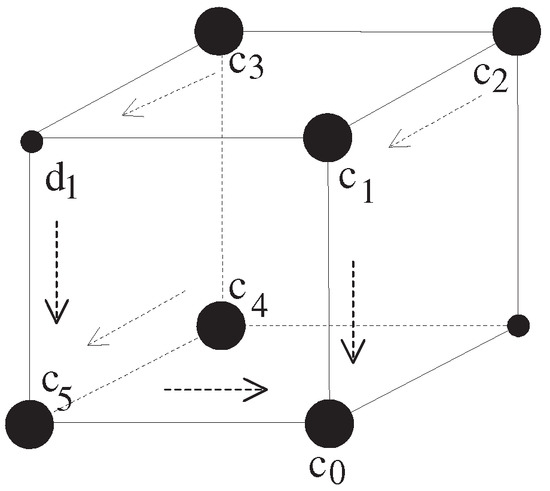
Let us consider $S{C}_6^{3,6}:={\left(c_i\right)}_{i\in {[0,5]}_{\mathbb{Z}}}$ embedded in $(I^3,6)$ (see Figure 1), where $c_0:=(0,0,0),c_1:=(0,0,1),c_2:=(0,1,1),c_3:=(-1,1,1,),c_4:=(-1,1,0),c_5:=(-1,0,0)$. It is obvious that $S{C}_6^{3,6}$ itself is not 6-contractible (see Theorem 1) because its 6-fundamental group is an infinite cyclic group [17]. However, identity map $1_{S{C}_6^{3,6}}$ is clearly 6-null homotopic in $(I^3,6)$ (see Figure 1). To be specific, consider the map

$$H:S{C}_6^{3,6}\times {[0,3]}_{\mathbb{Z}}\to (I^3,6)$$

Figure 1. Configuration of the pointed 6-null homotopic of $1_{S{C}_6^{3,6}}$ in $(I^3,6)$.

such that for $x\in S{C}_6^{3,6}$

$$\left\{\begin{array}{c}H(x,0)=x,i.e.,H(x,0)=1_{S{C}_6^{3,6}}\left(x\right);\hfill \\ H(x,1)=\{c_0,c_1,d_1,c_5\}byusingthemappings\hfill \\ c_0\to c_0,\{c_1,c_2\}\to \left\{c_1\right\},c_3\to d_{1}and\{c_4,c_5\}\to \left\{c_5\right\};\hfill \\ H(x,2)=\{c_0,c_5\}intermsofthemappings\hfill \\ \{c_0,c_1,c_2\}\to \left\{c_0\right\}and\{c_3,c_4,c_5\}\to \left\{c_5\right\},\hfill \\ i.e.,c_3\to c_{5}via{c}_3\to d_1\to c_5;and\hfill \\ H(x,3)=\left\{c_0\right\},x\in S{C}_6^{3,6},i.e.,H(x,3)=c_{\left\{c_0\right\}}\left(x\right).\hfill \end{array}\right\}$$

Then we see that the map H is a 6-homotopy making $1_{S{C}_6^{3,6}}$ 6-null homotopic in $(I^3,6)$.

In view of Example 1, we observe that $S{C}_6^{3,6}$ is not 6-contractible in itself because its digital 6-fundamental group is an infinite cyclic group (see Theorem 1, for the details, see [4,17]).

Remark 1.

The digital image $(I^3,6)$ is 6-contractible (see [34]).

Hereafter, we denote the n-dimensional digital cube (or digital n-cube) with

$$I^n:=\prod _{i=1}^n{[x_i,x_i+1]}_{\mathbb{Z}}\subset {\mathbb{Z}}^n,n\in \mathbb{N}.$$

Based on the 6-contractibility of $(I^3,6)$ (see [34]), using a similar method as the proof of it (see Remark 2 of [8]), it is obvious that $(I^n,k)$ is pointed k-contractible for any k-adjacency of ${\mathbb{Z}}^n$, where the k-adjacency is that of (3) according to the dimension “$n$”.

Let us now examine if a k-isomorphism preserves a k-homotopy between two k-continuous maps.

Theorem 2.

A k-isomorphism preserves a k-homotopy.

Proof. 

Given two spaces $X:=(X,k)$, $Y:=(Y,k)$ in ${\mathbb{Z}}^n$, consider two k-continuous functions $f,g:X\to Y$, relating to a k-homotopy $F:X\times {[a,b]}_{\mathbb{Z}}\to Y$, i.e., $f{\simeq }_{k}g$. Besides, further assume two k-isomorphisms $h_1:X\to X^{\prime }$ and $h_2:Y\to Y^{\prime }$, where $(X^{\prime },k)$ and $(Y^{\prime },k)$ are considered in ${\mathbb{Z}}^n$. Then, it is clear that the two composites

$$h_2\circ f\circ h_1^{-1}\mathrm{and}{h}_2\circ g\circ h_1^{-1}$$

are also k-continuous maps from $X^{\prime }$ to $Y^{\prime }$. Based on the given k-homotopy and the two k-isomorphisms $h_1$ and $h_2$, we now define the new map

$$G:=h_2\circ F\circ h_1^{-1}:X^{\prime }\times {[a,b]}_{\mathbb{Z}}\to Y^{\prime }.$$

Then, we obtain the following:

(1)

for all $x^{\prime }\in X^{\prime }$, $G(x^{\prime },a)=h_2\circ f\circ h_1^{-1}\left(x^{\prime }\right)$ and $G(x^{\prime },b)=h_2\circ g\circ h_1^{-1}\left(x^{\prime }\right)$;

(2)

for all $x^{\prime }\in X^{\prime }$, the induced function $G_{x^{\prime }}:{[a,b]}_{\mathbb{Z}}\to Y^{\prime }$ defined by $G_{x^{\prime }}\left(t\right):=G(x^{\prime },t)$ for all $t\in {[a,b]}_{\mathbb{Z}}$ is k-continuous;

(3)

for all $t\in {[a,b]}_{\mathbb{Z}}$, the induced function $G_t:X^{\prime }\to Y^{\prime }$ defined by $G_t\left(x^{\prime }\right):=G(x^{\prime },t)$ for all $x^{\prime }\in X^{\prime }$ is k-continuous.

Thus we have a conclusion that G is a k-homotopy between $h_2\circ f\circ h_1^{-1}$ and $h_2\circ g\circ h_1^{-1}$. □

Corollary 1.

A k-isomorphism preserves the k-contractibility.

Proof. 

In Theorem 2, consider a k-contractible space $(X,k)$ such that $X{\simeq }_{k·h·e}\left\{x_0\right\}$ for some point $x_0\in X$. Then, after replacing f (resp.g) by $1_X$ (resp. the constant map $c_{\left\{x_0\right\}}$), we prove the assertion. □

Corollary 2.

A k-isomorphism preserves the pointed k-contractibility.

Proof. 

In Theorem 2 and Corollary 1, consider a pointed k-contractible space $(X,k)$ such that $1_X$ is k-homotopic to the constant map in the space $\left\{x_0\right\}$ relative to $\left\{x_0\right\}$. After replacing f (resp.g) with $1_X$ (resp. the constant map $c_{\left\{x_0\right\}}$), we complete the proof. □

Using a method similar to the proof of Theorem 2, we obtain the following:

Corollary 3.

A $(k_0,k_1)$-isomorphism preserves a $(k_0,k_1)$-homotopy equivalence.

3. Utilities of the Minimal Simple Closed 6-, 18- and 26-Surfaces; $MS{S}_6$, $MS{S}_{18}$, $MS{S}_{18}^{\prime },MS{S}_{26}^{\prime }$

This section stresses some utilities of the minimal simple closed 6-, 18-, 26-surfaces, e.g., $MS{S}_6$, $MS{S}_{18}$, $MS{S}_{18}^{\prime },MS{S}_{26}^{\prime }$ [6] from the viewpoints of digital surface and digital homotopy theory. Indeed, these models for simple closed k-surfaces play important roles in digital homotopy theory, digital surface theory, and fixed point theory. Furthermore, these have been used in formulating connected sums of some simple closed k-surfaces, $k\in \{6,18,26\}$ [5,6,7]. Besides, these were essentially used in proceeding with geometric realizations of digital k-surfaces [7,8].

In order to study closed k-surfaces in ${\mathbb{Z}}^n$, let us recall some terminology from digital surface theory, as follows: A point $x\in (X,k)$ is called a k-corner if x is k-adjacent to two and only two points y, $z\in X$ such that y and z are k-adjacent to each other [2]. The k-corner x is called simple if y, z are not k-corners and if x is the only point k-adjacent to both y, z. $(X,k)$ is called a generalized simple closedk-curve if what is obtained by removing all simple k-corners of X is a simple closed k-curve [2,9]. For a k-connected digital image $(X,k)$ in $X\subset {\mathbb{Z}}^3$, we recall [1,2,6]

$${\left|X\right|}^x:=N_{26}(x,1)\backslash \left\{x\right\}.$$

(9)

In general, for a k-connected digital image $(X,k)$ in ${\mathbb{Z}}^n,n\ge 3$, we can state [7]

$${\left|X\right|}^x:=N_{3^n-1}(x,1)\backslash \left\{x\right\}.$$

(10)

Hereafter, for a k-surface in ${\mathbb{Z}}^n,n\in \mathbb{N}\backslash \{1,2\}$ [5,6], we call the set ${\left|X\right|}^x$ of (9) the minimal $(3^n-1)$-adjacency neighborhood of x in X.

We say that two subsets, $(A,k)$ and $(B,k)$ of $(X,k)$, are k-adjacent if $A\cap B=\varnothing$ and there are points $a\in A$ and $b\in B$ such that a and b are k-adjacent [19]. In particular, in the case that B is a singleton, say $B=\left\{x\right\}$, we say that A is k-adjacent to x.

Papers [5,6,7] introduced the notion of a closed k-surface in ${\mathbb{Z}}^n,n\ge 3$ and various properties of it. However, in the present paper, we will stress the study of closed k-surfaces in ${\mathbb{Z}}^3$ with the following approach in [3,9,10].

Definition 5.

[3,10] Let $(X,k)$ be a digital image in ${\mathbb{Z}}^3$, and $\overline{X}:={\mathbb{Z}}^3\backslash X$. Then, X is called a closed k-surface if it satisfies the following.

(1) 

In the case $(k,\overline{k})\in \{(26,6),(6,26)\}$, for each point $x\in X$,

(a) 

${\left|X\right|}^x$ has exactly one k-component k-adjacent to x;

(b) 

$|\overline{X}{|}^x$ has exactly two $\overline{k}$-components which are $\overline{k}$-adjacent to x; we denote by $C^{xx}$ and $D^{xx}$ these two components; and

(c) 

for any point $y\in N_k\left(x\right)\cap X$ (or $N_k(x,1)$ in $(X,k)$), $N_{\overline{k}}\left(y\right)\cap C^{xx}\ne \varphi$ and $N_{\overline{k}}\left(y\right)\cap D^{xx}\ne \varphi$.

Furthermore, if a closed k-surface X does not have a simple k-point, then X is called simple.

(2) 

In the case $(k,\overline{k})=(18,6)$,

(a) 

X is k-connected,

(b) 

for each point $x\in X$, ${\left|X\right|}^x$ is a generalized simple closed k-curve.

Furthermore, if the image ${\left|X\right|}^x$ is a simple closed k-curve, then the closed k-surface X is called simple.

Hereafter, we denote by $MS{S}_k$ a minimal simple closed k-surface in ${\mathbb{Z}}^3$ (see Figure 2). Furthermore, we recall the following closed k-surfaces, $k\in \{6,18,26\}$ [5]:

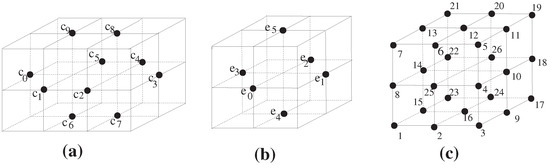
Figure 2. (a) $MS{S}_{18}$ [5,6]: (b) $MS{S}_{18}^{\prime }=MS{S}_{26}^{\prime }$ [5,6]; (c) $MS{S}_6$ [5].

Remark 2.

(1)$MS{S}_6{\approx }_6{[-1,1]}_{\mathbb{Z}}^3\backslash \left\{0_3\right\}$, where $0_3:=(0,0,0)$. Then, $MS{S}_6$ is the minimal simple closed 6-surface which is not 6-contractible (see Figure 2c). Namely, we obtain the digital picture $({\mathbb{Z}}^3,6,26,MS{S}_6)$ according to (1).

(2) $MS{S}_{18}^{\prime }{\approx }_{18}\{p\in {\mathbb{Z}}^3|d(p,0_3)=1\}$, where d is the typical Euclidean distance in ${\mathbb{R}}^3$. Thus we obtain the digital picture $({\mathbb{Z}}^3,18,6,MS{S}_{18}^{\prime })$ according to (1).

Papers [5,6] indeed stated that $MS{S}_{18}^{\prime }$ is 18-contractible and it is the minimal simple closed 18-surface. Besides, a paper [5] proved the simply 18-connectedness of $MS{S}_{18}^{\prime }$ and $MS{S}_{18}$. In addition, we see that $MS{S}_6$ is simply 6-connected [6,8].

Let us further recall two simple closed k-surface, $k\in \{18,26\}$, as follows:

• $MS{S}_{18}{\approx }_{18}(MS{C}_8\times \left\{1\right\})\cup (Int\left(MS{C}_8\right)\times \{0,2\})$ [5,6]. Thus we obtain the digital picture $({\mathbb{Z}}^3,18,6,MS{S}_{18})$ according to (1).
• $MS{S}_{26}^{\prime }:=MS{S}_{18}^{\prime }$ which is 26-contractible [5,6] and is the minimal simple closed 26-surface (see Figure 2b). Finally, we obtain the binary digital picture $({\mathbb{Z}}^3,26,6,MS{S}_{26}^{\prime })$ according to (1). Besides, we recall the following:

Remark 3.

[8] $MS{S}_{18}$ is pointed 18-contractible.

Proposition 2.

If given a digital image $(X,k)$ is not k-connected, then it is not k-contractible.

Proof. 

Owing to the second property of Definition 3, the assertion is proved. □

• (Correction) In the Figure 4c of [35], the given K-topological space $(Z,{\kappa }_Z^2)$ should be referred to as “non-K-retractible” instead of “$K$-retractible”.

4. Several Types of Models for ${\mathcal{C}}_6^n:=\stackrel{n-\mathrm{times}}{\overbrace{MS{S}_6♯\cdots ♯MS{S}_6}}$

From now on we denote a (simple) closed k-surface in ${\mathbb{Z}}^3$ with $S_k$, $k\in \{6,18,26\}$, which will be used in this paper. In particular, we will mainly consider an $S_k$, $k\in \{6,18,26\}$ in the picture as referred to in (1), i.e.,

$$\{({\mathbb{Z}}^3,26,6,S_{26}),({\mathbb{Z}}^3,18,6,S_{18}),({\mathbb{Z}}^3,6,26,S_6)\}.$$

(11)

Definition 6.

[5] In ${\mathbb{Z}}^3$, let $S_{k_0}$ (resp. $S_{k_1}$) be a closed $k_0$-(resp. a closed $k_1$-)surface, where $k_0=k_1\in \{6,18,26\}$.

• Consider $A_{k_0}^{\prime }\subset A_{k_0}\subset S_{k_0}$ and take $A_{k_0}\backslash A_{k_0}^{\prime }\subset S_{k_0}$, where $A_{k_0}{\approx }_{(k_0,4)}MS{C}_4^{*}$ or $A_{k_0}{\approx }_{(k_0,8)}MS{C}_8^{*}$, or $A_{k_0}{\approx }_{(k_0,8)}MS{C_8^{\prime }}^{*}$, and further, $A_{k_0}^{\prime }{\approx }_{(k_0,4)}$$Int\left(MS{C}_4\right)$ or $A_{k_0}^{\prime }{\approx }_{(k_0,8)}$$Int\left(MS{C}_8\right)$, or $A_{k_0}^{\prime }{\approx }_{(k_0,8)}$$Int\left(MS{C}_8^{\prime }\right)$, respectively.
• Let $f:A_{k_0}\to f\left(A_{k_0}\right)\subset S_{k_1}^{\prime }$ be a $(k_0,k_1)$-isomorphism. Remove $A_{k_0}^{\prime }$ and $f\left(A_{k_0}^{\prime }\right)$ from $S_{k_0}$ and $S_{k_1}$, respectively.
• Identify $A_{k_0}\backslash A_{k_0}^{\prime }$ and $f(A_{k_0}\backslash A_{k_0}^{\prime })$ by using the $(k_0,k_1)$-isomorphism f. Then, the quotient space $S_{k_0}^{\prime }\cup S_{k_1}^{\prime }/\sim$ is obtained by $i\left(x\right)\sim f\left(x\right)\in S_{k_1}^{\prime }$ for $x\in A_{k_0}\backslash A_{k_0}^{\prime }$ and is denoted by $S_{k_0}♯S_{k_1}$, where $S_{k_0}^{\prime }=S_{k_0}\backslash A_{k_0}^{\prime }$, $S_{k_1}^{\prime }=S_{k_1}\backslash f\left(A_{k_0}^{\prime }\right)$, and the map $i:A_{k_0}\backslash A_{k_0}^{\prime }\to S_{k_0}^{\prime }$ is the inclusion map.

Owing to Definition 6, $S_{k_0}♯S_{k_1}$ is obtained in ${\mathbb{Z}}^3$. Besides, the digital topological type of $S_{k_0}♯S_{k_1}$ absolutely depends on the choice of the subset $A_{k_0}\subset S_{k_0}$ [7]. Furthermore, the k-adjacency of $S_{k_0}♯S_{k_1}$ is required as follows:

Remark 4.

[5] In the quotient space $S_{k_0}♯S_{k_1}:=S_{k_0}^{\prime }\cup S_{k_1}^{\prime }/\sim$, the subsets $A:=S_{k_0}^{\prime }\backslash (A_{k_0}\backslash A_{k_0}^{\prime })$ and $B:=S_{k_1}^{\prime }\backslash f(A_{k_0}\backslash A_{k_0}^{\prime })$ in $S_{k_0}♯S_{k_1}$ are assumed to be disjoint and there are no points $x\in A$ and $x^{\prime }\in B$ such that x and $x^{\prime }$ are k-adjacent, where $k:=k_0=k_1$. Then, the digital image $(S_{k_0}♯S_{k_1},k)$ is called a (digital) connected sum of $S_{k_0}$ and $S_{k_1}$.

As mentioned in Remark 4, the requirement involving the k-adjacency of $(S_{k_0}♯S_{k_1},k)$ in ${\mathbb{Z}}^3$ plays an important role in studying connected sums of closed $k_i$-surfaces, $i\in \{0,1\},k=k_i$. Indeed, it turns out that [8] $(S_k♯S_k^{\prime },k)$ is also a closed k-surface in the picture $({\mathbb{Z}}^3,k,\overline{k},S_k♯S_k^{\prime })$, where $S_k$ and $S_k^{\prime }$ are closed k-surfaces in the pictures $({\mathbb{Z}}^3,k,\overline{k},S_k)$ and $({\mathbb{Z}}^3,k,\overline{k},S_k^{\prime })$, respectively.

This section explores several methods of formulating the digital connected sums $MS{S}_6♯MS{S}_6$, $MS{S}_{18}♯MS{S}_{18}$ and an n-times iterated connected sum of $MS{S}_6$ and that of $MS{S}_{18}$.

At the moment, let us recall the previously-mentioned queries in Section 1:

• (Q1) After replacing $(6,26)$ in Definition 5(1) with $(6,18)$, we may ask if it is possible to propose the simple closed 6-surface $MS{S}_6$ in the picture $({\mathbb{Z}}^3,6,18,MS{S}_6)$ instead of $({\mathbb{Z}}^3,6,26,MS{S}_6)$.
  This query is a reminder of the importance of the $\overline{k}$-adjacency of ${\mathbb{Z}}^3\backslash S_k$ of a simple closed k-surface $S_k$ in the picture $({\mathbb{Z}}^3,k,\overline{k},S_k)$.
  (Q2) Given the $MS{S}_6$, how many models for $MS{S}_6♯MS{S}_6$ exist ?
  Let ${\mathcal{C}}_6^n:=\stackrel{n-\mathrm{times}}{\overbrace{MS{S}_6♯\cdots ♯MS{S}_6}}$. Then we also have the following question:
  (Q3) How can we formulate ${\mathcal{C}}_6^n,n\in \mathbb{N}\backslash \left\{1\right\}$ ?

To address these queries, we now study some properties of $MS{S}_6$ and ${\mathcal{C}}_6^n$. First of all, let us represent the question (Q1), as follows:

Unlike the three cases of (1), we may ask if there are other binary relations $(6,\overline{k})$ for $MS{S}_6$, $\overline{k}\in \{6,18\}$.

Remark 5.

Regarding the question (Q1), we have a negative answer.

Proof. 

Consider the point indicated by the number “$3$” in Figure 2c. Since the set $|\overline{MS{S}_6}{|}^3$ does not satisfy the properties of Definition 5(b) and (c), we cannot consider the picture $({\mathbb{Z}}^3,6,18,MS{S}_6)$ for the simple closed 6-surface $MS{S}_6$.

Similarly, using a method similar to the above approach, we cannot take the picture $({\mathbb{Z}}^3,6,6,MS{S}_6)$ for $MS{S}_6$. □

To address the above question (Q2), we have the following:

Lemma 1.

Given an $MS{S}_6$, the only one type of $MS{S}_6♯MS{S}_6$ exists up to 6-isomorphism.

Proof. 

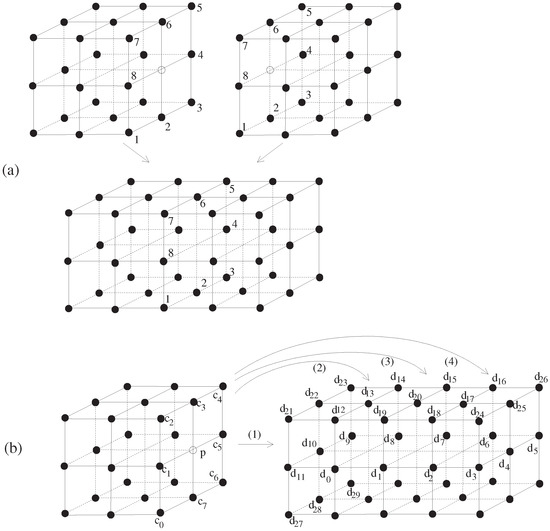
In order to formulate $MS{S}_6♯MS{S}_6$, we should follow Definition 6 and Remark 4. In this situation, it is obvious that we obtain six cases of $MS{S}_6♯MS{S}_6$ (see one of the cases in Figure 3a) which are 6-isomorphic to each other. Regarding the establishment of a connected sum $MS{S}_6♯MS{S}_6$, suppose some possibility of taking one of the points indicated by the numbers “$8$” or “$7$” in Figure 3a except the above-mentioned six points of $MS{S}_6$, e.g., the point p of Figure 3b. Then we have a contradiction to Remark 4. Hence we have the only one type of $MS{S}_6♯MS{S}_6$ as suggested in Figure 3a up to 6-isomorphism. □

Figure 3. (a) Process of constructing $MS{S}_6♯MS{S}_6$ [5]; (b) Configuration of ${\mathcal{C}}_6^3:=MS{S}_6♯MS{S}_6♯MS{S}_6$.

Regarding the question (Q3), we obtain the following:

Theorem 3.

In the case of ${\mathcal{C}}_6^n,n\in \mathbb{N}\backslash \{1,2\}$, many types of models for ${\mathcal{C}}_6^n$ exist.

Proof. 

Let us formulate ${\mathcal{C}}_6^3:=MS{S}_6♯MS{S}_6♯MS{S}_6$. As shown in Figure 3b, take a certain subset of $MS{S}_6$ which is $(6,4)$-isomorphic to the set $MS{C}_4^{*}$, e.g., the set ${\left(c_i\right)}_{i\in {[0,7]}_{\mathbb{Z}}}\cup \left\{p\right\}$ in $MS{S}_6$ (Figure 3b). Depending on the choice of the corresponding part in $MS{S}_6♯MS{S}_6$ (see Figure 3b), e.g., (1), (2), (3), and (4) in Figure 3b, we have different types of shapes for ${\mathcal{C}}_6^3:=MS{S}_6♯MS{S}_6♯MS{S}_6$. To be precise, if we follow Case (1) in Figure 3b, after deleting the two points p and $d_{10}$ in Figure 3b, we obtain ${\mathcal{C}}_6^3$ by identifying the two sets $\left\{c_i\right|i\in {[0,7]}_{\mathbb{Z}}\}$ and $\{d_{27},d_{11},d_{21},d_{22},d_{23},d_9,d_{29},d_{28}\}$ (see the method of Definition 6).

If we follow Case (2) in Figure 3b, after deleting the two points p and $d_{13}$ in Figure 3b, we obtain ${\mathcal{C}}_6^3$ by identifying the two sets $\left\{c_i\right|i\in {[0,7]}_{\mathbb{Z}}\}$ and $\{d_{12},d_{19},d_{20},d_{15},d_{14},d_{23},d_{22},d_{21}\}$ (see the method of Definition 6).

Using a method similar to these two approaches, after following Cases (3) and (4), we can also obtain ${\mathcal{C}}_6^3$. Then we observe some different shapes between the ${\mathcal{C}}_6^3$ established via (2) and those formulated via (1) or (3). As a generalization of ${\mathcal{C}}_6^3$, we obviously obtain several types of models for ${\mathcal{C}}_6^n,n\in \mathbb{N}\backslash \{1,2\}$. □

Motivated by Theorem 1 of [8], we obtain the following:

Remark 6.

[7] Given a closed 6-surface $S_6$ in the picture $({\mathbb{Z}}^3,6,26,S_6)$, we obtain that $S_6♯MS{S}_6$ is a simple closed 6-surface in the picture $({\mathbb{Z}}^3,6,26,S_6♯MS{S}_6)$.

5. Existence of Only Two Types of ${\mathcal{C}}_{18}^n:=\stackrel{n-\mathrm{times}}{\overbrace{MS{S}_{18}♯\cdots ♯MS{S}_{18}}},n\ge 2$

This section proves an existence of only two types of ${\mathcal{C}}_{18}^n:=\stackrel{n-\mathrm{times}}{\overbrace{MS{S}_{18}♯\cdots ♯MS{S}_{18}}},n\ge 2$. When establishing ${\mathcal{C}}_{18}^n$, we assume ${\mathcal{C}}_{18}^n:={\mathcal{C}}_{18}^{n-1}♯MS{S}_{18},n\ge 2$. Before studying ${\mathcal{C}}_{18}^n,n\ge 2$, we now investigate some properties of $MS{S}_{18}$ involving a choice of a suitable digital picture for $MS{S}_{18}$.

Remark 7.

Using a similar method as that of Remark 5, we obtain the following:

(1) 

The set $MS{S}_{18}$ cannot be a simple closed 18-surface in the picture $({\mathbb{Z}}^3,18,18,MS{S}_{18})$.

(2) 

The set $MS{S}_{26}^{\prime }$ cannot be a simple closed 26-surface in the picture $({\mathbb{Z}}^3,26,18,MS{S}_{26}^{\prime })$.

Based on the digital connected sums of $MS{S}_6$, $MS{S}_{18}$, $MS{S}_{18}^{\prime }$, and $MS{S}_{26}^{\prime }$ introduced [5], in order to study them more systematically, we need to address the following query.

(Q4) Given an $MS{S}_{18}$, how many types of $MS{S}_{18}♯MS{S}_{18}$ exist ?

Let ${\mathcal{C}}_{18}^n:=\stackrel{n-\mathrm{times}}{\overbrace{MS{S}_{18}♯\cdots ♯MS{S}_{18}}}$. Then we have the following question:

(Q5) How can we formulate ${\mathcal{C}}_{18}^n,n\in \mathbb{N}\backslash \left\{1\right\}$ ?

Based on the establishment of $MS{S}_{18}♯MS{S}_{18}$ in [5,7], we need to address the query of (Q4), as follows:

Theorem 4.

Given an $MS{S}_{18}$, we obtain the following:

(1) 

Only two types of $MS{S}_{18}♯MS{S}_{18}$ exist up to 18-isomorphism.

(2) 

In the case of ${\mathcal{C}}_{18}^n,n\in \mathbb{N}\backslash \{1,2\}$, only two methods are admissible in establishing ${\mathcal{C}}_{18}^n$ up to 18-isomorphism.

Proof. 

First of all, we need to ask if there is a certain possibility of taking a set $A_{18}(\subset MS{S}_{18})$ which is respectively $(18,4)$- and $(18,8)$-isomorphic to $MS{C}_4^{*}$ and $MS{C}_8^{*}$, or $MS{C_8^{\prime }}^{*}$ (see Definition 6). Then we can recognize that there are only six subsets in $MS{S}_{18}$ satisfying this requirement, such as (see the set in Figure 4a)

$$\left\{\begin{array}{c}\left(1\right)\{c_0,c_1,c_2,c_3,c_4,c_5,c_8,c_9\},\left\{c_i\right|i\in {[0,7]}_{\mathbb{Z}}\},\hfill \\ \left(2\right)\{c_0,c_1,c_2,c_3,c_6,c_7,c_8,c_9\},\{c_0,c_6,c_7,c_3,c_4,c_5,c_8,c_9\},\hfill \\ \left(3\right)\{c_2,c_7,c_4,c_8,c_3\},\{c_1,c_6,c_5,c_9,c_0\}.\hfill \end{array}\right\}$$

(12)

Figure 4. Explanation of the only two types of $MS{S}_{18}♯MS{S}_{18}$ in terms of the processes via (a) or (b) [5].

According to these considerations of (12), we now consider two cases, as follows:

• (Case 1) Based on the cases of (12) (1)–(2), in the case that we follow the method suggested in Figure 4a, we obtain $MS{S}_{18}♯MS{S}_{18}=MS{S}_{18}$ [5]. Eventually, if we take this process for obtaining ${\mathcal{C}}_{18}^n$, then we have ${\mathcal{C}}_{18}^n=MS{S}_{18}$.
  (Case 2) Based on the cases of (12) (3), according to the method suggested in Figure 4b, i.e., in the case $MS{S}_{18}♯MS{S}_{18}\ne MS{S}_{18}$, we now prove that there is only one type of $MS{S}_{18}♯MS{S}_{18}$ up to 18-isomorphism. To be precise, after identifying two sets denoted by the set $\{1,2,3,4\}$ of $MS{S}_{18}$ (see Figure 4b), we obtain $MS{S}_{18}♯MS{S}_{18}$. Hence, we have only one way to proceed to $MS{S}_{18}♯MS{S}_{18}$ as proposed in Figure 4b up to 18-isomorphism. Eventually, we uniquely obtain ${\mathcal{C}}_{18}^n$ in terms of ${\mathcal{C}}_{18}^n:={\mathcal{C}}_{18}^{n-1}♯MS{S}_{18}$. □

Remark 8.

When constructing $MS{S}_{18}♯MS{S}_{18}^{\prime }$, we only take the part suggested in (12) (3) so that we obtain $MS{S}_{18}♯MS{S}_{18}^{\prime }=MS{S}_{18}$ [5].

As mentioned in [5], we obtain the following:

Corollary 4.

(1) For a simple closed 18-surface $S_{18}$, $MS{S}_{18}^{\prime }♯S_{18}$ is a simple closed 18-surface.

(2) $MS{S}_{18}^{\prime }♯MS{S}_{18}^{\prime }=MS{S}_{18}^{\prime }$ [7].

6. Digital 18-Contractibility of ${\mathcal{C}}_{18}^n$ and Simply k-Connectedness of ${\mathcal{C}}_k^n$, $k\in \{6,18,26\}$

This section explores the digital 18-contractibility of ${\mathcal{C}}_{18}^n$ and the simply k-connectedness of ${\mathcal{C}}_k^n$, $k\in \{6,18,26\}$. Hereafter, we consider the process ${\mathcal{C}}_{18}^n:={\mathcal{C}}_{18}^{n-1}♯MS{S}_{18}$ and assume the case $MS{S}_{18}^{\prime }♯MS{S}_{18}\ne MS{S}_{18}$. As stated in the proof of Theorem 4, we obtain the following:

Lemma 2.

In case ${\mathcal{C}}_{18}^2:=MS{S}_{18}♯MS{S}_{18}\ne MS{S}_{18}$, ${\mathcal{C}}_{18}^3={\mathcal{C}}_{18}^2♯MS{S}_{18}$ uniquely exists up to 18-isomorphism.

Definition 7.

[17] For a k-connected digital image $(X,k)$, if ${\pi }_1^k\left(X\right)$ trivial, then we say that $(X,k)$ is simply k-connected.

Lemma 3.

[4,5,6,8] Each of ${\pi }_1^6\left(MS{S}_6\right)$, ${\pi }_1^{18}\left(MS{S}_{18}\right)$, ${\pi }_1^{18}\left(MS{S}_{18}^{\prime }\right)$, and ${\pi }_1^{26}\left(MS{S}_{26}^{\prime }\right)$ is trivial.

Proof. 

First of all, we see that the 6-fundamental group of $MS{S}_6$ is a trivial group [8]. Next, we see that each of $MS{S}_{18}$ and $MS{S}_{18}^{\prime }$ is 18-contractible and further, $MS{S}_{26}^{\prime }$ is 26-contractible, the proof is completed. □

Proposition 3.

A simple closed 6-surface $S_6$ is simply 6-connected.

Proof. 

It is obvious that $S_6$ is 6-connected. Using a trivial extension of a 6-loop on $S_6$, we see that any 6-loop on $S_6$ is 6-null homotopic in $S_6$ so that ${\pi }_1^6\left(S_6\right)$ is trivial, which completes the proof. □

Indeed, in [5] we stated the simple closed k-surface structure of a connected sum of two simple closed k-surfaces (see Theorem 5.4 of [5]).

Corollary 5.

[8] Given two simple closed k-surfaces $S_k$ and $S_k^{\prime }$ in ${\mathbb{Z}}^3$, $S_k♯S_k^{\prime }$ is a simple closed k-surface in ${\mathbb{Z}}^3$.

Theorem 5.

The n-times of connected sums of $MS{S}_6$, ${\mathcal{C}}_6^n:=\stackrel{n-\mathrm{times}}{\overbrace{MS{S}_6♯\cdots ♯MS{S}_6}}$, is simply 6-connected.

Proof. 

For convenience, for ${\mathcal{C}}_6^n:=\stackrel{n-\mathrm{times}}{\overbrace{MS{S}_6♯\cdots ♯MS{S}_6}}$, using a method similar to the proof of the triviality of ${\pi }_1^6\left(MS{S}_6\right)$, since any 6-loop on ${\mathcal{C}}_6^n$ is proved to be 6-null homotopic in ${\mathcal{C}}_6^n$ by using a trivial extension, we obtain that ${\pi }_1^6\left({\mathcal{C}}_6^n\right)$ is trivial. Besides, since ${\mathcal{C}}_6^n$ is 6-connected, the proof is completed. □

Since $MS{S}_6$ is not 6-contractible, we obtain the following:

Remark 9.

The connected sum ${\mathcal{C}}_6^n$ is not 6-contractible.

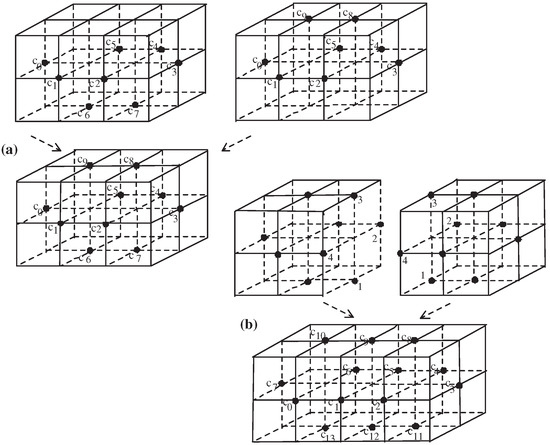
Let us now prove the 18-contractibility of ${\mathcal{C}}_{18}^n,n\in \mathbb{N}$, as follows:

Theorem 6.

The n-times of connected sums of $MS{S}_{18}$, ${\mathcal{C}}_{18}^n:=\stackrel{n-\mathrm{times}}{\overbrace{MS{S}_{18}♯\cdots ♯MS{S}_{18}}}$, is 18-contractible.

Before proving the assertion, as mentioned in (Case 1) of Theorem 4, at the moment we may only deal with the case $MS{S}_{18}♯MS{S}_{18}\ne MS{S}_{18}$ because $MS{S}_{18}$ is 18-contractible (see the 18-homotopy of (9) of [8] and Figure 2b of [8]).

Proof. 

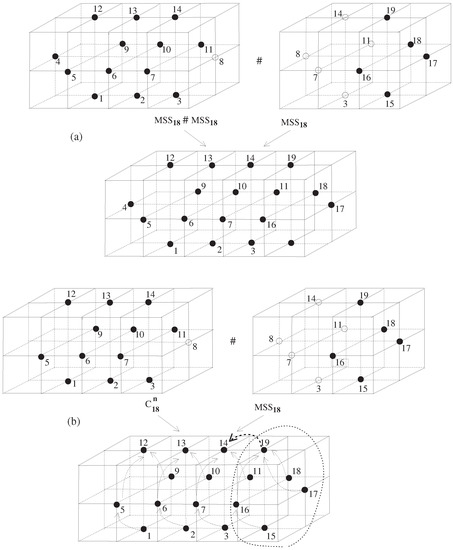
Let us prove the assertion using the mathematical induction.

(Step 1) A paper [8] proved that ${\mathcal{C}}_{18}^1:=MS{S}_{18}$ is 18-contractible (Remark 3 or the 18-homotopy of (9) proposed at the just above of Remark 2 of [8]).

(Step 2) For any $n\in \mathbb{N}$, assume that ${\mathcal{C}}_{18}^n$ is 18-contractible.

Let us now prove that ${\mathcal{C}}_{18}^{n+1}$ is 18-contractible. Owing to the 18-contractibility of ${\mathcal{C}}_{18}^n$, for some $m\in \mathbb{N}$, we may assume an 18-homotopy

$$H:{\mathcal{C}}_{18}^n\times {[0,m]}_{\mathbb{Z}}\to {\mathcal{C}}_{18}^n$$

(13)

supporting

$$1_{{\mathcal{C}}_{18}^n}{\simeq }_{18}{c}_{\left\{x_0\right\}}$$

for a certain point $x_0\in {\mathcal{C}}_{18}^n$.As usual, let

$${\mathcal{C}}_{18}^{n+1}:={\mathcal{C}}_{18}^n♯MS{S}_{18}.$$

(14)

At the moment we should assume that the point $x_0$ is not deleted in the process of (14). Then we now establish a map

$$H^{\prime }:{\mathcal{C}}_{18}^{n+1}\times {[0,m+m^{\prime }]}_{\mathbb{Z}}\to {\mathcal{C}}_{18}^{n+1},m^{\prime }\ge 1$$

(15)

such that the restriction of $H^{\prime }$ of (15) to the set $B:={\mathcal{C}}_{18}^{n+1}\backslash MS{S}_{18}$ is equal to the 18-homotopy H of (13) on B, where this $MS{S}_{18}$ is that of (14). Besides, we may assume $x_0\in B$ and the singleton $\left\{x_0\right\}$ is that of (13). We now need only consider the remaining part ${\mathcal{C}}_{18}^{n+1}\backslash {\mathcal{C}}_{18}^n$ (see the right part of the dotted arrow of Figure 5b). Using a method of the 18-contractibility of $MS{S}_{18}$ combined with the given 18-homotopy H of (13) (see Figure 5b), we finally have an 18-homotopy $H^{\prime }$ on ${\mathcal{C}}_{18}^{n+1}$ as in (15) supporting

$$1_{{\mathcal{C}}_{18}^{n+1}}{\simeq }_{18}{c}_{\left\{x_0\right\}}$$

for a the point $x_0\in {\mathcal{C}}_{18}^{n+1}$ (see the right part of Figure 5b shown by using the bold dotted arrow or the dotted ones). □

Figure 5. (a) Explanation of the process of establishing ${\mathcal{C}}_{18}^3:={\mathcal{C}}_{18}^2♯MS{S}_{18}$. (b) Configuration of an 18-homotopy $H:{\mathcal{C}}_{18}^{n+1}\times {[0,m+m^{\prime }]}_{\mathbb{Z}}\to {\mathcal{C}}_{18}^{n+1},m^{\prime }\ge 1$.

To explain the process of the proof of Theorem 6.7, motivated by the 18-contractibility of $MS{S}_{18}$ (see Lemma 1 and Figure 2 of [8]), we now consider the following:

Corollary 6.

${\mathcal{C}}_{18}^2$ is 18-contractible.

Proof. 

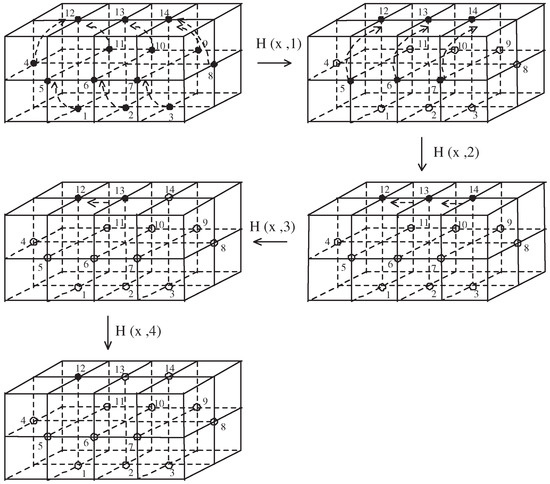
Let us consider the map (see Figure 6)

$$H:{\mathcal{C}}_{18}^2\times {[0,4]}_{\mathbb{Z}}\to {\mathcal{C}}_{18}^2$$

(16)

defined by

$$H(x,0)=1_{{\mathcal{C}}_{18}^2}\left(x\right),x\in {\mathcal{C}}_{18}^2.$$

$$H(x,1)=\left\{\begin{array}{c}5,x\in \{1,5\};\hfill \\ 12,x\in \{4,11,12\};\hfill \\ 6,x\in \{2,6\};\hfill \\ 13,x\in \{10,13\};\hfill \\ 7,x\in \{3,7\};\mathrm{and}\hfill \\ 14,x\in \{8,9,14\}.\hfill \end{array}\right\}$$

$$H(x,2)=\left\{\begin{array}{c}12,x\in \{1,4,5,11,12\}\hfill \\ 13,x\in \{2,6,10,13\};\mathrm{and}\hfill \\ 14,x\in \{3,7,8,9,14\}.\hfill \end{array}\right\}$$

$$H(x,3)=\left\{\begin{array}{c}12,x\in \{1,2,4,5,6,10,11,12,13\};\mathrm{and}\hfill \\ 13,x\in \{3,7,8,9,14\}.\hfill \end{array}\right\}$$

$$H(x,4)=c_{\left\{12\right\}}\left(x\right),x\in {\mathcal{C}}_{18}^2.$$

Then the map of $\left(16\right)$ is an 18-homotopy making ${\mathcal{C}}_{18}^2$ 18-contractible, i.e., $1_{{\mathcal{C}}_{18}^2}{\simeq }_{18}{c}_{\left\{12\right\}}$. □

Figure 6. Configuration of the 18-homotopy of (16) involving the 18-contractibility of ${\mathcal{C}}_{18}^2$ (see the proof of Corollary 6).

Corollary 7.

The n-times of connected sum of $MS{S}_{26}^{\prime }$, denoted by ${\mathcal{C}}_{26}^n$, is 26-contractible.

Proof. 

Since there is only one type of $MS{S}_{26}^{\prime }♯MS{S}_{26}^{\prime }=MS{S}_{26}^{\prime }$, ${\mathcal{C}}_{26}^n$ is equal to $MS{S}_{26}^{\prime }$ which is 26-contractible, the proof is completed. □

7. Non-almost Fixed Point Property of ${\mathcal{C}}_k^n,k\in \{6,18\}$

This section investigates if each of ${\mathcal{C}}_6^2$ and ${\mathcal{C}}_{18}^n$ has the AFPP. In order to address the problems proposed with (Q6)–(Q8), let us now recall the category of digital topological spaces and further, the fixed point property and the almost fixed point property from the viewpoint of digital topology.

• We denote by $DTC$ the category consisting of two data: The set of digital images $(X,k)$ as $Ob\left(DTC\right)$ and the set of $(k_0,k_1)$-continuous maps between every pair of digital images $(X,k_0)$ and $(Y,k_1)$ in $Ob\left(DTC\right)$ as $Mor\left(DTC\right)$ [18].
• We say that a digital image $(X,k)$ in ${\mathbb{Z}}^n$ has the fixed point property (for short FPP) [23] if for every k-continuous map $f:(X,k)\to (X,k)$ there is a point $x\in X$ such that $f\left(x\right)=x$.

Due to the study of the non-FPP of a digital picture (or digital image) in [23] (see Theorem 4.1 of [23]), it is clear that only the digital image (or a digital picture) $(X,k)$ with $\left|X\right|=1$ has the FPP because a singleton set obviously has the FPP in DTC. Thus we need to recall the following (see Theorem 4.1 of [23] and Remark 4.3 of [34]):

Remark 10.

[23,34] Only a digital image $(X,k)$ with $\left|X\right|=1$ has the FPP.

This property is obviously a certain implication of Theorems 3.3 and 4.1 of [23]. For the convenience of readers, we now confirm the assertion more precisely.

Proof. 

To wit the assertion, when establishing the notion of AFPP in [23] (see the bottom of the page 179 of [23]), we obviously find that Rosenfeld [23] stated two theorems such as Theorems 3.3 and 4.1 of [23] relating to the above assertion. More precisely, as mentioned in the above part (see the part just below Section 4 of [23]), a paper [23] finally mentioned the AFPP of an n-dimensional digital picture $(I^n,3^n-1)$ or a general picture $(X,3^n-1)$ in ${\mathbb{Z}}^n$. For instance, for the case of $({[a,b]}_{\mathbb{Z}},2),a\ne b$, Rosenfeld [23] proved the AFPP of it (see Theorem 3.3 of [23]). To be precise, for any 2-continuous self-map f of $({[a,b]}_{\mathbb{Z}},2)$, it turns out that $({[a,b]}_{\mathbb{Z}},2)$ has the AFPP instead of the FPP. Then, Theorem 3.3 implies that not every 2-continuous self-map f of $({[a,b]}_{\mathbb{Z}},2)$ support the FPP of it. However, the assertion supports the AFPP of $({[a,b]}_{\mathbb{Z}},2)$ instead of the FPP. Obviously, take a point $x\in {[a,b]}_{\mathbb{Z}}$ and $N_2(x,1)\subset {[a,b]}_{\mathbb{Z}}$. Then consider any point $x^{\prime }(\ne x)\in N_2(x,1)$ and further, according to Theorem 3.3 of [23], consider a self-map f of $({[a,b]}_{\mathbb{Z}},2)$ defined by $f\left(t\right)=x$ for all $t(\ne x)\in {[a,b]}_{\mathbb{Z}}$, and $f\left(x\right)=x^{\prime }$. Then, the map f is obviously 2-continuous and f implies that $({[a,b]}_{\mathbb{Z}},2)$ does not have the FPP. As a good example, consider a simple digital interval $({[0,1]}_{\mathbb{Z}},2)$ and consider the self-map f of it, say $f\left(0\right)=1$ and $f\left(1\right)=0$ which supports Theorem 3.3 of [23], which implies the AFPP of it instead of the FPP. Similarly, as mentioned in the beginning part of Section 4 of [23], the paper [23] proved that the n-dimensional case $(I^n,3^n-1)$ or a general picture $(X,3^n-1)$ in ${\mathbb{Z}}^n$ (see Theorem 4.1 of [23]) has the AFPP instead of the FPP. Eventually, with the same method as above, for any general digital image $(X,k)$ in ${\mathbb{Z}}^n$, we confirm the assertion of Remark 10. □

Owing to Remark 10, it turns out that the study of the FPP in DTC is very trivial. Henceforth, Rosenfeld [23] firstly studied the almost fixed point property for digital images. Hence we need to stress the AFPP in DTC.

• We say that a digital image $(X,k)$ in ${\mathbb{Z}}^n$ has the almost fixed point property (for short AFPP) [23] if for every k-continuous self-map f of $(X,k)$, there is a point $x\in X$ such that $f\left(x\right)=x$ or $f\left(x\right)$ is k-adjacent to x.

Furthermore, a paper [8] proved that each of $MS{S}_{18}$ and $MS{S}_{18}^{\prime }$ does not have the AFPP (see Theorem 7 below). Thus the study of the AFPP of ${\mathcal{C}}_k^n,n\in \mathbb{N}\backslash \left\{1\right\},k\in \{6,18\}$ remains. Let us now address this issue.

Theorem 7.

[8] (1) $MS{S}_{18}$ does not have the AFPP.

(2) $MS{S}_{18}^{\prime }$ does not have the AFPP.

For ${\mathcal{C}}_6^n:=\stackrel{n-\mathrm{times}}{\overbrace{MS{S}_6♯\cdots ♯MS{S}_6}}$ and ${\mathcal{C}}_{18}^n:=\stackrel{n-\mathrm{times}}{\overbrace{MS{S}_{18}♯\cdots ♯MS{S}_{18}}}$, motivated by Theorem 7, we may impose the following queries involving the AFPP of ${\mathcal{C}}_6^n$ and ${\mathcal{C}}_{18}^n$.

(Q6) How about the AFPP of ${\mathcal{C}}_6^n,n\in \mathbb{N}$ ?

(Q7) How about the AFPP of ${\mathcal{C}}_{18}^n,n\in \mathbb{N}$ ?

To address these two queries, we first prove the non-AFPP of $MS{S}_6$, as follows:

Lemma 4.

$MS{S}_6$ does not have the AFPP.

Proof. 

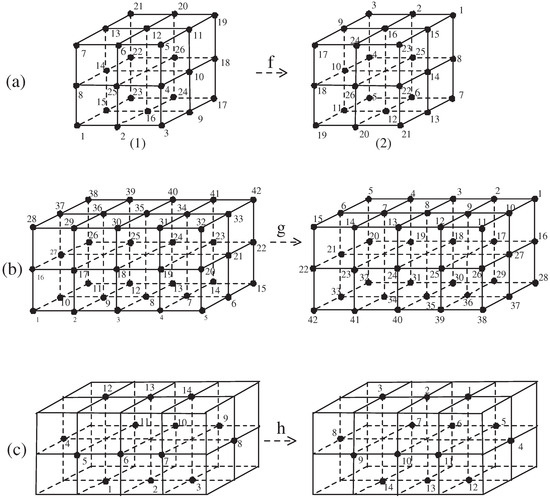
Consider the set $MS{S}_6$ in Figure 7a(1). Then, let f be a self-map of $MS{S}_6$ which is the composite of the three times reflections of $MS{S}_6$ according to the three $xy$-, $yz$-, and $xz$-planes in ${\mathbb{R}}^3$ (see the image of the map f on the set $MS{S}_6$ of Figure 7a(2)). Whereas the map f of Figure 7a is obviously a 6-continuous self-bijection of $MS{S}_6$, it does not support the AFPP of $MS{S}_6$. □

Figure 7. (a) Configuration of the AFPP of $MS{S}_6$. (b) Configuration of the non-AFPP of ${\mathcal{C}}_6^2:=MS{S}_6♯MS{S}_6$. (c) In case $MS{S}_{18}♯MS{S}_{18}\ne MS{S}_{18}$, configuration of the non-AFPP of ${\mathcal{C}}_{18}^2$.

Theorem 8.

The digital image ${\mathcal{C}}_6^2$ in the binary picture $({\mathbb{Z}}^3,6,26,{\mathcal{C}}_6^2)$ does not have the $AFPP$.

Before proving the assertion, due to Lemma 1, we recall that ${\mathcal{C}}_6^2$ uniquely exists up to 6-isomorphism.

Proof. 

Consider the set ${\mathcal{C}}_6^2$ in Figure 7a(2). Then assume a self-map g of ${\mathcal{C}}_6^2$ which is the composite of the three times reflections of $MS{S}_6$ according to the three $xy$-, $yz$-, and $xz$-planes in ${\mathbb{R}}^3$ (see the image of the map g of ${\mathcal{C}}_6^2$ in Figure 7a(2)). Whereas the map g is obviously a 6-continuous bijection, it does not support the AFPP of ${\mathcal{C}}_6^2$. □

Corollary 8.

Let ${\mathcal{C}}_6^n$ be assumed as the set formulated via the method suggested in Figure 3b(1). The image ${\mathcal{C}}_6^n$ in the binary picture $({\mathbb{Z}}^3,6,26,{\mathcal{C}}_6^n)$ does not have the $AFPP$.

As a generalization of the non-AFPP of $MS{S}_{18}$ referred to in Theorem 7, we obtain the following:

Theorem 9.

The digital image ${\mathcal{C}}_{18}^n$ in the binary picture $({\mathbb{Z}}^3,18,6,{\mathcal{C}}_{18}^n)$ does not have the $AFPP$.

Proof. 

(Case 1) In case $MS{S}_{18}♯MS{S}_{18}=MS{S}_{18}$, we observe that ${\mathcal{C}}_{18}^n=MS{S}_{18}$. To be specific, by Theorem 7, we obtain ${\mathcal{C}}_{18}^n:={\mathcal{C}}_{18}^{n-1}♯MS{S}_{18}$ does not have the AFPP in DTC.

(Case 2) In case $MS{S}_{18}♯MS{S}_{18}\ne MS{S}_{18}$, let us now prove the non-AFPP of ${\mathcal{C}}_{18}^n$. With the hypothesis, by Theorem 4, we see that ${\mathcal{C}}_{18}^n$ has the shape suggested in Figure 7c (just an example for ${\mathcal{C}}_{18}^2$ in Figure 7c). Then, let h be a self-map of ${\mathcal{C}}_{18}^n$ which is the composite of the three times reflections of ${\mathcal{C}}_{18}^n$ according to the $xy$-, $yz$-, and $xz$-planes in ${\mathbb{R}}^3$. Whereas the map h is obviously an 18-continuous map, it does not support the AFPP of ${\mathcal{C}}_{18}^n$. □

In order to generalize Theorem 9, we need the following notion which is stronger than the isomorphism of Definition 1.

Definition 8.

We say that a closed k-surface $S_k$ in the picture $({\mathbb{Z}}^3,k,\overline{k},S_k)$ is $(k,\overline{k})$-isomorphic to $(X,k)$ in the picture $({\mathbb{Z}}^3,k,\overline{k},X)$, $k\in \{6,18,26\}$ if

(1) 

$S_k(\subset {\mathbb{Z}}^3)$ is k-isomorphic to $(X,k)$ and

(2) 

$({\mathbb{Z}}^3\backslash S_k,\overline{k})$ is $\overline{k}$-isomorphic to $({\mathbb{Z}}^3\backslash X,\overline{k})$.

Remark 11.

Comparing the isomorphism of Definition 1 and that of Definition 8, we observe that they are different.

As a generalization of Theorems 8 and 9, and Corollary 8, we obtain the following:

Proposition 4.

Consider a (simple) closed k-surface $S_k$ in $({\mathbb{Z}}^3,k,\overline{k},S_k)$, $k\in \{6,18,26\}$ with the binary relations of (11). If it is $(k,\overline{k})$-isomorphic to $(X,k)$ in the picture $({\mathbb{Z}}^3,k,\overline{k},X)$ and the set X is symmetric according to each of $xy$-, $yz$-, and $xz$-planes of ${\mathbb{R}}^3$, then $S_k$ does not have the AFPP.

Proof. 

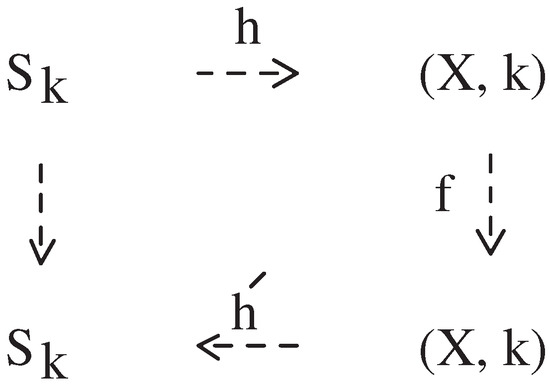
With the hypothesis, we proceed with the following several steps for proving the assertion. For convenience we may assume $S_k:=\left\{s_i\right|i\in {[1,m]}_{\mathbb{Z}}\}$ for some $m\in \mathbb{Z}$.

(Step 1) Take a $(k,\overline{k})$-isomorphism h from $S_k$ to $(X,k)$ in the given digital pictures (see Figure 8), where $X:=\left\{x_i\right|i\in {[1,m]}_{\mathbb{Z}},x_i:=h\left(s_i\right)\}$. Namely, we may assume a $(k,\overline{k})$-isomorphism $h:S_k\to (X,k)$ defined by $h\left(s_i\right)=x_i,i\in {[1,m]}_{\mathbb{Z}}$.

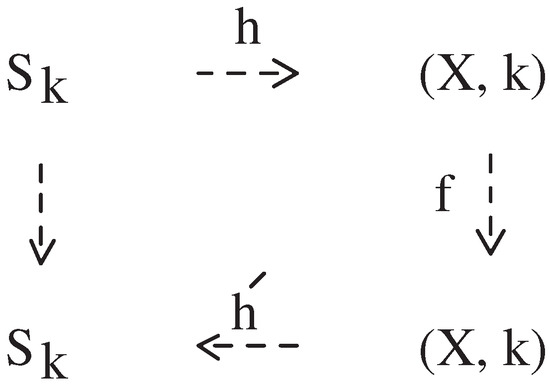
Figure 8. Explanation of the composite $h^{\prime }\circ f\circ h$.

(Step 2) Given the set $(X,k)$, proceed to the composite of the three times of different reflections of $(X,k)$ according to the certain $xy$-, $yz$-, and $xz$-planes in ${\mathbb{R}}^3$ which is a k-continuous bijection (or a k-isomorphism). Then we denote the composite with the self-map f of $(X,k)$. For convenience, put $f\left(x_i\right)=x_j$, $i,j\in {[1,m]}_{\mathbb{Z}}$ and we see $i\ne j$.

(Step 3) We denote the digital image being proceeded with (Step 2) with $(X^{\prime },k)$, i.e., $f\left(X\right):=X^{\prime }:=\{x_j|x_j=f\left(x_i\right)|j\in {[1,m]}_{\mathbb{Z}}\}$. Then we see that the k-isomorphism f supports the non-AFPP (see the proof of Theorem 8). Indeed, although the set $X^{\prime }$ is equal to the set X, the subscript of each of all elements is completely changed from $x_i$ to $x_j$, $i\ne j$.

(Step 4) After assigning each element $s_i\in S_k$ with $s_j\in S_k$ such that

$$s_j:=h^{-1}\circ f^{-1}\left(x_i\right),i,j\in {[1,m]}_{\mathbb{Z}},$$

we obtain the set $S_k^{\prime }:=\left\{s_j\right|j\in {[1,m]}_{\mathbb{Z}}\}$. Indeed, although $S_k^{\prime }=S_k$ as a set, we see that each element $s_i\in S_k$ is changed into another element $s_j\in S_k$. Consider the map $h^{\prime }:(X(=X^{\prime }),k)\to S_k(=S_k^{\prime })$ defined by

$$h^{\prime }\left(x_j\right)=s_j\in S_k^{\prime }=S_k,j\in {[1,m]}_{\mathbb{Z}}.$$

(Step 5) We finally obtain the composite of h, f, and $h^{\prime }$(see Figure 8), i.e.,

$$h^{\prime }\circ f\circ h:S_k\to S_k,$$

(17)

such that

$$h^{\prime }\circ f\circ h\left(s_i\right)=h^{\prime }\left(f\left(h\left(s_i\right)\right)\right)=h^{\prime }\left(f\left(x_i\right)\right)=h^{\prime }\left(x_j\right)=s_j.$$

Finally, we see that the composite $h^{\prime }\circ f\circ h$ is a certain k-continuous bijection (or a k-isomorphism) of $S_k$ which does not support the AFPP of $S_k$. □

Remark 12.

Proposition 4 includes the assertions of Theorems 7, 8, 9, and Lemma 4.

8. Conclusions and Further Work

After formulating ${\mathcal{C}}_k^n$, $k\in \{6,18,26\}$, the present paper proved that there are only two types of connected sums $MS{S}_{18}♯MS{S}_{18}$ up to 18-isomorphism, only one type of $MS{S}_6♯MS{S}_6$ up to 6-isomorphism and further, several types of connected sums ${\mathcal{C}}_6^3:=MS{S}_6♯MS{S}_6♯MS{S}_6$. Furthermore, it turns out that there are several types of connected sums for ${\mathcal{C}}_6^3:=MS{S}_6♯MS{S}_6♯MS{S}_6$. Besides, in case $MS{S}_{18}♯MS{S}_{18}\ne MS{S}_{18}$ up to 18-isomorphism, we proved that ${\mathcal{C}}_{18}^n:=\stackrel{\mathrm{n}-\mathrm{times}}{\overbrace{MS{S}_{18}♯\cdots ♯MS{S}_{18}}}$ uniquely exists up to 18-isomorphism. In addition, we proved the digital k-contractibility of ${\mathcal{C}}_k^n:=\stackrel{\mathrm{n}-\mathrm{times}}{\overbrace{MS{S}_k♯\cdots ♯MS{S}_k}},k\in \{18,26\}$ and further, the simply k-connectedness of ${\mathcal{C}}_k^n$, $k\in \{6,18,26\}$, $n\in \mathbb{N}$. Finally, we explored the non-AFPP of each of ${\mathcal{C}}_6^2$, ${\mathcal{C}}_{18}^n$ and ${\mathcal{C}}_{26}^n$. In view of several homotopic properties of $MS{S}_6$, $MS{S}_{18}$, $MS{S}_{18}^{\prime }$, and $MS{S}_{26}^{\prime }$ and further, the non-AFPP of them and their connected sums, we obtain the following:

As a further work, based on Proposition 4, we need to further study the AFPP of ${\mathcal{C}}_6^n,n\in \mathbb{N}\backslash \{1,2\}$ according to the processes associated with Figure 3b(2), (3), and (4). As mentioned above, some homotopic features of the models $MS{S}_6$, $MS{S}_{18}$, $MS{S}_{18}^{\prime }$, $MS{S}_{26}^{\prime }$ play important roles in digital topology and digital geometry because each of them can be considered to be the typical sphere-like model in Euclidean topology. Hence, the features referred to in Figure 9 facilitate studying many objects involving AFPP for digital images. Furthermore, the notion of digital connected sum also plays a crucial role in digital geometry because it can contribute to formulating another surface from two given surfaces. Besides, using the new topological structures in [36], we can study the FPP and AFPP of $S_k$ as subspaces of the newly-established topological structures. Finally, considering the geometric realization of a digital k-surface with an $SST$-structure in [37], we can deal with them from the viewpoint of computational geometry. In addition, after establishing a certain cone metric on a digital image [38,39,40,41,42], we need to further compare the current digital metric spaces using a length of simple k-path with cone metric spaces.

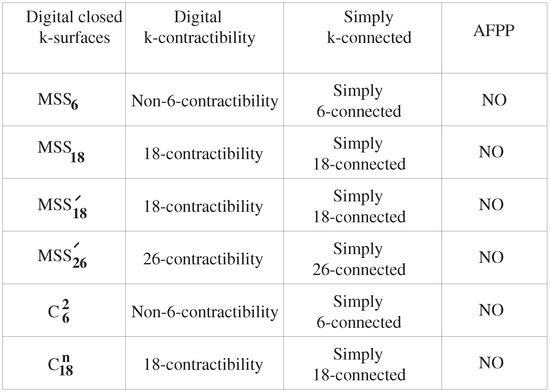
Figure 9. Digital topological properties of the non-AFPP of the minimal simple closed k-surfaces $MS{S}_6$, $MS{S}_{18}$, $MS{S}_{18}^{\prime }$, $MS{S}_{26}^{\prime }$, ${\mathcal{C}}_6^2$, and ${\mathcal{C}}_{18}^n$.