Adaptive Output Synchronization of General Complex Dynamical Network with Time-Varying Delays

Abstract

This paper is concerned with the output synchronization problems for a class of delayed complex dynamical networks. Based on the invariant principle of functional differential equations and Lyapunov stability theory, the feedback controller and parameter update laws are constructed for a large-scale network with uncertainties. The general complex delayed network can achieve synchronization by adaptively adjusting their feedback gains. Numerical examples are presented to further verify the effectiveness of the proposed control scheme.

1. Introduction

Ever since small-world and scale-free features were discovered in many real-world networks (see [1,2] and the references therein) synchronization in complex dynamical network has attracted much attention for its potential application in [3,4,5,6,7,8,9,10,11,12,13]. It is motivated by a broad area of potential applications: Networks of robots, formations of flying and underwater vehicles, control of industrial, electrical, communication, and production networks, etc. Thus, synchronization control for a general complex dynamical network becomes a new subject of active research. By introducing various complex dynamical network models, fruitful theoretical and applicable results have been studied for the corresponding synchronization issues in [14,15,16,17]. It is well known that under some extremely strict conditions, complex dynamical network models can achieve synchronization, especially for chaotic synchronization. In the past decades, many control methods have been proposed for chaotic synchronization, see [11,18,19] and the references therein. Min et al. [18] studied the synchronization of three different chaotic systems by using the theory of discontinuous dynamical systems. Chen et al. designed a nonlinear synchronization controller with exponential function, and realized the projection synchronization of two magnetically controlled memory chaotic systems in [19]. However, these methods focused mainly on synchronization of two identical systems, which is quite different from synchronization of complex networks. A key reason is that there are numerous mutual coupled cells in complex networks, with each one being a subsystem. What should be pointed out is that the coupling strengths of many complex networks are more likely to vary; they can even vary widely, e.g., [20].

Besides, there exist time delays in transmission due to limited transmission speeds or heavy traffic. It is almost impossible to learn the exact information of strength between cells or time delays, especially for a large-scale network. The existences of time delays can deteriorate the control performance and cause instability, see, e.g., [21,22,23,24,25,26,27,28,29]. In [21], an adaptive feedback strategy is proposed for a class of Takagi–Sugeno fuzzy complex networks with unknown topological structure and distributed time-varying delay, and the designed controller is only related to the dynamic behavior of directly related nodes. The authors of [22] researched the exponential synchronization of second-order nodes in dynamic networks with time-varying communication delays and switched communication topologies. The problem of synchronization control of complex dynamic networks with time-varying delays is studied in [27], a study in which is designed the synchronization controller of sampling system, which can make the generated synchronization error system stable. In [28], a global exponential synchronization criterion considering discrete time communication unit and delay is obtained by introducing a larger decision matrix. Hence, how to determine the appropriate feedback gain becomes an unavoidable problem if one adopts common error feedback control schemes. Actually, adaptive adjustment mechanisms are conveniently applied to the oretical analysis of uncertain closed-loop controlled systems. Motivated by the above discourse and examination, this paper will concentrate on adaptive output synchronization of general complex dynamical networks with time-varying delays.

The main contributions are listed as follows:

(i).

An appropriate adaptive output feedback synchronize problem is successfully solved for every cell output of general complex networks with time-varying delays.

(ii).

Based on the invariant principle of functional differential equations, the feedback controller and parameter update laws are constructed for a large-scale network with uncertainties. In addition, the general complex delayed network can achieve synchronization by adaptively adjusting their feedback gains.

(iii).

Numerical examples are presented to demonstrate the effectiveness of the control scheme. Compared with the state-feedback case, the output synchronization of the general complex dynamical network is closer to the real application.

The rest of this article is arranged as follows. The general delayed complex dynamical networks are introduced in Section 2. The adaptive output feedback synchronization criteria and corresponding numerical simulations are given in Section 3 and Section 4, respectively. Section 5 concludes the paper.

2. Preliminaries and Model Description

Throughout the whole paper, R is the set of real numbers; $R^{+}$ denotes the set of all non-negative real numbers; $R^i$ is the i-dimensional Euclidean space; $\parallel ·\parallel$ denotes the Euclidean norm of a vector or its induced matrix norm and $|·|$ stands for the absolute value of a function or constant.

Lemma 1

(see [30]). For any vectors x, $y\in R^n$ and positive definite matrix $P\in R^{n\times n}$, the following linear matrix inequality holds: $2x^{T}y\le x^{T}Px+y^T{P}^{-1}y$.

The design goal of this paper is to design an output feedback controller for a class of nonlinear time-varying delay coupled complex dynamical network to achieve synchronous control. Without loss of generality, we consider a general dynamical network with time-varying delays [11], the network consists of N identical cells with diffusion linear coupling, each of which is an n-dimensional dynamic subsystem.

One considers

$$\left\{\begin{array}{c}{\dot{x}}_i\left(t\right)=f_i\left(x_i\right)+{\sum }_{j=1}^N{G}_{ij}\left(t\right)y_j\left(t\right)+{\sum }_{j=1}^N{\widehat{G}}_{ij}\left(t\right)y_j(t-\tau \left(t\right))+u_i\left(t\right),\hfill \\ y_i\left(t\right)=C{x}_i\left(t\right),i\in L=\{1,2,\cdots ,N\},\hfill \end{array}\right.$$

(1)

where $f_i(·)\in R^n$ is continuously differentiable, governing the dynamics of the isolated cell, $x_i={[x_{i1},x_{i2},\cdots ,x_{in}]}^T$ stands for the state variable of the i-th cell, $\tau \left(t\right)\ge 0$ represents the time delay, and $u_i\left(t\right)$ is the controller, $C\in R^{n\times n}$ is the output matrix with an inverse, the coupling matrices $G_{ij}\left(t\right),{\widehat{G}}_{ij}\left(t\right)\in R^{N\times N}$ describe the topology of the network and coupling strength between cells at time t, with $G_{ii}\left(t\right)$ (the diagonal entries ${\widehat{G}}_{ii}\left(t\right)$ can be defined in the same way) being

$$G_{ii}\left(t\right)=-\sum _{j=1,j\ne i}^N{G}_{ij}\left(t\right),i\in L.$$

(2)

Obviously, all entries of coupling matrices are time-varying bounded uncertainties such that

$$\begin{array}{c}\hfill \left\{\begin{array}{c}|G_{ij}\left(t\right)|<m\hfill \\ |{\widehat{G}}_{ij}\left(t\right)|<n\hfill \end{array}\right.\hspace{1em}\forall i,j=1,2,\cdots ,n\end{array}$$

with m, $n\in R^{+}$. For $f_i(·)\in R^n$, one has

$$f_i\left(x\right)-f_i\left(y\right)=M_{x,y}(x-y),\forall x,y\in R^n,$$

where $M_{x,y}=M(x,y)$ is a bounded matrix such that $\left|\right|M_{x,y}\left|\right|\le \alpha$ with $\alpha \in R^{+}$.

Remark 1.

Since $M_{x,y}$ is a bounded matrix, there must exist a constant ${\lambda }_m$ such that $\lambda (M_{x,y}+M_{x,y}^T)<{\lambda }_m$, where $\lambda (·)$ is the eigenvalue of the corresponding matrix.

The objective of this paper is to achieve an asymptotical output synchronization for (1). Such that

$$\underset{t\to \infty }{lim}(y_i\left(t\right)-\widehat{y}\left(t\right))=0,\forall i\in L,$$

(3)

where $\widehat{y}\left(t\right)=C^{T}s\left(t\right)$ is the synchronous output of the whole network. Consider

$$\dot{s}\left(t\right)=f\left(s\left(t\right)\right),$$

(4)

$s\left(t\right)$ is one solution of an isolated cell can be an equilibrium point, a periodic orbit, and an aperiodic orbit, or a chaotic orbit in the phase space. To realize the objective, the following assumption is imposed on System (1).

Assumption A1.

In general delayed systems, time delay $\tau \left(t\right)$, usually written as τ for simplification, satisfies

$$\left\{\begin{array}{c}0\le \tau \left(t\right)\le {\varsigma }_1\hfill \\ \dot{\tau }\left(t\right)\le {\varsigma }_2\le 1,\hfill \end{array}\right.$$

(5)

where ${\varsigma }_1$ and ${\varsigma }_2$ are both positive constants.

Remark 2.

This paper mainly studies a general dynamical network with time-varying delays. What should be emphasized is that Assumption 1 is reasonable and widely applied. Assumption 1 is generally and commonly adopted, see [7,8,10,11]. If the delay is too large or the delay changes too fast, the controller will fail. Assumption 1 can limit the time variation of the system to a certain range, and the model closer to the real application.

Let

$$\begin{array}{c}\hfill e_i\left(t\right)=x_i\left(t\right)-s\left(t\right),\\ \hfill {\epsilon }_i\left(t\right)=y_i\left(t\right)-\widehat{y}\left(t\right),\end{array}$$

(6)

the dynamical network (1) can achieve output synchronization if

$$\underset{t\to \infty }{lim}\left|\right|{\epsilon }_i{\left(t\right)\left|\right|}_2=\underset{t\to \infty }{lim}\left|\right|e_i\left(t\right){\left|\right|}_2=0,\forall i\in L.$$

(7)

3. Output Synchronization in Complex Delayed Networks

Consider Systems (1) and (6), the following error dynamical system can be achieved:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{e}}_i=M_{x_i,s}{e}_i+{\sum }_{j=1}^N{G}_{ij}{\epsilon }_j+{\sum }_{j=1}^N{\widehat{G}}_{ij}{\epsilon }_j^{\tau }+u_i,\hfill \\ {\epsilon }_i=C{e}_i,\hfill \end{array}\right.\end{array}$$

(8)

where ${\epsilon }_j^{\tau }={\epsilon }_j(t-\tau \left(t\right))$. Choose Lyapunov function,

$$\begin{array}{ccc}\hfill V\left(t\right)& =& \sum _{i=1}^N{V}_i(e_i,e_i^{\tau }),\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill V_i(e_i,e_i^{\tau })& =& \frac{1}{2}{e}_i^T{e}_i+\frac{1}{2}{H}^T{(K_i-l{I}_n)}^{2}H+\frac{1}{2(1-{\varsigma }_2)}{\int }_{t-\tau }^t{e}_i^T\left(\theta \right)e_i\left(\theta \right)d\theta ,\hfill \end{array}$$

(10)

where $e_i^{\tau }=e_i(t-\tau \left(t\right))$, $H={[1,1,\cdots ,1]}^T$, $I_n$ is an $n\times n$ unit matrix, and l is the normal constant to be determined. The time derivative of $V_i$ along the error dynamic system trajectory (8) is given by

$$\begin{array}{cc}\hfill {\dot{V}}_i& =\frac{1}{2}{\dot{e}}_i^T{e}_i+\frac{1}{2}{e}_i^T{\dot{e}}_i+H^T(K_i-l{I}_n){\dot{K}}_{i}H+\frac{1}{2}{\delta }_1{e}_i^T{e}_i-\frac{1}{2}{\delta }_2{e}_i^{\tau T}{e}_i^{\tau }\hfill \\ \hfill & =\frac{1}{2}{e}_i^T(M_{x_1,s}+M_{x_1,s}^T)e_i+\sum _{j=1}^N{G}_{ij}{e}_i^{T}C{e}_j+\sum _{j=1}^N{\widehat{G}}_{ij}{e}_i^{T}C{e}_j^{\tau }-\frac{1}{2}{e}_i^T(K_{i}C+C^T{K}_i)e_i\hfill \\ \hfill & +{\epsilon }_i^T(K_i{\mathsf{\Gamma }}_i-l{I}_n){\epsilon }_i+\frac{1}{2}{\delta }_1{e}_i^T{e}_i-\frac{1}{2}{\delta }_2{e}_i^{\tau T}{e}_i^{\tau }\hfill \\ \hfill & =\frac{1}{2}{e}_i^T(M_{x_1,s}+M_{x_1,s}^T-2l{C}^{T}C)e_i+\sum _{j=1}^N{G}_{ij}{e}_i^{T}C{e}_j+\sum _{j=1}^N{\widehat{G}}_{ij}{e}_i^{T}C{e}_j^{\tau }+\frac{1}{2}{\delta }_1{e}_i^T{e}_i-\frac{1}{2}{\delta }_2{e}_i^{\tau T}{e}_i^{\tau }\hfill \\ \hfill & +\frac{1}{2}{e}_i^T(2C^T{K}_i{\mathsf{\Gamma }}_{i}C-K_{i}C-C^T{K}_i)e_i,\hfill \end{array}$$

where ${\delta }_1=1/(1-{\varsigma }_2)$, ${\delta }_2=(1-\dot{\tau })/(1-{\varsigma }_2)$. According to (5), one has

$$0\le 1-{\varsigma }_2\le 1-\dot{\tau }.$$

It is obvious that ${\delta }_2>1$. Then, (14) can be rewritten as

$$K_{ij}={\mathsf{\Gamma }}_{ij}{\int }_0^t{\epsilon }_{ij}^2\left(v\right)dv+K_{ij}\left(0\right).$$

On the other hand, since (15) holds and $C^T{\mathsf{\Gamma }}_i^{2}C>0$, one can obtain

$$\begin{array}{cc}\hfill K_i\left(0\right)C+C^T{K}_i\left(0\right)-2C^T{K}_i\left(0\right)C& >{\theta }_1{I}_n>0,\hfill \\ \hfill a_i(2C^T{\mathsf{\Gamma }}_i^{2}C-C^T{\mathsf{\Gamma }}_i-{\mathsf{\Gamma }}_{i}C)& >{\theta }_2{I}_n>0,\hfill \end{array}$$

by properly selecting ${\mathsf{\Gamma }}_i>0$, where ${\theta }_1$, ${\theta }_2\in R^{+}$ such that ${\theta }_1>{\theta }_2$, and

$$a_i=min\{{\int }_0^t{\epsilon }_{ij}^2\left(v\right)dv|j=1,2,\cdots ,n\}>0.$$

Therefore, it holds that

$$2C^T{K}_i{\mathsf{\Gamma }}_{i}C\le K_{i}C+C^T{K}_i.$$

Thus, it can be received that

$$\begin{array}{cc}\hfill {\dot{V}}_i& \le \frac{1}{2}{e}_i^T(M_{x_1,s}+M_{x_1,s}^T-2l{C}^{T}C)e_i+\sum _{j=1}^N{G}_{ij}{e}_i^{T}C{e}_j+\sum _{j=1}^N{\widehat{G}}_{ij}{e}_i^{T}C{e}_j^{\tau }+\frac{1}{2}{\delta }_1{e}_i^T{e}_i-\frac{1}{2}{e}_i^{\tau T}{e}_i^{\tau }\hfill \\ \hfill & \le \frac{1}{2}({\lambda }_m+{\delta }_1-2l{\lambda }_c)e_i^T{e}_i+\sum _{j=1}^N{G}_{ij}{e}_i^{T}C{e}_j+\sum _{j=1}^N{\widehat{G}}_{ij}{e}_i^{T}C{e}_j^{\tau }-\frac{1}{2}{e}_i^{\tau T}{e}_i^{\tau },\hfill \end{array}$$

(11)

where ${\lambda }_c={\lambda }_{min}\left(C^{T}C\right)>0$ is the minimal eigenvalue of $C^{T}C$. Substituting System (11) into System (9), one can get

$$\begin{array}{cc}\hfill \dot{V}& \le \frac{1}{2}({\lambda }_m+{\delta }_1-2l{\lambda }_c)e^{T}e-\frac{1}{2}{e}^{\tau T}{e}^{\tau }+\sum _{i=1}^N\sum _{j=1}^N{G}_{ij}{e}_i^{T}C{e}_j+\sum _{i=1}^N\sum _{j=1}^N{\widehat{G}}_{ij}{e}_i^{T}C{e}_j^{\tau },\hfill \end{array}$$

(12)

where $e={[e_1^T,e_2^T,\cdots ,e_N^T]}^T$.

Now, we give the main result in the following theorem.

Theorem 1.

With the controller

$$u_i\left(t\right)=-K_i\left(t\right){\epsilon }_i\left(t\right),$$

(13)

and the parameter updating laws

$${\dot{K}}_{ij}\left(t\right)={\mathsf{\Gamma }}_{ij}{\epsilon }_{ij}^2\left(t\right),$$

(14)

with $1\le j\le n$, the general delayed network (1) is synchronous with $\widehat{y}\left(t\right)$ starting from any initial condition $x_i\left(0\right)$ and $s\left(0\right)$, where $K_i\left(t\right)$ and ${\mathsf{\Gamma }}_i$ are both diagonal matrices with $K_i\left(0\right)$ being selected by

$$K_i\left(0\right)C+C^T{K}_i\left(0\right)>0,$$

(15)

and ${\mathsf{\Gamma }}_{ij}>0$ for all $i\in L$.

Proof. 

Using Lemma 1, (12), and $\lambda \left(C^{T}C\right)=\lambda \left(C{C}^T\right)$, one can yield

$$\begin{array}{cc}\hfill \dot{V}& \le \frac{1}{2}({\lambda }_m+{\delta }_1-2l{\lambda }_c)e^{T}e-\frac{1}{2}{e}^{\tau T}{e}^{\tau }+\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N(e_i^T{G}_{ij}^{2}C{C}^T{e}_i+e_j^T{e}_j)\hfill \\ \hfill & +\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N(e_i^T{\widehat{G}}_{ij}^{2}C{C}^T{e}_i+e_j^{\tau T}{e}_j^{\tau })\hfill \\ \hfill & \le \frac{1}{2}({\lambda }_m+{\delta }_1+N({\lambda }_c{m}^2+1+{\lambda }_c{n}^2)-2l{\lambda }_c)e^{T}e.\hfill \end{array}$$

Selecting

$$l=\frac{{\lambda }_m+{\delta }_1+N({\lambda }_c{m}^2+1+{\lambda }_c{n}^2)+2}{2{\lambda }_c},$$

one can get $\dot{V}\le -e^{T}e$. Obviously, $\dot{V}=0$ if and only if $e\left(t\right)=0$. According to the invariant principle of functional differential [31], $e\left(t\right)\to 0$ as $t\to \infty$. Thus, the output error $\epsilon \left(t\right)$ of (8) is asymptotically stable under the adaptive controllers (13) and updating laws (14). Namely, the dynamical network (1) achieves output synchronization, which completes the proof. □

Remark 3.

In fact, one cannot always find a diagonal matrix $K_i\left(0\right)$ to satisfy (15). A sufficient condition is that all diagonal entries of an output matrix are not equal to zero. Let us explain how to select $K_i\left(0\right)$.

Consider a linear matrix inequality

$$M_{\left(n\right)}=K_{\left(n\right)}{C}_{\left(n\right)}+C_{\left(n\right)}^T{K}_{\left(n\right)}>0,$$

(16)

where $K_{\left(n\right)}$ is an $n\times n$ diagonal matrix to be determined, and $C_{\left(n\right)}\in R^{n\times n}$ can be any matrix whose entries $C_{ii}\ne 0$ for all $i\le n$.

Let ${ϵ}_i$ be a large enough positive constant with $i=1,2,\cdots ,n$.

(1)

If $n=1$, it is easy to select ${ϵ}_1>K_{\left(1\right)}{C}_{\left(1\right)}>0$.

(2)

If $n=2$, one can select $K_{ii}$ which is satisfied

$$\begin{array}{c}\hfill K_{11}{C}_{11}>0,K_{11}{K}_{22}\left|C_{\left(2\right)}\right|>0,\end{array}$$

where $K_{11}=K_{\left(1\right)}$, $C_{11}=C_{\left(1\right)}$. Thus, ${ϵ}_2{I}_2>M_{\left(2\right)}>0$ holds.

One supposes that ${ϵ}_m{I}_m>M_{\left(m\right)}>0$ holds by selecting proper $K_{ii}$ for all $i\le m$ and $m=1,2,\cdots ,n$. If $n=m+1$, $M_{(m+1)}$ can be rewritten as

$$M_{(m+1)}=\left[\begin{array}{cc}{M}_{\left(m\right)}& K_{\left(m\right)}x+ky\\ x^T{K}_{\left(m\right)}+k{y}^T& 2kc\end{array}\right],$$

where $x,y\in R^n$, $c=C_{m+1,m+1}$, $k=K_{m+1,m+1}$, and

$$C_{(m+1)}=\left[\begin{array}{cc}{C}_{\left(m\right)}& x\\ y^T& c\end{array}\right],K_{(m+1)}=\left[\begin{array}{cc}{K}_{\left(m\right)}& 0\\ 0& k\end{array}\right].$$

Since

$$2kc-(x^T{K}_{\left(m\right)}+k{y}^T)M_{\left(m\right)}^{-1}(K_{\left(m\right)}x+ky)>0,$$

one has $M_{(m+1)}>0$. By solving the above inequality, one can easily derive that k has solutions if and only if

$$\begin{array}{c}\hfill c>2x^T{M}_{\left(m\right)}^{-1}y\mathrm{or}c<2x^T{M}_{\left(m\right)}^{-1}y.\end{array}$$

(17)

(17) holds if

$$\begin{array}{c}\hfill c>2{ϵ}_m^{-1}{x}^{T}y\mathrm{or}c<2{ϵ}_m^{-1}{x}^{T}y.\end{array}$$

(18)

Since ${ϵ}_m$ is large enough, (18) always holds. Therefore, one gets $M_{\left(n\right)}>0$.

4. Numerical Simulations

In this part, the nonlinear examples are presented to further verify the effectiveness of the proposed adaptive feedback. Consider a nine-node network with each cell being an identical Lorenz system, which is described by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{x}}_{i1}=a_1(x_{i2}-x_{i1})\hfill \\ {\dot{x}}_{i2}=b_1{x}_{i1}-x_{i2}-x_{i1}{x}_{i3}\hfill \\ {\dot{x}}_{i3}=-c_1{x}_{i3}+x_{i1}{x}_{i2},\hfill \end{array}\right.\end{array}$$

(19)

where $a_1=10$, $b_1=8/3$, $c_1=28$. The system has a bounded, zero volume, globally attracting set [32]. Therefore, the state trajectories $x_{ij}$ with $j=1,2,3$ are always bounded and continuously differentiable, and $M_{x,y}$ is a bounded matrix. The output matrix C is

$$C=\left[\begin{array}{ccc}1& 2& 3\\ 2& -1& 1\\ 0& 1& 2\end{array}\right].$$

Given time delay $\tau =e^t/(1+e^t)$ and the coupling matrices being

$$G\left(t\right)=\left[\begin{array}{ccccccccc}-2e^{-t}& e^{-t}& 0& 0& 0& 0& 0& 0& e^{-t}\\ arctant& -2arctant& arctant& 0& 0& 0& 0& 0& 0\\ 0& -e^{-2t}& 3e^{-2t}& -2e^{-2t}& 0& 0& 0& 0& 0\\ 0& 0& 1& -4& 3& 0& 0& 0& 0\\ 0& 0& 0& -\mathrm{th}\left(t\right)& 0& \mathrm{th}\left(t\right)& 0& 0& 0\\ 0& 0& 0& 0& -2sint& sint& sint& 0& 0\\ 0& 0& 0& 0& 0& 0& arctant& -arctant& 0\\ 0& 0& 0& 0& 0& 0& -2\mathrm{th}\left(t\right)& \mathrm{th}\left(t\right)& \mathrm{th}\left(t\right)\\ -3e^{-3t}& 0& 0& 0& 0& 0& 0& e^{-3t}& 2e^{-3t}\end{array}\right],$$

$$\widehat{G}=\left[\begin{array}{ccccccccc}-3& 2& 0& 0& 0& 0& 0& 0& 1\\ 3& -2& -1& 0& 0& 0& 0& 0& 0\\ 0& 1& -2& 1& 0& 0& 0& 0& 0\\ 0& 0& 2& -5& 3& 0& 0& 0& 0\\ 0& 0& 0& 1& -4& 3& 0& 0& 0\\ 0& 0& 0& 0& -1& -2& 3& 0& 0\\ 0& 0& 0& 0& 0& 2& -2& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0& -1\\ 1& 0& 0& 0& 0& 0& 0& 1& -2\end{array}\right],$$

where $\mathrm{th}\left(t\right)=(e^t-e^{-t})/(e^t+e^{-t})$.

By exactly following the design procedue in Section 3 with

$$K_i\left(0\right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& -1& 0\\ 0& 0& 2\end{array}\right],$$

${\mathsf{\Gamma }}_i=I_n$ for all $i\in L$. According to Theorem 1, the synchronous solution $s\left(t\right)$ of the obtained dynamical network is globally asymptotically stable.

If the isolated cell is a Chua’s oscillator, which is given by

$$\left\{\begin{array}{c}{\dot{x}}_{i1}=a_2(x_{i2}-x_{i1}-h\left(x_{i1}\right))\hfill \\ {\dot{x}}_{i2}=b_2(x_{i1}-x_{i2})+c_2{x}_{i3}\hfill \\ {\dot{x}}_{i3}=-d{x}_{i2},\hfill \end{array}\right.$$

where $a_2=7$, $b_2=0.35$, $c_2=0.5$, $d=7$, and

$$h\left(x\right)=m_{1}x+\frac{1}{2}(m_2-m_1)\left(\right|x+1|-|x-1\left|\right),$$

with $m_1=-1/7$ and $m_2=-40/7$. One can easily derive

$$\begin{array}{c}\hfill {|h\left(x\right)-h\left(s\right)|}_2\le m_0{e}_{i1}+(m_0-m_1)|e_{i1}|\le -m_1\left|e_{i1}\right|.\end{array}$$

Thus, Chua’s oscillator satisfies the Lipschitz condition. The synchronous error $e_i\left(t\right)$ is shown in Figure 1, where $s\left(0\right)={[1.5,-4.4,0.15]}^T$. Obviously, the zero error is globally asymptotically stable for (8). Thus, the designed controller can make the closed-loop systems asymptotically stable.

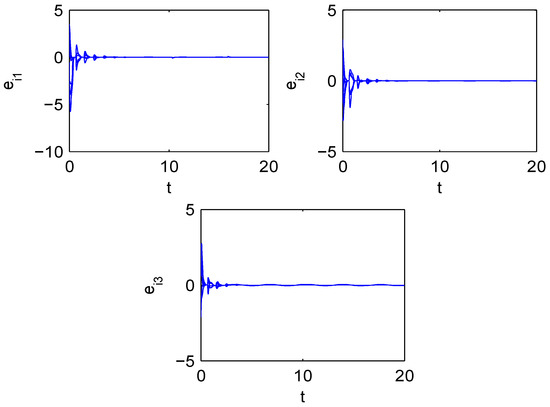
Figure 1. The errors between the cell output and synchronous output, with a chaotic Chua system being a cell.

5. Conclusions

An appropriate adaptive output feedback synchronize problem is introduced for a general dynamical network with time-varying delays. The general complex delayed network can achieve synchronization by adaptively adjusting their feedback gains. Based on the invariant principle of functional differential equations, the feedback controller and parameter update laws are constructed for a large-scale network with uncertainties. Numerical examples are given to demonstrate validity of the control scheme. A problem under investigation is how to design a controller with better performance in terms of timing and speed of synchronous control for System (1).