Super-Fast Computation for the Three-Asset Equity-Linked Securities Using the Finite Difference Method
Abstract
1. Introduction
2. Numerical Method
2.1. Three-Dimensional Black–Scholes Equation
2.2. Step-Down Type ELS
2.3. Solution Algorithm
2.4. Weak Condition of Time Step
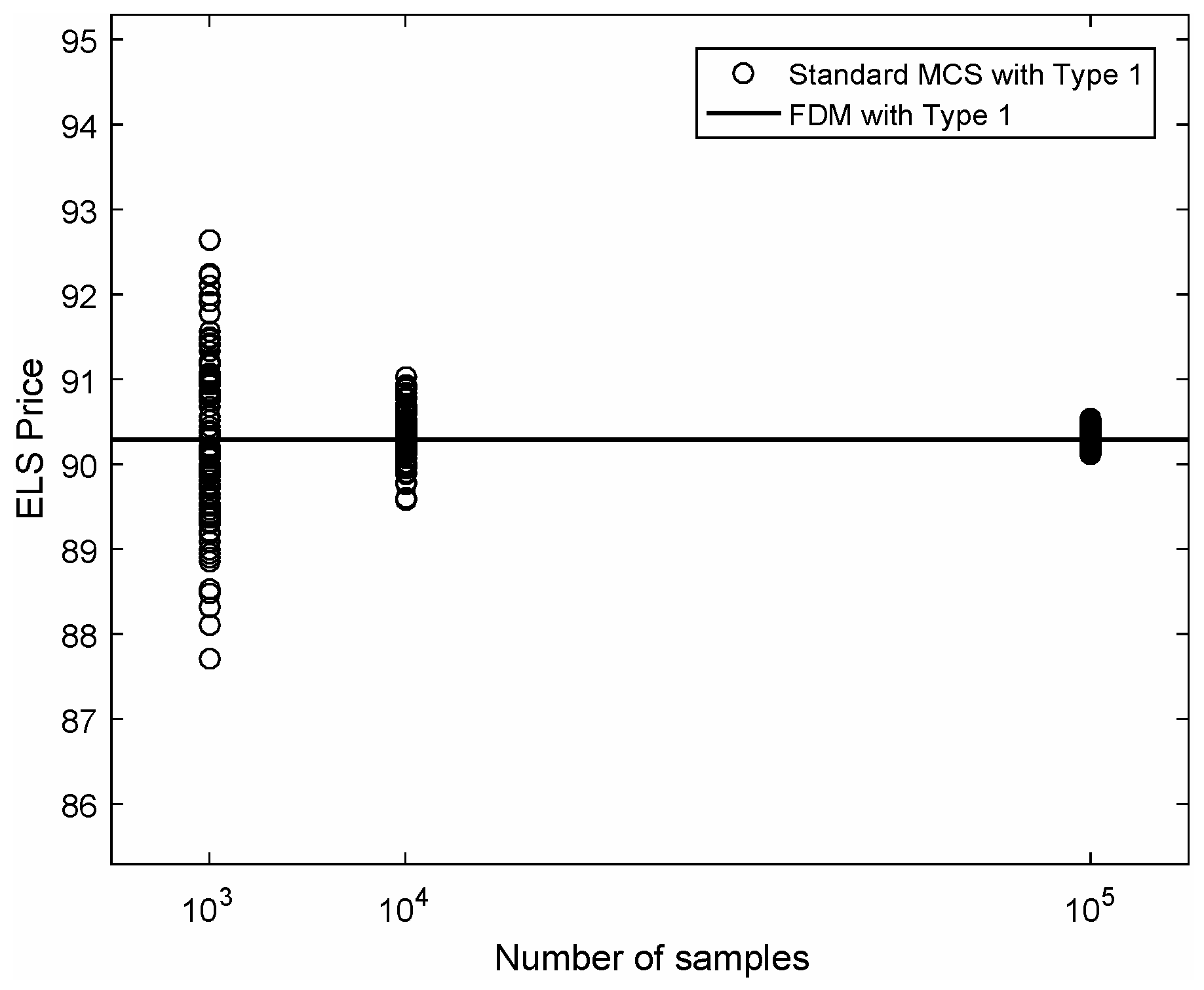
3. Numerical Experiments
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Deng, G.; Mallett, J.; McCann, C. Modeling autocallable structured products. In Derivatives and Hedge Funds; Palgrave Macmillan: London, UK, 2016; pp. 323–344. [Google Scholar]
- Haugh, M.B.; Kogan, L. Pricing American options: A duality approach. Oper. Res. 2004, 52, 258–270. [Google Scholar] [CrossRef]
- Pagés, G. The Monte Carlo Method and Applications to Option Pricing. In Numerical Probability; Springer: Cham, Germany, 2018; pp. 27–47. [Google Scholar]
- Moon, K.S.; Kim, H. A multi-dimensional local average lattice method for multi-asset models. Quant. Finance 2013, 13, 873–884. [Google Scholar] [CrossRef]
- Cen, Z.; Le, A. A robust and accurate finite difference method for a generalized Black–Scholes equation. J. Comput. Appl. Math. 2011, 235, 3728–3733. [Google Scholar] [CrossRef]
- Jeong, D.; Yoo, M.; Kim, J. Finite difference method for the Black–Scholes equation without boundary conditions. Comput. Econ. 2018, 51, 961–972. [Google Scholar] [CrossRef]
- Gulen, S.; Popescu, C.; Sari, M. A New Approach for the Black–Scholes Model with Linear and Nonlinear Volatilities. Mathematics 2019, 7, 760. [Google Scholar] [CrossRef]
- Zhang, R.; Song, H.; Luan, N. Weak Galerkin finite element method for valuation of American options. Front. Math. China 2014, 9, 455–476. [Google Scholar] [CrossRef]
- Mehrdoust, F. A new hybrid Monte Carlo simulation for Asian options pricing. J. Stat. Comput. Simul. 2015, 85, 507–516. [Google Scholar] [CrossRef]
- Wang, S. A novel fitted finite volume method for the Black–Scholes equation governing option pricing. IMA J. Numer. Anal. 2014, 24, 699–720. [Google Scholar] [CrossRef]
- Ma, J. A stochastic correlation model with mean reversion for pricing multi-asset options. Asia-Pac Financ Markets 2009, 16, 97–109. [Google Scholar] [CrossRef]
- Leentvaar, C.C.W.; Oosterlee, C.W. Pricing multi-asset options with sparse grids and fourth order finite differences. In Pricing Multi-Asset Options with Sparse Grids and Fourth Order Finite Differences; de Castro, A.B., Gómez, D., Quintela, P., Salgado, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 809–814. [Google Scholar]
- Ikonen, S.; Toivanen, J. Operator splitting methods for American option pricing. Appl. Math. Lett. 2004, 17, 809–814. [Google Scholar] [CrossRef]
- Heinecke, A.; Schraufstetter, S.; Bungartz, H.J. A highly parallel Black–Scholes solver based on adaptive sparse grids. Int. J. Comput. Math. 2012, 89, 1212–1238. [Google Scholar] [CrossRef]
- Guillaume, T. Autocallable structured products. J. Deriv. 2015, 22, 73–94. [Google Scholar] [CrossRef]
- Guillaume, T. On the multidimensional Black–Scholes partial differential equation. Ann. Oper. Res. 2019, 281, 229–251. [Google Scholar] [CrossRef]
- Yoo, M.; Jeong, D.; Seo, S.; Kim, J. A comparison study of explicit and implicit numerical methods for the equity-linked securities. Honam Math. J. 2015, 37, 441–455. [Google Scholar] [CrossRef][Green Version]
- O’Sullivan, S.; O’Sullivan, C. On the acceleration of explicit finite difference methods for option pricing. Quant. Finance 2011, 11, 1177–1191. [Google Scholar] [CrossRef]
- Boyle, P.P.; Tian, Y. An explicit finite difference approach to the pricing of barrier options. Appl. Math. Finance 1998, 5, 17–43. [Google Scholar] [CrossRef]
- Kim, J.; Kim, T.; Jo, J.; Choi, Y.; Lee, S.; Hwang, H.; Yoo, M.; Jeong, D. A practical finite difference method for the three-dimensional Black–Scholes equation. Eur. J. Oper. Res. 2016, 252, 183–190. [Google Scholar] [CrossRef]
- Choi, Y.; Jeong, D.; Kim, J.; Kim, Y.R.; Lee, S.; Seo, S.; Yoo, M. Robust and accurate method for the Black–Scholes equations with payoff-consistent extrapolation. Commun. Korean Math. Soc. 2015, 30, 297–311. [Google Scholar] [CrossRef][Green Version]
- Jo, J.; Kim, Y. Comparison of numerical schemes on multi-dimensional Black–Scholes equations. Bull. Korean Math. Soc. 2013, 50, 2035–2051. [Google Scholar] [CrossRef]
- Heston, S.L. A closed-form solution for options with stochastic volatility with applications to bond and currency options. Rev. Financ. Stud. 1993, 6, 327–343. [Google Scholar] [CrossRef]
- Ullah, M.Z. Numerical Solution of Heston–Hull–White Three-Dimensional PDE with a High Order FD Scheme. Mathematics 2019, 7, 704. [Google Scholar] [CrossRef]







| Case | Price | CPU Time (s) |
|---|---|---|
| Standard MCS | 90.3002 | 369.4568 |
| Fast FDM | 90.2910 | 2.3900 |
| Case | Price | CPU Time (s) |
|---|---|---|
| Standard MCS | 89.1673 | 386.3436 |
| Fast FDM | 89.0452 | 3.3280 |
| Case | Price | CPU Time (s) |
|---|---|---|
| Standard MCS | 90.8376 | 369.9680 |
| Fast FDM | 90.7650 | 5.1090 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.; Lyu, J.; Park, E.; Lee, W.; Kim, S.; Jeong, D.; Kim, J. Super-Fast Computation for the Three-Asset Equity-Linked Securities Using the Finite Difference Method. Mathematics 2020, 8, 307. https://doi.org/10.3390/math8030307
Lee C, Lyu J, Park E, Lee W, Kim S, Jeong D, Kim J. Super-Fast Computation for the Three-Asset Equity-Linked Securities Using the Finite Difference Method. Mathematics. 2020; 8(3):307. https://doi.org/10.3390/math8030307
Chicago/Turabian StyleLee, Chaeyoung, Jisang Lyu, Eunchae Park, Wonjin Lee, Sangkwon Kim, Darae Jeong, and Junseok Kim. 2020. "Super-Fast Computation for the Three-Asset Equity-Linked Securities Using the Finite Difference Method" Mathematics 8, no. 3: 307. https://doi.org/10.3390/math8030307
APA StyleLee, C., Lyu, J., Park, E., Lee, W., Kim, S., Jeong, D., & Kim, J. (2020). Super-Fast Computation for the Three-Asset Equity-Linked Securities Using the Finite Difference Method. Mathematics, 8(3), 307. https://doi.org/10.3390/math8030307






