A Spectral Conjugate Gradient Method with Descent Property

Abstract

Spectral conjugate gradient method (SCGM) is an important generalization of the conjugate gradient method (CGM), and it is also one of the effective numerical methods for large-scale unconstrained optimization. The designing for the spectral parameter and the conjugate parameter in SCGM is a core work. And the aim of this paper is to propose a new and effective alternative method for these two parameters. First, motivated by the strong Wolfe line search requirement, we design a new spectral parameter. Second, we propose a hybrid conjugate parameter. Such a way for yielding the two parameters can ensure that the search directions always possess descent property without depending on any line search rule. As a result, a new SCGM with the standard Wolfe line search is proposed. Under usual assumptions, the global convergence of the proposed SCGM is proved. Finally, by testing 108 test instances from 2 to 1,000,000 dimensions in the CUTE library and other classic test collections, a large number of numerical experiments, comparing with both SCGMs and CGMs, for the presented SCGM are executed. The detail results and their corresponding performance profiles are reported, which show that the proposed SCGM is effective and promising.

1. Introduction

Conjugate gradient method (CGM) is one class of the prevailing methods commonly used for solving large-scale optimization problems, since it possesses simple iterations, fast convergence properties and low memory requirements. In this paper, we consider the following unconstrained optimization problem:

$$min\left\{f(x)\right|x\in R^n\},$$

(1)

where $f:R^n\to R$ is a continuously differentiable function and its gradient is denoted by $g(x)=\nabla f(x)$. The iterates of the classical CGM can be formulated as

$$\begin{array}{c}{x}_{k+1}=x_k+{\alpha }_k{d}_k,\end{array}$$

(2)

and

$$d_k=\left\{\begin{array}{cc}-g_k,& \mathrm{if}k=1,\\ -g_k+{\beta }_k{d}_{k-1},\hspace{1em}& \mathrm{if}k>1,\end{array}\right.$$

(3)

where $g_k=g(x_k)$, $d_k$ is the search direction, ${\beta }_k$ is the so-called conjugate parameter, and ${\alpha }_k$ is the steplength which obtained by a suitable exact or inexact line search. However, as the high cost of the exact line search, ${\alpha }_k$ is usually generated by an inexact line search, such as the Wolfe line search

$$\left\{\begin{array}{c}f(x_k+{\alpha }_k{d}_k)\le f(x_k)+\delta {\alpha }_k{g}_k^T{d}_k,\hfill \\ g{(x_k+{\alpha }_k{d}_k)}^T{d}_k\ge \sigma g_k^T{d}_k,\hfill \end{array}\right.$$

(4)

or the strong Wolfe line search

$$\left\{\begin{array}{c}f(x_k+{\alpha }_k{d}_k)\le f(x_k)+\delta {\alpha }_k{g}_k^T{d}_k,\hfill \\ |g{(x_k+{\alpha }_k{d}_k)}^T{d}_k|\le \sigma |g_k^T{d}_k|.\hfill \end{array}\right.$$

(5)

The parameters $\delta$ and $\sigma$ above generally are required to satisfy $0<\delta <\sigma <1$. As we know, different choice for ${\beta }_k$ would generate different CGM. The most well-known CGMs are the Hestenes-Stiefel (HS, 1952) method [1], Fletcher-Reeves (FR, 1964) method [2], Polak-Ribière-Polyak (PRP, 1969) method [3,4] and the Dai-Yuan (DY, 1999) method [5], where the corresponding formulas for ${\beta }_k$ are

$${\beta }_k^{\mathrm{HS}}=\frac{g_k^T(g_k-g_{k-1})}{d_{k-1}^T(g_k-g_{k-1})},{\beta }_k^{\mathrm{FR}}=\frac{\parallel g_k{\parallel }^2}{\parallel g_{k-1}{\parallel }^2},{\beta }_k^{\mathrm{PRP}}=\frac{g_k^T(g_k-g_{k-1})}{\parallel g_{k-1}{\parallel }^2},{\beta }_k^{\mathrm{DY}}=\frac{\parallel g_k{\parallel }^2}{d_{k-1}^T(g_k-g_{k-1})},$$

respectively, where $\parallel ·\parallel$ is the standard Euclidean norm. Generally, these four methods are often referred to the classical CGMs. Under the corresponding assumptions, the authors analysed the convergence properties and tested the numerical performance of the four CGMs in References [2,3,4,5,6], respectively.

It is well known that the FR CGM and DY CGM possess nice convergence properties. However, their numerical performances are not so good. Inversely, the PRP and HS methods have excellent performance in practical computation. But their convergence properties are hardly to be obtained. Thus, to overcome these shortcomings of the classical CGMs, many researchers pay great attention to improve the CGMs. As a result, many improvements with excellent theoretical properties and numerical performance of the CGMs results were proposed, for example, References [7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Where, the spectral conjugate gradient method (SCGM) proposed by Birgin and Martinez [12] can be seen as an important development of CGM. The main difference between SCGM and CGM lies in the computation of the search direction. The search direction of SCGM is usually yielded as follows:

$$d_k=\left\{\begin{array}{cc}-g_k,\hfill & \mathrm{if}k=1,\hfill \\ -{\theta }_k{g}_k+{\beta }_k{d}_{k-1},\hfill & \mathrm{if}k>1,\hfill \end{array}\right.$$

(6)

where ${\theta }_k$ is a spectral parameter. Obviously, for a SCGM, the selection techniques for the spectral parameter ${\theta }_k$ and the conjugate parameter ${\beta }_k$ are core work and very important.

In Reference [12], after giving the concrete conjugate parameter ${\beta }_k$, Birgin and Martinez required the spectral search direction yielded by (6) satisfying $g_k^T{d}_k=-{\parallel g_k\parallel }^2$ (a special sufficient descent property), and then obtained the corresponding spectral parameter:

$${\theta }_k=\frac{s_k^T{s}_k}{s_k^T{y}_k},\mathrm{where}{s}_k=x_k-x_{k-1},y_k=g_k-g_{k-1}.$$

(7)

Under suitable line search, the SCGM yielded by (2) and (6) as well as (7) performs superiorly to the PRP CGM, the FR CGM and the Perry method [21].

Yielding the conjugate parameter ${\beta }_k$ by a modified DY formula, based on the Newton’s direction and the quasi-Newton equation as well as the conjugate conditions, respectively, Andrei [13] considered two approaches to generate the spectral parameter ${\theta }_k$, namely,

$${\theta }_k^{\mathrm{N}}=\frac{1}{y_k^T{g}_k}(\parallel g_k{\parallel }^2-\frac{\parallel g_k{\parallel }^2{s}_k^T{g}_k}{y_k^T{s}_k}+s_k^T{g}_k),$$

and

$${\theta }_k^{\mathrm{C}}=\frac{1}{y_k^T{g}_k}(\parallel g_k{\parallel }^2-\frac{\parallel g_k{\parallel }^2{s}_k^T{g}_k}{y_k^T{s}_k}).$$

The two SCGMs associated with ${\theta }_k^{\mathrm{N}}$ and ${\theta }_k^{\mathrm{C}}$ are all sufficient descent without depending on any line search, and are global convergent with the Wolfe line search (4). Also, the numerical results show that the SCGM associated with ${\theta }_k^{\mathrm{N}}$ is more encouraging.

Recently, by requiring the spectral direction $d_k$ defined by (6) satisfying the special sufficient descent condition $g_k^T{d}_k=-{\parallel g_k\parallel }^2$ for general ${\beta }_k$, Liu et al. [15] proposed a class of choice for ${\theta }_k$ as follows:

$${\theta }_k^{\mathrm{LFZ}}=-\frac{g_{k-1}^T{d}_{k-1}}{\parallel g_{k-1}\parallel }+{\beta }_k\frac{g_k^T{d}_{k-1}}{\parallel g_k{\parallel }^2}.$$

Under the conventional assumptions and request $|{\beta }_k|\le |{\beta }_k^{\mathrm{FR}}|$ as well as the Wolfe line search (4), the SCGM developed by ${\theta }_k^{\mathrm{LFZ}}$ is global convergent, and implemented with good computation performance.

On the other hand, Jiang et al. [19] considered to improve both the FR method and the DY method by utilizing the strong Wolfe line search (5), and achieved their good numerical effect. As a result, two schemes for the conjugate parameter are proposed, namely,

$${\beta }_k^{\mathrm{IFR}}=\frac{|g_k^T{d}_{k-1}|}{-g_{k-1}^T{d}_{k-1}}·\frac{\parallel g_k{\parallel }^2}{\parallel g_{k-1}{\parallel }^2},{\beta }_k^{\mathrm{IDY}}=\frac{|g_k^T{d}_{k-1}|}{-g_{k-1}^T{d}_{k-1}}·\frac{\parallel g_k{\parallel }^2}{d_{k-1}^T(g_k-g_{k-1})}.$$

Interestingly, it is found, from formulas (3) and (6), that the SCGM can lead to more decrease than the classical CGM for a same ${\beta }_k$ and any ${\theta }_k>1$. Therefore, in this work, motivated by the ideas of the modified FR method and DY method [19], and making full use of the second condition of the strong Wolfe line search (5), we first introduce a new approach for yielding the spectral parameter as follows:

$${\theta }_k^{\mathrm{JYJLL}}=1+\frac{|g_k^T{d}_{k-1}|}{-g_{k-1}^T{d}_{k-1}}.$$

(8)

Obviously, ${\theta }_k^{\mathrm{JYJLL}}\ge 1$ if the previous $d_{k-1}$ is a descent direction.

Secondly, based on the scheme of the conjugate parameter in Reference [20] with the form

$${\beta }_k^{\mathrm{JYJ}}=\frac{\parallel g_k{\parallel }^2-\frac{{(g_k^T{d}_{k-1})}^2}{\parallel d_{k-1}{\parallel }^2}}{\parallel g_{k-1}{\parallel }^2+u\left|d_{k-1}^T{g}_k\right|},$$

and fully absorbing the hybrid idea of Reference [11], we propose a new conjugate parameter in the following manner

$${\beta }_k^{\mathrm{JYJLL}}=\frac{\parallel g_k{\parallel }^2-\frac{{(g_k^T{d}_{k-1})}^2}{\parallel d_{k-1}{\parallel }^2}}{max\{\parallel g_{k-1}{\parallel }^2,d_{k-1}^T(g_k-g_{k-1})\}}.$$

(9)

So far, a basic conception of our SCGM has been formed. As a result, a new SCGM is proposed, and the theoretical features and numerical performance is analysed and reported.

2. Algorithm and the Descent Property

Based on the formulas (2) and (6) as well as (9), we establish the new SCGM as follows (Algorithm 1).

Algorithm 1: JYJLL-SCGM

Step 0. Given any initial point $x_1\in R^n$, parameters $\delta$ and $\sigma$ satisfying $0<\delta <\sigma <1$, and an accuracy tolerance $ϵ>0$. Let $d_1=-g_1$, set $k:=1$.

Step 1. If $\parallel g_k\parallel \le ϵ$, terminate. Otherwise, go to Step 2.

Step 2. Determine a steplength ${\alpha }_k$ by an inexact line search.

Step 3. Generate the next iterate by $x_{k+1}=x_k+{\alpha }_k{d}_k$, compute gradient $g_{k+1}:=g(x_{k+1})$ and the spectral parameter ${\theta }_{k+1}:={\theta }_{k+1}^{\mathrm{JYJLL}}$ by (8), as well as the conjugate parameter ${\beta }_{k+1}:={\beta }_{k+1}^{\mathrm{JYJLL}}$ by (9).

Step 4. Let $d_{k+1}=-{\theta }_{k+1}{g}_{k+1}+{\beta }_{k+1}{d}_k$. Set $k:=k+1$, repeat Step 1.

The following lemma indicates that the JYJLL-SCGM always satisfies the descent condition without depending on any line search, and the conjugate parameter ${\beta }_k^{\mathrm{JYJLL}}$ has the similar properties as the DY formula.

Lemma 1.

Suppose that the search direction $d_k$ is generated by JYJLL-SCGM. Then, we have $g_k^T{d}_k<0$ for $k\ge 1$, that is, the search direction satisfies the descent condition. Furthermore, we obtain $0\le {\beta }_k^{\mathrm{JYJLL}}\le \frac{g_k^T{d}_k}{g_{k-1}^T{d}_{k-1}}.$

Proof. 

We first prove the former claim by induction. For $k=1$, it is easy to see that $g_1^T{d}_1=-{\parallel g_1\parallel }^2<0$. Assume that $g_{k-1}^T{d}_{k-1}<0$ holds for $k-1(k\ge 2)$. Now, we prove that $g_k^T{d}_k<0$ holds for $k.$ Let ${\widehat{\theta }}_k$ be the angle between $g_k$ and $d_{k-1}$. The proof is divided into two cases as follows.

(a) If $d_{k-1}^T(g_k-g_{k-1})>{\parallel g_{k-1}\parallel }^2$, then $d_{k-1}^T(g_k-g_{k-1})>0$. It follows from (8) and (9) that

$$\begin{array}{c}\begin{array}{cc}{g}_k^T{d}_k& =g_k^T(-{\theta }_k^{\mathrm{JYJLL}}{g}_k+{\beta }_k^{\mathrm{JYJLL}}{d}_{k-1})\\ & =-(1+\frac{|g_k^T{d}_{k-1}|}{-g_{k-1}^T{d}_{k-1}}){\parallel g_k\parallel }^2+\frac{\parallel g_k{\parallel }^2(1-{cos}^2{\widehat{\theta }}_k)}{d_{k-1}^T(g_k-g_{k-1})}{g}_k^T{d}_{k-1}\\ & =-\frac{|g_k^T{d}_{k-1}|}{-g_{k-1}^T{d}_{k-1}}\parallel g_k{\parallel }^2-{\parallel g_k\parallel }^2{cos}^2{\widehat{\theta }}_k+\frac{\parallel g_k{\parallel }^2(1-{cos}^2{\widehat{\theta }}_k)}{d_{k-1}^T(g_k-g_{k-1})}{g}_{k-1}^T{d}_{k-1}\\ & =-({cos}^2{\widehat{\theta }}_k+\frac{|g_k^T{d}_{k-1}|}{-g_{k-1}^T{d}_{k-1}}){\parallel g_k\parallel }^2+{\beta }_k^{\mathrm{JYJLL}}{g}_{k-1}^T{d}_{k-1}<0.\end{array}\end{array}$$

(10)

(b) If $d_{k-1}^T(g_k-g_{k-1})\le {\parallel g_{k-1}\parallel }^2$, then $g_k^T{d}_{k-1}\le {\parallel g_{k-1}\parallel }^2+g_{k-1}^T{d}_{k-1}$, and hence by (8) and (9), we have

$$\begin{array}{c}\begin{array}{cc}{g}_k^T{d}_k& =g_k^T(-{\theta }_k^{\mathrm{JYJLL}}{g}_k+{\beta }_k^{\mathrm{JYJLL}}{d}_{k-1})\\ & =-{\theta }_k^{\mathrm{JYJLL}}{\parallel g_k\parallel }^2+\frac{\parallel g_k{\parallel }^2(1-{cos}^2{\widehat{\theta }}_k)}{\parallel g_{k-1}{\parallel }^2}{g}_k^T{d}_{k-1}\\ & \le -(1+\frac{|g_k^T{d}_{k-1}|}{-g_{k-1}^T{d}_{k-1}})\parallel g_k{\parallel }^2+\frac{\parallel g_k{\parallel }^2(1-{cos}^2{\widehat{\theta }}_k)}{\parallel g_{k-1}{\parallel }^2}(\parallel g_{k-1}{\parallel }^2+g_{k-1}^T{d}_{k-1})\\ & =-({cos}^2{\widehat{\theta }}_k+\frac{|g_k^T{d}_{k-1}|}{-g_{k-1}^T{d}_{k-1}}){\parallel g_k\parallel }^2+{\beta }_k^{\mathrm{JYJLL}}{g}_{k-1}^T{d}_{k-1}<0.\end{array}\end{array}$$

(11)

Thus, $g_k^T{d}_k<0$ holds for $k\ge 1$.

Now we prove the second assertion. From (10) and (11), it follows that $g_k^T{d}_k\le {\beta }_k^{\mathrm{JYJLL}}{g}_{k-1}^T{d}_{k-1}$. This together with $g_k^T{d}_k<0$ implies that ${\beta }_k^{\mathrm{JYJLL}}\le \frac{g_k^T{d}_k}{g_{k-1}^T{d}_{k-1}}$, furthermore, we deduce that $0\le {\beta }_k^{\mathrm{JYJLL}}$ from (9), and the proof is complete. □

3. Convergence Analysis

To analyze and ensure the global convergence of the JYJLL-SCGM, we choose the Wolfe line search (4) to yield the steplength ${\alpha }_k$. Further, a basic assumption about the objective function as follows is needed.

Assumption 1.

(H1) For any initial point $x_1\in R^n$, the level set $\mathsf{\Lambda }=\{x\in R^n|f(x)\le f(x_1)\}$ is bounded; (H2) $f(x)$ is continuously differentiable in a neighborhood U of Λ, and its gradient $g(x)$ is Lipschitz continuous, namely, there exists a constant $L>0$ such that $\parallel g(x)-g(y)\parallel \le L\parallel x-y\parallel ,\forall x,y\in U.$

In the following lemma, we review the well-known Zoutendijk condition [6], which plays an important role in the convergence analysis of CGMs. Also, the Zoutendijk condition is suitable for the convergence analysis of the JYJLL-SCGM.

Lemma 2.

Suppose that Assumption 1 holds. Consider a general iterative method $x_{k+1}=x_k+{\alpha }_k{d}_k,$ where $d_k$ is a descent direction such that $g_k^T{d}_k<0$, and the steplength ${\alpha }_k$ satisfies the Wolfe line search condition (4). Then ${\sum }_{k=1}^{\infty }\frac{{(g_k^T{d}_k)}^2}{\parallel d_k{\parallel }^2}<\infty .$

Based on Lemmas 1 and 2, we can establish the global convergence of the JYJLL-SCGM.

Theorem 1.

Suppose that Assumption 1 holds, and let the sequence $\left\{x_k\right\}$ be generated by the JYJLL-SCGM with the wolfe line search (4). Then $\underset{k\to \infty }{lim\; inf}\parallel g_k\parallel =0.$

Proof. 

By contradiction, suppose that the conclusion is not true. Then there exists a positive constant $\gamma >0$ such that $\parallel g_k{\parallel }^2\ge \gamma ,\forall k$. Again, from (8), we obtain $d_k+{\theta }_k^{\mathrm{JYJLL}}{g}_k={\beta }_k^{\mathrm{JYJLL}}{d}_{k-1}$. Combining this equation and Lemma 1, we have

$$\begin{array}{cc}\parallel d_k{\parallel }^2& ={({\beta }_k^{\mathrm{JYJLL}})}^2\parallel d_{k-1}{\parallel }^2-2{\theta }_k^{\mathrm{JYJLL}}{g}_k^T{d}_k-{({\theta }_k^{\mathrm{JYJLL}})}^2{\parallel g_k\parallel }^2\\ & \le {(\frac{g_k^T{d}_k}{g_{k-1}^T{d}_{k-1}})}^2\parallel d_{k-1}{\parallel }^2-2{\theta }_k^{\mathrm{JYJLL}}{g}_k^T{d}_k-{({\theta }_k^{\mathrm{JYJLL}})}^2{\parallel g_k\parallel }^2.\end{array}$$

Next, dividing both sides of the above inequality by ${(g_k^T{d}_k)}^2$, we obtain

$$\begin{array}{cc}\frac{\parallel d_k{\parallel }^2}{{(g_k^T{d}_k)}^2}& \le \frac{\parallel d_{k-1}{\parallel }^2}{{(g_{k-1}^T{d}_{k-1})}^2}-\frac{2{\theta }_k^{\mathrm{JYJLL}}}{g_k^T{d}_k}-\frac{{({\theta }_k^{\mathrm{JYJLL}})}^2{\parallel g_k\parallel }^2}{{(g_k^T{d}_k)}^2}\\ & =\frac{\parallel d_{k-1}{\parallel }^2}{{(g_{k-1}^T{d}_{k-1})}^2}+\frac{1}{\parallel g_k{\parallel }^2}-{(\frac{1}{\parallel g_k\parallel }+\frac{{\theta }_k^{\mathrm{JYJLL}}\parallel g_k\parallel }{g_k^T{d}_k})}^2\\ & \le \frac{\parallel d_{k-1}{\parallel }^2}{{(g_{k-1}^T{d}_{k-1})}^2}+\frac{1}{\parallel g_k{\parallel }^2}.\end{array}$$

In terms of $\frac{\parallel d_1{\parallel }^2}{{(g_1^T{d}_1)}^2}=\frac{1}{\parallel g_1{\parallel }^2}$, together with the above relations and $\parallel g_k{\parallel }^2\ge \gamma$, we have

$$\begin{array}{cc}\frac{\parallel d_k{\parallel }^2}{{(g_k^T{d}_k)}^2}& \le \frac{\parallel d_{k-1}{\parallel }^2}{{(g_{k-1}^T{d}_{k-1})}^2}+\frac{1}{\parallel g_k{\parallel }^2}\\ & \le \frac{\parallel d_{k-2}{\parallel }^2}{{(g_{k-2}^T{d}_{k-2})}^2}+\frac{1}{\parallel g_k{\parallel }^2}+\frac{1}{\parallel g_{k-1}{\parallel }^2}\\ & \le \cdots \le \sum _{i=1}^k\frac{1}{\parallel g_i{\parallel }^2}\le \frac{k}{\gamma },\end{array}$$

that is, $\frac{{(g_k^T{d}_k)}^2}{\parallel d_k{\parallel }^2}\ge \frac{\gamma }{k}$. Hence ${\sum }_{k=1}^{\infty }\frac{{(g_k^T{d}_k)}^2}{\parallel d_k{\parallel }^2}=\infty$, which contradicts Lemma 2. Therefore, the proof is complete. □

4. Numerical Results

In this section, we test the numerical performance of our method (denoted by JYJLL for short) via 108 test problems, and compare it with the four methods HZ [7], KD [8], AN1 [13] and LFZ [15]. The HZ and KD methods belong to the CGMs with excellent effect, and the AN1 and LFZ methods are the SCGMs with more efficient performance. The first 53 (from $\mathrm{bard}$ to $\mathrm{woods}$) test problems are taken from the CUTE library in N. I. M. Gould et al. [22], and the last 55 are from References [23,24], their dimensions ranging from 2 to 1,000,000. All codes were written in Matlab 2016a and run on a DELL PC with 4GB of memory and windows 10 operating system. All the steplength ${\alpha }_k$ is generated by the Wolfe line search with $\sigma =0.1$ and $\delta =0.01$.

In the experiments, notations Itr, NF, NG, and Tcpu and $\parallel g_{*}\parallel$ denote the number of iteration, function evaluation, gradient evaluation, computing time of CPU and gradient values, respectively. We stop the iteration, if one of the following two cases is satisfied: (i) $\parallel g_k\parallel \le {10}^{-6}$; (ii) $\mathrm{Itr}>2000$. When case (ii) appears, the method is deemed to be invalid and is denoted by “F”.

To show the numerical performance of the tested methods, we observed and reported the values of Itr, NF, NG, Tcpu and $\parallel g_{*}\parallel$ generated by the five tested methods for each test instance, see Table 1 and Table 2 below. On the other hand, to visually characterize and compare the numerical results in Table 1 and Table 2, we use the performance profiles introduced by Dolan and Morè [25] to describe the performance of the five tested methods according to Itr, NF, NG and Tcpu, respectively, see Figure 1, Figure 2, Figure 3 and Figure 4 below.

Table 1. Numerical test reports for the five tested methods.

Problems	JYJLL	KD	AN1	HZ	LFZ
Name/n	Itr/ NF/ NG/ Tcpu/ $\parallel g_{*}\parallel$	Itr/ NF/ NG/ Tcpu/ $\parallel g_{*}\parallel$	Itr/ NF/ NG/ Tcpu/ $\parallel g_{*}\parallel$	Itr/ NF/ NG/ Tcpu/ $\parallel g_{*}\parallel$	Itr/ NF/ NG/ Tcpu/ $\parallel g_{*}\parallel$
bard 3	178/218/259/0.171/8.74 $\times {10}^{-7}$	1565/48,617/19,915/4.657/8.01 $\times {10}^{-7}$	81/206/156/0.051/8.35 $\times {10}^{-7}$	620/18,622/7190/1.732/3.95 $\times {10}^{-7}$	265/6647/3284/0.691/1.72 $\times {10}^{-7}$
beale 2	67/93/87/0.015/9.28 $\times {10}^{-7}$	326/9668/4385/0.429/7.71 $\times {10}^{-7}$	44/150/92/0.012/9.17 $\times {10}^{-7}$	251/7325/3130/0.318/6.17 $\times {10}^{-7}$	171/4757/2347/0.214/4.31 $\times {10}^{-8}$
box 3	139/193/207/0.026/6.64 $\times {10}^{-7}$	330/10,108/4330/0.504/5.98 $\times {10}^{-7}$	36/104/64/0.009/7.52 $\times {10}^{-7}$	475/14,246/5816/0.702/8.94 $\times {10}^{-7}$	68/1569/764/0.083/3.17 $\times {10}^{-7}$
cosine 2000	17/55/19/0.104/2.48 $\times {10}^{-7}$	493/13,783/6221/3.593/8.15 $\times {10}^{-7}$	247/673/556/0.438/9.68 $\times {10}^{-7}$	435/11,148/5281/3.126/4.62 $\times {10}^{-7}$	F/F/F/F/1.88 $\times {10}^3$
cosine 4000	20/61/24/0.050/9.50 $\times {10}^{-8}$	F/F/F/F/6.04 $\times {10}^{-3}$	246/908/671/0.964/5.96 $\times {10}^{-7}$	178/4537/2189/3.495/8.83 $\times {10}^{-7}$	F/F/F/F/7.43 $\times {10}^{-4}$
cosine 20,000	26/65/32/0.228/6.76 $\times {10}^{-7}$	F/F/F/F/3.13 $\times {10}^{-3}$	163/207/240/1.029/7.51 $\times {10}^{-7}$	1730/48,495/21,578/161.976/6.59 $\times {10}^{-7}$	F/F/F/F/1.85 $\times {10}^4$
dixmaana 3000	21/63/22/0.318/8.90 $\times {10}^{-7}$	17/266/117/0.683/3.09 $\times {10}^{-7}$	20/60/22/0.178/9.35 $\times {10}^{-7}$	26/520/206/1.282/1.33 $\times {10}^{-7}$	24/393/169/1.012/1.85 $\times {10}^{-7}$
dixmaanb 3000	12/59/12/0.159/3.75 $\times {10}^{-7}$	12/150/49/0.370/3.26 $\times {10}^{-7}$	14/59/14/0.145/8.48 $\times {10}^{-7}$	49/1246/565/3.231/9.61 $\times {10}^{-8}$	14/180/72/0.458/1.48 $\times {10}^{-7}$
dixmaanc 3000	15/64/15/0.197/8.85 $\times {10}^{-7}$	25/458/217/1.207/5.54 $\times {10}^{-7}$	19/61/19/0.174/9.87 $\times {10}^{-7}$	33/678/323/1.829/1.92 $\times {10}^{-7}$	35/659/315/1.718/8.03 $\times {10}^{-7}$
dixmaand 3000	19/68/19/0.194/1.05 $\times {10}^{-8}$	25/389/167/0.977/3.58 $\times {10}^{-7}$	21/67/21/0.191/3.53 $\times {10}^{-7}$	54/1304/627/3.484/2.30 $\times {10}^{-7}$	45/822/409/2.179/6.68 $\times {10}^{-7}$
dixmaane 3000	564/525/797/3.316/8.67 $\times {10}^{-7}$	787/22,182/9876/60.145/9.62 $\times {10}^{-7}$	406/249/500/2.203/9.08 $\times {10}^{-7}$	1239/35,277/14,918/96.673/7.67 $\times {10}^{-7}$	369/9463/4622/26.732/7.85 $\times {10}^{-7}$
dixmaanf 3000	486/470/691/3.060/5.26 $\times {10}^{-7}$	720/20,789/8946/56.355/7.80 $\times {10}^{-7}$	395/238/483/2.094/7.12 $\times {10}^{-7}$	1387/40,775/17,299/111.617/9.92 $\times {10}^{-7}$	283/7443/3631/21.630/8.83 $\times {10}^{-7}$
dixmaang 3000	291/286/403/1.872/8.98 $\times {10}^{-7}$	557/15,559/6999/43.071/8.50 $\times {10}^{-7}$	430/266/531/2.370/6.61 $\times {10}^{-7}$	1492/43,815/18,382/120.388/6.52 $\times {10}^{-7}$	441/11,502/5595/32.348/6.66 $\times {10}^{-7}$
dixmaanh 3000	501/499/719/3.300/8.91 $\times {10}^{-7}$	933/26,886/11971/73.607/9.35 $\times {10}^{-7}$	428/245/518/2.273/9.72 $\times {10}^{-7}$	F/F/F/F/2.23 $\times {10}^{-5}$	478/12,359/6015/35.150/9.39 $\times {10}^{-7}$
dixmaanj 3000	874/829/1258/5.304/7.87 $\times {10}^{-7}$	1201/34,580/15,144/93.734/9.58 $\times {10}^{-7}$	1038/575/1295/5.617/7.20 $\times {10}^{-7}$	F/F/F/F/3.16 $\times {10}^{-6}$	642/16,203/7988/45.658/9.24 $\times {10}^{-7}$
dixmaank 3000	891/876/1297/5.757/9.74 $\times {10}^{-7}$	1158/33,535/14,587/89.969/7.82 $\times {10}^{-7}$	978/551/1222/5.291/6.98 $\times {10}^{-7}$	F/F/F/F/2.66 $\times {10}^{-5}$	1899/49,488/24,316/139.479/8.81 $\times {10}^{-7}$
dixon3dq 5	51/54/54/0.011/5.58 $\times {10}^{-7}$	136/3776/1687/0.156/4.24 $\times {10}^{-7}$	52/58/58/0.007/5.73 $\times {10}^{-7}$	77/1803/786/0.072/7.91 $\times {10}^{-7}$	168/4217/2066/0.165/4.14 $\times {10}^{-7}$
dixon3dq 40	631/600/908/0.076/9.98 $\times {10}^{-7}$	1164/34,979/14,945/1.418/5.17 $\times {10}^{-7}$	394/114/427/0.041/7.07 $\times {10}^{-7}$	1789/52,134/21,597/1.999/7.37 $\times {10}^{-7}$	477/12,218/5965/0.492/3.93 $\times {10}^{-7}$
dqdrtic 10,000	105/159/144/0.174/8.38 $\times {10}^{-7}$	275/7800/3415/3.965/2.96 $\times {10}^{-7}$	78/124/99/0.159/7.25 $\times {10}^{-7}$	911/28,054/11,907/15.545/7.25 $\times {10}^{-7}$	191/5281/2547/3.215/3.10 $\times {10}^{-7}$
dqdrtic 100,000	118/176/164/1.740/9.70 $\times {10}^{-7}$	455/13,662/6077/53.011/3.67 $\times {10}^{-7}$	104/232/178/2.033/8.42 $\times {10}^{-7}$	685/20,674/8804/82.583/5.80 $\times {10}^{-7}$	293/7575/3761/30.040/3.73 $\times {10}^{-7}$
dqdrtic 1,000,000	67/143/96/13.649/2.81 $\times {10}^{-7}$	256/7211/3161/354.291/7.07 $\times {10}^{-7}$	84/185/132/19.420/9.45 $\times {10}^{-7}$	854/26,185/11,120/1264.582/5.93 $\times {10}^{-7}$	214/5856/2872/297.431/3.91 $\times {10}^{-7}$
dqrtic 480	33/89/33/0.043/6.19 $\times {10}^{-7}$	F/F/F/F/4.77 $\times {10}^9$	43/100/51/0.037/2.83 $\times {10}^{-7}$	F/F/F/F/4.77 $\times {10}^9$	F/F/F/F/4.77 $\times {10}^9$
dqrtic 510	28/89/28/0.028/2.08 $\times {10}^{-7}$	F/F/F/F/5.90 $\times {10}^9$	F/F/F/F/1.16 $\times {10}^9$	F/F/F/F/5.90 $\times {10}^9$	F/F/F/F/5.90 $\times {10}^9$
edensch 4000	39/326/155/0.683/9.42 $\times {10}^{-7}$	45/855/380/1.666/6.67 $\times {10}^{-7}$	F/F/F/F/7.59 $\times {10}^{-6}$	51/1123/490/2.195/8.67 $\times {10}^{-7}$	F/F/F/F/1.22 $\times {10}^{-5}$
edensch 5000	34/196/83/0.573/6.12 $\times {10}^{-7}$	66/1491/715/3.760/6.48 $\times {10}^{-7}$	F/F/F/F/1.99 $\times {10}^{-6}$	48/1035/475/2.590/6.56 $\times {10}^{-7}$	F/F/F/F/2.25 $\times {10}^{-5}$
edensch 7500	35/259/96/0.956/2.94 $\times {10}^{-7}$	68/1673/797/4.458/3.76 $\times {10}^{-7}$	F/F/F/F/2.64 $\times {10}^{-6}$	F/F/F/F/2.13 $\times {10}^{-6}$	F/F/F/F/9.86 $\times {10}^{-6}$
eg2 30	66/84/79/0.036/6.82 $\times {10}^{-7}$	F/F/F/F/3.05 $\times {10}^{-1}$	62/138/102/0.016/7.12 $\times {10}^{-7}$	F/F/F/F/3.20 $\times {10}^{-3}$	F/F/F/F/2.61 $\times {10}^{-5}$
eg2 100	111/156/157/0.025/7.73 $\times {10}^{-7}$	156/4392/1951/0.320/5.40 $\times {10}^{-7}$	45/289/160/0.031/5.13 $\times {10}^{-7}$	F/F/F/F/7.42 $\times {10}^{-6}$	F/F/F/F/2.74 $\times {10}^{-5}$
fletchcr 50	51/107/81/0.028/4.96 $\times {10}^{-7}$	88/2309/1016/0.239/4.70 $\times {10}^{-7}$	63/108/89/0.025/7.14 $\times {10}^{-7}$	140/3679/1711/0.383/1.92 $\times {10}^{-7}$	181/4599/2284/0.539/3.65 $\times {10}^{-7}$
fletchcr 100	59/75/69/0.016/5.93 $\times {10}^{-7}$	157/4341/1989/0.306/4.38 $\times {10}^{-7}$	F/F/F/F/4.08 $\times {10}^{-6}$	86/2125/978/0.127/5.68 $\times {10}^{-7}$	67/1635/810/0.093/9.77 $\times {10}^{-7}$
fletchcr 200	59/75/72/0.012/7.79 $\times {10}^{-7}$	117/3079/1414/0.205/7.30 $\times {10}^{-7}$	75/288/195/0.032/4.41 $\times {10}^{-7}$	F/F/F/F/8.57 $\times {10}^{-6}$	F/F/F/F/1.00 $\times {10}^{-5}$
freuroth 5	269/390/421/0.061/9.04 $\times {10}^{-7}$	941/28,582/12,159/1.563/3.39 $\times {10}^{-8}$	F/F/F/F/1.56 $\times {10}^{-5}$	1580/48,118/19,484/2.562/6.79 $\times {10}^{-7}$	F/F/F/F/5.26 $\times {10}^{-6}$
genrose 5000	283/292/397/0.537/7.01 $\times {10}^{-7}$	371/10,726/47,41/6.456/3.94 $\times {10}^{-7}$	219/194/283/0.441/7.91 $\times {10}^{-7}$	1070/31,988/13,201/16.842/4.83 $\times {10}^{-7}$	616/16,065/7855/5.567/8.05 $\times {10}^{-7}$
genrose 100,000	142/170/193/2.068/9.01 $\times {10}^{-7}$	416/12,351/5418/62.603/9.70 $\times {10}^{-7}$	166/203/233/2.965/9.99 $\times {10}^{-7}$	494/14,196/6016/71.947/9.73 $\times {10}^{-7}$	361/9600/4616/54.420/9.84 $\times {10}^{-7}$
genrose 1000	233/266/335/0.077/8.18 $\times {10}^{-7}$	295/8492/3729/0.942/8.13 $\times {10}^{-7}$	224/197/291/0.087/7.28 $\times {10}^{-7}$	701/20,368/8502/2.625/4.17 $\times {10}^{-7}$	393/10,221/5053/1.526/9.81 $\times {10}^{-7}$
gulf 3000	2/1/2/0.008/0.00 $\times {10}^0$	2/1/2/0.001/0.00 $\times {10}^0$	2/1/2/0.000/0.00 $\times {10}^0$	2/1/2/0.000/0.00 $\times {10}^0$	2/1/2/0.000/0.00 $\times {10}^0$
helix 20,000	133/203/199/0.064/7.70 $\times {10}^{-7}$	282/8168/3481/0.733/4.20 $\times {10}^{-7}$	119/258/212/0.044/8.96 $\times {10}^{-7}$	731/21,643/8941/2.214/6.74 $\times {10}^{-7}$	F/F/F/F/4.06 $\times {10}^1$
himmelbg 30,000	3/6/7/0.051/8.71 $\times {10}^{-28}$	3/6/7/0.043/7.27 $\times {10}^{-28}$	3/6/7/0.043/8.73 $\times {10}^{-28}$	3/6/7/0.042/6.57 $\times {10}^{-28}$	3/6/7/0.043/8.75 $\times {10}^{-28}$
himmelbg 50,000	3/6/7/0.075/1.12 $\times {10}^{-27}$	3/6/7/0.067/9.38 $\times {10}^{-28}$	3/6/7/0.081/1.13 $\times {10}^{-27}$	3/6/7/0.066/8.48 $\times {10}^{-28}$	3/6/7/0.072/1.13 $\times {10}^{-27}$
himmelbg 10	3/6/7/0.001/1.59 $\times {10}^{-29}$	3/6/7/0.001/1.33 $\times {10}^{-29}$	3/6/7/0.001/1.59 $\times {10}^{-29}$	3/6/7/0.001/1.20 $\times {10}^{-29}$	3/6/7/0.001/1.60 $\times {10}^{-29}$
kowosb 10	449/470/668/0.097/9.29 $\times {10}^{-7}$	817/24,298/10,391/1.768/4.66 $\times {10}^{-7}$	118/285/243/0.042/6.03 $\times {10}^{-7}$	F/F/F/F/5.22 $\times {10}^{-4}$	312/8413/4176/0.666/7.72 $\times {10}^{-7}$
liarwhd 15	59/95/73/0.018/9.69 $\times {10}^{-7}$	72/1725/753/0.127/4.53 $\times {10}^{-7}$	35/129/68/0.013/7.67 $\times {10}^{-7}$	229/6565/2858/0.417/5.51 $\times {10}^{-7}$	47/1028/474/0.072/6.32 $\times {10}^{-7}$
liarwhd 1000	258/421/426/0.094/6.91 $\times {10}^{-7}$	F/F/F/F/1.33 $\times {10}^{-4}$	39/211/102/0.027/7.23 $\times {10}^{-7}$	1267/38,967/15,799/3.867/9.84 $\times {10}^{-7}$	224/5956/2888/0.612/5.39 $\times {10}^{-7}$
nondquar 10	385/461/586/0.085/9.98 $\times {10}^{-7}$	F/F/F/F/2.49 $\times {10}^{-4}$	F/F/F/F/2.76 $\times {10}^{-3}$	F/F/F/F/1.28 $\times {10}^{-3}$	F/F/F/F/1.99 $\times {10}^1$
penalty1 1000	14/75/14/0.279/6.45 $\times {10}^{-8}$	15/253/94/1.084/1.21 $\times {10}^{-7}$	14/75/14/0.279/7.70 $\times {10}^{-8}$	15/253/94/0.996/1.21 $\times {10}^{-7}$	15/253/94/0.954/1.21 $\times {10}^{-7}$
penalty1 8000	17/79/17/13.954/3.44 $\times {10}^{-7}$	114/3407/1633/545.410/1.79 $\times {10}^{-7}$	17/79/17/11.996/3.00 $\times {10}^{-7}$	114/3407/1624/568.693/1.79 $\times {10}^{-7}$	114/3407/1607/573.841/1.77 $\times {10}^{-7}$
quartc 50	23/67/23/0.010/5.57 $\times {10}^{-7}$	28/516/226/0.034/1.42 $\times {10}^{-8}$	21/68/23/0.006/1.03 $\times {10}^{-7}$	26/449/192/0.028/8.61 $\times {10}^{-7}$	85/2319/1093/0.157/6.36 $\times {10}^{-7}$
quartc 300	25/86/26/0.019/4.33 $\times {10}^{-7}$	34/562/249/0.100/3.74 $\times {10}^{-7}$	29/87/32/0.020/2.30 $\times {10}^{-7}$	37/633/284/0.116/8.92 $\times {10}^{-8}$	108/2821/1345/0.494/4.26 $\times {10}^{-7}$
tridia 400	1196/1131/1723/0.225/8.86 $\times {10}^{-7}$	F/F/F/F/1.07 $\times {10}^{-3}$	865/482/1067/0.152/6.41 $\times {10}^{-7}$	F/F/F/F/3.76 $\times {10}^{-5}$	832/22,141/10,798/1.437/5.76 $\times {10}^{-7}$
tridia 500	1163/1073/1661/0.230/9.65 $\times {10}^{-7}$	1655/47,555/20,693/3.330/4.97 $\times {10}^{-7}$	F/F/F/F/1.52 $\times {10}^3$	F/F/F/F/3.97 $\times {10}^{-3}$	991/25,621/12,586/1.797/5.03 $\times {10}^{-7}$
sinquad 3	202/284/320/0.032/6.77 $\times {10}^{-8}$	272/7998/3343/0.334/8.95 $\times {10}^{-7}$	86/220/173/0.018/6.56 $\times {10}^{-8}$	501/14,834/5870/0.639/2.96 $\times {10}^{-7}$	166/4182/2052/0.201/9.27 $\times {10}^{-7}$
vardim 2	10/54/10/0.014/5.74 $\times {10}^{-7}$	10/124/36/0.005/9.89 $\times {10}^{-8}$	10/54/10/0.003/5.74 $\times {10}^{-7}$	10/124/36/0.009/9.89 $\times {10}^{-8}$	10/124/36/0.006/9.89 $\times {10}^{-8}$
woods 10,000	662/760/998/1.323/9.70 $\times {10}^{-7}$	1851/54,675/25,702/47.380/9.00 $\times {10}^{-7}$	215/321/331/0.640/5.16 $\times {10}^{-7}$	1122/32,157/13,925/29.130/8.10 $\times {10}^{-7}$	515/13,196/6550/12.415/1.79 $\times {10}^{-7}$

Table 2. Numerical test reports for the five tested methods (Continue).

Problems	JYJLL	KD	AN1	HZ	LFZ
Name/n	Itr/ NF/ NG/ Tcpu/ $\parallel g_{*}\parallel$	Itr/ NF/ NG/ Tcpu/ $\parallel g_{*}\parallel$	Itr/ NF/ NG/ Tcpu/ $\parallel g_{*}\parallel$	Itr/ NF/ NG/ Tcpu/ $\parallel g_{*}\parallel$	Itr/ NF/ NG/ Tcpu/ $\parallel g_{*}\parallel$
bdexp 50,000	3/2/3/0.079/1.33 $\times {10}^{-109}$	3/2/3/0.075/1.28 $\times {10}^{-109}$	3/2/3/0.072/1.32 $\times {10}^{-109}$	3/2/3/0.073/1.25 $\times {10}^{-109}$	3/2/3/0.074/1.33 $\times {10}^{-109}$
bdexp 100,000	3/2/3/0.134/1.73 $\times {10}^{-109}$	3/2/3/0.129/1.70 $\times {10}^{-109}$	3/2/3/0.132/1.73 $\times {10}^{-109}$	3/2/3/0.123/1.68 $\times {10}^{-109}$	3/2/3/0.123/1.73 $\times {10}^{-109}$
bdexp 1,000,000	3/2/3/1.245/5.09 $\times {10}^{-109}$	3/2/3/1.276/5.08 $\times {10}^{-109}$	3/2/3/1.341/5.09 $\times {10}^{-109}$	3/2/3/1.239/5.08 $\times {10}^{-109}$	3/2/3/1.259/5.09 $\times {10}^{-109}$
exdenschnf 100,000	24/84/25/0.751/8.51 $\times {10}^{-7}$	69/1886/922/16.019/6.00 $\times {10}^{-7}$	74/130/97/2.004/8.07 $\times {10}^{-7}$	59/1490/692/12.027/2.21 $\times {10}^{-7}$	123/3284/1568/26.773/8.35 $\times {10}^{-7}$
exdenschnf 1,000,000	29/86/30/8.772/3.60 $\times {10}^{-7}$	72/1974/940/155.062/9.90 $\times {10}^{-8}$	57/114/73/16.513/3.88 $\times {10}^{-7}$	123/3517/1677/281.678/5.75 $\times {10}^{-8}$	220/6391/3128/520.133/6.92 $\times {10}^{-7}$
mccormak 2	23/58/30/0.024/7.24 $\times {10}^{-7}$	19/364/163/0.021/8.11 $\times {10}^{-7}$	33/55/39/0.005/7.39 $\times {10}^{-7}$	39/900/404/0.039/1.21 $\times {10}^{-7}$	F/F/F/F/2.89 $\times {10}^4$
exdenschnb 15,000	24/62/25/0.067/3.34 $\times {10}^{-7}$	28/600/263/0.496/8.71 $\times {10}^{-7}$	32/61/33/0.101/7.18 $\times {10}^{-7}$	38/787/367/0.764/9.24 $\times {10}^{-8}$	134/3726/1766/3.688/8.57 $\times {10}^{-7}$
exdenschnb 120,000	23/62/24/0.497/7.31 $\times {10}^{-7}$	30/632/282/3.333/2.86 $\times {10}^{-7}$	33/63/34/0.638/8.21 $\times {10}^{-7}$	28/523/223/2.688/2.98 $\times {10}^{-7}$	89/2344/1134/12.149/4.31 $\times {10}^{-7}$
genquartic 120,000	35/78/41/0.793/9.37 $\times {10}^{-7}$	46/929/437/6.281/1.34 $\times {10}^{-7}$	47/83/57/1.178/5.73 $\times {10}^{-7}$	59/1355/643/9.081/9.61 $\times {10}^{-7}$	166/4182/2080/28.307/9.70 $\times {10}^{-7}$
genquartic 100,000	28/67/31/0.556/5.69 $\times {10}^{-7}$	37/736/306/4.120/5.17 $\times {10}^{-7}$	39/74/44/0.786/6.59 $\times {10}^{-7}$	81/2048/984/11.667/8.80 $\times {10}^{-7}$	174/4464/2191/25.852/9.57 $\times {10}^{-7}$
biggsb1 110	790/738/1136/0.118/7.29 $\times {10}^{-7}$	F/F/F/F/2.37 $\times {10}^{-4}$	522/143/571/0.065/9.63 $\times {10}^{-7}$	1868/55,264/23,430/2.526/9.82 $\times {10}^{-7}$	594/15,762/7618/0.728/4.96 $\times {10}^{-7}$
biggsb1 200	1717/1618/2504/0.255/8.47 $\times {10}^{-7}$	1809/52,361/22,385/2.674/9.04 $\times {10}^{-7}$	1148/205/1228/0.163/9.09 $\times {10}^{-7}$	F/F/F/F/2.38 $\times {10}^{-3}$	866/22,409/11,027/1.192/7.31 $\times {10}^{-7}$
sine 750,000	111/147/156/31.089/8.79 $\times {10}^{-7}$	141/3661/1775/379.752/3.73 $\times {10}^{-11}$	F/F/F/F/1.65 $\times {10}^{-3}$	101/2714/1330/318.993/5.72 $\times {10}^{-7}$	F/F/F/F/5.77 $\times {10}^{-3}$
sine 1,000,000	238/407/412/110.321/2.67 $\times {10}^{-7}$	72/2052/994/297.446/2.56 $\times {10}^{-7}$	89/198/160/47.856/2.98 $\times {10}^{-7}$	150/3798/1858/538.100/9.23 $\times {10}^{-8}$	F/F/F/F/4.35 $\times {10}^1$
fletcbv3 55	667/488/895/0.408/2.07 $\times {10}^{-7}$	1381/26,076/12,787/1.507/8.07 $\times {10}^{-8}$	F/F/F/F/2.03 $\times {10}^{-4}$	1388/26,927/13,220/1.712/8.48 $\times {10}^{-7}$	F/F/F/F/1.59 $\times {10}^{-4}$
fletcbv3 85	1654/911/2080/0.348/5.69 $\times {10}^{-7}$	F/F/F/F/7.89 $\times {10}^{-4}$	F/F/F/F/7.43 $\times {10}^{-4}$	F/F/F/F/8.15 $\times {10}^{-4}$	772/13,968/7106/1.214/2.55 $\times {10}^{-7}$
nonscomp 30,000	F/F/F/F/2.14 $\times {10}^{-4}$	147/3574/1604/6.135/8.57 $\times {10}^{-7}$	95/124/119/0.409/4.82 $\times {10}^{-7}$	927/27600/11616/41.504/5.89 $\times {10}^{-7}$	F/F/F/F/4.08 $\times {10}^{-3}$
nonscomp 25000	60/78/62/0.217/6.47 $\times {10}^{-7}$	1164/35,210/14,738/47.678/6.09 $\times {10}^{-7}$	93/125/118/0.381/9.82 $\times {10}^{-7}$	199/4988/2234/6.920/4.66 $\times {10}^{-7}$	1006/26,503/13,011/38.180/4.78 $\times {10}^{-7}$
power1 100	1588/1500/2295/0.277/7.70 $\times {10}^{-7}$	F/F/F/F/8.27 $\times {10}^{-5}$	1496/908/1907/0.181/9.52 $\times {10}^{-7}$	F/F/F/F/2.49 $\times {10}^{-1}$	1178/31,067/15,281/1.268/7.06 $\times {10}^{-7}$
power1 90	1614/1548/2346/0.201/9.42 $\times {10}^{-7}$	F/F/F/F/5.18 $\times {10}^{-5}$	F/F/F/F/1.03 $\times {10}^{-2}$	F/F/F/F/5.28 $\times {10}^{-2}$	1043/27,237/13,510/1.104/8.22 $\times {10}^{-7}$
raydan1 1000	320/362/470/0.141/6.35 $\times {10}^{-7}$	527/14,585/6962/1.225/8.97 $\times {10}^{-7}$	F/F/F/F/1.91 $\times {10}^{-5}$	1029/29,815/13,278/2.239/7.75 $\times {10}^{-7}$	F/F/F/F/4.19 $\times {10}^{-5}$
raydan1 1200	404/391/568/0.101/2.46 $\times {10}^{-7}$	601/17,005/7837/1.484/7.66 $\times {10}^{-7}$	1971/2141/3002/0.527/8.77 $\times {10}^{-7}$	850/24,008/10,762/1.970/9.80 $\times {10}^{-7}$	F/F/F/F/1.31 $\times {10}^{-4}$
raydan2 5000	17/52/17/0.067/9.00 $\times {10}^{-7}$	21/456/230/0.265/7.22 $\times {10}^{-8}$	17/52/17/0.033/9.35 $\times {10}^{-7}$	38/972/472/0.461/2.67 $\times {10}^{-7}$	21/458/205/0.207/8.34 $\times {10}^{-7}$
raydan2 10,000	17/56/20/0.069/1.63 $\times {10}^{-7}$	18/364/149/0.374/1.55 $\times {10}^{-7}$	23/60/28/0.089/6.20 $\times {10}^{-7}$	17/303/143/0.326/3.56 $\times {10}^{-7}$	33/780/348/0.819/8.82 $\times {10}^{-7}$
raydan2 20,000	13/50/14/0.100/7.46 $\times {10}^{-7}$	29/662/305/1.224/3.55 $\times {10}^{-7}$	20/83/44/0.185/6.68 $\times {10}^{-7}$	14/238/81/0.602/8.97 $\times {10}^{-7}$	21/413/163/0.867/5.83 $\times {10}^{-7}$
diagonal1 50	69/67/72/0.047/6.89 $\times {10}^{-7}$	152/4438/2120/0.247/8.73 $\times {10}^{-7}$	79/244/169/0.017/7.22 $\times {10}^{-7}$	204/5701/2669/0.239/9.74 $\times {10}^{-7}$	188/4914/2287/0.218/5.44 $\times {10}^{-7}$
diagonal1 80	100/321/228/0.063/8.82 $\times {10}^{-7}$	227/6698/3133/0.355/5.49 $\times {10}^{-7}$	F/F/F/F/1.81 $\times {10}^{-5}$	215/5707/2704/0.267/8.70 $\times {10}^{-7}$	F/F/F/F/1.11 $\times {10}^{-5}$
diagonal2 5000	821/775/1183/1.415/7.04 $\times {10}^{-7}$	1614/47,941/22,089/25.459/9.28 $\times {10}^{-7}$	470/415/652/0.717/7.50 $\times {10}^{-7}$	F/F/F/F/1.33 $\times {10}^{-1}$	619/15,686/7753/8.985/9.65 $\times {10}^{-7}$
diagonal2 10,000	1043/974/1505/3.503/5.89 $\times {10}^{-7}$	F/F/F/F/1.93 $\times {10}^{-4}$	873/775/1235/5.941/9.42 $\times {10}^{-7}$	F/F/F/F/2.20 $\times {10}^{-1}$	819/21,318/10,576/30.265/7.97 $\times {10}^{-7}$
diagonal3 150	164/575/422/0.058/7.53 $\times {10}^{-7}$	194/5161/2419/0.294/7.94 $\times {10}^{-7}$	F/F/F/F/2.95 $\times {10}^{-5}$	F/F/F/F/5.99 $\times {10}^{-6}$	F/F/F/F/2.13 $\times {10}^{-5}$
diagonal3 200	144/655/421/0.056/9.54 $\times {10}^{-7}$	F/F/F/F/3.24 $\times {10}^{-6}$	F/F/F/F/2.96 $\times {10}^{-5}$	F/F/F/F/2.85 $\times {10}^{-5}$	F/F/F/F/6.48 $\times {10}^{-5}$
bv 1000	19/13/23/0.152/8.69 $\times {10}^{-7}$	29/805/356/3.956/6.69 $\times {10}^{-7}$	82/25/90/0.705/7.51 $\times {10}^{-7}$	33/931/383/4.416/9.42 $\times {10}^{-7}$	143/4195/1754/19.534/8.70 $\times {10}^{-7}$
bv 2000	5/5/5/0.125/5.84 $\times {10}^{-7}$	14/385/172/5.830/3.11 $\times {10}^{-7}$	42/9/44/0.964/8.45 $\times {10}^{-7}$	9/225/93/3.519/4.59 $\times {10}^{-7}$	123/3714/1509/55.763/5.77 $\times {10}^{-7}$
ie 215	13/40/13/0.977/8.36 $\times {10}^{-7}$	13/183/64/3.470/7.39 $\times {10}^{-7}$	15/42/15/1.083/9.11 $\times {10}^{-7}$	17/294/120/6.959/9.65 $\times {10}^{-8}$	40/889/394/21.664/3.31 $\times {10}^{-7}$
singx 900	F/F/F/F/1.46 $\times {10}^{-5}$	1479/44741/16,996/180.509/2.36 $\times {10}^{-7}$	223/580/477/3.497/8.63 $\times {10}^{-7}$	F/F/F/F/4.08 $\times {10}^{-5}$	366/9279/4616/38.993/4.12 $\times {10}^{-7}$
band 3	20/64/22/0.024/1.48 $\times {10}^{-7}$	67/1838/860/0.089/6.29 $\times {10}^{-7}$	40/96/57/0.007/4.87 $\times {10}^{-7}$	77/2156/1006/0.097/6.95 $\times {10}^{-7}$	46/1025/467/0.048/8.94 $\times {10}^{-8}$
gauss 3	23/38/28/0.029/4.72 $\times {10}^{-7}$	47/1263/533/0.085/6.39 $\times {10}^{-7}$	12/30/13/0.003/6.97 $\times {10}^{-7}$	14/245/114/0.018/8.13 $\times {10}^{-7}$	30/743/361/0.052/7.35 $\times {10}^{-7}$
jensam 2	69/113/98/0.024/8.86 $\times {10}^{-7}$	119/3545/1697/0.155/6.69 $\times {10}^{-7}$	37/139/82/0.009/2.89 $\times {10}^{-7}$	211/6152/2894/0.271/6.99 $\times {10}^{-7}$	188/5415/2603/0.242/3.45 $\times {10}^{-8}$
lin 200	2/2/2/0.012/1.71 $\times {10}^{-13}$	2/2/2/0.006/1.71 $\times {10}^{-13}$	2/2/2/0.006/1.71 $\times {10}^{-13}$	2/2/2/0.006/1.71 $\times {10}^{-13}$	2/2/2/0.007/1.71 $\times {10}^{-13}$
lin 500	2/2/2/0.021/9.93 $\times {10}^{-14}$	2/2/2/0.021/9.93 $\times {10}^{-14}$	2/2/2/0.020/9.93 $\times {10}^{-14}$	2/2/2/0.021/9.93 $\times {10}^{-14}$	2/2/2/0.020/9.93 $\times {10}^{-14}$
lin 500	2/2/2/0.023/9.93 $\times {10}^{-14}$	2/2/2/0.021/9.93 $\times {10}^{-14}$	2/2/2/0.022/9.93 $\times {10}^{-14}$	2/2/2/0.020/9.93 $\times {10}^{-14}$	2/2/2/0.020/9.93 $\times {10}^{-14}$
osb2 11	1266/1180/1833/0.415/9.27 $\times {10}^{-7}$	F/F/F/F/2.54 $\times {10}^{-3}$	615/483/831/0.200/5.98 $\times {10}^{-7}$	F/F/F/F/6.43 $\times {10}^{-4}$	F/F/F/F/5.58 $\times {10}^{-2}$
pen1 50	121/233/192/0.035/8.32 $\times {10}^{-7}$	222/6619/2668/0.414/7.03 $\times {10}^{-7}$	58/152/89/0.016/2.20 $\times {10}^{-7}$	691/21,027/8471/1.298/7.18 $\times {10}^{-7}$	21/427/184/0.027/7.53 $\times {10}^{-7}$
pen1 90	260/411/417/0.069/9.04 $\times {10}^{-7}$	340/10,061/4115/0.750/8.46 $\times {10}^{-7}$	104/284/194/0.035/2.08 $\times {10}^{-7}$	348/10,351/4128/0.768/4.68 $\times {10}^{-7}$	93/2475/1171/0.190/5.09 $\times {10}^{-9}$
pen2 105	135/360/265/0.116/5.37 $\times {10}^{-7}$	224/6471/3041/1.603/7.59 $\times {10}^{-7}$	F/F/F/F/4.85 $\times {10}^{-5}$	F/F/F/F/7.28 $\times {10}^{-5}$	F/F/F/F/2.24 $\times {10}^{-4}$
pen2 100	F/F/F/F/1.09 $\times {10}^{-5}$	274/7792/3688/1.809/6.18 $\times {10}^{-7}$	F/F/F/F/8.89 $\times {10}^{-6}$	430/12,042/5778/3.055/8.95 $\times {10}^{-7}$	F/F/F/F/7.94 $\times {10}^{-6}$
rose 2	166/261/263/0.063/4.08 $\times {10}^{-7}$	911/28,228/11,815/1.219/8.56 $\times {10}^{-7}$	58/239/145/0.016/4.35 $\times {10}^{-7}$	1075/32,570/13,545/1.405/9.49 $\times {10}^{-7}$	148/3833/1917/0.174/8.42 $\times {10}^{-8}$
rosex 100	377/471/577/0.089/1.30 $\times {10}^{-7}$	1077/33,420/13,972/2.948/8.43 $\times {10}^{-7}$	66/317/190/0.041/8.67 $\times {10}^{-7}$	811/23,841/10,191/2.349/2.55 $\times {10}^{-7}$	148/4021/1954/0.423/8.91 $\times {10}^{-8}$
rosex 500	292/415/463/2.101/3.95 $\times {10}^{-7}$	1160/36,016/15,090/88.764/7.03 $\times {10}^{-7}$	60/241/146/0.751/6.09 $\times {10}^{-7}$	891/26,552/11,144/65.695/7.84 $\times {10}^{-7}$	150/4066/1960/10.359/4.00 $\times {10}^{-7}$
sing 4	896/1018/1373/0.142/7.31 $\times {10}^{-7}$	380/11052/4591/0.502/6.68 $\times {10}^{-7}$	153/388/314/0.032/5.24 $\times {10}^{-7}$	F/F/F/F/5.50 $\times {10}^{-6}$	360/8971/4386/0.427/9.01 $\times {10}^{-7}$
trid 50	82/79/93/0.029/9.78 $\times {10}^{-7}$	201/5551/2510/0.475/5.26 $\times {10}^{-7}$	81/89/96/0.019/9.39 $\times {10}^{-7}$	196/5383/2389/0.451/4.84 $\times {10}^{-7}$	317/8411/4103/0.723/9.60 $\times {10}^{-7}$
trid 90	87/87/101/0.026/3.19 $\times {10}^{-7}$	240/6330/2957/0.737/9.36 $\times {10}^{-7}$	103/105/126/0.033/8.56 $\times {10}^{-7}$	182/4501/2012/0.531/4.11 $\times {10}^{-7}$	207/5447/2632/0.654/8.16 $\times {10}^{-7}$
wood 4	351/391/509/0.074/8.86 $\times {10}^{-7}$	631/17,914/8171/0.865/7.97 $\times {10}^{-7}$	210/342/341/0.037/7.14 $\times {10}^{-7}$	1284/36,519/15,935/1.768/7.91 $\times {10}^{-7}$	375/9721/4715/0.479/4.73 $\times {10}^{-7}$

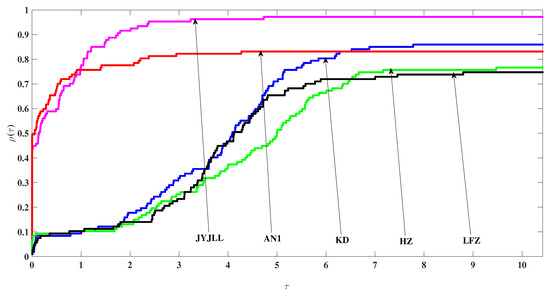
Figure 1. Performance profiles on Tcpu.

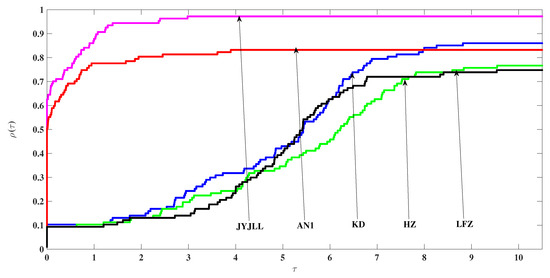
Figure 2. Performance profiles on NF.

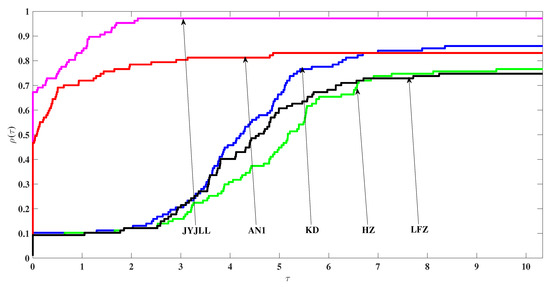
Figure 3. Performance profiles on NG

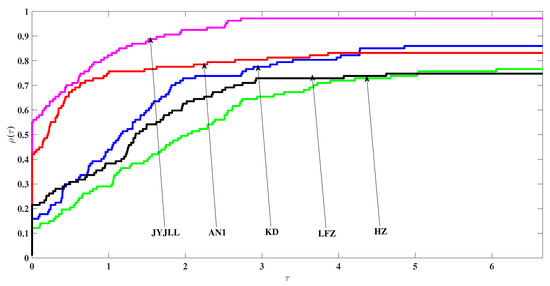
Figure 4. Performance profiles on Itr.

5. Discussion of Results

First, it is known, from the characters of the performance profiles, that the higher the curve in the figures, the better the associated method. Second, by summarizing the convergence analysis and numerical reports in Table 1 and Table 2 and Figure 1, Figure 2, Figure 3 and Figure 4, the proposed JYJLL-SCGM shows the following three advantages.

(i) It has good global convergence under mild assumptions.

(ii) It is practically effective, at least for the 108 tested instances.

(iii) It is the most effective in the five tested methods. In addition, the numerical performance of AN1 [13] method and the JYJLL-SCGM is relatively stable.

Of cause, the advantages above are attributed to the choice techniques (8) and (9) for the spectral parameter and the conjugate parameter.

6. Conclusions

The contributions of this work are two aspects. The one is to design a new computing schemes for the spectral parameter which ensures the ${\theta }_k>1$. The other is to propose a new computing method for the conjugate parameter. These two techniques such that the search directions always possess descent property independent of the line search technique. As a result, the presented JYJLL-SCGM possesses global convergence if using the Wolfe line search to yield the steplength. A lot of numerical experiments in comparison with relative methods show that our SCGM is promising.

As further works, we think the following two problems are interesting and worth studying. The one is to design new approaches for the spectral parameter to guarantee ${\theta }_k>1$, such as, combining the Newton direction and some new quasi-Newton equations, or the new conjugate conditions. The other is to find new computation techniques for the conjugate parameter with the help of the existing approaches, for example, the hybrid parameter, the three–term conjugate parameter et al.