A Novel Tabu Search Algorithm for Multi-AGV Routing Problem
Abstract
1. Introduction
2. Problem Formulation
2.1. Work Flow of Picking Up Goods
2.2. Problem Description and Mathematical Formulation
- (1)
- One only focuses on the issue of taking out goods, while the time of taking out goods is not counted.
- (2)
- The number of AGVs is fixed.
- (3)
- Since one only considers the case that the goods volume or quality is small enough and will not exceed the AGV capacity, the capacity limitations are ignored.
- (4)
- One must consider each AGV as a particle with a constant velocity, regardless of turning time and acceleration.
- (5)
- The starting and ending points of each AGV pickup path are the entrance and exit, respectively.
- (6)
- Each pickup point is processed only once.
- (7)
- The distance to the adjacent cell is 1, and the time taken to traverse that distance is 1.
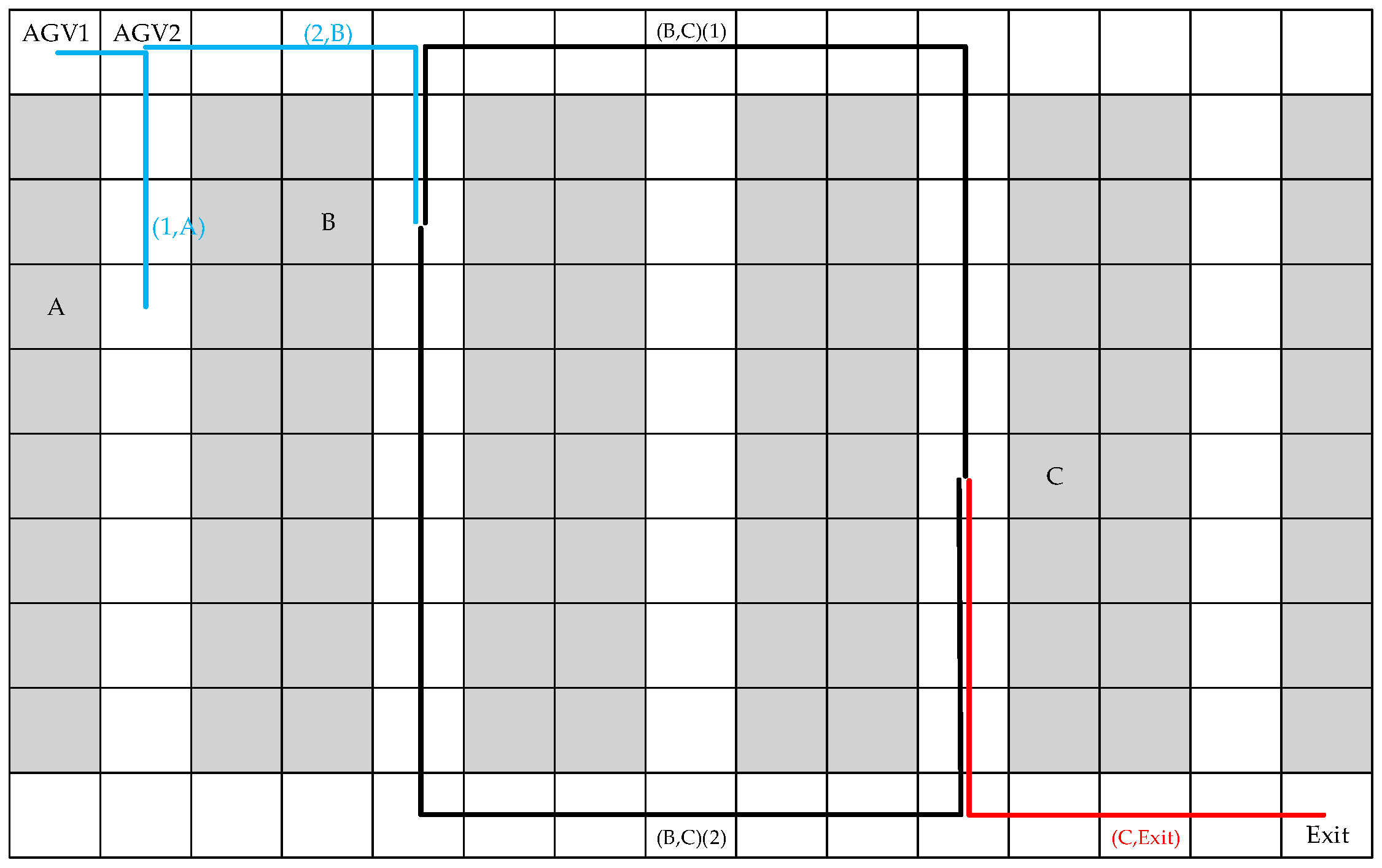
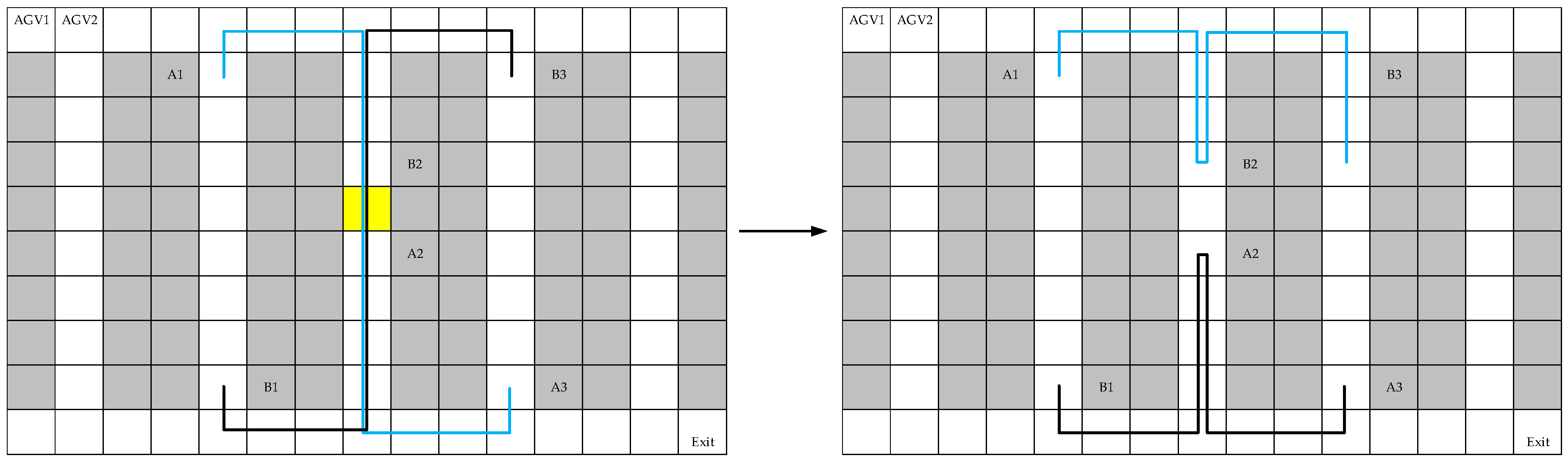
3. Conflict Types and Solving Approaches
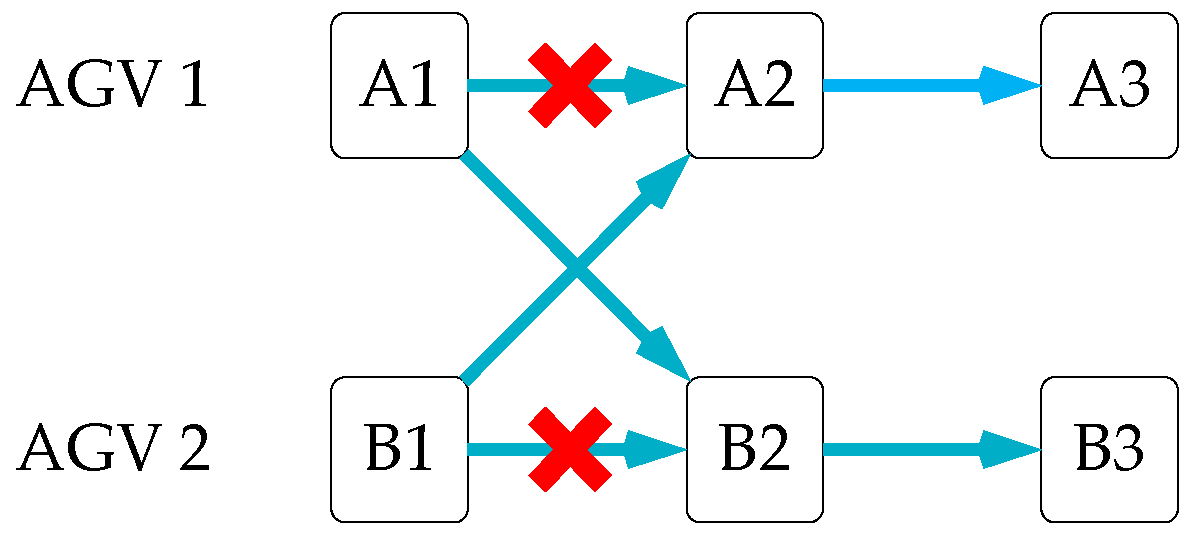
3.1. Opposite Direction Conflict
3.2. Uniform Direction Conflict
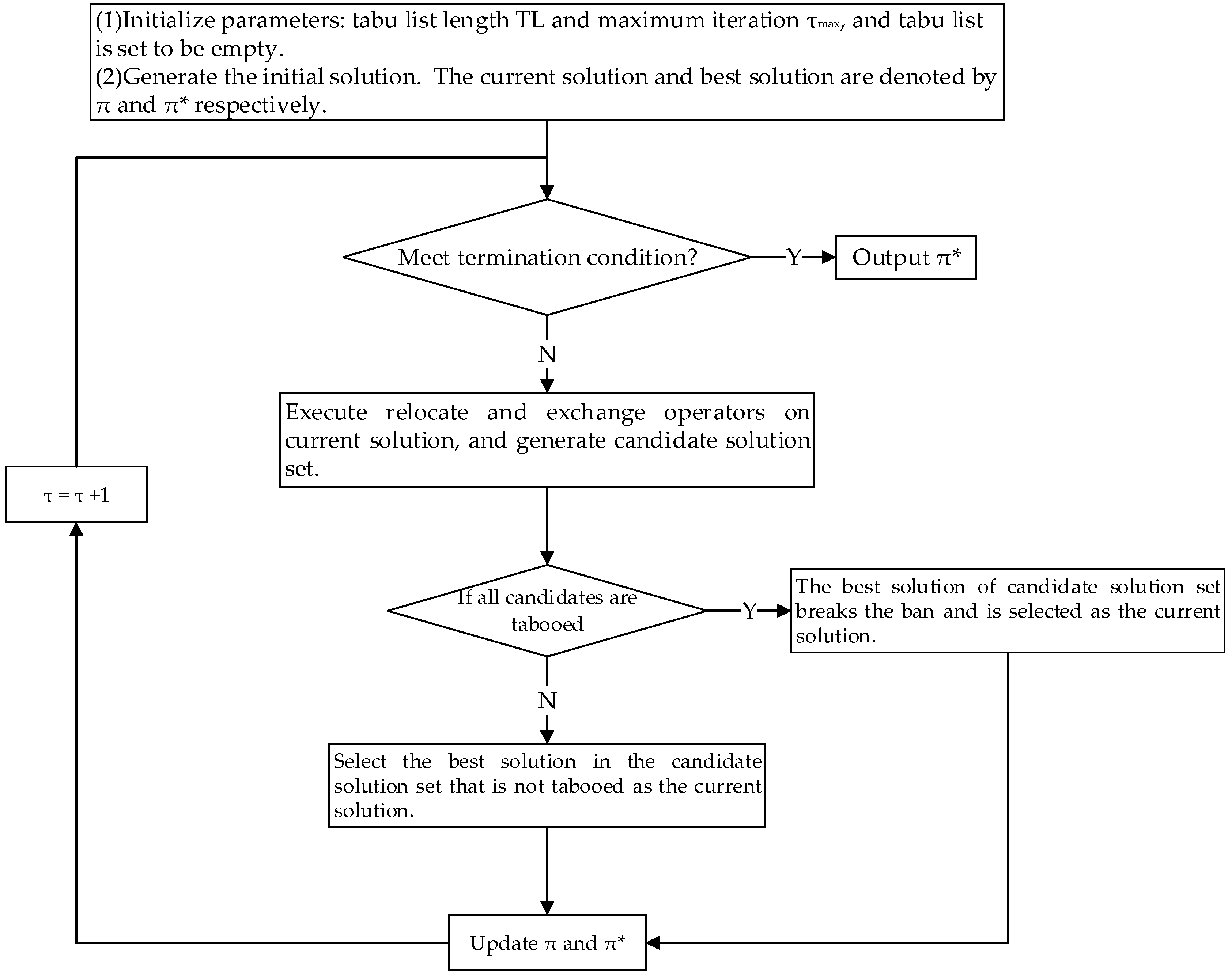
4. Tabu Search Algorithm
4.1. Initial Solution Generation
- (1)
- First, arrange the first pickup point for each AGV as the one that is closest to the AGV’s entrance.
- (2)
- Arrange the next nearest pickup point for the AGVs that takes shortest time to pick up all arranged goods.
- (3)
- Arrange exit after all pickup points have been arranged.
4.2. Neighborhood Search
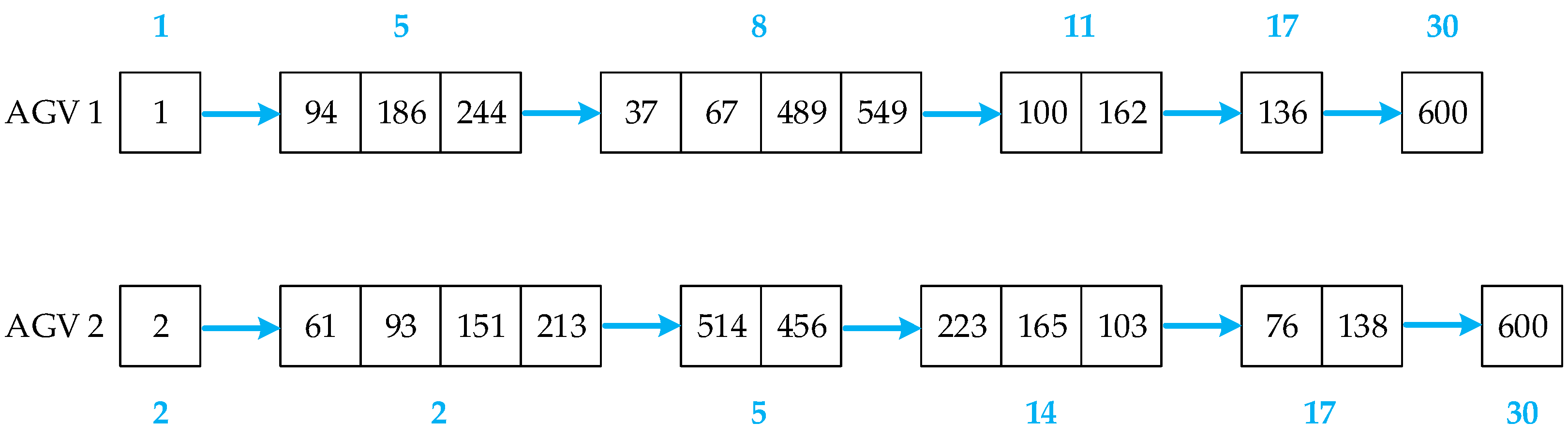
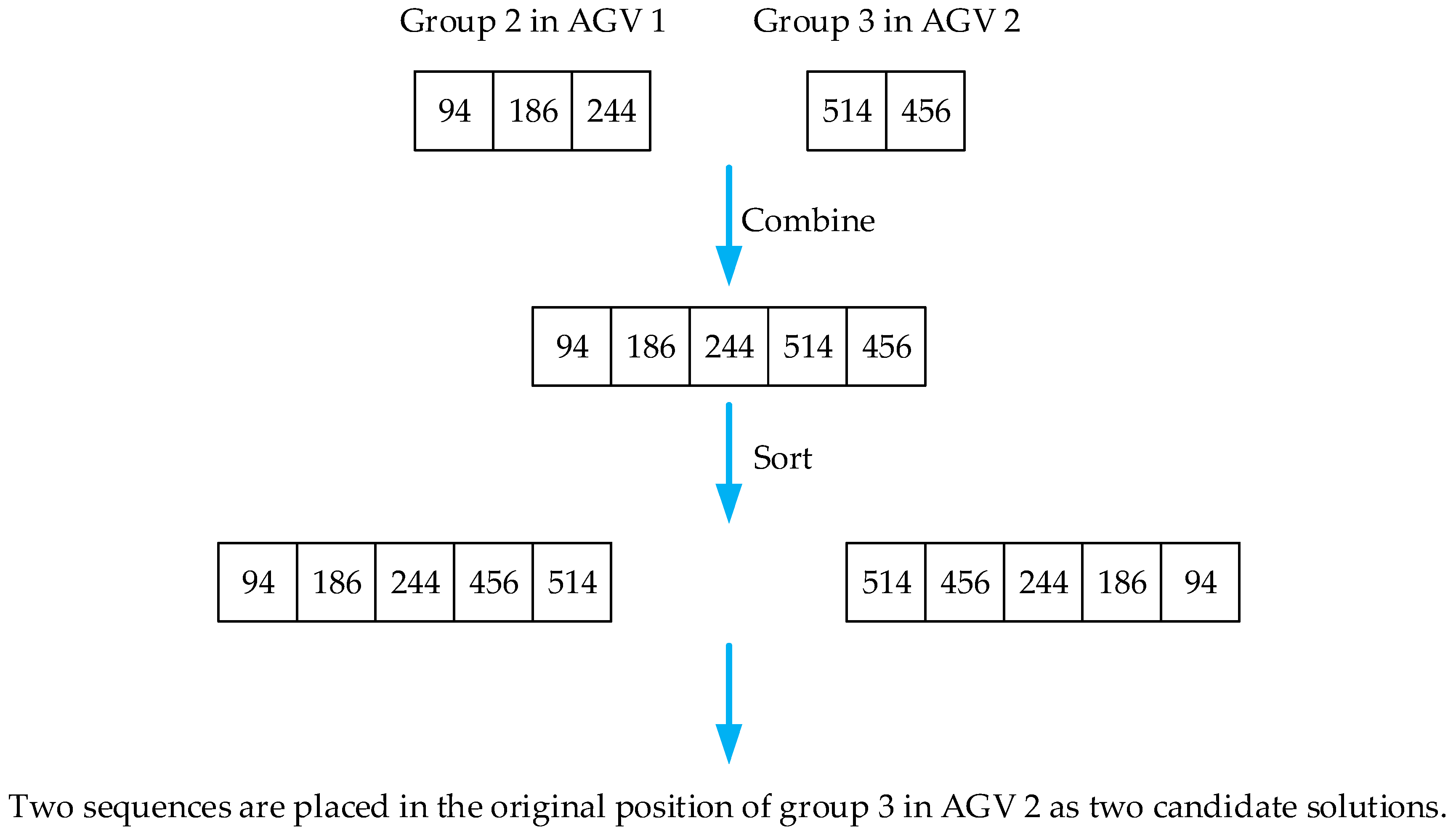
4.2.1. Relocation Operation
4.2.2. Exchanging Operation
4.3. Tabu Object and Aspiration Criterion
4.4. Flow Chart of our TS Algorithm
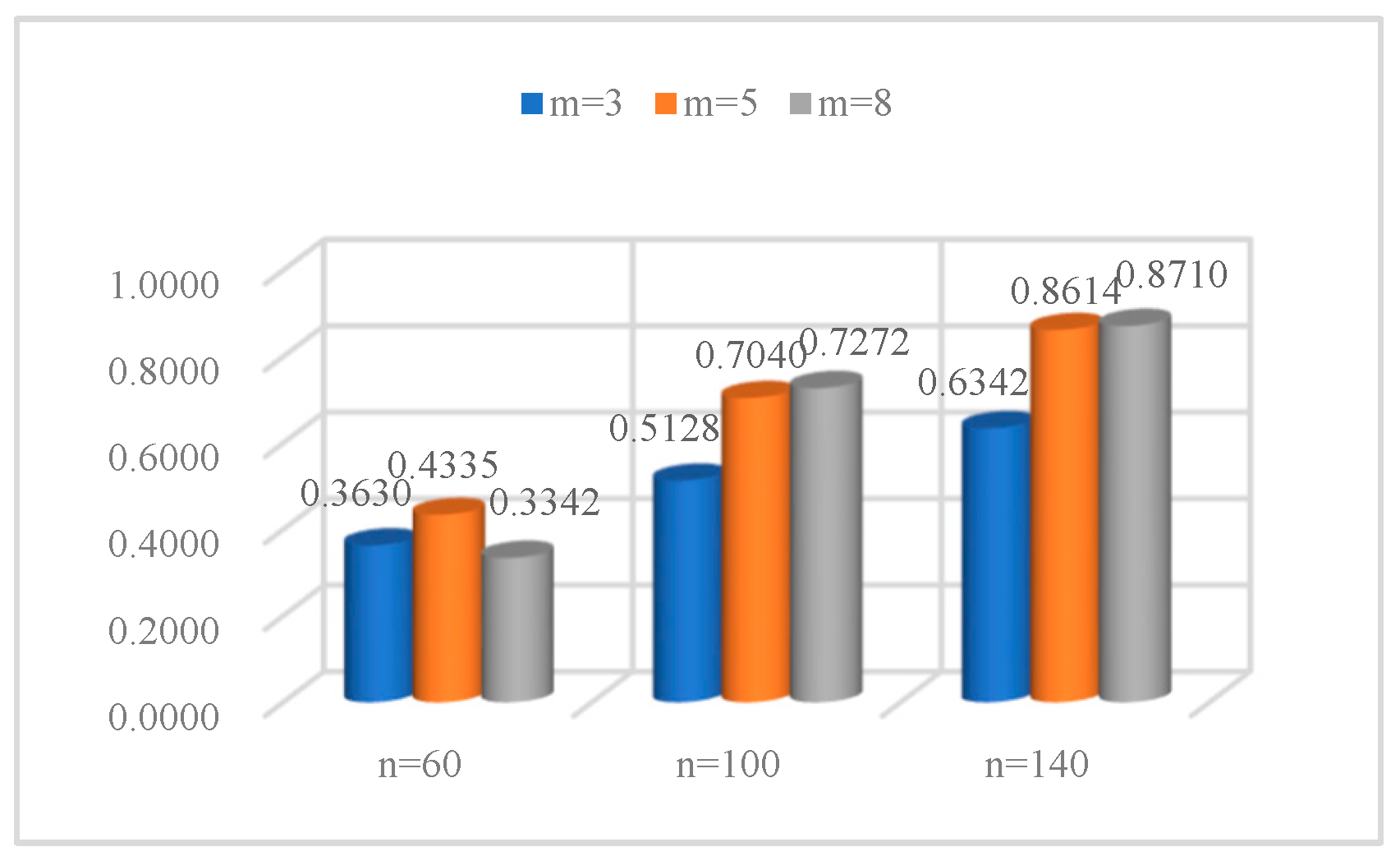
5. Computational Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Factors | Tabu List Length | Maximum Number of Iterations |
|---|---|---|
| Level 1 | 3 | 100 |
| Level 2 | 5 | 200 |
| Level 3 | 7 | 300 |
| Level 4 | 400 | |
| Level 5 | 500 |
| Factors | Tabu List Length | Maximum Number of Iterations | Experimental Result | |
|---|---|---|---|---|
| Trail 1 | 3 | 100 | 40.85 | |
| Trail 2 | 3 | 200 | 32.14 | |
| Trail 3 | 3 | 300 | 30.39 | |
| Trail 4 | 3 | 400 | 40.19 | |
| Trail 5 | 3 | 500 | 34.39 | |
| Trail 6 | 5 | 100 | 39.31 | |
| Trail 7 | 5 | 200 | 37.40 | |
| Trail 8 | 5 | 300 | 38.71 | |
| Trail 9 | 5 | 400 | 31.89 | |
| Trail 10 | 5 | 500 | 32.15 | |
| Trail 11 | 7 | 100 | 41.57 | |
| Trail 12 | 7 | 200 | 32.07 | |
| Trail 13 | 7 | 300 | 39.07 | |
| Trail 14 | 7 | 400 | 34.74 | |
| Trail 15 | 7 | 500 | 35.37 | |
| Trail 16 | 5 | 100 | 35.31 | |
| Trail 17 | 5 | 200 | 37.67 | |
| Trail 18 | 5 | 300 | 37.05 | |
| Trail 19 | 5 | 400 | 36.64 | |
| Trail 20 | 5 | 500 | 34.07 | |
| Trail 21 | 5 | 100 | 36.28 | |
| Trail 22 | 5 | 200 | 34.41 | |
| Trail 23 | 5 | 300 | 41.39 | |
| Trail 24 | 5 | 400 | 37.01 | |
| Trail 25 | 5 | 500 | 36.66 | |
| (Sum of experimental results at level i) | 177.954 | 193.314 | - | |
| 545.947 | 173.679 | - | ||
| 182.814 | 186.608 | - | ||
| - | 180.475 | - | ||
| - | 172.639 | - | ||
| (Mean of experimental results at level i) | 35.591 | 38.663 | - | |
| 36.396 | 34.736 | - | ||
| 36.563 | 37.322 | - | ||
| - | 36.095 | - | ||
| - | 34.528 | - | ||
| Sources of Variation | Sum of Squares of Deviations | Degree of Freedom | Mean Square | F Value | Significance |
| Tabu list length | 2.975 | 2 | 1.488 | - | - |
| Maximum number of iterations | 61.255 | 4 | 15.314 | - | - |
| Error | 175.544 | 18 | 9.752 | - | - |
| Total | 239.774 | 24 | - | - | - |
| Incorporate the Factor Tabu List Length into the Error Column and Recalculate | |||||
| Sources of Variation | Sum of Squares of Deviations | Degree of Freedom | Mean Square | F Value | Significance |
| Tabu list length | 2.975 | 2 | 1.488 | - | No influence |
| Maximum number of iterations | 61.255 | 4 | 15.314 | 1.716 | No influence |
| Error | 178.519 | 20 | 8.926 | - | - |
| Total | 239.774 | 24 | - | - | - |
References
- Mostafa, N.; Hamdy, W.; Alawady, H. Impacts of Internet of Things on supply chains: A framework for warehousing. Soc. Sci. 2019, 8, 84. [Google Scholar] [CrossRef]
- Richards, G. Warehouse Management: A Complete Guide to Improving Efficiency and Minimizing Costs in the Modern Warehouse, 3rd ed.; Kogan Page: London, UK, 2017; pp. 7–25. [Google Scholar]
- Moshayedi, A.J.; Li, J.; Liao, L. AGV (automated guided vehicle) robot: Mission and obstacles in design and performance. J. Simul. Anal. Nov. Technol. Mech. Eng. 2019, 12, 5–18. [Google Scholar]
- Gotting, H.H. Automation and steering of vehicles in ports. Port Technol. Int. 2000, 10, 101–111. [Google Scholar]
- Liu, J.E.; Zhang, S.; Liu, H. Research on AGV Path Planning under “Parts-to-Picker” Mode. Open J. Soc. Sci. 2019, 7, 1–14. [Google Scholar] [CrossRef]
- Petersen, C.G.; Schmenner, R.W. An evaluation of routing and volume-based storage policies in an order picking operation. Decis. Sci. 1999, 30, 481–501. [Google Scholar] [CrossRef]
- Roodbergen, K.J.; De Koster, R. Routing order pickers in a warehouse with a middle aisle. Eur. J. Oper. Res. 2001, 133, 32–43. [Google Scholar] [CrossRef]
- Grosse, E.H.; Glock, C.H. The effect of worker learning on manual order picking processes. Int. J. Prod. Econ. 2015, 170, 882–890. [Google Scholar] [CrossRef]
- Giannikas, V.; Lu, W.; Robertson, B.; McFarlane, D. An interventionist strategy for warehouse order picking: Evidence from two case studies. Int. J. Prod. Econ. 2017, 189, 63–76. [Google Scholar] [CrossRef]
- Koo, P.H. The use of bucket brigades in zone order picking systems. OR Spectr. 2009, 31, 759. [Google Scholar] [CrossRef]
- Koster, R.D.; Le-Duc, T.; Roodbergen, K.J. Design and control of warehouse order picking: A literature review. Eur. J. Oper. Res. 2007, 182, 481–501. [Google Scholar] [CrossRef]
- Manzini, R. Warehousing in the Global Supply Chain; Springer: London, UK, 2012; pp. 104–137. [Google Scholar]
- Yener, F.; Yazgan, H.R. Optimal warehouse design: Literature review and case study application. Comput. Ind. Eng. 2019, 129, 1–13. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Qu, H.; Yi, Z.; Tang, H. A columnar competitive model for solving multi-traveling salesman problem. Chaos Solitons Fractals 2007, 31, 1009–1019. [Google Scholar] [CrossRef]
- Kelly, J.P.; Xu, J. A set-partitioning-based heuristic for the vehicle routing problem. Inf. J. Comput. 1999, 11, 161–172. [Google Scholar] [CrossRef][Green Version]
- Fan, X.; Luo, X.; Yi, S.; Yang, S.; Zhang, H. Optimal Path Planning for Mobile Robots Based on Intensified Ant Colony Optimization Algorithm. In Proceedings of the 2003 IEEE International Conference on Robotics, Intelligent Systems and Signal, Changsha, China, 8–13 October 2003. [Google Scholar]
- Tian, G.; Zhang, P.; Li, X.; Yin, J.; Lu, F. Research on one class of optimization problem of the automated warehouse using a new kind of hybrid genetic algorithm. J. Syst. Simul. 2004, 16, 1198–1201. [Google Scholar]
- Saska, M.; Macas, M.; Preucil, L.; Lhotska, L. Robot Path Planning Using Particle Swarm Optimization of Ferguson Splines. In Proceedings of the 2006 IEEE Conference on Emerging Technologies and Factory Automation, Prague, Czech Republic, 20–22 September 2006. [Google Scholar]
- Zheng, K.; Tang, D.; Gu, W.; Dai, M. Distributed control of multi-AGV system based on regional control model. Prod. Eng. 2013, 7, 433–441. [Google Scholar] [CrossRef]
- Zhang, B.; Li, L.; Zhao, Y.; Li, J. The Research on E-Commerce Logistics Picking AGV Path Optimization Method Based on the Improved A* Algorithm. In Proceedings of the 2016 International Conference on Cybernetics, Robotics and Control (CRC), Hong Kong, China, 19–21 August 2016. [Google Scholar]
- Kim, D.H.; Hai, N.T.; Joe, W.Y. A Guide to Selecting Path Planning Algorithm for Automated Guided Vehicle (AGV). In Proceedings of the AETA 2017—Recent Advances in Electrical Engineering and Related Sciences: Theory and Application, Ho Chi Minh, Vietnam, 7–9 December 2017. [Google Scholar]
- Zhang, Z.; Guo, Q.; Chen, J.; Yuan, P. Collision-free route planning for multiple agvs in automated warehouse based on collision classification. IEEE Access 2018, 6, 26022–26035. [Google Scholar] [CrossRef]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Lee, T.K.; Baek, S.H.; Choi, Y.H.; Oh, S.Y. Smooth coverage path planning and control of mobile robots based on high-resolution grid map representation. Robot. Auton. Syst. 2011, 59, 801–812. [Google Scholar] [CrossRef]
- Yerpude, S.; Singhal, T.K. SMART Warehouse with Internet of Things supported Inventory Management System. Int. J. Pure Appl. Math. 2018, 118, 1–15. [Google Scholar]
- Habazin, J.; Glasnović, A.; Bajor, I. Order picking process in warehouse: Case study of dairy industry in Croatia. Promet-Traffic Trans. 2017, 29, 57–65. [Google Scholar] [CrossRef]
- Liu, Y.; Ji, S.; Su, Z.; Guo, D. Multi-objective AGV scheduling in an automatic sorting system of an unmanned (intelligent) warehouse by using two adaptive genetic algorithms and a multi-adaptive genetic algorithm. PLoS ONE 2019, 14, e0226161. [Google Scholar] [CrossRef] [PubMed]
- Zuniga, C.A.; Olivares-Benitez, E.; Tenahua, A.M.; Mujica, M.A. A methodology to solve the Order Batching Problem. IFAC-PapersOnLine 2015, 48, 1380–1386. [Google Scholar] [CrossRef]
- Nosrati, M.; Khamseh, A. Bi objective hybrid vehicle routing problem with alternative paths and reliability. Decis. Sci. Lett. 2020, 9, 145–162. [Google Scholar] [CrossRef]



| Notation | Meaning |
|---|---|
| m | The number of AGVs. |
| n | The number of pickup points. |
| G | A set of all cells. G = {1,…,g}, where g is the number of cells. |
| G’ | A set of all goods which are waiting to be take out, G’ ⊆ G, |G’| = n. |
| Travel distance between pickup point (or entrance) i and pickup point (or exit) j. | |
| The line number of the pickup location for the pickup point i or the line number of entrance and exit. , and there are r rows. | |
| The column number of the pickup location for the pickup point i or the column number of entrance and exit. , and there are c columns. | |
| A binary variable that is 1 when AGV k travel from point i to point j; 0 otherwise. |
| n = 60 | n = 100 | n = 140 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NTS | TS | HDDE | NTS | TS | HDDE | NTS | TS | HDDE | ||
| m = 3 | Trail 1 | 281 | 283 | 387 | 277 | 281 | 431 | 285 | 367 | 487 |
| Trail 2 | 277 | 277 | 359 | 283 | 295 | 445 | 283 | 369 | 407 | |
| Trail 3 | 271 | 277 | 385 | 281 | 289 | 367 | 285 | 357 | 481 | |
| Trail 4 | 279 | 299 | 383 | 283 | 325 | 391 | 281 | 371 | 467 | |
| Trail 5 | 279 | 293 | 371 | 281 | 285 | 429 | 283 | 297 | 409 | |
| Trail 6 | 275 | 305 | 369 | 283 | 301 | 487 | 281 | 363 | 483 | |
| Trail 7 | 275 | 299 | 403 | 281 | 319 | 419 | 285 | 327 | 477 | |
| Trail 8 | 281 | 285 | 381 | 277 | 293 | 387 | 285 | 313 | 467 | |
| Trail 9 | 275 | 275 | 377 | 283 | 293 | 483 | 285 | 331 | 477 | |
| Trail 10 | 273 | 307 | 355 | 283 | 293 | 415 | 285 | 365 | 483 | |
| average | 277 | 290 | 377 | 281 | 297 | 425 | 284 | 346 | 464 | |
| m = 5 | Trail 1 | 332 | 332 | 488 | 328 | 382 | 576 | 336 | 408 | 600 |
| Trail 2 | 328 | 340 | 466 | 334 | 454 | 556 | 334 | 418 | 612 | |
| Trail 3 | 324 | 334 | 428 | 330 | 370 | 546 | 336 | 360 | 632 | |
| Trail 4 | 330 | 326 | 488 | 334 | 438 | 582 | 332 | 380 | 612 | |
| Trail 5 | 330 | 332 | 506 | 332 | 370 | 572 | 334 | 380 | 614 | |
| Trail 6 | 332 | 344 | 466 | 332 | 340 | 554 | 332 | 388 | 638 | |
| Trail 7 | 326 | 402 | 508 | 332 | 376 | 628 | 336 | 344 | 632 | |
| Trail 8 | 328 | 344 | 446 | 330 | 410 | 514 | 336 | 384 | 624 | |
| Trail 9 | 326 | 348 | 444 | 332 | 362 | 574 | 336 | 370 | 620 | |
| Trail 10 | 324 | 344 | 462 | 334 | 382 | 552 | 336 | 400 | 648 | |
| average | 328 | 345 | 470 | 332 | 388 | 565 | 335 | 383 | 623 | |
| m = 8 | Trail 1 | 394 | 432 | 522 | 394 | 482 | 694 | 394 | 510 | 698 |
| Trail 2 | 394 | 422 | 540 | 394 | 448 | 676 | 394 | 498 | 742 | |
| Trail 3 | 392 | 430 | 526 | 406 | 464 | 680 | 394 | 528 | 866 | |
| Trail 4 | 394 | 394 | 534 | 394 | 460 | 714 | 394 | 478 | 694 | |
| Trail 5 | 394 | 466 | 530 | 394 | 496 | 676 | 394 | 474 | 712 | |
| Trail 6 | 394 | 414 | 512 | 394 | 474 | 616 | 394 | 468 | 758 | |
| Trail 7 | 394 | 420 | 558 | 394 | 488 | 668 | 394 | 510 | 710 | |
| Trail 8 | 394 | 422 | 514 | 394 | 464 | 716 | 394 | 536 | 786 | |
| Trail 9 | 394 | 432 | 484 | 394 | 488 | 700 | 394 | 516 | 742 | |
| Trail 10 | 394 | 402 | 534 | 394 | 460 | 686 | 424 | 470 | 720 | |
| average | 394 | 423 | 525 | 395 | 472 | 683 | 397 | 499 | 743 | |
| n = 60 | n = 100 | n = 140 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NTS | TS | HDDE | NTS | TS | HDDE | NTS | TS | HDDE | ||
| m = 3 | Trail 1 | 1.951 | 3.079 | 500.397 | 3.715 | 8.128 | 10393.339 | 6.934 | 19.609 | 18,961.581 |
| Trail 2 | 1.976 | 3.340 | 481.716 | 4.195 | 7.505 | 6626.229 | 6.913 | 19.374 | 15,427.298 | |
| Trail 3 | 1.939 | 3.246 | 575.057 | 3.926 | 8.440 | 3634.481 | 7.386 | 17.116 | 24,877.259 | |
| Trail 4 | 1.948 | 3.393 | 435.070 | 3.929 | 8.798 | 5256.536 | 6.945 | 19.320 | 19,682.740 | |
| Trail 5 | 1.945 | 2.994 | 727.229 | 4.019 | 7.853 | 3738.185 | 7.169 | 14.811 | 16,561.710 | |
| Trail 6 | 2.097 | 3.653 | 892.122 | 3.979 | 8.063 | 3964.789 | 6.895 | 18.527 | 22,405.243 | |
| Trail 7 | 1.920 | 3.544 | 472.420 | 3.963 | 8.769 | 3698.056 | 7.130 | 17.053 | 16,051.987 | |
| Trail 8 | 1.836 | 3.504 | 506.553 | 4.180 | 8.235 | 4511.152 | 6.800 | 15.419 | 17,810.505 | |
| Trail 9 | 1.921 | 3.619 | 526.601 | 3.937 | 8.293 | 5317.399 | 6.803 | 16.498 | 21,293.276 | |
| Trail 10 | 1.882 | 3.255 | 610.396 | 3.957 | 8.216 | 4840.318 | 6.902 | 16.684 | 19,258.136 | |
| average | 1.942 | 3.363 | 572.756 | 3.980 | 8.230 | 5198.048 | 6.988 | 17.441 | 19,232.974 | |
| m = 5 | Trail 1 | 3.943 | 5.118 | 1512.533 | 8.161 | 13.505 | 8391.081 | 13.857 | 25.214 | 23,283.422 |
| Trail 2 | 3.744 | 5.729 | 1118.698 | 8.226 | 15.769 | 5361.342 | 14.364 | 25.011 | 25,869.500 | |
| Trail 3 | 4.162 | 5.285 | 1415.852 | 8.122 | 12.086 | 6211.561 | 13.974 | 22.084 | 19,439.788 | |
| Trail 4 | 3.847 | 5.137 | 1005.755 | 8.715 | 14.787 | 8971.270 | 13.817 | 23.234 | 19,355.222 | |
| Trail 5 | 3.943 | 5.283 | 1002.492 | 8.794 | 12.581 | 5422.703 | 14.377 | 23.769 | 32,212.212 | |
| Trail 6 | 4.175 | 5.018 | 1660.255 | 8.335 | 11.313 | 5428.650 | 13.936 | 23.018 | 27,777.053 | |
| Trail 7 | 3.781 | 6.661 | 1097.204 | 9.005 | 12.915 | 5506.001 | 14.149 | 20.961 | 18,425.203 | |
| Trail 8 | 3.926 | 5.121 | 747.236 | 9.171 | 13.433 | 7585.026 | 13.968 | 22.647 | 19,667.650 | |
| Trail 9 | 3.886 | 5.397 | 1090.556 | 8.063 | 13.870 | 6643.318 | 15.191 | 21.957 | 26,439.659 | |
| Trail 10 | 3.831 | 5.343 | 774.069 | 8.194 | 12.069 | 7663.535 | 15.621 | 24.568 | 36,381.835 | |
| average | 3.924 | 5.409 | 1142.465 | 8.479 | 13.233 | 6718.449 | 14.325 | 23.246 | 24,885.154 | |
| m = 8 | Trail 1 | 7.909 | 8.179 | 3591.557 | 15.968 | 21.845 | 21426.231 | 26.412 | 37.348 | 65,224.116 |
| Trail 2 | 7.944 | 9.163 | 1993.240 | 16.141 | 20.724 | 16625.712 | 27.428 | 37.365 | 52,793.295 | |
| Trail 3 | 7.439 | 8.678 | 2572.098 | 16.060 | 21.320 | 12983.184 | 26.943 | 38.875 | 40,496.482 | |
| Trail 4 | 7.476 | 8.928 | 2486.247 | 16.141 | 20.554 | 15421.759 | 26.965 | 37.227 | 58,480.069 | |
| Trail 5 | 7.427 | 9.956 | 5021.107 | 15.853 | 22.104 | 21253.317 | 26.223 | 35.783 | 37,094.787 | |
| Trail 6 | 7.735 | 9.127 | 4354.038 | 16.463 | 21.325 | 18642.408 | 26.408 | 35.057 | 59,505.527 | |
| Trail 7 | 7.310 | 9.180 | 1994.660 | 16.198 | 20.710 | 16229.108 | 26.940 | 37.375 | 37,644.008 | |
| Trail 8 | 7.694 | 9.268 | 6158.387 | 16.981 | 19.987 | 12600.642 | 27.410 | 40.199 | 47,251.975 | |
| Trail 9 | 7.676 | 9.435 | 6523.730 | 15.497 | 21.908 | 10957.605 | 26.486 | 39.158 | 36,420.641 | |
| Trail 10 | 7.538 | 9.511 | 5716.876 | 15.832 | 20.071 | 16501.993 | 26.127 | 35.850 | 77,484.502 | |
| average | 7.615 | 9.143 | 4041.194 | 16.113 | 21.055 | 16264.196 | 26.734 | 37.424 | 51,239.540 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, L.; Liu, Y.; Li, H.; Wu, C.-C.; Lin, W.-C.; Chen, X. A Novel Tabu Search Algorithm for Multi-AGV Routing Problem. Mathematics 2020, 8, 279. https://doi.org/10.3390/math8020279
Xing L, Liu Y, Li H, Wu C-C, Lin W-C, Chen X. A Novel Tabu Search Algorithm for Multi-AGV Routing Problem. Mathematics. 2020; 8(2):279. https://doi.org/10.3390/math8020279
Chicago/Turabian StyleXing, Lining, Yuanyuan Liu, Haiyan Li, Chin-Chia Wu, Win-Chin Lin, and Xin Chen. 2020. "A Novel Tabu Search Algorithm for Multi-AGV Routing Problem" Mathematics 8, no. 2: 279. https://doi.org/10.3390/math8020279
APA StyleXing, L., Liu, Y., Li, H., Wu, C.-C., Lin, W.-C., & Chen, X. (2020). A Novel Tabu Search Algorithm for Multi-AGV Routing Problem. Mathematics, 8(2), 279. https://doi.org/10.3390/math8020279





