A New Look at the Single Ladder Problem (SLP) via Integer Parametric Solutions to the Corresponding Quartic Equation

Abstract

The aim is to put new light on the single ladder problem (SLP). Some new methods for finding complete integer solutions to the corresponding quartic equation $z^4-2L{z}^3+(L^2-a^2-b^2)z^2+2L{a}^{2}z-L^2{a}^2=0$ are developed. For the case $L\ge L_{\min }$, these methods imply a complete parametric representation for integer solutions of SLP in the first quadrant. Some corresponding (less complete) results for the case $L>L_{\min }$ are also pointed out.

1. Introduction

There are a number of algebraic-geometrical problems that have been given names referring to a common geometric feature, the so-called ladder problems. They are separated into two main categories: the single ladder problem (SLP), and where two ladders are involved, the crossed ladder problem (CLP); see Figure 1 and Figure 2. Figure 1 shows a version of SLP also labeled the ladder box problem. Other SLP-varieties are the ladder corner problem, where a ladder is required to be transferred through a corner in a narrow corridor, and the ladder wall problem, where a ladder is raised to a wall and the bottom part of the ladder is sliding along the floor. The authors of this paper have previously studied the properties of CLP in several articles; see, e.g., [1,2,3,4,5,6]. In the current paper the intention has been to research the conditions for finding complete integer parametric solutions to a complex geometrical problem. For this purpose we have found that the ladder box problem of SLP is particularly well suited.

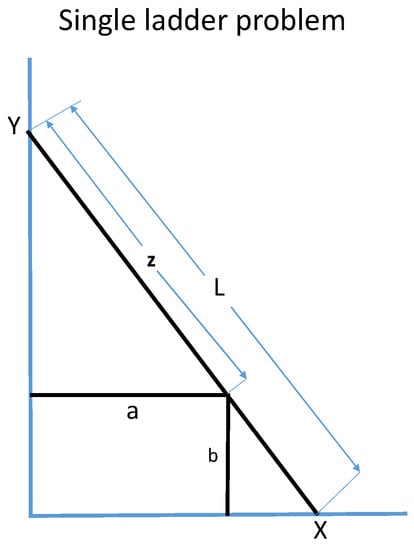
Figure 1. The single ladder problem (SPL).

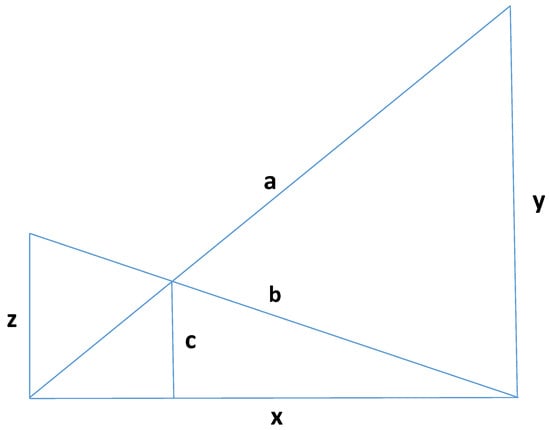
Figure 2. The crossed ladder problem (CLP): find a complete integer parametric representation of the CLP variables.

It is well known (see, e.g., [7] ) that the solutions to the quartic

$$z^4-2L{z}^3+(L^2-a^2-b^2)z^2+2L{a}^{2}z-L^2{a}^2=0$$

(1)

give solutions to the single ladder problem (SLP). This problem reads: A ladder of length L is raised to a wall and touches the corner of a rectangular box with sides a and b; see Figure 1. The problem is to determine how high the ladder reaches on the wall, or, as in this case, the distance of the ladder between the corner of the rectangle and the wall; see, e.g., [8]. Finding solutions to a nonlinear equation like (1) one would normally require approximate methods, such as Newton’s procedure, or recently developed methods (see, e.g., [9,10]), but in this case we are looking for integer solutions and must, in accordance with the legacy of Diophantos, find individually oriented methods. The quartic (1) follows from eliminating the variable y from the two simultaneous second degree equations that can be formulated from Figure 1:

$$z^2=a^2+{(Y-b)}^2,$$

and

$$\frac{z}{Y-b}=\frac{L-z}{b}.$$

If $a=b$, then the quartic (1) can by algebraic manipulations be reduced to solving quadratic equations. If $a\ne b$, then we need to find an algebraic solution to the quartic which requires us to use the traditional and cumbersome methods for solving quartics.

Historically, the problem has attracted great interest from professional mathematicians. The first reference to work on similar problems dates back to classic Greek mathematicians; for example Appolonius (see, e.g., [11]). In the late renaissance or birth of modern mathematics, Decartes and Newton published several works considering variations over the same basic problem; see, e.g., [12,13]. In the eighteenth century, Simpson and Lagrange included work on this problem in textbooks on algebra; see [14,15].

Let $L_{\min }$ denote the minimum length of the ladder in quadrant one for a given set of a and $b$. It has been shown that if $L>L_{\min }$, then the problem has four real solutions, two in the first quadrant, one in the third quadrant and one in the fourth quadrant. If $L=L_{\min }$, then the problem has two real solutions in the first quadrant and one real solution in each of the quadrants three and four, and if $L<L_{\min }$, then it has two complex roots in the first quadrant and one real solution in each of the quadrants three and four; see [7] and cf. also Figure 3.

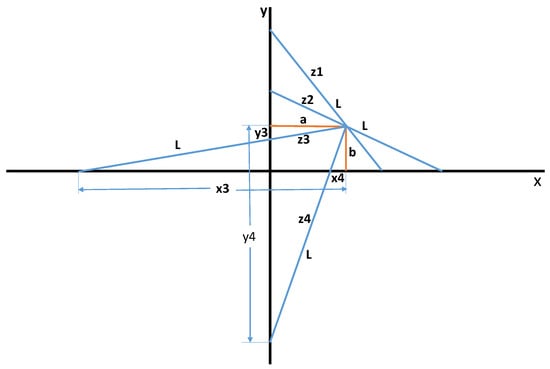
Figure 3. SPL: the four real solutions to the quartic.

Later on, the single ladder problem became a popular subject in both professional and recreational mathematics, and a number of papers have been published; see, e.g., [7,16,17,18,19,20,21,22,23,24,25] and also especially the recent review article [26] by H.S.M. Coxeter and the references given therein.

The authors of this paper claim that by reformulating the problem, other methods are able to be tested and new understanding can be found in the interplay between geometric and algebraic avenues for treating and understanding this problem.

The following idea has especially guided us:

• Find complete integer solutions by parametric representation for the quartic in question, both for the two solutions in the first quadrant and for all four solutions.
• Use this information to find new information concerning SLP.

The paper is organized as follows: In Section 1 we prove a new complete integer parametric representation of the two solutions of the quartic in quadrant one. In Section 2 we present some new methods for deriving integer parametric representation of all four solutions of the quartic. Section 3 is reserved further contributions to the understanding of and new information concerning the open problem related to Section 2 (see Remark 15).

2. Complete Parametric Representation for Integer Solutions in the First Quadrant

In [16] the authors have presented a method to determine (incomplete) integer solutions to the SLP in the first quadrant by parametric representation. In this Section we present another method, which gives complete parametric integer solutions to all the SLP variables in quadrant one.

Theorem 1.

A complete integer parametric representation of the two real solutions $(a,b,L)$ of the SLP in the first quadrant when $L\ge L_{\min }$ can be determined by using four parameters, $r,s,t$ and $w$, where $r>s>0,t>w>0$ and $r,s,t,w\in Z_{+}$:

$$\begin{array}{l}a=4rstw(st+rw)\\ b=(rt-sw)(r^2-s^2)(t^2-w^2)\\ L=\left(t^2+w^2\right)\left(r^2+s^2\right)\left(rt+sw\right).\end{array}$$

(2)

Proof. 

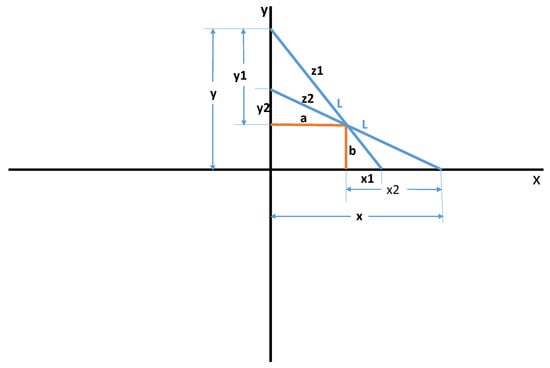
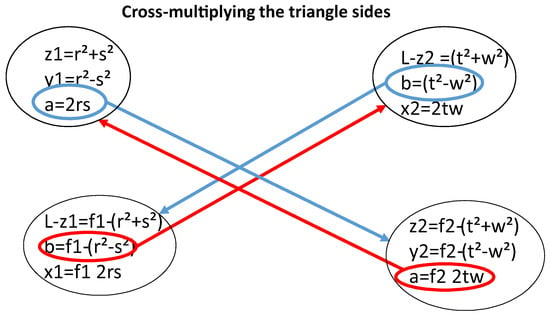
From similar triangles and using Pythagorean triples, we can write the following complete representation of the four right-angle triangles in Figure 4 with a and b as triangle sides and $z_i$ and $L-z_i$ as hypotenuses.

Figure 4. SPL, with the solutions in quadrant one.

We have that

$$\begin{array}{cc}\hfill z_1& =r^2+s^2\hfill \\ \hfill y_1& =r^2-s^2\hfill \\ \hfill a& =2rs,\hfill \end{array}$$

$$\begin{array}{cc}\hfill L-z_1& =f_1(r^2+s^2)\hfill \\ \hfill b& =f_1(r^2-s^2)\hfill \\ \hfill x_1& =f_{1}2rs,\hfill \end{array}$$

$$\begin{array}{cc}\hfill z_2& =f_2(t^2+w^2)\hfill \\ \hfill y_2& =f_2(t^2-w^2)\hfill \\ \hfill a& =f_{2}2tw,\hfill \end{array}$$

$$\begin{array}{cc}\hfill L-z_2& =(t^2+w^2)\hfill \\ \hfill b& =(t^2-w^2)\hfill \\ \hfill x_2& =2tw,\hfill \end{array}$$

where $r,s,t,w$ are integer parameters and $f_1$ and $f_2$ are factoring constants. To find integer solutions to $a,b,L,x_{1,}{x}_2,y_1,y_2,z_1$ and $z_2$, and to $f_1$ and $f_2$, we arrange the triangle parameters as shown in Figure 5 and cross-multiply the variables as indicated with arrows in the figure.

Figure 5. The cross-multiplying method.

This leads to the following set without loss of generality or completeness:

$$\begin{array}{cc}\hfill z_{1m}& =f_{2}2tw(r^2+s^2)\hfill \\ \hfill y_{1m}& =f_{2}2tw(r^2-s^2)\hfill \\ \hfill a_m& =f_{2}4rstw,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {(L-z_1)}_m& =f_1(r^2+s^2)(t^2-w^2)\hfill \\ \hfill b_m& =f_1(r^2-s^2)(t^2-w^2)\hfill \\ \hfill x_{1m}& =f_{1}2rs(t^2-w^2),\hfill \end{array}$$

$$\begin{array}{cc}\hfill z_{2m}& =f_{2}2rs(t^2+w^2)\hfill \\ \hfill y_{2m}& =f_{2}2rs(t^2-w^2)\hfill \\ \hfill a_m& =f_{2}4rstw,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {(L-z_2)}_m& =f_1(r^2-s^2)(t^2+w^2)\hfill \\ \hfill b_m& =f_1(r^2-s^2)(t^2-w^2)\hfill \\ \hfill x_{2m}& =f_{1}2tw(r^2-s^2),\hfill \end{array}$$

where the index m indicates the value of each variable after using this “cross-multiplication method.” By this, we have found that a and b are invariant:

$$a_m=f_{2}4rstw,$$

and

$$b_m=f_1(r^2-s^2)(t^2-w^2).$$

In [1] the authors proved that the procedure shown above results in complete parametric representation of the four right-angle triangles in Figure 4 with a and b as sides. We can now, without loss of generality, determine the factoring constants $f_1$ and $f_2$ by requiring that L is invariant. We have

$${(L-z_1)}_m=f_1(r^2+s^2)(t^2-w^2),$$

giving that

$$L_{m1}=z_{1m}+f_1(r^2+s^2)(t^2-w^2)=f_{2}2tw(r^2+s^2)+f_1(r^2+s^2)(t^2-w^2),$$

and

$${(L-z_2)}_m=f_1(r^2-s^2)(t^2+w^2),$$

resulting in

$$L_{m2}=z_{2m}+f_1(r^2-s^2)(t^2+w^2)=f_{2}2rs(t^2+w^2)+f_1(r^2-s^2)(t^2+w^2).$$

We require that

$$L_{m1}=L_{m2},$$

i.e.,

$$f_{2}2tw(r^2+s^2)+f_1(r^2+s^2)(t^2-w^2)=f_{2}2rs(t^2+w^2)+f_1(r^2-s^2)(t^2+w^2),$$

which implies that

$$f_1((r^2+s^2)(t^2-w^2)-(r^2-s^2)(t^2+w^2))=f_2(2rs(t^2+w^2)-2tw(r^2+s^2)),$$

leading to that

$$\frac{f_1}{f_2}=\frac{(2rs(t^2+w^2)-2tw(r^2+s^2))}{((r^2+s^2)(t^2-w^2)-(r^2-s^2)(t^2+w^2))}=\frac{rt-sw}{st+rw}.$$

We set

$$\begin{array}{cc}\hfill F_1& =S(rt-sw)\hfill \\ \hfill F_2& =S(st+rw),\hfill \end{array}$$

where S is a scaling factor. This factor will appear as a constant factor in all the variables and can therefore be eliminated. Hence, we may without loss of generality set

$$\begin{array}{cc}\hfill f_1& =(rt-sw)\hfill \\ \hfill f_2& =(st+rw).\hfill \end{array}$$

Multiplying the variables after the cross-multiplication with these values, we get the following complete integer parametric solutions to $\left(a,b,L\right)$ in quadrant one:

$$\begin{array}{cc}\hfill a& =4rstw(st+rw)\hfill \\ \hfill b& =(rt-sw)(r^2-s^2)(t^2-w^2)\hfill \\ \hfill L& =\left(t^2+w^2\right)\left(r^2+s^2\right)\left(rt+sw\right).\hfill \end{array}$$

The corresponding complete parametric solutions to the other line elements mentioned before are:

$$\begin{array}{cc}\hfill x_1& =2rs(rt-sw)(t^2-w^2)\hfill \\ \hfill x_2& =2tw(rt-sw)(r^2-s^2)\hfill \\ \hfill y_1& =2tw(st+rw)(r^2-s^2)\hfill \\ \hfill y_2& =2rs(st+rw)(t^2-w^2)\hfill \\ \hfill z_1& =2tw(st+rw)(r^2+s^2)\hfill \\ \hfill z_2& =2rs(st+rw)(t^2+w^2)\hfill \\ \hfill L-z_1& =\left(t^2-w^2\right)\left(r^2+s^2\right)\left(rt-sw\right)\hfill \\ \hfill L-z_2& =\left(t^2+w^2\right)\left(r^2-s^2\right)\left(rt-sw\right)\hfill \\ \hfill X_1& =x_1+a=2rs\left(t^2+w^2\right)\left(rt+sw\right)\hfill \\ \hfill X_2& =x_2+a=2tw\left(r^2+s^2\right)\left(rt+sw\right)\hfill \\ \hfill Y_1& =y_1+b=\left(t^2+w^2\right)\left(r^2-s^2\right)\left(rt+sw\right)\hfill \\ \hfill Y_2& =y_2+b=\left(t^2-w^2\right)\left(r^2+s^2\right)\left(rt+sw\right).\hfill \end{array}$$

(3)

 □

Example 1

(Numerical Example). If $r=3,s=2,t=2,w=1$, then we get the following integer solution of SLP, after scaling for common factors:

$$(a,b,L)=(84,15,130).$$

Moreover, $(x_1,x_2,y_1,y_2)=(36,20,35,63)$ in this case.

Remark 1.

We shortly discuss the connection between the two so-called ladder problems: the single ladder problem (SLP) and the crossed ladder problem (CLP). They are both geometrical problems defined by several right-angled triangles that require the solution of a fourth degree equation (derived from two simultaneous second degree equations); namely:

$$z^4-2Lz{}^3+(L{}^2-a{}^2-b{}^2)z{}^2+2La{}^{2}z-L{}^{2}a{}^2=0,$$

and

$$z^4-2cz{}^3+(a{}^2-b{}^2)z{}^2-2c(a{}^2-b{}^2)z+c{}^2(a{}^2-b{}^2)=0,$$

respectively.

By comparing SLP in Figure 4 with CLP in Figure 2, we see that the right-angle triangles consisting of the sides $(z_1,y_1,a)$ and $(z_2,y_2,a)$ and also $((L-z_1),x_1,b)$ and $((L-z_2),x_2,b),$ by rotating one of the triangles, constitute CLPs just lacking the line segment c. But $c=(yz)/(y+z)$ only constitute a factoring constant in transforming the SLP-triangels to true CLPs. That is to say that if we multiply $(a,y_1,y_2,z_1,z_2)$ with $(y_1+y_2)$ and $(b,x_1,x_2,(L-z1),(L-z_2))$ with $(x_1+x_2)$ from (3), we have transformed the SLP variables to the corresponding line segments in integer CLPs, where $c=y_1{y}_2$ and $c=x_1{x}_2$, respectively.

There are several interesting mathematical directions to be derived from the ladder problems; for instance, in relation to power means and to finding integer valued relations between nominators and denominators of fourth degree; see e.g., [3,4,5,6] and the references therein.

Next, we seek for the minimum length of the ladder, $L_{\min }$ for a given set of $a,b.$ Instead of calculating the derivative of L to determine $L_{\min },$ we see directly from Figure 4 that the minimum value of L must appear when $x_1=x_2.$ Hence, according to (3) above, we require that

$$2rs(rt-sw)(t^2-w^2)=2tw(rt-sw)(r^2-s^2),$$

leading to that

$$st=rw,$$

or

$$\begin{array}{c}r=t\hfill \\ \hfill s=w.\end{array}$$

Inserting these values in the variables into (3), we get the following result in the case of $L=L_{\min }$:

Corollary 1.

A complete parametric solution for the two real integer solutions $\left(a,b,L\right)$ of the SLP when $L=L_{\min }$ is given by

$$\begin{array}{cc}\hfill a& =8t^3{w}^3\hfill \\ \hfill b& ={\left(t^2-w^2\right)}^3\hfill \\ \hfill L_{\min }& ={\left(t^2+w^2\right)}^3,\hfill \end{array}$$

where $t>w>0$ and $t,w,z\in Z_{+}$.

Remark 2.

The corresponding parametric expressions for the variables $x_1,y_1,z_1$, X and Y are:

$$\begin{array}{cc}\hfill x_1& =x_2=2tw{\left(t^2-w^2\right)}^2\hfill \\ \hfill y_1& =y_2=4t^2{w}^2\left(t^2-w^2\right)\hfill \\ \hfill z_1& =z_2=4t^2{w}^2\left(t^2+w^2\right)\hfill \\ \hfill X& =x_1+a=2tw{\left(t^2+w^2\right)}^2\hfill \\ \hfill Y& =y_1+b=\left(t^2-w^2\right){\left(t^2+w^2\right)}^2.\hfill \end{array}$$

Example 2

(Numerical Example). If $t=2$ and $w=1$, then we have the following integer solution of SLP in this minimum case:

$$\left(a,b,L\right)=\left(64,27,125\right).$$

3. Parametric Representation for Integer Solutions to All Four Real Solutions to the Quartic (1) When $\mathit{L}>{\mathit{L}}_{\mathbf{min}}$

The generating quartic is

$$z_1^4-2L{z}_1^3+(L^2-a^2-b^2)z_1^2+2L{a}^2{z}_1-L^2{a}^2=0.$$

Geometrically, the four solutions to the quartic, when $L>L_{\min }$, are shown in Figure 3. Our first result in this Section reads:

Theorem 2.

Complete integer parametric representations to the four solutions to the quartic (1) when $L>L_{\min }$ can be calculated by determining all rational solutions of

$$t^4{r}^4+4st{w}^3{r}^3+6s^2{t}^2{w}^2{r}^2+4s^3{t}^{3}wr+s^4{w}^4=Q^2,$$

(4)

where Q is any positive rational number (an algorithm to find these solutions is described in Remark 3 and the sequel).

Proof. 

From the theory of algebraic equations, we know that the four solutions to a quartic equation are symmetric functions of the coefficients of the equation (see [27]). From (1) we then have that

$$z_1+z_2+z_3+z_4=-(-2L),$$

resulting in

$$z_3+z_4=2L-(z_1+z_2)=2(rt+sw){(rt-sw)}^2.$$

(5)

We also have that

$$z_1{z}_2{z}_3{z}_4=-L^2{a}^2,$$

so that

$$z_3{z}_4=-\frac{L^2{a}^2}{z_1{z}_2}=-4rstw{(rt+sw)}^2(r^2+s^2)(t^2+w^2).$$

We therefore find that

$${(z_3-z_4)}^2={(z_3+z_4)}^2-4z_3{z}_4=4(t^4{r}^4+4st{w}^3{r}^3+6s^2{t}^2{w}^2{r}^2+4s^3{t}^{3}wr+s^4{w}^4){(rt+sw)}^2.$$

If we can determine all rational solutions of (4), then we have that

$$(z_3-z_4)=2Q\left(rt+sw\right).$$

(6)

We will then from (5) and (6) have

$$z_3+z_4=\mathrm{rational},$$

(7)

and

$$z_3-z_4=\mathrm{rational},$$

(8)

and can then, by eventual scaling for common factors, calculate all integer solutions to $z_3$ and $z_4,$ and to all the other involved variables. □

Remark 3.

There are infinitely many rational solutions of (4), and there are several ways to find the solutions. Each solution will result in an integer parametric solution to all the SPL variables. Hence, to find all integer solutions $(a,b,L)$ to the four solutions of (1) we do as follows:

1. 

Determine all rational values of $r,s,t,w$ that give solutions to (4).

2. 

Calculate corresponding values of $z_3$ and $z_4$ for (7) and (8).

3. 

Calculate corresponding $(a,b,L)$ and the other SPL variables and scale for common factors to arrive at a parametric integer solution.

The next step is to continue by describing how to use this technique in practise. The crucial step is to birationally transform (4) to an elliptic curve and use known methods to find all rational solutions. By setting

$$\begin{array}{cc}\hfill \frac{r}{s}& =x\hfill \\ \hfill \frac{w}{t}& =a\hfill \\ \hfill \frac{Q}{s^2{t}^2}& =y,\hfill \end{array}$$

(9)

we can write (4) as

$$y^2=x^4+4a^3{x}^3+6a^2{x}^2+4ax+a^4.$$

(10)

A rational solution to this quartic is

$$(x_1,y_1)=(-\frac{1}{a},\pm \frac{\left(a^4-1\right)}{a^2}).$$

(11)

We then use the transformation description given in [2] and arrive at the elliptic cuve

$$j^2=k^3+12\frac{{\left(a^4-1\right)}^2}{a^2}{k}^2+48\frac{{\left(a^4-1\right)}^4}{a^4}k+16{\left(a^4+1\right)}^2\frac{{\left(a^4-1\right)}^6}{a^{10}}.$$

(12)

All rational solutions of (12) can be transformed to rational solutions of (10). The reverse transformation formula is given by (see, e.g., [2])

$$x=x_1-\frac{2k{y}_1^2}{2\frac{a^4-1}{a^3}k+4\left(a^4+1\right)\frac{{\left(a^4-1\right)}^3}{a^5}-j}.$$

(13)

By inspection we see that (12) has a rational solution

$$(k_0,j_0)=(0,4\left(a^4+1\right)\frac{{\left(a^4-1\right)}^3}{a^5}).$$

This point lead to a trivial solution to the SPL, but a tangent to (12) through this point will cross (12) at another rational point; namely,

$$(k_1,j_1)=(-12{\left(a^4-1\right)}^2\frac{-a^4+a^8+1}{a^2{\left(a^4+1\right)}^2},4(-14a^4+24a^8-14a^{12}+a^{16}+1)\frac{{\left(a^4-1\right)}^3}{a^5{\left(a^4+1\right)}^3}).$$

Using (13) and (11) we find that

$$x=a^3\frac{a^4-2}{2a^4-1}.$$

Moreover, from (9) we have that

$$(x,a)=(\frac{r}{s},\frac{w}{t})$$

and obtain that

$$\frac{r}{s}=w^3\frac{2t^4-w^4}{t^3\left(t^4-2w^4\right)};$$

i.e.,

$$r=w^3(2t^4-w^4)$$

$$s=t^3\left(t^4-2w^4\right).$$

These values of r and s give a rational solution to (4), and consequently to the four solutions to (1). Using (10) and (9) we determine the corresponding values for y and $Q$, and from (5) and (6) we calculate $z_3$ and $z_4$. By inserting the obtained values for r and s as functions of t and w in (3) we obtain integer parametric representations to the SLP variables:

$$\begin{array}{cc}\hfill a& =4t^3{w}^3\left(t^4-2w^4\right)\left(2t^4-w^4\right)\left(t^4+w^4\right)\hfill \\ \hfill b& =\left(t^2-w^2\right)\left(-tw+t^2-w^2\right)\left(tw+t^2-w^2\right)\left(t^{2}w+t^3+w^3\right)\hfill \\ \hfill & \left(-t^{2}w+t^3-w^3\right)\left(t{w}^2+t^3-w^3\right)\left(t{w}^2+t^3+w^3\right)\hfill \\ \hfill L& =\left(t^2+w^2\right)\left(3t^2{w}^2+t^4+w^4\right)\left(-2t^2{w}^4+t^4{w}^2+t^6+w^6\right)\left(t^2{w}^4-2t^4{w}^2+t^6+w^6\right).\hfill \end{array}$$

By using the well established methods for finding rational points on elliptic curves (see, e.g., [28]), we can determine all rational points on (12). Each rational point on (12) will, through transformation, lead to a rational point on (10) and eventually on (4). All different rational points on (4) lead to a another integer parametric representations to the four solutions to the quartic (1).

Going further, we prefer in this case to use the classical methods developed by Euler (see [2]).

We will start by finding rational solutions of (4) corresponding to fixed Q by Euler’s method and set

$$\begin{array}{l}{Q}_1=t^2{r}^2+2\frac{s{w}^3}{t}r+s^2{w}^2\\ Q_2=t^2{r}^2+2\frac{s{w}^3}{t}r-s^2{w}^2.\end{array}$$

When we use $Q_1,$ we see that

$$t^4{r}^4+4st{w}^3{r}^3+6s^2{t}^2{w}^2{r}^2+4s^3{t}^{3}wr+s^4{w}^4-Q_1^2=4r{s}^{2}w\left(t-w\right)\left(t+w\right)\left(t^2+w^2\right)\frac{st+rw}{t^2}=0.$$

All solutions to

$$4r{s}^{2}w\left(t-w\right)\left(t+w\right)\left(t^2+w^2\right)\frac{st+rw}{t^2}=0$$

give only trivial solutions to the SLP.

Using $Q_2$ we find that

$$t^4{r}^4+4st{w}^3{r}^3+6s^2{t}^2{w}^2{r}^2+4s^3{t}^{3}wr+s^4{w}^4-Q_2^2=4r{s}^{2}w\frac{s{t}^5-r{w}^5+2r{t}^{4}w+st{w}^4}{t^2}=0.$$

We must then require that

$$s{t}^5-r{w}^5+2r{t}^{4}w+st{w}^4=0,$$

which implies that

$$\frac{r}{s}=\frac{t(t^4+w^4)}{w\left(w^4-2t^4\right)};$$

(14)

i.e.,

$$\begin{array}{cc}\hfill r& =t(t^4+w^4)\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill s& =w\left(w^4-2t^4\right).\hfill \end{array}$$

(16)

From the fact that

$$Q_2=(t^2{r}^2+2\frac{s{w}^3}{t}r-s^2{w}^2),$$

and (5) and (6), it follows that

$$z_3-z_4=2Q(rt+sw)=2(t^2{r}^2+2\frac{s{w}^3}{t}r-s^2{w}^2)(rt+sw),$$

and

$$z_3+z_4=2L-(z_1+z_2)=2(rt+sw){(rt-sw)}^2,$$

leading to

$$z_3=2r(r{t}^3+s{w}^3-s{t}^{2}w)\frac{rt+sw}{t},$$

and

$$z_4=-2sw\left(rt+sw\right)\frac{r{t}^2+r{w}^2-stw}{t}.$$

Inserting the values from (15) and (16) we find that

$$z_3=2\left(t^4+w^4\right)\left(t^2+w^2\right)\left(t^2{w}^4-2t^4{w}^2+t^6+w^6\right)\left(-2t^2{w}^4+t^4{w}^2+t^6+w^6\right),$$

and

$$z_4=2t^2{w}^2\left(2t^4-w^4\right)\left(t^2{w}^4-2t^4{w}^2+t^6+w^6\right)\left(3t^2{w}^2+t^4+w^4\right).$$

Hence, by inserting the values for r and s from (15) and (16) in the formulas in (3) and scaling for common factors, we can determine a set of integer parametric representation for all four solutions to (1) to all the variables; namely, we have that

$$\begin{array}{cc}a\hfill & =4t^3{w}^3\left(t^4-2w^4\right)\left(2t^4-w^4\right)\left(t^4+w^4\right)\hfill \\ b\hfill & =\left(t^2-w^2\right)\left(-tw+t^2-w^2\right)\left(tw+t^2-w^2\right)\left(t^{2}w+t^3+w^3\right)\hfill \\ & \left(-t^{2}w+t^3-w^3\right)\left(t{w}^2+t^3-w^3\right)\left(t{w}^2+t^3+w^3\right)\hfill \\ L\hfill & =\left(t^2+w^2\right)\left(3t^2{w}^2+t^4+w^4\right)\left(-2t^2{w}^4+t^4{w}^2+t^6+w^6\right)\left(t^2{w}^4-2t^4{w}^2+t^6+w^6\right)\hfill \\ x_1\hfill & =-2tw\left(2t^4-w^4\right)\left(t^4+w^4\right)\left(t^2-w^2\right)\left(t{w}^2+t^3+w^3\right)\left(t{w}^2+t^3-w^3\right)\hfill \\ x_2\hfill & =2tw\left(tw+t^2-w^2\right)\left(-tw+t^2-w^2\right)\left(t^{2}w+t^3+w^3\right)\left(-t^{2}w+t^3-w^3\right)\left(t{w}^2+t^3-w^3\right)\left(t{w}^2+t^3+w^3\right)\hfill \\ x_3\hfill & =2t^3{w}^3\left(2t^4-w^4\right)\left(t^4-2w^4\right)\left(-tw+t^2-w^2\right)\left(tw+t^2-w^2\right)\hfill \\ x_4\hfill & =2tw\left(t^2-w^2\right)\left(t^4-2w^4\right)\left(t^4+w^4\right)\left(-t^{2}w+t^3-w^3\right)\left(t^{2}w+t^3+w^3\right)\hfill \\ y_1\hfill & =-2t^2{w}^2\left(t^4-2w^4\right)\left(-tw+t^2-w^2\right)\left(tw+t^2-w^2\right)\left(-t^{2}w+t^3-w^3\right)\left(t^{2}w+t^3+w^3\right)\hfill \\ y_2\hfill & =2t^2{w}^2\left(t^2-w^2\right)\left(t^4-2w^4\right)\left(2t^4-w^4\right)\left(t^4+w^4\right)\hfill \\ y_3\hfill & =2\left(t^2-w^2\right)\left(t^4+w^4\right)\left(t{w}^2+t^3+w^3\right)\left(t{w}^2+t^3-w^3\right)\left(t^{2}w+t^3+w^3\right)\left(-t^{2}w+t^3-w^3\right)\hfill \\ y_4\hfill & =2t^2{w}^2\left(2t^4-w^4\right)\left(tw+t^2-w^2\right)\left(-tw+t^2-w^2\right)\left(t{w}^2+t^3-w^3\right)\left(t{w}^2+t^3+w^3\right)\hfill \\ z_1\hfill & =-2t^2{w}^2\left(t^4-2w^4\right)\left(3t^2{w}^2+t^4+w^4\right)\left(-2t^2{w}^4+t^4{w}^2+t^6+w^6\right)\hfill \\ z_2\hfill & =2t^2{w}^2\left(t^4-2w^4\right)\left(2t^4-w^4\right)\left(t^2+w^2\right)\left(t^4+w^4\right)\hfill \\ z_3\hfill & =2\left(t^4+w^4\right)\left(t^2+w^2\right)\left(t^2{w}^4-2t^4{w}^2+t^6+w^6\right)\left(-2t^2{w}^4+t^4{w}^2+t^6+w^6\right)\hfill \\ z_4\hfill & =2t^2{w}^2\left(2t^4-w^4\right)\left(t^2{w}^4-2t^4{w}^2+t^6+w^6\right)\left(3t^2{w}^2+t^4+w^4\right),\hfill \end{array}$$

(17)

where $t>w$ and $t,w\in Z_{+}$. The variables $x_3,y_3$ and $x_4,y_4$ are determined by the formulas:

$$\begin{array}{l}{x}_3^2={(L-z_3)}^2-b^2\\ y_3^2=z_3^2-a^2,\end{array}$$

and

$$\begin{array}{l}{x}_4^2={(z_4-L)}^2-b^2\\ y_4^2=z_4^2-a^2.\end{array}$$

The integer parametric representation of all four solutions of (1) shown in (17) is not complete. As written above, that would involve finding all solutions to (4). Each solution will result in a separate table of parametric representations of the variables.

Example 3

(Numerical Example). If $t=2$ and $w=1,$ then we obtain the following integer solution $(a,b,L)$ to the SLP:

$$\left(a,b,L\right)=\left(236096,57915,391645\right).$$

The four solutions to SLP in this case will look approximately like in Figure 6.

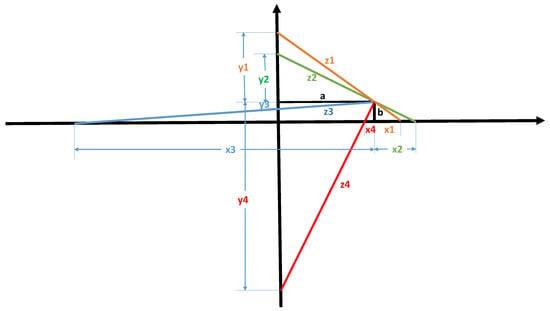
Figure 6. SPL: four integer solutions to the quartic.

Remark 4.

The parametric solutions presented in (17) has degree 18 in t and $w$. In fact, we can, by using some of the findings in the calculations above, determine solutions of other degrees, still using the classical methods. Is it then natural to ask if we can find parametric integer solutions of other degrees? The answer is “yes,” and we proceed by giving two examples of such alternative integer solutions.

Example 4.

By inspection we can easily find a number of “low hanging” solutions to (4):

$$r=0,s,-s,\frac{sw}{t},-\frac{st}{w}.$$

(18)

These solutions can be used to find other parametric solutions to the SPL, where the degree of the parametric solution has degree 10 in t and w (see (24) below).

Proof. 

Consider

$$Q^2=t^4{r}^4+4st{w}^3{r}^3+6s^2{t}^2{w}^2{r}^2+4s^3{t}^{3}wr+s^4{w}^4.$$

We set

$$Q=t^2{r}^2+2\frac{s{w}^3}{t}r+y.$$

We can then formulate two identical second degree equations with y and r as variables, respectively:

$$-t^2{y}^2+\left(-2r^2{t}^4-4srt{w}^3\right)y+\left(6r^2{s}^2{t}^4{w}^2-4r^2{s}^2{w}^6+4r{s}^3{t}^{5}w+s^4{t}^2{w}^4\right)=0,$$

(19)

and

$$\left(6s^2{t}^4{w}^2-4s^2{w}^6-2y{t}^4\right)r^2+\left(4s^3{t}^{5}w-4st{w}^{3}y\right)r+\left(s^4{t}^2{w}^4-t^2{y}^2\right)=0.$$

(20)

The solutions to (4) listed in (18) will in each of them, when inserted into (19), result in two rational solutions $y$. When these values of y are inserted into (20), then they will give two rational solutions in $r$. When this procedure is continued, we find infinitely many new solutions to r as a function of $s,t,w$, eventually of increasing degree, that all are solutions to (4). □

From this procedure we find after a few iterations that

$$\frac{r}{s}=\frac{w(tw+t^2-w^2)}{-t^{2}w+t^3-w^3},$$

i.e.,

$$\begin{array}{c}r=w(tw+t^2-w^2)\end{array}$$

(21)

$$\begin{array}{c}s=-t^{2}w+t^3-w^3.\end{array}$$

(22)

This results in

$$Q=\pm w\left(t-w\right)\left(3t{w}^5+2t^3{w}^3+2t^6+w^6\right).$$

(23)

By inserting (21), (22) and (23) into (5) and (6) we can determine $z_3$ and $z_4$:

$$\begin{array}{l}{z}_3=2t{w}^2\left(t-w\right)\left(-2tw+t^2+2w^2\right)\left(tw+t^2-w^2\right)\left(t^2+w^2\right)\left(2tw+2t^2+w^2\right)\\ z_4=-2w^2\left(t-w\right)\left(2tw+2t^2+w^2\right)\left(-t^{2}w+t^3-w^3\right)\left(t^4+w^4\right).\end{array}$$

Inserting (21) and (22) into (3) and scaling for common factors we find a set of integer parametric representation for all four solutions to (1); namely, the following:

$$\begin{array}{cc}\hfill a& =4tw\left(-t^{2}w+t^3-w^3\right)\left(tw+t^2-w^2\right)\left(t{w}^2+t^3+w^3\right)\hfill \\ \hfill b& =-tw\left(t^2-w^2\right)\left(tw+t^2+2w^2\right)\left(-tw+2t^2+w^2\right)\left(-2tw+t^2-w^2\right)\hfill \\ \hfill L& =\left(t^2+w^2\right)\left(t^4+w^4\right)\left(-2tw+t^2+2w^2\right)\left(2tw+2t^2+w^2\right)\hfill \\ \hfill x_1& =2w^2\left(t+w\right)\left(-tw+2t^2+w^2\right)\left(-t^{2}w+t^3-w^3\right)\left(tw+t^2-w^2\right)\hfill \\ \hfill x_2& =-2t^2\left(-2tw+t^2-w^2\right)\left(tw+t^2+2w^2\right)w^2\left(-tw+2t^2+w^2\right)\hfill \\ \hfill x_3& =2\left(t^2-w^2\right)\left(-2tw+t^2-w^2\right)\left(t{w}^2+t^3+w^3\right)\left(-t^{2}w+t^3-w^3\right)\hfill \\ \hfill x_4& =2t^2\left(t-w\right)\left(tw+t^2+2w^2\right)\left(tw+t^2-w^2\right)\left(t{w}^2+t^3+w^3\right)\hfill \\ \hfill y_1& =-2t^2\left(t-w\right)\left(tw+t^2+2w^2\right)\left(-2tw+t^2-w^2\right)\left(t{w}^2+t^3+w^3\right)\hfill \\ \hfill y_2& =2\left(t-w\right)\left(t{w}^2+t^3+w^3\right)\left(t+w\right)\left(-t^{2}w+t^3-w^3\right)\left(tw+t^2-w^2\right)\hfill \\ \hfill y_3& =2t^2{w}^2\left(tw+t^2-w^2\right)\left(tw+t^2+2w^2\right)\left(-tw+2t^2+w^2\right)\hfill \\ \hfill y_4& =2w^2\left(t+w\right)\left(-tw+2t^2+w^2\right)\left(-2tw+t^2-w^2\right)\left(-t^{2}w+t^3-w^3\right)\hfill \\ \hfill z_1& =2t\left(t{w}^2+t^3+w^3\right)\left(-2tw+t^2+2w^2\right)\left(t^4+w^4\right)\hfill \\ \hfill z_2& =2\left(t{w}^2+t^3+w^3\right)\left(t^2+w^2\right)\left(-t^{2}w+t^3-w^3\right)\left(tw+t^2-w^2\right)\hfill \\ \hfill z_3& =2tw\left(t^2+w^2\right)\left(tw+t^2-w^2\right)\left(-2tw+t^2+2w^2\right)\left(2tw+2t^2+w^2\right)\hfill \\ \hfill z_4& =-2w\left(t^4+w^4\right)\left(-t^{2}w+t^3-w^3\right)\left(2tw+2t^2+w^2\right),\hfill \end{array}$$

(24)

where $t>w$ and $t,w\in Z_{+}$. Note that in this case the parametric integer solutions we have found have degree 10 in each case.

Example 5

(Numerical Example). If $t=2$ and $w=1$, then we obtain the following integer solution $(a,b,L)$ to the SLP:

$$\left(a,b,L\right)=\left(660,168,1105\right).$$

Moreover,

$$\begin{array}{cc}\hfill (x_1,x_2,x_3,x_4)& =(315,224,-99,1760)\hfill \\ \hfill (y_1,y_2,y_3,y_4)& =(352,495,1120,-63)\hfill \\ \hfill (z_1,z_2,z_3,z_4)& =(748,825,1300,-663).\hfill \end{array}$$

Example 6.

We see from (18) that (4) has solutions for

$$rt=sw,$$

and for

$$rw=-st.$$

Thus, some solutions to (4) are

$$Q^2=16m^4{n}^4{\left(m-n\right)}^2{\left(m+n\right)}^2{\left(m^2+n^2\right)}^2,$$

and

$$Q^2=64m^6{n}^6{\left(m^2+n^2\right)}^2,$$

respectively. Both $rt=sw$ and $rw=-st$ give trivial solutions when they are inserted in the variables in (3), $b=0$ and $a=0$, respectively. It is tempting then to investigate if it is possible to find simple two-parameter representations to $r,s,t,w$ that give, say, $rs=tw$ and that also give solutions to (4). A quick search shows that

$$r,s,t,w=m(m^2+n^2),n(m^2-n^2),m(m^2-n^2),n(m^2+n^2),$$

leading to

$$Q^2={\left(m^4-n^4\right)}^2{\left(6m^4{n}^4+m^8+n^8\right)}^2.$$

When we insert the above values of $r,s,t,w$ in the variables in (3), we find a set of integer parametric representations for all four solutions to (1) of degree 14; namely, the following:

$$\begin{array}{cc}\hfill a& =8m^3{n}^3(m^8-n^8)\hfill \\ \hfill b& =(m^2-n^2)\left(-m{n}^2-m^{2}n+m^3-n^3\right)\left(m{n}^2+m^{2}n+m^3-n^3\right)\hfill \\ \hfill & \left(m{n}^2-m^{2}n+m^3+n^3\right)\left(-m{n}^2+m^{2}n+m^3+n^3\right)\hfill \\ \hfill L& =\left(m^2+n^2\right)\left(-m^2{n}^4+3m^4{n}^2+m^6+n^6\right)\left(3m^2{n}^4-m^4{n}^2+m^6+n^6\right)\hfill \\ \hfill x_1& =2mn\left(m^2+n^2\right){\left(m^2-n^2\right)}^2\left(-m{n}^2+m^{2}n+m^3+n^3\right)\left(-m{n}^2-m^{2}n+m^3-n^3\right)\hfill \\ \hfill x_2& =2mn\left(m^2+n^2\right){\left(m^2-n^2\right)}^2\left(m{n}^2-m^{2}n+m^3+n^3\right)\left(m{n}^2+m^{2}n+m^3-n^3\right)\hfill \\ \hfill x_3& =4m^{3}n\left(m^4+n^4\right)\left(m{n}^2-m^{2}n+m^3+n^3\right)\left(m{n}^2+m^{2}n+m^3-n^3\right)\hfill \\ \hfill x_4& =4m{n}^3\left(m^4+n^4\right)\left(-m{n}^2+m^{2}n+m^3+n^3\right)\left(-m{n}^2-m^{2}n+m^3-n^3\right)\hfill \\ \hfill y_1& =14m^2{n}^2\left(m^4+n^4\right)\left(m{n}^2-m^{2}n+m^3+n^3\right)\left(m{n}^2+m^{2}n+m^3-n^3\right)\hfill \\ \hfill y_2& =14m^2{n}^2\left(m^4+n^4\right)\left(-m{n}^2+m^{2}n+m^3+n^3\right)\left(-m{n}^2-m^{2}n+m^3-n^3\right)\hfill \\ \hfill y_3& =2n^2\left(m^2+n^2\right){\left(m^2-n^2\right)}^2\left(-m{n}^2-m^{2}n+m^3-n^3\right)\left(-m{n}^2+m^{2}n+m^3+n^3\right)\hfill \\ \hfill y_4& =2m^2\left(m^2+n^2\right){\left(m^2-n^2\right)}^2\left(m{n}^2+m^{2}n+m^3-n^3\right)\left(m{n}^2-m^{2}n+m^3+n^3\right)\hfill \\ \hfill z_1& =4m^2{n}^2\left(m^4+n^4\right)\left(-m^2{n}^4+3m^4{n}^2+m^6+n^6\right)\hfill \\ \hfill z_2& =4m^2{n}^2\left(m^4+n^4\right)\left(3m^2{n}^4-m^4{n}^2+m^6+n^6\right)\hfill \\ \hfill z_3& =-2n^2\left(m^2-n^2\right){\left(m^2+n^2\right)}^2\left(-m^2{n}^4+3m^4{n}^2+m^6+n^6\right)\hfill \\ \hfill z_4& =2m^2\left(m^2-n^2\right){\left(m^2+n^2\right)}^2\left(3m^2{n}^4-m^4{n}^2+m^6+n^6\right),\hfill \end{array}$$

where $m>n$ and $m,n\in Z_{+}$.

Example 7

(Numerical Example). If $m=2$ and $n=1$, then we obtain the following solution $(a,b,L)$ to the SLP:

$$(a,b,L)=(16320,3003,33245).$$

4. Final Examples and Remarks

Remark 5.

As we have seen, to find a complete set of integer solutions to SLP for the case $L>L_{\min }$ is still a challenging, open problem. However, via the methods presented in this paper we can find several different types of such integer solutions which hopefully can be guidelines to find the final solutions of this problem.

Example 8.

We seek solutions for a quadratic box instead of a rectangular one; i.e., when

$$a=b.$$

From (3) we see that this requires that

$$4rstw(st+rw)=(rt-sw)(r^2-s^2)(t^2-w^2)$$

leading to

$$(rt-st-rw-sw)(r^2{t}^2+s^2{w}^2+rs{t}^2-rs{w}^2+r^{2}tw-s^{2}tw+2rstw)=0.$$

We then have to check two possibilities:

(i)

$$\left(r^2{t}^2+s^2{w}^2+rs{t}^2-rs{w}^2+r^{2}tw-s^{2}tw+2rstw\right)=0,$$

implying that

$$\frac{r}{s}=\frac{1}{2}\frac{1}{t\left(t+w\right)}\left(\sqrt{-8t{w}^3+8t^{3}w+2t^2{w}^2+t^4+w^4}-2tw-t^2+w^2\right).$$

For r and s to be integer valued, we must require

$$-8{tw}^3+8t^{3}w+2t^2{w}^2+t^4+w^4$$

to be perfect square. The only solutions are $t=\pm w$, which give only trivial solutions to the problem.

(ii)

$$\left(rt-st-rw-sw\right)=0,$$

which gives that

$$\frac{r}{s}=\frac{t+w}{t-w},$$

which, without loss of generality, leads to

$$\begin{array}{l}r=t+w\\ s=t-w.\end{array}$$

Inserting these values in the variables in (3) gives the complete integer parametric representation of the variables in quadrant one for the case $a=b$:

$$\begin{array}{cc}\hfill a& =2tw\left(t^4-w^4\right)\hfill \\ \hfill b& =2tw\left(t^4-w^4\right)\hfill \\ \hfill L& ={\left(t^2+w^2\right)}^2\left(2tw+t^2-w^2\right)\hfill \\ \hfill x_1& =\left(t^2+w^2\right){\left(t^2-w^2\right)}^2\hfill \\ \hfill x_2& =4t^2{w}^2\left(t^2+w^2\right)\hfill \\ \hfill y_1& =4t^2{w}^2\left(t^2+w^2\right)\hfill \\ \hfill y_2& =\left(t^2+w^2\right){\left(t^2-w^2\right)}^2\hfill \\ \hfill z_1& =2tw{\left(t^2+w^2\right)}^2\hfill \\ \hfill z_2& ={\left(t^2+w^2\right)}^2\left(t^2-w^2\right).\hfill \end{array}$$

Example 9

(Numerical Example). We see that when $a=b$, then $x_1=y_2$ and $x_2=y_1$. In particular, if $t=2$ and $w=1$, then

$$\left(a,b,L\right)=\left(12,12,45\right),$$

and, moreover,

$$\left(x_1,x_2\right)=\left(9,16\right),$$

$$\left(y_1,y_2\right)=\left(16,9\right),$$

and

$$\left(z_1,z_2\right)=\left(20,15\right).$$

Example 10.

What are the requirements for $z_1=L-z_1$, (or equivalently, $z_2=L-z_2$)? From (3) we then must have that

$$2tw(st+rw)(r^2+s^2)=\left(t^2-w^2\right)\left(r^2+s^2\right)\left(rt-sw\right),$$

so that

$$\left(r^2+s^2\right)\left(r{t}^3+s{w}^3-3rt{w}^2-3s{t}^{2}w\right)=0,$$

which leads to

$$\begin{array}{l}r=w(3t^2-w^2)\\ s=t\left(t^2-3w^2\right).\end{array}$$

When we insert these values into the formulas in (3), then we find the following complete integer parametric solution for the variables in quadrant one for the case $z_1=L-z_1$.

$$\begin{array}{cc}\hfill a& =2tw\left(t^2+w^2\right)\left(t^2-3w^2\right)\left(3t^2-w^2\right)\hfill \\ \hfill b& =-\left(t^4-w^4\right)\left(-4tw+t^2+w^2\right)\left(4tw+t^2+w^2\right)\hfill \\ \hfill L& =2{\left(t^2+w^2\right)}^4\hfill \\ \hfill x_1& =2tw\left(t^2+w^2\right)\left(t^2-3w^2\right)\left(3t^2-w^2\right)\hfill \\ \hfill x_2& =-2tw\left(t^2+w^2\right)\left(-4tw+t^2+w^2\right)\left(4tw+t^2+w^2\right)\hfill \\ \hfill y_1& =-\left(t^4-w^4\right)\left(-4tw+t^2+w^2\right)\left(4tw+t^2+w^2\right)\hfill \\ \hfill y_2& =\left(t^4-w^4\right)\left(t^2-3w^2\right)\left(3t^2-w^2\right)\hfill \\ \hfill z_1& ={\left(t^2+w^2\right)}^4\hfill \\ \hfill z_2& ={\left(t^2+w^2\right)}^2\left(t^2-3w^2\right)\left(3t^2-w^2\right)\hfill \\ \hfill L-z_1& ={\left(t^2+w^2\right)}^4\hfill \\ \hfill L-z_2& =-{\left(t^2+w^2\right)}^2\left(4tw+t^2+w^2\right)\left(-4tw+t^2+w^2\right).\hfill \end{array}$$

Example 11

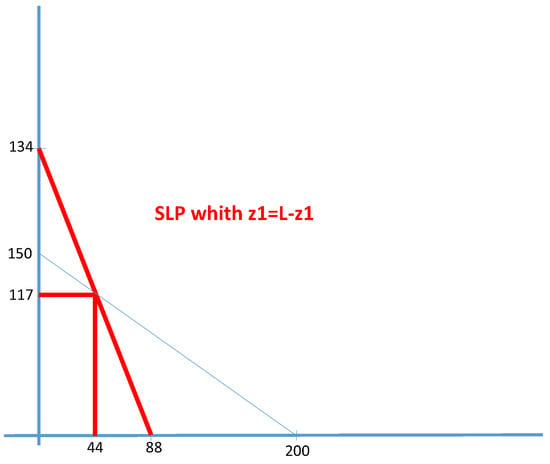
(Numerical Example). We see that when $z_1=L-z_1,$ then $x_1=a$ and $y_1=b$. In particular, if $t=2$ and $w=1$, we obtain that

$$\left(a,b,L\right)=\left(44,117,250\right),$$

$$\left(x_1,x_2\right)=\left(44,156\right),$$

$$\left(y_1,y_2\right)=\left(117,33\right),$$

and

$$\left(z_1,z_2\right)=\left(125,55\right).$$

This case is illustrated in Figure 7.

Figure 7. SPL where the two parts of the ladder are equal.