Abstract
A multidimensional two-sex branching process is introduced to model the evolution of a pedigree originating from the mutation of an allele of a Y-linked gene in a monogamous population. The study of the extinction of the mutant allele and the analysis of the dominant allele in the pedigree is addressed on the basis of the classical theory of multi-type branching processes. The asymptotic behavior of the number of couples of different types in the pedigree is also derived. Finally, using the estimates of the mean growth rates of the allele and its mutation provided by a Gibbs sampler, a real Y-linked pedigree associated with hearing loss is analyzed, concluding that this mutation will persist in the population although without dominating the pedigree.
Keywords:
Y-linked genes; pedigree; Markov chains; two-sex branching processes; multi-type branching processes; Gibbs sampler; hearing loss MSC:
60J80; 60J85; 92D10
1. Introduction
Branching Processes (BPs) (see [1]) are stochastic mathematical models widely used in population genetics (see [2]) as an alternative approach to the Wright–Fisher model when the classical assumption of constant population size is dropped (see [3]). Not only the simplest model, the Bienaymé–Galton–Watson BP, has been applied (see, for example, the pioneering work [4], or more recently [5,6], or [7]), but also more complex BPs have been used to better describe newly arisen genetic issues (see, for example, logistic BP [8], infinite-allele BP [9], or multi-type self-regulating BP [10].)
In this setting, those processes that model sexual reproduction merit particular attention. Deriving from the standard two-sex BP (see [11]), several multi-type discrete time two-sex BPs have been proposed to model various genetic problems. In particular, in [12] and in Chapters 11 and 12 in [13], two-sex multi-type self-regulating BPs were considered to model the evolution of autosomal loci with several alleles. Furthermore, the evolution of the number of carriers of the alleles of sex-linked genes has been considered for both Y-linked and X-linked cases. In particular, a Y-linked two-sex BP was introduced in [14] in which a preference of females to mate with males having a specific allele was modeled. In [15,16], it was considered that the Y-linked gene (without and with mutant alleles, respectively) had no influence on the mating process, i.e., females chose their mates blindly. An X-linked two-sex BP was introduced in [17] to study X-linked recessive diseases.
All those studies considered two-sex monogamous populations, i.e., one individual can mate with at most one individual of the opposite sex, forming a couple or mating unit, which gives rise to female and male offspring with different genotypes according to certain inheritance rules. Each couple is classified according to its components’ genotypes. The total number of different types of couple formed in a generation depends on the total number of females and males in that generation and is determined by the mating scheme (preference or blind choice) that defines the sexual interaction. Those studies considered an overall population, dealing with such problems as its extinction, the fixation of specific alleles, the coexistence of different alleles, their rates of growth, etc. In many real cases, however, only a part of the population was observed, usually a pedigree or a family tree (see, for example, in [18,19,20] for human populations and [21,22,23,24,25,26] for populations of other animals) related to a target genetic trait (usually originating from mutation), so that the total number of females and males in the overall population to which the pedigree belongs is unknown. The pedigree usually has its own characteristics since, for example, mating with relatives (i.e., individuals within the pedigree) may be forbidden so that external individuals to the pedigree from the rest of the overall population have to be chosen as mates. These features are shown in Figure 1, which illustrates the evolution of the first generations of a simulated Y-linked pedigree evolving within an overall population. Notice that, in this genetic framework (the Y-linked gene case), the evolution of the number of carriers of different genotypes in the overall population could be modeled by the Y-linked two-sex BP with the mutant allele that was introduced in [16]. If one is dealing only with a pedigree, however, this is not the case either with the aforementioned model or with other Y-linked two-sex BPs without mutation. The reason is that the total numbers of females and of each type of male are unknown. This also implies that the inferential methods developed in [27,28,29,30,31] are inadequate to quantify the presence of the different alleles of the gene within the Y-linked pedigree.
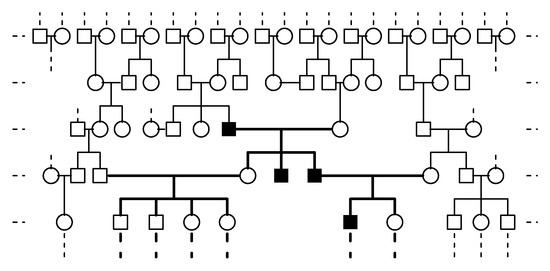
Figure 1.
Generation-by-generation evolution of a simulated Y-linked pedigree (bold line) within an overall population. ◯ Female, □ male without the target allele, and ■ male with the target allele.
In general therefore, the characteristics that typify a pedigree mean that the existing models introduced to describe the evolution in an overall population of the number of carriers of alleles linked to sex chromosomes are not fully appropriate. Hence, there is need for proposals of new ad hoc processes that can model, analyze, and infer the behavior of pedigrees that form part of an overall population. As a first attempt to address this practical problem, we shall here focus on modeling Y-linked pedigrees through BPs. With this aim, we have split this communication into seven sections. In Section 2, which follows, a Y-linked pedigree two-sex BP is introduced. Its basic properties are studied in Section 3, including how to consider part of the model as a specific multi-type BP. Then, the extinction problem of the Y-linked gene in the pedigree, as well as its asymptotic growth rate in the event of survival is considered in Section 4. An application to real data is described in Section 5, where a Y-linked pedigree associated with the inheritance of non-syndromic hearing impairment is analyzed. Finally, the conclusions to be drawn are reported in Section 6, and some technical mathematical results together with the limiting behavior of the total number of mating units of each genotype, which is not deduced directly from the multi-type BP results, are included as an Appendix A.
2. Description of the Model
We shall now introduce a discrete-time Y-linked two-sex BP, which determines generation-by-generation the evolution of a pedigree associated with a Y-linked gene with two alleles, r and R, where R originates from a mutation of the r allele and will be the target characteristic. Moreover, it is considered that any other mutation of the r allele will not give rise to the same characteristic as the R allele, so that we can take all individuals with the R allele to stem from the first individual with that allele. Thus, for every , , , and denote the total numbers of females and of r- and R-type males that belong to the pedigree at generation n, respectively. The total numbers of r- and R-type couples or mating units related to the pedigree at generation n are denoted by and , respectively, where the type of a mating unit is the same as the genotype of its male. The numbers of females and of males of each type at the initial generation () are fixed, and we suppose that R-type males exist at this generation since the pedigree is originated by the R genotype. From the vector , the size of the family tree in each generation is determined by taking into account two phases: mating and reproduction.
In the mating phase, the number of couples of each genotype in generation n is obtained by assuming that generations do not overlap and that there are females, males with the r genotype, and males with the R genotype in the Y-linked pedigree. The point here is perfect fidelity mating, i.e., each individual mates at most with one individual of the opposite sex. Mating with relatives is forbidden, so that external individuals to the pedigree from the overall population are chosen as mates. Furthermore, we assume that females generated in the family tree only form couples with external r males (since, as explained at the beginning of the section, we suppose that there are no external R males). Hence, each mating unit is one-to-one, with only one of the two individuals belonging to the family tree. Hence, the R-type male of an R-type mating unit belongs to the pedigree, but for an r-type mating unit, either the male or the female (but not both) belongs to the family tree. Denoting by and the numbers of r-type mating units whose females and males, respectively, belong to the pedigree, one therefore has that .
We now consider the following probabilities: that each R-type male of the pedigree mates with one external female is , ; that a female of the pedigree mates with an external r-type male is , ; and that an r-type male of the pedigree mates with an external female is , . These probabilities may be different. Assuming that the probability that any given individual of the pedigree mates is independent of the others, if there are , , and females and r- and R-types males, respectively, then in the pedigree at generation n, the number of couples that are formed is given by:
where denotes the binomial distribution of size N and probability p. Notice that, for generation n, external females and external r-type males were chosen from the overall population (they are not considered in the pedigree).
To guarantee conditions that allow this model to be applicable, we assume that the pedigree exists within an overall population that is large enough for it to be a continual source of females and r-type males for the pedigree, allowing each individual in the pedigree to choose its mate by itself and independently of the others and for the probability of its mating to be constant from generation-to-generation, although possibly different for each type of individual.
In the reproduction phase, as was done in other Y-linked BPs (see [14,15]), each couple is assumed to produce offspring independently of the other couples according to a probability distribution, which will be the same for all the couples with a given genotype, irrespective of the generation to which they belong. This will be termed the reproduction law of the corresponding genotype. Formally, we consider the following independent sequences:
of independent, identically distributed, non-negative, and integer-valued bivariate random vectors, where (resp. ) represents the number of females and males generated by the couple of type r in generation n, with the female () or the male () belonging to the pedigree (resp. type R).
Notice that and have the same distribution since both stem from couples of type r. However, for and may have different distributions, meaning that there may be differences in the reproductive capacities of r-type and R-type couples. With respect to the distribution of these vectors, we assume the binomial reproduction scheme introduced in [11], which we shall refer to throughout the paper as Daley’s scheme. This is that the total number of offspring generated by an r-type (resp. R-type) couple is specified by a given probability distribution, (resp. ), where , with and (resp. , with ). Moreover, we denote by (resp. ) the average number of offspring generated by an r-type (resp. R-type) couple. Furthermore, an offspring will be female with probability , , or male with probability . These sex designations are made independently among the offspring of any couple, and it is assumed that the genotype has no influence on the sex determination, so that is the same for both genotypes. Then, if an r-type (resp. R-type) couple produces l (resp. k) offspring, i.e., , with (resp. ), the number of females among these, (resp. ) follows a binomial distribution of size l (resp. k) and probability . Hence, the average number of females and males per r-type (resp. R-type) couple will be and , respectively, independently of t (resp. and ).
On the basis of the rules described above, for a generation n with known and , i.e., the total number of r-type couples at generation n whose females and males belong to the Y-linked pedigree, respectively, and the total number of R-type couples at generation n, , one has that the total number of females in generation stemming from all couples in generation n is given by:
where . Moreover, the male offspring of all r-type and R-type couples in generation n are the total of r-type and R-type males in the pedigree in generation , respectively. Their numbers are given by the following expressions:
We shall term the six-dimensional process a Y-linked pedigree two-sex branching process.
Remark 1.
The values of the β parameters may be determined in many different ways depending on the population one is modeling. For example, if the behavior of the individuals in the population is that every individual that can mate mates (and this behavior is also followed by the individuals of the pedigree), i.e., the population evolves as a two-sex BP with perfect fidelity mating (see [11]), then, when, it would be reasonable to consider thatand, because the total number of females is eventually greater than the total number of males in the survival set of the population, and then eventually, all males mate, and the ratio between males and females in the population stabilizes at around(see [32]). Analogously, when, and are reasonable choices since the total number of males is eventually greater than the total number of females in the survival set of the population, and in the mating process, there is no preference for either one of the alleles. Nevertheless, in some situations, R-males may be preferred by females as mates. In this case, the reasonable choice for would be . Notice that these examples of modeling have some similarity with those given in [15] for “blind choice” mating and in [14] for mating with preference, respectively.
3. Basic Properties
From the foregoing description of the model, one deduces that the number of females and males of each genotype belonging to the Y-linked pedigree in the next generation depends only on the current number of individuals in the pedigree, and not on the number of ancestors in the pedigree or in the overall population of any past generation.
Therefore, if the current numbers of females and of each type of male in the Y-linked pedigree are known and given the parameters of the model, i.e., the probability of an offspring to be female, , the probabilities of mating, , , and , and the reproduction laws of both types, and , which remain the same from generation-to-generation, then the numbers of mating units, of females, and of males of each type in the following generations are generated recursively by Equations (1)–(3), respectively. Mathematically therefore, a Y-linked pedigree two-sex BP is a homogeneous multi-type Markov chain in discrete time, whose states are vectors with non-negative integer coordinates.
Moreover, since each mating unit is related to only one individual of the pedigree, then from Lemma A1 in Appendix A, the marginal three-dimensional process could be regarded as a multi-type BP (see [33]). In fact, for all ,
where denotes equality in distribution, and with and being independent sequences of independent and identically distributed random variables following Bernoulli distributions with probabilities , , and , respectively, determining for each individual whether it has mated or not.
Therefore, the basic properties of the process are deduced from those of a multi-type BP. In particular, we derive the following expression for the matrix of means of the offspring distributions (see Proposition A1 in Appendix A for mathematical details):
which depends on the sex ratio, , the probabilities of mating, , , and , and the reproduction means, and , in a usual way. To avoid trivialities, we henceforth consider that these parameters are non-null.
Then, using the multi-type BP terminology (see [33]), is a reducible process with two classes determined by the genotypes of the mating units. Specifically, females and r-type males belonging to the pedigree form r-type mating units (first class), each of which gives rise to females and r-type males, but not to R-type males, while R-type males form R-type mating units (second class), which give rise to females and R-type males, but not to r-type males. Then, since the pedigree is originated by the R allele, individuals of all types, including r-type males, may be present generation-by-generation. However, if the R allele becomes extinct, then only females and r-type males may be present in future generations. Furthermore, to avoid trivial non-branching situations, we shall henceforth consider that , i.e., r-type mating units do not almost surely produce one single offspring (see Proposition A2 in the Appendix A for technical details).
Finally, the eigenvalues of the matrix of means are , , and . These will play an important role in the evolution of the Y-linked pedigree. Intuitively, represents the mean growth rate of R-type males in the pedigree, and unifies the reproductive capacities of females and r-type males by themselves since they form the same type of mating unit.
Notice that, although the mating rules do not appear explicitly in the marginal process since this does not record the number of mating units of each type, they are implicit in the mating probabilities.
4. Asymptotic Behavior
In this section, we deduce the generation-to-generation behavior of a Y-linked pedigree two-sex BP by applying the theory of multi-type BPs (see [33,34]) to the marginal process . Since throughout this work, we are assuming that the pedigree is initiated by the R genotype, we focus our attention on the case that there are only R-type males in the initial generation. Moreover, taking into account the additive property of the marginal process and without loss of generality, we consider that .
Hence, from Proposition A3 in Appendix A, one derives that only two limiting behaviors are possible almost surely for each class: either it goes to zero (i.e., it becomes extinct) or it grows without limit. Mathematically,
The same behavior is derived for the marginal process associated with mating units. From Equations (1)–(3) and the properties of the binomial distribution, one deduces that if at some generation there are no individuals of one type, then neither are there any mating units associated with that type, i.e., , , and imply almost surely that , , and , respectively. Furthermore, if there are no R-type mating units, then neither are there any males of this type, i.e., when , which implies the extinction of this genotype independently of the existence of mating units of type r. However, females and r-type males could be generated even when there are no r-type mating units, i.e., does not imply that and since R-type mating units give rise to females that can only mate with r-type males forming mating units that can generate r-type males. Therefore, a.s.,
Now, in order to quantify the Y-linked pedigree extinction probability, i.e., , by Theorem 10.1, Chapter II, in [34] (p. 46), one has that this probability is unity if and only if and (recall that and are the greatest eigenvalues of the matrix of means). From (5), one can also derive results concerning the extinction probability of mating units related to the family tree. Notice that the event has positive probability if and only if (in this case, Theorem 7.1, Chapter II, in [34] (p. 41) is being applied) independently of , which is only associated with females and r-type males.
Finally, with respect to the growth rates in the cases of non-extinction, we derive from [35] geometric growths defined by and for each type of individual. Moreover, taking into account Daley’s scheme, the properties of the binomial distribution and the logarithmic conditions for and that are typical in branching process theory, i.e.,
and
one also derives the limiting behavior of the mating units inherited from them (see Theorem A1 in Appendix A). In particular, if and (6) holds, then there exists a positive random variable, , on the non-extinction set such that:
Furthermore, when , with , and (6) and (7) hold, there exist positive random variables, and , on the non-extinction set such that if , then:
while if , then:
Thus, one also derives that there are just two limiting behaviors (extinction or unlimited growth) almost surely for each type of mating unit since:
Furthermore, from Theorem A1 in Appendix A, one has that:
since R- and r-type mating units generate females and r-type males, respectively, following a binomial scheme. Notice that the case and is special since the probability of the event is non-null even if females do not reproduce.
Therefore, when and , i.e., , the numbers of females and r-type males, and also of r-type mating units, dominate the Y-linked pedigree. However, when and , i.e., , all types of individuals and mating units have the same geometric growth, defined by .
Remark 2.
Taking into account Remark 1 and the foregoing results, one can deduce the same asymptotic behavior for both R-type males and R-type mating units as those derived in [36,37] since these kinds of individuals and mating units are unrelated to either females or r-type males. This is not the case, however, for r-type males and mating units or for females since r-type males can be generated not only by r-type males, but also by females originating from R- or r-type males or females of the pedigree.
Remark 3.
The behavior of mating units associated with a Y-linked pedigree was derived from the marginal process of individuals since each mating unit is related to just one individual belonging to the family tree.
5. Analyzing Real Data
A Y-linked pedigree associated with the inheritance of non-syndromic hearing impairment was reported in [20]. In particular, data on seven generations of a Chinese family were collected by the Institute of Otolaryngology of the Chinese People’s Liberation Army General Hospital in Beijing in which the inheritance pattern was likely due to a mutation that occurred in an ancestor’s putative Y-chromosome linked gene. The hearing loss was not transmitted by females of this family who mated with unrelated males with normal hearing. Thus, the Y-linked pedigree two-sex BP introduced in this paper may be used to model this inheritance pattern, with the R allele meaning the hearing loss disorder and the r allele normal hearing. The numbers of females and of r- and R-type males belonging to the pedigree, as well as the numbers of each type of couple in the first six generations () are presented in Figure 2 and Table 1. One more observed generation (the seventh) was described in [20], but we discarded its data since that generation was still open when the data were collected. Neither could generation be completed since the number of R-type males fell, as did the numbers of each type of mating unit (see Figure 2). Henceforth therefore, we shall consider the observed sample to be:
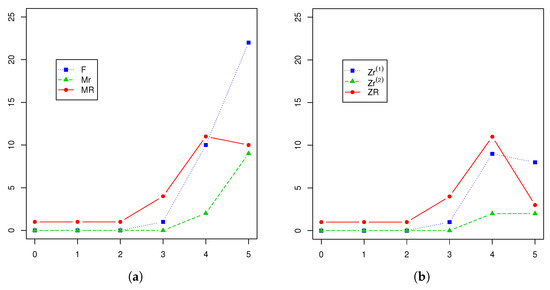
Figure 2.
Evolution generation-by-generation of (a) and (b).

Table 1.
Number of individuals and couples of each type in the first six generations for the Y-linked pedigree associated with the inheritance of non-syndromic hearing impairment reported in [20].
Moreover, the last observed generation, , will be useful in order to assess the goodness of the predictions given by the model.
Given the data , we took a Bayesian approach in a non-parametric framework based on Markov chain Monte Carlo methods to estimate the key parameters and . In particular, we applied the Gibbs sampler algorithm proposed in [38], since a Y-linked pedigree two-sex BP could be regarded as a multi-type BP. To this end, we simulated 150 chains formed by 20,000 iterations of the method. According to the Gelman–Rubin–Brooks diagnostic tools, Five thousand was a sufficient burn-in period with a batch size of 200. In this way, we obtained a sample of size 11,400 from the conditional distribution of the parameter vector . Summary statistics for this posterior distribution are given in Table 2, and the estimates of its marginal density and joint density contour plot are presented in Figure 3 and the left-hand-side of Figure 4, respectively. We deduced that both growth rates were greater than unity, with that of R-type males, , being less than that of females and r-type males, , since our estimates were that and were approximately equal to unity and , with Bayes factors greater than unity.

Table 2.
Summary statistics for the posterior distribution of , , , , , , and , given . SD: standard deviation; MCSE: Monte Carlo standard error; TSSE: time-series standard error.
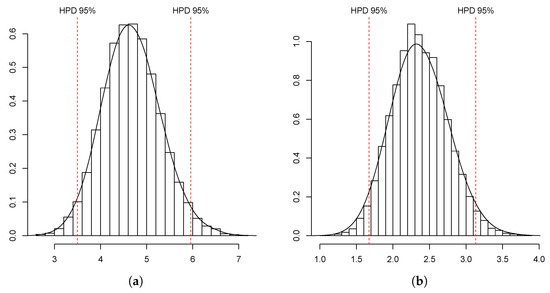
Figure 3.
Estimated density for (a) and for (b), with 95% HPD (highest posterior density) sets.
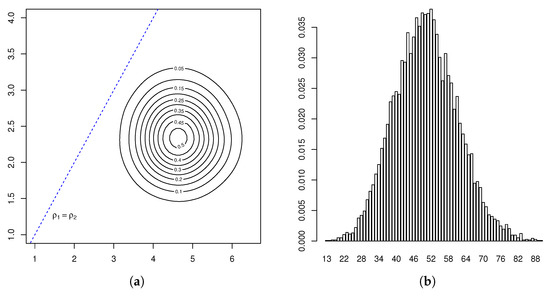
Figure 4.
Contour plot of (a) and estimated predictive distribution (b).
Applying these results therefore, we deduced that there existed a positive probability for the hearing impairment not to disappear from this family, in which the presence of r-type males and females would dominate the Y-linked pedigree in the following generations. Indeed, this behavior was confirmed from the Monte Carlo estimated predictive posterior distributions of the number of individuals of each type at Generations 5 and 9 (Figure 4, Figure 5 and Figure 6) in which the R allele became extinct only in one simulated path of 11,400. Notice that almost all estimates at Generation 5 exceeded the observed values, coherent with our comment above that this generation was incomplete. Moreover, couples of the different types could not be compared with the observed values in the pedigree because they were not archivable from the multi-type BP. However, we deduced that their growth rates were the same as the individuals. Figure 7 plots the logarithms of the number of individuals and mating units of each type generation by generation together with the logarithms of the estimated mean growth rates (straight lines). It indicates that the evolution of the observed Y-linked pedigree was in agreement with the behavior predicted by the two-sex BPs introduced in this communication. Note that the fit was better for the R genotype since this genotype was observed over more generations than females and r-type males of the pedigree.
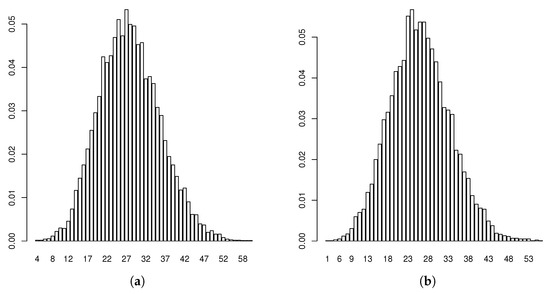
Figure 5.
Estimated predictive distributions of (a) and (b).
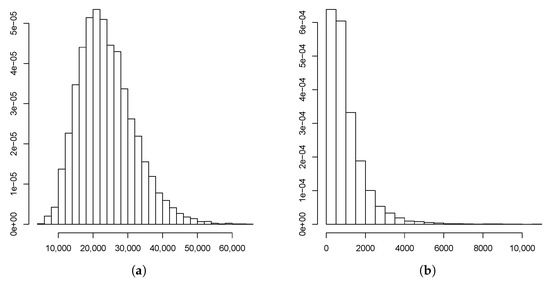
Figure 6.
Estimated predictive distributions of (a) and (b).
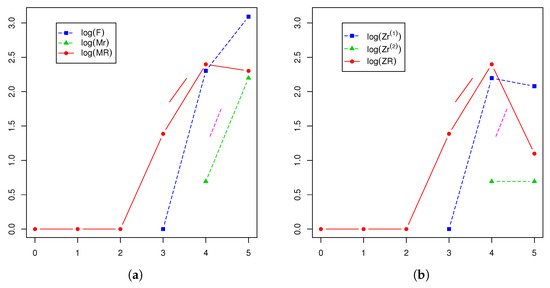
Figure 7.
Evolution generation-by-generation of (a) and (b), together with (solid straight line) and (dotted straight line).
Remark 4.
In this study, we used the statistical computing and graphics language and environment R (“GNU S”) ([39]), the CODA package ([40]) to analyze the convergence of the Gibbs sampler algorithm, and the GenKern package ([41]) for the two-dimensional kernel density estimation.
6. Conclusions
Motivated by the study of a real Y-linked pedigree associated with hearing loss (see [20]), we presented and evaluated a model that should be very useful for studies of the evolution of Y-linked pedigrees. Specifically, a Y-linked two-sex branching process was introduced aimed at studying the generation-by-generation evolution of a pedigree, which appeared in a population from the mutation of an allele linked to a gene on the male Y chromosome. Assuming that the population comprised females and two types of males, r and its mutation R, the model was defined in a two-phase structure: mating and reproduction. In the mating phase, two types of couple were formed depending on the genotype of the male. The number of each type of couple was given by a binomial scheme under the main assumptions of perfect fidelity mating and of each individual of the pedigree mating only with external individuals, i.e., mating with relatives was forbidden. In the reproduction phase, each couple produced offspring independently according to some probability distribution, which was the same for a given genotype and was independent of the generation.
It was proven that the marginal process formed by the total number of females and males with r and R genotypes belonging to the pedigree could be regarded as a reducible multi-type branching process with two classes determined by the genotypes of the mating units. It was then not difficult to obtain the matrix of means of the offspring distributions, whose greatest eigenvalues ( and ) were directly related to the asymptotic behavior of the process. In particular, (with being the probability that a female in the pedigree mates with an external r-type male, the probability that an r-type male in the pedigree mates with an external female, the probability of an offspring being female, and the mean number of offspring generated by an r-type couple) represented the unified reproductive capacity of females and r-type males belonging to the pedigree, and (with being the probability that an R-type male mates with an external female and the mean number of offspring generated by an R-type couple) represented the mean (geometric) growth rate of R-type males and couples on the non-extinction set. The mean growth rate of females and of r-type males and couples was given by the greater of and . When , both grew geometrically in the long term. However, if , the sequence that normalized them was . It was then deduced that, on the non-extinction set, the r allele dominated the pedigree when , while if , then the two genotypes had the same geometric growth given by . Mathematically, it has to be observed that the results related to the asymptotic behavior of the number of couples of each type were not a direct consequence of those obtained from the reducible multi-type branching model.
Finally, we evaluated the practical performance of the model against some real data. In particular, the model allowed us to study the evolution of Y-linked patterns associated with the real pedigree presented in [20]. From the observed sample given in that reference, which had the structure given in Equation (8), we estimated the parameters and using the Gibbs sampler algorithm proposed in [30] and deduced that there existed a positive probability for the hearing disorder not to disappear from the family even though the dominant allele was the one that transmitted normal hearing. The future population size of the total number of individuals of each type was estimated from the approximation of the predictive posterior distributions, indicative that the present results showed the usefulness of the model from a realistic perspective.
Author Contributions
All the authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Ministerio de Economía y Competitividad and the Fondo Europeo de Desarrollo Regional (MINECO/FEDER, UE) (Grant MTM2015-70522-P) and by the Junta de Extremadura/European Regional Development Fund (Grant IB16099).
Acknowledgments
The authors thank the referees for their careful reading of the paper and for their constructive comments, which improved its presentation.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this section, we provide some technical details of the results that were used in the study.
Lemma A1.
Letandbe fixed. Furthermore, letbe independent random variables such thatis an n-dimensional random variable with probability generating function, Y follows a binomial distribution with parameters N and θ, andfollows a Bernoulli distribution with probability θ, for every. Then:
wheredenotes equality in distribution.
Proof.
For all , with , one has that:
where . Furthermore,
and the proof is complete. □
Proposition A1.
Letbe the marginal process of a Y-linked pedigree two-sex branching process as defined in Equation (4). It holds that for all with :
with and being the probability generating functions of the reproduction laws and , respectively.
Proof.
Taking into account Daley’s scheme and that the reproduction phase of the process is independent of the mating phase, we have that:
The rest of the equations are derived in a similar manner. □
The following proposition is easily deduced from the previous one and is related to the singular multi-type branching process (see Definition 5.2 in [33] (p. 11)).
Proposition A2.
Letbe the marginal process of a Y-linked pedigree two-sex branching process. The processis singular whenand, whileis singular when, , and, withsuch that.
From Chapter II, Section 6 in [34], we derived the following result:
Proposition A3.
Letbe the marginal process of a Y-linked pedigree two-sex branching process such thatandare non-singular processes. Then,is an absorbing state, and every non-null state is transient. Moreover,
Finally, from the asymptotic behavior of reducible multi-type BPs given in [35], we obtain the following limiting behavior:
Theorem A1.
Letbe a Y-linked pedigree two-sex branching process. Ifand Equation (6) holds, then there exists a positive random variable,, on the non-extinction set such that:
with, Furthermore, when, with, and Equations (6) and (7) hold, there exist positive random variables,and, on the non-extinction set such that if, then:
while if, then:
with,
Proof.
First, from Equations (6) and (7), we deduce the logarithmic conditions for the multi-type branching process . In particular, taking into account Equation (4), Daley’s scheme, and that the reproduction phase of the process is independent of the mating phase, one has that:
The other logarithmic conditions are derived in a similar manner.
Finally, since all limiting assertions are obtained in a similar manner, we confine ourselves to proving that if and Equation (6) holds, then:
where is the almost sure limit of , which is non-degenerate at zero (applying the classical theory of multi-type BPs given in [35]).
To this end, fix , and define for :
By appeal to Chebyshev’s inequality and taking into account that on , we infer that, a.s. on ,
with . Moreover, by the conditional Borel–Cantelli lemma,
and the result is derived, so that the proof is concluded. □
References
- Haccou, P.; Jagers, P.; Vatutin, V. Branching Processes: Variation, Growth and Extinction of Populations; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Pakes, A. Biological applications of branching processes. In Handbook of Statistic, Vol. 21 Stochastic Processes: Modelling and Simulation; Shanbhag, D.N., Rao, C.R., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2003; pp. 693–773. [Google Scholar]
- Cyran, K.; Kimmel, M. Alternatives to the Wright-Fisher model: The robustness of mitochondrial Eve dating. Theor. Popul. Biol. 2010, 78, 165–172. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R. On dominace ratio. Proc. Roy. Soc. Edinburgh 1922, 50, 205–220. [Google Scholar]
- Burden, C.; Simon, H. Genetic drift in populations governed by a Galton-Watson branching process. Theor. Popul. Biol. 2016, 109, 63–74. [Google Scholar] [CrossRef] [PubMed]
- Neves, A.; Moreira, C. Applications of the Galton-Watson process to human DNA evolution and demography. Physica A 2006, 368, 132–146. [Google Scholar] [CrossRef][Green Version]
- O’Conell, N. The genealogy of branching processes and the age of our more recent common ancestor. Adv. Appl. Probab. 1995, 27, 418–442. [Google Scholar] [CrossRef]
- Campbell, R. A logistic branching process for population genetics. J. Theor. Biol. 2003, 225, 195–203. [Google Scholar] [CrossRef]
- McDonald, T.; Kimmel, M. A multitype infinite-allele branching process with applications to cancer evolution. J. Appl. Probab. 2015, 52, 864–876. [Google Scholar] [CrossRef]
- Mode, C.; Sleeman, C.; Raj, T. On the inclusion of self-regulating branching processes in the working paradigm of evolutianary and population Genetics. Front. Genet. 2013, 4, 11. [Google Scholar] [CrossRef]
- Daley, D.J. Extinction conditions for certain bisexual Galton-Watson branching processes. Z. Wahrscheinlichkeitsth. 1968, 9, 315–322. [Google Scholar] [CrossRef]
- Mode, C.; Raj, T.; Sleeman, C. Monte Carlo implementations of two sex density dependent branching processes and their applications in evolutionary Genetics. In Applications of Monte Carlo Methods in Biology, Medicine and Other Fields of Science; Mode, C.J., Ed.; IntechOpen: London, UK, 2011; pp. 273–296. [Google Scholar]
- Mode, C.J.; Sleemam, C.K. Stochastic Processes in Genetics and Evolution: Computer Experiments in the Quantification of Mutation and Selection; World Scientific: Singapore, 2012. [Google Scholar]
- González, M.; Hull, D.; Martínez, R.; Mota, M. Bisexual branching processes in a genetic context: The extinction problem for Y-linked genes. Math. Biosci. 2006, 202, 227–247. [Google Scholar] [CrossRef]
- González, M.; Martínez, R.; Mota, M. Bisexual branching processes to model extinction conditions for Y-linked genes. J. Theor. Biol. 2009, 258, 478–488. [Google Scholar] [CrossRef] [PubMed]
- González, M.; Gutiérrez, C.; Martínez, R. Extinction conditions for Y-linked mutant-alleles through two-sex branching processes with blind-mating structure. J. Theor. Biol. 2012, 307, 104–116. [Google Scholar] [CrossRef] [PubMed]
- González, M.; Gutiérrez, C.; Martínez, R.; Mota, M. Extinction probability of some recessive alleles of X-linked genes in the context of two-sex branching processes. In Branching Processes and Their Applications; Lecture Notes in Statistics; Springer: Berlin/Heidelberg, Germany, 2016; Volume 219, pp. 287–305. [Google Scholar]
- Fu, S.; Yan, J.; Wang, X.; Dong, J.; Chen, P.; Wang, C.; Chen, G. The audiological characteristics of a hereditary Y-linked hearing loss in a Chinese ethnic Tujia pedigree. Int. J. Pediatr. Otorhinolaryngol. 2011, 75, 202–206. [Google Scholar] [CrossRef] [PubMed]
- Reed, S.; Cambier, R.; Applen, J. A color vision anomaly showing holandric (Y-linked) transmission. Am. J. Hum. Genet. 1951, 3, 282–284. [Google Scholar] [CrossRef]
- Wang, Q.; Lu, C.; Li, N.; Rao, S.; Shi, Y.; Han, D.; Li, X.; Cao, J.; Yu, L.; Li, Q.; et al. Y-linked inheritance of non-syndromic hearing impairment in a large Chinese family. J. Med. Genet. 2004, 41, e80. [Google Scholar] [CrossRef]
- Abitbol, M.; Bosse, P.; Thomas, A.; Tiret, L. A deletion in FOXN1 is associated with a syndrome characterized by congenital hypotrichosis and short life expectancy in Birman cats. PLoS ONE 2015, 10, e0120668. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, S.; Rubinstein, B.; Ross, E.; Sánchez, A. Widespread maintenance of genome heterozygosity in Schmidtea Mediterranea. Nat. Ecol. Evol. 2016, 1, 1–19. [Google Scholar] [CrossRef]
- Metzger, J.; Wohlke, A.; Mischke, R.; Hoffmann, A.; Hewicker-Trautwein, M.; Kuch, E.; Naim, H.; Distl, O. A novel SLC27A4 splice acceptor sitemutation in Great Daneswith ichthyosis. PLoS ONE 2015, 10, e0141514. [Google Scholar] [CrossRef]
- Murgiano, L.; Sacchetto, R.; Testoni, S.; Dorotea, T.; Mascarello, F.; Liguori, R.; Gentile, A.; Drogemuller, C. Pseudomyotonia in Romagnola cattle caused by novel ATP2A1 mutations. BMC Vet. Res. 2012, 8, 186. [Google Scholar] [CrossRef]
- Reinartz, S.; Mohwinkel, H.; Surie, C.; Hellige, M.; Feige, K.; Eikelberg, D.; Beineke, A.; Metzger, J.; Distl, O. Germline mutation within COL2A1 associated with lethal chondrodysplasia in a polled Holstein family. BMC Genom. 2015, 18, 762. [Google Scholar] [CrossRef]
- Yamato, O.; Jo, E.; Chang, H.; Satoh, H.; Shoda, T.; Sato, R.; Uechi, M.; Kawasaki, N.; Naito, Y.; Yamasaki, M.; et al. Molecular screening of canine GM1 gangliosidosis using blood smear specimens after prolonged storage: Detection of carriers among Shiba dogs in northern Japan. J. Vet. Diagn. Investig. 2008, 20, 68–71. [Google Scholar] [CrossRef] [PubMed]
- González, M.; Gutiérrez, C.; Martínez, R. Parametric inference for Y-linked gene branching models: Expectation-maximization method. In Workshop on Branching Processes and Their Applications; Lecture Notes in Statistics-Proceedings; Springer: Berlin/Heidelberg, Germany, 2010; Volume 197, pp. 191–204. [Google Scholar]
- González, M.; Gutiérrez, C.; Martínez, R. Expectation-maximization algorithm for determining natural selection of Y-linked genes through two-sex branching processes. J. Comput. Biol. 2012, 19, 1015–1026. [Google Scholar] [CrossRef] [PubMed]
- González, M.; Gutiérrez, C.; Martínez, R. Parametric Bayesian inference for Y-linked two-sex branching models. Stat. Comput. 2013, 23, 727–741. [Google Scholar] [CrossRef]
- González, M.; Gutiérrez, C.; Martínez, R. Non-parametric Bayesian inference through MCMC method for Y-linked two-sex branching processes with blind choice. J. Stat. Comput. Sim. 2018, 88, 3565–3587. [Google Scholar] [CrossRef]
- González, M.; Gutiérrez, C.; Martínez, R. Bayesian inference in Y-linked two-sex branching processes with mutations: ABC approach. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019. [Google Scholar] [CrossRef]
- González, M.; Molina, M. On the limit behavior of a superadditive bisexual Galton-Watson branching process. J. Appl. Probab. 1996, 33, 960–967. [Google Scholar] [CrossRef]
- Mode, C. Multitype Branching Processes; Elsevier: Amsterdam, The Netherlands, 1971. [Google Scholar]
- Harris, T. The Theory of Branching Processes; Springer: Berlin/Heidelberg, Germany, 1964. [Google Scholar]
- Kesten, H.; Stigum, B. Limit theorems for decomposable multi-dimensional Galton-Watson processes. J. Math. Anal. Appl. 1967, 17, 309–338. [Google Scholar] [CrossRef]
- Alsmeyer, G.; Gutiérrez, C.; Martínez, R. Limiting geneotype frequencies of Y-linked genes through bisexual branching processes with blind choice. J. Theor. Biol. 2011, 275, 42–51. [Google Scholar] [CrossRef]
- González, M.; Martínez, R.; Mota, M. Bisexual branching processes in a genetic context: Rates of growth for Y-linked genes. Math. Biosci. 2008, 215, 167–176. [Google Scholar] [CrossRef]
- González, M.; Martín, J.; Martínez, R.; Mota, M. Non-parametric Bayesian estimation for multitype branching processes through simulation-based methods. Comput. Statist. Data Anal. 2008, 52, 1281–1291. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Plummer, M.; Best, N.; Cowles, K.; Vines, K. Coda: Output Analysis and Diagnostics for MCMC; R Package Version 0.19-1: Vienna, Austria, 2016; Available online: https://cran.r-project.org/web/packages/coda/index.html (accessed on 1 January 2020).
- Lucy, D.; Aykroyd, R. Genkern: Functions for Generating And manipulating Binned Kernel Density Estimates; R Package Version 1.2-60: Vienna, Austria, 2013; Available online: https://cran.r-project.org/web/packages/GenKern/index.html (accessed on 1 January 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).