Secret Image Sharing with Dealer-Participatory and Non-Dealer-Participatory Mutual Shadow Authentication Capabilities

Abstract

A $(k,n)$ threshold secret image sharing (SIS) method is proposed to divide a secret image into n shadows. The beauty of this scheme is that one can only reconstruct a secret image with k or more than k shadows, but one cannot obtain any information about the secret from fewer than k shadows. In the $(k,n)$ threshold SIS, shadow authentication means the detection and location of manipulated shadows. Traditional shadow authentication schemes require additional bits for authentication; need much information to be public; or need to put each shadow into a host image, utilizing the information hiding technique, which makes the generation, recovery and authentication complexity higher. Besides, most existing schemes work when a dealer participates in recovery. Our contribution is that we propose a SIS method for a $(k,n)$ threshold with dealer-participatory and non-dealer-participatory mutual shadow authentication capabilities which integrates polynomial-based SIS and visual secret sharing (VSS) through using the result of VSS to “guide” the polynomial-based SIS by a screening operation. In our scheme, when an authentication image is public, all involved actors (participants and dealer) can mutually authenticate each other by exchange the lowest level plane instead of the whole shadow. Our scheme is suitable for the case with and without a dealer participate recovery. In addition, the proposed scheme has characteristics of low generation and authentication complexity, no pixel expansion, 100% detection rate and lossless recovery.

1. Introduction

In a $(k,n)$ threshold secret image sharing (SIS) scheme, where $k\le n$, a secret image is divided into n shadow images without any secret information leakage, and it can be reconstructed only when a sufficient number of shadow images are combined together, but one cannot obtain any information of the secret image from fewer than k shadow images. There are two major categories in secret image sharing scheme: one is the visual secret sharing (VSS) [1,2] (i.e., visual cryptography), and the other is the polynomial-based secret image sharing [3]. The beauty of visual cryptography scheme (VCS) is the stack-to-see property, which indicates the secret can be visually recognized by human visual system (HVS) just with sufficient shares stacking. This natural property of VCS is based on OR operation, so it has several drawbacks, such as lossy recovery and low visual quality of recovered images. Shamir [3] designed the first $(k,n)$ threshold polynomial-based secret sharing method to achieve high quality of recovered secret images. Other research [4,5,6,7,8], based on Shamir’s work, developed some improved polynomial-based SIS schemes in order to get superior results.

The SIS schemes mentioned above have not taken the shadow authentication ability into account. However, many applications, such as e-voting, e-auctions, secret image sharing and audio sharing, are very dependent on verifiable secret sharing. The novelty of verifiable secret sharing is that it enables a dealer to divide a secret into n shares and allows shareholders to verify all received shadows of the secret without revealing what the secret and shares are. Primitive “verifiable secret sharing” was first used by Chor et al. [9]; they verified by simultaneous broadcast network. In the practical application of SIS, shadow authentication plays an increasingly important role. Through authentication, a dishonest participant can be identified by a combiner before secret reconstruction process, thereby saving time for the combiner. In general, there are three roles, namely, dealer, participant and combiner, in a secret image sharing scheme. The dealer is authorized to share a secret image and distributes the shares to the participants. Participants hold the shares assigned by a dealer, and finally, the combiner is given the function to choose the threshold or a higher number of participants and gather shares from them. The combiner may be one of the participants or the dealer, or another with the authority to recover the secret image from the collected shares. There are two types of verifiable secret sharing scheme: one is the interactive verifiable secret sharing, and the other is non-interactive verifiable secret sharing. In interactive verifiable secret sharing, all the participants and the dealer can exchange information with each other. In non-interactive verifiable secret sharing, only the dealer is allowed to send messages; in particular, the participants (shareholders) cannot talk with each other or the dealer when verifying a share.

Based on commitment property, Feldman [10] proposed verifiable secret sharing. The dealer checks whether the shares he/she gathered are generated from same polynomial. To verify the identity of each participant, the combiner performs the authentication of the shares submitted by the participants from the commitments, and when he/she detects any fake share submitted by a participant, the secret reconstruction process is halted by a broadcast that there is act of swindling. However, the scheme is based on the premise that a lot of information is public, which increases the risk of information disclosure. In Pedersen’s scheme [11] which uses the two entry commitment property, the combiner is considered honest, which not always be the case. Laih et al. [12] proposed a dynamic secret sharing scheme to change the number of participants dynamically. Charnes et al. [13] introduced the idea of hierarchical delegation within a secret sharing scheme, and they attempted to share secrets among the participants in different levels. Each scheme referred to involves not only the participants, but also an honest dealer.

Pioneer works [14] added a verification function to image secret sharing. Recently, in GF(251) based on improved polynomial-based SIS, Liu et al. [15] proposed an extended polynomial-based SIS for a $(k,n)$ threshold with shadow authentication. A secret image is divided into t blocks where each block includes $2k-2$ secret pixels. The dealer selects an integer, and generates two $k-1$ degree polynomials. The coefficient of the two polynomials satisfies certain conditions over $GF\left(251\right)$. For each block the dealer computes the sub-shadow. In the image reconstruction phase, they reconstruct the two $k-1$ degree polynomials using Lagrange interpolation respectively, and then they check if there is a common integer satisfying the conditions over $GF\left(251\right)$, and thus detect the cheating. However, it suffers from hard dishonest participant location, lossy reconstruction, auxiliary encryption, high generation complexity, high recovery complexity and high authentication complexity.

Recently, Hu et al. [16] proposed a verifiable secret sharing scheme suitable for the combinatorial auctions domain in which they represent the bidding price as a polynomial’s degree. Authors propose this scheme to counter conspiracy attacks which may implemented by a dishonest auctioneer and participant. Besides, multi-servers in the scheme are allowed to randomly choose secret shares and mutually verify the legitimacy of them. They use the degree of the sum/product of the two polynomials to construct the maximum/sum of the degree of two polynomials, and they utilize the verifiable secret sharing scheme to resist collusion attack. The shortcoming of the scheme is that if the number of nodes is large, the framework may not work, because the combinatorial auction’s winner determination problem is NP-complete.

One way to implement verifiable secret sharing is to use fragile watermarks. A fragile watermark can be easily destroyed, even the watermarked image is tampered with quietly. It is usually embedded in an image. Additionally, a fragile watermark is used to authenticate by inspecting the existence of the embedded signal in an image. In Wang’s verifiable secret sharing scheme [17], a watermark image with size of $n\times n$ was used with the secret image to generate shadows. Before reconstructing the secret image, the reliability from shadow images is determined by the accuracy of watermark image. Through determining the accuracy of watermark image, the recovered secret image could be verified. To slightly distort the quality of shadow, Lin and Tsai [18] embedded the shared bits and authentication bit in a four-pixel block. They combined information hiding and authentication features to prevent accidentally bringing an incorrect shadow or deliberately submitting a fake shadow by using the parity check bit. Unfortunately, parity checking bits lead to the leakage of the information of authentication, and dishonest participants can easily fake a shadow that easily passes validation. Besides the visual quality of the shadows is not good enough.

Yang et al. [19] improved the authentication by hashing the four-pixel block, block ID and image ID. They used a hash function to prevent participants from manipulating shadows. The shortcomings are high generation and authentication complexity and poor visual quality.

Yang et al. [20] presented a novel approach which is based on a symmetric bivariate polynomial without needing parity bits. In addition, their $(k,n)$ steganography and authenticated image sharing (SAIS) scheme provides better visual quality and has a higher detection ratio. They combine both authentication and secret sharing features into shared bits without needing additional authentication bits. The shortcoming of the scheme is that it generates a stegoimage four times larger than the secret image, which leads to the increase of storage space and transmission bandwidth.

Yan et al. [21] proposed a $(k,n)$ threshold SIS scheme capable of separate shadow authentication. Yan et al.’s work cleverly integrates polynomial-based SIS and visual secret sharing. They utilize $(2,2)$ RG-VSS to split every pixel of authentication image into two temporary bits. One is assigned to binary authentication shadow, and the other one guide to the generation of secret shadows in polynomial-based SIS. Their scheme has the ability of separate shadow authentication. It achieves low generation complexity, low recovery complexity, low authentication complexity, no pixel expansion and lossless recovery. However, their scheme is only suitable for the case with dealer.

In this paper, we propose a $(k,n)$ threshold SIS authentication with dealer-participatory and non-dealer-participatory mutual shadow authentication capabilities which integrates polynomial-based SIS and visual secret sharing (VSS) through using the result of VSS to “guide”the polynomial-based SIS. We input a public binary authentication image and a grayscale secret image into the proposed scheme to obtain n grayscale shadows when specifying 257 as a prime. The least significant bit (LSB) of each shadow pixel is exactly the value of the appropriate bit of binary authentication shadows generated by $(2,n)$ RG-VSS, and each shadow’s pixel value is less than 256 by selecting the random coefficients of the established polynomials. By Lagrange interpolation operation, the secret image is losslessly reconstructed, and the dealer and each participant are authenticated by only stacking or the XOR operation. All involved participants and the dealer can mutually authenticate other participants. Besides, in our scheme the participants only need to exchange the lowest level plane instead of the whole shadow, and only require an authentication image to be public. The proposed scheme has low generation complexity, low recovery complexity, low authentication complexity, no pixel expansion and lossless recovery. In order to validate the proposed scheme, we give illustrations, theoretical analyses and comparisons.

The following sections are organized as follows. In Section 2, we focus on preliminaries for our work. The motivation and contribution of our paper are described in Section 3. In Section 4, we present the proposed SIS scheme authentication with dealer-participatory and non-dealer-participatory mutual shadow authentication capabilities and its performance analysis in detail. Section 5 illustrates the details of the experiments and comparisons, and Section 6 is the conclusion.

2. Preliminaries

We introduce some preliminaries for our work in this section, including a traditional polynomial-based SIS scheme and random grid-based $(2,n)$ threshold VSS (RG-VSS). The conventional polynomial based SIS scheme means Shamir’s primitive polynomial-based secret sharing scheme, which is used as the foundation of our scheme to achieve a mutual shadow authentication, and a $(2,n)$ threshold RG-VSS is used to output n random bits from each binary authentication image pixel.

2.1. Polynomial-Based SIS Scheme

In 1979, Shamir [3] did a landmark job in which he constructed a $(k,n)$ threshold sharing algorithm by replacing the constant term $a_0$ of a $K-1$ degree polynomial with secret information and randomly selecting other coefficients of the polynomial. N shadow images ($f\left(i\right),fori=1,2,\cdots ,n.$) are generated by a dealer by using different variables (say i∈[1,n]). The polynomial is defined as

$$f\left(x\right)=(a_0+a_{1}x+\cdots +a_{k-1}{x}^{k-1})modP$$

(1)

where P is a prime number, the secret is $f\left(0\right)=a_0$ and $a_i$ is random, for $i=1,2,\cdots ,k-1$.

In the recovery phase, by using Lagrange interpolation, any k shadows can together rebuild this $k-1$ degree polynomial $f\left(x\right)$ following the Lagrange interpolation formula, and the secret information can be derived from $a_0=f\left(0\right)$. Less than k shadow images can not recover any secret information.

Due to a digital image being a special form of digital data, Shamir’s primitive polynomial-based secret sharing scheme can be directly applied to the sharing of images, and the prime P is generally set to 251. Figure 1 shows experimental results of $(3,4)$ threshold PSIS based on Shamir’s PSS. Figure 1a denotes secret image S. As is displayed in Figure 1b, one out of four shadow images $S{C}_1$ did not reveal any secrets. Figure 1c shows the recovered image $S_{t=2}^{\prime }$ with not enough shares, where $S_{t=2}^{\prime }$ represents recovery with any 2 shares. Images $S_{t=3}^{\prime }$ and $S_{t=4}^{\prime }$, which are similar to S, denote the recovered image with any three and four shares, respectively.

As shown in Figure 1d–e, there are black shadows in the recovered images. Since $p=251$, all the values in Equation (1) ($x,f\left(x\right),a_0,a_1,\cdots ,a_{k-1}$) are within the interval $[0,250]$. However, the grayscale image includes 256 gray levels from 0 to 255. As a result, pixel values from 251 to 255 can not be processed, so classic PSISs have lossy recovery. Besides, the classic PSISs have not take shadow authentication ability into account which leads to the shadows involved in recovery possibly being faked.

2.2. Random Grid-Based VSS – $(k,n)$ RG-VSS

It is necessary to review RG-VSS before introducing $(k,n)$ RG-VSS. In RG-VSS [22,23], “1” and “0” represent black and white pixel respectively. In what follows, symbols ⊗ and ⊕ denote the Boolean OR and XOR operations. The generation and recovering phases of a classical $(2,2)$ RG-VSS are given below.

Generating Step 1: Pseudo-randomly generate RG $S_1{C}_1$.

Generating Step 2: Calculate $S_1{C}_2$ as in Equation (2).

Recovering phase: ${S_1}^{\prime }=S_1{C}_1\otimes S_1{C}_2$ as Equation (3). For example, suppose the value of a secret pixel $s_1=S_1(h,w)$ of $S_1$ is 1; then, the recovered bit $S_1{C}_1\otimes S_1{C}_2=1$ is always black. While the value of a secret pixel is 0, the reconstructed bit $S_1{C}_1\otimes S_1{C}_2=S_1{C}_1(h,w)\otimes S_1{C}_1(h,w)$ has a 50% chance to be black or white since $S_1{C}_1$ is pseudo-randomly generated.

$$S_1{C}_2(h,w)=\left\{\begin{array}{c}{S}_1{C}_1(h,w)if{S}_1(h,w)=0\hfill \\ \overline{S_1{C}_1(h,w)}if{S}_1(h,w)=1\hfill \end{array}\right.$$

(2)

$$\begin{array}{cc}\hfill S_1^{\prime }(h,w)=& S_1{C}_1(h,w)\otimes S_1{C}_2(h,w)\hfill \\ \hfill =& \left\{\begin{array}{c}{S}_1{C}_1(h,w)\otimes S_1{C}_1(h,w)if{S}_1(h,w)=0\hfill \\ S_1{C}_1(h,w)\otimes \overline{S_1{C}_1(h,w)}=1if{S}_1(h,w)=1\hfill \end{array}\right.\hfill \end{array}$$

(3)

Equation (2) is equal to $S_1(h,w)=S_1{C}_1(h,w)\oplus S_1{C}_2(h,w)$. Thus, we can losslessly reconstruct $S_1(h,w)$ by Boolean XOR operation.

In [23], Yan et al. proposed a $(k,n)$ $\left(generallyn, k\in Z^{+}, 2\le k\le n\right)$ VSS based on RG. The generating phase of a typical $(k,n)$ RG-VSS are demonstrated in Algorithm 1.

Algorithm 1 $(k,n)$ RG-VSS.

Input: A $M\times N$ binary secret image S, a pair of threshold parameters $(k,n)$.

Output: n shadows $S{C}_i$, $i=1,2,\cdots n$.

Step 1: For each position $(h,w)\in \left\{\right(h,w\left)\right|1\le h\le M,1\le w\le N\}$, repeat Steps 2–4.

Step 2: Sequentially calculate $b_1$, $b_2$, ⋯, $b_k$ repeatedly using Equation (2) where $b_x$ is the provisional pixels,

$x=1,2,\cdots n-1,n$.

Step 3: Set $b_{k+1}=b_1$, $b_{k+2}=b_2$, ⋯ $b_{2k}=b_k$, $b_{2k+1}=b_1$, ⋯ if $\left(nmodk\right)=0$, $b_n=b_k$ else $b_n=b_{nmodk}$.

Step 4: Rearrangement $b_1$, $b_2$, ⋯, $b_n$ to $S{C}_1(i,j)$, $S{C}_2(i,j)$, ⋯, $S{C}_n(i,j)$ randomly.

Step 5: Output n shadows $S{C}_1,S{C}_2,\cdots S{C}_n$.

It is remarkable that the k bits are utilized to gain the threshold mechanism in Step 2, and Step 3 is designed to improve the visual quality of reconstructed secret image by a different way to use the last $n-k$ bits, through which the chance of covering $b_1$, $b_2$, ⋯, $b_k$ in the recovered t bits is improved. While Step 4 aims to make all the shadows be equal to each other, the generated n bits are rearranged to corresponding n shadow images.

The secret recovery of the scheme is also based on stacking or the HVS.

3. Motivation and Contribution

In our scheme, there are three roles, namely, dealer, participant and combiner, as described in Section 1. To simplify and make it easier to understand, we assume the combiner is one of the participants or the dealer in this paper. Additionally, it is assumed that the three roles all store the authentication image.

As shown in Figure 2, we give an example of the general application scenario regarding the $(k,n)$ threshold SIS with dealer-participatory and non-dealer-participatory mutual shadow authentication. For Case 1: $(k,n)$ threshold SIS with dealer-participation and no deception. Any k of the participants send their shadows; the dealer authenticates the k shadows and successfully recovers the secret image. For Case 2: $(k,n)$ threshold SIS with dealer-participation and deception. Any k of the participants send their shadows to the dealer; the dealer authenticates the k shadows, and then detects a fake shadow. The dealer stops the recovery phase and broadcasts the dishonest participant to the other participants. For Case 3: $(3,5)$ threshold SIS with no dealer-participation and no deception. Participant 1, Participant 2 and Participant 3 mutually send shadows to each other then authenticate each other. Every participant collects three shadows, and these shadows all pass authentication. Finally, every participant successfully recovers the secret image. For Case 4: $(3,5)$ threshold SIS with deception and no dealer-participation. Dishonest participant, Participant 2 and Participant 3 mutually send shadows to each other, and then authenticate each other. Every participant collects three shadows. Through authentication, Participant 2 and Participant 3 detect that the shadow sent by dishonest participant is fake. Then, Participant 2 and Participant 3 stop the recovery phase and broadcast the dishonest participant to Participant 4 and Participant 5. Of course, there may be multiple cheaters. Here we only give the example of the case where there is only one cheater.

Our motivation is to propose an SIS scheme which is suitable for shadow verification with and without a dealer. Further, it is great if the proposed scheme has characteristics of lossless recovery, low recovery complexity, low authentication complexity and no auxiliary encryption.

It is easy to think that it is the best case that any two participants can verify each other. It means that every honest participant’s detection rate of fake shadows is 100%. Based on the ability of mutual authentication ability, we can design a variety of shadow authentication protocols. For example, it is reasonable to design a shadow authentication protocol like majority rule. As described in Yang et al.’s work [20], majority rule is a decision rule that selects the valid shadows which have more than half the votes. Suppose that the k shadows are all valid. k participants exchange their shadows mutually; then, each participant authenticates other $k-1$ shadows and votes for them. If any one shadow gains less than $(k-1)$ votes, we stop recovery and proceed with the auxiliary authentication procedure of other $(n-k)$ participants. Remaining participants vote for these k shadows. If the shadow gains less than T votes from $(n-1)$ participants, we affirm this shadow as fake; otherwise it is valid. Here, we suppose more than half participants are honest. The maximum number of votes from other participants is $(n-1)$ votes. Therefore, a majority-voting threshold is chosen as $T=\lfloor (n-1)/2\rfloor$. Since $T=\lfloor (n-1)/2\rfloor =\lfloor n/2\rfloor$, it implies that we need a majority $T=\lfloor (n/2)\rfloor +1$ of trustworthy participants among all n participants to achieve the threshold.

For example, see Case 4 in Figure 2—$(3,5)$ for threshold SIS without a dealer when there is a dishonest participant. Suppose that Participant 2, Participant 3 and the dishonest participant send their shadows to each other at the same time. If every shadow gain two votes from other two participants, the shadows are authenticated successfully. Otherwise, we proceed with the authentication procedure with the help of Participant 4 and Participant 5.

In this paper, we propose a $(k,n)$ threshold SIS with dealer-participatory and non-dealer-participatory mutual shadow authentication which integrates polynomial-based SIS and visual secret sharing (VSS) through using the result of VSS to “guide” the polynomial-based SIS by screening operation. In this paper, we assume that the dealer can be both the producer and distributor of shadow and the combiner. In our scheme, all involved participants and the dealer can mutually authenticate other participants. If a dealer is responsible for recovering secret image, participants can verify the credibility of the dealer too. Our scheme is suitable for the case with and without dealer and only requires an authentication image to be public. If the recovery is done by entities other than the participants and the dealer, our scheme applies. Besides, in our scheme the participants only need to exchange the lowest level plane instead of the whole shadow. The proposed scheme has features of low generation complexity, low authentication complexity and no pixel expansion. It achieves lossless recovery and 100% detection rate. In terms of classification, our scheme uses the interactive verifiable secret sharing mentioned in Section 1.

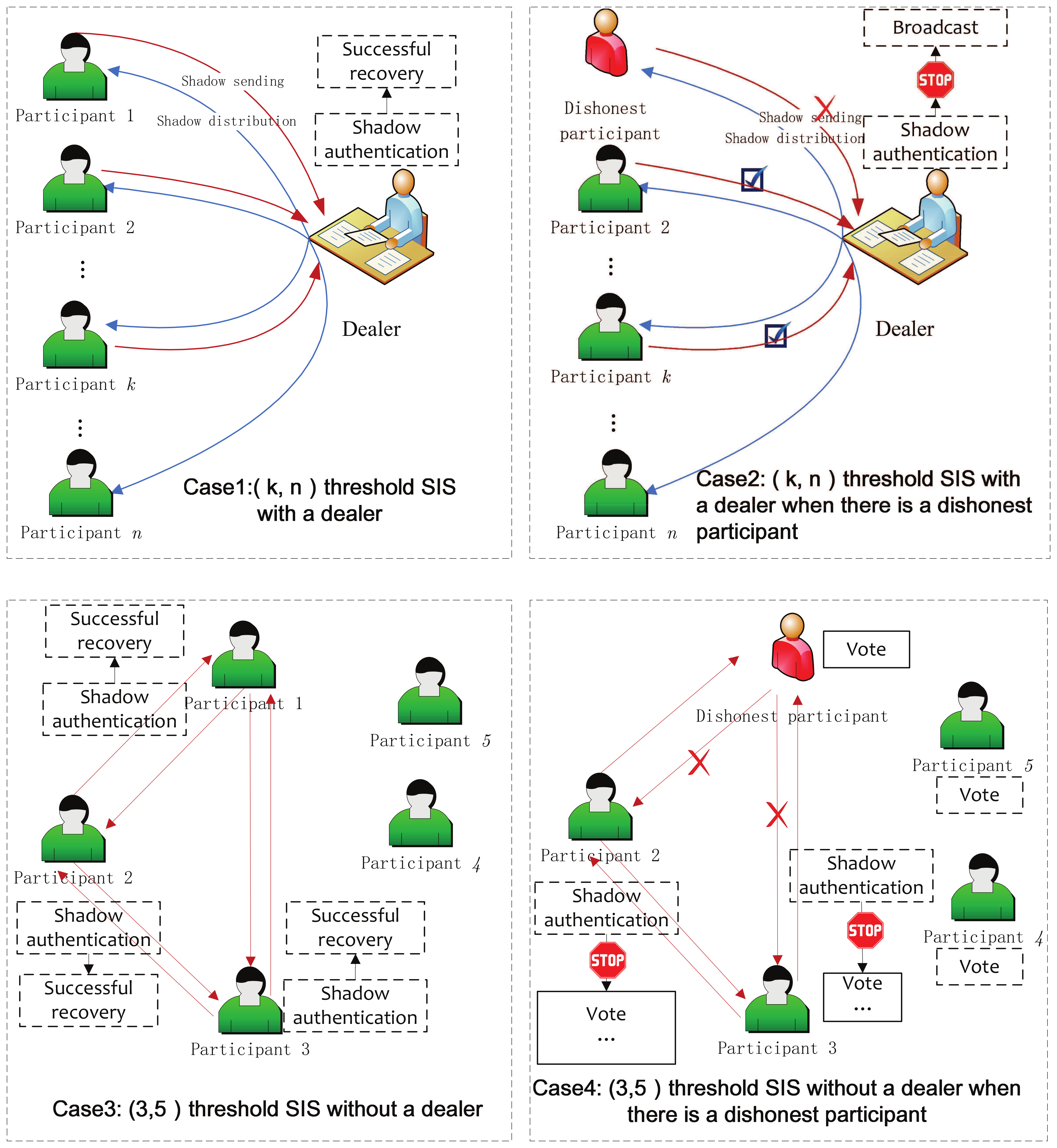
4. The Proposed $(\mathit{k},\mathit{n})$ SIS with the Mutual Shadow Authentication Ability

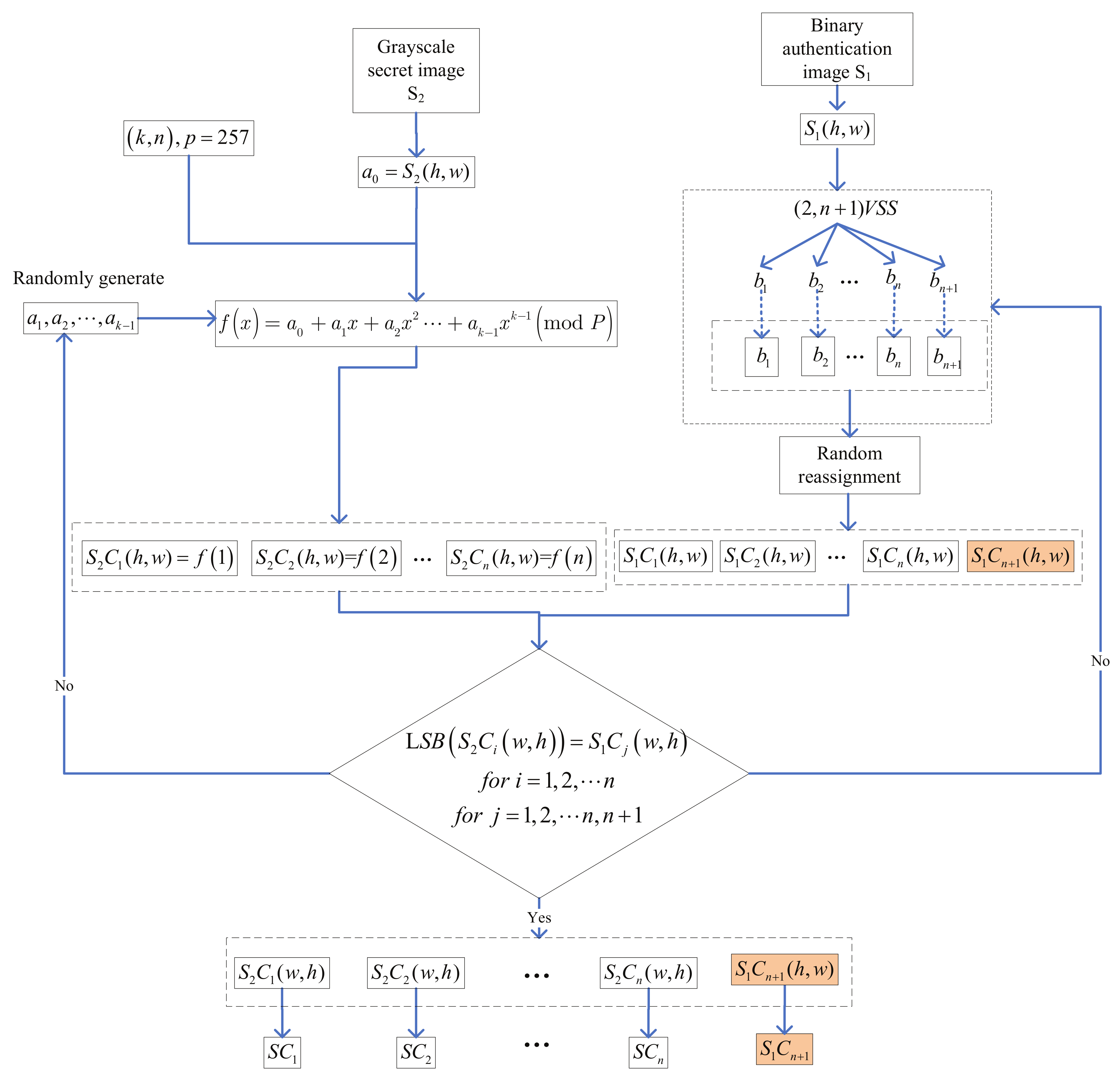
4.1. The Proposed Scheme

Figure 3 shows the design mentality of the proposed $(k,n)$ SIS authentication with dealer-participatory and non-dealer-participatory mutual shadow authentication capabilities. The explicit generating algorithm is illustrated in Algorithm 2, and its matching authentication and recovery algorithm is in Algorithm 3.

Algorithm 2 The proposed secret image sharing for $(k,n)$ threshold authentication with dealer-participatory

and non-dealer-participatory mutual shadow authentication capabilities.

Input: A H×W grayscale secret image $S_2$; a H×W binary authentication image $S_1$; the threshold parameters

$(k,n)$, where $2\le k\le n$.

Output: Shadow $S{C}_i$, $i=1,2,\cdots n$; a binary authentication shadow $S_1{C}_{n+1}$.

Step 1: Specify a prime number $P=257$. For each position $(h,w)\in \left\{\right(h,w\left)\right|1\le h\le H,1\le w\le W\}$,

repeat Steps 2–5.

Step 2: Utilize $(2,n+1)$ RG-VSS to split $S_1(h,w)$ to $n+1$ temporary bits, denoted by $b_1$, $b_2$, ⋯, $b_{n+1}$.

Randomly reassign $b_1$, $b_2$, ⋯, $b_{n+1}$ to $S_1{C}_1(h,w)$, $S_1{C}_2(h,w)$, ⋯, $S_1{C}_{n+1}(h,w)$.

Step 3: Construct a $k-1$ degree polynomial, as shown below. $$f\left(x\right)=(a_0+a_{1}x+\cdots +a_{k-1}{x}^{k-1})modP$$

where $a_0=S_2(h,w)$, $a_i$ is random, for $i=1,2,\cdots k-1$.

Compute $S_2{C}_i\left(h,w\right)=f\left(i\right)$, for $i=1,2,\cdots n$.

Step 4: Randomly pick up n numbers from $\{1,2,\cdots ,n,n+1\}$, scrambling these n numbers, denoted by

$\{i_1,i_2,\cdots ,i_n\}$. If $S_2{C}_i\left(h,w\right)<P-1$ and $LSB\left(S_2{C}_i\left(h,w\right)\right)=S_1{C}_j\left(h,w\right)$, for $i=1,2,\cdots n$,

$j=i_1,i_2,\cdots i_n$, go to Step 5 or go to Step 2.

Step 5: Specify $S_2{C}_i\left(h,w\right)$ to $S{C}_i\left(h,w\right)$, for $i=1,2,\cdots n$.

Step 6:n grayscale shadows $S{C}_1,S{C}_2,\cdots S{C}_n$ and a binary authentication shadow $S_1{C}_{n+1}$ which assigned

to the dealer if there exists are output.

Regarding Algorithm 2, we remark that:

1.

$S_1$ is a binary authentication image with size of $H\times W$ which is held or known by all participants involved and the dealer. In other words, $S_1$ is public.

2.

In Step 1, we set a prime number $P=257$; thus, in Step 4 $S_2{C}_i\left(h,w\right)<P-1$ to guarantee the value of the shadow pixel is within $[0,255]$ and lossless recovery by utilizing the screening operation.

3.

Step 3 aims at guaranteeing the $(k,n)$ threshold attribute and no pixel expansion by using the polynomial.

4.

Step 4 is designed to satisfy $LSB\left(S_2{C}_i\left(h,w\right)\right)=S_1{C}_j\left(h,w\right)$ to achieve mutual shadow authentication.

5.

Since $a_1,a_2,\cdots ,a_{k-1}$ and $b_1$ are random, when $n-k$ is small, we can find a set of random values to satisfy $S_2{C}_i\left(h,w\right)<P-1$ and $LSB\left(S_2{C}_i\left(h,w\right)\right)=S_1{C}_j\left(h,w\right)$, for $i=1,2,\cdots n$, $j=i_1,i_2,\cdots ,i_n$ (randomly pick up n numbers from $\{1,2,\cdots ,n,n+1\}$, Scrambling these n numbers, denoted by $\{i_1,i_2,\cdots ,i_n\}$) in Step 4. This way, $S_2$ can be losslessly recovered and mutual shadow authentication ability can be realized.

Algorithm 3 The authentication and recovery in the proposed secret image sharing for $(k,n)$ threshold

authentication with dealer-participatory and non-dealer-participatory mutual shadow authentication

capabilities.

Input: The binary authentication image $S_1$ and dealer’s binary authentication shadow $S_1{C}_{n+1}$, any k

grayscale shadows $S{C}_{i_1},S{C}_{i_2},\cdots S{C}_{i_k}$.

Output: k authenticating results of $S{C}_{i_j}$ for $j=1,2,\cdots ,k$ or $(k-1)$ authenticating results of $S{C}_{i_j}$

for $j=1,2,\cdots ,k$ for each participant involved depends on there is a dealer participant or not.

Recovered grayscale secret image $S_2^{\prime }$ with a size of H×W.

Step 1: If there is a dealer, for $j=1,2,\cdots ,k$, take the LSB (least significant bit) of $S{C}_{i_j}$, denoted by

$S_1{C}_1$, obtain the reconstructed binary authentication image $S_1^{\prime }$ through the stacking or XORing

operation of $S_1{C}_1$ and $S_1{C}_{n+1}$. If $S_1^{\prime }$ is recognized as $S_1$ by HVS or $S_1^{\prime }=S_1$, pass the authentication

and go to Step 3; otherwise, a fake shadow is identified, denoted by $i_j^{*}$, and broadcast the dishonest

participant to the other participants.

Step 2: If there is not a dealer involved, take the LSB (least significant bit) of the participant itself’s

shadow, denoted by $S_1{C}_1$, take the LSB (least significant bit) of $S{C}_{i_j}$ for $j=1,2,\cdots ,k$, denoted by

$S_1{C}_{i_j}$ for $j=1,2,\cdots ,k-1$, obtain the reconstructed binary authentication image $S_1^{\prime }$ through the

stacking or XORing operation of $S_1{C}_1$ and $S_1{C}_{i_j}$. If all the $S_1^{\prime }$ are recognized as $S_1$ by HVS or $S_1^{\prime }=S_1$,

pass the authentication and go to Step 3; otherwise, a fake shadow is identified, denoted by $i_j^{*}$,

and broadcast the dishonest participant to the other participants.

Step 3: For each position $(h,w)\in \left\{(h,w)|1\le h\le H,1\le w\le W\right\}$, repeat Steps 4–5.

Step 4: Solve the following equation to get $a_0$ by Lagrange interpolation function. $$\begin{array}{c}\hfill f\left(i_1\right)=(a_0+a_{}{i}_1+\cdots +a_{k-1}{i_1}^{k-1})modP\\ \hfill f\left(i_2\right)=(a_0+a_{}{i}_2+\cdots +a_{k-1}{i_2}^{k-1})modP\\ \hfill \cdots \\ \hfill f\left(i_{k-1}\right)=(a_0+a_{}{i}_{k-1}+\cdots +a_{k-1}{i_{k-1}}^{k-1})modP\\ f\left(i_k\right)=(a_0+a_{}{i}_k+\cdots +a_{k-1}{i_k}^{k-1})modP\\ \hfill \end{array}$$

Step 5: Compute $S_2^{\prime }(h,w)=a_0$.

Step 6: Output recovered grayscale secret image $S_2^{\prime }$ with a size of H×W and k authenticating results of

$S{C}_{i_j}$ for $j=1,2,\cdots ,k$ or $(k-1)$ authenticating results of $S{C}_{i_j}$ for $j=1,2,\cdots ,k$ for each

participant.

For Algorithm 3, we note the following.

1.

If there is a dealer, the dealer generates k authenticating results of $S{C}_{i_j}$ for $j=1,2,\cdots ,k$. If there is not a dealer, each participant involved generates the $(k-1)$ authenticating result of $S{C}_{i_j}$ for $j=1,2,\cdots ,k$. When we mention each participant involved, it means k participants in the final recovery.

2.

The LSB of $S{C}_{i_j}$ can be gotten by bitwise operation.

3.

In Step 1, dealer or participants authenticate each gathered shadow to estimate whether $S_1^{\prime }$ is recognized as $S_1$ by HVS or $S_1^{\prime }=S_1$; thus, mutual shadow authentication is achieved by stacking or XOR operation.

4.

In Step 2, every participant involved authenticates other $(k-1)$ participants’ shadows. $S{C}_{i_j}$ for $j=1,2,\cdots ,k-1$ denote shadows held by other $(k-1)$ participants. Each participant involved takes his/her shadow’s LSB, denoted by $S_1{C}_1$. The other $(k-1)$ participants involved take their shadows’ LSBs, denoted by $S_1{C}_{i_j}$ for $j=1,2,\cdots ,k-1$. Since authentication is performed in pairs in our scheme, we achieve mutual shadow authentication.

5.

In Step 2, every participant involved authenticates other $(k-1)$ participants’ shadows. So if $k\times \left(k-1\right)$ $S_1^{\prime }$ are recognized as $S_1$ by HVS or $S_1^{\prime }=S_1$, pass the authentication and go to Step 3.

6.

In Step 2, when detecting a fake shadow, the participant broadcasts the dishonest participant to the other participants and stops recovery phase. Here, the scheme supposes that the participant performing shadow authentication is honest. There is no further discussion on how to authenticate and recover in the case of more than one dishonest participant in our scheme. In this paper, we focus on designing a SIS with mutual authentication capability, rather than the rules or protocols of mutual authentication among participants. However, one can design many protocols for authentication and recovery based on the proposed scheme with mutual authentication ability. For example, one can design to allow participants to perform authentication by using a vote-based protocol. Every participant authenticates other shadows, and decides whether to vote for the shadows. According to the result of a majority vote, the authenticity of the shadows is then determined by peers.

Here we will give a simple numerical example of $(3,4)$ threshold to illustrate the algorithm process of our scheme. Let us take the current processing positions $S_1(h,w)=0$ and $S_2(h,w)=161$ as an example.

In the generation phase, use $(2,5)$ RG-VSS to divide $S_1(h,w)$ into [0, 0, 0, 0, 0]. Assign $S_1{C}_1(h,w)=0$, $S_1{C}_2(h,w)=0$, $S_1{C}_3(h,w)=0$, $S_1{C}_4(h,w)=0$ and $S_1{C}_5(h,w)=0$; $S_1{C}_5(h,w)$ is always assigned to the dealer if one exists. Construct a 2-degree polynomial as $f\left(x\right)=(161+a_{1}x+a_2{x}^2)mod257$. Screen $a_1$ and $a_2$ to satisfy $S_2{C}_i\left(h,w\right)<256$ and $LSB\left(S_2{C}_i\left(h,w\right)\right)=1$, for $i=1,2,\cdots n$; for example, $a_1=229$ and $a_2=216$. Then, the corresponding shadow pixel values are $S_2{C}_1\left(h,w\right)=32$, $S_2{C}_2\left(h,w\right)=64$, $S_2{C}_3\left(h,w\right)=172$ and $S_2{C}_4\left(h,w\right)=248$.

In the authentication phase, when the dealer is responsible for verifying and recovering images, assume $S_1{C}_i(h,w)=LSB\left(S{C}_i(h,w)\right)$, for $i=1,2,\cdots ,5$. To authenticate $S{C}_1$, obtain the recovered binary authentication image $S_1^{\prime }$ through the stacking or XORing operation of $S_1{C}_1$ and $S_1{C}_5$; if all the $S_1^{\prime }$ are recognized as $S_1$ by HVS or $S_1^{\prime }=S_1$, pass the authentication. When there is not a dealer, suppose Participant 1 and Participant 2 who hold $S{C}_1$ and $S{C}_2$ respectively mutually verify each other. To authenticate $S{C}_1$ and $S{C}_2$, obtain the recovered binary authentication image $S_1^{\prime }$ through the stacking or XORing operation of $S_1{C}_1$ and $S_1{C}_2$; if all the $S_1^{\prime }$ are recognized as $S_1$ by HVS or $S_1^{\prime }=S_1$, pass the authentication.

In the recovery phase, when two shadows (such as $S{C}_1(h,w)=32$ and $S{C}_2(h,w)=64$) are gathered, solve $f\left(1\right)=(a_0+a_1)mod257$ and $f\left(2\right)=(a_0+2a_1)mod257$ to obtain $a_0=113$ by Lagrange interpolation; thus, the recovery fails; when $S{C}_1(h,w)=32$, $S{C}_2(h,w)=64$ and $S{C}_3(h,w)=172$ are collected, solve $f\left(1\right)=(a_0+a_1+a_2)mod257$, $f\left(2\right)=(a_0+2a_1+4a_2)mod257$ and $f\left(3\right)=(a_0+3a_1+9a_2)mod257$ to obtain $a_0=161$ by Lagrange interpolation; thus, the recovery is successful.

4.2. Security Analysis, Time and Space Complexity Analyses and Performance Proof

Herein, we provide the performance and security analysis of the proposed $(k,n)$ threshold SIS authentication with dealer-participatory and non-dealer-participatory mutual shadow authentication capabilities. In the next analyses, we suppose that the authentication image $S_1$ and the secret image $S_2$ are natural images, and they have no relevance.

We denote the gathered any k grayscale pixels as $s{c}_{i_1},s{c}_{i_2},\cdots s{c}_{i_k}$ in the recovery phase corresponding to $S{C}_{i_1}(h,w),S{C}_{i_2}(h,w),\cdots S{C}_{i_k}(h,w)$. $s_1$ and $s_2$ mean $S_1(h,w)$ and $S_2(h,w)$, respectively.

Lemma 1.

$s_2$ can be within $[0,255]$, and $s{c}_i$ is restricted to $[0,255]$ where $i=1,2,\cdots n$.

Proof. 

Due to $P=257$, $s_2$ is limited within $[0,255]$. $S_2{C}_i\left(h,w\right)<P-1$, $s{c}_i$ is limited within $[0,255]$ for $i=1,2,\cdots n$. □

Lemma 2.

One can losslessly recover the secret pixel $s_2$ with $s{c}_{i_1},s{c}_{i_2},\cdots s{c}_{i_k}$.

Proof. 

Using the equation mentioned in Algorithm 3 and the Lagrange interpolation, we can calculate the value of $a_0$ and $a_i$ uniquely for $i=1,2,\cdots k-1$. Based on the Lemma 1, since $s_2=a_0<P$, $s_2$ can be recovered with $s{c}_{i_1},s{c}_{i_2},\cdots s{c}_{i_k}$ without distortion. □

Theorem 1.

Using $S{C}_i$, $S_1$ and $S{C}_{i_j}$ ($S_1{C}_{n+1}$), we can recognize whether $S{C}_i$ is fake, for $i=1,2,\cdots n$.

Proof. 

In Step 4 of Algorithm 2, we make $LSB\left(S{C}_i\left(h,w\right)\right)=S_1{C}_1\left(h,w\right)$, $LSB\left(S{C}_i\right)=S_1{C}_1$, $LSB\left(S{C}_{i_j}\left(h,w\right)\right)=S_1{C}_{i_j}\left(h,w\right)$ and $LSB\left(S{C}_{i_j}\right)=S_1{C}_{i_j}$. According to $(k,n)$ RG-VSS [23], we can visually reveal $S_1$ by stacking and XORing $S_1{C}_1$ and $S_1{C}_{i_j}$ ($S_1{C}_{n+1}$). According to Equation (2), the probability of correctly inferring $S_1{C}_1$ is ${(1/2)}^{HW}$. As a result, using $S{C}_i$, $S_1$ and $S_1{C}_{i_j}$ ($S_1{C}_{n+1}$), we can judge whether $S{C}_i$ is fake for $i=1,2,\cdots n$. □

Lemma 3.

When gathering $k-1$ or fewer shadows, The secret image $S_2$ cannot be recovered.

Proof. 

If only $k-1$ equations are built in the equation mentioned in Algorithm 3, we have P solutions rather than only one to the equation mentioned in Algorithm 3. Thus, the secret image $S_2$ cannot be recovered when gathered $k-1$ or fewer shadows. □

5. Experimental Results and Discussion

In this section, we implement a set of experiments to verify the effectiveness of the proposed $(k,n)$ threshold SIS authentication with dealer-participatory and non-dealer-participatory mutual shadow authentication capabilities in which we set the value of n from 2 to 5, and the value of k from 2 to n accordingly. Then, comparisons with related scheme will be given to show the features of our scheme. In the future, we intend to use machine learning (i.e., [24]) to perform shadow verification.

5.1. Experimental Illustration

Due to the characteristics of no pixel expansion of the proposed SIS, all the experimental images are have same size $128\times 128$ in our experiments. Here we only introduce the experimental results of $(2,2)$ threshold and $(3,4)$ threshold SIS with dealer-participatory and non-dealer-participatory mutual shadow authentication ability.

Figure 4 exhibits the results of $(3,4)$ threshold SIS authentication with dealer-participatory and non-dealer-participatory mutual shadow authentication capabilities, the binary authentication image $S_1$ is shown in Figure 4a and the input secret image $S_2$ which is grayscale is displayed in Figure 4e. Figure 4b–d denotes the output binary shadows $S_1{C}_1$, $S_1{C}_2$, $S_1{C}_3$, where $S_1{C}_3$ is the binary authentication shadow assigned to the dealer. Figure 4f–g presents the outputs of two shadows $S{C}_1$ and $S{C}_2$. Figure 4h illustrates a fake shadow which is denoted by $S{C}_1^{*}$. Figure 4i–l denotes the recovered binary authentication images obtained through the stacking and XORing operations of $S_1{C}_3$ and $S{C}_1$, $S{C}_2$, respectively, where the recovered binary authentication image can be well recognized; thus, the shadows $S{C}_1$ and $S{C}_2$ are authenticated by the dealer. Meanwhile, participants holding the shadows $S{C}_1$ and $S{C}_2$ can verify the credibility of the dealer responsible for recovering secret image. Figure 4m,n denotes the recovered binary authentication images obtained through the stacking and XORing operations of $S{C}_1$ and $S{C}_2$, respectively, where the recovered binary authentication image can be well recognized; thus, the shadows $S{C}_1$ and $S{C}_2$ are authenticated. In other words, the two participants are mutually authenticated successfully. Suppose there is an attacker posing as Participant 1, or that Participant 1 is an dishonest participant who sends a fake shadow $S{C}_1^{*}$ to other participants or the dealer. The recovered binary authentication images with $S{C}_1^{*}$ and $S{C}_1$, $S{C}_2$ by stacking and XORing, respectively, are presented in Figure 4o–r, and it is obvious that the binary authentication image is not disclosed or recovered, and thus the shadow $S{C}_1^{*}$ is fake. Figure 4s exhibits the secret image reconstructed with the two shadows by Lagrange interpolation, and we can see that the secret image is reconstructed losslessly. Figure 4t demonstrates the secret image recovered with $S{C}_1^{*}$ and $S{C}_2$ by Lagrange interpolation operation, which is not recognized as the secret image; thus, the recovery is failed. Additional instructions are needed here. In our scheme, participants exchange and authenticate their shadows’ LSB planes mutually in the case of non-dealer-participation. In the case of dealer-participation, the dealer authenticates the LSB planes of shadows sent by participants. Thus, the $S{C}_1$ and $S{C}_2$ we are talking about here are actually the LSB planes of them.

Figure 5 exhibits the results of $(3,4)$ threshold SIS authentication with dealer-participatory and non-dealer-participatory mutual shadow authentication capabilities. The input binary authentication image $S_1$ is shown in Figure 5a. Figure 5c shows the input grayscale secret image $S_2$. Figure 5b denotes the output binary authentication shadow $S_1{C}_5$. Figure 5d–g presents the output 4 shadows. Suppose $S{C}_1$, $S{C}_2$ and $S{C}_3$ are specified to recover the secret image. When the dealer is in charge of the authentication, he/she takes his/her binary shadow and the shadow (the LSB plane of shadow) sent to him/her by the participant to perform stacking and XORing. Figure 5h–m denotes the binary authentication images recovered through the stacking and XORing operations of $S_1{C}_5$ and $S{C}_1$, $S{C}_2$, $S{C}_3$, respectively, where the recovered binary authentication image can be well recognized, and thus the three shadows are authenticated. Meanwhile, participants holding the shadows $S{C}_1$, $S{C}_2$ and $S{C}_3$ can verify the credibility of the dealer responsible for recovering secret image. When there is not a dealer, the participants holding $S{C}_1$ or $S{C}_2$ or $S{C}_3$ mutually authenticate each other. Figure 5n–s shows binary authentication images mutually recovered through the stacking and XORing operations of $S{C}_1$, $S{C}_2$ and $S{C}_3$, respectively, where the recovered binary authentication image can be well recognized; thus, the shadows $S{C}_1$, $S{C}_2$ and $S{C}_3$ are authenticated. In other words, the three participants are mutually authenticated successfully. Figure 5t shows the secret image recovered with the three shadows by Lagrange interpolation, and we can see that the secret image is reconstructed losslessly.

Figure 6 exhibits the results of our proposed $(3,4)$ threshold SIS authentication with dealer-participatory and non-dealer-participatory mutual shadow authentication capabilities, when there is a fake shadow participating in recovery. A randomly generated fake shadow, denoted by $S{C}_1^{*}$, is illustrated in Figure 6a. Suppose there is an attacker posing as Participant 1 or Participant 1 is an dishonest participant who sends a fake shadow $S{C}_1^{*}$ to other participants or dealer. The binary authentication images recovered $S{C}_1^{*}$, $S{C}_2$ and $S{C}_1$ by stacking and XORing, respectively, are presented in Figure 6b–e, and the binary authentication images are not correctly identified; thus the shadow $S{C}_1^{*}$ is fake. Figure 6f demonstrates the recovered secret images $S_2^{*}$ with $S{C}_1^{*}$ and $S{C}_2$, $S{C}_3$ by stacking and XORing, respectively by Lagrange interpolation, which displays no secret information; thus, the recovery is failed.

According to the above experimental results, we draw the following conclusions:

1.

The shadow generated by our scheme has no cross-interference and no pixel expansion of the secret image.

2.

Figure 7 shows the security of the proposed SIS when recovered with fewer than k shadows; the recovered image leaks no secret details.

3.

One can losslessly reconstruct the secret image with any number k or more of shadows.

4.

The binary authentication image is lossily reconstructed, so one can carry out authentication by only stacking or XORing operation.

5.

The mutual authentication ability is gained based on SIS itself rather than another technique.

6.

An SIS with dealer-participatory and non-dealer-participatory mutual shadow authentication for a general $(k,n)$ threshold is achieved, where $n\ge k\ge 2$. Since when k is fixed, as n increases more requirements should be satisfied. Through experiments, we give the suggestion that the condition is $\frac{n-k}{n}\le \frac{3}{5}$.

Moreover, in Algorithm 2, we use $(2,n+1)$ RG-VSS to split every pixel of authentication image into $n+1$ temporary bits; one is assigned to binary authentication shadow, and the others are used to guide the generation of secret shadows in polynomial-based SIS. The specific guidance method is as follows: we continue to screen $a_1,a_2,\cdots ,a_{k-1}$ until we find a set of random values to satisfy $S_2{C}_i\left(h,w\right)<P-1$ and $LSB\left(S_2{C}_i\left(h,w\right)\right)=S_1{C}_j\left(h,w\right)$, for $i=1,2,\cdots n$, $j=i_1,i_2,\cdots ,i_n$ (randomly pick up n numbers from $\{1,2,\cdots ,n,n+1\}$. So, what we change and influence are the LSBs of the shadows generated by the polynomial-based SIS, and the shadow itself is noise like, so it is difficult to be detected even if we modify the LSBs of all pixels of all shadows. Figure 8 shows that the shadows are randomly generated by the polynomial-based SIS.

5.2. Comparisons with Relative Schemes

Herein, we will compare the proposed SIS with Yan et al.’s work [21].

1.

Inspired by Yan et al.’s work [21], we improve the SIS scheme to be suitable for the case with and without dealer by extending the sharing method of the authentication image from $(2,2)$ RG-VSS to $(2,n+1)$ RG-VSS. Yan et al. utilize the $(2,2)$ RG-VSS to split every pixel of authentication image into two temporary bits; one is assigned to binary authentication shadow, and another one guides the generation of secret pixels in polynomial-based SIS. We use $(2,n+1)$ RG-VSS to split every pixel of authentication image into $n+1$ temporary bits; one is assigned to the binary authentication shadow, and the others are used to guide the generation of secret shadows in polynomial-based SIS. Thus, in our scheme, any actor (participants or dealer) can be specified as a combiner. Yan et al.’s scheme works when there is a dealer.

2.

As shown in Figure 9, when we share extreme image Figure 9a by Yan et al.’s and our $(2,3)$ threshold SISs respectively, we can see through our eyes that the shadows (Figure 9b–d) generated by Yan et al.’s reveal the secret, while ours (Figure 9e–g do not). The reason is that we use the pixels generated by $(2,n+1)$ RG-VSS to guide the LSBs of pixels generated by the polynomial-based SIS, while Yan et al. use the pixels generated by $(2,2)$ RG-VSS to guide the MSBs of pixels generated by the polynomial-based SIS. Besides, based on the above Lemmas 2 and 3, the conditions are satisfied. Unfortunately, Yan et al.’s use MSBs of pixels, which is the most significant bit, may cause information disclosure when $n-k$ gets larger and larger. In contrast, we use the LSB, which will be better.

3.

Due to the characteristics of $(2,2)$ RG-VSS and $(2,n+1)$ RG-VSS, in the authentication phase, the shadow passes verification when the binary authentication image is always well recognized in our scheme. The shadow passes verification when the binary authentication image recovered respectively, by stacking or XORing, is always well recognized or losslessly recovered in Yan et al.’s scheme.

Besides, we compare the proposed SIS with Bhattacharjee et al.’s work [25]. Bhattacharjee et al. propose an image-in-image communication scheme which is a data-hiding-based SIS scheme. The process includes encoding and decoding stages. In the encoding stage, they first M-bit signal modulates all the pixels of the secret image, and then n shadows of reduced size are generated by their shadow generation algorithm; finally stegoimages are generated by a series of steps which include generation of Walsh code, a block-based discrete cosine transform (DCT) operation, SS embedding and an inverse DCT transformation operation. It should be noted that the SS embedding in Bhattacharjee et al.’s work means spread spectrum watermarking which is used to resist attacks and unexpected operations. Correspondingly, the decoding stage includes the share image’s extraction (the stegoimage’s decomposition, correlation calculation and secret rearrangement) and secret reconstruction.

The comparisons between the proposed scheme and Bhattacharjee et al.’s scheme are summarized as follows.

1.

The proposed scheme is $(k,n)$ threshold SIS scheme. Contrarily, the scheme in Bhattacharjee et al.’s [25] work is $(n,n)$ threshold.

2.

Bhattacharjee et al. embed the shares into several cover images; this leads to the need to extract shares from stegoimages during the recovery phase, and thus increases decoding complexity. Contrarily, we do not use a cover image at all. In addition, Bhattacharjee et al.’s scheme generates shadows of reduced size in the encoding phase by using a kind of encryption technology which increases encoding complexity.

3.

Bhattacharjee et al.’s scheme has the characteristics of no key requirements but several cover image requirements, while our scheme only requires an authentication image to be public.

Table 1. Comparison of our scheme, Yan et al.’s scheme [21] and Bhattacharjee et al.’s scheme [25].

Properties	Our Scheme	Yan et al. [21]	Bhattacharjee et al. [25]
Threshold	$(k,n)$	$(k,n)$	$(n,n)$ progressive quality access
Dealer participatory	No	Yes	No
Verification operation	VCS(OR/XOR)	VCS(OR/XOR)	Watermark
Recovery operation	Lagrange interpolation	Lagrange interpolation	Pixel rearrangement
Cover images	No	No	Yes
Pixel expansion	No	No	No (reduced shadow size)
Technology	Polynomial-based SIS and $(2,n+1)$ RG-VSS	Polynomial-based SIS and $(2,2)$ RG-VSS	Data hiding

shows the comparison of the properties between our scheme and the schemes proposed in [21,25].

In particular, compared with traditional schemes, the proposed SIS for the $(k,n)$ threshold achieves the features of mutual shadow authentication, low recovery operation, no pixel expansion and lossless recovery. Besides, in our scheme the actors only need to exchange the lowest level plane instead of the whole shadow, and it only requires an authentication image to be public.

6. Conclusions

In this paper, the proposed SIS for a $(k,n)$ threshold authentication with dealer-participatory and non-dealer-participatory mutual shadow authentication capabilities integrates polynomial-based SIS and visual secret sharing (VSS) through using the result of VSS to "guide" the polynomial-based SIS by screening operation. We input a public binary authentication image and a grayscale secret image into the proposed scheme to obtain n grayscale shadows when specifying 257 as a prime. The least significant bit (LSB) of each shadow pixel is exactly the value of the appropriate bit of binary authentication shadows generated by $(2,n)$ RG-VSS, and each shadow’s pixel value is less than 256 by selecting the random coefficients of the established polynomials. In our scheme, we can assign any participant as a combiner. By Lagrange interpolation operation, the secret image is losslessly reconstructed, and the dealer and each participant are authenticated by only stacking or XORing operation. All involved participants and the dealer can mutually authenticate other participants. Besides, in our scheme the participants only need to exchange the lowest level plane instead of the whole shadow, and it only requires an authentication image to be public. The proposed scheme has low generation complexity, low recovery complexity, low authentication complexity, no pixel expansion, lossless recovery and a 100% detection rate.