A Virus Infected Your Laptop. Let’s Play an Escape Game
Abstract
1. Introduction
2. Engaging and Motivating Students with Escape Games
3. Description of the Breakout
3.1. History
3.2. Material
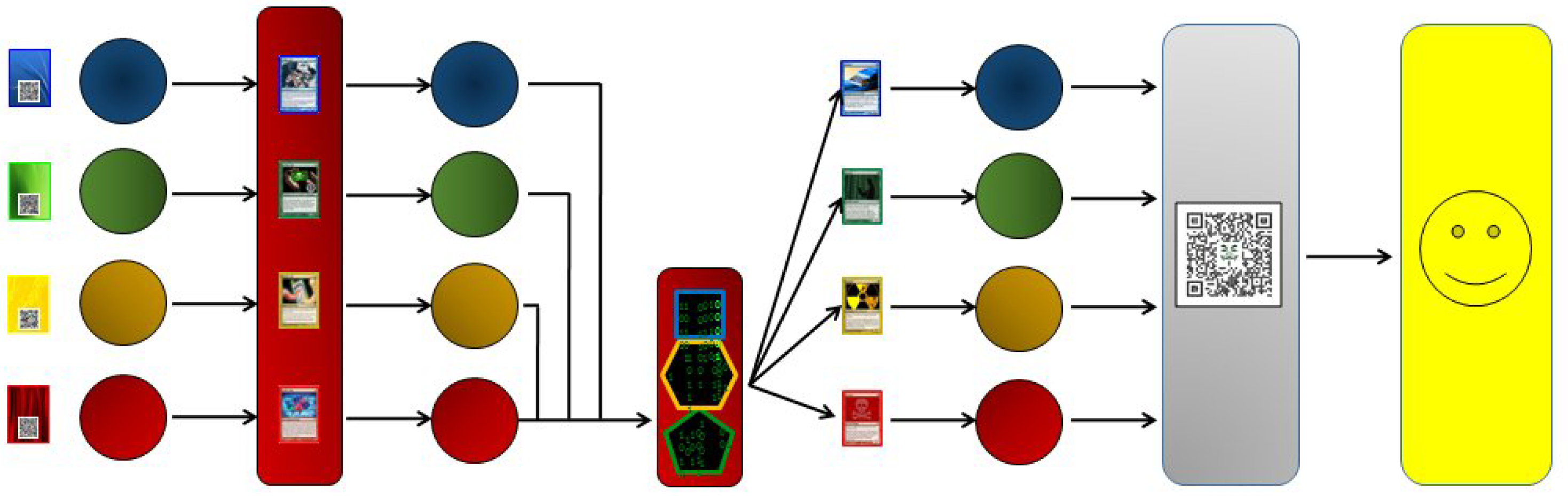
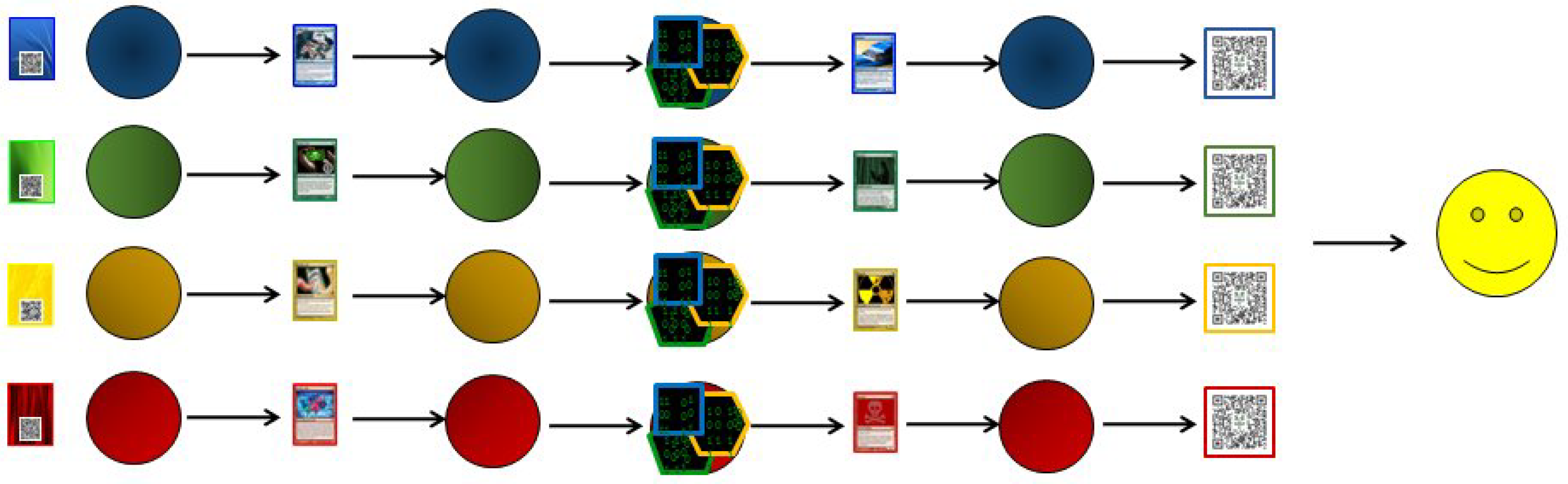
- Blue, red, green, and yellow Magic cards with different figures and text written on them. All of them with the name of different malware.
- Black and purple border Magic cards. These are clue cards to help gamers.
- A Domino game.
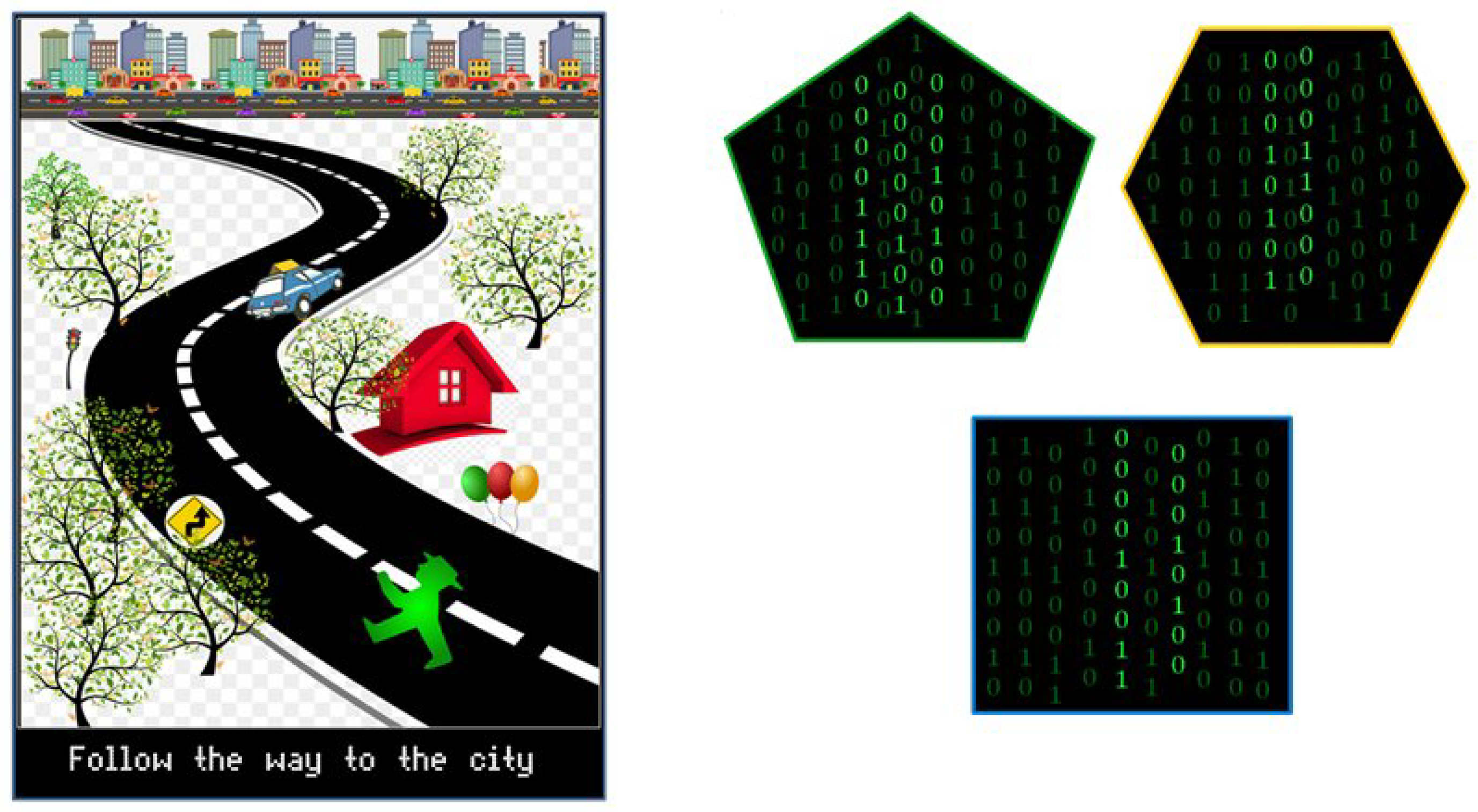
- Black Matrix figures: a square, a hexagon, and a pentagon with some 0’s and 1’s similar to the Matrix film.
- Some boarding cards like the one shown in Figure 3 belonging to Isaac Newton, Leonardo De Pisa, Albert Einstein, Evariste Galois, etc.
- Some other riddles and puzzles.
- The HP Reveal App will be needed during the breakout. This augmented reality application triggers overlays when the smartphone scans a selected image. Gamers are told that they will need this App and that they must follow the gamemaster’s account (if they don’t do it, it will not work).
3.3. First Step: Riddle from Identification Cards
- Blue riddle: September, 2019; November, 2015; June, 1969; August, 1999; October, 2000. What have these dates in common? (All those months have the same weekday for the 13th, which is Friday).
- Green riddle is to solve a system of linear equations and find the value of y: ; ; .
- Yellow riddle is to solve a second-order equation: Find the x-coordinate where the parabola cuts the line . Although the answer is double: and 13, there is no malware’s name related to .
- Red riddle: We are looking for information in these books: Algebra, page 85; Calculus, page 184; Statistics, page 229; Numerical methods, page 76. What do these pages have in common? (The sum of the digits of each page is the same: 13).
3.4. Second Step: Riddle from Friday 13th Cards
- Results from green, yellow, and blue teams are numbers.
- Red team will use these numbers and the “green man” riddle to find the order of black Matrix figures to get the name of the next malware.
- Blue card image hides a domino piece. This team must play domino and find a number after some derivation and integration operations. The final number is 6.
- Green card image includes the U.S. National Security Agency logo. The real logo says “NATIONAL SECURITY AGENCY” and “UNITED STATES OF AMERICA”, but the game’s logo has changed the second sentence to “QR CODE - ALBERT EINSTEIN”. Gamers must look for some other material related to Albert Einstein, i.e., the boarding card. The card QR code leads us to an Adobe Spark video where we can see a man (similar to Einstein) that says: “The number that you are looking for is number four”.
- Yellow card contains the information: “magic card game” and something about this cards game: “You will lose if you lose all your cards”. Among the materials that are available for all players, there is a riddle with the figure of a Magic card game in a table (see Figure 5). The answer to this riddle is 5.
- Red card: from the road map, players know that red team needs the numbers found by the rest of teams (6, 4, and 5), and the “green man” riddle to find the order of black Matrix figures (see Figure 6) to get the name of the next malware. This is a difficult riddle because gamers must pay attention to the green man and realise that green, yellow, and blue figures (in that order) are directed towards the city. This is the order of the Matrix geometric figures (the same as left figure): blue at the top (square, 4), yellow in the middle (hexagon, 6), and green at the bottom (pentagon, 5). After getting this, it is easy to convert binary numbers to decimal, and then get the corresponding letters: 19 (S)-20 (T)-21 (U)-24 (X)-14 (N)-5 (E)-20 (T).
3.5. Third Step: Riddle from Stuxnet Cards
3.5.1. Blue Stuxnet
- ”Integrate what you find”.
- ”The orientation must be taken into account”.
- ”We have to cover this area with a piece of resistant material. Which is the area of the hole that we need to cover?”.
- ”When we need to calculate the area of a surface, we use the definite integrals. Do you remember how to calculate integrals?”.
- The link to this video: https://youtu.be/9_fkoUHXrck.
3.5.2. Green Stuxnet
- ”Pipeline system”.
- ”This system is similar to a traffic flow, where everything coming into must leave, i.e., everything that go inside has to go out”.
- ”You must pose a solution using linear equations”.
- A link to genial.ly that includes information about the pipeline system (https://bit.ly/2tanbjo).
3.5.3. Yellow Stuxnet
- ”Earthquake and vibrations”.
- A link to online information located at https://bit.ly/366PuOe.
- A Mathematica file with the solution is also available as part of the materials.
3.5.4. Red Stuxnet
- Law of cooling.
- Newton’s law of cooling states that the rate of change of the temperature of an object is proportional to the difference between its own temperature and the ambient temperature.
- Online information at genial.ly platform. The link https://bit.ly/36bEgby includes some interactive elements such as the link to a Mathematica file, called breakout-Newton-CLUE.nb with the problem almost solved.
4. Discussion and Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bodnar, C.A.; Anastasio, D.; Enszer, J.A.; Burkey, D.D. Engineers at play: Games as teaching tools for undergraduate engineering students. J. Eng. Educ. 2016, 105, 147–200. [Google Scholar] [CrossRef]
- Haoran, G.; Bazakidi, E.; Zary, N. Serious Games in Health Professions Education: Review of Trends and Learning Efficacy. Yearb. Med. Inform. 2019, 28, 240–248. [Google Scholar] [CrossRef]
- Low, L.; Elimur, E. 2018 Escape Room Enthusiast Survey. 2018. Available online: https://thecodex.ca/2018-escape-room-enthusiast-survey/ (accessed on 22 January 2020).
- Kinio, A.E.; Dufresne, L.; Brandys, T.; Jetty, P. Break out of the classroom: The use of escape rooms as an alternative teaching strategy in surgical education. J. Surg. Educ. 2019, 76, 134–139. [Google Scholar] [CrossRef] [PubMed]
- Monaghan, S.; Nicholson, S. Bringing escape room concepts to pathophysiology case studies. HAPS Educ. 2017, 21, 49–62. [Google Scholar] [CrossRef]
- Hermanns, M.; Deal, B.; Campbell, A.M.; Hillhouse, S.; Opella, J.B.; Faigle, C.; Campbell, R.H., IV. Using an “Escape Room” toolbox approach to enhance pharmacology education. J. Nurs. Educ. Pract. 2018, 8, 89. [Google Scholar] [CrossRef]
- Caraballo Martín, A.; Paralera, C.; González, M.M.S.; Tenorio, Á.F. Evaluación y Breakout. Anales de ASEPUMA 2018, 26, 6. [Google Scholar]
- Laal, M.; Laal, M.; Kermanshahi, Z.K. 21st century learning; learning in collaboration. Procedia-Soc. Behav. Sci. 2012, 47, 1696–1701. [Google Scholar] [CrossRef]
- Robles, M.M. Executive perceptions of the top 10 soft skills needed in today’s workplace. Bus. Commun. Q. 2012, 75, 453–465. [Google Scholar] [CrossRef]
- Adams, V.; Burger, S.; Crawford, K.; Setter, R. Can you escape? Creating an escape room to facilitate active learning. J. Nurses Prof. Dev. 2018, 34, E1–E5. [Google Scholar] [CrossRef]
- López-Pernas, S.; Gordillo, A.; Barra, E.; Quemada, J. Examining the Use of an Educational Escape Room for Teaching Programming in a Higher Education Setting. IEEE Access 2019, 7, 31723–31737. [Google Scholar] [CrossRef]
- Borrego, C.; Fernández, C.; Blanes, I.; Robles, S. Room escape at class: Escape games activities to facilitate the motivation and learning in computer science. JOTSE 2017, 7, 162–171. [Google Scholar] [CrossRef]
- Ho, A.M. Unlocking ideas: Using escape room puzzles in a cryptography classroom. PRIMUS 2018, 28, 835–847. [Google Scholar] [CrossRef]
- Santos, M.J.; Miguel, M.; Queiruga-Dios, A.; Encinas, A.H. Looking for the Antidote for Contaminated Water: Learning Through an Escape Game. In Proceedings of the International Joint Conference: 12th International Conference on Computational Intelligence in Security for Information Systems (CISIS 2019) and 10th International Conference on EUropean Transnational Education (ICEUTE 2019), Seville, Spain, 13–15 May 2019; pp. 217–226. [Google Scholar]
- Vörös, A.I.V.; Sárközi, Z. Physics escape room as an educational tool. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2017; Volume 1916, p. 050002. [Google Scholar]
- Peleg, R.; Yayon, M.; Katchevich, D.; Moria-Shipony, M.; Blonder, R. A Lab-Based Chemical Escape Room: Educational, Mobile, and Fun! J. Chem. Educ. 2019, 96, 955–960. [Google Scholar] [CrossRef]
- Clarke, S.; Peel, D.J.; Arnab, S.; Morini, L.; Keegan, H.; Wood, O. escapED: A framework for creating educational escape rooms and Interactive Games for Higher/Further Education. Int. J. Serious Games 2017, 4, 73–86. [Google Scholar] [CrossRef]
- Caridade, C.M.; Encinas, A.H.; Martín-Vaquero, J.; Queiruga-Dios, A.; Rasteiro, D.M. Project-based teaching in Calculus courses: Estimation of the surface and perimeter of the Iberian Peninsula. Comput. Appl. Eng. Educ. 2018, 26, 1350–1361. [Google Scholar] [CrossRef]
- Queiruga-Dios, A.; Encinas, A.H.; Sánchez, G.R.; del Rey, Á.M.; Vaquero, J.M.; Encinas, L.H. Case study: Malware propagation models for undergraduate engineering students. In Proceedings of the Fourth International Conference on Technological Ecosystems for Enhancing Multiculturality, Salamanca, Spain, 2–4 November 2016; pp. 931–935. [Google Scholar]
- Hauge, J.B.; Riedel, J.C. Evaluation of simulation games for teaching engineering and manufacturing. Procedia Comput. Sci. 2012, 15, 210–220. [Google Scholar] [CrossRef]
- Ahmed, A.; Sutton, M.J. Gamification, serious games, simulations, and immersive learning environments in knowledge management initiatives. World J. Sci. Technol. Sustain. Dev. 2017, 14, 78–83. [Google Scholar] [CrossRef]
- Bodnar, C.A.; Clark, R.M. Can game-based learning enhance engineering communication skills? IEEE Trans. Prof. Commun. 2017, 60, 24–41. [Google Scholar] [CrossRef]
- Nicholson, S. Peeking behind the Locked Door: A Survey of Escape Room Facilities. White Paper. 2015. Available online: http://scottnicholson.com/pubs/erfacwhite.pdf (accessed on 22 January 2020).
- Wiemker, M.; Elumir, E.; Clare, A. Escape room games: ’Can you transform an unpleasant situation into a pleasant one?’. In Game Based Learning-Dialogorientierung & Spielerisches Lernen Analog und Digital; Ikon Verlags Gmbh: Brunn am Gebirge, Austria, 2015; pp. 55–68. [Google Scholar]
- Heikkinen, O.; Shumeyko, J. Designing an Escape Room with the Experience Pyramid Model. Bachelor’s Thesis, Haaga-Helia University of Applied Sciences, Helsinki, Finland, 2016. [Google Scholar]
- Czikszentmihalyi, M. Flow: The Psychology of Optimal Experience; Harper & Row: New York, NY, USA, 1990. [Google Scholar]
- Clare, A. Escape the Game: How to Make Puzzles and Escape Rooms; Wero Creative Press: Toronto, ON, Canada, 2016. [Google Scholar]
- Jack, B.M.; Lin, H.S. Making learning interesting and its application to the science classroom. Stud. Sci. Educ. 2017, 53, 137–164. [Google Scholar] [CrossRef]
- Abdul Jabbar, A.I.; Felicia, P. Gameplay engagement and learning in game-based learning: A systematic review. Rev. Educ. Res. 2015, 85, 740–779. [Google Scholar] [CrossRef]
- Davies, D.; Jindal-Snape, D.; Digby, R.; Howe, A.; Collier, C.; Hay, P. The roles and development needs of teachers to promote creativity: A systematic review of literature. Teach. Teach. Educ. 2014, 41, 34–41. [Google Scholar] [CrossRef]
- Eukel, H.N.; Frenzel, J.E.; Cernusca, D. Educational Gaming for Pharmacy Students–Design and Evaluation of a Diabetes-themed Escape Room. Am. J. Pharm. Educ. 2017, 81, 6265. [Google Scholar]
- Cain, J. Exploratory implementation of a blended format escape room in a large enrollment pharmacy management class. Curr. Pharm. Teach. Learn. 2019, 11, 44–50. [Google Scholar] [CrossRef] [PubMed]
- Nelson, M.; Calandrella, C.; Schmalbach, P.; Palmieri, T. 159 Escape the Conference Room. Ann. Emerg. Med. 2017, 70, S64. [Google Scholar] [CrossRef]
- Low, L.; Elimur, E. 2017 Escape Room Enthusiast Survey. 2017. Available online: https://thecodex.ca/2017-escape-room-enthusiast-survey/ (accessed on 22 January 2020).
- Tarssanen, S.; Kylänen, M. Handbook for experience stagers. In Lapland Center of Expertise for the Experience Industry; OY Sevenprint Ltd.: Rovaniemi, Finland, 2009. [Google Scholar]
- Cagiltay, N.E. Teaching software engineering by means of computer-game development: Challenges and opportunities. Br. J. Educ. Technol. 2007, 38, 405–415. [Google Scholar] [CrossRef]
- Gilbert, J.K. Eclectic perspectives on the preparation of informal science Educators. Stud. Sci. Educ. 2017, 53, 235–237. [Google Scholar] [CrossRef]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Queiruga-Dios, A.; Santos Sánchez, M.J.; Queiruga Dios, M.; Gayoso Martínez, V.; Hernández Encinas, A. A Virus Infected Your Laptop. Let’s Play an Escape Game. Mathematics 2020, 8, 166. https://doi.org/10.3390/math8020166
Queiruga-Dios A, Santos Sánchez MJ, Queiruga Dios M, Gayoso Martínez V, Hernández Encinas A. A Virus Infected Your Laptop. Let’s Play an Escape Game. Mathematics. 2020; 8(2):166. https://doi.org/10.3390/math8020166
Chicago/Turabian StyleQueiruga-Dios, Araceli, María Jesús Santos Sánchez, Marián Queiruga Dios, Víctor Gayoso Martínez, and Ascensión Hernández Encinas. 2020. "A Virus Infected Your Laptop. Let’s Play an Escape Game" Mathematics 8, no. 2: 166. https://doi.org/10.3390/math8020166
APA StyleQueiruga-Dios, A., Santos Sánchez, M. J., Queiruga Dios, M., Gayoso Martínez, V., & Hernández Encinas, A. (2020). A Virus Infected Your Laptop. Let’s Play an Escape Game. Mathematics, 8(2), 166. https://doi.org/10.3390/math8020166







