1. Introduction
One of the oldest mechanisms in order to sell an item is by auction. In an auction there is a seller (the auctioneer) with one or more items to sell and a set of potential buyers (bidders) bidding for them, according to the corresponding auction mechanism. Therefore in an auction we have two sides: the auctioneer and the bidders. From the point of view of the bidders, an auction would be reasonable if it satisfies at least the following two characteristics: (1) bidders with the highest bids obtain the items for sale –fairness– and (2) winning bidders do not pay for the objects acquired more than they are actually willing to pay for them—no over-payment. Likewise, from the auctioneer perspective, the auction should be firstly designed to provide her with the highest (expected) revenue –optimality– and, secondly (in many situations firstly), to assign the objects to whoever has given them the highest value—efficiency [
1]. Today we can find many examples of the use of auctions to sell or assign objects [
2,
3]. Not all auctions are the same, and therefore we can find in the literature different types of auctions with their own characteristics [
1,
2,
3]. In particular, multiple-object auctions when the objects are commonly ranked. This kind of auctions is used in numerous contexts [
4]. Especially, ranked objects auctions are closely related to keyword auctions in search engines on the Internet [
5]. In this paper, we will focus on the relevant problems of designing and choosing auctioning mechanisms for multiple commonly ranked objects taking into account not only the properties referred to above but also the risk for the auctioneer.
In the literature on multi-object auctions when the objects are commonly ranked, we can find numerous papers where different problems are addressed [
4]. In most of these, a new auction mechanism is proposed or one already known is studied or extended to the case of ranked objects auctions. The best known case is the generalized second-price auction (GSP), about which Gomes and Sweeney [
6] wrote the following: “
Over the last few years a new multi-unit auction format known as the generalized second-price (GSP) auction has received much attention from economist. This auction format has been applied to diverse problems such as routing in fixed and wireless networks (see Reference [7]) and the allocation of capacity in electricity markets (see References [8,9]). Most remarkably, search engines use the GSP to sell sponsored advertising links in the Internet, with revenues that exceeded 20 billion dollars industry-wide in 2009”. Although the relevance of the GSP is evident both from its simplicity and from its applicability, nevertheless, the GSP is not actually an extension of the second price auction and, moreover, it has not, in general, an efficient symmetric Bayesian Nash equilibrium [
6]. Furthermore, we do not find in the literature a parametric analysis of auction mechanisms for ranked objects that attempts to extend and encompass the best-known auction mechanisms, except for the case of 1 or 2 objects [
10,
11], but the latter is completely insufficient for a more complete and general analysis of the problem in hand. Finally, although variance is a reasonable measure for the variability of a random variable, perhaps it is not suitable for comparing auction mechanisms, because variance does not indicate the sign of the revenue deviations with respect to the expected revenue. Hence, since an auctioneer is not negatively affected if revenue is higher than expected, it seems reasonable to be interested only in obtaining a measure for the risk of losses. This engages with risk assessment and risk management problems [
12,
13,
14]. However, we have not found any paper in the literature on risk assessment of auction mechanisms, only in the paper by Crowley and Hancher [
15] the risk assessment of competitive procurement is studied. Therefore, the main purpose of this paper is aimed at trying to fill all these research gaps in the ranked objects auction literature.
In order to address all the issues mentioned above, we introduce a parametric family of auction mechanisms for ranked objects auctions extending the ideas in Alonso and Tejada [
10], and Alonso, Sanchez-Soriano and Tejada [
11]. These auction mechanisms would not be difficult to implement and apply in real situations, such as keywords auctions in search engines on the Internet, although they have a more complex structure than, for example, the GSP. Apart from the auction family, we obtain the following results. We first show that this family contains, as particular cases, extensions of the well-known discriminatory, uniform and Vickrey (second-price) auctions [
16]. Furthermore, these three auctions correspond to only three of many other vertices of the polyhedron which we can associate with the members of the parametric family. Hence, the family is much larger than the simple convex combination of all the three. Therefore, we apply a wider approach to the problem of designing and choosing an auction mechanism. Second, we show that all members of the family satisfy the properties of fairness, no over-payment, optimality and efficiency, and all have the same expected revenue. In addition, the symmetric Bayesian Nash equilibria [Harsanyi [
17,
18,
19] for all auctions in the family are determined, which is more difficult to obtain than in the cases of 1 or 2 objects [
10,
11] because as the number of objects to be auctioned increases, this calculation is increasingly complex. Moreover, when analyzing a parametric family of auctions, instead of just one, the proofs have an added difficulty due to the number of parameters increases with the number of objects. Likewise, under the same hypotheses that we consider in this paper, the expression of the Bayesian Nash equilibria in Theorem 1 collects, in particular, all the expressions of the equilibria obtained in the corresponding literature so far. Third, we prove that all auctions in the family have the same expected revenue as the GSP, and we show the GSP is not an extension of the Vickrey auction to the case of ranked objects auctions, whereas one of the auctions in the family is. Finally, since the expected revenue of both the auctions in the family (Corollary 1) and the GSP (Theorem 2) coincide, all of them are compared by using the value at risk (VaR), which is a measure of risk of loss widely used in economic contexts [
20]. This comparison is carried out by simulation for 2, 3 and 4 objects, but an algorithm to do this for any number of objects is provided. In this computational experience, we observe that the auctions with lower VaR have in common that, in contrast with the GSP, the payment of bidder in the top position depends on his own bid as much as possible. Furthermore, depending on the ratio between the objects to be auctioned, the auction with the lowest VaR is on many occasions an auction in the family which is different from the classical mechanisms.
The rest of the paper is organized as follows. In
Section 2 we review the related literature. In
Section 3 we provide the notation used in the paper, introduce the parametric family of auction mechanisms and we obtain their respective Bayesian Nash equilibrium. Furthermore, we show that all auction mechanisms in the parametric family satisfy efficiency, no over-payment and fairness. Likewise, we prove that any auction mechanism in the parametric family yields the same expected revenue for the auctioneer.
Section 4 is devoted to the GSP and we prove that the expected revenues of the auctioneer for the GSP auction and the auction mechanisms belonging to the parametric family are the same. In
Section 5, by using simulation, we assess the risk of the auction mechanisms in the parametric family and the GSP auction with respect to their auctioneer revenue value at risk.
Section 6 concludes. Finally, the proofs of all results are included in the
Appendix A.
2. Literature Review
From the earliest work by Milgrom and Weber ([
21,
22]) in the early 1980s up to the present day (see, for example, Reference [
23]), multi-object auctions have received wide attention due to their use in numerous money-generating markets. Some relevant examples of these markets that have received special attention are Treasury bill and bond markets, raw materials or other product markets (fish, flowers…), electricity wholesale spot markets, licenses allocations, especially spectrum licenses, or more recently, sponsored keywords search on the Internet. For this reason, in the literature we can find numerous works dedicated to studying different aspects of this type of auction. Hortacsu and McAdams [
4] survey multi-object auctions from an empirical point of view and divide these auctions into three groups: (1) auctions of identical objects, (2) auctions of dissimilar objects, and (3) auctions of ranked objects. Hortacsu [
24] and Bajo-Buenestado [
25] review the case of auctions of identical objects. Perhaps, electricity wholesale spot markets are one of most relevant situations in which these types of auction are applied. Therefore we can find many papers in the literature devoted to different aspects of them (see, for example, References [
9,
26,
27,
28,
29,
30,
31,
32]). The most studied auctions of heterogeneous objects have been those of licenses allocations, in particular spectrum licenses in telecommunications (see, for example, References [
33,
34,
35,
36,
37,
38,
39,
40,
41,
42]. Finally, auctions of ranked objects are used in several contexts, in particular, in sponsored keywords search on the Internet, which have received great attention in recent years due to their economic impact. This paper is related to the latter group of multi-object auctions. Therefore, below we review the corresponding literature in more detail.
In the ranked objects auctions literature, we can find different research topics, of all of which we consider the following: (a) theoretical and empirical analysis of the generalized first price auction (GFP), and generalized second price auction (GSP), which are those commonly used by the search engines, particularly the second; (b) proposal of new auction models and their comparison with GFP, and mainly with GSP; (c) optimal choice or design of auctions following the ideas of the pioneer works by Myerson, Riley and Samuelson ([
43,
44]), usually from the point of view of the expected revenues; (d) analysis of ranked objects auctions by using their relation with the well-known assignment games [
45]; and (e) analysis of the behavior of the agents involved such as bidders or consumers. Our work makes contributions to the research topics (a), (b), and (c).
Regarding the analysis of the GSP auction, Aggarwal, Goel and Motwani [
46] study the GSP auction under complete information and prove that the GSP is not truthful in general. Varian [
47] also studies the GSP auction under complete information, shows that the resulting game is closely related to the assignment game, and analyzes its Nash equilibria. Moreover, he carries out an empirical analysis to check that the Nash equilibria are close to the observed data in Edelman, Ostrovsky and Schwarz [
48] define and analyze a ranked objects auction model from two perspectives, as a static game with complete information and as a dynamic game with incomplete information. In the first case, the game induced by the GSP is again related to the assignment game, and they study the locally envy-free equilibria of this game. In the game with incomplete information, they relate the GSP with the generalized English auction, and they prove the existence of a unique Bayesian equilibrium which is an ex post equilibrium that results in the same payoffs to all players as the dominant strategy equilibrium of Vickrey-Clarke-Groves (VCG) mechanism. Yenmez [
49] extends the results in Edelman, Ostrovsky and Schwarz [
48] to the case of ascending auctions with general pricing rules where the price for an object depends on the bids of agents who win lower ranked objects. Gomes and Sweeney [
6] study the GSP under incomplete information and prove that, in general, the GSP does not admit an efficient symmetric Bayesian Nash equilibrium. However, they provide conditions under which this equilibrium exists. Lu and Riis [
50] complement the analysis of Gomes and Sweeney [
6] by considering allocative externalities arising from the heterogeneous match rates of bidders, obtaining similar results concerning the existence of a Bayesian Nash equilibrium. In addition, applications of the GSP to other fields different than sponsored keywords markets can be found in the literature, see for example, Reference [
7] or Reference [
51]. Menezes and Monteiro [
52], Han and Liu [
53], and Dutting, Fischer and Parkes [
54] study the GFP auction under incomplete information. In the first paper, the authors study simultaneous pooled auctions and analyze the bidding strategies and the expected revenue of the GFP when bidders make only one bid which is paid whenever one of the objects is awarded. In the second, the authors prove how efficient symmetric Bayesian Nash equilibrium bidding strategies of bidders are, and give the expression of the expected revenue in equilibrium; while in the third paper, they prove that when each bidder submits a bid for each position, then the GFP mechanism has an efficient Bayesian Nash equilibrium with the same payoffs as the truthful equilibrium of the VCG mechanism. However, we have not found any reference related to the risk assumed by the auctioneer when the GSP is used. In this paper, from the perspective of risk assessment and risk management, we analyze by simulation the relative value at risk (see, for example, Reference [
20]) of the auctioneer in the GSP. We observe that for two objects the higher the number of bidders, the lower the relative value at risk (RVaR) is, however, for three or more objects, the auctioneer cannot control the RVaR because the GSP auction mechanism does not always have an efficient equilibrium. When this equilibrium exists the RVaR behavior depends on the relationship between the values of the ranked objects.
Generally research topics (b) and (c) tend to go hand in hand, and when a new auction model is proposed, it intends to have a certain improved property with respect to other existing ones, usually with respect to the GSP. Aggarwal, Goel and Motwani [
46] propose a new auction by slightly modifying with respect to the GSP what the winning bidders have to pay for the objects. They prove that this new auction is truthful. Garg and Narahari [
55] propose a new auction mechanism based on an optimization problem which maximizes the expected revenue subject to achieving Bayesian incentive compatibility and individual rationality. They prove that, when the bidders are symmetric, the expected revenue of the new mechanism is the same as the GSP and VCG. Gomes and Sweeney [
6], and Han and Liu [
53] consider ranked objects auctions with reserve price under incomplete information and determine the optimal reserve price in order to optimize the expected revenue of the GSP and the GFP, respectively. Edelman and Schwarz [
56] also determine the optimal reserve price in the GSP by using the so-called non-contradiction criteria (NCC) to determine which equilibria in a complete information game that approximates the behavior of players in a corresponding game of incomplete information are admissible. In the case of auctions, NCC establishes an upper bound on equilibrium revenues. Yenmez [
49] also studies how to improve the seller’s expected revenue by setting a reserve price in the case of winning bidders paying what they bid. Since some bidders can incur in over-payment, the authors design a tailored VCG mechanism with same expected revenue but without the problem of the over-payment. Feng [
57] studies how to design auctions of commonly-ranked objects when the bidders have different rates of decrease valuation of the objects and the seller establishes a reserve price for each object. She determines the optimal allocation and payment rules for four different situations of valuations. Alonso, Sanchez-Soriano and Tejada [
11] study two ranked objects auctions, propose a parametric family of mechanisms, determine the unique Bayesian-Nash equilibrium of each member of the family, and analyze the risk of the auctioneer for each auction. Liu, Chen and Whinston [
58] study the design of ranked object auctions when bids are weighted and there are minimum bids. They consider two types of bidders and determine t he weighting schemes and minimum-bid policies that on the one hand, maximize total expected valuation created, and on the other hand, that maximize the auctioneer’s expected revenue. Li, Liu and Liu [
59] introduce shadow costs in the definitions of the allocation rule and the payment rule. Then they analyze the problem following the ideas of Myerson [
43] in order to optimize the expected revenues in their general model and under special cases. In this review we basically observe three issues: (1) new auction mechanisms are usually introduced by simply modifying the payment function to obtain the desired properties; (2) the optimization and choice of the mechanisms is mainly based on introducing reserve prices and then determining that which maximizes the expected revenue; and (3) the optimization and choice of the mechanisms are based on the design of the allocation rule. Moreno and Wooders [
60], and Yang et al. [
61] depart from the common assumption of a risk neutral auctioneer by analyzing how the auction and the reserve prices depend on the assumption of a risk averse auctioneer. Only in Alonso, Sanchez-Soriano and Tejada [
11] the approach changes basing the auction choice on the associated risk, but only for the case of two objects which has a very limited scope. In this paper, we extend and generalize the results in Alonso, Sanchez-Soriano and Tejada [
11] to the case of a general number of objects. Our contributions to the literature in research topics (b) and (c) are the following:
Following the idea of modifying the auction payment function, a parametric family of auction mechanisms for commonly ranked objects is introduced and is much broader than in Alonso, Sanchez-Soriano and Tejada [
11], which also includes the three classical ones: discriminatory-price auction, uniform- price auction and Vickrey auction.
The parameters are chosen to avoid the over-payment problem.
The unique symmetric Bayesian-Nash equilibrium of each member of the family is determined to the general case of any number of objects. This extension of the analogous result in Alonso, Sanchez-Soriano and Tejada [
11] is not trivial because as many parameters are used as there are objects.
It is shown that the GSP is not in the family, and that the expected revenue of the GSP and all the mechanisms in the family are the same.
As in Alonso, Sanchez-Soriano and Tejada [
11], the risk associated with each auction, including the GSP, is used as a selection criterion from the auctioneer’s perspective, using the concepts of risk assessment and risk management. Due to the analytical complexity, this analysis has been carried out by simulation.
Regarding the last contribution, we emphasize once again that we have not found any paper in the literature on risk assessment of auction mechanisms, only in Crowley and Hancher [
15] the risk assessment of competitive procurement is studied. We can find works that study variability in terms of variance, the auctioneer’s risk profile or mean-preserving (see, for example, References [
16,
62,
63,
64]), but although these approaches are reasonable, in our opinion an analysis from the perspective of risk assessment is better since an auctioneer is not negatively affected if revenue is higher than expected. On the other hand, risk assessment is a relevant decision tool in many other fields (see, for example, References [
29,
65,
66,
67,
68]), and, therefore, we think that we contribute with this to fill a gap in the literature on auctions.
To conclude the review of the literature, we give some tips on several results of the other two mentioned research topics, (d) and (e). The relation with the assignment game when complete information is considered can be found, for example, in References [
47,
48], and [
69]. On the other hand, Aparicio et al. [
70] design and implement from the perspective of bidders a decision support system to analyze discriminatory price ranked object auctions. In this sense, the tool is useful for a bidder makes a better bid. Kim et al. [
71] study the effects of consumer involvement on keyword performance. To end, Kamijo [
72] studies the behavior of bidders along a number of periods in the GSP model.
3. A Parametric Family of Efficient Auction Mechanisms for Ranked Objects Auctions
We consider the ranked objects auction model described, for example, by Varian [
47] and Gomes and Sweeney [
6], which is used in most of the papers about this type of auctions, and can be considered as a canonical model for this kind of works. For the sake of completeness, we provide a brief description of the model, at the same time that we introduce the notation that we use throughout this paper.
An auctioneer sells k ranked objects to risk-neutral bidders through a mechanism which assigns the objects in decreasing order of bids. The objects have an associated relevance or impact which are common knowledge. We can assume without loss of generality that . The valuation for each object j of bidder i is given by , where is information only known to bidder i. This is an independent realization of a continuous random variable (possible types of bidders) with c.d.f. F, continuously differentiable, and with density function f, strictly positive on the interval (we consider that the maximum value is normalized to 1). Each bidder i simultaneously and independently, submits his single bid, , to the auctioneer specifying the maximum unit-price offer at which he is willing to pay, that is, at most for the j-th object. Thus, a strategy for bidder i is a function . We assume, given the symmetry of the model, that is the bid function used in equilibrium by all bidders, where is a strictly monotone and differentiable function. The objects are allocated based on the rank of the bids. The bidder with the highest bid obtains the highest-ranked object, the bidder with the second-highest bid obtains the second-ranked object and so on until to allocate the k objects to the bidders with the k highest bids. The remaining bidders obtain nothing. We assume that the bidders with highest bids obtain their desired objects, therefore this mechanism has the property of fairness.
Once determined who wins what in an auction, the next step in the design of an auction is how much the winning bidders have to pay for the objects they win. There are many different methods of payment which give name to the different types of auction mechanisms. In this paper, we consider a parametric family in order to generalize the analysis, since this family includes the most well-known auctions in the literature. Next we describe the profit function of the bidders taking into account their gains and their payments in the auction.
The price paid by each bidder depend on a linear combination of his own bid and the ordered list of bids below his bid. In particular, the profit function in the
parametric family of auctions, for bidder
i, is given by
where, given a set of
n bids,
,
denotes the set of all bids except bid
i, and
is the highest bid of the set
b,
is the second highest bid of the set
b, and so on; and
are auction design parameters to weigh the effect of the lower bids on what a bidder with a higher bid has to pay.
In order to avoid negative coefficients in the linear combinations of bids, the k parameters must be chosen verifying , , . Moreover, the profit function has been defined by imposing that it meets three requirements: (1) the extension of the 3 classical auction models can be obtained from suitable combinations of the parameters, that is, the family is a reasonable extension from one object to many ranked objects; (2) the payment for a wining bidder is a linear combination with positive coefficients of his bid and the ordered list of bids below it, that is, lower bids should not prejudice bidders with higher bids; (3) over-payment must be avoided. It is easy to check that the addition of all the coefficients of the linear combination corresponding to the payment of the winner of the object j is exactly , therefore this payment will be always below times his bid. The following example illustrates how the profit function works.
Example 1. Let us consider a search engine that sells three positions for a particular keyword, and the search engines announces for a strategic reason that those positions provide C, and clicks, respectively, where . There are four bidders (1, 2, 3 and 4) interested in that keyword whose average profits per click, ,, and , are between 0 and 1 m.u. This is an example of ranked objects auction in which , and . If the search engines uses as auction mechanism the member of the parametric family with and , and the bids are 0.8, 0.6, 0.4 and 0.2, respectively, then the winning bidders have to pay per click
And the profit per click for each bidder is given by , . Now, if we take into account the parameter C, we obtain the total profit obtained in each position for each bidder.
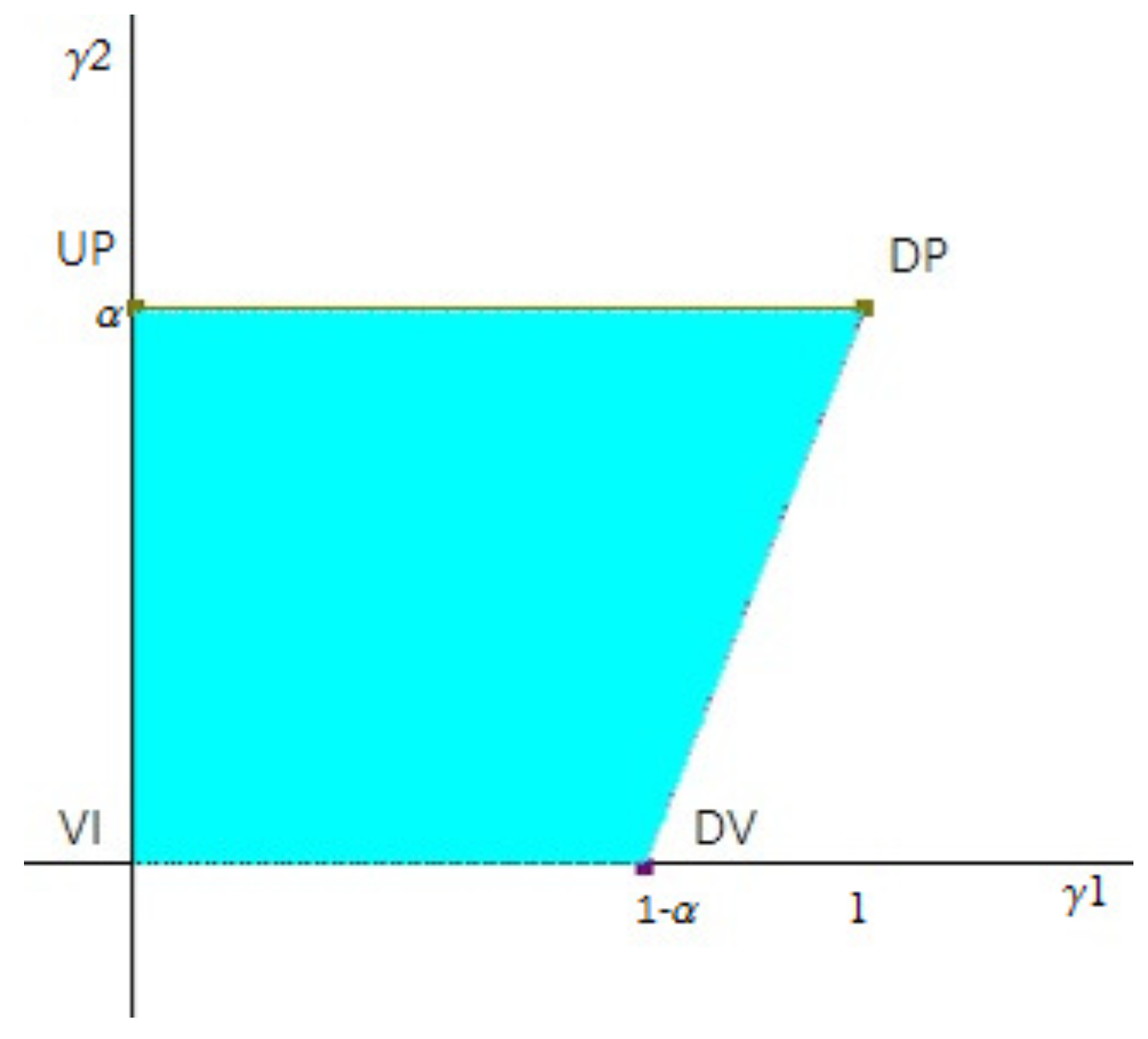
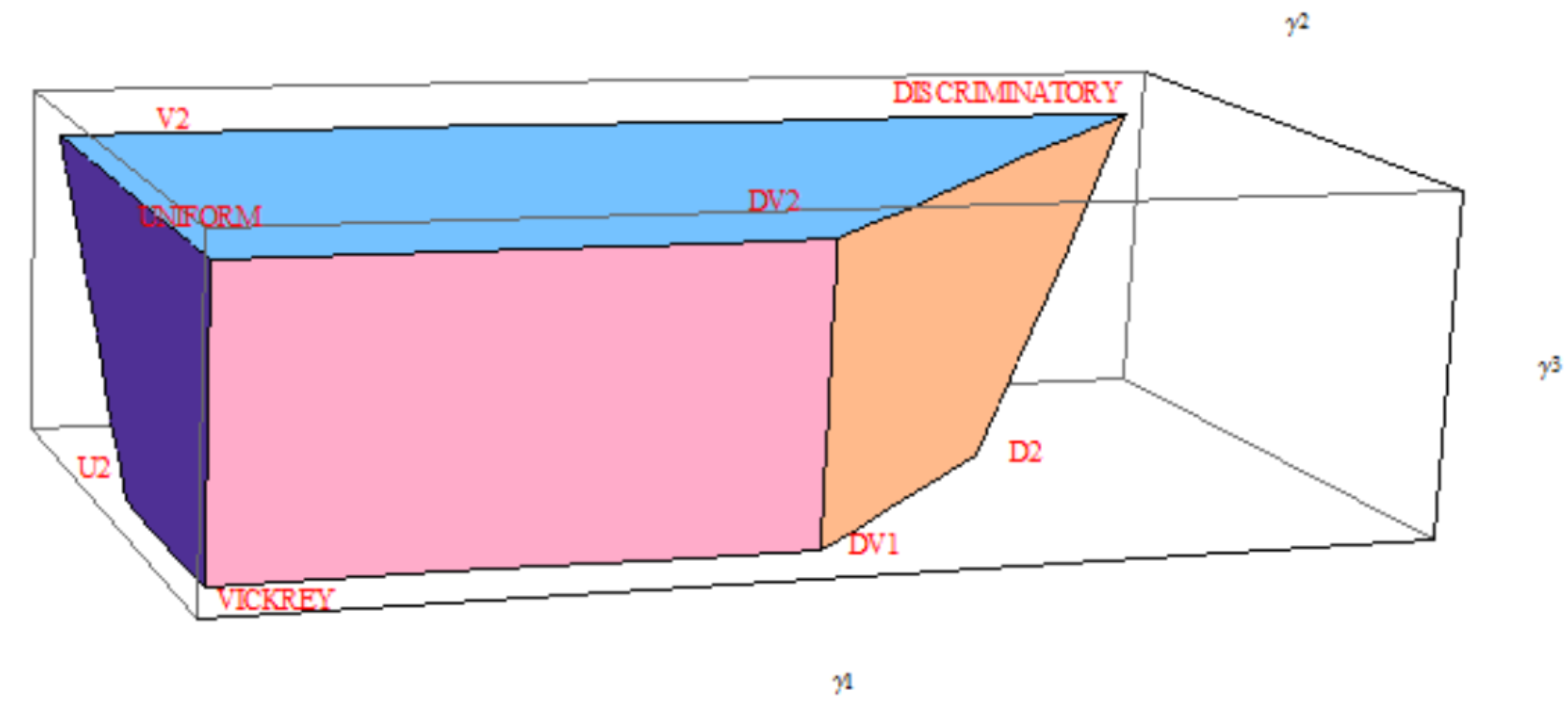
Note also that we have defined a parametric family of auctions which contains generalizations of the discriminatory-price (DP) (, , the uniform-price (UP) (, ) and the Vickrey (VI) () auctions. In fact if , , then we obtain k identical objects auctions and DP, UP and VI in this work are the respective three classical auctions. As it can be observed in Figures 1 and 3 these auctions just correspond to three of all vertices of the polyhedron that represents the members of the parametric family through their parameters. Therefore, the parametric family is much larger than the convex hull of the DP, UP and VI auctions. The following example illustrates the above comment for the case of 3 object.
Example 2. There are 3 ranked objects to sell () and bidders. If we consider in particular:
, and , then we obtain the profit function, for bidder i, in UP: and when the objects to sell are homogeneous the previous expression is reduced to the classical Uniform auction in which all bidders pay a per unit price equal to the lowest winning bid.
, and , then we obtain the profit function, for bidder i, in DP: where each winner pays his own bid. The previous expression is reduced to the classical Discriminatory or GFP auction.
, and , then we obtain the profit function, for bidder i, in VI: where each winner pays for the harm he causes to displaced bidders.
When the objects to sell are homogeneous the previous expression is reduced to the classical Vickrey auction in which all winning bidders pay the amount of the highest non-winning bid (the price of the object sold if he removes his bid).
Remark 1. is the coefficient that multiplies the highest bid and one of the parameters determining the specific auction model in the family. This parameter takes values within the interval . Throughout this work, we will demonstrate that, in terms of risk, the most advantageous auction models for the auctioneer are those with . They are the auction mechanisms of the parametric family with the highest possible value of for fixed (i.e., the payment of the bidder in the highest position depends on his own bid as much as possible).
The following theorem shows that all members of the parametric family have a unique efficient symmetric Bayesian Nash equilibrium.
Theorem 1. All auction mechanisms in the parametric family have a unique symmetric Bayesian Nash equilibrium , with the condition , which is efficient:
Otherwise,whereandis the probability that the bidder of type x wins the object.
Remark 2. Theorem 1 generalizes all particular cases that have appeared in the literature so far.
If only one object is auctioned then , and the proof of Theorem 1 is reduced to the differential equation obtained in Alonso and Tejada [10]. If two objects are auctioned then , and the proof of Theorem 1 is reduced to the differential equation obtained in Alonso, Sanchez-Soriano and Tejada [11]. From Theorem 1 is possible to obtain the Bayesian Nash equilibrium for particular cases as VI (substituting ) and DP (substituting , :whereis the probability that the bidder of type x buys the object. Notice that this last expression is obtained in Han and Liu [53]. Not only can we find that Theorem 1 generalizes particular cases that have already appeared in the literature but also we can find Bayesian Nash equilibrium not obtained before as UP auction (substituting , ).
In addition, if , , then we obtain k identical objects auctions and the Bayesian Nash equilibrium of DP, UP and VI in classical auctions.
Therefore, taking into account how the allocation of objects is made, the structure of the profit function and Theorem 1, we conclude that all auction mechanisms in the parametric family satisfy fairness, no over-payment and efficiency. Furthermore, given a particular situation with n bidders, k objects and their corresponding ratios among them, all auction mechanisms in the parametric family provide the same expected payment for the bidders and the same expected revenue for the auctioneer as the following corollary states.
Corollary 1. All auction mechanisms belonging to the parametric family provide the same expected payment for the bidders and the same expected revenue for the auctioneer and they do not depend on the parameters of the auction family.
Therefore, we have defined a family of auction mechanisms, which includes the DP, UP and VI auctions, and show that all of them have the same properties in terms of the above mentioned criteria used in auctions. However, as we will show later, they have different risks for the auctioneer.
4. Generalized Second Price (GSP) Auction for Ranked Objects
Another relevant auction mechanism in (commonly) ranked object is the Generalized Second Price (GSP) auction. Since this does not belong to the parametric family defined in
Section 3, in this section we will briefly analyze it. One of the most interesting auction mechanisms is the second price auction which was generalized to environments where more than one object is auctioned by Vickrey [
16]. The Vickrey auction is defined as follows: Each winner pays the harm caused to displaced bidders. Another extension of the second price auction, in the context of ranked auctions, is the so-called GSP auction (Edelman, Ostrovsky and Schwarz [
48]) which is defined as follows: Each winner bidder pays for a click in his link the bid submitted by the bidder below him in the ordered list.
In the GSP auction for
k ranked objects, the profit function for bidder
i is given by
It is obvious the GSP auction does not belong to the parametric family of auctions defined before because it is not possible to find a combination of parameters
...,
such that
. Moreover, Gomes and Sweeney [
6] proved that the GSP auction may not have an efficient symmetric Bayesian Nash equilibrium but we prove in Theorem 1 that all auctions in the parametric family have such equilibrium.
Although we already know that the GSP auction, the Vickrey auction, and the auction mechanism VI of the parametric family with parameter are not the same, an interesting question is whether these auctions always provide the same result. The answer to this question is negative as the following example shows.
Example 3. In the conditions of Example 3, Table 1 shows the results when the search engines uses as auction mechanisms the GSP auction, the Vickrey auction and the member of the parametric family with : Procedure to calculate the Vickrey payments:
- 1.
Let be the value that bidder i obtains from the efficient allocation.
- 2.
Let V be the total surplus from the efficient allocation ().
- 3.
Let be the total surplus that could be generated if i did not participate (and the seller allocated efficiently the goods among the other bidders).
- 4.
Then is the Vickrey payment for bidder i.
Therefore, we observe that the Vickrey auction and the auction mechanism of the parametric family VI with parameters coincide, but they are different from the GSP auction. It is not difficult to prove that the auction mechanism VI of the parametric family with parameters follows the same idea of the Vickrey auction (see Example 2). Thus, they always coincide. Therefore, we can say that VI is an extension of the Vickrey auction to the case of commonly ranked objects auctions.
After analyzing some relationships between the GSP auction, the Vickrey auction and some members of the parametric family, the next question is: what happens with the expected revenues? In terms of expected revenues of the auctioneer, the GSP auction and the auction mechanisms belonging to the parametric family are equivalent as the following theorem states.
Theorem 2. When the GSP has an efficient Bayesian Nash equilibrium, the expected revenues of the auctioneer for the GSP auction and the auction mechanisms belonging to the parametric family are the same.
Therefore, we can conclude that when there is an efficient equilibrium in the GSP auction the corresponding expected revenue for the auctioneer coincides with the expected revenue for her when she uses whatever of the auctions in the parametric family introduced in this paper. Thus, from the viewpoint of the expected revenue, when an efficient equilibrium exists, all auctions in the parametric family and the GSP are indifferent, accordingly other criteria are necessary in order to select one or another. The next section deals with introducing an additional choice criterion when the equivalence of expected revenue among different auctions mechanisms occurs.
5. Analysis of the Risk Assumed by the Auctioneer
In this section, we analyze the risk assumed by the auctioneer when an auction of the parametric family or the GSP is implemented. Risk analysis of the different decision alternatives is always important before making a decision, but when all the alternatives are equivalent in terms of expected revenues, this can become a decisive criterion for choosing one of the alternatives. Thus, if an auctioneer only took into account expected revenues (risk-neutral auctioneer), then any auction mechanism that satisfies the Revenue Equivalence Theorem would be indifferent to him, which would imply that he could choose one of the mechanisms at random. However, the risk associated with each of the mechanisms may be different and, therefore, some will be better than others according to this criterion. Since an auctioneer is never unhappy if revenue is higher than expected, it seems reasonable to be only interested in obtaining a measure for the risk of losses with respect to the expected revenue. A widely used measure of the risk of loss in different economic and business contexts is the value at risk (VaR) (see, for instance, Reference [
20]). In our context, this measures how much is the most the auctioneer admits to losing with respect to the expected revenue. Therefore, the lower the VaR, the better for the auctioneer. More precisely, given a confidence level
, the VaR on the auctioneer revenue of an auction mechanism
M is the smallest
x such that the probability that the difference between the expected and the actual revenue was less than
x is greater than or equal to
. Formally,
where
is the random variable that provides the auctioneer revenue at equilibrium which is given by
where
is the
-highest order statistic of
and
is the expected revenue for the auctioneer in an auction mechanism
M.
In order to avoid the effect of the size of
we use the relative VaR, RVaR, that is given by
We next evaluate the RVaR of several auction mechanisms in the parametric family and GSP. In this way, we have the opportunity to differentiate among them using this criterion, given all these auction mechanisms have the same expected auctioneer revenue , when an efficient equilibrium exists, as we have shown previously.
At this point, we have all the tools to be able to calculate the RVaR of any auction model in the family within a specific market. Therefore, we could now establish which are the auction models with the lowest risk for the auctioneer. However, the problem of finding the parameters which minimize the RVaR is extremely difficult, for this reason we resort to simulation in order to illustrate and to analyze how the RVaR of several auction mechanisms introduced above performs in different scenarios. We run simulations using the following Algorithm 1:
| Algorithm 1: Algorithm for computing VaR. |
INPUT: Auction model , the values of the objects , the number of bidders n, the random vector of bidder types, R, where each coordinate is assumed to be uniformly distributed on and the confidence level . OUTPUT: The VaR on the auctioneer revenue of the auction mechanism M. . ; } Return Quantile
|
A brief explanation of the algorithm is the following. At each step j, R is formed by n random numbers in -which represent the n valuations from the bidders. This is how we obtain which is the difference between actual and expected revenue to the auctioneer, assuming that each player bids according to the corresponding equilibrium model M (equilibria are calculated in Theorem 1). We repeat this operation 100,000 times to obtain a sample () and calculate its -quantile (sample VaR). As usual in the auction literature, when there is no information about the valuation of the bidders, bidder types are assumed to be uniformly distributed on [0,1]. In the following subsections we compute by simulation the value at risk for the auctioneer for two, three and four objects auctions, under different scenarios. We consider these three situations are reasonable and sufficient because, for example, in real situations in keywords auctions in search engines on the Internet, they are the most common values for n, and they are enough to illustrate how important it is to take into account the risk in order to select one auction or another.
5.1. Simulations of Two Objects Auctions
In this case the ratios between the values of the objects are taken to be
and
Then we obtain the parametric family for two ranked objects auctions that was studied by Alonso, Sanchez-Soriano and Tejada [
11]. In that paper, the VaR and the RVaR of the auction mechanisms in the parametric family were analyzed and the authors showed that the auction mechanisms of the parametric family with smaller VaR and RVaR were those in the segment whose vertices were DP (
,
and DV (
,
(see
Figure 1). They are the auction mechanisms of the parametric family mentioned in Remark 1 with the highest possible value of
for fixed
(i.e., the payment of bidder in the highest position depends on his own bid as much as possible).
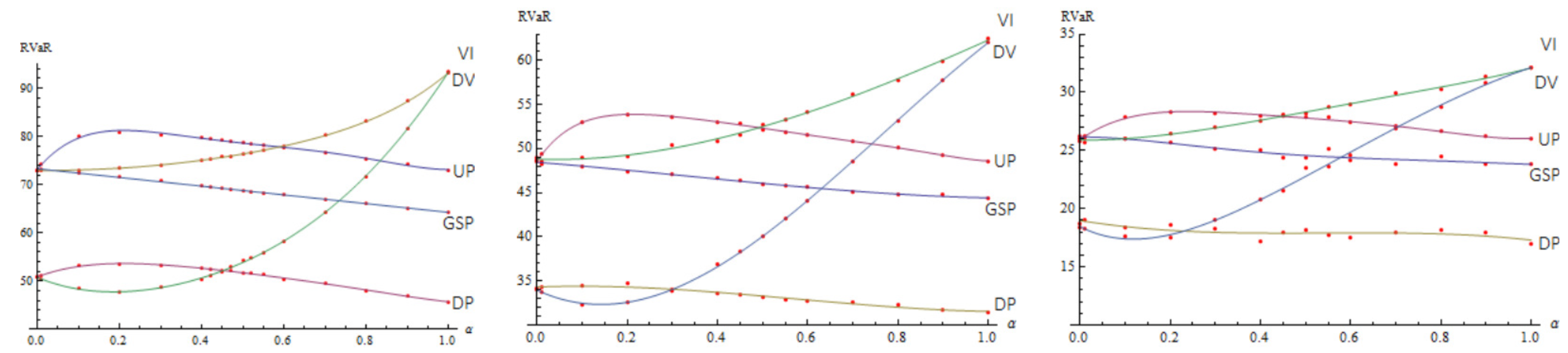
Now, we compare the RVaR of some auction mechanisms in the parametric family with the RVaR for the GSP for bidders.
The results are depicted in
Figure 2 where we can observe that the higher the number of bidders, the lower the RVaR is. Likewise, we also observe that the relative positions of the auction mechanisms depicted in
Figure 2 with respect to the RVaR are approximately the same for each pair
and
n. Moreover, we can observe that DV is the best auction for small values of
, and DP is the best for large values.
Although Gomes and Sweeney [
6] proved the equilibrium of the GSP is inefficient for large values of
(for example, for two objects, three bidders and
), we have used it to compute reward in order not to cut the graphs. Therefore, for large values of
, the auctioneer cannot predict the behaviour of the bidders and the RVAR of the GSP. Nevertheless, we observe that the GSP auction performs better than the Vickrey and Uniform auctions in all cases and better than DV for values of
greater than 0.6 with respect to the RVaR. In general, we observe that there will be auction mechanisms belonging to the parametric family different from DP that perform better than the GSP auction.
5.2. Simulations of Three Objects Auctions
For this case, the ratios are taken to be
,
and
. If we represent graphically this family of auctions with respect to the parameters
,
and
, then we observe that the generalizations of the three classical mechanisms correspond to three vertices of the polyhedron (see
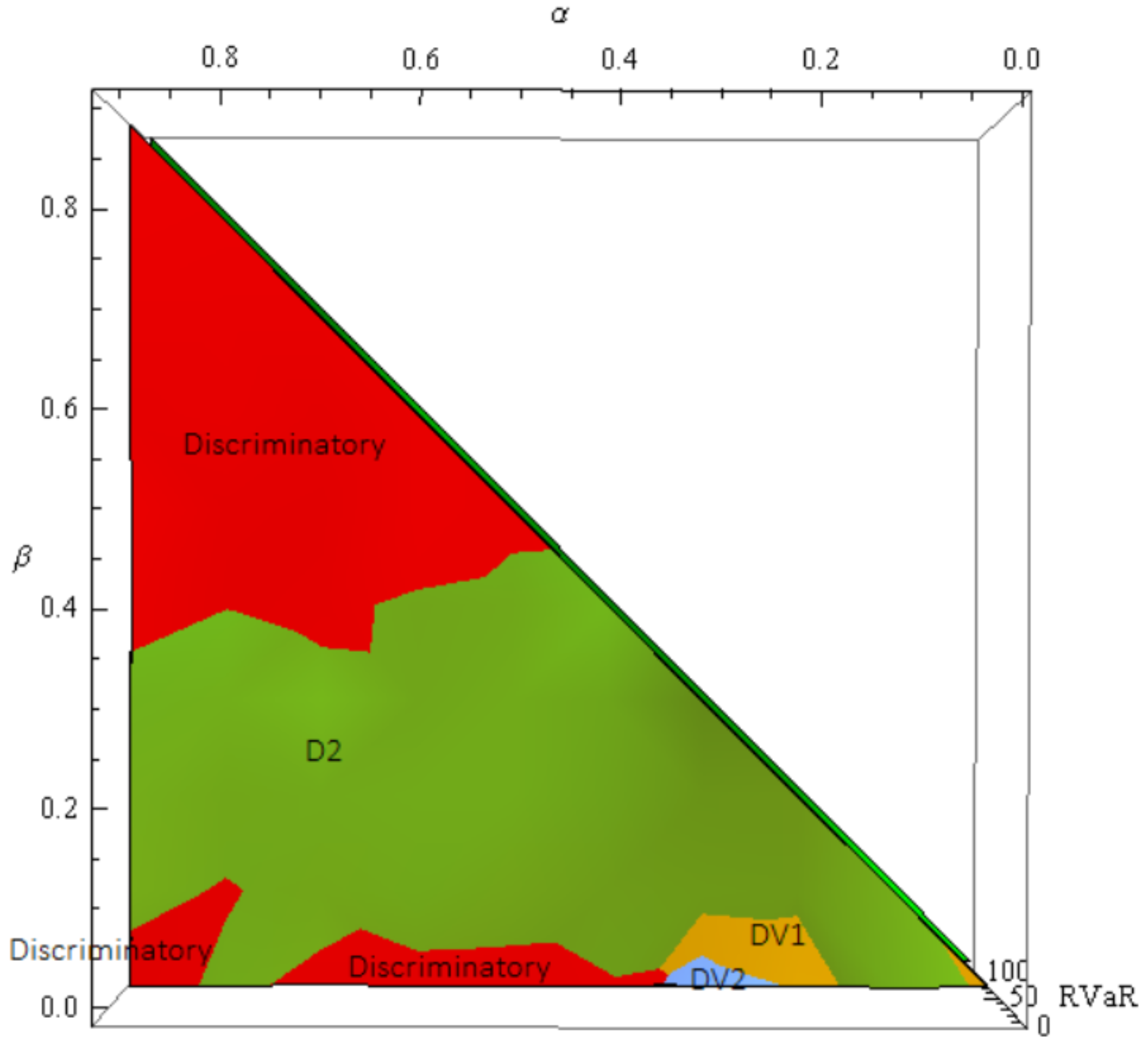
Figure 3) and the other vertices correspond to new auction mechanisms.
For this case, we calculate the RVaR for the auction mechanisms of the parametric family corresponding to the eight vertices in
Figure 3 and the GSP.
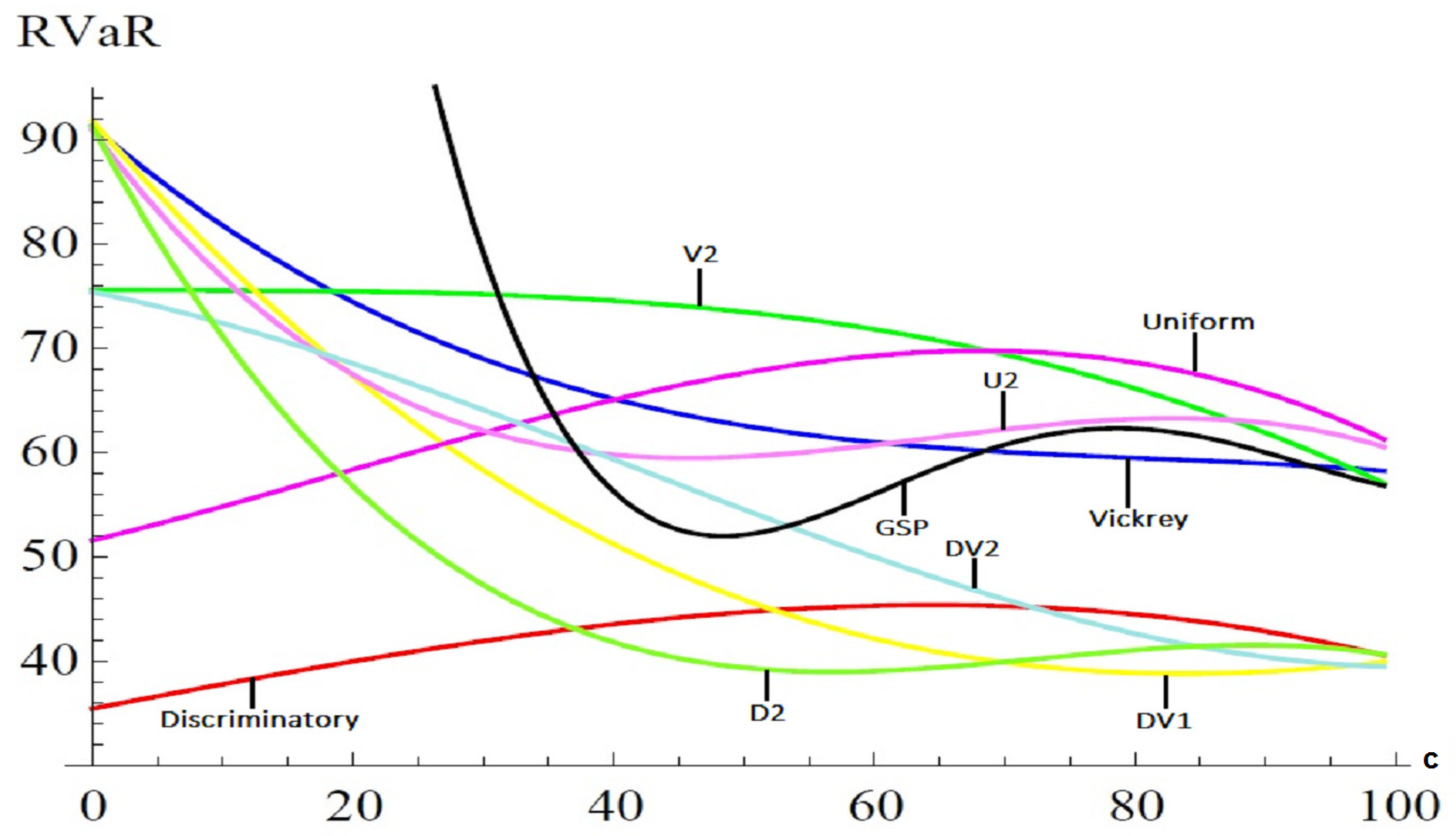
In order to avoid three dimensional representation, we distinguish two simulation scenarios. In a first simulation scenario, we consider that when a bidder loses a position, he loses a fix proportion of clicks, in particular we consider that and , .
For this scenario, the results are depicted in
Figure 4 where we can observe that, for values of
c below 40, the RVaR of the GSP auction goes to infinity because we are in a region in which the equilibrium for the GSP auction is not efficient ([
6]). Therefore, since the GSP auction mechanism does not have always an efficient equilibrium, the auctioneer has no control on the RVaR, but even in the case where the GSP auction mechanism has an efficient equilibrium there will be auction mechanisms in the parametric family which perform better than the GSP with respect to the RVaR. Depending on the value of
c the lowest RVaR is reached in the facet whose vertices are DV1 (
,
,
, D2 (
,
,
, DP (Discriminatory,
,
,
and DV2 (
,
,
. In any case, DP, D2 and DV1 have always a lower RVaR than the GSP and Vickrey for all
c.
Therefore, depending on the value of c, there are new auction mechanisms in the parametric family which perform better than the classical ones with respect to the RVaR. This is an interesting aspect to be taken into account when an auctioneer has to select an auction mechanism.
In a second simulation scenario, we take
and
with step
. For this case, the best auction mechanisms in the parametric family with the smallest RVaR are shown in
Figure 5. In general, we observe that the best auction mechanisms of the parametric family are the same as the first scenario. Again, they are auction mechanisms of the parametric family with the highest possible value of
for fixed
and
.
5.3. Simulations of Four Objects Auctions
In this case, we take , , and . Moreover, taking into account what we have observed for cases and , we will choose some of those auction mechanisms of the parametric family with the highest possible value of given , and : DP (, , ), Dis2 (, , ) and D21 (, , ).
Then these auctions are compared with the GSP auction mechanism, for which the payment of the winning bidders do not directly depend on their bids.
In order to run the simulation, we consider the following scenario similar to the first one simulated for three objects: when a bidder loses a position, he loses a fixed proportion of clicks, in particular, we consider that and , .
For the scenario described above, the results obtained are depicted in
Figure 6, where we can also observe that the three selected auction mechanisms of the parametric family perform better than the GSP in all cases. We can observe that there will be auction mechanisms in the parametric family which perform better with respect to the RVaR than the Discriminatory auction mechanism for values of
c higher than 35, that is, for situations in which the difference between the number of clicks from one position to the following increases.
6. Conclusions and Further Research
In this paper a parametric family of bidders’ payment functions is used to define new auctions for commonly ranked objects, while the allocation rule is the higher the bid, the higher the rank of the object assigned to the corresponding bidder. The number of parameters used coincides with the number of objects to sell, and the price paid by each winning bidder depends on a linear combination of his own bid and the ordered list of bids below his bid. One possible shortcoming of this family is that the coefficients of the linear combinations depend on both the parameters and the impact of the commonly ranked objects. Nevertheless, from the point of view of the auctioneer this may not be a problem because of the previous information. For example, in keyword auctions on the Internet, the search engine has enough information about the number of clicks for each position, and therefore a good estimate of the impact in terms of the number of clicks of the positions. Likewise, this information could become common knowledge depending on the auctioneer’s own interests (see, for example, Reference [
73]).
We have proved that all auctions in the parametric family have a unique efficient symmetric Bayesian Nash equilibrium and satisfy fairness, no over-payment, efficiency and revenue equivalence. Moreover, the family includes generalizations of the classical DP, UP, VI auctions to the case of commonly ranked auctions. However the GSP is not in the family, but the expected revenue of the GSP and all auctions in the family coincide when the GSP has an efficient equilibrium. Therefore, the auction mechanisms introduced in this paper have interesting properties to be applied in real situations, because although, in general, they are more complex than the GSP, their implementation is not difficult.
In order to select the best mechanism for the auctioneer, the criterion of maximizing the expected revenue (with or without a reserve price) is very often used in the literature (see
Section 2). However, when the alternative mechanisms have equal, similar or satisfactory expected revenue, a safety criterion must be taken into account: minimizing the associate risk of obtaining such expected revenue. Since all the auctions that we have presented in this paper have the same expected revenue, we have chosen to compare them from the point of view of that second criterion. In particular, we have calculated by simulation the the RVaR for several cases. The main conclusion of this analysis is that, in general, auction mechanisms in the parametric family can be found that are more advantageous in terms of risk for the auctioneer than the GSP and the remaining mechanisms in the parametric family. In particular, those for which the payment of the bidder winning the top position depends on his own bid as much as possible. Of course, this does not mean that there are no other criteria for the GSP and other auction mechanisms to be better than the auction mechanisms in the parametric family with respect to them. However, we would like to highlight that when an auctioneer has to select an auction mechanism to be implemented in a particular market, she should take into account that it is possible to define new auction mechanisms which could perform better than the classical examples with respect to some relevant criteria for the auctioneer.
Some future research directions are the following. First, it would be interesting to study the case in which reserve prices are considered, analyze what equilibria are obtained, if any, and determine the reserve price that maximizes the expected revenue for each of the auctions in the family. At this point, the relationship between the reserve price that maximizes the expected revenue and the parameters that define the auction could be analyzed. Moreover, a comparison between the different maximum expected revenues could be carried out, including the GSP. Second, further research would be needed to know whether it is possible to determine the member of the family with the lowest RVaR in terms of the parameters defining the family and the impacts of the objects, or at least to implement an algorithm for doing this numerically. Third, it would also be interesting to study the effect of the bidders’ learning when the parametric family auctions are used. Fourth, following the scheme in Reference [
47], an analysis of the case with complete information for the parametric family of auctions could be carried out and compared with the results obtained for the GSP and the GFP. Fifth, it would be of interest to analyze the collusive behavior of bidders when the auctions introduced in this paper are used. And, finally, related to the latter, cooperative games arising from the auctions in the parametric family could be studied.