Finitistic Homological Dimensions Relative to Subcategories

Abstract

Let $\mathcal{C}\subseteq \mathcal{T}$ be subcategories of an abelian category $\mathcal{A}$. Under some certain conditions, we show that the $\mathcal{C}$-finitistic and $\mathcal{T}$-finitistic global dimensions of $\mathcal{A}$ are identical. Some applications are given; in particular, some known results are obtained as corollaries.

1. Introduction

In homological algebra, homological dimensions are important and fundamental invariants, which play an important role in studying the properties of modules and rings. It is known that every homological dimension of modules is defined relative to some subcategory of modules. For example, (Gorenstein) projective, flat and injective dimensions of modules are defined relative to the categories of (Gorenstein) projective, flat and injective modules respectively, and so on. The relationship between the homological dimensions relative to a category and a subcategory has been investigated in [1].

Let $\mathcal{C}\subseteq \mathcal{T}$ be subcategories of an abelian category $\mathcal{A}$. It is trivial that the $\mathcal{T}$-projective dimension of an object in $\mathcal{A}$ is at most its $\mathcal{C}$-projective dimension, and hence the $\mathcal{T}$-global dimension of $\mathcal{A}$ is at most its $\mathcal{C}$-global dimension. However, we do not know the relation between the $\mathcal{T}$-finitistic global dimension of $\mathcal{A}$ and its $\mathcal{C}$-finitistic global dimension in general. So, a natural question is: when is there a relationship between these two finitistic global dimensions? For any ring, it was shown in [2] that if $\mathcal{C}$ and $\mathcal{T}$ are the classes of projective and Gorenstein projective left R-modules respectively, then the $\mathcal{C}$-finitistic and $\mathcal{T}$-finitistic global dimensions are identical. Furthermore, when R is an artin algebra and $\mathcal{C}$ and $\mathcal{T}$ are the classes of finitely generated projective and Gorenstein projective left R-modules respectively, it was shown in [3] that the $\mathcal{C}$-finitistic and $\mathcal{T}$-finitistic global dimensions are also identical. In this paper, we will study this question in a general case.

The paper is organized as follows. In Section 2, we give some notions and notations which will be used in the sequel. Let $\mathcal{C}\subseteq \mathcal{T}$ and $\mathcal{E}$ be subcategories of an abelian category $\mathcal{A}$ that satisfy certain hypotheses that will be presented in detail in Section 2. In Section 3, we first prove that any object in $\mathcal{A}$ with finite $\mathcal{T}$-projective dimension is isomorphic to a kernel (resp. a cokernel) of a morphism from an object with finite $\mathcal{C}$-projective dimension to an object in $\mathcal{T}$. By using it, we give some sufficient conditions such that the $\mathcal{C}$-finitistic and $\mathcal{T}$-finitistic global dimensions of $\mathcal{A}$ are identical (Theorem 1 and Corollary 1). Then we apply this result to some special module categories (Theorems 3 and 4). Some known results are obtained as corollaries.

A referee comments that the results in this paper are important in the spirit of operad theory and quantization issues ([4,5,6]).

2. Preliminaries

Throughout this paper, $\mathcal{A}$ is an abelian category admitting enough projective and injective objects, and all subcategories of $\mathcal{A}$ considered are full and additive. We use $\mathcal{P}\left(\mathcal{A}\right)$ (resp. $\mathcal{I}\left(\mathcal{A}\right)$) to denote the subcategory of $\mathcal{A}$ consisting of projective (resp. injective) objects.

Let $\mathcal{X}$ be a subcategory of $\mathcal{A}$. We write

$${}^{\perp }\mathcal{X}:=\{A\in \mathcal{A}\mid {Ext}_{\mathcal{A}}^{\ge 1}(A,X)=0 \mathrm{for} \mathrm{any}X\in \mathcal{X}\},$$

$${\mathcal{X}}^{\perp }:=\{A\in \mathcal{A}\mid {Ext}_{\mathcal{A}}^{\ge 1}(X,A)=0 \mathrm{for} \mathrm{any}X\in \mathcal{X}\}.$$

For subcategories $\mathcal{X},\mathcal{Y}$ of $\mathcal{A}$, we write $\mathcal{X}\perp \mathcal{Y}$ if ${Ext}_{\mathcal{A}}^{\ge 1}(X,Y)=0$ for any $X\in \mathcal{X}$ and $Y\in \mathcal{Y}$. An exact sequence (of finite or infinite length)

$$\cdots \to X_n\to \cdots \to X_1\to X_0\to M\to 0$$

in $\mathcal{A}$ is called an $\mathcal{X}$-resolution of M if all $X_i$ are in $\mathcal{X}$. Let M be an object of $\mathcal{A}$. The $\mathcal{X}$-projective dimension$\mathcal{X}$-$\mathrm{pd}M$ of M is defined as $\inf \{n\mid$ there exists an $\mathcal{X}$-resolution

$$0\to X_n\to \cdots \to X_1\to X_0\to M\to 0$$

of M in $\mathcal{A}\}$. Dually, the notions of an $\mathcal{X}$-coresolution and the $\mathcal{X}$-injective dimension$\mathcal{X}$-$\mathrm{id}M$ of M are defined. We use $\mathcal{X}$-${\mathrm{pd}}^{<\infty }$ (resp. $\mathcal{X}$-${\mathrm{id}}^{<\infty }$) to denote the subcategory of $\mathcal{A}$ consisting of objects with finite $\mathcal{X}$-projective (resp. $\mathcal{X}$-injective) dimension. We write

$$\mathcal{X}-\mathrm{FPD}:=\sup \{\mathcal{X}-\mathrm{pd}M\mid M\in \mathcal{X}-{\mathrm{pd}}^{<\infty }\},$$

$$\mathcal{X}-\mathrm{FID}:=\sup \{\mathcal{X}-\mathrm{id}M\mid M\in \mathcal{X}-{\mathrm{id}}^{<\infty }\}.$$

For any $n\ge 0$, we use $\mathcal{X}$-${\mathrm{pd}}^{\le n}$ (resp. $\mathcal{X}$-${\mathrm{id}}^{\le n}$) to denote the subcategory of $\mathcal{A}$ consisting of objects with $\mathcal{X}$-projective (resp. $\mathcal{X}$-injective) dimension at most n.

Let $\mathcal{E}$ be a subcategory of $\mathcal{A}$. Recall from [7] that a sequence

$$\mathbb{S}:\cdots \to S_1\to S_2\to S_3\to \cdots$$

in $\mathcal{A}$ is called ${\mathrm{Hom}}_{\mathcal{A}}(\mathcal{E},-)$-exact (resp. ${\mathrm{Hom}}_{\mathcal{A}}(-,\mathcal{E})$-exact) if ${\mathrm{Hom}}_{\mathcal{A}}(E,\mathbb{S})$ (resp. ${\mathrm{Hom}}_{\mathcal{A}}(\mathbb{S},E)$) is exact for any $E\in \mathcal{E}$. Let $\mathcal{C}\subseteq \mathcal{T}$ be subcategories of $\mathcal{A}$. Recall from [1] that $\mathcal{C}$ is called an $\mathcal{E}$-proper generator (resp. $\mathcal{E}$-coproper cogenerator) for $\mathcal{T}$ if for any $T\in \mathcal{T}$, there exists a ${\mathrm{Hom}}_{\mathcal{A}}(\mathcal{E},-)$ (resp. ${\mathrm{Hom}}_{\mathcal{A}}(-,\mathcal{E})$)-exact exact sequence

$$0\to T^{\prime }\to C\to T\to 0(\mathrm{resp}.0\to T\to C\to T^{\prime }\to 0)$$

in $\mathcal{A}$ with $C\in \mathcal{C}$ and $T^{\prime }\in \mathcal{T}$. When $\mathcal{E}=\mathcal{P}\left(\mathcal{A}\right)$ (resp. $\mathcal{I}\left(\mathcal{A}\right)$), an $\mathcal{E}$-proper generator (resp. $\mathcal{E}$-coproper cogenerator) is exactly a usual generator (resp. cogenerator).

Definition 1.

([1]) Let $\mathcal{E}$ and $\mathcal{T}$ be subcategories of $\mathcal{A}$.

(1) 

The subcategory$\mathcal{T}$is called$\mathcal{E}$-preresolving in$\mathcal{A}$if the following conditions are satisfied.

(1.1) 

$\mathcal{T}$admits an$\mathcal{E}$-proper generator.

(1.2) 

$\mathcal{T}$is closed under$\mathcal{E}$-proper extensions, that is, for any${\mathrm{Hom}}_{\mathcal{A}}(\mathcal{E},-)$-exact exact sequence

$$0\to A_1\to A_2\to A_3\to 0$$

in$\mathcal{A}$, if both$A_1$and$A_3$are objects in$\mathcal{T}$, then$A_2$is also an object in$\mathcal{T}$.

(2) 

The subcategory$\mathcal{T}$is called$\mathcal{E}$-precoresolving in$\mathcal{A}$if the following conditions are satisfied.

(2.1) 

$\mathcal{T}$ admits an $\mathcal{E}$-coproper cogenerator.

(2.2) 

$\mathcal{T}$is closed under$\mathcal{E}$-coproper extensions, that is, for any${\mathrm{Hom}}_{\mathcal{A}}(-,\mathcal{E})$-exact exact sequence

$$0\to A_1\to A_2\to A_3\to 0$$

in$\mathcal{A}$, if both$A_1$and$A_3$are objects in$\mathcal{T}$, then$A_2$is also an object in$\mathcal{T}$.

Definition 2.

([8,9]). Let R and S be arbitrary associative rings. An (R-S)-bimodule ${}_R{C}_S$ is called semidualizing if the following conditions are satisfied.

(a1) 

${}_{R}C$admits a degreewise finite R-projective resolution.

(a2) 

$C_S$admits a degreewise finite$S^{op}$-projective resolution.

(b1) 

The homothety map${}_R{R}_R\stackrel{{}_R\gamma }{\to }{\mathrm{Hom}}_{S^{op}}(C,C)$is an isomorphism.

(b2) 

The homothety map${}_S{S}_S\stackrel{{\gamma }_S}{\to }{\mathrm{Hom}}_R(C,C)$is an isomorphism.

(c1) 

${\mathrm{Ext}}_R^{\ge 1}(C,C)=0$.

(c2) 

${\mathrm{Ext}}_{S^{op}}^{\ge 1}(C,C)=0$.

Typical examples of semidualizing bimodules include the free module of rank one and the dualizing module over a Cohen-Macaulay local ring.

3. Main Results

3.1. General Results

In this subsection, assume that $\mathcal{C}\subseteq \mathcal{T}$ and $\mathcal{E}$ are subcategories of an abelian category $\mathcal{A}$ and $\mathcal{C}$ is closed under direct summands.

The following result shows that under some conditions, any object in $\mathcal{A}$ with finite $\mathcal{T}$-projective dimension is isomorphic to a kernel (resp. a cokernel) of a morphism from an object with finite $\mathcal{C}$-projective dimension to an object in $\mathcal{T}$.

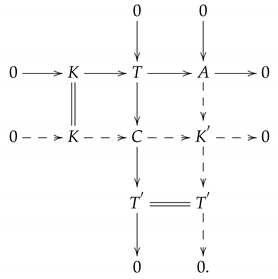
Lemma 1.

Let$\mathcal{T}$be an$\mathcal{E}$-precoresolving subcategory of$\mathcal{A}$admitting an$\mathcal{E}$-coproper cogenerator$\mathcal{C}$. If$A\in \mathcal{A}$satisfies$\mathcal{T}$-$\mathrm{pd}A\le n$with$n\ge 0$, then there exist exact sequences

$$0\to K\to T\to A\to 0,$$

(1)

$$0\to A\to K^{\prime }\to T^{\prime }\to 0$$

(2)

in$\mathcal{A}$with$T,T^{\prime }\in \mathcal{T}$,$\mathcal{C}$-$\mathrm{pd}K\le n-1$and$\mathcal{C}$-$\mathrm{pd}{K}^{\prime }\le n$.

Proof. 

Let $\mathcal{T}$-$\mathrm{pd}A\le n$. By ([1], Theorem 4.7) we get the exact sequence (1). Since $\mathcal{C}$ is an $\mathcal{E}$-coproper cogenerator for $\mathcal{T}$, there exists an exact sequence

$$0\to T\to C\to T^{\prime }\to 0$$

in $\mathcal{A}$ with $C\in \mathcal{C}$ and $T^{\prime }\in \mathcal{T}$. Consider the following push-out diagram

By the middle row in the above diagram, we have $\mathcal{C}$-$\mathrm{pd}{K}^{\prime }\le n$. Thus the rightmost column is the desired exact sequence (2). □

By using Lemma 1, we get the following result.

Theorem 1.

Let$\mathcal{T}$be an$\mathcal{E}$-precoresolving subcategory of$\mathcal{A}$admitting an$\mathcal{E}$-coproper cogenerator$\mathcal{C}$. If$\mathcal{C}$-${\mathrm{pd}}^{\le n}$is closed under direct summands for all$n\ge 0$, then we have

(1) 

For any$A\in {\mathcal{T}}^{\perp }$,$\mathcal{T}$-$\mathrm{pd}A=\mathcal{C}$-$\mathrm{pd}A$.

(2) 

If$\mathcal{T}\perp \mathcal{C}$, then we have

(2.1) 

For any$A\in \mathcal{C}$-${\mathrm{pd}}^{<\infty }$,$\mathcal{T}$-$\mathrm{pd}A=\mathcal{C}$-$\mathrm{pd}A$.

(2.2) 

$\mathcal{C}-\mathrm{FPD}\le \mathcal{T}-\mathrm{FPD}$.

(2.3) 

Assume that the following condition$(\star )$is satisfied: in any exact sequence

$$0\to A\to B\to T\to 0$$

in$\mathcal{A}$with$T\in \mathcal{T}$and$A\ne 0$,$\mathcal{T}$-$\mathrm{pd}A=\mathcal{T}$-$\mathrm{pd}B$. Then$\mathcal{C}-\mathrm{FPD}=\mathcal{T}-\mathrm{FPD}$.

Proof. 

(1) For any $A\in \mathcal{A}$, it is trivial that $\mathcal{T}$-$\mathrm{pd}A\le \mathcal{C}$-$\mathrm{pd}A$. Let $A\in {\mathcal{T}}^{\perp }$. It suffices to prove $\mathcal{C}$-$\mathrm{pd}A\le \mathcal{T}$-$\mathrm{pd}A$. Without loss of generality, suppose $\mathcal{T}$-$\mathrm{pd}A=n<\infty$. By Lemma 1, there exists an exact sequence

$$0\to A\to K^{\prime }\to T^{\prime }\to 0$$

(3)

in $\mathcal{A}$ with $T^{\prime }\in \mathcal{T}$ and $\mathcal{C}$-$\mathrm{pd}{K}^{\prime }\le n$. Since $A\in {\mathcal{T}}^{\perp }$, this exact sequence splits and A is a direct summand of $K^{\prime }$. Notice that $\mathcal{C}$-${\mathrm{pd}}^{\le n}$ is closed under direct summands by assumption, so we have $\mathcal{C}$-$\mathrm{pd}A\le n$.

(2) If $\mathcal{T}\perp \mathcal{C}$, then $\mathcal{C}$-${\mathrm{pd}}^{<\infty }\subseteq {\mathcal{T}}^{\perp }$ by the dimension shifting. Now the assertion (2.1) follows from (1), and (2.2) is an immediate consequence of (2.1).

Suppose $\mathcal{T}$-$\mathrm{pd}A=n<\infty$. Consider the exact sequence (3) again. If the condition $(\star )$ is satisfied, then $\mathcal{T}$-$\mathrm{pd}{K}^{\prime }=n$, and thus $\mathcal{C}$-$\mathrm{pd}{K}^{\prime }\ge \mathcal{T}$-$\mathrm{pd}{K}^{\prime }=n$. Since $\mathcal{C}$-$\mathrm{pd}{K}^{\prime }\le n$ by construction, we have $\mathcal{C}$-$\mathrm{pd}{K}^{\prime }=n$. From this fact, it follows that $\mathcal{T}-\mathrm{FPD}\le \mathcal{C}-\mathrm{FPD}$. □

As a consequence, we get the following result.

Corollary 1.

Let$\mathcal{T}$be an$\mathcal{E}$-precoresolving subcategory of$\mathcal{A}$admitting an$\mathcal{E}$-coproper cogenerator$\mathcal{C}$. If$\mathcal{T}\perp \mathcal{C}$, then we have

(1) 

For any$A\in {\mathcal{T}}^{\perp }$,$\mathcal{T}$-$\mathrm{pd}A=\mathcal{C}$-$\mathrm{pd}A$.

(2) 

For any$A\in \mathcal{C}$-${\mathrm{pd}}^{<\infty }$,$\mathcal{T}$-$\mathrm{pd}A=\mathcal{C}$-$\mathrm{pd}A$.

(3) 

$\mathcal{C}-\mathrm{FPD}\le \mathcal{T}-\mathrm{FPD}$.

(4) 

If the condition$(\star )$in Theorem 1 (2.3) is satisfied, then$\mathcal{C}-\mathrm{FPD}=\mathcal{T}-\mathrm{FPD}$.

Proof. 

It is trivial that $\mathcal{C}$ is a $\mathcal{C}$-precoresolving subcategory of $\mathcal{A}$ admitting a $\mathcal{C}$-coproper cogenerator $\mathcal{C}$. The assumption $\mathcal{T}\perp \mathcal{C}$ implies $\mathcal{C}\perp \mathcal{C}$ clearly, it follows from ([1], Corollaty 3.9) that $\mathcal{C}$-${\mathrm{pd}}^{\le n}$ is closed under direct summands for all $n\ge 0$. Now the assertions follow from Theorem 1. □

The following three results are completely dual to Lemma 1, Theorem 1 and Corollary 1. We omit their proofs.

Lemma 2.

Let$\mathcal{T}$be an$\mathcal{E}$-preresolving subcategory of$\mathcal{A}$admitting an$\mathcal{E}$-proper generator$\mathcal{C}$. If$A\in \mathcal{A}$satisfies$\mathcal{T}$-$\mathrm{id}A\le n$with$n\ge 0$, then there exist exact sequences

$$0\to A\to T\to K\to 0,$$

$$0\to T^{\prime }\to K^{\prime }\to A\to 0$$

in$\mathcal{A}$with$T,T^{\prime }\in \mathcal{T}$,$\mathcal{C}$-$\mathrm{id}K\le n-1$and$\mathcal{C}$-$\mathrm{id}{K}^{\prime }\le n$.

Theorem 2.

Let$\mathcal{T}$be an$\mathcal{E}$-preresolving subcategory of$\mathcal{A}$admitting an$\mathcal{E}$-proper generator$\mathcal{C}$. If$\mathcal{C}$-${\mathrm{id}}^{\le n}$is closed under direct summands for all$n\ge 0$, then we have

(1) 

For any$A\in {}^{\perp }\mathcal{T}$,$\mathcal{T}$-$\mathrm{id}A=\mathcal{C}$-$\mathrm{id}A$.

(2) 

If$\mathcal{C}\perp \mathcal{T}$, then we have

(2.1) 

For any$A\in \mathcal{C}$-${\mathrm{id}}^{<\infty }$,$\mathcal{T}$-$\mathrm{id}A=\mathcal{C}$-$\mathrm{id}A$.

(2.2) 

$\mathcal{C}-\mathrm{FID}\le \mathcal{T}-\mathrm{FID}$.

(2.3) 

Assume that the following condition$(\star \star )$is satisfied: in any exact sequence

$$0\to T\to B\to A\to 0$$

in$\mathcal{A}$with$T\in \mathcal{T}$and$A\ne 0$,$\mathcal{T}$-$\mathrm{id}A=\mathcal{T}$-$\mathrm{id}B$. Then$\mathcal{C}-\mathrm{FID}=\mathcal{T}-\mathrm{FID}$.

Corollary 2.

Let$\mathcal{T}$be an$\mathcal{E}$-preresolving subcategory of$\mathcal{A}$admitting an$\mathcal{E}$-proper generator$\mathcal{C}$. If$\mathcal{C}\perp \mathcal{T}$, then we have

(1) 

For any$A\in {}^{\perp }\mathcal{T}$,$\mathcal{T}$-$\mathrm{id}A=\mathcal{C}$-$\mathrm{id}A$.

(2) 

For any$A\in \mathcal{C}$-${\mathrm{id}}^{<\infty }$,$\mathcal{T}$-$\mathrm{id}A=\mathcal{C}$-$\mathrm{id}A$.

(3) 

$\mathcal{C}-\mathrm{FID}\le \mathcal{T}-\mathrm{FID}$.

(4) 

If the condition$(\star \star )$in Theorem 2 (2.3) is satisfied, then$\mathcal{C}-\mathrm{FID}=\mathcal{T}-\mathrm{FID}$.

Definition 3.

([10]) The Gorenstein subcategory $\mathcal{G}\left(\mathcal{C}\right)$ of $\mathcal{A}$ is defined as $\mathcal{G}\left(\mathcal{C}\right)=\{A\in \mathcal{A}\mid$ there exists an exact sequence

$$\cdots \to C_1\to C_0\to C^0\to C^1\to \cdots$$

in $\mathcal{A}$ with all $C_i,C^i$ in $\mathcal{C}$, which is both ${\mathrm{Hom}}_{\mathcal{A}}(\mathcal{C},-)$-exact and ${\mathrm{Hom}}_{\mathcal{A}}(-,\mathcal{C})$-exact, such that $A\cong \mathrm{Im}(C_0\to C^0)\}$.

The Gorenstein subcategory unifies the following notions: modules of Gorenstein dimension zero ([11]), Gorenstein projective modules, Gorenstein injective modules ([12]), V-Gorenstein projective modules, V-Gorenstein injective modules ([13]), $\mathcal{W}$-Gorenstein modules ([14]), and so on (see ([15], Remark 2.7) for the details).

Corollary 3.

If$\mathcal{C}\perp \mathcal{C}$, then we have

(1) 

$\mathcal{C}-\mathrm{FPD}=\mathcal{G}\left(\mathcal{C}\right)-\mathrm{FPD}$.

(2) 

$\mathcal{C}-\mathrm{FID}=\mathcal{G}\left(\mathcal{C}\right)-\mathrm{FID}$.

Proof. 

(1) Let $\mathcal{C}\perp \mathcal{C}$. By ([10], Corollaries 4.5 and 4.7), we have that $\mathcal{G}\left(\mathcal{C}\right)$ is closed under extensions and $\mathcal{G}\left(\mathcal{C}\right)\perp \mathcal{C}$. It follows from the definition of Gorenstein subcategories that $\mathcal{G}\left(\mathcal{C}\right)$ is $\mathcal{C}$-precoresolving in $\mathcal{A}$ admitting a $\mathcal{C}$-coproper cogenerator $\mathcal{C}$. ([15], Corollary 5.10) implies that the condition $(\star )$ is satisfied. Now the assertion follows from Corollary 1.

(2) It is dual to (1). □

3.2. Applications

In this subsection, all rings are associative rings with units. For a ring R, $\mathrm{Mod}R$ is the category of left R-modules and $\mathrm{mod}R$ is the category of finitely presented left R-modules. For a left R-module M, we use ${\mathrm{Add}}_{R}M$ (${\mathrm{add}}_{R}M$) to denote the class consisting of all modules isomorphic to direct summands of direct sums of (finitely many) copies of M.

From now on, R and S are arbitrary rings and we fix a semidualizing bimodule ${}_R{C}_S$. Following [9], set

$${\mathcal{P}}_C\left(R\right):=\{C{\otimes }_{S}P\mid P\mathrm{is}\mathrm{projective}\mathrm{in}\mathrm{Mod}S\},$$

$${\mathcal{F}}_C\left(R\right):=\{C{\otimes }_{S}F\mid F\mathrm{is}\mathrm{flat}\mathrm{in}\mathrm{Mod}S\},$$

$${\mathcal{I}}_C\left(S\right):=\{{\mathrm{Hom}}_R(C,I)\mid I\mathrm{is}\mathrm{injective}\mathrm{in}\mathrm{Mod}R\},$$

$${\mathcal{I}}_C\left(R^{op}\right):=\{{\mathrm{Hom}}_{S^{op}}(C,I^{\prime })\mid I^{\prime }\mathrm{is}\mathrm{injective}\mathrm{in}\mathrm{Mod}{S}^{op}\}.$$

The modules in ${\mathcal{P}}_C\left(R\right)$, ${\mathcal{F}}_C\left(R\right)$ and ${\mathcal{I}}_C\left(S\right)$ (${\mathcal{I}}_C\left(R^{op}\right)$) are called C-projective, C-flat and C-injective respectively. Note that ${\mathcal{P}}_C\left(R\right)={\mathrm{Add}}_{R}C$ ([16], Proposition 2.4 (1)). When ${}_R{C}_S={}_R{R}_R$, C-projective, C-flat and C-injective modules are exactly projective, flat and injective modules respectively.

Recall that a sequence in $\mathrm{Mod}R$ is called $({\mathcal{I}}_C\left(R^{op}\right){\otimes }_R-)$-exact if it is exact after applying the functor $E{\otimes }_R-$ for any $E\in {\mathcal{I}}_C\left(R^{op}\right)$.

3.2.1. C-Gorenstein Modules

The following notions were introduced by Holm and Jøgensen in [17] for commutative rings. The following are their non-commutative versions.

Definition 4.

([16])

(1) 

A module$M\in \mathrm{Mod}R$is called C-Gorenstein projective if there exists a${\mathrm{Hom}}_R(-,{\mathrm{Add}}_{R}C)$-exact exact sequence

$$\cdots \to P_1\to P_0\to G^0\to G^1\to \cdots$$

in$\mathrm{Mod}R$with all$P_i$projective and$G^i$in${\mathrm{Add}}_{R}C$, such that$M\cong \mathrm{Im}(P_0\to G^0)$.

(2) 

A module$M\in \mathrm{Mod}R$is called C-Gorenstein flat if there exists an$({\mathcal{I}}_C\left(R^{op}\right){\otimes }_R-)$-exact exact sequence

$$\cdots \to F_1\to F_0\to Q^0\to Q^1\to \cdots$$

in$\mathrm{Mod}R$with all$F_i$flat and$Q^i$in${\mathcal{F}}_C\left(R\right)$, such that$M\cong \mathrm{Im}(F_0\to Q^0)$.

(3) 

A module$N\in \mathrm{Mod}S$is called C-Gorenstein injective if there exists a${\mathrm{Hom}}_S({\mathcal{I}}_C\left(S\right),-)$-exact exact sequence

$$\cdots \to E_1\to E_0\to I^0\to I^1\to \cdots$$

in$\mathrm{Mod}S$with all$I^i$injective and$E_i$in${\mathcal{I}}_C\left(S\right)$.

We use ${\mathcal{GP}}_C\left(R\right)$ (resp. ${\mathcal{GF}}_C\left(R\right)$) to denote the subcategory of $\mathrm{Mod}R$ consisting of C-Gorenstein projective (resp. flat) modules, and use ${\mathcal{GI}}_C\left(S\right)$ to denote the subcategory of $\mathrm{Mod}S$ consisting of C-Gorenstein injective modules. When ${}_R{C}_S={}_R{R}_R$, C-Gorenstein projective, flat and injective modules are exactly Gorenstein projective, flat and injective modules respectively ([2,7]).

Theorem 3.

(1) 

${\mathcal{P}}_C\left(R\right)-\mathrm{FPD}={\mathcal{GP}}_C\left(R\right)-\mathrm{FPD}$.

(2) 

${\mathcal{I}}_C\left(S\right)-\mathrm{FID}={\mathcal{GI}}_C\left(S\right)-\mathrm{FID}$.

Proof. 

(1) By ([16], Lemma 3.2 (3)), we have that ${\mathcal{GP}}_C\left(R\right)$ is closed under extensions. It follows from the definition of C-Gorenstein projective modules that ${\mathcal{GP}}_C\left(R\right)\perp {\mathcal{P}}_C\left(R\right)$ and ${\mathcal{GP}}_C\left(R\right)$ is ${\mathcal{P}}_C\left(R\right)$-precoresolving in $\mathrm{Mod}R$ admitting a ${\mathcal{P}}_C\left(R\right)$-coproper cogenerator ${\mathcal{P}}_C\left(R\right)$. ([16], Proposition 3.3 (1))implies that the condition $(\star )$ is satisfied. Now the assertion follows from Corollary 1.

(2) It is dual to (1). □

We define $\mathcal{G}{p}_C\left(R\right):=\{M\in \mathrm{mod}R\mid$ there exists a ${\mathrm{Hom}}_R(-,{\mathrm{add}}_{R}C)$-exact exact sequence

$$\cdots \to P_1\to P_0\to G^0\to G^1\to \cdots$$

(4)

in $\mathrm{mod}R$ with all $P_i$ projective and $G^i$ in ${\mathrm{add}}_{R}C$, such that $M\cong \mathrm{Im}(P_0\to G^0)\}$.

Proposition 1.

If R is a left coherent ring, then

$$\mathcal{G}{p}_C\left(R\right)={\mathcal{GP}}_C\left(R\right)\cap \mathrm{mod}R.$$

Proof. 

We first prove $\mathcal{G}{p}_C\left(R\right)\subseteq {\mathcal{GP}}_C\left(R\right)\cap \mathrm{mod}R$. Let $M\in \mathcal{G}{p}_C\left(R\right)$. Then there exists an exact sequence as (4). Then ${\mathrm{Ext}}_R^{\ge 1}(M,C)=0$. It follows from ([7], Lemma 10.2.4) that ${\mathrm{Ext}}_R^{\ge 1}(M,{\mathrm{Add}}_{R}C)=0$, and so the exact sequence

$$\cdots \to P_1\to P_0\to M\to 0$$

is ${\mathrm{Hom}}_R(-,{\mathrm{Add}}_{R}C)$-exact. Similarly, the exact sequence

$$0\to M\to G^0\to G^1\to \cdots$$

is ${\mathrm{Hom}}_R(-,{\mathrm{Add}}_{R}C)$-exact. Thus the exact sequence (4) is also ${\mathrm{Hom}}_R(-,{\mathrm{Add}}_{R}C)$-exact and $M\in {\mathcal{GP}}_C\left(R\right)\cap \mathrm{mod}R$.

Next we will prove ${\mathcal{GP}}_C\left(R\right)\cap \mathrm{mod}R\subseteq \mathcal{G}{p}_C\left(R\right)$. Let $M\in {\mathcal{GP}}_C\left(R\right)\cap \mathrm{mod}R$. Since R is left coherent, there exists a ${\mathrm{Hom}}_R(-,{\mathrm{add}}_{R}C)$-exact exact sequence

$$\cdots \to P_1\to P_0\to M\to 0$$

(5)

in $\mathrm{mod}R$ with all $P_i$ projective. On the other hand, by the definition of C-Gorenstein projective modules and ([16], Theorem 2.10), there exists a ${\mathrm{Hom}}_R(-,{\mathrm{Add}}_{R}C)$-exact exact sequence

$$0\to M\to G\to M^{\prime }\to 0$$

in $\mathrm{Mod}R$ with $G\in {\mathrm{Add}}_{R}C$ and $M^{\prime }\in {\mathcal{GP}}_C\left(R\right)$. We may assume that $G=C^{\left(I\right)}$ for some indexed set I. Since M is finitely presented, there exists a decomposition $G=G^0\oplus G^{\prime }$ with $G^0\in {\mathrm{add}}_{R}C$, such that there exists a ${\mathrm{Hom}}_R(-,{\mathrm{Add}}_{R}C)$-exact exact sequence

$$0\to M\to G^0\to M^1\to 0$$

with $M^{\prime }\cong M^1\oplus G^{\prime }$. So $M^1\in {\mathcal{GP}}_C\left(R\right)\cap \mathrm{mod}R$. Repeating this procedure, we get a ${\mathrm{Hom}}_R(-,{\mathrm{Add}}_{R}C)$-exact (and hence ${\mathrm{Hom}}_R(-,{\mathrm{add}}_{R}C)$-exact) exact sequence

$$0\to M\to G^0\to G^1\to \cdots$$

(6)

in $\mathrm{mod}R$ with all $G^i$ in ${\mathrm{add}}_{R}C$. It follows from the exact sequences (5) and (6) that $M\in \mathcal{G}{p}_C\left(R\right)$. □

For a left R-module M, we use ${\mathrm{pd}}_{R}M$ and ${\mathrm{Gpd}}_{R}M$ to denote the projective and Gorenstein projective dimensions of M respectively. We write

$$\mathrm{Fin}.\dim R:=\sup \{{\mathrm{pd}}_{R}M\mid M\in \mathrm{Mod}R\mathrm{with}{\mathrm{pd}}_{R}M<\infty \},$$

$$G-\mathrm{Fin}.\dim R:=\sup \{{\mathrm{Gpd}}_{R}M\mid M\in \mathrm{Mod}R\mathrm{with}{\mathrm{Gpd}}_{R}M<\infty \},$$

$$\mathrm{fin}.\dim R:=\sup \{{\mathrm{pd}}_{R}M\mid M\in \mathrm{mod}R\mathrm{with}{\mathrm{pd}}_{R}M<\infty \},$$

$$G-\mathrm{fin}.\dim R:=\sup \{{\mathrm{Gpd}}_{R}M\mid M\in \mathrm{mod}R\mathrm{with}{\mathrm{Gpd}}_{R}M<\infty \}.$$

In the following result, the first assertion is ([2], Theorem 2.28), and the second one was proved in ([3], Lemma 4.6) when R is an artin algebra.

Corollary 4.

(1) 

$\mathrm{Fin}.\dim R=G-\mathrm{Fin}.\dim R$.

(2) 

If R is a left coherent ring, then$\mathrm{fin}.\dim R=G-\mathrm{fin}.\dim R$.

Proof. 

(1) Putting $\mathcal{A}=\mathrm{Mod}R$ and $\mathcal{C}=\mathcal{P}\left(R\right)$ (the subcategory of $\mathrm{Mod}R$ consisting of projective modules) in Corollary 3 (1), or putting ${}_R{C}_S={}_R{R}_R$ in Theorem 3 (1), the assertion follows.

(2) Let R be a left coherent ring. Then $\mathrm{mod}R$ is an abelian category. By putting ${}_R{C}_S={}_R{R}_R$ in Proposition 1, we have that $\mathcal{G}{p}_R\left(R\right)$ is exactly the subcategory of $\mathrm{mod}R$ consisting of Gorenstein projective modules. It is trivial that $\mathcal{G}\left(p\left(R\right)\right)=\mathcal{G}{p}_R\left(R\right)$, where $p\left(R\right)$ is the subcategory of $\mathrm{mod}R$ consisting of projective modules. Now putting $\mathcal{A}=\mathrm{mod}R$ and $\mathcal{C}=p\left(R\right)$ in Corollary 3 (1), the assertion follows. □

It is well known that projective left R-modules are flat. However, it is an open question:

$$Are Gorenstein project left R-modules Gorenstein flat?$$

The answer to this question is positive when R is a right coherent ring and $\mathrm{Fin}.\dim R<\infty$ ([2], Proposition 3.4).

Set ${(-)}^{+}:={\mathrm{Hom}}_{\mathbb{Z}}(-,\mathbb{Q}/\mathbb{Z})$, where $\mathbb{Z}$ is the additive group of integers and $\mathbb{Q}$ is the additive group of rational numbers. We write ${\mathcal{I}}_C{\left(R^{op}\right)}^{+}:=\{E^{+}\mid E\in {\mathcal{I}}_C\left(R^{op}\right)\}$. We have the following result.

Proposition 2.

If${\mathcal{I}}_C{\left(R^{op}\right)}^{+}\subseteq {\mathcal{F}}_C\left(R\right)$and${\mathcal{P}}_C\left(R\right)-\mathrm{FPD}<\infty$, then any C-Gorenstein projective left R-module is C-Gorenstein flat.

Proof. 

Let M be a C-Gorenstein projective left R-module. Then there exists a ${\mathrm{Hom}}_R(-,{\mathrm{Add}}_{R}C)$-exact exact sequence

$$\cdots \to P_1\to P_0\to G^0\to G^1\to \cdots$$

(7)

in $\mathrm{Mod}R$ with all $P_i$ projective and $G^i$ in ${\mathrm{Add}}_{R}C$, such that $M\cong \mathrm{Im}(P_0\to G^0)$. By using induction on the dimension, it is easy to verify that the exact sequence (7) is ${\mathrm{Hom}}_R(-,H^{\prime })$-exact for any $H^{\prime }\in \mathrm{Mod}R$ with ${\mathcal{P}}_C\left(R\right)$-$\mathrm{pd}{H}^{\prime }<\infty$.

Now let $E\in {\mathcal{I}}_C\left(R^{op}\right)$. Then $E^{+}\in {\mathcal{F}}_C\left(R\right)$ by assumption. Since ${\mathcal{P}}_C\left(R\right)-\mathrm{FPD}<\infty$ by assumption, we have ${\mathcal{P}}_C\left(R\right)$-$\mathrm{pd}{E}^{+}<\infty$ by ([18], Proposition 3.1). It follows that the exact sequence (7) is ${\mathrm{Hom}}_R(-,E^{+})$-exact, and hence $(E{\otimes }_R-)$-exact by the adjoint isomorphism theorem. Thus M is C-Gorenstein flat. □

When ${}_R{C}_S={}_R{R}_R$, we have ${\mathcal{P}}_C\left(R\right)-\mathrm{FPD}=\mathrm{Fin}.\dim R$. Moreover, if R is a right coherent ring, then ${\mathcal{I}}_R{\left(R^{op}\right)}^{+}\subseteq {\mathcal{F}}_R\left(R\right)$ by ([2], Theorem 3.6). Thus ([2], Proposition 3.4) is an immediate consequence of Proposition 2.

3.2.2. Auslander and Bass Classes

Let $M\in \mathrm{Mod}R$ and $N\in \mathrm{Mod}S$. Then we have the following two canonical evaluation homomorphisms

$${\theta }_M:C{\otimes }_S{\mathrm{Hom}}_R(C,M)\to M$$

defined by ${\theta }_M(c\otimes f)=f\left(c\right)$ for any $c\in C$ and $f\in {\mathrm{Hom}}_R(C,M)$; and

$${\mu }_N:N\to {\mathrm{Hom}}_R(C,C{\otimes }_{S}N)$$

defined by ${\mu }_N\left(x\right)\left(c\right)=c\otimes x$ for any $x\in N$ and $c\in C$.

Definition 5.

([9])

(1) 

The Auslander class${\mathcal{A}}_C\left(S\right)$with respect to C consists of all left S-modules N satisfying the following conditions.

(A1) 

${\mathrm{Tor}}_{\ge 1}^S(C,N)=0$.

(A2) 

${\mathrm{Ext}}_R^{\ge 1}(C,C{\otimes }_{S}N)=0$.

(A3) 

${\mu }_N$is an isomorphism in$\mathrm{Mod}S$.

(2) 

The Bass class${\mathcal{B}}_C\left(R\right)$with respect to C consists of all left R-modules M satisfying the following conditions.

(B1) 

${\mathrm{Ext}}_R^{\ge 1}(C,M)=0$

(B2) 

${\mathrm{Tor}}_{\ge 1}^S(C,{\mathrm{Hom}}_R(C,M))=0$.

(B3)

${\theta }_M$is an isomorphism in$\mathrm{Mod}R$.

It follows from ([9], Lemma 5.1) that ${\mathcal{I}}_C\left(S\right)\subseteq {\mathcal{A}}_C\left(S\right)$ and ${\mathcal{P}}_C\left(R\right)\subseteq {\mathcal{B}}_C\left(R\right)$. We have the following result.

Theorem 4.

(1) 

${\mathcal{I}}_C\left(S\right)-\mathrm{FPD}={\mathcal{A}}_C\left(S\right)-\mathrm{FPD}$.

(2) 

${\mathcal{P}}_C\left(R\right)-\mathrm{FID}={\mathcal{B}}_C\left(R\right)-\mathrm{FID}$.

Proof. 

(1) It follows from ([9], Theorems 2 and 6.2) that ${\mathcal{A}}_C\left(S\right)$ is ${\mathcal{I}}_C\left(S\right)$-precoresolving in $\mathrm{Mod}S$ admitting an ${\mathcal{I}}_C\left(S\right)$-coproper cogenerator ${\mathcal{I}}_C\left(S\right)$. By ([19], Lemma 3.5 (2)), we have ${\mathcal{A}}_C\left(S\right)\perp {\mathcal{I}}_C\left(S\right)$.

Let

$$0\to A\to B\to T\to 0$$

be an exact sequence in $\mathrm{Mod}S$ with $T\in {\mathcal{A}}_C\left(S\right)$ and $A\ne 0$. Then ${\mathrm{Tor}}_{\ge 1}^S(C,T)=0$, and hence ${\mathrm{Tor}}_i^S(C,A)$ $\cong {\mathrm{Tor}}_i^S(C,B)$ for any $i\ge 1$. By ([20], Proposition 4.2), ${\mathcal{A}}_C\left(S\right)$-${\mathrm{pd}}^{<\infty }$ is closed under extensions and kernels of epimorphisms. So ${\mathcal{A}}_C\left(S\right)$-${\mathrm{id}}_{S}A<\infty$ if and only if ${\mathcal{A}}_C\left(S\right)$-${\mathrm{id}}_{S}B<\infty$. Then ([20], Theorem 4.4) yields

$${\mathcal{A}}_C\left(S\right)-\mathrm{pd}A\le n\iff {\mathrm{Tor}}_{\ge n+1}^S(C,A)=0\iff {\mathrm{Tor}}_{\ge n+1}^S(C,B)=0\iff {\mathcal{A}}_C\left(S\right)-\mathrm{pd}B\le n,$$

which implies ${\mathcal{A}}_C\left(S\right)-\mathrm{pd}A={\mathcal{A}}_C\left(S\right)-\mathrm{pd}B$. Now the assertion follows from Corollary 1.

(2) It follows from ([9], Theorems 6.1 and 6.2) that ${\mathcal{B}}_C\left(R\right)$ is ${\mathcal{P}}_C\left(R\right)$-preresolving in $\mathrm{Mod}R$ admitting a ${\mathcal{P}}_C\left(R\right)$-proper generator ${\mathcal{P}}_C\left(R\right)$. By ([18], Lemma 2.5 (1)), we have ${\mathcal{P}}_C\left(R\right)\perp {\mathcal{B}}_C\left(R\right)$.

Let

$$0\to T\to B\to A\to 0$$

be an exact sequence in $\mathrm{Mod}R$ with $T\in {\mathcal{B}}_C\left(R\right)$ and $A\ne 0$. Then ${\mathrm{Ext}}_R^{\ge 1}(C,T)=0$, and hence ${\mathrm{Ext}}_R^i(C,B)$ $\cong {\mathrm{Ext}}_R^i(C,A)$ for any $i\ge 1$. By the dual of ([20], Proposition 4.2), ${\mathcal{B}}_C\left(R\right)$-${\mathrm{id}}^{<\infty }$ is closed under extensions and cokernels of monomorphisms. So ${\mathcal{B}}_C\left(R\right)$-$\mathrm{id}B<\infty$ if and only if ${\mathcal{B}}_C\left(R\right)$-$\mathrm{id}A<\infty$. Then ([21], Theorem 4.2) yields

$${\mathcal{B}}_C\left(R\right)-\mathrm{id}B\le n\iff {\mathrm{Ext}}_R^{\ge n+1}(C,B)=0\iff {\mathrm{Ext}}_R^{\ge n+1}(C,A)=0\iff {\mathcal{B}}_C\left(R\right)-\mathrm{id}A\le n,$$

which implies ${\mathcal{B}}_C\left(R\right)-\mathrm{id}B={\mathcal{B}}_C\left(R\right)-\mathrm{id}A$. Now the assertion follows from Corollary 2. □