Abstract
We present a constructive approach to Bernstein copulas with an admissible discrete skeleton in arbitrary dimensions when the underlying marginal grid sizes are smaller than the number of observations. This prevents an overfitting of the estimated dependence model and reduces the simulation effort for Bernstein copulas a lot. In a case study, we compare different approaches of Bernstein and Gaussian copulas regarding the estimation of risk measures in risk management.
MSC:
62H05; 62H12; 62H17; 11K45
1. Introduction
Since the pioneering paper [1] by Serge Bernstein in 1912, Bernstein polynomials have been an indispensable tool in calculus and approximation theory (see, e.g., [2]). Bernstein copulas, which can be considered to be Bernstein polynomials for empirical and other copula functions, have a long tradition in nonparametric modelling of dependence structures in arbitrary dimensions, in particular, with applications in risk management, and have come into a deeper focus in the recent years. There is an extensive list of research papers on this topic, for instance, [3,4,5,6,7,8,9,10,11,12,13,14]. In particular, the monographs [15,16] have devoted separate chapters to the topic of Bernstein copulas.
A very important aspect of Bernstein copulas lies in Monte Carlo simulation techniques of dependence structures, in particular, in higher dimensions. The structure of such procedures ranges from very complex (see, e.g., [10]) to extremely simple (see, e.g., [5]), such that Monte Carlo simulations could, for instance, be performed easily with ordinary spreadsheets, in particular, in applications concerning quantitative risk management.
From a statistical point of view, the problem of a potential overfitting of the true underlying dependence structure with Bernstein polynomials emerges naturally when the pertaining Bernstein polynomial degree increases, i.e., with an increasing number of observations. This has been discussed extensively, for instance, in [6] (Section 3.1), [7] (Section 4), [17] (Section 3.2.1) or [14] (Remark 4). This leads to the fact that the Bernstein copula density becomes more wiggly the more empirical observations are used in the analysis. In comparison with classical parametric dependence models such as elliptically contoured or Archimedean copulas, this is probably a nondesirable property. In particular, this problem has been tackled seemingly first in [10] by approximating the underlying discrete skeleton for the Bernstein copula by a least-squares approach and recently in the Ph.D. thesis [18], where cluster analytic methods were used.
In the present paper, we propose a simple but yet effective approach to reduce the complexity of Bernstein copulas in a two-step approach, namely first an augmentation step in combination with a second reduction step. The reduction step is also discussed in [12]; however, without a possible application to a general complexity reduction of Bernstein copulas.
2. Some Important Facts about Multivariate Bernstein Polynomials
Let f be an arbitrary bounded real-valued function on the unit cube with dimension . Furthermore, let , …, be integers. The corresponding multivariate Bernstein polynomial is defined by
with (see, e.g., [2] (p. 51)). It is known that for multivariate Bernstein polynomials converge to f at any point of continuity and approximate f uniformly if f is continuous on .
Another important property of multivariate Bernstein polynomials, which is perhaps less known in the mathematical community, is the fact that the multivariate Bernstein polynomial density given by
can be written as a linear combination of product beta densities. For this purpose, consider univariate beta densities
where denotes the Euler beta function, i.e., . We need the following definition to proceed.
Definition 1.
Let g be a real-valued bounded function on . We call
the Δ-difference of g over the interval with , and , . (We adopt here a notation similar to that in [19] (Definition 2.1), which is slightly different from the notation in [20] (Definition 1.2.10).)
Proposition 1.
With the above notation, the Bernstein polynomial density can be represented as
with and .
Proof.
This follows immediately from the arguments in the proof of Theorem 2.2. in [5]; compare also the line of proofs in [21]. □
Example 1.
We consider the polynomial , , with , . In this case, the two-dimensional Bernstein polynomial differs from f due to smaller polynomial degrees. We have
with
Please note that here
or, in tabular form, the values are given in Table 1.

Table 1.
Values of for the polynomial in Example 1.
After a little computation it is easy to see that indeed here
The plots of , and are shown in Figure 1.
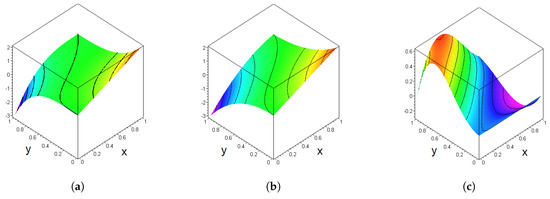
Figure 1.
Plots of the functions in Example 1. (a) Plot of f(x,y). (b) Plot of Bnf(x,y). (c) Plot of f(x,y) − Bnf(x,y).
A direct consequence of Proposition 1 concerns the monotonicity behavior of multivariate Bernstein polynomials.
Definition 2.
Let g be a real-valued function on . We call g d-monotone iff for all , with , .
It is obvious by the iterated mean value theorem that for a sufficiently smooth function g, d-monotonicity is equivalent to
Please note that in the case that g is a d-dimensional cumulative distribution function of a probability measure on the d-dimensional Borel -field , then .
Proposition 2.
Let f be a real-valued d-monotone function on . Then the corresponding multivariate Bernstein polynomial is also d-monotone. In particular, the Bernstein polynomial density is a positive linear combination of product beta densities.
Proof.
By the arguments above and the notation as in Proposition 1, we have
which is a sufficient condition for to be d-monotone. □
Please note that the polynomial f from Example 1 is not 2-monotone since with and . However, the slightly modified polynomial is 2-monotone since with the unique global minimum point and . With respect to the corresponding multivariate Bernstein polynomial, we now obtain the values given in Table 2, which also explicitly shows that the Bernstein polynomial is 2-monotone.

Table 2.
Values of for the modified polynomial .
3. From Bernstein Polynomials to Bernstein Copulas
Remark 1.
Seemingly Proposition 2 can be usefully applied to arbitrary d-dimensional cumulative distribution functions F concentrated on the unit cube (continuous or not) such that the corresponding multivariate Bernstein polynomial
is also a cumulative distribution function since is non-negative and d-increasing with and . In particular, the Bernstein polynomial density is always a (probabilistic) mixture of product beta densities, as explicitly noted in [5,12] for Bernstein copulas. Note also that this observation was the motivation for the setup in [22].
Example 2.

We consider a two-dimensional random vector with a discrete distribution concentrated on with and given by Table 3.

Table 3.
Distribution of the vector in Example 2.
Let H denote the Heaviside unit step function, i.e.,
Then the corresponding cumulative distribution function F for the given discrete distribution is
The graphs in Figure 2, Figure 3 and Figure 4 show the corresponding cumulative distribution function F as well as the corresponding Bernstein polynomials and densities for various choices of according to relations (11) and (12) above.
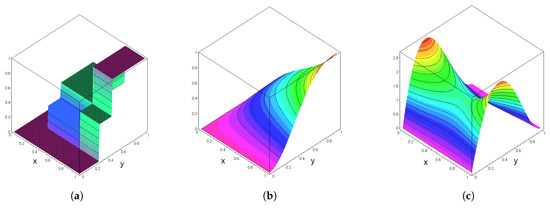
Figure 2.
Plots of the functions in Example 2, n1 = 3 and n2 = 5. (a) Plot of F(x,y). (b) Plot of BnF(x,y). (c) Plot of bnF(x,y).
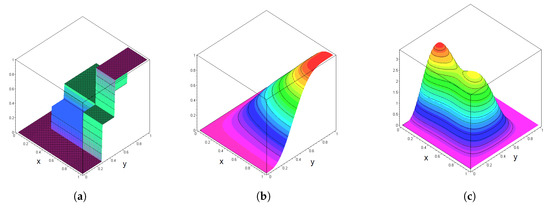
Figure 3.
Plots of the functions in Example 2, n1 = 11 and n2 = 7. (a) Plot of F(x,y). (b) Plot of BnF(x,y). (c) Plot of bnF(x,y).
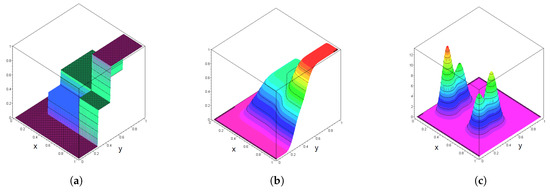
Figure 4.
Plots of the functions in Example 2, n1 = 50 and n2 = 50. (a) Plot of F(x,y). (b) Plot of BnF(x,y). (c) Plot of bnF(x,y).
The graphs in Figure 2, Figure 3 and Figure 4 clearly visualize the approximation effect of multivariate Bernstein polynomials for discrete multivariate distributions if gets large. In particular, the Bernstein polynomial density has spikes around the support points of the underlying discrete distribution.
To simplify notation, we will use the following convention. Let be a natural number and be arbitrary. Then, for , let
denote the vector , where the k-th component is replaced by y.
Proposition 3.
Suppose that for , there is a cumulative distribution function with and such that for given natural numbers we have for , , , where . Then the d-dimensional Bernstein polynomial with associated with F is a copula.
Proof.
By Remark 1, we know that is also a cumulative distribution function with and , and (note that )
for and ( is the expectation of the Binomial distribution with trials and success probability x). Hence the marginal distributions induced by B are continuous uniform, which means that B is indeed a copula. □
Please note that Proposition 3 is already implicitly formulated in [5,10] (see also [15] (Chapter 4.1.2)). We reformulate the corresponding statements there in an appropriate way.
Corollary 1.
Let be a discrete random vector whose marginal component follows a discrete uniform distribution over with integers , . Then the multivariate Bernstein polynomial derived from the cumulative distribution function F for the scaled random vector given by , , is a copula. The corresponding Bernstein copula density is given by
Proof.
For , , we have
and hence
□
Remark 2.
We call the Bernstein copula induced by . In coincidence with [10] we also call the discrete skeleton of the Bernstein copula and the number its grid size. If is an arbitrary discrete random vector over , we call an admissible discrete skeleton if the marginal distributions are discrete uniform. So every admissible skeleton over induces a corresponding Bernstein copula via the multivariate Bernstein polynomial of its rescaled cumulative distribution function. The corresponding Bernstein copula density is a mixture of product beta kernels with weights given by the individual probabilities representing the admissible skeleton.
4. Empirical Bernstein Copulas
Bernstein copulas can be easily constructed from independent samples , …, , , of d-dimensional random vectors with the same intrinsic dependence structure and the same marginal distributions. For simplicity, we assume here that the marginal distributions are continuous in order to avoid ties in the observations. The simplest way to construct an empirical Bernstein copula is on the basis of Deheuvel’s empirical copula in the form of a cumulative distribution function (see [20]), which can be represented by an admissible discrete skeleton derived from the individual ranks , , , of the observation vectors , , given by the order statistics , i.e., iff is the k-largest value of the i-th observed component. Here the discrete skeleton is given by a random vector over with a discrete uniform distribution over the n support points , …, , where , . Since the empirical copula converges in distribution to the true underlying copula as , it follows that the corresponding empirical Bernstein copula does so likewise (cf. [15] (Chapter 4.1.2)). This provides—in the light of relation (16)—in particular, a simple way to generate samples from an empirical Bernstein copula by Monte Carlo methods in two steps:
- Step 1: Select an index N randomly and uniformly among 1, …, n.
- Step 2: Generate d independent beta distributed random variables , …, (also independent of N), where follows a beta distribution with parameters and , .
Then is a sample point from the empirical Bernstein copula.
This was also observed in [12], but was known earlier (see, e.g., [5]). In what follows, we will discuss the data set presented in [10] (Section 3) in more detail.
Example 3.

Table 4 contains the ranks for observed insurance data from windstorm () and flooding () losses in central Europe for 34 consecutive years discussed in [10].

Table 4.
Ranks for observed insurance data from windstorm () and flooding () losses in Example 3.
The graphs in Figure 5 show some plots for the empirical Bernstein copula.
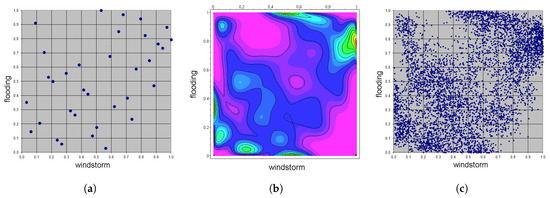
Figure 5.
Plots for the empirical Bernstein copula in Example 3. (a) Support points of scaled skeleton. (b) Empirical Bernstein copula density contour plot. (c) Simulation of 5000 empirical Bernstein copula pairs.
It is clearly to be seen from the shape of the contour lines in Figure 5b that the empirical Bernstein copula density is quite bumpy here, e.g., in comparison with the Gaussian copula density fitted to the data set above (see Figure 6).
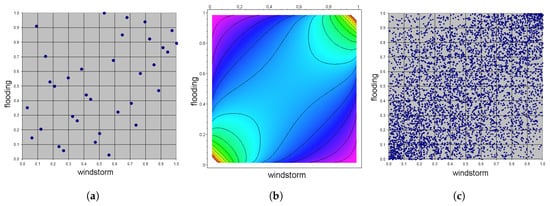
Figure 6.
Plots for the Gaussian copula in Example 3. (a) Support points of scaled skeleton. (b) Gaussian copula density contour plot. (c) Simulation of 5000 Gaussian copula pairs.
From a practical point of view, it might therefore be desirable to adapt the empirical Bernstein copula to a smaller support set for the underlying discrete skeleton. This is the central idea in [10]. However, the disadvantage of the method proposed in that paper is that the number of support points of gets dramatically larger and is typically of exponential order with increasing grid sizes. This is due to the fact that the number of support points is usually in the range of because by the specific method of least squares used there, most support points of will get a positive weight. Therefore, we propose a simpler way how to find a smaller discrete approximating skeleton with an arbitrary given grid size in Section 5.
5. Adaptive Bernstein Copula Estimation
We start with the individual ranks of the observation vectors , . Let denote the canonical admissible discrete skeleton as described in Section 4, derived from the empirical copula. Our aim is to find a good approximating admissible discrete skeleton with a given grid size , where the are typically smaller than n. We proceed in two steps:
- Step 1: AugmentationSelect an integer M such that all , , are divisors of M, for instance, their least common multiple. We construct pseudo-ranks in the following way:Here , , stands for “rounding up”. Let be the uniformly discretly distributed random vector over with support points , …, , where , . Please note that the probability mass is for each support point, and that is an admissible discrete skeleton.
- Step 2: ReductionConstruct the final ranks in the following way:It follows from the above definition that there will be replicates in the final ranks and that takes values in the set . A point will be a support point of the final admissible skeleton if there exist final ranks such that for some . The probability mass attached to is given by the number , where K is the number of rank combinations that lead to the same . This also enables very simple Monte Carlo realizations of the corresponding Bernstein copula as described in Section 4 by first selecting an index N randomly and uniformly among 1, …, and then by proceeding as in Step 2 there with all of the .
Please note that the above augmentation step creates permutations of the set in each component so that the pseudo-ranks actually lead to an admissible discrete skeleton (cf. [5] (Section 4)). The mathematical correctness of the reduction step follows from the proof of Proposition 2.5 in [12].
In the augmentation step, M-wise partial permutations would not change the result but would create a more “random” augmentation of the original ranks.
Example 4.

Consider Table 5 with ranks and probabilities for .

Table 5.
Ranks and probabilities in Example 4.
We want to create approximate final ranks with and . Both numbers are not a divisor of n, so we choose . We show a part of the resulting pseudo-ranks and probabilities in Table 6.

Table 6.
Resulting pseudo-ranks and probabilities in Example 4.
For the final ranks and probabilities , we obtain Table 7.

Table 7.
Final ranks and probabilities in Example 4.
From , , and , , we see that the induced skeleton is indeed admissible.
The graphs in Figure 7 show the corresponding copula densities and induced by and . Seemingly the shape of both densities is similar, reflecting the structure of the original ranks quite well. However, the density is less wiggly than the density , as intended.
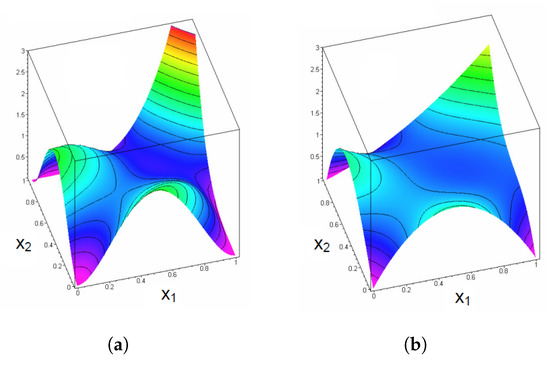
Figure 7.
Plots of the copula densities in Example 4. (a) Copula density . (b) Copula density
Note also that a reduction of complexity for copulas in the sense discussed here is also an essential topic in [23] (Section 3) (see, in particular, Figure 2 there). However, the underlying problem of a consistent reduction of complexity is not really discussed there.
6. Applications to Risk Management
In this section, we first want to investigate the data set of Example 3 in more detail. It is the basis data set in [10]. In particular, we want to discuss the effect of different adaptive Bernstein copula estimations on the estimation of risk measures such as Value at Risk, which is, for instance, the basis for Solvency II.
In [10], the number of the original observations is first reduced to by a least squares technique. The resulting optimal discrete skeleton with probabilities , , , is presented in Table 8 with . We have highlighted the non-zero entries in Table 8 and Table 9 in order to illustrate the effect of a reduction in complexity by an appropriate application of adaptive Bernstein copulas.

Table 8.
Probabilities in the resulting optimal discrete skeleton in Example 3.

Table 9.
Probabilities after application of the adaptive strategy in Example 3.
An application of the adaptive strategy described in Section 5 gives alternatively Table 9, which is less complex. Here we have chosen . Seemingly the number of support points for the adaptive probabilities are much less than before.
The graphs in Figure 8 show contour plots for the corresponding Bernstein copula densities. Here denotes the Bernstein copula density derived from Table 8, denotes the Bernstein copula density derived from Table 9. In the first case we have chosen , in the second case . Seemingly the differences are only marginal. However, in comparison with Figure 5b, the smoothing effect of the adaptive procedure is clearly visible.
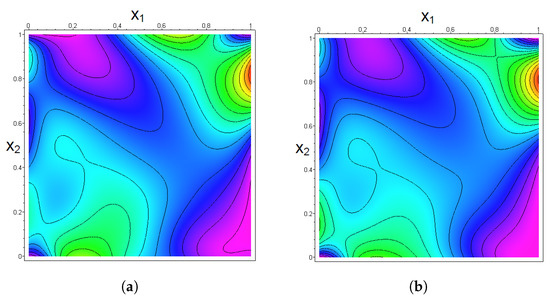
Figure 8.
Contour plots for the Bernstein copula densities in Example 3. (a) Bernstein copula density . (b) Bernstein copula density
The graphs in Figure 9 show contour plots for the adaptive Bernstein copula densities and with the choices and , respectively.
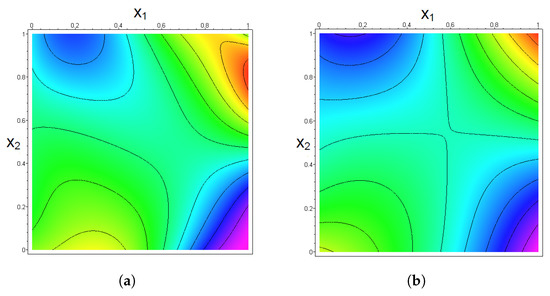
Figure 9.
Contour plots for the adaptive Bernstein copula densities in Example 3. (a) Adaptive Bernstein copula density . (b) Adaptive Bernstein copula density
In the next step, we compare estimates for the risk measure Value at Risk with the risk level —corresponding to a return period of 200 years—on the basis of a Monte Carlo study with 1,000,000 repetitions each for the aggregated risk of windstorm and flooding losses. We consider the full Bernstein copula of Example 3 with as well as the adaptive Bernstein copulas with , and . For the sake of completeness, we also add estimates from the Gaussian copula, the independence as well as the co- and countermonotonicity copulas (see [15] (p. 11) for definitions).
The graphs in Figure 10 show the support points of the underlying adaptive scaled discrete skeletons as well as 5000 simulated pairs of the adapted Bernstein copulas.
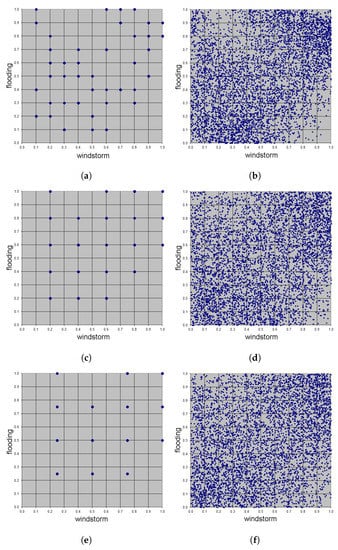
Figure 10.
Plots related to the adaptive Bernstein copulas in Example 3. (a) Support points of the adaptive scaled discrete skeleton, n1 = n2 = 10. (b) Simulation of 5000 adapted Bernstein copula pairs, n1 = n2 = 10. (c) Support points of the adaptive scaled discrete skeleton, n1 = n2 = 5. (d) Simulation of 5000 adapted Bernstein copula pairs, n1 = n2 = 5. (e) Support points of the adaptive scaled discrete skeleton, n1 = n2 = 5. (f) Simulation of 5000 adapted Bernstein copula pairs, n1 = n2 = 5.
Table 10 provides estimated values of the risk measures from the Monte Carlo simulations, which are given in Mio. monetary units. For the marginal distributions, the assumptions in [10] are used.

Table 10.
Estimated values of for different grid types in Example 3.
Seemingly the comonotonicity copula provides the largest -estimate due to an extreme tail dependence, whereas the countermonotonicity copula provides the smallest -estimate. Surprisingly, the -estimates for the adaptive Bernstein copulas do not differ very much from each other (at most 2.5%) and are almost identical to the estimate from the independence copula here. Please note that the -estimate for the Gaussian copula is slightly larger.
However, significant differences are visible if we look at the densities of the aggregated risk. The graphs in Figure 11 show empirical histograms for these densities under the models considered above, from 100,000 simulations each. Please note that the histogram for the full Bernstein copula has two peaks, whereas the other histograms show a more smooth behavior.
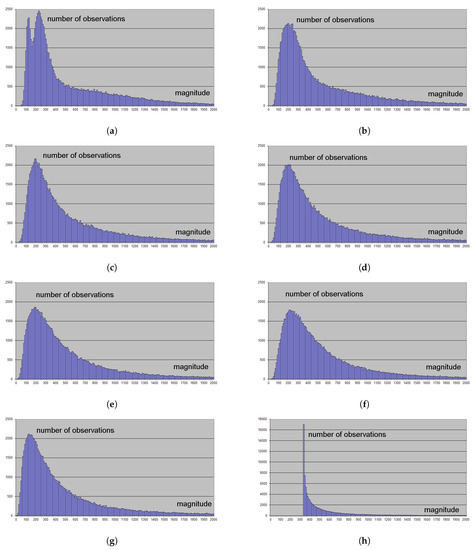
Figure 11.
Empirical histograms for the densities of the aggregated risk in Example 3. (a) Bernstein copula, grid type 34 × 34. (b) Bernstein copula, grid type 10 × 10. (c) Bernstein copula, grid type 5 × 5. (d) Bernstein copula, grid type 4 × 4. (e) Gaussian copula. (f) Independence copula. (g) Comonotonicity copula. (h) Countermonotonicity copula.
Example 5.


Finally, we discuss a high-dimensional data set, which is also analyzed in [24]. It represents economically adjusted windstorm losses in 19 adjacent areas in Central Europe over a time period of 20 years. In Table 11 and Table 12, the losses are given in Mio. monetary units.

Table 11.
Insurance losses in Example 5, part I.

Table 12.
Insurance losses in Example 5, part II.
A statistical analysis of the data shows a good fit to lognormal -distributions for the losses per Area k, . Thus, the parameters and for Area k can be estimated from the log data by calculating means and standard deviations (see Table 13 and Table 14).

Table 13.
Values of the parameters and estimated from the log data in Example 5, part I.

Table 14.
Values of the parameters and estimated from the log data in Example 5, part II.
As expected, insurance losses in locally adjacent areas show a high degree of stochastic dependence, which can also be seen from the correlation Table 15 and Table 16. In Table 15, correlations above 0.9 are highlighted.

Table 15.
Correlations between original losses in adjacent areas in Example 5.

Table 16.
Correlations between log losses in adjacent areas in Example 5.
The following results have been achieved by Monte Carlo studies of 1,000,000 simulations each, based on various choices of the grid constants for fixed numbers m. We first show scatter plots of each 5000 simulated adaptive Bernstein copula points for selected area combinations with high correlations (Area 1 vs. Area 13, Area 3 vs. Area 4, Area 7 vs. Area 16) and a low correlation (Area 3 vs. Area 18).
For comparison purposes, we start with , which corresponds to an extreme overfitting of the given data (see Figure 12). The scatter plots in Figure 13 correspond to the choice , which represents the ordinary Bernstein copula approach. The scatter plots in Figure 14 correspond to the choice , which represents a slightly adapted Bernstein copula approach. The scatter plots in Figure 15 correspond to the choice , which represents a moderately adapted Bernstein copula approach. The final scatter plots in Figure 16 correspond to the choice , which represents a strongly adapted Bernstein copula approach.
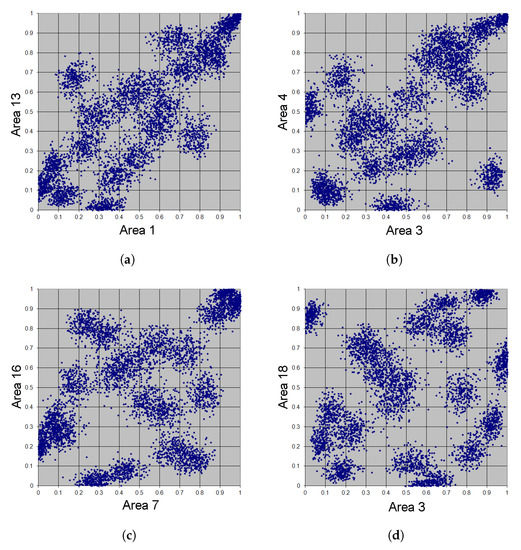
Figure 12.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 100. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
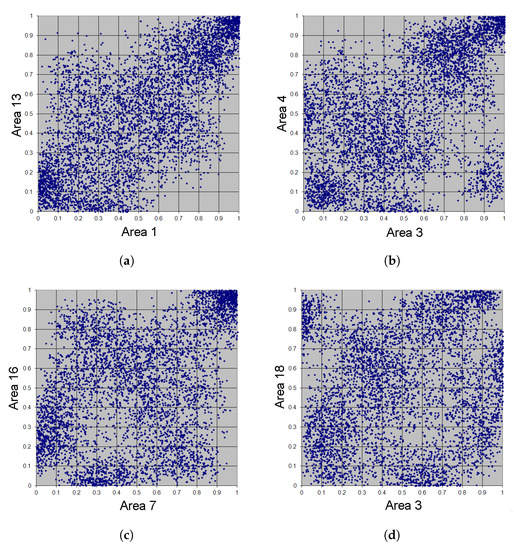
Figure 13.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 20. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
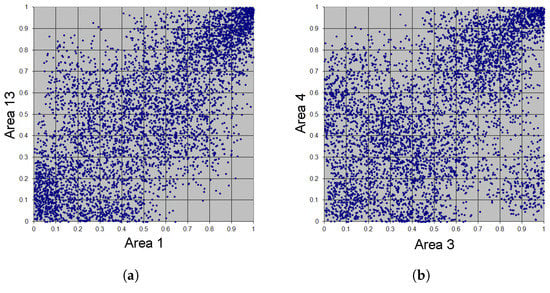
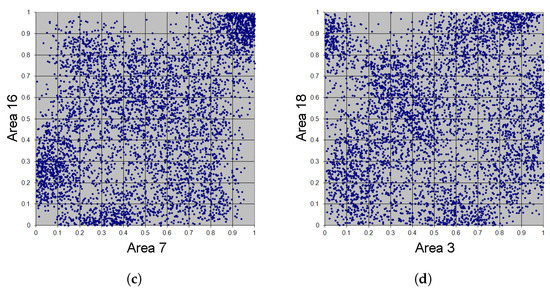
Figure 14.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 17. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
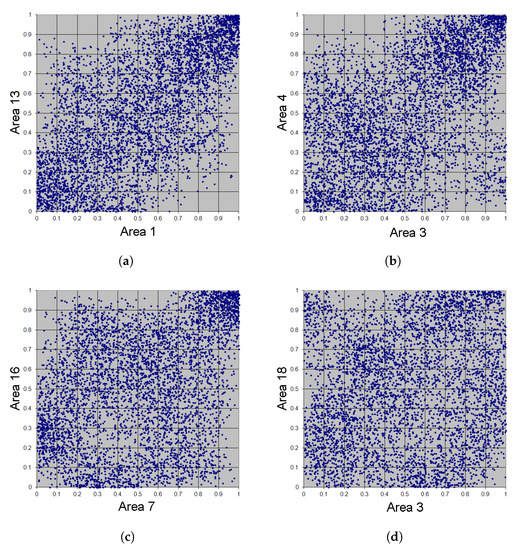
Figure 15.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 13. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
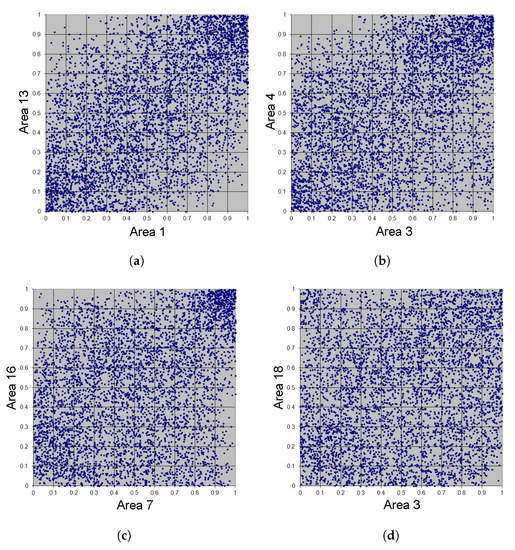
Figure 16.
Simulation of 5000 adaptive Bernstein copula points in Example 5, m = 7. (a) Area 1 vs. Area 13. (b) Area 3 vs. Area 4. (c) Area 7 vs. Area 16. (d) Area 3 vs. Area 18.
As can clearly be seen, the choice of m influences significantly the shape of the adapted Bernstein copula. With decreasing magnitude of m, we see a more uniform distribution of adapted Bernstein copula points, as expected. Table 17 shows -estimates depending on the choice of m.

Table 17.
-estimates for different values of m in Example 5.
In contrast to the analysis of Example 3 (cf. Table 10), we see here that the choice of grid constants has a major influence on the estimated risk measure. The overfitted for is more than 50% higher than the for .
7. Conclusions
Adaptive Bernstein copulas are an interesting tool for smoothing or, if desired, also sharpening the empirical dependence structure, in particular, in risk management applications when the number of observations and dimensions is moderate to large. The possibility of a smoothing of the dependence structure prevents in particular a kind of overfitting to copula models. In particular, the choice of the grid constants in the reduction procedure is arbitrary, the selected grid constants need not to be divisors of the number of observations. The method presented here also enables Monte Carlo studies for the comparison of different estimates of risk measures or the shape of the aggregate risk distribution. If the various estimates for the risk measure do not differ much for several adaptive strategies, this could make a sensitivity analysis, for instance, under Solvency II more profound. In other cases, when significant differences in the estimation of risk measures become apparent under various adaptive strategies, one should be cautious with a mere statistical risk assessment. Anyway, a kind of a worst case analysis derived from different approaches could be helpful here.
The method of reducing (or, if desired, sharpening) the complexity in the rank structures of the data might also be applied to partition-of-unity copulas (see [24,25,26]). With such copulas, tail dependence can be introduced to the dependence models, which cannot be obtained by Bernstein copulas alone due to the boundedness of the corresponding densities.
Author Contributions
The authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
The publication of this paper was funded by the University of Oldenburg.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bernstein, S. Démonstration du théorème de Weierstrass fondée sur le calcul des probabilités. Commun. Kharkov Math. Soc. 1912, 13, 1–2. [Google Scholar]
- Lorentz, G.G. Bernstein Polynomials, 2nd ed.; Chelsea Publishing Company: New York, NY, USA, 1986. [Google Scholar]
- Babu, G.J.; Canty, A.J.; Chaubey, Y.P. Application of Bernstein polynomials for smooth estimation of a distribution and density function. J. Statist. Plann. Inference 2002, 105, 377–392. [Google Scholar] [CrossRef]
- Cheng, C. The Bernstein polynomial estimator of a smooth quantile function. Statist. Probab. Lett. 1995, 24, 321–330. [Google Scholar] [CrossRef]
- Cottin, C.; Pfeifer, D. From Bernstein polynomials to Bernstein copulas. J. Appl. Funct. Anal. 2014, 9, 277–288. [Google Scholar]
- Guan, Z. Efficient and robust density estimation using Bernstein type polynomials. J. Nonparametr. Stat. 2016, 28, 250–271. [Google Scholar] [CrossRef]
- Guan, Z. Bernstein polynomial model for grouped continuous data. J. Nonparametr. Stat. 2017, 29, 831–848. [Google Scholar] [CrossRef]
- Leblanc, A. On estimating distribution functions using Bernstein polynomials. Ann. Inst. Statist. Math. 2012, 64, 919–943. [Google Scholar] [CrossRef]
- Pfeifer, D.; Nešlehová, J. Modeling dependence in finance and insurance: The copula approach. Bl. DGVFM 2003, 26, 177–191. [Google Scholar] [CrossRef]
- Pfeifer, D.; Straßburger, D.; Philipps, J. Modelling and simulation of dependence structures in nonlife insurance with Bernstein copulas. In Proceedings of the Paper presented on the occasion of the International ASTIN Colloquium, Helsinki, Finland, 1–4 June 2009. [Google Scholar]
- Sancetta, A.; Satchell, S. The Bernstein copula and its applications to modeling and approximations of multivariate distributions. Econom. Theory 2004, 20, 535–562. [Google Scholar] [CrossRef]
- Segers, J.; Sibuya, M.; Tsukahara, H. The empirical beta copula. J. Multivar. Anal. 2017, 155, 35–51. [Google Scholar] [CrossRef]
- Vil’chevskii, N.O.; Shevlyakov, G.L. On the Bernstein polynomial estimators of distribution and quantile functions. J. Math. Sci. 2001, 105, 2626–2629. [Google Scholar] [CrossRef]
- Wang, T.; Guan, Z. Bernstein polynomial model for nonparametric multivariate density. Statistics 2018, 53, 321–338. [Google Scholar] [CrossRef]
- Durante, F.; Sempi, C. Principles of Copula Theory; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Ibragimov, R.; Prokhorov, A. Heavy Tails and Copulas. Topics in Dependence Modelling in Economics and Finance; World Scientific: Singapore, 2017. [Google Scholar]
- Rose, D. Modeling and Estimating Multivariate Dependence Structures with the Bernstein Copula. Ph.D. Thesis, Ludwig-Maximilians-Universität, München, Germany, 8 October 2015. Available online: https://edoc.ub.uni-muenchen.de/18757/ (accessed on 8 December 2020).
- Avomo Ngomo, J.S.-L. Entwicklung und Implementierung eines Verfahrens zur Optimierung des Speicheraufwands bei Bernstein-und Verwandten Copulas. Ph.D. Thesis, Carl von Ossietzky Universität, Oldenburg, Germany, 18 December 2017. Available online: http://oops.uni-oldenburg.de/3457/ (accessed on 8 December 2020).
- Masuhr, A.; Trede, M. Bayesian estimation of generalized partition of unity copulas. Depend. Model. 2020, 8, 119–131. [Google Scholar] [CrossRef]
- Deheuvels, P. La fonction de dépendance empirique et ses propriétés. Un test non paramétrique d’indépendance. Acad. R. Belg. Bull. Sci. 1979, 65, 274–292. [Google Scholar] [CrossRef]
- Butzer, P.L. On two-dimensional Bernstein polynomials. Canad. J. Math. 1953, 5, 107–113. [Google Scholar] [CrossRef]
- Pfeifer, D.; Ragulina, O. Generating VaR scenarios under Solvency II with product beta distributions. Risks 2018, 6, 122. [Google Scholar] [CrossRef]
- Junker, R.R.; Griessenberger, F.; Trutschnig, W. Estimating scale-invariant directed dependence of bivariate distributions. Comput. Statist. Data Anal. 2021, 153, 107058. [Google Scholar] [CrossRef]
- Pfeifer, D.; Mändle, A.; Ragulina, O.; Girschig, C. New copulas based on general partitions-of-unity (part III)—the continuous case. Depend. Model. 2019, 7, 181–201. [Google Scholar] [CrossRef]
- Pfeifer, D.; Tsatedem, H.A.; Mändle, A.; Girschig, C. New copulas based on general partitions-of-unity and their applications to risk management. Depend. Model. 2016, 4, 123–140. [Google Scholar] [CrossRef]
- Pfeifer, D.; Mändle, A.; Ragulina, O. New copulas based on general partitions-of-unity and their applications to risk management (part II). Depend. Model. 2017, 5, 246–255. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).