Author Contributions
Conceptualization, R.G.-D., E.M., E.P.-H. and B.R.; Investigation, R.G.-D., E.M., E.P.-H. and B.R.; Methodology, R.G.-D., E.M., E.P.-H. and B.R.; Software, R.G.-D., E.M., E.P.-H. and B.R.; Supervision, R.G.-D., E.M., E.P.-H. and B.R.; Validation, R.G.-D., E.M., E.P.-H. and B.R.; Writing—original draft, R.G.-D., E.M., E.P.-H. and B.R.; Writing—review and editing, R.G.-D., E.M., E.P.-H. and B.R. All authors have read and agreed to the published version of the manuscript.
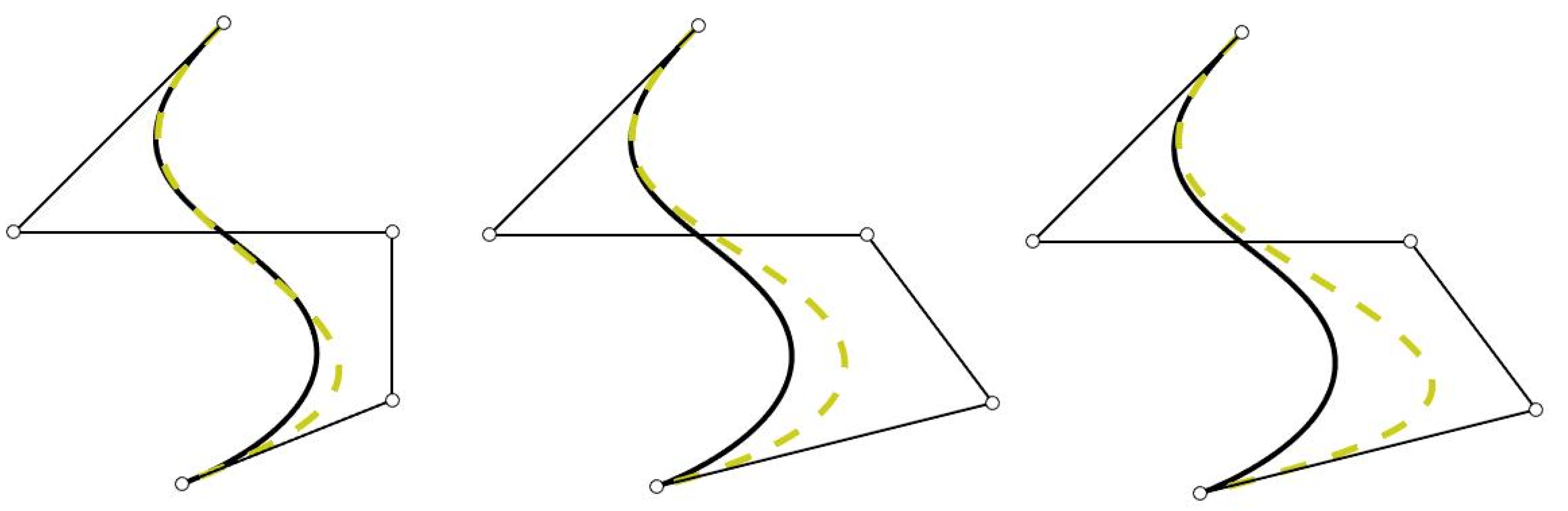
Figure 1.
Initial curve (line) and curve obtained (dotted line) after changing the weights and/or control points. Left: changing the fourth weight; center: changing the fourth control point; and right: changing the fourth weight and the fourth control point.
Figure 1.
Initial curve (line) and curve obtained (dotted line) after changing the weights and/or control points. Left: changing the fourth weight; center: changing the fourth control point; and right: changing the fourth weight and the fourth control point.
Figure 2.
(
Left): Rational basis (
2) using
,
,
. Weights
(black line) and weights
(blue dotted line). (
Right): Rational basis (
2) using
,
,
. Weights
(black line) and weights
(blue dotted line).
Figure 2.
(
Left): Rational basis (
2) using
,
,
. Weights
(black line) and weights
(blue dotted line). (
Right): Rational basis (
2) using
,
,
. Weights
(black line) and weights
(blue dotted line).
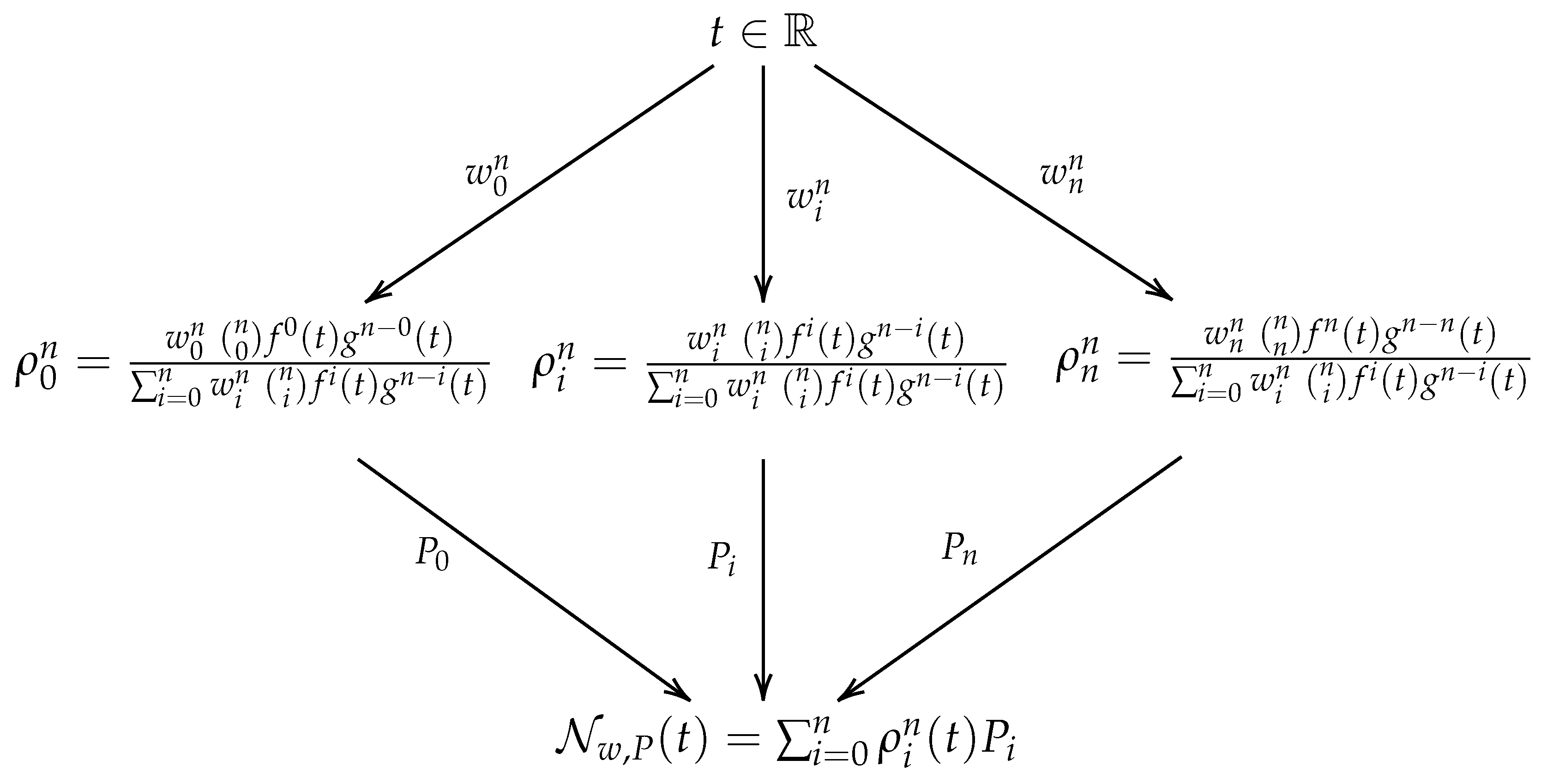
Figure 3.
From top to bottom. The input layer has the parameter as input. The hidden layer is of width and its parameters are the weights. Then, the output layer computes the approximation of the target curve and its parameters are the control points.
Figure 3.
From top to bottom. The input layer has the parameter as input. The hidden layer is of width and its parameters are the weights. Then, the output layer computes the approximation of the target curve and its parameters are the control points.
Figure 4.
Evolution of the fitting curve . Set of data points from the target curve (dotted) and the fitting curve (line). From top to bottom and left to right: Increment , , , , , and .
Figure 4.
Evolution of the fitting curve . Set of data points from the target curve (dotted) and the fitting curve (line). From top to bottom and left to right: Increment , , , , , and .
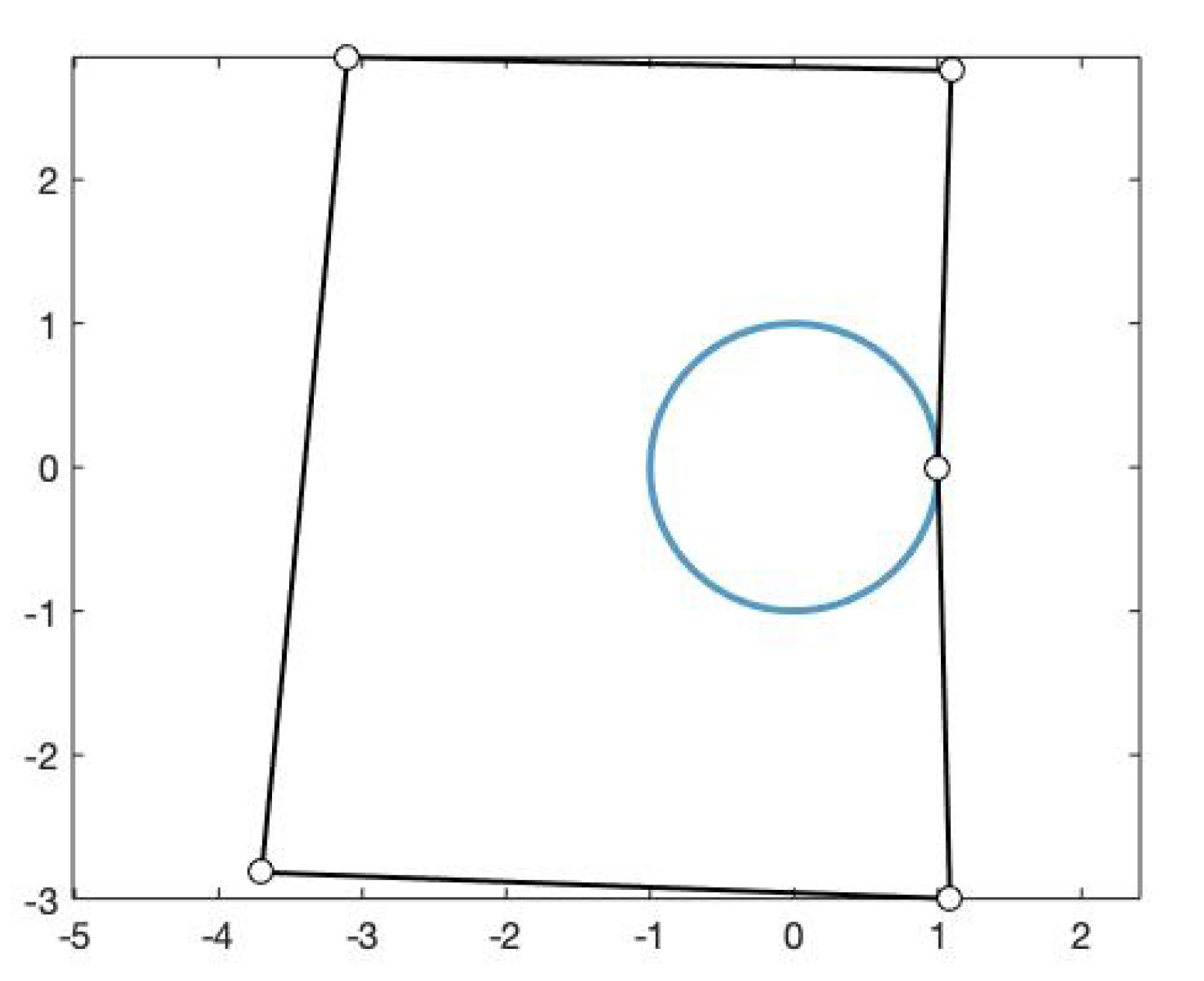
Figure 5.
Fitting curve of degree 5 obtained using the functions and , , and its corresponding control polygon.
Figure 5.
Fitting curve of degree 5 obtained using the functions and , , and its corresponding control polygon.
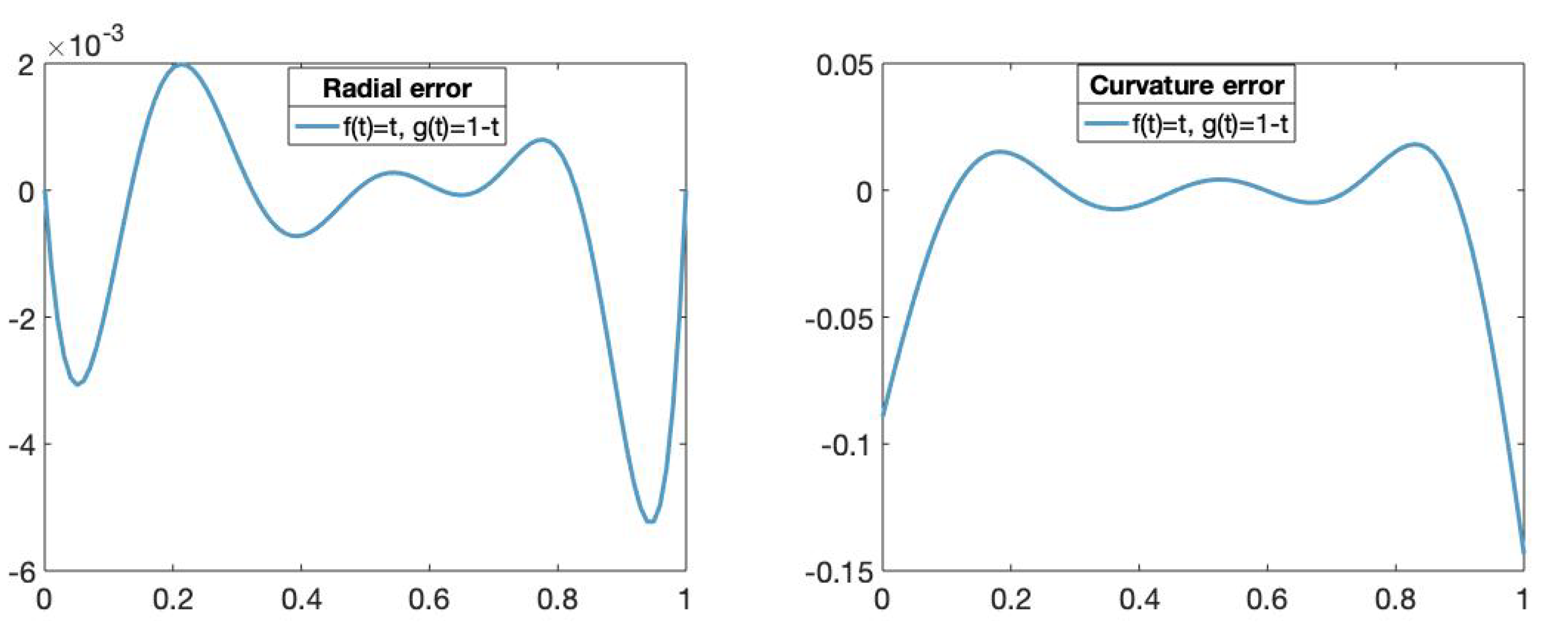
Figure 6.
(Left): The x-axis represents the parameters t in and the y-axis represents the radial error value of the fitting curve obtained using the functions and , . (Right): The x-axis represents the parameters t in and the y-axis represents the curvature error value of fitting curve obtained using the functions and , .
Figure 6.
(Left): The x-axis represents the parameters t in and the y-axis represents the radial error value of the fitting curve obtained using the functions and , . (Right): The x-axis represents the parameters t in and the y-axis represents the curvature error value of fitting curve obtained using the functions and , .
Figure 7.
Fitting curve of degree 5 using and , , and its control polygon.
Figure 7.
Fitting curve of degree 5 using and , , and its control polygon.
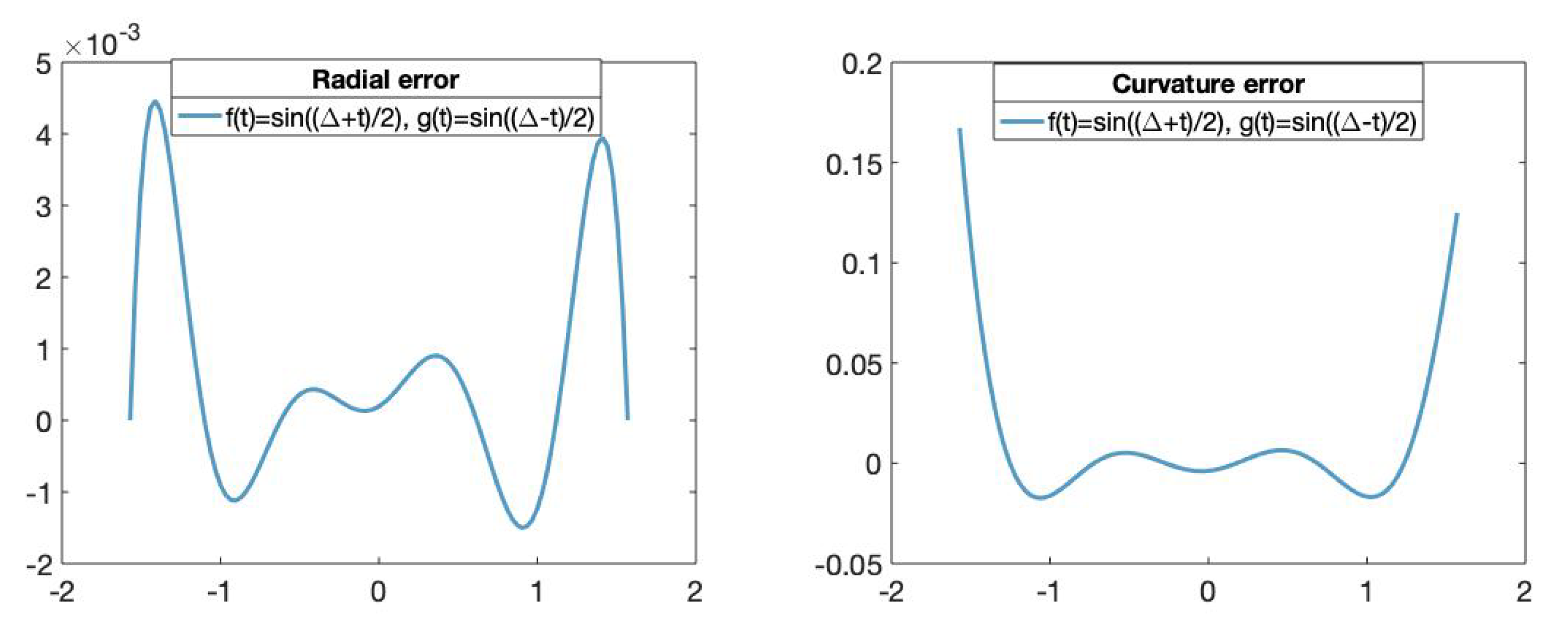
Figure 8.
(Left): The x-axis represents the parameters t in and the y-axis represents the radial error value of the fitting curve obtained using the trigonometric basis. (Right): The x-axis represents the parameters t in and the y-axis represents the curvature error value of the fitting curves obtained using the trigonometric basis.
Figure 8.
(Left): The x-axis represents the parameters t in and the y-axis represents the radial error value of the fitting curve obtained using the trigonometric basis. (Right): The x-axis represents the parameters t in and the y-axis represents the curvature error value of the fitting curves obtained using the trigonometric basis.
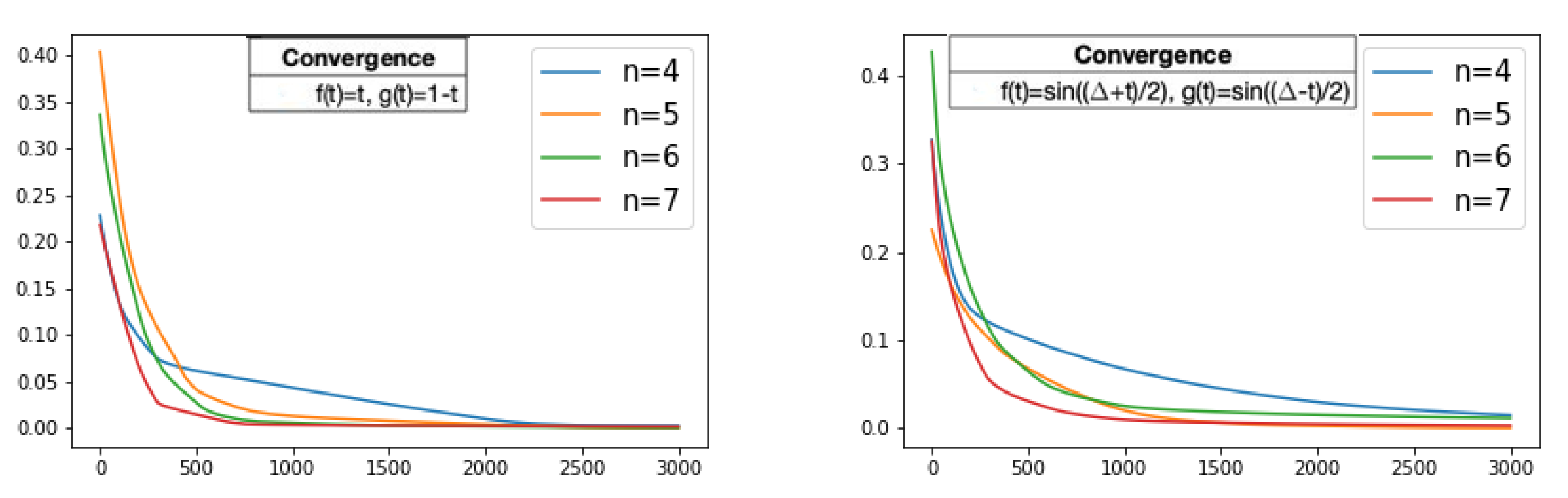
Figure 9.
For different values of n, the history of the loss function, i.e., the mean absolute error values, through the training process on 3000 iterations while the fitting curves converges. (Left): Loss values of the fitting curve using , , . (Right): Loss values of the fitting curve using , , . The x-axis represents the iteration of the training algorithm and the y-axis represents the mean absolute error value.
Figure 9.
For different values of n, the history of the loss function, i.e., the mean absolute error values, through the training process on 3000 iterations while the fitting curves converges. (Left): Loss values of the fitting curve using , , . (Right): Loss values of the fitting curve using , , . The x-axis represents the iteration of the training algorithm and the y-axis represents the mean absolute error value.
Figure 10.
(Left): Set of data points on the cycloid (dotted), fitting curve obtained using the functions , , (blue) and fitting curve obtained using the functions ,, (green). (Right): Fitting error comparison.The x-axis represents the parameters t in and the y-axis represents the fitting error value of the fitting curves obtained using the functions , , (green) and the functions , , (blue).
Figure 10.
(Left): Set of data points on the cycloid (dotted), fitting curve obtained using the functions , , (blue) and fitting curve obtained using the functions ,, (green). (Right): Fitting error comparison.The x-axis represents the parameters t in and the y-axis represents the fitting error value of the fitting curves obtained using the functions , , (green) and the functions , , (blue).
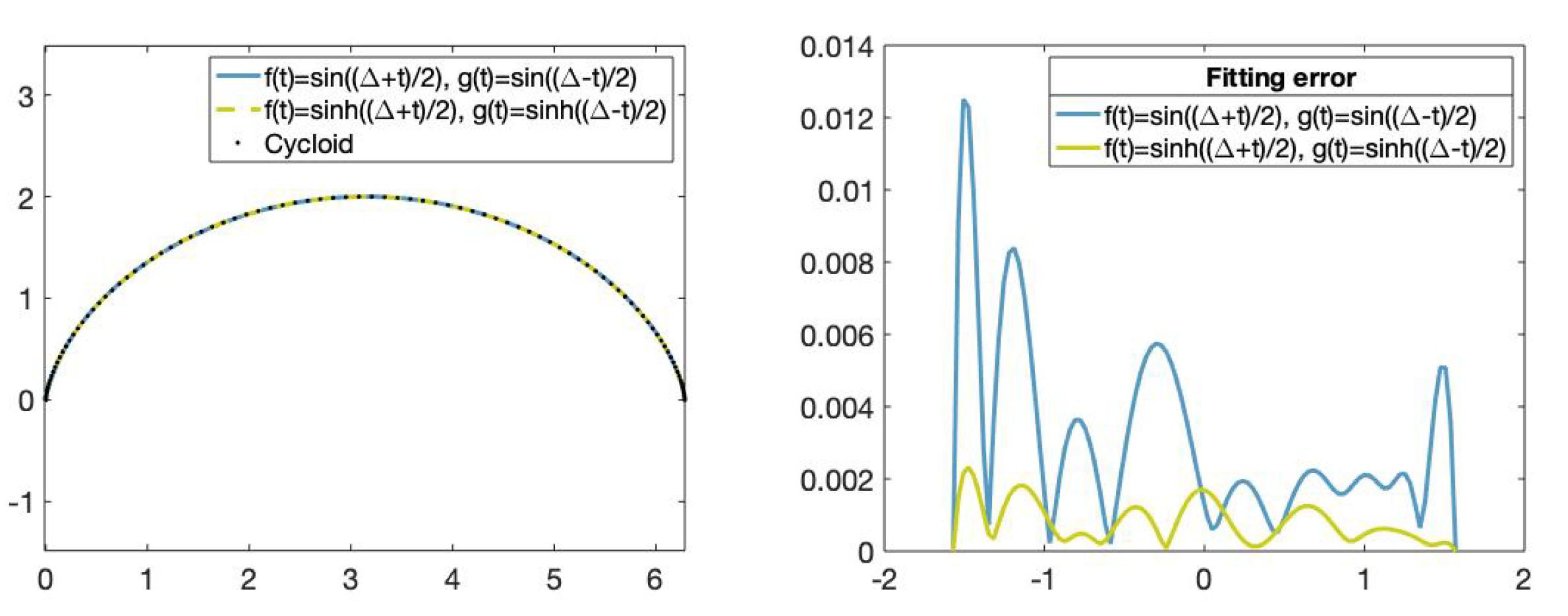
Figure 11.
(Left): Set of data points on the cycloid (dotted), fitting curve obtained using the trigonometric functions and and fitting curve obtained using the hyperbolic functions and . (Right): Fitting error comparison. The x-axis represents the parameters t in and the y-axis represents the curvature error value of the fitting curve obtained using the trigonometric and hyperbolic bases.
Figure 11.
(Left): Set of data points on the cycloid (dotted), fitting curve obtained using the trigonometric functions and and fitting curve obtained using the hyperbolic functions and . (Right): Fitting error comparison. The x-axis represents the parameters t in and the y-axis represents the curvature error value of the fitting curve obtained using the trigonometric and hyperbolic bases.
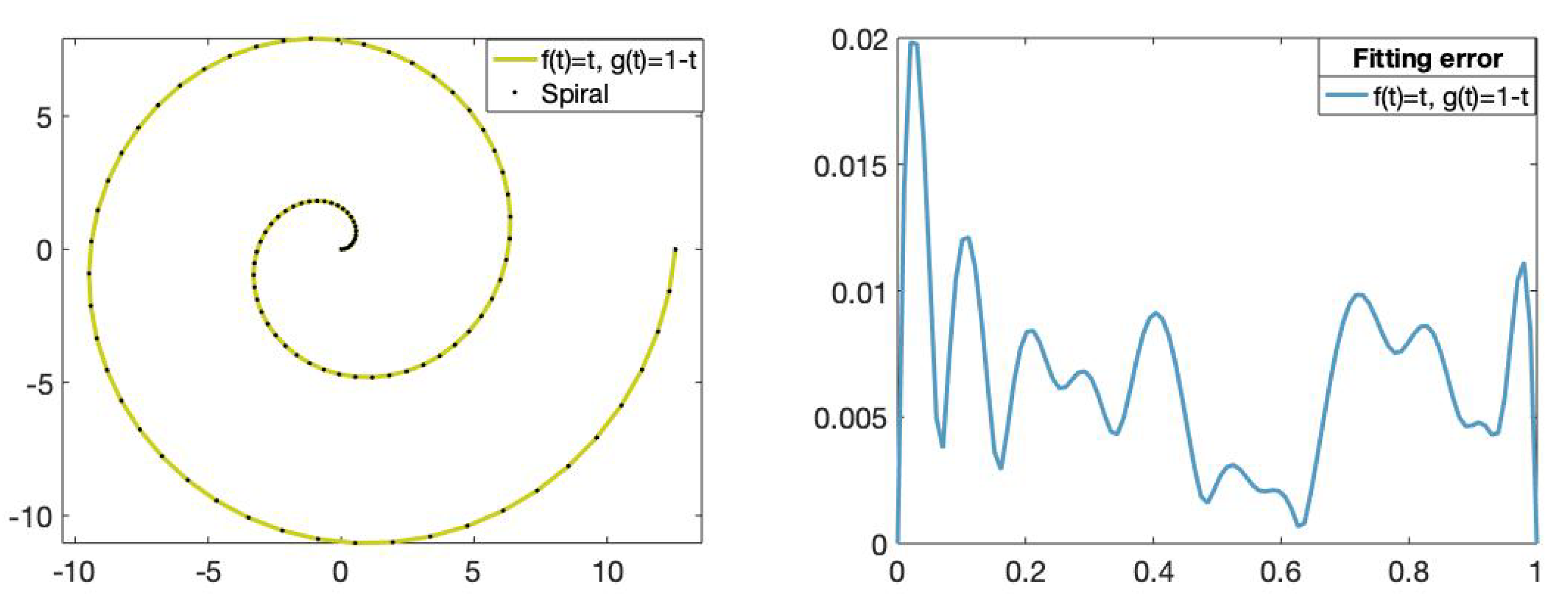
Figure 12.
(Left): Set of data points on the Archimedean spiral (dotted) and the fitting curve of degree 11 obtained using the functions and , . (Right): The x-axis represents the parameters t in and the y-axis represents the fitting error value of the fitting curve obtained using the functions and .
Figure 12.
(Left): Set of data points on the Archimedean spiral (dotted) and the fitting curve of degree 11 obtained using the functions and , . (Right): The x-axis represents the parameters t in and the y-axis represents the fitting error value of the fitting curve obtained using the functions and .
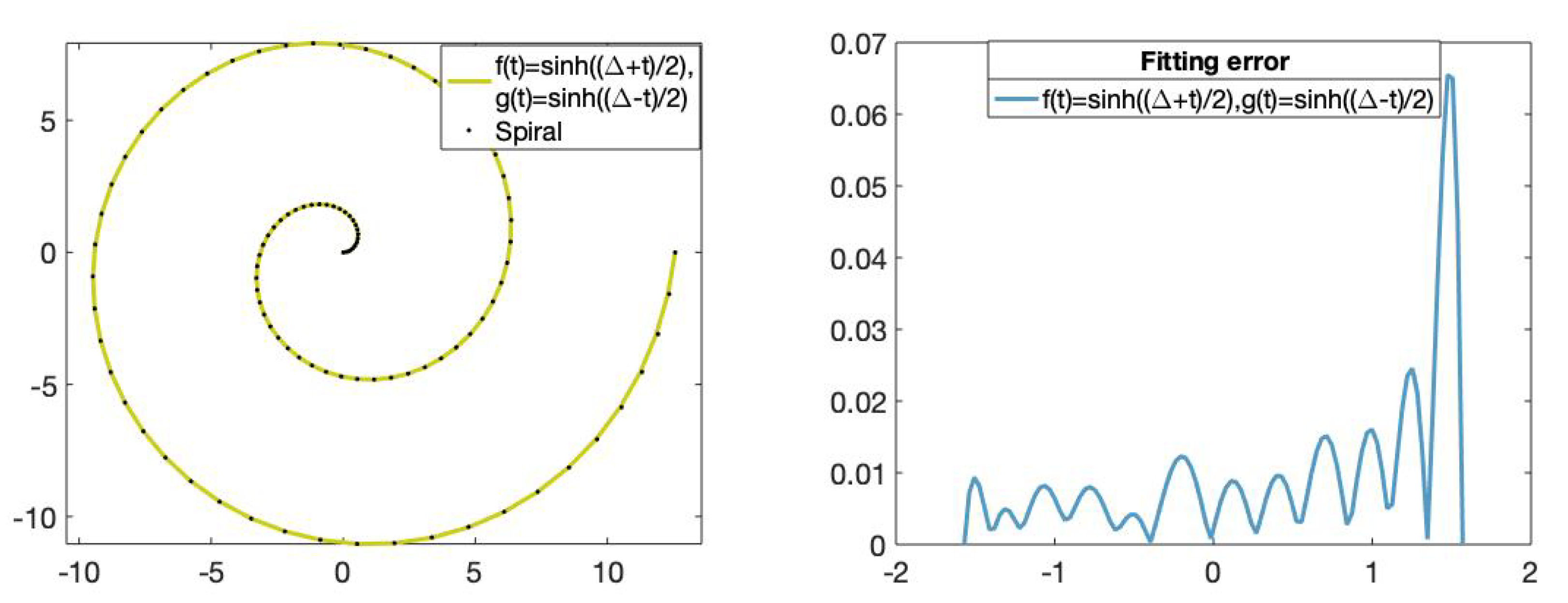
Figure 13.
(Left): Set of data points on the Archimedean spiral (dotted) and the fitting curve of degree 11 with the functions and . (Right): The x-axis represents the parameters t in and the y-axis represents the fitting error value of the fitting curve obtained using the hyperbolic basis.
Figure 13.
(Left): Set of data points on the Archimedean spiral (dotted) and the fitting curve of degree 11 with the functions and . (Right): The x-axis represents the parameters t in and the y-axis represents the fitting error value of the fitting curve obtained using the hyperbolic basis.
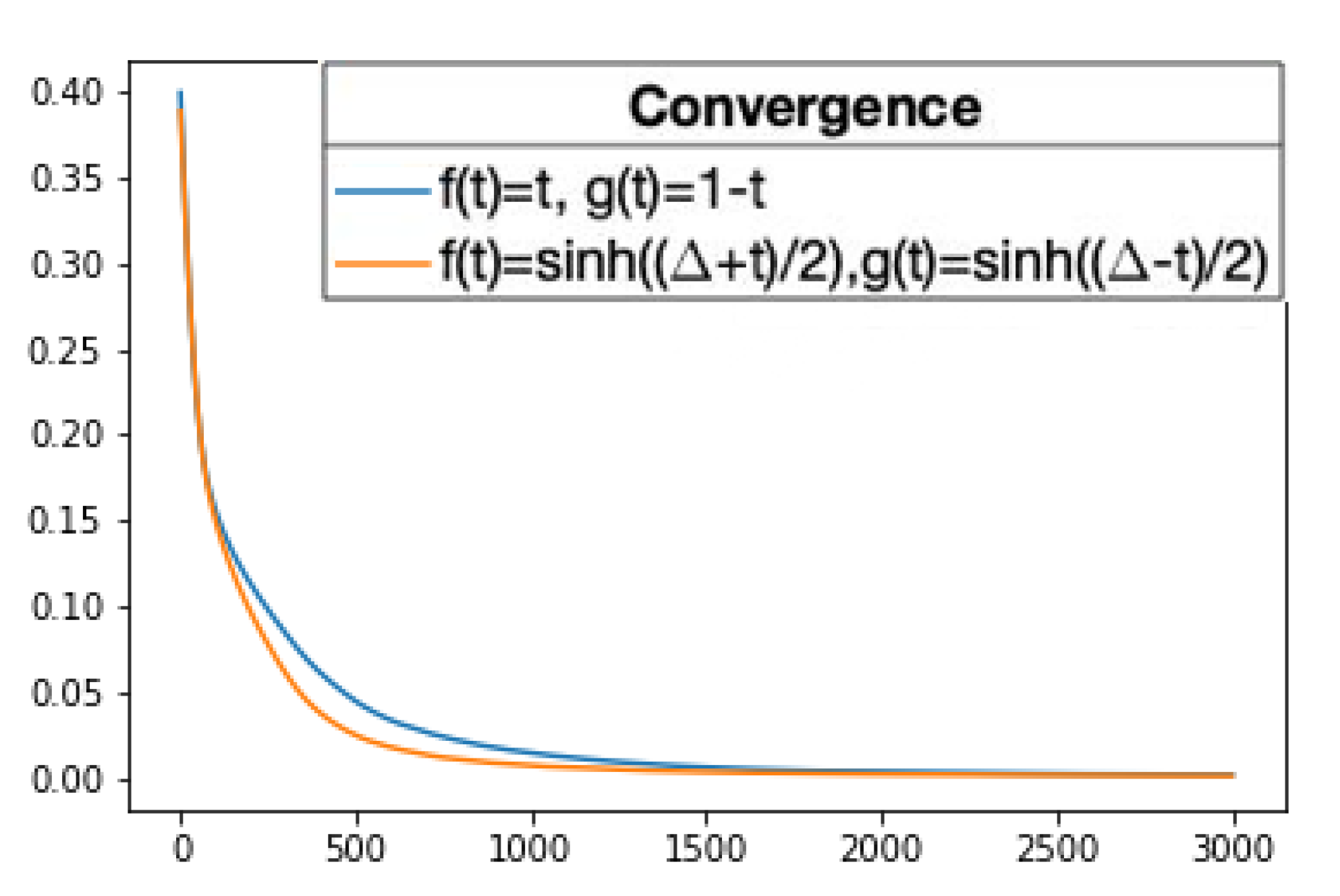
Figure 14.
The history of the loss values, i.e., the mean absolute error values, through 3000 iterations of the training algorithm while the fitting curves converge is pictured. The blue line corresponds to the fitting curve of degree 11 obtained using and , , and the orange line corresponds to the fitting curve of degree 11 obtained using and . The x-axis represents the iteration of the training algorithm and the y-axis represents the mean absolute error value. The values are the mean of 50 repetitions.
Figure 14.
The history of the loss values, i.e., the mean absolute error values, through 3000 iterations of the training algorithm while the fitting curves converge is pictured. The blue line corresponds to the fitting curve of degree 11 obtained using and , , and the orange line corresponds to the fitting curve of degree 11 obtained using and . The x-axis represents the iteration of the training algorithm and the y-axis represents the mean absolute error value. The values are the mean of 50 repetitions.
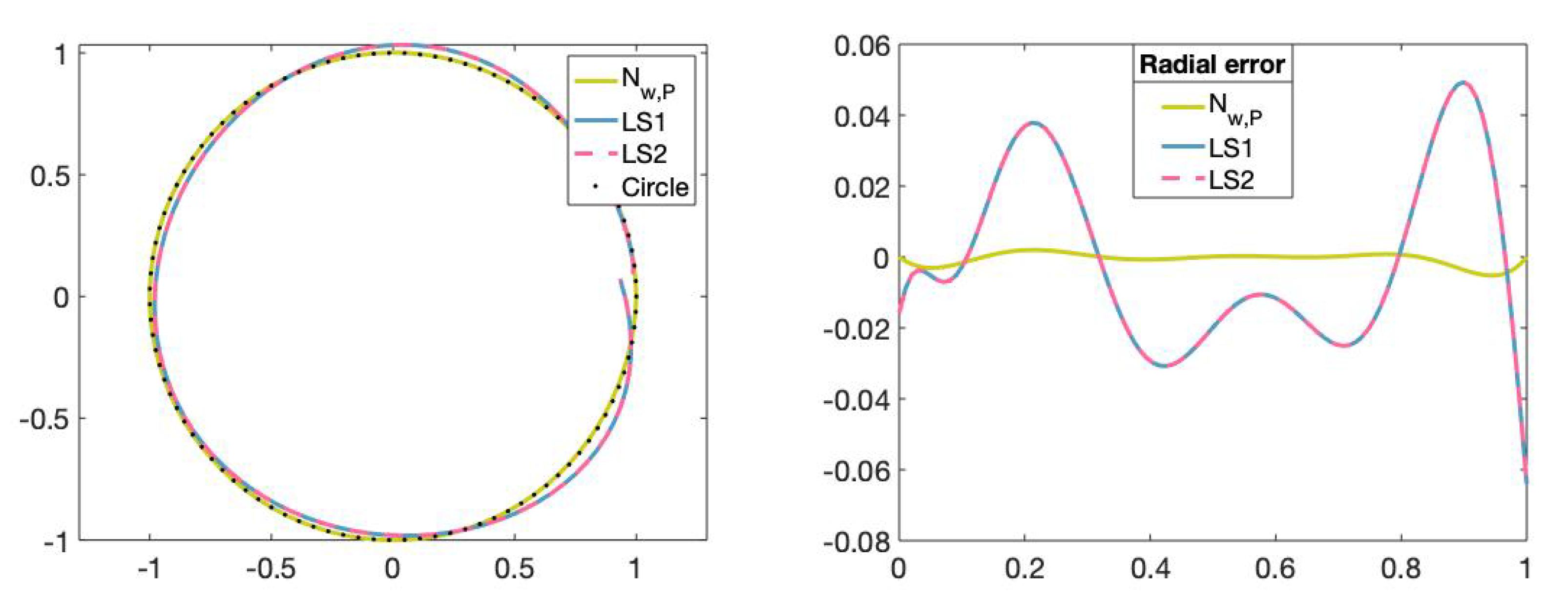
Figure 15.
(Left): Set of data points on circle (dotted), fitting curve of degree 5 obtained with the neural network, fitting curve of degree 5 obtained with the least-squares method by using the Matlab commmand mldivide (LS1), fitting curve of degree 5 obtained with the least-squares method by using the Matlab command SVD (LS2). (Right): The x-axis represents the parameters t in and the y-axis represents the radial error value of the fitting curves obtained with the different methods.
Figure 15.
(Left): Set of data points on circle (dotted), fitting curve of degree 5 obtained with the neural network, fitting curve of degree 5 obtained with the least-squares method by using the Matlab commmand mldivide (LS1), fitting curve of degree 5 obtained with the least-squares method by using the Matlab command SVD (LS2). (Right): The x-axis represents the parameters t in and the y-axis represents the radial error value of the fitting curves obtained with the different methods.
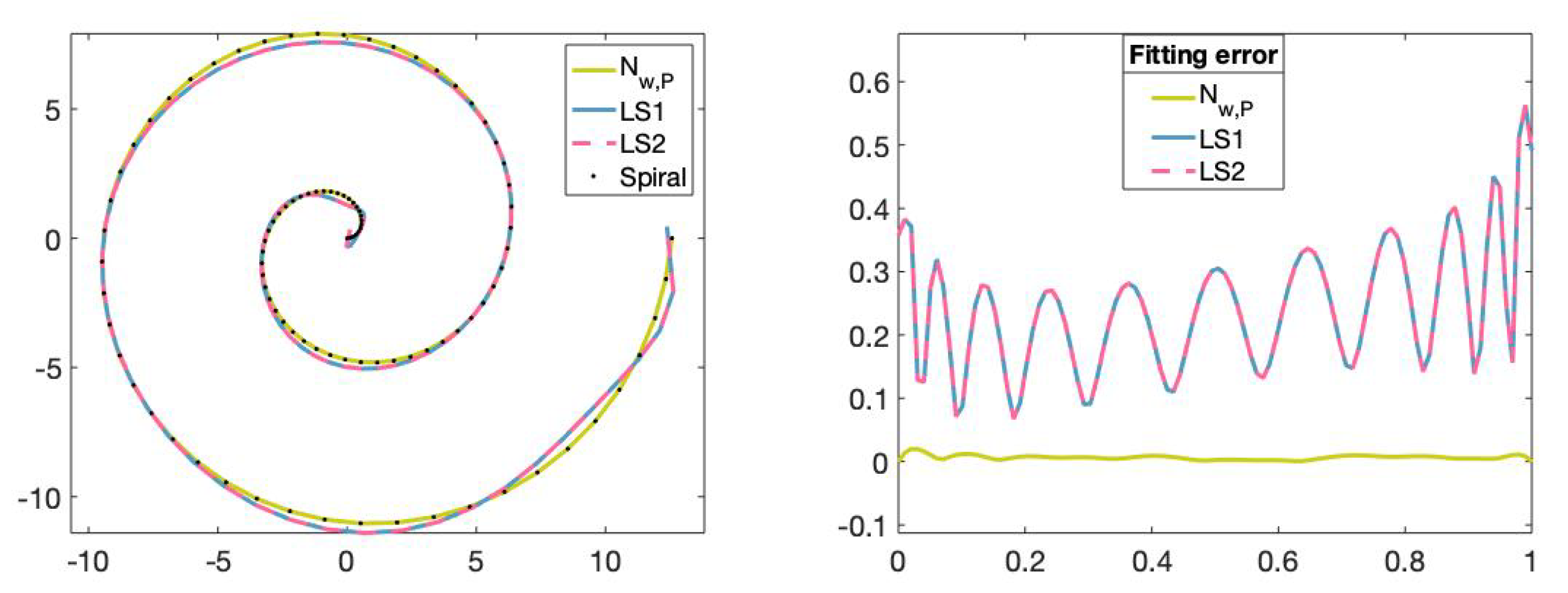
Figure 16.
(Left): Set of points on the Archimedean spiral curve, fitting curve of degree 11 obtained with the neural network, fitting curve of degree 11 obtained with the least-squares method by using the Matlab command mldivide (LS1) and fitting curve of degree 11 obtained with the least-squares method using the Matlab command SVD (LS2). (Right): The x-axis represents the parameters t in and the y-axis represents the fitting error value of the fitting curves obtained with the different methods.
Figure 16.
(Left): Set of points on the Archimedean spiral curve, fitting curve of degree 11 obtained with the neural network, fitting curve of degree 11 obtained with the least-squares method by using the Matlab command mldivide (LS1) and fitting curve of degree 11 obtained with the least-squares method using the Matlab command SVD (LS2). (Right): The x-axis represents the parameters t in and the y-axis represents the fitting error value of the fitting curves obtained with the different methods.
Figure 17.
Noisy set of data points obtained from the baroque image (points in blue), fitting curve obtained by training the proposed neural network (points in green) and fitting curve obtained using the regularized least-squares method (pink). Baroque motif image source:
Freepik.com.
Figure 17.
Noisy set of data points obtained from the baroque image (points in blue), fitting curve obtained by training the proposed neural network (points in green) and fitting curve obtained using the regularized least-squares method (pink). Baroque motif image source:
Freepik.com.
Table 1.
Loss values of the mean absolute error (
12) for different fitting curves of degree
n with
,
,
(Basis 1),
and
,
, (Basis 2),
and
,
,
,
, (Basis 3) and finally
and
,
,
, (Basis 4). They were all trained with 4000 iterations,
,
,
,
. The process was repeated 5 times, with the loss values provided being the best values reached.
Table 1.
Loss values of the mean absolute error (
12) for different fitting curves of degree
n with
,
,
(Basis 1),
and
,
, (Basis 2),
and
,
,
,
, (Basis 3) and finally
and
,
,
, (Basis 4). They were all trained with 4000 iterations,
,
,
,
. The process was repeated 5 times, with the loss values provided being the best values reached.
| n | Basis 1 | Basis 2 | Basis 3 | Basis 4 |
|---|
| Circle |
| 3 | 3.3946 × | 3.7129 × | 7.0468 × | 3.6438 × |
| 4 | 2.1757 × | 1.5338 × | 3.1678 × | 2.5582 × |
| 5 | 1.7333 × | 9.2269 × | 2.8083 × | 2.2488 × |
| Cycloid |
| 8 | 1.0849 × | 3.6855 × | 3.6017 × | 3.1674 × |
| 9 | 4.6163 × | 3.6855 × | 3.6017 × | 2.4914 × |
| 10 | 3.3944 × | 3.6855 × | 3.6017 × | 2.4914 × |
| Archimedean spiral |
| 11 | 1.5982 × | 1.0474 × | 2.2349 × | 7.8109 × |
| 12 | 1.5982 × | 7.8916 × | 5.7801 × | 7.8109 × |
| 13 | 1.4106 × | 5.2853 × | 5.7801 × | 7.8109 × |
Table 2.
Time of execution of the proposed algorithm measured in seconds for different numbers of units and iterations. The values provided are the mean of 5 repetitions with a set of data points of size 100.
Table 2.
Time of execution of the proposed algorithm measured in seconds for different numbers of units and iterations. The values provided are the mean of 5 repetitions with a set of data points of size 100.
| Number of Iterations |
|---|
| 1 | 25 | 50 | 100 | 3000 |
|---|
| 5 | 0.1259 | 1.4284 | 2.8381 | 5.7259 | 189.5386 |
| 10 | 0.0989 | 2.0781 | 4.1325 | 10.2672 | 268.8726 |
| 15 | 0.1244 | 2.7142 | 5.3781 | 10.9886 | 347.6139 |
| 50 | 0.6479 | 8.2589 | 13.3576 | 27.4398 | 850.6713 |
| 100 | 1.1624 | 14.3999 | 32.6576 | 65.3298 | 1521.3971 |
Table 3.
For different number of weights and control points, the time of execution of the least-squares method using the Matlab commands mldivide and SVD, and the time of execution of the Algorithm 1 for 3000 iterations are provided. The values have been measured in seconds with a set of data points of size 100 and they are the mean of 5 repetitions.
Table 3.
For different number of weights and control points, the time of execution of the least-squares method using the Matlab commands mldivide and SVD, and the time of execution of the Algorithm 1 for 3000 iterations are provided. The values have been measured in seconds with a set of data points of size 100 and they are the mean of 5 repetitions.
| Least-Squares Method | Algorithm 1 |
|---|
| mldivide | SVD | 3000 Iterations |
|---|
| 5 | 63.3014 | 65.6015 | 189.5386 |
| 10 | 167.0402 | 237.0386 | 268.8726 |
| 15 | 309.5811 | 457.8987 | 347.6139 |
| 20 | 478.1141 | 774.3472 | 429.2819 |
| 30 | 961.2860 | 978.6830 | 568.5647 |
| 50 | 2552.4064 | 4097.9278 | 850.6713 |