Abstract
This paper presents the visual navigation method for determining the position and orientation of a ground robot using a diffusion map of robot images (obtained from a camera in an upper position—e.g., tower, drone) and for investigating robot stability with respect to desirable paths and control with time delay. The time delay appears because of image processing for visual navigation. We consider a diffusion map as a possible alternative to the currently popular deep learning, comparing the possibilities of these two methods for visual navigation of ground robots. The diffusion map projects an image (described by a point in multidimensional space) to a low-dimensional manifold preserving the mutual relationships between the data. We find the ground robot’s position and orientation as a function of coordinates of the robot image on the low-dimensional manifold obtained from the diffusion map. We compare these coordinates with coordinates obtained from deep learning. The algorithm has higher accuracy and is not sensitive to changes in lighting, the appearance of external moving objects, and other phenomena. However, the diffusion map needs a larger calculation time than deep learning. We consider possible future steps for reducing this calculation time.
1. Introduction
Currently, deep learning (based on artificial neural networks) [1,2,3,4,5,6,7] is a very popular and powerful instrument for arriving at the solution of complex problems of classification and function regression. The main advantage of this method is that we need not develop some complex features describing the group of investigated objects. We obtain these features automatically. In addition, deep learning is a very effective method for function regression. For example, we cannot only recognize a ground robot but can also find its position and orientation.
“PoseNet is [1] is based on the GoogLeNet architecture. It processes RGB-images and is modified so that all three softmax and fully connected layers are removed from the original model and replaced by regressors in the training phase. In the testing phase the other two regressors of the lower layers are removed and the prediction is done solely based on the regressor on the top of the whole network.
Bayesian PoseNet Kendall et al. [2] propose a Bayesian convolutional neural network to estimate uncertainty in the global camera pose which leads to improving localization accuracy. The Bayesian convolutional neural is based on PoseNet architecture by adding dropout after the fully connected layers in the pose regressor and after one of the inception layers (layer 9) of GoogLeNet architecture.
LSTM-Pose [3] is otherwise similar to PoseNet, but applies LSTM networks for output feature coming from the final fully connected layer. In detail, it is based on utilizing the pre-trained GoogLeNet architecture as a feature extractor followed by four LSTM units applying in the up, down, left and right directions. The outputs of LSTM units are then concatenated and fed to a regression module consisting of two fully connected layers to predict camera pose.
VidLoc [4] is a CNN-based system based on short video clips. As in PoseNet and LSTM-Pose, VidLoc incorporates similarly modified pre-trained GoogLeNet model for feature extraction. The output of this module is passed to bidirectional LSTM units predicting the poses for each frame in the sequence by exploiting contextual information in past and future frames.” (cited from [5]). Here RGB is Red, Green, Blue; CNN is Convolutional Neural Network; GoogLeNet is a well-known 22 layers deep network (googlenet in Matlab).
In the paper [5], we propose an encoder–decoder convolutional neural network (CNN) architecture for estimating camera pose (orientation and location) from a single RGB image. The architecture has an hourglass shape consisting of a chain of convolution and up-convolution layers followed by a regression part.
In the paper [6], similar to PoseNet, MapNet also learns a deep learning neural network (DNN) that estimates the 6-DoF camera pose from an input RGB image on the training set via supervised learning. The main difference, however, is that MapNet minimizes both the loss of the per-image absolute pose and the loss of the relative pose between image pairs.
The corresponding results can be found in our paper [8]. However, the principal difference between [1,2,3,4,5,6] and [8] is the following: in [1,2,3,4,5,6], a camera is on a moving object, while in [8], we used a camera which is external with respect to the moving object and established on an upper position (e.g., tower, drone or tethered flying platform). This is our new original patented technology [9].
Because of the popularity of deep learning, many scientists think that only deep learning has these remarkable properties. However, competing methods exist with the same advantages–they can generate features automatically and are very effective methods for function regression. We must remember these methods and investigate their advantages and disadvantages with respect to deep learning. Hence, we would like to consider one such method–the diffusion map [10,11,12,13,14,15,16,17] and compare it with deep learning using a very interesting task of visual navigation of a ground robot from an upper position [8,9].
We can give an example of using the diffusion map in navigation [10]. However, the diffusion map is not used in this paper for visual navigation, i.e., identification position and orientation of a moving object with respect to a camera. The diffusion map was used for path planning inside a 2D grid map.
In this paper, we apply methods based on low-dimensional manifolds, which are widely used in image recognition, to the problem of the determination of ground robot coordinates. The main idea is that multidimensional image data are, in fact, distributed close to some embedded mathematical manifold of low dimension. The diffusion map projects an image (described by a point in the multidimensional space) to this low-dimensional manifold preserving the mutual relationships between the data [11,12,13,14,15,16,17]. The coordinates of the point on the low-dimensional manifold represent the coordinates of the object. We find the ground robot coordinates as a function of coordinates of the robot image on the low-dimensional manifold obtained from the diffusion map. We compare these coordinates with coordinates obtained from deep learning. We also give a short description of robot control with a time delay on the basis of these coordinates found from the diffusion map.
The structure of the paper is the following:
Part 1 is the Introduction. In this part, we explain the importance and novelty of the paper. Indeed, we seek methods that can compete with deep learning in universality and the possibility of automatic generation of features for recognition and regression. The diffusion map is such a method. In this paper, we offer an important practical example (the ground robot navigation), demonstrating that the diffusion map can indeed compete with deep learning. We also offer in this section a list of relevant references and describe the structure of the paper.
Part 2 is the Materials and Methods section. In this part, we describe methods used for the solution of the ground robot navigation using a diffusion map and provide a block diagram describing the solution flowchart.
Part 3 is the Results. In this part, we introduce the diffusion map using four steps. First, we define the function for comparing similar images based on the Lucas–Kanade method [18] for finding optical flow. In the second step, we define diffusion space and its eigenbasis. In the third step, we define how an arbitrary image can be expanded using the eigenbasis. However, finding the ground robot position and orientation is only half of the problem of navigation. Hence, in the fourth step, we consider the problem of controlling the robot’s motion. The paper presents a method for stabilization of the moving robot controlled by autopilot with time delay using results developed herein [8]. Indeed, image processing for visual navigation demands much time and results in time delay. However, the proposed method allows us to achieve stable control in the presence of this time delay.
Part 4 is the Discussion section. In this part, we describe the results of the diffusion map algorithm and the deep learning algorithm, drawing conclusions on the efficiency of the diffuse map method.
Part 5 is the Conclusion. In this part, we conclude with the main results of our paper, compare the diffusion map with deep learning, describe the advantages and disadvantages of the methods and also discuss future plans to improve the diffusion map.
2. Materials and Methods
In this paper, we use two sets of images—a training set (900 images) and a validation set (5000 images). The training set is used for training the diffusion map algorithm, and the validation set is used for verification of the diffusion map algorithm. The diffusion map algorithm allows us to find the coordinates of the ground robot on an image in the diffusion space.
We also know the usual space coordinates of the ground robot with respect to the camera. Hence, using 1800 images (900 from the training set and 900 from the validation set) and some interpolation functions, we can find values of the usual space coordinates for any values of the diffusion space coordinates.
The rest of the images from the validation set are used for finding error values for two coordinates and the angle describing the position of the ground robot with respect to the camera.
The diffusion map, as a data analysis tool, was introduced in 2006 [11,12]. The authors showed that the eigenfunctions of the Markov matrices could be used to construct embedded low-dimensional manifold coordinates, obtained by the diffusion map, that create effective representations for complex geometric structures. It is very useful for dimensionality reduction and data parameterization.
For many cases, the data sample is represented by a set of numeric attributes. In this situation, the condition that two nodes can be connected and the strength of this connection is calculated on the basis of closeness for the corresponding data points of the feature space.
The basic idea is to treat the eigenvectors of the Markov matrices (the matrix of translation probability for all node connections) as coordinates on a dataset. Therefore, the data initially considered as a graph can be considered as a point cloud.
This algorithm demonstrates two main advantages with respect to classical dimensionality reduction methods (for example, classical multivariate scaling or principal component analysis): it is nonlinear and preserves local structures.
Let us briefly describe the diffusion map algorithm. Suppose that images , where –multifold in . Let us define up to multifold measure μ, such that:
Let us build using an weighted graph, where will be nodes of the graph and will be graph distances, connecting the nodes i and k. These distances create distance matrix M. At the next step from the graph matrix M we define weight matrix W that is called the Laplace matrix. Moreover, in the next step from the weight matrix W, we create the Markov matrix . The first m eigenvectors of the Markov matrix may be considered as coordinates in the diffusion space with m-dimensions, produced by .
If we get a new point , by using the vector we can find point in diffusion space . These coordinates provide us essential information about the new point .
We can build the diffusion space up to the basic set of ground robot images . This diffusion space will allow us to find with high precision coordinates in the diffusion space for any additional image y, which is not included in the set
For finding the diffusion map, we must define the function of similarity for two images . To do it, we look for intrinsic points by the Harris–Stephens corner detector [17] and then use the Lucas–Kanade algorithm [18] to find corresponding intrinsic points.
Finally, we describe the robot control with time delay based on diffusion map algorithm measurements using the results of the papers [19,20].
The flowchart for the full ground robot navigation and control algorithm using a diffusion map is the following:
- Start;
- We define the similarity of two robot images using the Harris–Stephens corner detector [17] and then use the Lucas–Kanade algorithm [18] to find correspondent intrinsic points;
- We choose the set of n robot images describing its possible rotations and translations with some small steps;
- Using the set of n images and the similarity function, we find the diffusion map with correspondent n eigenvalues and eigenvectors;
- Using these eigenvalues and eigenvector, we find the correspondent reduced m-dimension (m « n) diffusion space;
- We describe the method for finding coordinates of an arbitrary robot image in the diffusion space;
- We add n new images and find their coordinates in the diffusion space;
- Using these two sets of n images and any interpolation method, we can find correspondence between the position and orientation of the robot and its image coordinates in the diffusion space;
- Using the found correspondence, we can find the position and orientation of the robot on any image;
- Using the theory for the robot control with time delay, we can find control signals for decreasing difference between the found and desirable robot position and orientation;
- Finish.
3. Results
3.1. Basic and Additional Sets of Images
Images of a ground robot on a neutral background with pixel size 100 × 100 were created in the Unity program (Figure 1). Because of the properties of our image processing algorithm, we choose a special pattern for the upper surface of the robot with a large number of intrinsic points and nonuniform environments of these points: The black strip borders with the upper robot surface. We need this strip to separate the upper robot surface from the surrounding background.
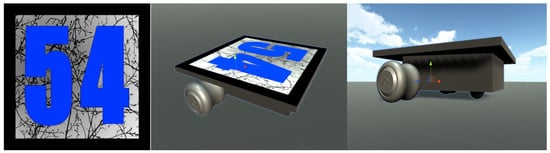
Figure 1.
The ground robot images.
The basic set (the training set) of images includes 900 images with a pixel size of 100 × 100, where coordinates of the robots and their rotation angle are some discrete set. Some examples are shown in Figure 2. The set of the horizontal coordinates u are −16 pixels, −8 pixels, 0 pixels, 8 pixels, 16 pixels. A similar set is defined for the vertical coordinates v. The rotation angle α changes from −170° to 180° with angle step 10°. The coordinate origin (for the robot body) is pointed in the middle of the line connecting the centers of the back wheels because this point is a center of robot rotation during motion, and we need to know the origin of the coordinates for controlling the robot. In addition, 0° corresponds to the robot pointed down with respect to the image, with a clockwise direction corresponding to the robot angle increasing.
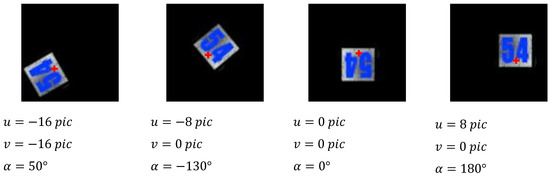
Figure 2.
Examples of images from the basic set (the red plus sign denotes the robot body origin).
The set of the basic robot images corresponds to a table with the robot coordinates and robot angle sin() and cos() correspondent to the robot position and orientation on the images. We use sin() and cos() to prevent a gap (for ) in the point between −180° and 180°.
The set of additional images (the validation set) includes 5000 images with random angles and coordinates in the same range.
Images can be considered as points of the multifold in the space, where N is equal to the pixel number of an image multiplied by the number of the layers, i.e., N = 100 × 100 × 3 = 30,000. As far as images, are different only by the coordinates and rotation angle of the robot. It is evident that and . However, for the description of the robot position and orientation, we will use 4 values– to prevent mistakes for rotation angle close to values −180° or 180°.
3.2. Intrinsic Points
On the image of the robot with pixel coordinates and rotation angle we found 25 intrinsic points by the Harris–Stephens corner detector [17] (Figure 3). These points can be easily found on any image of the robot with a different position and orientation. We also found coordinates of all these points on all images of the basic set (900 images).

Figure 3.
Image of the robot with pixel coordinates and rotation angle with 25 intrinsic points found by the Harris–Stephens corner detector [17].
These points have the following properties [17]:
- distinctness–the intrinsic point must be clearly different from the background and have a special (one-of-a-kind) environment.
- invariance–the recognition of an intrinsic point must be independent with respect to affine transformation.
- stability–the recognition of an intrinsic point must be independent with respect to noise and errors.
- uniqueness–except for local distinctness (already described above), the intrinsic point must also have global uniqueness for the distinction of repeating patterns.
- interpretability–the intrinsic point must be defined in such a way to use them for analysis of correspondences and finding interpretive information from images.
3.3. Measure Definition
We defined as a measure of similarity between images (one of the basic images) and by the following:
- Both images and we transform to gray images;
- Twenty-five intrinsic points on the first image we take from prepared data of basic images with already previously found intrinsic points;
- Using the Lucas–Kanade algorithm [18], we find correspondent points on the second image (Figure 4);
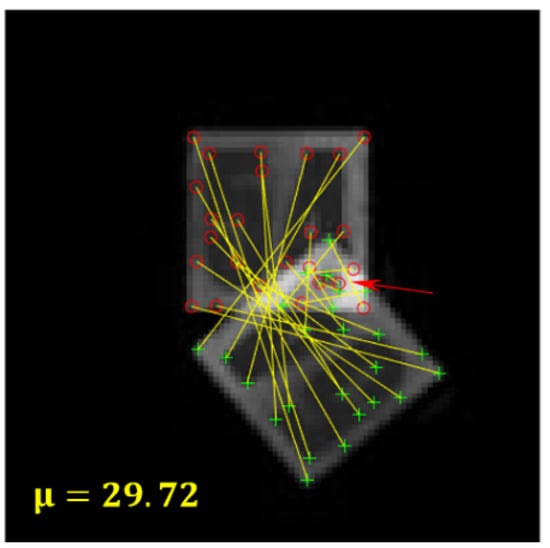 Figure 4. Correspondent points on the two images and the found measure .
Figure 4. Correspondent points on the two images and the found measure . - We find distances between correspondent points. If no correspondent point is found for some intrinsic point of the first image, we suppose the distance to be equal to 100;
- The Lucas–Kanade algorithm gives us information about the error value of the found correspondence. If this error value is larger than the threshold value 30, we suppose the distance to be equal to 100. The example of such correspondence is denoted by a red arrow in Figure 4;
- All 25 found distances are arranged in increasing order;
- The measure of similarity between images and is the median value of the distances.
3.4. Definition of Weight Matrix
- Using the described above measure based on the Lucas–Kanade algorithm, we can define the distance matrix M with size 900 × 900, where any matrix element is defined by measure between -th and -th images.
- In the next step, we define weight matrix W:where ε-is a correctly chosen scale coefficient.To choose ε, we use the recommendation described in the paper (Bah, 2008), specifically:
- we calculate the value:
- we draw the function on a logarithmic scale (Figure 5). This graph has two asymptotes for and for .
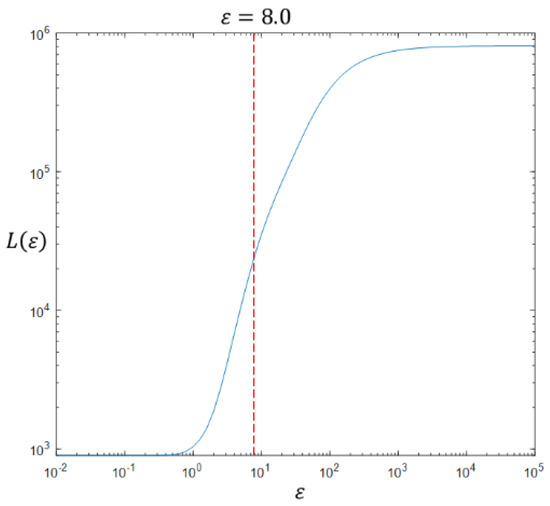 Figure 5. The function in logarithmic scale.
Figure 5. The function in logarithmic scale. - we choose the final value of on the middle of the linear part of the graph in the inflection point.
3.5. Creation of Diffusion Space
For the creation of the diffusion space, we need to find eigenvectors of the Markov matrix. Markov matrix is created from matrix W by normalization of its rows. To do this, we need to:
- Create the diagonal matrix D using the following formulas:
- Find eigenvectors of the Markov matrix that we previously need to create the symmetric matrix instead of (element of Markov matrix can be interpreted as the probability of transition from node i to node j of the graph). It was demonstrated in the paper [13] that symmetric matrix has the same eigenvectors as up to multiplication to . Specifically, if are eigenvectors and are eigen values of matrix , then eigenvectors and eigen values of matrix will be, correspondingly:The first eigenvector is trivial and equal to (1, 1, 1, …, 1) T with eigen value 1.
- Image coordinates of in diffusion space can be defined as the following:where is the -th element of the -th eigenvector. As demonstrated [13], the distance between points and in the diffusion space is equal:Using only the first m eigenvectors, we get a low-dimension representation of the initial set of basic images. The corresponding diffusion space can be defined as follows:
In this connection, the information about the position and orientation of the robot in the images is included in the first eigenvectors (Figure 6). In Figure 6, we can see that the second eigenvector is correlated with sin(α − 65), the third vector is correlated with cos(α + 205) = cos(α − 65 + 270) = sin(α − 65), the sixth vector is correlated with , and the seventh vector is correlated with .
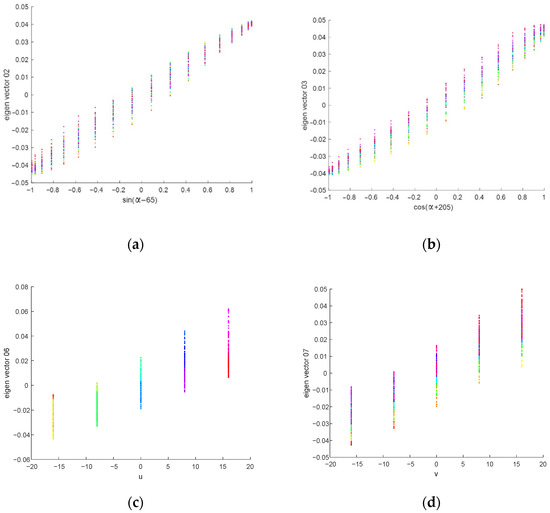
Figure 6.
Correlation of eigenvectors with the robot coordinates and rotation angle: (a) correlation of the second eigenvector with sin(α − 65) of rotation angle α; (b) correlation of the third eigenvector with cos(α + 205) = sin(α − 65) of rotation angle α; (c) correlation of the sixth eigenvector with robot coordinate u; (d) correlation of the seventh eigenvector with robot coordinate v.
3.6. Finding the Diffusion Coordinate for an Arbitrary Image not Included in the Basic Set
Currently, we need to find the diffusion coordinate for an arbitrary image not included in the basic set:
- Using the above-described measure for arbitrary image , we can create the vector:We can rewrite the vector in weight form similar to elements of matrix (see Equation (2)):
- However, to find the diffusion coordinate for an arbitrary image not included in the basic set, it is necessary to use the method of geometric harmonics based on the Nyström extension [12] and [15].According to the definition of eigenvectors and eigenvalues νW, λW of matrix from Equation (2), we can write the following equations:Using the Nyström extension, we can approximate for images not included in the basic set:Eigen vectors {νW} form the orthonormal basis in . Consequently, any function f(x), defined in the basic set of images, can be approximate as the linear combination of basic eigenvectors {νW}:whereUsing the Nyström extension, we can approximate f(x) for an arbitrary value :Applying the last equation for the eigenvectors of Markov matrix instead of function f, we derive from Equations (14) and (17):These values can be used for the calculation of the diffusion coordinates of the image .
- Diffusion coordinates of the image can be found as follows:
3.7. Finding the Robot Coordinates and Rotation Angle from Image Coordinates in the Diffusion Space
We can form the learning set including 900 basic images and 900 images (not included in the basic set) with the robot’s two known coordinates, sin() and cos() of rotation angle and find the coordinates of these images in the diffusion space. In the next step, we can consider the robot’s two coordinates, sin() and cos() of rotation angle as a function of its image coordinates in the diffusion space. Indeed, we can find these 4 functions using 1800 images described above with the help of any known interpolation method (for example, artificial neural network, inverse distance weighting and so on).
3.8. Automatic Control
We define the following parameters and variables used in the ground robot motion equations (Figure 7):

Figure 7.
Ground robot, the picture on the surface of the robot was used for navigation with the help of the deep learning network.
- (1)
- motion variables:и —ground robot coordinates; α-robot rotation angle on the plane; —robot translation velocity; ω-robot angular velocity
- (2)
- parameters of the ground robot:R–radius of the robot wheels; —distance between robot wheels
- (3)
- Command signals for control:—angular rotation velocities for the left and right wheels.
We can see from [19] that rotation and forward movement can be described using the following system of equations:
As a result of system nonlinearity, it is too difficult to use those equations for stability analysis. It is thus necessary to linearize them. The parameters x(t), y(t), α(t), v(t), ω(t) correspond to steady-state flight (x0(t), y0(t), α0(t), v0(t), ω0(t)) perturbated by small increments δx(t), δy(t),δα(t), δv(t-τ), δω(t-τ).
The robot trajectory can be estimated by a polygonal chain path. This path is a set of rotations in vertices with zero translational velocity and constant angular velocity (rotation), and linear motion along straight-line segments with zero angular velocity and constant translational velocity (linear motion).
In case the stationary parameters themselves cannot guarantee stability for the desirable steady-state trajectory, an autopilot is necessary (see Figure 8). This autopilot must state the controlling parameters δv(t-τ), δω(t-τ) controlled by autopilot as functions of the output parameters (δx(t), δy(t),δα(t)), which are perturbations with respect to the desirable steady-state path. The autopilot gets the output parameter values from navigation: from vision-based navigation, satellite navigation, inertial navigation, and so on. Using these measurements, the autopilot can find signals of control for decreasing undesirable perturbations. Unfortunately, for any measurement, some delay always exists in getting output parameters used for control. As a result, we are faced with a problem because we have a lack of information for control. From [20], we can see that even for such conditions with the time delay, we can generate a signal of control that guarantees a stable trajectory.
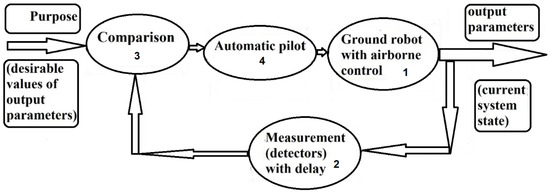
Figure 8.
Automatic control: the ground robot has output parameters (output of block 1) describing its position, orientation, and velocity. These parameters are measured and calculated by the measurement system with some time delay (output of block 2). These measured parameters and their desirable values, calculated from the desirable trajectory (inputs of block 3), can be compared, and deviation from desirable trajectory can be calculated (output of block 3). The automatic pilot receives these deviations and calculates the control parameters for the ground robot to decrease these deviations. Then the ground robot changes its output parameters (output of block 1). This cycle repeats for the duration of the motion.
From [20] the final solution is the following:
The steady state solution for rotation is as follows:
where control parameters are the following:
α(t) = ωt + φ; v(t) = 0; φ = 0
The steady-state solution for linear motion is as follows:
where values of control parameters can be found by:
α(t) = α; v(t) = v;
Time of delay can be found by:
4. Discussion
In [8], we used the deep learning network for the solution of the same task: looking for the orientation and position of a ground robot. The deep learning network was developed using AlexNet with small changes in training mode and structure. AlexNet [7] is a popular CNN (convolutional neural network), which was developed by Alex Krizhevsky and described by Ilya Sutskever, Alex Krizhevsky and Geoffrey Hinton. On 30 September 2012, AlexNet took part in the ImageNet large scale visual recognition challenge and was the winner. Initially, AlexNet had eight levels (five convolutional levels and three fully connected levels). In our case, we replaced the last two fully connected layers with one fully connected layer having four outputs (trigonometric functions sin(α) and cos(α), where α-angle of rotation, and x, y coordinates) or seven outputs (sin(α), cos(α), x, y, angle error, coordinate errors, and total error) and also one regression layer. The pre-trained modified AlexNet network was used for the solution of the regression problem: finding the course angle and two coordinates of the ground robot (Figure 2 in [8]).
With this deep learning network, it is possible to find the ground robot angle with an accuracy of 4° and ground robot position with an accuracy of 2.6 pixels (6 cm) (Table 1) for any 227 × 227 pixel-sized image. For training, we used the set of 10,000 images and the “adam” solver, with training carried out in 200 epochs with a batch size equal to 500. Using Unity modeling, we programmatically generated the dataset.

Table 1.
Error of coordinates and rotation angle for the ground robot for navigation by the artificial neural network; size of the robot is 50 cm × 50 cm; pixel size corresponds to the distance 2.30 cm on the ground.
At every step, robot rotation angle, robot position, and working platform element location were selected randomly. We simulated lighting as sunlight falling from various directions and angles. We used 50 different textures for the background to be sure that the ground robot coordinates would be independent of the background. In addition, 12,000 3036 × 3036-pixel sized RGB images were generated which contain the ground robot. There also were images where the robot was completely or partially occluded by the camera tower or some objects of the environment. We also prepared a file with data about the angle of rotation and coordinates for the ground robot. After using these images, we prepared the set of reduced 227 × 227-pixel sized images.
We have the train set (used for the ANN or artificial neural network training) and the validation set for the verification of the pre-trained ANN.
All errors were found for the validation set of images as differences between positions and orientations, obtained from the pre-trained artificial neural network, and known positions and orientations used for the creation of images by the Unity program. The root-mean-squares of these errors are written in the second row of Table 1.
Let us consider the visual navigation again with the help of the diffusion map algorithm.
In Figure 6, we can see that the second eigenvector is correlated with sin(), the third vector is correlated with cos(), the sixth vector is correlated with , and the seventh vector is correlated with .
We can see that the basis of the diffusion space, in fact, corresponds to the robot position and orientation. The first seven eigenvectors give us full information about these parameters.
Our experiment demonstrates that for optimal results, the number of the first eigenvectors of the diffusion space m = 40 (from maximal value n = 900).
In Table 2, we can see the error value for four variables describing the ground robot position: coordinate (u and v) and rotation angle (cos(α), sin(α), α). We give the results for the training set (used for the creation of the diffusion space and interpolation function) and the independent validation set.

Table 2.
Error of coordinates and rotation angle for the ground robot for navigation by the diffusion map; size of the robot is 50 cm × 50 cm; pixel size corresponds to 1.47 cm on the ground.
We have the training set (used for finding the diffusion map) and the validation set for the verification of the diffusion map method results.
First, all errors were found for the training set of images as differences between positions and orientations, obtained from the diffusion map method, and known positions and orientations used for the creation of the images by the Unity program. The root-mean-square of these errors is written in the first row of Table 2.
Second, all errors were found for the validation set of images as differences between positions and orientations, obtained from the diffusion map method, and known positions and orientations used for the creation of the images by the Unity program. The root-mean-square of these errors is written in the second row of Table 2.
The following conclusions can be made about the diffusion map:
- The computing time used for the diffusion map is high because of the large number of basic images;
- The diffusion map needs very high localization for the area of the possible robot position. We can use motion detection for this localization;
- Under correct estimation of similarity between images, the diffusion map has higher precision;
- The diffusion map operates according to the known algorithm, and we automatically get features for recognition and function regression, describing position and orientation. It is the seven first axes of the diffusion space.
5. Conclusions
In our previous paper [8], we used the artificial neural network (deep learning) for the solution of the same task: finding the position and orientation of the ground robot. The developed network allowed us to find the coordinates with a precision of 6 cm and a rotation angle with a precision of 4° (Table 1).
We can calculate robot recognition error in a deep learning network using three (from seven outputs) with position and orientation errors (in a seven output network, described above). We can conclude that the robot does not exist on an image or is partially occluded if there are very big position and orientation errors.
For the deep learning and diffusion map algorithms, we chose the robot surface and background to be strongly different, so recognition quality is almost ideal. This is not because of the high quality of the network or the diffusion map, but because of choosing the robot surface, which is very different from the background. Indeed, we need to choose robot surfaces for robust navigation, which are strongly different from the background. The chosen robot surfaces, which are optimal for recognition, are different for the two methods (see Figure 1 and Figure 7).
The diffusion map allows us to find the position and orientation of the ground robot with better precision for coordinates and similar precision for the rotation angle.
The following differences exist with respect to deep learning [8]:
- The computing time used for the diffusion map is higher than the computer time, which is necessary for deep learning. We need longer computer time for the diffusion map because of the large number of images in the basic set;
- The artificial neural network can find the robot in a large area, but the diffusion map claims very high localization for the area of the possible robot position. We can use motion detection for this localization;
- Under correct estimation of similarity between images, the diffusion map has higher precision than deep learning;
- The diffusion map operates according to a known algorithm, so we need not look for some artificial neural network structure.
We see that the main disadvantage of the diffusion map is the long calculation time. Our future plans are to resolve this problem. The time can be reduced using the following methods:
- Using parallel processing for calculation of the measure of similarity for the pair of images and parallel calculations for different images in the basic set;
- Reduction of time by optimization of an algorithm for calculation of the measure of similarity between a pair of images;
- Reduction of the number of images in the basic set;
- Preprocessing clustering of close images in the basic set. Hence, we can then calculate only measures of similarity between an investigated image and images only from its closest clusters.
Image processing for visual navigation needs a great deal of time. As a result, we are faced with a time delay. We can see in Figure 8 that the time delay exists in the measurement block because of the long duration of time, which is necessary for image processing of visual navigation. As a result, we can also find the perturbations of the robot coordinates with the time delay. However, the proposed method allows us to get a stable control in the presence of the time delay if this time delay is small enough (see Equation (28)).
Author Contributions
All authors have written this paper, and the final form of this paper is approved by all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kendall, A.; Grimes, M.; Cipolla, R. PoseNet: A convolutional network for real-time 6-dof camera relocalization. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Kendall, A.; Cipolla, R. Geometric loss functions for camera pose regression with deep learning. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Walch, F.; Hazirbas, C.; Leal-Taixe, L.; Sattler, T.; Hilsenbeck, S.; Cremers, D. Image-based localization using LSTMs for structured feature correlation. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Clark, R.; Wang, S.; Markham, A.; Trigoni, N.; Wen, H. VidLoc: A Deep Spatio-Temporal Model for 6-DoF Video-Clip Relocalization. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Melekhov, I.; Ylioinas, J.; Kannala, J.; Rahtu, E. Image-based Localization using Hourglass Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Brahmbhatt, S.; Gu, J.; Kim, K.; Hays, J.; Kautz, J. Geometry-Aware Learning of Maps for Camera Localization. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Kupervasser, O.; Kutomanov, H.; Sarychev, V.; Yavich, R. The new advanced prototype of airborne visual control of a ground robot. In Proceedings of the Geomate 2020, Melbourne, Australia, 11–13 November 2020; Available online: https://www.researchgate.net/publication/344925210_THE_NEW_ADVANCED_PROTOTYPE_OF_AIRBORNE_VISUAL_CONTROL_OF_A_GROUND_ROBOT (accessed on 28 October 2020).
- Kupervasser, O.Y. Russian Invention: Method for Coordination of Ground Moving Automated Devices with the Help of Single Central Control. System. Patent No. 2691788, 5 July 2015. [Google Scholar]
- Chen, Y.F.; Liu, S.-Y.; Liu, M.; Miller, J.; How, J.P. Motion Planning with Diffusion Maps. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, South Korea, 9–14 October 2016. [Google Scholar]
- Coifman, R.; Lafon, S. Diffusion maps. Appl. Comput. Harmon. Anal. 2006, 21, 5–30. [Google Scholar] [CrossRef]
- Coifman, R.; Lafon, S. Geometric harmonics: A novel tool for multiscale out-of-sample. Appl. Comput. Harmon. Anal. 2006, 21, 31–52. [Google Scholar] [CrossRef]
- De la Portey, J.; Herbsty, B.M.; Hereman, W.; van der Walt, S.J. An Introduction to Diffusion Maps. In 19th Symposium of the Pattern Recognition Association of South Africa; University of Stellenbosch: Stellenbosch, South Africa, 2008. [Google Scholar]
- Koltyrin, A. Hyperspectral Imaging dataclustering by constructing a diffusion map, Technical sciences-from theory to practice. In Proceedings of the X International Science and Practice Conference, Novosibirsk, Russia, 12 June 2012. [Google Scholar]
- Averbuch, A.; Hochman, K.; Rabin, N.; Schclar, A.; Zheludev, V. A diffusion framework for detection of moving vehicles. Digit. Signal Process. 2010, 20, 111–122. [Google Scholar]
- Bah, B. Diffusion Maps: Analysis and Applications; University of Oxford: Oxford, UK, 2008. [Google Scholar]
- Haralick, R.M.; Shapiro, L.G. Computer and Robot Vision; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1992. [Google Scholar]
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the DARPA Imaging Understanding Workshop, Washington, DC, USA, 23 April 1981; pp. 121–130. [Google Scholar]
- Longoria, R.G. Turning Kinematically. 2015. Available online: https://docplayer.net/31417021-Turning-kinematically.html (accessed on 25 August 2020).
- Domoshnitsky, A.; Kupervasser, O.; Kutomanov, H.; Yavich, R. A Method for Stabilization of Ground Robot Path Controlled by Airborne Autopilot with Time Delay; Book Chapter; Springer Nature Singapore Pte Ltd.: Singapore, 2020. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).