A Fuzzy Method for Solving Fuzzy Fractional Differential Equations Based on the Generalized Fuzzy Taylor Expansion

Abstract

In this field of research, in order to solve fuzzy fractional differential equations, they are normally transformed to their corresponding crisp problems. This transformation is called the embedding method. The aim of this paper is to present a new direct method to solve the fuzzy fractional differential equations using fuzzy calculations and without this transformation. In this work, the fuzzy generalized Taylor expansion by using the sense of fuzzy Caputo fractional derivative for fuzzy-valued functions is presented. For solving fuzzy fractional differential equations, the fuzzy generalized Euler’s method is introduced and applied. In order to show the accuracy and efficiency of the presented method, the local and global truncation errors are determined. Moreover, the consistency, convergence, and stability of the generalized Euler’s method are proved in detail. Eventually, the numerical examples, especially in the switching point case, show the flexibility and the capability of the presented method.

1. Introduction

Fuzzy set theory is a powerful tool for modeling uncertain problems. Therefore, large varieties of natural phenomena have been modeled using fuzzy concepts. Particularly, the fuzzy fractional differential equation is a common model in different scientific fields, such as population models, evaluating weapon systems, civil engineering, and modeling electro-hydraulics. Therefore, the concept of the fractional derivative is a very important topic in fuzzy calculus. Therefore, fuzzy fractional differential equations have attracted much attention in mathematics and engineering fields. The first work devoted to the subject of fuzzy fractional differential equations is the paper by Agarwal et al. [1]. They have defined the Riemann–Liouville differentiability concept under the Hukuhara differentiability to solve fuzzy fractional differential equations.

In recent years, fractional calculus has been introduced as an applicable topic to produce the accurate results of mathematical and engineering problems such as aerodynamics and control systems, signal processing, bio-mathematical problems, and others [1,2,3,4,5].

Furthermore, fractional differential equations in the fuzzy case [1] have been studied by many authors and they have been solved by various methods [6,7,8,9]. In [10], Hoa studied the fuzzy fractional differential equations under Caputo gH-differentiability, and in [11] Agarwal et al. had a survey on mentioned problem to show the its relation with optimal control problems. Furthermore, Long et al. [12] illustrated the solvability of fuzzy fractional differential equations, and Salahshour et al. [13] applied the fuzzy Laplace transforms to solve this problem.

There are many numerical methods to solve the fuzzy fractional differential equations by transforming to crisp problems [14,15,16]. In this paper, a new direct method is introduced to solve the mentioned problem without changing to the crisp form. The Taylor expansion method is one of the famous and applicable methods to solve the linear and nonlinear problems [17,18,19]. In this paper, the fuzzy generalized Taylor expansion based on the fuzzy Caputo fractional derivative is expanded. Then, Euler’s method is applied to solve the fuzzy fractional differential equations. Furthermore, the local and global truncation errors are considered, and finally the consistency, the convergence and the stability of the generalized fuzzy Euler’s method are demonstrated. Furthermore, some examples with the switching point are solved by using the presented method. The numerical results show the precision of the generalized Euler’s method to solve the fuzzy fractional differential equations.

2. Basic Concepts

At first, a brief summary of the fuzzy details and some preliminaries is revisited [20,21,22,23,24,25].

Definition 1.

Set ${\mathbb{R}}_{\mathcal{F}}=\{u:{\mathbb{R}}^n\to [0,1]$ such that u satisfies in the conditions I to IV. }

I. 

u is normal: there exists an $x_0\in {\mathbb{R}}^n$ such that $u(x_0)=1$.

II. 

u is fuzzy convex: for $0\le \lambda \le 1,u({\lambda }_{x_1}+(1-{\lambda }_{x_2}))\ge min\{u(x_1),u(x_2)\}$.

III. 

u is upper semi-continuous: for any $x_0\in {\mathbb{R}}^n$, it holds that $u(x_0)\ge {lim}_{x\to x_0^{\pm }}u(x)$.

IV. 

${\left[u\right]}_0=\overline{supp(u)}=cl\{x\in {\mathbb{R}}^n\mid u(x)>0\}$ is a compact subset.

is called the space of fuzzy numbers or the fuzzy numbers set. The r-level set is ${\left[u\right]}_r=\{x\in {\mathbb{R}}^n\mid u(x)\ge r,0<r\le 1\}$. Then, from I to IV, it follows that, the r-level sets of $u\in {\mathbb{R}}_{\mathcal{F}}$ are nonempty, closed, and bounded intervals.

Definition 2.

A triangular fuzzy number is defined as a fuzzy set in ${\mathbb{R}}_{\mathcal{F}}$, that is specified by an ordered triple $u=(a,b,c)\in {\mathbb{R}}^3$ with $a\le b\le c$ such that $u^{-}(r)=a+(b-a)r$ (or lower bound of u) and $u^{+}(r)=c-(c-b)r$ (or upper bound of u) are the endpoints of r-level sets for all $r\in [0,1]$.

A crisp number k is simply represented by $u^{-}(r)=u^{+}(r)=k,0\le r\le 1$ and called singleton. For arbitrary $u,v\in {\mathbb{R}}_{\mathcal{F}}$ and scalar $k,$ we might summarize the addition and the scalar multiplication of two fuzzy numbers by

$◃addition:{[u\oplus v]}_r=[u^{-}(r)+v^{-}(r),u^{+}(r)+v^{+}(r)],$

$◃scalarmultiplication:\left\{\begin{array}{c}{[k\odot u]}_r=[k{u}^{-}(r),k{u}^{+}(r)],k\ge 0,\\ {[k\odot u]}_r=[k{u}^{+}(r),k{u}^{-}(r)],k<0.\end{array}\right.$

The Hausdorff distance between fuzzy numbers is given by $\mathcal{H}:{\mathbb{R}}_{\mathcal{F}}\times {\mathbb{R}}_{\mathcal{F}}\to {\mathbb{R}}^{+}\cup \left\{0\right\}$ as

$$\mathcal{H}(u,v)=\underset{0\le r\le 1}{sup}max\left\{\right|u^{-}(r)-v^{-}(r)|,|u^{+}(r)-v^{+}(r)\left|\right\},$$

where ${\left[u\right]}_r=[u^{-}(r),u^{+}(r)],{\left[v\right]}_r=[v^{-}(r),v^{+}(r)]$. The metric space $({\mathbb{R}}_{\mathcal{F}},\mathcal{H})$ is complete, separable, and locally compact where the following conditions are valid for metric $\mathcal{H}$:

I.

$\mathcal{H}(u\oplus w,v\oplus w)=\mathcal{H}(u,v),\forall u,v,w\in {\mathbb{R}}_{\mathcal{F}}.$

II.

$\mathcal{H}(\lambda u,\lambda v)=\mid \lambda \mid \mathcal{H}(u,v),\forall \lambda \in \mathbb{R},\forall u,v\in {\mathbb{R}}_{\mathcal{F}}.$

III.

$\mathcal{H}(u\oplus v,w\oplus z)\le \mathcal{H}(u,w)+\mathcal{H}(v,z),\forall u,v,w,z\in {\mathbb{R}}_{\mathcal{F}}.$

Definition 3.

Let $u,v\in {\mathbb{R}}_{\mathcal{F}}$, if there exists $w\in {\mathbb{R}}_{\mathcal{F}},$ such that $u=v+w,$ then $w$ is called the Hukuhara difference (H-difference) of $u$ and $v,$ and it is denoted by $u\ominus v$. Furthermore, the generalized Hukuhara difference ($gH$-difference) of two fuzzy numbers $u,v\in {\mathbb{R}}_{\mathcal{F}}$ is defined as follows,

$$u{\ominus }_{gH}v=w\iff \left\{\begin{array}{c}(i)u=v\oplus w,\hfill \\ or\hfill \\ (ii)v=u\oplus (-1)w,\hfill \end{array}\right.$$

it is easy to show that conditions (i) and (ii) are valid if and only if $w$ is a crisp number. The conditions of the existence of $u{\ominus }_{gH}v\in {\mathbb{R}}_{\mathcal{F}}$ are given in [22]. Through the whole of the paper, we suppose that the $gH$-difference exists.

In this paper, the meaning of fuzzy-valued function is a function $f:A\to {\mathbb{R}}_{\mathcal{F}},A\in \mathbb{R}$ where $\mathbb{R}$ is the set of all real numbers and ${\left[f(t)\right]}_r=[f^{-}(t;r),f^{+}(t;r)]$ is the so-called r-cut or parametric form of the fuzzy-valued function f.

Definition 4.

A fuzzy-valued function $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ is said to be continuous at $t_0\in [a,b]$ if for each $\epsilon >0$ there is $\delta >0$ such that $\mathcal{H}(f(t),f(t_0))<\epsilon$, whenever $t\in [a,b]$ and $\mid t-t_0\mid <\delta$. We say that f is fuzzy continuous on $[a,b]$ if f is continuous at each $t_0\in [a,b]$.

Throughout the rest of this paper, the notation ${\mathcal{C}}_f([a,b],{\mathbb{R}}_{\mathcal{F}})$ is called the set of fuzzy-valued continuous functions which are defined on $[a,b]$.

If $f:[a,b]\subseteq \mathbb{R}\to {\mathbb{R}}_{\mathcal{F}}$ is continuous by the metric $\mathcal{H}$, then ${\int }_a^{t}f(s)ds$ is a continuous function in $t\in [a,b]$ and the function f is integrable on $[a,b]$. Furthermore, it holds

$${\left[{\int }_a^{b}f(s)ds\right]}_r=\left[{\int }_a^b{f}^{-}(s;r)ds,{\int }_a^b{f}^{+}(s;r)ds\right].$$

Definition 5.

Let $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$, $t_0\in (a,b)$ with $f^{-}(t;r)$ and $f^{+}(t;r)$ both differentiable at $t_0$ for all $r\in [0,1]$ and $D{f}_{gH}$ (gH-derivative) exists:

I. 

The function f is ${}^F[(i)-gH]$-differentiable at $t_0$ if ${\left[D{f}_{i.gH}(t_0)\right]}_r=[D{f}^{-}(t_0;r),D{f}^{+}(t_0;r)]$.

II. 

The function f is ${}^F[(ii)-gH]$-differentiable at $t_0$ if ${\left[D{f}_{ii.gH}(t_0)\right]}_r=[D{f}^{+}(t_0;r),D{f}^{-}(t_0;r)].$

3. Definitions and Properties of Fractional $\mathit{g}\mathit{H}$-Differentiability

In this section, let us focus on some definitions and properties related to the fuzzy fractional generalized Hukuhara derivative which are useful in the sequel of this paper.

Definition 6

([26]). Let $f(t)$ be a fuzzy Lebesque integrable function. The fuzzy Riemann–Liouville fractional (for short $(F.RL)$-fractional) integral of order $\alpha >0$ is defined as follows,

$${}^{F.RL}{I}_{[a,t]}^{\alpha }f(t)=\frac{1}{\Gamma (\alpha )}{\int }_a^t{(t-s)}^{\alpha -1}f(s)ds.$$

Definition 7

([26]). Let $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$. The fuzzy fractional derivative of $f(t)$ in the Caputo sense is in the following form,

$${}^{FC}{D}_{*}^{\alpha }f(t)={}^{F.RL}{I}_{[a,t]}^{m-\alpha }(D^m{f}_{gH})(t)=\frac{1}{\Gamma (m-\alpha )}{\int }_a^t{(t-s)}^{m-\alpha -1}{D}^m{f}_{gH}(s)ds,$$

$$m-1<\alpha <m,m\in \mathbb{N},t>a,$$

where $\forall m\in \mathbb{N},D^m{f}_{gH}(s)$ ($gH$-derivatives of f) are integrable. In this paper, we consider fuzzy Caputo generalized Hukuhara derivative (for short ${}^{FC}\left[gH\right]$-derivative) of order $0<\alpha \le 1$, for fuzzy-valued function f, so the ${}^{FC}\left[gH\right]$-derivative will be expressed by

$${}^{FC}{D}_{*}^{\alpha }f(t)={}^{F.RL}{I}_{[a,t]}^{1-\alpha }(D{f}_{gH})(t)=\frac{1}{\Gamma (1-\alpha )}{\int }_a^t{(t-s)}^{-\alpha }D{f}_{gH}(s)ds,t>a.$$

(1)

Lemma 1.

Let $f:[a,b]\subseteq \mathbb{R}\to {\mathbb{R}}_{\mathcal{F}}$ be continuous. Then, ${}^{F.RL}{I}_{[a,t]}^{\alpha }f(t)$ for $0<\alpha \le 1$ and $t\in [a,b]$ is a continuous function.

Proof. 

Under assumptions of the continuous functions, $f(s)$ is a fuzzy Lebesque integrable function. On the other hand, since $\forall 0<\alpha \le 1,{(t-s)}^{\alpha -1}\ge 0$ is continuous, so ${\int }_a^t{(t-s)}^{\alpha -1}f(s)ds$ is a continuous function and as a result ${}^{F.RL}{I}_{[a,t]}^{\alpha }f(t)$ is a continuous function in $t\in [a,b]$. □

Lemma 2.

Let $f\in {\mathcal{C}}_f(\mathbb{R},{\mathbb{R}}_{\mathcal{F}}),m\in \mathbb{N}$. Then, the fuzzy Riemann-Liouvil fractional integrals ${}^{F.RL}{I}_{[a,t_{m-1}]}^{\alpha }f(t_{m-1}),{}^{F.RL}{I}_{[a,t_{m-2}]}^{\alpha }{(}^{F.RL}{I}_{[a,t_{m-1}]}^{\alpha }f)(t_{m-1})),\dots {,}^{F.RL}{I}_{[a,t]}^{\alpha }{{(}^{F.RL}{I}_{[a,t_1]}^{\alpha }\dots (}^{F.RL}{I}_{[a,t_{m-2}]}^{\alpha }$

${(}^{F.RL}{I}_{[a,t_{m-1}]}^{\alpha }f)(t_{m-1}))\dots )$ for $0<\alpha \le 1$, are continuous functions in $t_{m-1},t_{m-2},\dots ,t$, respectively. Here, $t_{m-1},t_{m-2},\dots ,t\ge a$, and they are real numbers.

Proof. 

This lemma is a fairly straightforward generalization of Lemma 1. The proof will be done by introducing on $m\in \mathbb{N}$. Assume that the lemma holds for $(m)$-times applying operator $(F.RL)$-fractional integrating for function f, we will prove it will correct for $(m+1)$-times applying operator $(F.RL)$-fractional integrating for function f. By Lemma 1, as $f\in {\mathcal{C}}_f(\mathbb{R},{\mathbb{R}}_{\mathcal{F}})$, thus ${}^{F.RL}{I}_{[a,t_{m-1}]}^{\alpha }f(t_{m-1})$ is a continuous function in $t_{m-1}$. Furthermore, under the hypothesis of induction,

$${}^{F.RL}{I}_{[a,t_{m-2}]}^{\alpha }{(}^{F.RL}{I}_{[a,t_{m-1}]}^{\alpha }f)(t_{m-1}),\dots ,\stackrel{(m)-times}{\overbrace{{}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{F.RL}{I}_{[a,t_1]}^{\alpha }\dots {{(}^{F.RL}{I}_{[a,t_{m-2}]}^{\alpha }(}^{F.RL}{I}_{[a,t_{m-1}]}^{\alpha }}}f)(t_{m-1}))\dots ),$$

are continuous functions in $t_{m-1},t_{m-2},t_{m-3},\dots ,t,$ respectively. It follows easily that

$$\stackrel{(m+1)-times}{\overbrace{{}^{F.RL}{I}_{[a,t_{m+1}]}^{\alpha }{(}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{F.RL}{I}_{[a,t_1]}^{\alpha }\dots {{(}^{F.RL}{I}_{[a,t_{m-2}]}^{\alpha }(}^{F.RL}{I}_{[a,t_{m-1}]}^{\alpha }}}f)(t_{m-1}))\dots )),$$

is a continuous function in $t_{m+1}$, which is our claim. □

Definition 8

([26]). Let $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ be the fuzzy Caputo generalized Hukuhara differentiable (for short ${}^{FC}\left[gH\right]$-differentiable) at $t_0\in [a,b].$ Thus, $f$ is ${}^{FC}[(i)-gH]$-differentiable at $t_0\in [a,b]$ if for $0\le r\le 1$

$${{[}^{FC}{D}_{*}^{\alpha }{f}_{i.gH}(t_0)]}_r={[}^C{D}_{*}^{\alpha }{f}^{-}(t_0;r),{}^C{D}_{*}^{\alpha }{f}^{+}(t_0;r)],$$

and that f is ${}^{FC}[(ii)-gH]$-differentiable at $t_0$ if

$${{[}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(t_0)]}_r={[}^C{D}_{*}^{\alpha }{f}^{+}(t_0;r),{}^C{D}_{*}^{\alpha }{f}^{-}(t_0;r)],$$

where

$${}^C{D}_{*}^{\alpha }{f}^{-}(t_0;r)=\frac{1}{\Gamma (1-\alpha )}{\int }_a^{t_0}{(t_0-s)}^{-\alpha }D{f}^{-}(s;r)ds,$$

$${}^C{D}_{*}^{\alpha }{f}^{+}(t_0;r)=\frac{1}{\Gamma (1-\alpha )}{\int }_a^{t_0}{(t_0-s)}^{-\alpha }D{f}^{+}(s;r)ds.$$

Definition 9

([26]). Let $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ be a fuzzy-valued function on $[a,b]$. A point $t_0\in [a,b]$ is said to be a switching point for the ${}^{FC}\left[gH\right]$-differentiability of $f,$ if in any neighborhood $V$ of $t_0$ there exist points $t_1<t_0<t_2$ such that

(type I) 

f is ${}^{FC}[(i)-gH]$-differentiable at $t_1$ while f is not ${}^{FC}[(ii)-gH]$-differentiable at $t_1$, and

f is ${}^{FC}[(ii)-gH]$-differentiable at $t_2$ while f is not ${}^{FC}[(i)-gH]$-differentiable at $t_2,$

or

(type II) 

f is ${}^{FC}[(ii)-gH]$-differentiable at $t_1$ while f is not ${}^{FC}[(i)-gH]$-differentiable at $t_1,$

and f is ${}^{FC}[(i)-gH]$-differentiable at $t_2$ while f is not ${}^{FC}[(ii)-gH]$-differentiable at $t_2.$

Theorem 1

([1]). If $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$, ${\left[f(t)\right]}_r=[f^{-}(t;r),f^{+}(t;r)]$ and f is integrable for $0\le r\le 1,t\in [a,b]$ and $\alpha ,\beta >0$, then we have

$${}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{F.RL}{I}_{[a,t]}^{\beta }f)(t)={}^{F.RL}{I}_{[a,t]}^{\alpha +\beta }f(t).$$

Lemma 3

([1]). Suppose that $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ be a fuzzy-valued function and $D{f}_{gH}$ is exist, then for $0<\alpha \le 1,$

$${}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }f)(t)=f(t){\ominus }_{gH}f(a),0\le r\le 1.$$

The principal significance of this lemma is in the following theorem.

Theorem 2

([1]). Let $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ be the fractional $gH$-differentiable such that type of Caputo differentiability f in $[a,b]$ does not change. Then, for $a\le t\le b$ and $0<\alpha \le 1,$

I.  

If $f(s)$ is ${}^{FC}[(i)-gH]$-differentiable then ${}^{FC}{D}_{*}^{\alpha }{f}_{i.gH}(t)$ is $(F.RL)$-integrable over $[a,b]$ and

$$f(t)=f(a)\oplus {}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{i.gH})(t),$$

II.  

If $f(s)$ is ${}^{FC}[(ii)-gH]$-differentiable then ${}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(t)$ is $(F.RL)$-integrable over $[a,b]$ and

$$f(t)=f(a)\ominus (-1){}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH})(t).$$

Lemma 4.

Suppose that $f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ is the fractional $gH$-differentiable and ${}^{FC}{D}_{*}^{\alpha }{f}_{gH}(t)\in {\mathcal{C}}_f([a,b],{\mathbb{R}}_{\mathcal{F}})$ then for $0<\alpha \le 1,$

$${}^{F.RL}{I}_{[t,a]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{i.gH})(t)=(-1)\odot {}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH})(t),$$

Proof. 

As ${}^{FC}{D}_{*}^{\alpha }{f}_{i.gH}(t)$ is continuous, it follows that ${}^{FC}{D}_{*}^{\alpha }{f}_{i.gH}(t)$ is the Riemann–Liouville integrable, and by using Lemma 3 for $0\le r\le 1$

$$\begin{array}{ccc}\hfill {{[}^{F.RL}{I}_{[t,a]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{i.gH})(t)]}_r& =& {[}^{F.RL}{I}_{[t,a]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}^{-})(t;r){,}^{F.RL}{I}_{[t,a]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}^{+})(t;r)]\hfill \\ \hfill & =& [f^{-}(a;r)-f^{-}(t;r),f^{+}(a;r)-f^{+}(t;r)]\hfill \\ \hfill & =& {[f(a)\ominus f(t)]}_r,\hfill \end{array}$$

(2)

moreover,

$$\begin{array}{ccc}\hfill {{[}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH})(t)]}_r& =& {[}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}^{+})(t;r){,}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}^{-})(t;r)]\hfill \\ \hfill & =& [f^{+}(t;r)-f^{+}(a;r),f^{-}(t;r)-f^{-}(a;r)]\hfill \\ \hfill & =& {[(-1)\odot (f(a)\ominus f(t))]}_r,\hfill \end{array}$$

(3)

by combining Equations (2) with (3) the lemma is proved. □

Theorem 3.

Let ${}^{FC}{D}_{*}^{\alpha }f:[a,b]\to {\mathbb{R}}_{\mathcal{F}}$ and ${}^{FC}{D}_{*}^{n\alpha }f\in {\mathcal{C}}_f([a,t],{\mathbb{R}}_{\mathcal{F}})$. For all $t\in [a,b]$ and $0<\alpha \le 1,$

I.  

Let ${}^{FC}{D}_{*}^{j\alpha }f,j=1,\dots ,n$ be the ${}^{FC}[(i)-gH]$-differentiable, and they do not change in the type of differentiability on $[a,b],$ then

$${}^{FC}{D}_{*}^{(j-1)\alpha }{f}_{i.gH}(t)={}^{FC}{D}_{*}^{(j-1)\alpha }{f}_{i.gH}(a)\oplus {}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{j\alpha }{f}_{i.gH})(t).$$

II.  

If ${}^{FC}{D}_{*}^{j\alpha }f,j=1,\dots ,n$ are ${}^{FC}[(ii)-gH]$-differentiable and the type of their differentiability does not change in the interval $[a,b],$ then

$${}^{FC}{D}_{*}^{(j-1)\alpha }{f}_{ii.gH}(t)={}^{FC}{D}_{*}^{(j-1)\alpha }{f}_{ii.gH}(a)\oplus {}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{j\alpha }{f}_{ii.gH})(t).$$

III.  

Assume that ${}^{FC}{D}_{*}^{j\alpha }f,j=2k-1,k\in \mathbb{N}$ are the ${}^{FC}[(i)-gH]$-differentiable and they are ${}^{FC}[(ii)-gH]$-differentiable, for $j=2k,k\in \mathbb{N}$ then

$${}^{FC}{D}_{*}^{(j-1)\alpha }{f}_{i.gH}(t)={}^{FC}{D}_{*}^{(j-1)\alpha }{f}_{i.gH}(a)\ominus {(-1)}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{j\alpha }{f}_{ii.gH})(t).$$

IV.  

Suppose that ${}^{FC}{D}_{*}^{j\alpha }f,j=2k-1,k\in \mathbb{N}$ are ${}^{FC}[(ii)-gH]$-differentiable and they are ${}^{FC}[(i)-gH]$-differentiable for $j=2k,k\in \mathbb{N}$, so

$${}^{FC}{D}_{*}^{(j-1)\alpha }{f}_{ii.gH}(t)={}^{FC}{D}_{*}^{(j-1)\alpha }{f}_{ii.gH}(a)\ominus {(-1)}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{j\alpha }{f}_{i.gH})(t).$$

Proof. 

By assuming ${}^{FC}{D}_{*}^{j\alpha }f\in {\mathcal{C}}_f([a,b],{\mathbb{R}}_{\mathcal{F}}),j=0,\dots ,n$ we give the proof only for parts II and III. Proving the other parts are similar.

II. 

Our proof starts with the observation that ${}^{FC}{D}_{*}^{j\alpha }f,j=1,\dots ,n$ are ${}^{FC}[(ii)-gH]$-differentiable. Therefore, using the properties of fuzzy Caputo derivative and Theorem 2, we have

$$\begin{array}{cc}\hfill & {{[}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{j\alpha }{f}_{ii.gH})(t)]}_r\hfill \\ \hfill & ={[}^{RL}{I}_{[a,t]}^{\alpha }{(}^C{D}_{*}^{j\alpha }{f}^{+})(t;r),{}^{RL}{I}_{[a,t]}^{\alpha }{(}^C{D}_{*}^{j\alpha }{f}^{-})(t;r)]\hfill \\ \hfill & ={[}^{RL}{I}_{[a,t]}^{\alpha }{.}^C{D}_{*}^{\alpha }{(}^C{D}_{*}^{(j-1)\alpha }{f}^{+})(t;r),{}^{RL}{I}_{[a,t]}^{\alpha }{.}^C{D}_{[a,t]}^{\alpha }{(}^C{D}_{*}^{(j-1)\alpha }{f}^{-})(t;r)]\hfill \\ \hfill & ={[}^C{D}_{*}^{(i-1)\alpha }{f}^{+}(t;r)-{}^C{D}_{*}^{(j-1)\alpha }{f}^{+}(a;r),{}^C{D}_{*}^{(j-1)\alpha }{f}^{-}(t;r)-{}^C{D}_{*}^{(j-1)\alpha }{f}^{-}(a;r)]\hfill \\ \hfill & ={[}^C{D}_{*}^{(j-1)\alpha }{f}^{+}(t;r),{}^C{D}_{*}^{(j-1)\alpha }{f}^{-}(t;r)]-{[}^C{D}_{*}^{(j-1)\alpha }{f}^{+}(a;r),{}^C{D}_{*}^{(j-1)\alpha }{f}^{-}(a;r)]\hfill \\ \hfill & ={{[}^{FC}{D}_{*}^{(j-1)\alpha }{f}_{ii.gH}(t)\ominus {}^{FC}{D}_{*}^{(j-1)\alpha }{f}_{ii.gH}(a)]}_r,\hfill \end{array}$$

thus, we obtain

$${}^{FC}{D}_{*}^{(j-1)\alpha }{f}_{ii.gH}(t)={}^{FC}{D}_{*}^{(j-1)\alpha }{f}_{ii.gH}(a){\oplus }^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{j\alpha }{f}_{ii.gH})(t).$$

III. 

Under the conditions stated in the part III, ${}^{FC}{D}_{*}^{j\alpha }f$ is ${}^{FC}[(i)-gH]$-differentiable for $j=2k-1,k\in \mathbb{N}$ and it is ${}^{FC}[(ii)-gH]$-differentiable for $j=2k,k\in \mathbb{N}$. In the sense of Section 2 and by Theorem 2, we get

$$\begin{array}{cc}\hfill & {{[}^{FC}{D}_{*}^{(j-1)\alpha }{f}_{i.gH}(t)\oplus {(-1)}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{j\alpha }{f}_{ii.gH})(t)]}_r\hfill \\ \hfill & ={[}^C{D}_{*}^{(j-1)\alpha }{f}^{-}(t;r){,}^C{D}_{*}^{(j-1)\alpha }{f}^{+}(t;r)]+[{-}^{RL}{I}_{[a,t]}^{\alpha }{(}^C{D}_{*}^{j\alpha }{f}^{-})(t;r),{-}^{RL}{I}_{[a,t]}^{\alpha }{(}^C{D}_{*}^{j\alpha }{f}^{+})(t;r)]\hfill \\ \hfill & ={[}^C{D}_{*}^{(j-1)\alpha }{f}^{-}(t;r),{}^C{D}_{*}^{(j-1)\alpha }{f}^{+}(t;r)]\hfill \\ \hfill & +{[}^C{D}_{*}^{(j-1)\alpha }{f}^{-}(a;r)-{}^C{D}_{*}^{(j-1)\alpha }{f}^{-}(t;r),{}^C{D}_{*}^{(j-1)\alpha }{f}^{+}(a;r)-{}^C{D}_{*}^{(j-1)\alpha }{f}^{+}(t;r)]\hfill \\ \hfill & ={[}^C{D}_{*}^{(j-1)\alpha }{f}^{-}(a;r),{}^C{D}_{*}^{(j-1)\alpha }{f}^{+}(a;r)]={{[}^{FC}{D}_{*}^{(j-1)\alpha }{f}_{i.gH}(a)]}_r,\hfill \end{array}$$

which completes the proof. □

4. Fuzzy Generalized Taylor Theorem

Theorem 4.

Let $T=[a,a+\beta ]\subset \mathbb{R}$, with $\beta >0$ and ${}^{FC}{D}_{*}^{j\alpha }f\in {\mathcal{C}}_f([a,b],{\mathbb{R}}_f),j=1,\dots ,n$. For $t\in T,0<\alpha \le 1$

I.  

If ${}^{FC}{D}_{*}^{j\alpha }f,j=0,1,\dots ,n-1$ are ${}^{FC}[(i)-gH]$-differentiable, provided that type of fuzzy Caputo differentiability has no change. Then,

$$\begin{array}{ccc}\hfill f(t)& =& f(a)\oplus {}^{FC}{D}_{*}^{\alpha }{f}_{i.gH}(a)\odot \frac{{(t-a)}^{\alpha }}{\Gamma (\alpha +1)}\oplus {}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(a)\odot \frac{{(t-a)}^{2\alpha }}{\Gamma (2\alpha +1)}\hfill \\ \hfill & \oplus & \dots \oplus {}^{FC}{D}_{*}^{(n-1)\alpha }{f}_{i.gH}(a)\odot \frac{{(t-a)}^{(n-1)\alpha }}{\Gamma ((n-1)\alpha +1)}\oplus R_n(a,t),\hfill \end{array}$$

where $R_n(a,t):={}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{F.RL}{I}_{[a,t_1]}^{\alpha }\dots {(}^{F.RL}{I}_{[a,t_{n-1}]}^{\alpha }{(}^{FC}{D}_{*}^{n\alpha }{f}_{i.gH})(t_n))\dots ).$

II.  

If ${}^{FC}{D}_{*}^{j\alpha }f,j=0,1,\dots n-1$ are ${}^{FC}[(ii)-gH]$-differentiable, provided that type of fuzzy Caputo differentiability has no change, then

$$\begin{array}{ccc}\hfill f(t)& =& f(a)\ominus (-1){}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(a)\odot \frac{{(t-a)}^{\alpha }}{\Gamma (\alpha +1)}\ominus (-1){}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH}(a)\odot \frac{{(t-a)}^{2\alpha }}{\Gamma (2\alpha +1)}\hfill \\ \hfill & \ominus & (-1)\dots \ominus (-1){}^{FC}{D}_{*}^{(n-1)\alpha }{f}_{ii.gH}(a)\odot \frac{{(t-a)}^{(n-1)\alpha }}{\Gamma ((n-1)\alpha +1)}\ominus (-1)R_n(a,t),\hfill \end{array}$$

where $R_n(a,t):={}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{F.RL}{I}_{[a,t_1]}^{\alpha }\dots {(}^{F.RL}{I}_{[a,t_{n-1}]}^{\alpha }{(}^{FC}{D}_{*}^{n\alpha }{f}_{ii.gH})(t_n))\dots ).$

III.  

If ${}^{FC}{D}_{*}^{j\alpha }f,j=1,\dots ,n,$ exist and in each order the type of ${}^{FC}\left[gH\right]$-differentiability changes on T

$$\begin{array}{ccc}\hfill f(t)& =& f(a)\ominus (-1){}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(a)\odot \frac{{(t-a)}^{\alpha }}{\Gamma (\alpha +1)}\oplus {}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(a)\odot \frac{{(t-a)}^{2\alpha }}{\Gamma (2\alpha +1)}\hfill \\ \hfill & \ominus & (-1)\dots \ominus (-1){}^{FC}{D}_{*}^{(\frac{j}{2}-1)\alpha }{f}_{ii.gH}(a)\odot \frac{{(t-a)}^{(\frac{j}{2}-1)\alpha }}{\Gamma (\frac{j}{2}\alpha )}\hfill \\ \hfill & \oplus & {}^{FC}{D}_{*}^{(\frac{j}{2})\alpha }{f}_{i.gH}(a)\odot \frac{{(t-a)}^{(\frac{j}{2})\alpha }}{\Gamma (\frac{j}{2}\alpha +1)}\ominus (-1)\dots \ominus (-1)R_n(a,t),\hfill \end{array}$$

where $R_n(a,t):={}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{F.RL}{I}_{[a,t_1]}^{\alpha }\dots {(}^{F.RL}{I}_{[a,t_{n-1}]}^{\alpha }{(}^{FC}{D}_{*}^{n\alpha }{f}_{i.gH})(t_n))\dots ).$

IV.  

For ${}^{FC}{D}_{*}^{k\alpha }f\in {\mathcal{C}}_f([a,b],{\mathbb{R}}_f),k\ge 3$, suppose that f on $[a,\xi ]$ is ${}^{FC}[(ii)-\left[gH\right]$-differentiable and on $[\xi ,b]$ is ${}^{FC}[(i)-gH]$-differentiable, in fact ξ is switching point (type II) for α-order derivative of f. Moreover, for $t_0\in [a,\xi ]$, let $2\alpha$-order derivative of f in ${\xi }_1$ of $[t_0,\xi ]$ have switching point (type I). On the other hand, the type of differentiability for ${}^{FC}{D}_{*}^{j\alpha }f,j\le k$ on $[\xi ,b]$ does not change. Therefore,

$$\begin{array}{ccc}\hfill f(t)& =& f(t_0)\ominus {(-1)}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(t_0)\odot \frac{{(\xi -t_0)}^{\alpha }}{\Gamma (\alpha +1)}\oplus {(-1)}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(t_0)\odot \frac{{(t_0-{\xi }_1)}^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ \hfill & \odot & \frac{{(\xi -t_0)}^{\alpha }}{\Gamma (\alpha +1)}\ominus {(-1)}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH}({\xi }_1)\odot \left[\frac{{(\xi -{\xi }_1)}^{2\alpha }}{\Gamma (2\alpha +1)}-\frac{{(t_0-{\xi }_1)}^{2\alpha }}{\Gamma (2\alpha +1)}\right]\hfill \\ \hfill & \oplus & {}^{FC}{D}_{*}^{\alpha }{f}_{i.gH}(\xi )\odot \frac{{(t-\xi )}^{\alpha }}{\Gamma (\alpha +1)}\oplus {}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(\xi )\odot \frac{{(t-\xi )}^{2\alpha }}{\Gamma (2\alpha +1)}\hfill \\ \hfill & \oplus & {}^{F.RL}{I}_{[t_0,\xi ]}^{\alpha }{.}^{F.RL}{I}_{[t_0,{\xi }_1]}{.}^{F.RL}{I}_{[t_0,t_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{i.gH})(t_4)\hfill \\ \hfill & \ominus & {(-1)}^{F.RL}{I}_{[t_0,\xi ]}^{\alpha }{.}^{F.RL}{I}_{[{\xi }_1,t_1]}{.}^{F.RL}{I}_{[{\xi }_1,t_3]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{ii.gH})(t_5).\hfill \\ \hfill & \oplus & {}^{F.RL}{I}_{[\xi ,t]}{.}^{F.RL}{I}_{[\xi ,s_1]}^{\alpha }{.}^{F.RL}{I}_{[a,s_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{i.gH})(s_3).\hfill \end{array}$$

Proof. 

Here, we prove parts II, III, and IV because the proof of part I is similar to the part II. Under the assumptions that ${}^{FC}{D}_{*}^{j\alpha }f\in {\mathcal{C}}_f([a,b],{\mathbb{R}}_f),j=1,\dots ,n,$ we conclude that ${}^{FC}{D}_{*}^{j\alpha }f$ are $(F.RL)$-fractional integrable on T,

II. 

As f is a continuous function and ${}^{FC}[(ii)-gH]$-differentiable, by Theorem 2, we get

$$f(t)=f(a)\ominus (-1){}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH})(t_1).$$

Under the hypotheses of Theorem, type of differentiability does not change, so by Theorem 3 and by attention to $(F.RL)$-integrability of ${}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}$ on T, we obtain

$${}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(t_1)={}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(a)\oplus {}^{F.RL}{I}_{[a,t_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH})(t_2).$$

Applying operator ${}^{F.RL}{I}_{[a,t]}^{\alpha }$ to ${}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(t_1)$, gives

$$\begin{array}{c}\hfill {}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH})(t_1)={}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(a)\odot \frac{{(t-a)}^{\alpha }}{\Gamma (\alpha +1)}\oplus {}^{F.RL}{I}_{[a,t]}^{\alpha }.{}^{F.RL}{I}_{[a,t_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH})(t_2).\end{array}$$

Lemma 2 implies that the last double $(F.RL)$-fractional integral belongs to ${\mathbb{R}}_f$. Therefore,

$$f(t)=f(a)\ominus (-1){}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(a)\odot \frac{{(t-a)}^{\alpha }}{\Gamma (\alpha +1)}\ominus (-1){}^{F.RL}{I}_{[a,t]}^{\alpha }.{}^{F.RL}{I}_{[a,t_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH})(t_2),$$

(4)

by repeating the above argument, we get

$${}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH}(t_2)={}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH}(a)\oplus {}^{F.RL}{I}_{[a,t_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{ii.gH})(t_3).$$

Therefore, we find that

$${}^{F.RL}{I}_{[a,t_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH})(t_2)={}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH}(a)\odot \frac{{(t_1-a)}^{\alpha }}{\Gamma (\alpha +1)}\oplus {}^{F.RL}{I}_{[a,t_1]}^{\alpha }.{}^{F.RL}{I}_{[a,t_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{ii.gH})(t_3),$$

moreover

$$\begin{array}{ccc}\hfill {}^{F.RL}{I}_{[a,t]}^{\alpha }{.}^{F.RL}{I}_{[a,t_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH})(t_2)& =& {}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH}(a)\odot \frac{{(t-a)}^{2\alpha }}{\Gamma (2\alpha +1)}\hfill \\ \hfill & \oplus & {}^{F.RL}{I}_{[a,t]}^{\alpha }.{}^{F.RL}{I}_{[a,t_1]}^{\alpha }.{}^{F.RL}{I}_{[a,t_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{ii.gH})(t_3).\hfill \end{array}$$

By Lemma 2, the last triple $(F.RL)$-fractional integral belongs to ${\mathbb{R}}_f$. Therefore, substituting above equation into Equation (4), we find that

$$\begin{array}{ccc}\hfill f(t)& =& f(a)\ominus (-1){}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(a)\odot \frac{{(t-a)}^{\alpha }}{\Gamma (\alpha +1)}\ominus (-1){}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH}(a)\hfill \\ \hfill & \odot & \frac{{(t-a)}^{2\alpha }}{\Gamma (2\alpha +1)}\ominus {(-1)}^{F.RL}{I}_{[a,t]}^{\alpha }.{}^{F.RL}{I}_{[a,t_1]}^{\alpha }.{}^{F.RL}{I}_{[a,t_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{ii.gH})(t_3),\hfill \end{array}$$

the high order of the last formula by Lemma 2 is a continuous function in terms of t so it belongs to ${\mathbb{R}}_f$. With the same manner, we can demonstrate that part $\mathbf{II}$ is satisfied.

III. 

Suppose that f is ${}^{FC}[(ii)-gH]$-differentiable. Using Theorem 2, we have

$$f(t)=f(a)\ominus (-1){}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH})(t_1).$$

Under the hypothesis of theorem, as f is ${}^{FC}[(ii)-gH]$-differentiable, ${}^{FC}{D}_{*}^{\alpha }f$ is ${}^{FC}[(i)-gH]$-differentiable. Therefore, by Theorem 3 we get

$${}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(t_1)={}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(a)\ominus (-1){}^{F.RL}{I}_{[a,t_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH})(t_2).$$

Now, applying operator $(F.RL)$-integral to ${(}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH})(t_1)$ gives

$$\begin{array}{ccc}\hfill & {}^{F.RL}{I}_{[a,t]}^{\alpha }& {(}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH})(t_1)\hfill \\ \hfill & & ={}^{F.RL}{I}_{[a,t]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH})(a)\ominus (-1){}^{F.RL}{I}_{[a,t]}^{\alpha }.{}^{F.RL}{I}_{[a,t_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH})(t_2)\hfill \\ \hfill & & ={}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(a)\odot \frac{{(t-a)}^{\alpha }}{\Gamma (\alpha +1)}\ominus {(-1)}^{F.RL}{I}_{[a,t]}^{\alpha }.{}^{F.RL}{I}_{[a,t_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH})(t_2).\hfill \end{array}$$

Lemma 2 now leads to the last double (F.RL)-fractional integral belongs to ${\mathbb{R}}_f$. Therefore,

$$f(t)=f(a)\ominus (-1){}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(a)\odot \frac{{(t-a)}^{\alpha }}{\Gamma (\alpha +1)}\oplus {}^{F.RL}{I}_{[a,t]}^{\alpha }.{}^{F.RL}{I}_{[a,t_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH})(t_2).$$

Similarly, as ${}^{FC}{D}_{*}^{\alpha }f$ is ${}^{FC}[(i)-gH]$-differentiable, ${}^{FC}{D}_{*}^{2\alpha }f$ is ${}^{FC}[(ii)-gH]$-differentiable and we get

$${}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(t_2)={}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH})(a)\ominus (-1){}^{F.RL}{I}_{[a,t_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{ii.gH})(t_3),$$

thus

$$\begin{array}{ccc}\hfill {}^{F.RL}{I}_{[a,t_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH})(t_2)& =& {}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(a)\odot \frac{{(t_1-a)}^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ \hfill & \ominus & (-1){}^{F.RL}{I}_{[a,t_1]}^{\alpha }.{}^{F.RL}{I}_{[a,t_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{ii.gH})(t_3).\hfill \end{array}$$

Now, applying operator ${}^{F.RL}{I}_{[a,t]}^{\alpha }$ gives

$$\begin{array}{ccc}\hfill {}^{F.RL}{I}_{[a,t]}^{\alpha }{.}^{F.RL}{I}_{[a,t_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH})(t_2)& =& {}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(a)\odot \frac{{(t-a)}^{2\alpha }}{\Gamma (2\alpha +1)}\hfill \\ \hfill & \ominus & (-1){}^{F.RL}{I}_{[a,t]}^{\alpha }.{}^{F.RL}{I}_{[a,t_1]}^{\alpha }.{}^{F.RL}{I}_{[a,t_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{ii.gH})(t_3),\hfill \end{array}$$

as this satisfies all the other conditions for the Lemma 2, the last triple $(F.RL)$-fractional integral belongs to ${\mathbb{R}}_f$. Then,

$$\begin{array}{ccc}\hfill f(t)& =& f(a)\ominus (-1){}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(a)\odot \frac{{(t-a)}^{\alpha }}{\Gamma (\alpha +1)}\oplus {}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(a)\hfill \\ \hfill & \odot & \frac{{(t-a)}^{2\alpha }}{\Gamma (2\alpha +1)}\ominus (-1){}^{F.RL}{I}_{[a,t]}^{\alpha }.{}^{F.RL}{I}_{[a,t_1]}^{\alpha }.{}^{F.RL}{I}_{[a,t_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{ii.gH})(t_3).\hfill \end{array}$$

with simple and similar method, the proof for this type of differentiability will be completed.

IV. 

As f is ${}^{FC}[(ii)-gH]$-differentiable in $[t_0,\xi ]$, Theorem 2 leads to

$$f(\xi )=f(t_0)\ominus {(-1)}^{F.RL}{I}_{[t_0,\xi ]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH})(t_1),$$

(5)

and in the interval $[\xi ,b]$, f is ${}^{FC}[(i)-gH]$-differentiable, so for $t\in [\xi ,b]$

$$f(t)=f(\xi )\oplus {}^{F.RL}{I}_{[\xi ,t]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{i.gH})(s_1).$$

(6)

According to the hypothesis, we know that $\xi$ is a switching point for differentiability f; thus, by substituting Equation (5) into Equation (6), we obtain

$$f(t)=f(t_0)\ominus {(-1)}^{F.RL}{I}_{[t_0,\xi ]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH})(t_1)\oplus {}^{F.RL}{I}_{[\xi ,t]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{i.gH})(s_1).$$

(7)

Consider the first $(F.RL)$-fractional integral on the right side of the Equation (7):

By noting the hypothesis of theorem, the fuzzy Caputo derivative of the function f has the switching point ${\xi }_1$ of type I. Therefore, ${}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}$ is ${}^{FC}[(i)-gH]$-differentiable on $[t_0,{\xi }_1]$, then type of differentiability can be changed. By these conditions, the Theorem 3, admits that

$${}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}({\xi }_1)={}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(t_0)\ominus {(-1)}^{F.RL}{I}_{[t_0,{\xi }_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH})(t_2).$$

(8)

On the other hand, we know that ${}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}$ is ${}^{FC}[(ii)-gH]$-differentiable on $[{\xi }_1,\xi ]$ and the type of differentiability does not change. Thus, for $t_1\in [{\xi }_1,\xi ]$ from Theorem 3, it follows that

$${}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(t_1)={}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}({\xi }_1)\oplus {}^{F.RL}{I}_{[{\xi }_1,t_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH})(t_3),$$

(9)

substituting Equation (8) into Equation (9) gives

$$\begin{array}{ccc}\hfill {}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(t_1)& =& {}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(t_0)\ominus {(-1)}^{F.RL}{I}_{[t_0,{\xi }_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH})(t_2)\hfill \\ \hfill & \oplus & {}^{F.RL}{I}_{[{\xi }_1,t_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH})(t_3),\hfill \end{array}$$

(10)

that

$$\begin{array}{ccc}\hfill & & {}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(t_2)={}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(t_0)\oplus {}^{F.RL}{I}_{[t_0,t_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{i.gH})(t_4),\hfill \\ \hfill & \Rightarrow & {}^{F.RL}{I}_{[t_0,{\xi }_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH})(t_2)\hfill \\ \hfill & =& {}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(t_0)\odot \frac{{({\xi }_1-t_0)}^{\alpha }}{\Gamma (\alpha +1)}\oplus {}^{F.RL}{I}_{[t_0,{\xi }_1]}{.}^{F.RL}{I}_{[t_0,t_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{i.gH})(t_4),\hfill \end{array}$$

(11)

follows from Theorem 3 and also

$$\begin{array}{ccc}\hfill & & {}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH}(t_3)={}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH}({\xi }_1)\oplus {}^{F.RL}{I}_{[{\xi }_1,t_3]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{ii.gH})(t_5),\hfill \\ \hfill & \Rightarrow & {}^{F.RL}{I}_{[{\xi }_1,t_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH})(t_3)\hfill \\ \hfill & =& {}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH}({\xi }_1)\odot \frac{{(t_1-{\xi }_1)}^{\alpha }}{\Gamma (\alpha +1)}\oplus {}^{F.RL}{I}_{[{\xi }_1,t_1]}{.}^{F.RL}{I}_{[{\xi }_1,t_3]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{ii.gH})(t_5),\hfill \end{array}$$

(12)

the insertion of Equations (11) and (12) in Equation (10) allows us to obtain

$$\begin{array}{ccc}\hfill {}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(t_1)& =& {}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(t_0)\ominus {}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(t_0)\odot \frac{{(t_0-{\xi }_1)}^{\alpha }}{\Gamma (\alpha +1)}\oplus {}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH}({\xi }_1)\hfill \\ \hfill & \odot & \frac{{(t_1-{\xi }_1)}^{\alpha }}{\Gamma (\alpha +1)}\ominus {(-1)}^{F.RL}{I}_{[t_0,{\xi }_1]}{.}^{F.RL}{I}_{[t_0,t_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{i.gH})(t_4)\hfill \\ \hfill & \oplus & {}^{F.RL}{I}_{[{\xi }_1,t_1]}{.}^{F.RL}{I}_{[{\xi }_1,t_3]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{ii.gH})(t_5).\hfill \end{array}$$

Finally, the first $(F.RL)$-fractional integral on the right side of the Equation (7) obtains as follows

$$\begin{array}{ccc}\hfill {}^{F.RL}{I}_{[t_0,\xi ]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH})(t_1)& =& {}^{FC}{D}_{*}^{\alpha }{f}_{ii.gH}(t_0)\odot \frac{{(\xi -t_0)}^{\alpha }}{\Gamma (\alpha +1)}\ominus {}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(t_0)\odot \frac{{(t_0-{\xi }_1)}^{\alpha }}{\Gamma (\alpha +1)}\hfill \\ \hfill & \odot & \frac{{(\xi -t_0)}^{\alpha }}{\Gamma (\alpha +1)}\oplus {}^{FC}{D}_{*}^{2\alpha }{f}_{ii.gH}({\xi }_1)\odot [\frac{{(\xi -{\xi }_1)}^{2\alpha }}{\Gamma (2\alpha +1)}-\frac{{(t_0-{\xi }_1)}^{2\alpha }}{\Gamma (2\alpha +1)}]\hfill \\ \hfill & \ominus & {(-1)}^{F.RL}{I}_{[t_0,\xi ]}^{\alpha }{.}^{F.RL}{I}_{[t_0,{\xi }_1]}{.}^{F.RL}{I}_{[t_0,t_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{i.gH})(t_4)\hfill \\ \hfill & \oplus & {}^{F.RL}{I}_{[t_0,\xi ]}^{\alpha }{.}^{F.RL}{I}_{[{\xi }_1,t_1]}{.}^{F.RL}{I}_{[{\xi }_1,t_3]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{ii.gH})(t_5),\hfill \end{array}$$

(13)

the only point remaining concerns the behavior of the second $(F.RL)$-fractional integral on the right side of the Equation (7). We can now proceed analogously to the first $(F.RL)$-fractional integral:

By noting the hypothesis of theorem, ${}^{FC}{D}_{*}^{j\alpha }{f}_{i.gH},j=2,3$ are ${}^{FC}[(i)-gH]$-differentiable on $[\xi ,b]$, and the type of differentiability does not change. By Theorem 3 we deduce that

$${}^{FC}{D}_{*}^{\alpha }{f}_{i.gH}(s_1)={}^{FC}{D}_{*}^{\alpha }{f}_{i.gH}(\xi )\oplus {}^{F.RL}{I}_{[\xi ,s_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH})(s_2),$$

(14)

and

$$\begin{array}{ccc}\hfill & & {}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(s_2)={}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(\xi )\oplus {}^{F.RL}{I}_{[\xi ,s_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{i.gH})(s_3).\hfill \\ \hfill & \Rightarrow & {}^{F.RL}{I}_{[\xi ,s_1]}^{\alpha }{(}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH})(s_2)\hfill \\ \hfill & =& {}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(\xi )\odot \frac{{(s_1-\xi )}^{\alpha }}{\Gamma (\alpha +1)}\oplus {}^{F.RL}{I}_{[\xi ,s_1]}{.}^{F.RL}{I}_{[\xi ,s_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{i.gH})(s_3),\hfill \end{array}$$

(15)

substituting (15) into (14) we obtain

$${}^{FC}{D}_{*}^{\alpha }{f}_{i.gH}(s_1)={}^{FC}{D}_{*}^{\alpha }{f}_{i.gH}(\xi )\oplus {}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(\xi )\odot \frac{{(s_1-\xi )}^{\alpha }}{\Gamma (\alpha +1)}\oplus {}^{F.RL}{I}_{[\xi ,s_1]}{.}^{F.RL}{I}_{[\xi ,s_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{i.gH})(s_3).$$

Thus, the second $(F.RL)$-fractional integral on the right side of the Equation (7) is as follows,

$$\begin{array}{ccc}\hfill {}^{F.RL}{I}_{[\xi ,t]}^{\alpha }{(}^{FC}{D}_{*}^{\alpha }{f}_{i.gH})(s_1)& =& {}^{FC}{D}_{*}^{\alpha }{f}_{i.gH}(\xi )\odot \frac{{(t-\xi )}^{\alpha }}{\Gamma (\alpha +1)}\oplus {}^{FC}{D}_{*}^{2\alpha }{f}_{i.gH}(\xi )\odot \frac{{(t-\xi )}^{2\alpha }}{\Gamma (2\alpha +1)}\hfill \\ \hfill & \oplus & {}^{F.RL}{I}_{[\xi ,t]}{.}^{F.RL}{I}_{[\xi ,s_1]}^{\alpha }{.}^{F.RL}{I}_{[\xi ,s_2]}^{\alpha }{(}^{FC}{D}_{*}^{3\alpha }{f}_{i.gH})(s_3),\hfill \end{array}$$

(16)

having disposed of this preliminary step, we can now return to the Equation (7).

By substituting Equations (13) and (16), in Equation (7), the desired result is achieved. □

5. Fuzzy Generalized Euler’s Method

In this section, we will touch on only a few aspects of the fuzzy generalized Taylor theorem and restrict the discussion to the fuzzy generalized Euler’s method. This case is important enough to be stated separately. We consider the following fuzzy fractional initial value problem,

$$\left\{\begin{array}{cc}{}^{FC}{D}_{*}^{\alpha }{y}_{gH}(t)=f(t,y(t)),\hfill & t\in [0,T],\hfill \\ y(0)=y_0\in {\mathbb{R}}_{\mathcal{F}},\hfill \end{array}\right.$$

(17)

where $f:[0,T]\times {\mathbb{R}}_{\mathcal{F}}\to {\mathbb{R}}_{\mathcal{F}}$ is continuous and $y(t)$ is an unknown fuzzy function of crisp variable t. Furthermore, ${}^{FC}{D}_{*}^{\alpha }{y}_{gH}(t)$ is the fuzzy fractional derivative $y(t)$ in the Caputo sense of order $0<\alpha \le 1$, with the finite set of switching points. Now, by dividing the interval $[0,T]$ with the step length of h, we have the partition ${\widehat{I}}_N=\{0=t_0<t_1<\dots <t_N=T\}$ where $t_k=kh$ for $k=0,1,2,\dots ,N.$

Case I. Unless otherwise stated we assume that the unique solution of the fuzzy fractional initial value problem (17), ${}^{FC}{D}_{*}^{2\alpha }y(t)\in {\mathcal{C}}_f([0,T],{\mathbb{R}}_{\mathcal{F}})\cap {\mathcal{L}}^{\zeta }([0,T],{\mathbb{R}}_{\mathcal{F}})$ is ${}^{FC}[(i)-gH]$-differentiable such that the type of differentiability does not change on $[0,T]$. Consider the fractional Taylor series expansion of the unknown fuzzy function $y(t)$ about $t_k$, for each $k=0,1,\dots N$.

$$y(t_{k+1})=y(t_k)\oplus \frac{{(t_{k+1}-t_k)}^{\alpha }}{\Gamma (\alpha +1)}\odot {}^{FC}{D}_{*}^{\alpha }{y}_{i.gH}(t_k)\oplus \frac{{(t_{k+1}-t_k)}^{2\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{i.gH}({\eta }_t),$$

for some points k lie between $t_k$ and $t_{k+1}$. As $h=t_{k+1}-t_k$, we have

$$y(t_{k+1})=y(t_k)\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot {}^{FC}{D}_{*}^{\alpha }{y}_{i.gH}(t_k)\oplus \frac{h^{2\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{i.gH}({\eta }_t),$$

and, y(t) satisfies in problem (5.1), so

$$y(t_{k+1})=y(t_k)\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y(t_k))\oplus \frac{h^{2\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{i.gH}({\eta }_t),$$

$$\begin{array}{ccc}\hfill & & \mathcal{H}(y(t_{k+1}),y(t_k)\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y(t_k))\oplus \frac{h^{2\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{i.gH}({\eta }_t))\hfill \\ \hfill & \le & \mathcal{H}(y(t_{k+1}),y(t_k)\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y(t_k))+\mathcal{H}(0,\frac{h^{2\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{i.gH}({\eta }_t)),\hfill \end{array}$$

as $h\to 0$ as

$$\begin{array}{ccc}\hfill & & \mathcal{H}(y(t_{k+1}),y(t_k)\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y(t_k))\to 0,\hfill \\ \hfill & & \mathcal{H}(0,\frac{h^{2\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{i.gH}({\eta }_t))\to 0,\hfill \end{array}$$

we conclude that

$$\begin{array}{ccc}\hfill & & \mathcal{H}(y(t_{k+1}),y(t_k)\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y(t_k))+\mathcal{H}(0,\frac{h^{2\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{i.gH}({\eta }_t))\to 0,\hfill \\ \hfill & \Rightarrow & {\mathcal{H}}_d(y(t_{k+1}),y(t_k)\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y(t_k))\oplus \frac{h^{2\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{i.gH}({\eta }_t))\to 0.\hfill \end{array}$$

Thus, for sufficiently small h we find that

$$y(t_{k+1})\approx y(t_k)\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y(t_k)),$$

and finally we get

$$\left\{\begin{array}{c}{y}_0=y_0,\hfill \\ y_{k+1}=y_k\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y_k),\hfill & k=0,1,\dots ,N-1.\hfill \end{array}\right.$$

(18)

Case II. Assume that ${}^{FC}{D}_{*}^{2\alpha }y(t)\in {\mathcal{C}}_f([0,T],{\mathbb{R}}_{\mathcal{F}})$ is ${}^{FC}[(ii)-gH]$-differentiable such that the type of differentiability does not change on $[0,T]$. Therefore, the fractional Taylor’s series expansion of $y(t)$ about the point $t_k$ at $t_{k+1}$ is

$$y(t_{k+1})=y(t_k)\ominus (-1)\frac{{(t_{k+1}-t_k)}^{\alpha }}{\Gamma (\alpha +1)}\odot {}^{FC}{D}_{*}^{\alpha }{y}_{ii.gH}(t_k)\ominus (-1)\frac{{(t_{k+1}-t_k)}^{2\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{ii.gH}({\eta }_t),$$

according to the process described in Case I, the generalized Euler’s method takes the form

$$\left\{\begin{array}{c}{y}_0=y_0,\hfill \\ y_{k+1}=y_k\ominus (-1)\frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y_k),\hfill & k=0,1,\dots ,N-1.\hfill \end{array}\right.$$

(19)

Case III. Let us suppose that $t_0=0,t_1,\dots ,t_j,\zeta ,t_{j+1},\dots ,t_N=T$ is a partition of interval $[0,T]$ and $y(t)$ has a switching point in $\zeta \in [0,T]$ of type I. Therefore, according to Equations (18) and (19), we have

$$\left\{\begin{array}{c}{y}_0=y_0,\hfill \\ y_{k+1}=y_k\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y_k),\hfill & k=0,1,\dots ,j.\hfill \\ y_{k+1}=y_k\ominus (-1)\frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y_k),\hfill & k=j+1,j+2,\dots ,N-1.\hfill \end{array}\right.$$

(20)

Case IV. Consider $y(t)$ has a switching point type II in $\zeta \in [0,T]$ such that $t_0,t_1,\dots ,t_j,\zeta ,t_{j+1},\dots ,t_N$ is a partition of interval $[0,T]$. Therefore, by Equations (18) and (19), we conclude that

$$\left\{\begin{array}{c}{y}_0=y_0,\hfill \\ y_{k+1}=y_k\ominus (-1)\frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y_k),\hfill & k=0,1,\dots ,j.\hfill \\ y_{k+1}=y_k\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y_k),\hfill & k=j+1,j+2,\dots ,N-1.\hfill \end{array}\right.$$

(21)

Our next concern will be the behavior of the fuzzy generalized Euler method.

6. Analysis of the Fuzzy Generalized Euler’s Method

In this section, the local and the global truncation errors of the fuzzy generalized Euler’s method are illustrated. Therefore, by applying them the consistency, the convergence, and the stability of the presented method are proved. Furthermore, several definitions and concepts of the fuzzy generalized Euler’s method are presented under ${}^{FC}\left[gH\right]$-differentiability [27].

6.1. Local Truncation Error, Consistent

Consider the unique solution of the fuzzy fractional initial value problem (17):

Definition 10.

If $y(t)$ is ${}^{FC}[(i)-gH]$-differentiable on $[0,T]$ and the type of differentiability does not change, now we define the residual ${\mathcal{R}}_k$ as

$${\mathcal{R}}_k=y(t_{k+1}){\ominus }_{gH}\left(y(t_k)\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y(t_k))\right),$$

and if $y(t)$ is ${}^{FC}[(ii)-gH]$-differentiable on $[0,T]$, we have

$${\mathcal{R}}_k=y(t_{k+1}){\ominus }_{gH}\left(y(t_k)\ominus (-1)\frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y(t_k))\right),$$

on the other hand, the local truncation error (LTE) $({\tau }_k)$ is defined as

$${\tau }_k=\frac{1}{h^{\alpha }}{\mathcal{R}}_k,$$

and the fuzzy generalized Euler’s method is said to be consistent if

$$\underset{h\to 0}{lim}\underset{t_k\le T}{max}\mathcal{H}({\tau }_k,0)=0,$$

therefore, due to the type of differentiability of $y(t)$ for ${\eta }_k\in [t_k,t_{k+1}]$, the residual $({\mathcal{R}}_k)$ and the LTE $({\tau }_k)$ are defined as follows.

$•\begin{array}{cc}& {\mathcal{R}}_k=\frac{h^{2\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{i.gH}({\eta }_k),\hfill \\ {}^{FC}[(i)-gH]-differentiability\Rightarrow \hfill \\ & {\tau }_k=\frac{h^{\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{i.gH}({\eta }_k),\hfill \end{array}$

$•\begin{array}{cc}& {\mathcal{R}}_k=\ominus (-1)\frac{h^{2\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{ii.gH}({\eta }_k),\hfill \\ {}^{FC}[(ii)-gH]-differentiability\Rightarrow \hfill \\ & {\tau }_k=\ominus (-1)\frac{h^{\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{ii.gH}({\eta }_k).\hfill \end{array}$

◃ Investigating the consistence of the fuzzy generalized Euler’s method:

For this purpose, assume that $\mathcal{H}{(}^{FC}{D}_{*}^{2\alpha }{y}_{ii.gH}({\eta }_k),0)\le M$. We have two following steps:

note that only one of the steps is proved and the proof of another one is similar.

Step I. If $y(t)$ be ${}^{FC}[(ii)-gH]$-differentiable, then

$$\begin{array}{ccc}\hfill {\displaystyle \underset{h\to 0}{lim}}{\displaystyle \underset{t_k\le T}{max}}\mathcal{H}({\tau }_k,0)& =& {\displaystyle \underset{h\to 0}{lim}}{\displaystyle \underset{t_k\le T}{max}}\mathcal{H}(\ominus (-1)\frac{h^{\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{ii.gH}({\eta }_k),0)\hfill \\ \hfill & =& {\displaystyle \underset{h\to 0}{lim}}\mid (-1)\frac{h^{\alpha }}{\Gamma (2\alpha +1)}\mid {\displaystyle \underset{t_k\le T}{max}}\mathcal{H}(\ominus {}^{FC}{D}_{*}^{2\alpha }{y}_{ii.gH}({\eta }_k),0)\hfill \\ \hfill & =& {\displaystyle \underset{h\to 0}{lim}}\frac{h^{\alpha }}{\Gamma (2\alpha +1)}.\mathcal{H}{(}^{FC}{D}_{*}^{2\alpha }{y}_{ii.gH}({\eta }_k),0)\le {\displaystyle \underset{h\to 0}{lim}}\frac{h^{\alpha }}{\Gamma (2\alpha +1)}.M=0.\hfill \end{array}$$

Step II. The same conclusion can be drawn for the ${}^{FC}[(i)-gH]$-differentiability of $y(t)$. Thus, note that we have actually proved that the fuzzy generalized Euler’s method is consistent as long as the solution belongs to ${\mathcal{C}}_f([0,T],{\mathbb{R}}_{\mathcal{F}}).$

6.2. Global Truncation Error, Convergence

Lemma 5

([28]). $\forall \mathrm{z}\in \mathbb{R},1+\mathrm{z}\le e^{\mathrm{z}}$.

Definition 11

([29]). The global truncation error is the agglomeration of the local truncation error over all the iterations, assuming perfect knowledge of the true solution at the initial time step.

In the fuzzy fractional initial value problem $(17)$, assume that $y(t)$ is ${}^{FC}[(i)-gH]$-differentiable, then the global truncation error is

$$\begin{array}{ccc}\hfill e_{k+1}& =& y(t_{k+1}){\ominus }_{gH}{y}_{k+1}=y(t_{k+1}){\ominus }_{gH}[y_0\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_0,y_0)\hfill \\ \hfill & \oplus & \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_1,y_1)\oplus \dots \oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y_k))],\hfill \end{array}$$

and for the ${}^{FC}[(ii)-gH]$-differentiability of $y(t)$, we have

$$\begin{array}{ccc}\hfill e_{k+1}& =& y(t_{k+1}){\ominus }_{gH}{y}_{k+1}=y(t_{k+1}){\ominus }_{gH}[y_0\ominus (-1)\frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_0,y_0)\hfill \\ \hfill & \ominus & (-1)\frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_1,y_1)\ominus (-1)\dots \ominus (-1)\frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y_k))].\hfill \end{array}$$

Definition 12.

If global truncation error leads to zero as the step size goes to zero, the numerical method is convergent, i.e.,

$$\underset{h\to 0}{lim}\underset{k}{max}\mathcal{H}(e_{k+1},0)=0,\Rightarrow \underset{h\to 0}{lim}\underset{k}{max}\mathcal{H}\left(y(t_{k+1}),y_{k+1}\right)=0,$$

in this case, the numerical solution converges to the exact solution.

◃ Investigating the convergence of the fuzzy generalized Euler’s method:

To suppose that ${}^{FC}{D}_{*}^{2\alpha }y(t)$ exists and $f(t,y)$ satisfies in Lipschitz condition on the $\{(t,y)\mid t\in [0,p],y\in \overline{B}(y_0,q),p,q>0\}$, the research on this subject will be divided into two steps:

Step I. Suppose that $y(t)$ is ${}^{FC}[(ii)-gH]$-differentiable, now by using Equation (18) and assumption $r_k=\ominus (-1)\frac{h^{2\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{ii.gH}(t_k)$, the exact solution of the Equation (17) satisfies

$$y(t_{k+1})=y(t_k)\ominus (-1)\frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,y(t_k))\oplus r_k.$$

$$\Rightarrow \mathcal{H}\left(y(t_{k+1}),y_{k+1}\right)=\mathcal{H}\left(y(t_k),y_k\right)+\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\left[\mathcal{H}\left(f(t_k,y_k){\ominus }_{gH}f(t_k,y(t_k)),0\right)\right]+\mathcal{H}(r_k,0),$$

the inequality

$$\mathcal{H}\left(f(t_k,y_k){\ominus }_{gH}f(t_k,y(t_k)),0\right)=\mathcal{H}\left(f(t_k,y_k),f(t_k,y(t_k))\right)\le {\ell }_k\mathcal{H}\left(y(t_k),y_k\right),$$

which is the conclusion of Lipschitz condition, implies that

$$\mathcal{H}\left(y(t_{k+1}),y_{k+1}\right)\le (1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.{\ell }_k)\mathcal{H}\left(y(t_k),y_k\right)+\mathcal{H}(r_k,0).$$

(22)

Now, assume that

$$\ell =\underset{0\le k\le N-1}{max}{\ell }_k,r=\underset{0\le k\le N-1}{max}\mathcal{H}(r_k,0),$$

and rewrite Equation (22) as

$$\mathcal{H}\left(y(t_{k+1}),y_{k+1}\right)\le (1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell )\mathcal{H}\left(y(t_k),y_k\right)+r,$$

as the inequality holds for all k, we get

$$\begin{array}{ccc}\hfill \mathcal{H}\left(y(t_{k+1}),y_{k+1}\right)& \le & (1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell )\left[(1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell )\mathcal{H}\left(y(t_{k-1}),y_{k-1}\right)+r\right]+r\hfill \\ \hfill & =& {(1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell )}^2.\mathcal{H}\left(y(t_{k-1}),y_{k-1}\right)+r\left[1+(1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell )\right].\hfill \end{array}$$

Repeated application of the above inequality enables us to write

$$\begin{array}{ccc}\hfill & & \mathcal{H}\left(y(t_{k+1}),y_{k+1}\right)\hfill \\ \hfill & \le & {(1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell )}^{k+1}.\mathcal{H}\left(y(t_0),y_0\right)+r\left[1+(1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell )+\dots +{(1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell )}^k\right],\hfill \end{array}$$

obviously, this sum is a geometric series, so we have

$$\sum _{i=0}^k{(1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell )}^i=\frac{1-{(1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell )}^{k+1}}{\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell },$$

that resulted to

$$\mathcal{H}\left(y(t_{k+1}),y_{k+1}\right)\le {(1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell )}^{k+1}\mathcal{H}\left(y(t_0),y_0\right)+\frac{r\Gamma (\alpha +1)}{h^{\alpha }\ell }\left[1-{(1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell )}^{k+1}\right],$$

(23)

with $z=-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell$ in Lemma 5 concludes that

$${(1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell )}^{k+1}\le e^{-\frac{h^{\alpha }}{\Gamma (\alpha +1)}.\ell (k+1)}\le e^{-\frac{\ell T}{\Gamma (\alpha +1)}},$$

where $0\le (k+1)h^{\alpha }\le T$ for $(k+1)\le (N-1).$ Thus in Equation (23), we obtain

$$\mathcal{H}\left(y(t_{k+1}),y_{k+1}\right)\le e^{-\frac{\ell T}{\Gamma (\alpha +1)}}\mathcal{H}\left(y(t_0),y_0\right)+\frac{r\Gamma (\alpha +1)}{h^{\alpha }\ell }[1-e^{-\frac{\ell T}{\Gamma (\alpha +1)}}].$$

Moreover,

$$r=\underset{0\le k\le N-1}{max}\mathcal{H}(r_k,0)=-\frac{h^{2\alpha }}{\Gamma (2\alpha +1)}\underset{0\le t\le T}{max}\mathcal{H}{(}^{FC}{D}_{*}^{2\alpha }{y}_{ii.gH}(t),0),$$

and the accuracy of the initial value, concludes that $\mathcal{H}\left(y(t_0),y_0\right)=0$, so

$$\mathcal{H}\left(y(t_{k+1}),y_{k+1}\right)\le -\frac{h^{\alpha }\Gamma (\alpha +1)}{\ell \Gamma (2\alpha +1)}[1-e^{-\frac{\ell T}{\Gamma (\alpha +1)}}]\underset{0\le t\le T}{max}\mathcal{H}{(}^{FC}{D}_{*}^{2\alpha }{y}_{ii.gH}(t),0),$$

now, letting $h\to 0$ then $\mathcal{H}\left(y(t_{k+1}),y_{k+1}\right)\to 0$, which is the desired conclusion, and we can say that the fuzzy generalized Euler’s method is convergent in this step.

Step II. To estimate the step II, consider $y(t)$ is ${}^{FC}[(i)-gH]$-differentiable, by using Equation (19) and let $r_k=\frac{h^{2\alpha }}{\Gamma (2\alpha +1)}\odot {}^{FC}{D}_{*}^{2\alpha }{y}_{i.gH}(t_k)$ the proof of this step is similar to step I, so the fuzzy generalized Euler’s method is convergent.

6.3. Stability

Now, the stability of the presented method is illustrated. For this aim, the following definition is presented.

Definition 13.

Assume that $y_{k+1},k+1\ge 0$ is the solution of fuzzy generalized Euler’s method where $y_0\in {\mathbb{R}}_{\mathcal{F}}$ and also $z_{k+1}$ is the solution of the same numerical method where $z_0=y_0\oplus {\delta }_0\in {\mathbb{R}}_{\mathcal{F}}$ shows its perturbed fuzzy initial condition. The fuzzy generalized Euler’s method is stable if there exists positive constant $\widehat{h}$ and $\mathcal{K}$ such that

$$\forall (k+1)h^{\alpha }\le T,k+1<N-1,h\in (0,\widehat{h})\Rightarrow \mathcal{H}\left(z_{k+1},y_{k+1}\right)\le \mathcal{K}\delta$$

whenever $\mathcal{H}\left({\delta }_0,0\right)\le \delta .$

◃ Investigating the stability of the fuzzy generalized Euler’s method:

The proof falls naturally into two steps:

Step I. If $y(t)$ is ${}^{FC}[(ii)-gH]$-differentiable, by using Equation (18) the perturbed problem is in the following form,

$$z_{k+1}=z_k\ominus (-1)\frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot f(t_k,z_k),z_0=y_0\oplus {\delta }_0.$$

(24)

According to the Equations (19) and (24), we have

$$\mathcal{H}\left(z_{k+1},y_{k+1}\right)\le \mathcal{H}\left(z_k,y_k\right)-\frac{h^{\alpha }}{\Gamma (\alpha +1)}\mathcal{H}\left(f(t_k,z_k),f(t_k,y_k)\right),$$

which we have been working under the assumption that specifications of the Hausdorff metric are satisfied. Using the Lipschitz condition, it can be concluded that

$$\mathcal{H}\left(z_{k+1},y_{k+1}\right)\le (1-\frac{h^{\alpha }}{\Gamma (\alpha +1)}\ell )\mathcal{H}\left(z_k,y_k\right),$$

repeating with the inequality and applying Lemma 5 lead us to the following inequality

$$\begin{array}{ccc}\hfill \mathcal{H}\left(z_{k+1},y_{k+1}\right)& \le & {(1-{\displaystyle \frac{h^{\alpha }}{\Gamma (\alpha +1)}}\ell )}^{k+1}\mathcal{H}\left(z_0,y_0\right)\hfill \\ \hfill & \le & e^{-{\displaystyle \frac{h^{\alpha }}{\Gamma (\alpha +1)}}.\ell (k+1)}\mathcal{H}\left(z_0{\ominus }_{gH}{y}_0,0\right)\hfill \\ \hfill & \le & e^{-{\displaystyle \frac{\ell T}{\Gamma (\alpha +1)}}}\mathcal{H}({\delta }_0,0)\le \mathcal{K}\delta ,\hfill \end{array}$$

where $\mathcal{K}=e^{-{\displaystyle \frac{\ell T}{\Gamma (\alpha +1)}}}$ and for $k+1<N-1\Rightarrow h^{\alpha }(k+1)\le T$. In this case, it is obvious the stability of the fuzzy generalized Euler’s method.

Step II. For ${}^{FC}[(i)-gH]$-differentiability of $y(t)$ the same process can be used. In general, the above-mentioned analysis, points out that the fuzzy generalized Euler method is a stable approach.

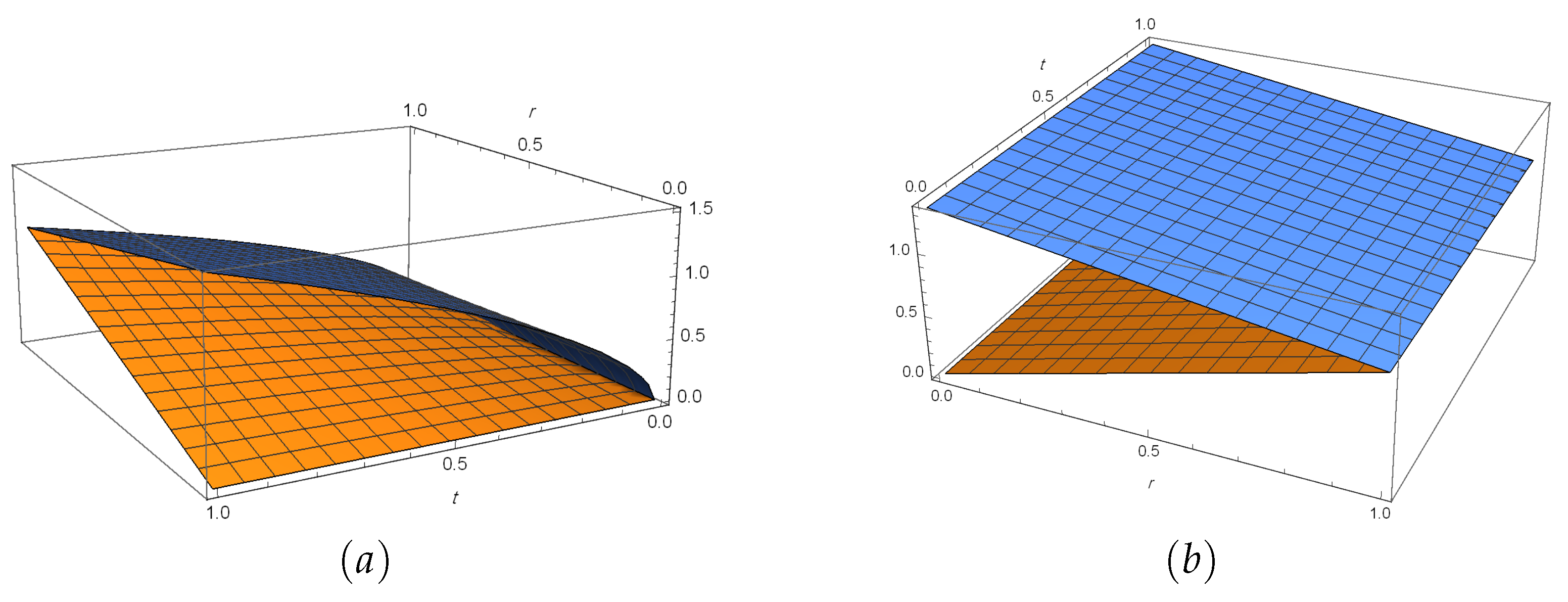
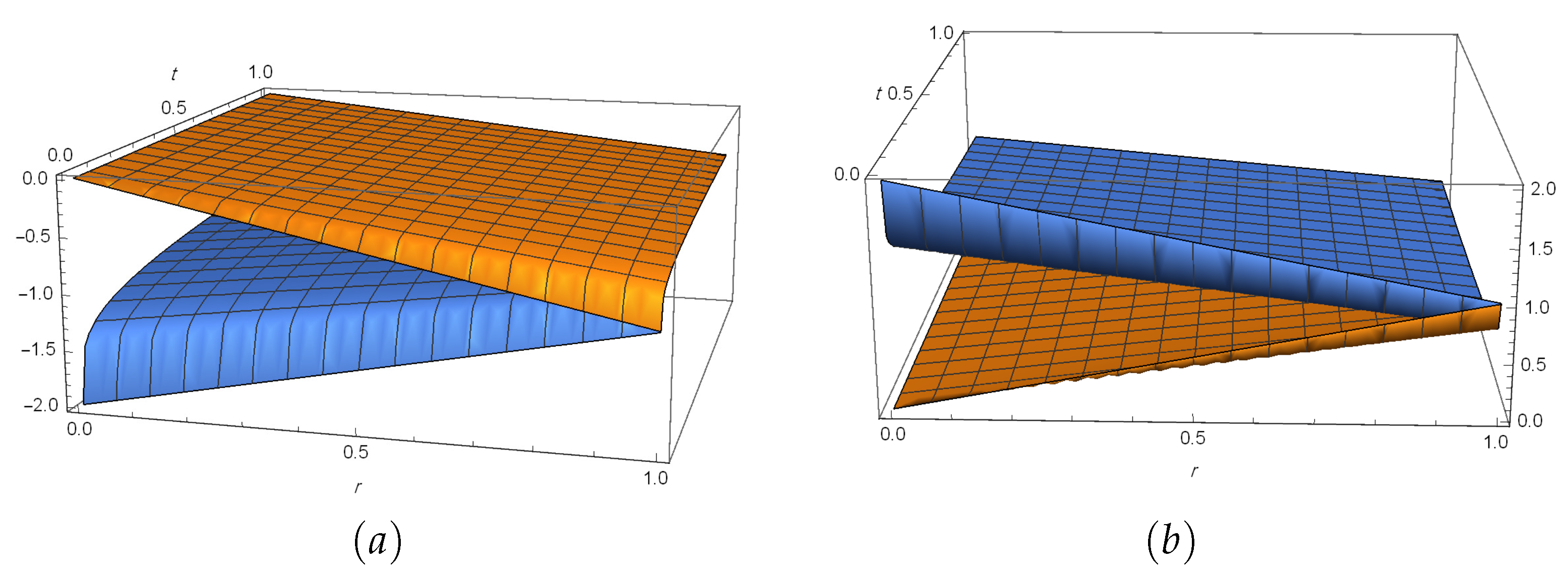
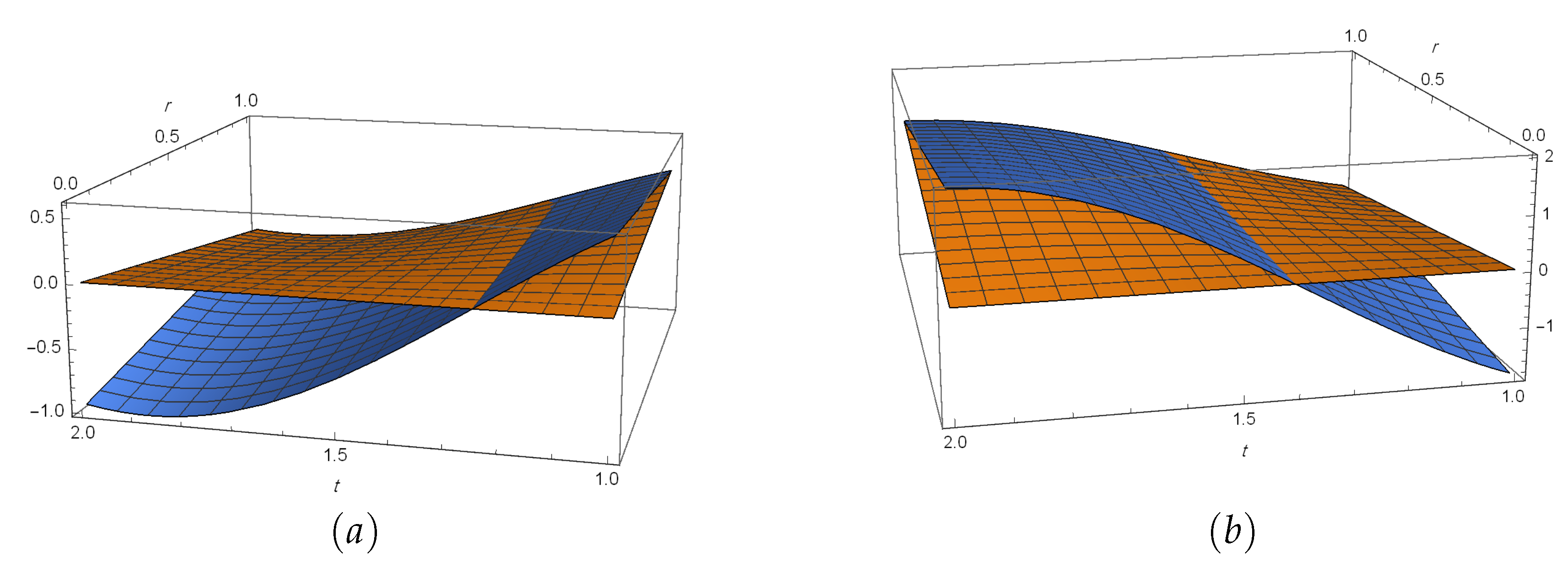
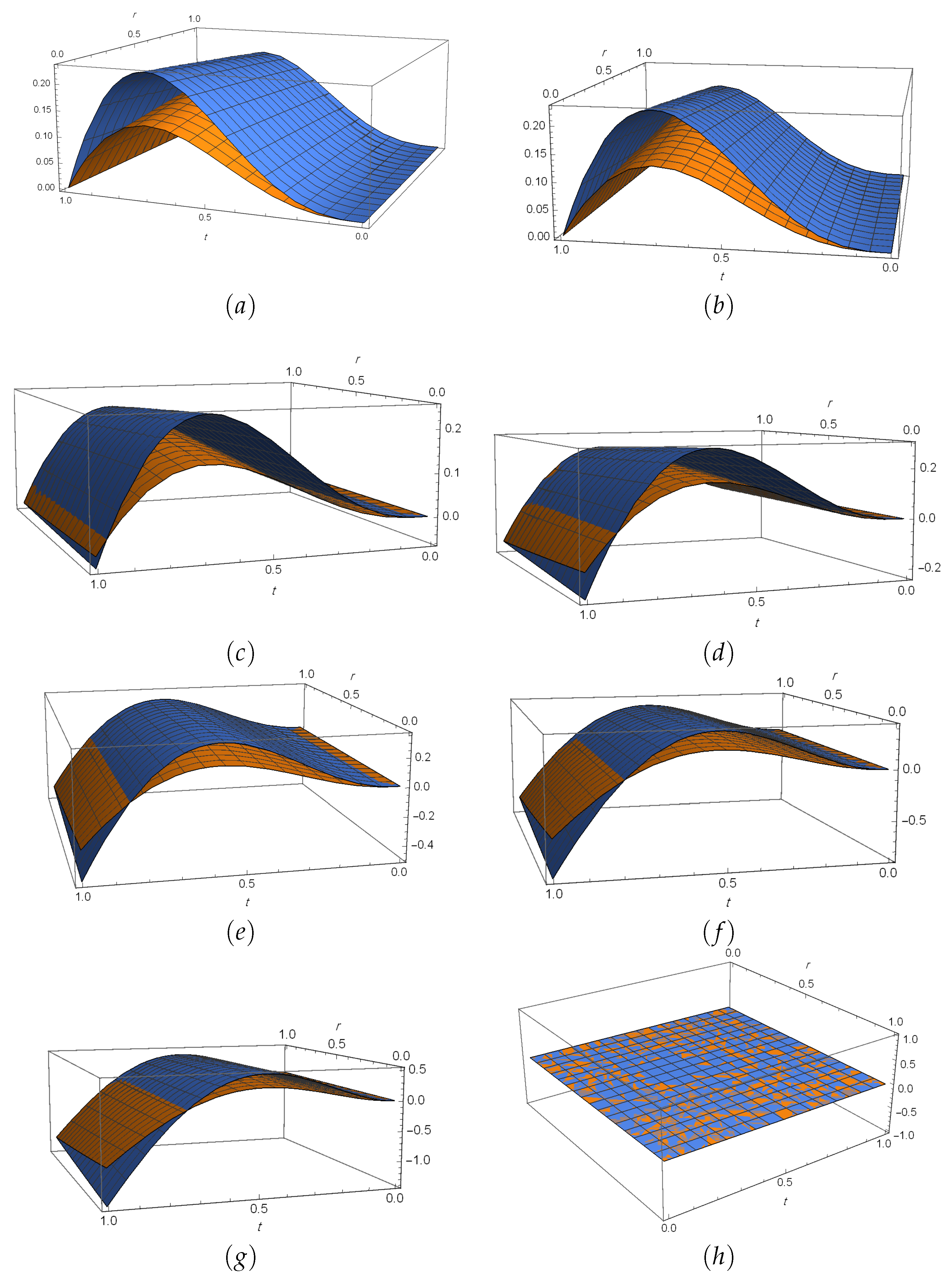
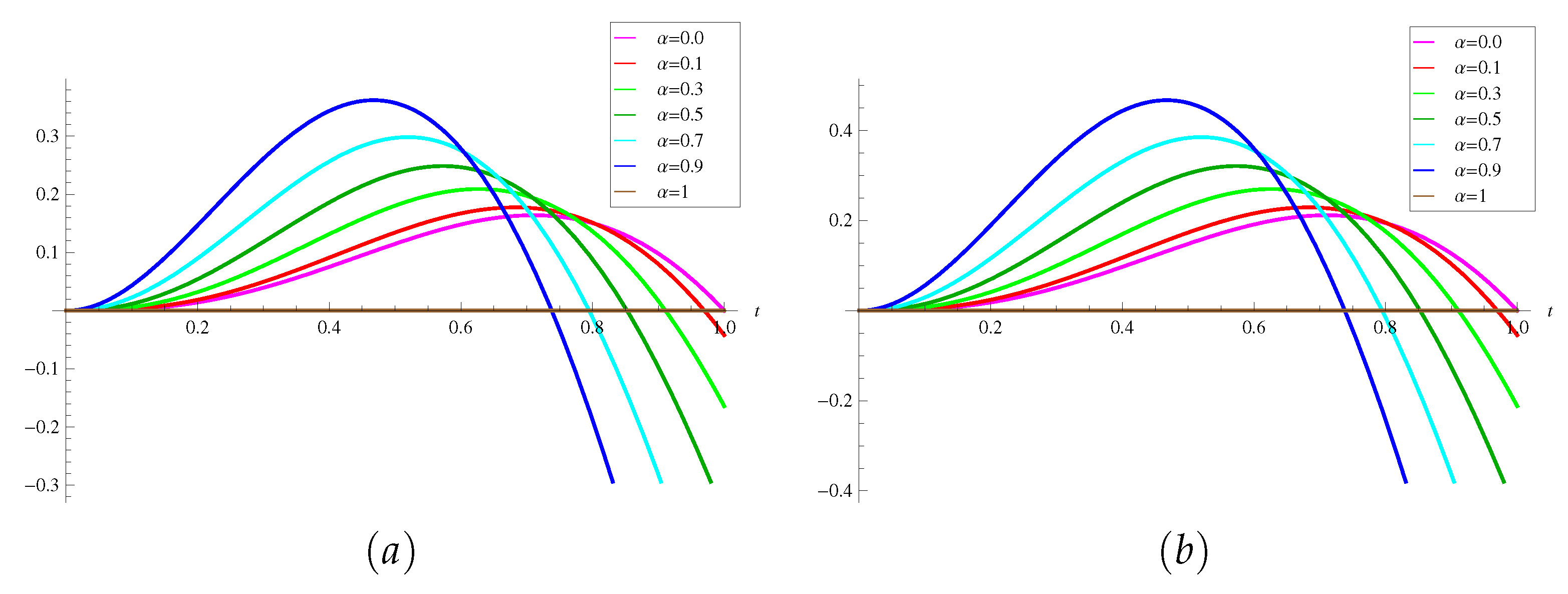
7. Numerical Simulations

In this section, several examples of the fractional differential equations are solved by using the full fuzzy generalized Euler method. Moreover, the numerical results are demonstrated on some tables for different values of h and t.

Example 1.

Let us consider the following initial value problem,

$${}^{FC}{D}_{*}^{\alpha }y(t)=(0,1,1.5)\odot \Gamma (\alpha +1),0<t\le 1,$$

where $y(0)=0$, and $y(t)=(0,1,1.5)\odot t^{\alpha }$ is the exact ${}^{FC}[i-gH]$-differentiable solution of problem. In order to find the numerical results we should construct the following iterative formula as

$$y_{k+1}=y_k\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot \left[(0,1,1.5)\odot \Gamma (\alpha +1)\right],k=0,1,\cdots ,N-1,$$

in

Table 1. Numerical results of Example 1 for various $t,\alpha$ and h.

$\mathit{\alpha }=0.3$			$\mathit{\alpha }=0.6$		$\mathit{\alpha }=0.9$
$\mathit{t}$	$\mathit{h}\mathbf{=}\mathbf{0.2}$	$\mathit{h}\mathbf{=}\mathbf{0.02}$	$\mathit{h}\mathbf{=}\mathbf{0.2}$	$\mathit{h}\mathbf{=}\mathbf{0.02}$	$\mathit{h}\mathbf{=}\mathbf{0.2}$	$\mathit{h}\mathbf{=}\mathbf{0.02}$
0.1	(0, 0.617034, 0.925551)	(0, 0.309249, 0.463874)	(0, 0.380731, 0.571096)	(0, 0.0956352, 0.143453)	(0, 0.234924, 0.352386)	(0, 0.0295752, 0.0443627)
0.2	(0, 1.23407, 1.8511)	(0, 0.618499, 0.927748)	(0, 0.761462, 1.14219)	(0, 0.19127, 0.286906)	(0, 0.469848, 0.704771)	(0, 0.0591503, 0.0887255)
0.3	(0, 1.8511, 2.77665)	(0, 0.927748, 1.39162)	(0, 1.14219, 1.71329)	(0, 0.286906, 0.430359)	(0, 0.704771, 1.05716)	(0, 0.0887255, 0.133088)
0.4	(0, 2.46814, 3.7022)	(0, 1.237, 1.8555)	(0, 1.52292, 2.28438)	(0, 0.382541, 0.573811)	(0, 0.939695, 1.40954)	(0, 0.118301, 0.177451)
0.5	(0, 3.08517, 4.62775)	(0, 1.54625, 2.31937)	(0, 1.90365, 2.85548)	(0, 0.478176, 0.717264)	(0, 1.17462, 1.76193)	(0, 0.147876, 0.221814)
0.6	(0, 3.7022, 5.5533)	(0, 1.8555, 2.78325)	(0, 2.28438, 3.42658)	(0, 0.573811, 0.860717)	(0, 1.40954, 2.11431)	(0, 0.177451, 0.266176)
0.7	(0, 4.31924, 6.47886)	(0, 2.16475, 3.24712)	(0, 2.66512, 3.99767)	(0, 0.669447, 1.00417)	(0, 1.64447, 2.4667)	(0, 0.207026, 0.310539)
0.8	(0, 4.93627, 7.40441)	(0, 2.474, 3.71099)	(0, 3.04585, 4.56877)	(0, 0.765082, 1.14762)	(0, 1.87939, 2.81909)	(0, 0.236601, 0.354902)
0.9	(0, 5.5533, 8.32996)	(0, 2.78325, 4.17487)	(0, 3.42658, 5.13987)	(0, 0.860717, 1.29108)	(0, 2.11431, 3.17147)	(0, 0.266176, 0.399265)
1.0	(0, 6.17034, 9.25551)	(0, 3.09249, 4.63874)	(0, 3.80731, 5.71096)	(0, 0.956352, 1.43453)	(0, 2.34924, 3.52386)	(0, 0.295752, 0.443627)

, the numerical results for different values of $t,\alpha$ and h are demonstrated. In Figure 1, the exact solution and the Caputo gH-derivative for $\alpha =0.6$ are demonstrated.

Example 2.

Consider the following problem,

$${}^{FC}{D}_{*}^{\alpha }y(t)=(-1)\odot y(t),0\le t\le 1,$$

where $y(0)=(0,1,2)$ and the exact ${}^{FC}[ii-gH]$-differentiable solution of problem is in the form $y(t)=(0,1,2)\odot E_{\alpha }(-t^{\alpha })$. In order to solve the mentioned problem the following formula should be applied as

$$\begin{array}{c}{y}_0=(0,1,2),\hfill \\ y_{k+1}=y_k{\ominus }_{gH}\frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot y_k,k=0,1,\cdots ,N-1,\hfill \end{array}$$

the numerical results based on the presented method are obtained in

Table 2. Numerical results of Example 2 for various $t,\alpha$ and h.

$\mathit{\alpha }=0.3$			$\mathit{\alpha }=0.6$		$\mathit{\alpha }=0.9$
$\mathit{t}$	$\mathit{h}\mathbf{=}\mathbf{0.2}$	$\mathit{h}\mathbf{=}\mathbf{0.02}$	$\mathit{h}\mathbf{=}\mathbf{0.2}$	$\mathit{h}\mathbf{=}\mathbf{0.02}$	$\mathit{h}\mathbf{=}\mathbf{0.2}$	$\mathit{h}\mathbf{=}\mathbf{0.02}$
0.1	(0, 0.312475, 0.624949)	(0, 0.655421, 1.31084)	(0, 0.573896, 1.14779)	(0, 0.892967, 1.78593)	(0, 0.755737, 1.51147)	(0, 0.969249, 1.9385)
0.2	(0, 0.0976404, 0.195281)	(0, 0.429577, 0.859154)	(0, 0.329356, 0.658712)	(0, 0.797391, 1.59478)	(0, 0.571138, 1.14228)	(0, 0.939444, 1.87889)
0.3	(0, 0.0305101, 0.0610203)	(0, 0.281554, 0.563107)	(0, 0.189016, 0.378032)	(0, 0.712044, 1.42409)	(0, 0.43163, 0.863261)	(0, 0.910555, 1.82111)
0.4	(0, 0.00953365, 0.0190673)	(0, 0.184536, 0.369072)	(0, 0.108476, 0.216951)	(0, 0.635832, 1.27166)	(0, 0.326199, 0.652398)	(0, 0.882555, 1.76511)
0.5	(0, 0.00297902, 0.00595805)	(0, 0.120949, 0.241898)	(0, 0.0622536, 0.124507)	(0, 0.567777, 1.13555)	(0, 0.246521, 0.493042)	(0, 0.855415, 1.71083)
0.6	(0, 0.000930869, 0.00186174)	(0, 0.0792725, 0.158545)	(0, 0.0357271, 0.0714542)	(0, 0.507007, 1.01401)	(0, 0.186305, 0.37261)	(0, 0.829111, 1.65822)
0.7	(0, 0.000290873, 0.000581746)	(0, 0.0519568, 0.103914)	(0, 0.0205036, 0.0410072)	(0, 0.45274, 0.905481)	(0, 0.140797, 0.281595)	(0, 0.803615, 1.60723)
0.8	(0, 0.0000908904, 0.000181781)	(0, 0.0340536, 0.0681072)	(0, 0.0117669, 0.0235339)	(0, 0.404282, 0.808565)	(0, 0.106406, 0.212812)	(0, 0.778903, 1.55781)
0.9	(0, 0.000028401, 0.0000568019)	(0, 0.0223195, 0.0446389)	(0, 0.00675299, 0.013506)	(0, 0.361011, 0.722022)	(0, 0.0804149, 0.16083)	(0, 0.754951, 1.5099)
1.0	(0,$8.87458\times {10}^{-6}$,0.0000177492)	(0, 0.0146286, 0.0292573)	(0, 0.00387551, 0.00775103)	(0, 0.322371, 0.644742)	(0, 0.0607725, 0.121545)	(0, 0.731735, 1.46347)

for various $t,\alpha =0.3,0.6,0.9$ and $h=0.2,0.02$. The figures of exact solution and the Caputo gH-derivative are shown in Figure 2.

Example 3.

Let us to consider the following problem,

$${}^{FC}{D}_{*}^{\alpha }y(t)=-\frac{{\pi }^2{t}^{2-\alpha }{\alpha }^2}{(2-3\alpha +{\alpha }^2)\Gamma (1-\alpha )}{}_p{F}_q\left(1;\left[\frac{3}{2}-\frac{\alpha }{2},2-\frac{\alpha }{2}\right];-\frac{1}{4}{\pi }^2{t}^2{\alpha }^2\right)\odot \left(0,\frac{1}{2},1\right),1\le t\le 2,$$

where $y(1)=\left(0,\frac{1}{2},1\right)\odot cos(\alpha \pi )$ and the exact solution is $y(t)=\left(0,\frac{1}{2},1\right)\odot cos(\alpha \pi t)$. We know that this problem has the switching point at $t=1.40426$. According to Equation (20), we should divide the interval $[1,2]$ to the N subinterval $[t_k,t_{k+1}]$, for $k=0,1,\dots ,N-1$, and assuming the switching point belongs to $[t_j,t_{j+1}]$, then the following iterative formulas are applied as

$$\begin{array}{c}{\displaystyle y_{k+1}=y_k\oplus \frac{h^{\alpha }}{\Gamma (\alpha +1)}\left(-\frac{{\pi }^2{t}^{2-\alpha }{\alpha }^2}{(2-3\alpha +{\alpha }^2)\Gamma (1-\alpha )}{}_p{F}_q\left(a;b;z{t}_k^2\right)\odot \left(0,\frac{1}{2},1\right)\right),}\hfill \\ k=0,1,\cdots ,j,\hfill \\ {\displaystyle y_{k+1}=y_k\ominus (-1)\frac{h^{\alpha }}{\Gamma (\alpha +1)}\left(-\frac{{\pi }^2{t}^{2-\alpha }{\alpha }^2}{(2-3\alpha +{\alpha }^2)\Gamma (1-\alpha )}{}_p{F}_q\left(a;b;z{t}_k^2\right)\odot \left(0,\frac{1}{2},1\right)\right),}\hfill \\ k=j+1,\cdots ,N-1,\hfill \end{array}$$

where $a=1,b=\left[\frac{3}{2}-\frac{\alpha }{2},2-\frac{\alpha }{2}\right]$ and $z=-\frac{1}{4}{\pi }^2{\alpha }^2$. Numerical results are demonstrated in

Table 3. Numerical results of Example 3 for $\alpha =0.8$, $h=0.2,0.02,0.002$ and various t.

$\mathit{\alpha }=0.8$
$\mathit{t}$	$\mathit{h}\mathbf{=}\mathbf{0.2}$	$\mathit{h}\mathbf{=}\mathbf{0.02}$	$\mathit{h}\mathbf{=}\mathbf{0.002}$
1.1	(0, −0.452376, −0.918699)	(0, −0.463549, −0.928996)	(0, −0.464888, −0.929776)
1.2	(0, −0.489654, −0.984721)	(0, −0.495423, −0.991934)	(0, −0.496057, −0.992115)
1.3	(0, −0.489654, −0.984721)	(0, −0.495423, −0.991934)	(0, −0.496057, −0.992115)
1.4	(0, −0.452376, −0.918699)	(0, −0.463549, −0.928996)	(0, −0.464888, −0.929776)
1.5	(0, −0.400112, −0.800241)	(0, −0.404397, −0.808832)	(0, −0.404508, −0.809017)
1.6	(0, −0.307754, −0.628932)	(0, −0.317689, −0.637143)	(0, −0.318712, −0.637424)
1.7	(0, −0.20878, −0.417784)	(0, −0.21233, −0.425584)	(0, −0.21289, −0.425779)
1.8	(0, −0.0927856, −0.176232)	(0, −0.0935876, −0.187196)	(0, −0.0936907, −0.187381)
1.9	(0, 0.0304523, 0.0618529)	(0, 0.0313271, 0.0627734)	(0, 0.0313953, 0.0627905)
2.0	(0, 0.146488, 0.301241)	(0, 0.15359, 0.308805)	(0, 0.154508, 0.309017)

for $\alpha =0.8$ and $h=0.2,0.02,0.002$. In Figure 3, the graphs of the exact solution and the Caputo gH-derivative are presented for $\alpha =0.8$.

Example 4.

Consider the following nonlinear fractional differential equations under uncertainty,

$$\sqrt{\eta }\odot {}^{FC}{D}_{*}^{\alpha }y(t)+y^2(t)=g(x),0<\alpha <1,t\in [0,1],$$

where

$$g(x)=\left[\frac{\Gamma (6)}{\Gamma (6-\alpha )}{t}^{5-\alpha }-\frac{3\Gamma (5)}{\Gamma (5-\alpha )}{t}^{3-\alpha }+\frac{\Gamma (5)}{\Gamma (4-\alpha )}{t}^{3-\alpha }+{(t^5-3t^4+2t^3)}^2\right]\odot \tilde{\eta },$$

and $\tilde{\eta }(r)=(1,2,3),y\ne 0$. Then, the exact solution of the problem is $y(t)=\sqrt{\eta }\odot (t^5-3t^4+2t^3)$. By solving the problem under ${}^{FC}$[(i)-gH]-differentiability using

$$y_{k+1}=y_k+\frac{h^{\alpha }}{\Gamma (\alpha +1)}\odot {\Gamma }_k,k=0,1,\cdots ,N-1,$$

we obtain the numerical solution shown in

Table 4. Absolute error of Example 4 at $t=1$.

h	$\mathit{\alpha }=0.1$	$\mathit{\alpha }=0.3$	$\mathit{\alpha }=0.5$	$\mathit{\alpha }=0.7$	$\mathit{\alpha }=0.9$
$\frac{1}{10}$	$7.20602\times {10}^{-2}$	$6.5418\times {10}^{-2}$	$5.8823\times {10}^{-2}$	$5.3707\times {10}^{-2}$	$5.0201\times {10}^{-2}$
$\frac{1}{20}$	$3.9603\times {10}^{-2}$	$3.3498\times {10}^{-2}$	$2.9368\times {10}^{-2}$	$2.6937\times {10}^{-2}$	$2.5668\times {10}^{-2}$
$\frac{1}{40}$	$2.0653\times {10}^{-2}$	$1.6611\times {10}^{-2}$	$1.4420\times {10}^{-2}$	$1.3384\times {10}^{-2}$	$1.2962\times {10}^{-2}$
$\frac{1}{80}$	$1.0448\times {10}^{-4}$	$8.1038\times {10}^{-3}$	$7.0482\times {10}^{-3}$	$6.6381\times {10}^{-3}$	$6.5091\times {10}^{-3}$

, with different order of differentiability and step size.

In Figure 4, the graphs of the exact solution and Caputo gH-derivatives are presented for $\alpha =0.1,0.3,0.5,0.7,0.9,1$, and in Figure 5 these Caputo gH-derivatives have been compared in $r=0.5$.

Remark 1.

Although we have obtained the solution under ${}^{FC}[(i)-gH]$-differentiability, it is easy to check that it is not ${}^{FC}[(i)-gH]$-differentiable on $(0,1)$. Actually, due to obtained results (see

Table 5. Switching points for different values of $\alpha$.

$\alpha$	$0.1$	$0.3$	$0.5$	$0.7$	$0.9$	1
t	$0.9701$	$0.9109$	$0.8525$	$0.7949$	$0.7381$	$0.7101$

), we can consider the proper interval that the given exact solution and its approximation is ${}^{FC}[(i)-gH]$-differentiable. Moreover, note that, we have computed the approximation of the solution of Example 4 at point $t=1$, which is clearly this point take place out of proper domain of ${}^{FC}[(i)-gH]$-differentiability. In fact, the computed error at point $t=1$, just obtained based on the lower-upper approximation of lower-upper of exact solution. For more clarification, we determined switching points regarding each order of differentiability.

Remark 2.

Indeed, using the results of Table 5, we in fact deduce that by considering the problem of fractional order instead of integer order (here, first order), we obtain some wider interval than the first order case; on the other hand, when $\alpha =1$, the valid interval that the given exact solution verify the assumption ${}^{FC}[(i)-gH]$-differentiability is $(0,0.7101)$, while for $\alpha =0.9$ and $\alpha =0.7$, the valid interval are $(0,0.7381)$ and $(0,0.7949)$, respectively. Actually, this is the first time in the literature that this new result, i.e., extending the length of valid interval that the type of differentiability remains unchanged, is investigated.

8. Conclusions

Fractional differential equations are one of the important topics of fuzzy arithmetic which have many applications in sciences and engineering. Thus finding the numerical and analytical methods to solve these problems is very important. This paper was presented based on the two main topics. First, proving the generalized Taylor series expansion for fuzzy valued function based on the concept of generalized Hukuhara differentiability. Second, introducing the fuzzy generalized Euler’s method as an application of the generalized Taylor expansion and applying it to solve the fuzzy fractional differential equations. The capabilities and abilities of the presented method were shown by presenting several theorems about the consistency, the convergence, and the stability of the generalized Euler’s method. Furthermore, the accuracy and efficiency of the method were illustrated by considering the local and global truncation errors. The numerical results especially in the switching point case showed the precision of the generalized Euler’s method to solve the fuzzy fractional differential equations.