Abstract
A subgraph H of a graph G with perfect matching is nice if has perfect matching. It is well-known that all fullerene graphs have perfect matchings and that all fullerene graphs contain some small connected graphs as nice subgraphs. In this contribution, we consider fullerene graphs arising from smaller fullerenes via the leapfrog transformation, and show that in such graphs, each pair of (necessarily disjoint) pentagons is nice. That answers in affirmative a question posed in a recent paper on nice pairs of odd cycles in fullerene graphs.
1. Introduction
It has been known for a long time that the stability of several classes of organic compounds is, to a great degree, determined by the presence and abundance of resonant electronic structures. A natural way to represent such structures is via perfect matchings in the corresponding graphs, and the general rule for polycyclic aromatic hydrocarbons and other conjugated systems is that the stability of a compound increases with the number of perfect matchings in the corresponding graph.
The study of matchings in fullerene graphs begun almost as soon as the fullerene structures were first observed. It turned out that the number of perfect matchings is not so decisive for the stability of fullerene structures as for the conjugated compounds [1]. However, the interest for matchings in fullerenes did not wane, driven by the fact that fullerene graphs can serve as useful stepping-stones toward establishing important results for larger classes of graphs. Among several matching-related structural properties of all fullerene graphs, the most productive one turned out to be their cyclical 5-edge connectivity [2,3,4,5], further leading to their bicriticality and 2-extendability. In a recent paper by the present author [6], some of the consequences of those structural properties, elaborated in a series of papers concerned with the so-called bricks [7,8,9,10,11,12], were applied to the study of nice addition patterns in fullerenes, that is, the addition/substitution patterns, such that the unaffected part of the molecule still has a resonant structure. It was observed that each fullerene graph contains two disjoint odd cycles whose union is a nice subgraph, and it was investigated whether one or both of those odd cycles could be pentagonal faces. The aim of this contribution is to settle one of the open problems listed at the end of that paper.
The next section introduces basic concepts and quotes some relevant results from previous research. Section 3 is devoted to our main findings. In the last section, we list some unsolved issues and indicate a couple of possible topics for future research.
2. Definitions and Preliminary Results
For a given graph G, we denote its vertex set by and its edge set by . For other basic graph-theoretic and matching-related notations and definitions, we refer the reader to [13] or [14].
A fullerene graph is a planar, 3-regular, and 3-connected graph with only pentagonal and hexagonal faces. Every fullerene graph must contain exactly 12 pentagonal faces; this follows easily from the Euler formula. Since the number of hexagons can be any non-negative integer except 1 [15], it follows that fullerene graphs on n vertices exist for (no hexagons) all for all even . A classical survey of early results on fullerene graphs is [16], and for a more recent comprehensive review we refer the reader to [17].
A matching M in a graph G is a collection of edges from , such that each vertex of G is incident to, at most, one edge from M. Hence, no two edges from M share a vertex. A matching M is perfect if every vertex of G is incident with (covered by) an edge from M. Every fullerene graph has at least one perfect matching; that follows from a celebrated result of Petersen, stating that every cubic graph with, at most, two bridges has a perfect matching [18].
Let G be a graph with perfect matchings. A subgraph H of G is nice if has a perfect matching. In molecular graphs, nice subgraphs represent the addition patterns, such that the rest of the molecule still has a resonant pattern. Fullerenes contain several small graphs as nice subgraphs; see [19,20,21] for a non-exhaustive list.
Several transformations of fullerene graphs result in other, usually larger, fullerene graphs. The most important are the so-called Goldberg-Coxeter transformations [17], and the most common among them is certainly the leapfrog transformation. For a given fullerene G on n vertices, its leapfrog transform is obtained by truncating its dual. Hence,
where denotes the dual graph of G. It is easily seen that the leapfrog transform of G has vertices and that it indeed is a fullerene graph. Further, it has isolated pentagons, and among its faces it is possible to distinguish between those that arise from the faces of G and those that arise from its vertices. In Figure 1 we show a portion of a leapfrog fullerene. The edges of the original fullerene are indicated in dashed lines. The faces arising from the original faces (we call them the facial faces) are shaded. One can see that they are isolated by faces arising from vertices of G. Furthermore, the edges not on the boundary of the facial faces, shown in thick full lines in Figure 1, form a perfect matching in . We call it the canonical perfect matching. Finally, all non-facial faces of are alternating with respect to the canonical perfect matching. That means that we can flip the edges on the boundary of any collection of disjoint non-facial faces and still have a perfect matching in . Four such faces are marked by circles in Figure 1. For more on leapfrog fullerenes and their remarkable properties and for more information on other fullerene-to-fullerene transformations, we refer the reader to [16,22,23,24,25].
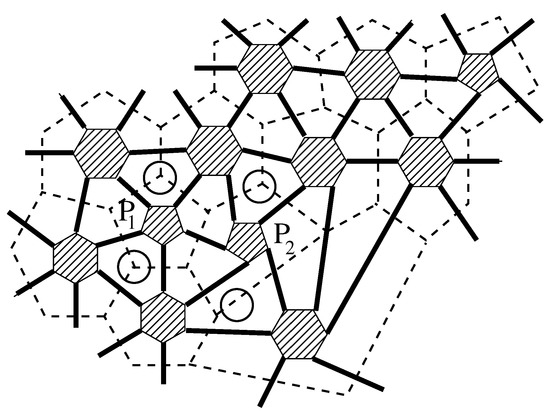
Figure 1.
A portion of a leapfrog fullerene.
The following result, observed by the present author in [6], depends on several structural properties of fullerene graphs, such as their cyclical 5-edge connectivity, bicriticality, and the fact that they are bricks. As those properties are not directly relevant for this paper, we omit the definitions and instead refer the interested reader to the series of papers [7,8,9,10,11,12].
Theorem 1.
Every fullerene graph G contains two disjoint odd cycles and , such that has a perfect matching.
Clearly, any odd cycle in a fullerene graph must involve at least one of its pentagonal faces. It is then natural to ask when the pentagonal faces suffice, or whether any two disjoint pentagons form a nice pair. These, as well as some other problems were analyzed to some extent in [6], and some of the findings turned out to be somewhat counter-intuitive. It was found that in almost all small fullerenes, any two disjoint pentagons do indeed form a nice pair. It was also found that, for a sufficiently large number of vertices, there always exists a fullerene graph with this property. However, an infinite class of fullerene graphs was found, such that this is not true—there are fullerenes, the narrow nanotubes, containing pairs of disjoint pentagons which are not nice. Altogether, there seems to remain a large gap between the patterns that were empirically observed and those that were strictly proved. In the next section, we narrow the gap a bit by proving that in a non-negligible fraction of all fullerenes, any two pentagons form a nice pair.
3. Main Results
Theorem 2.
Let G be a leapfrog fullerene. Then, any two pentagons in G form a nice pair.
Proof.
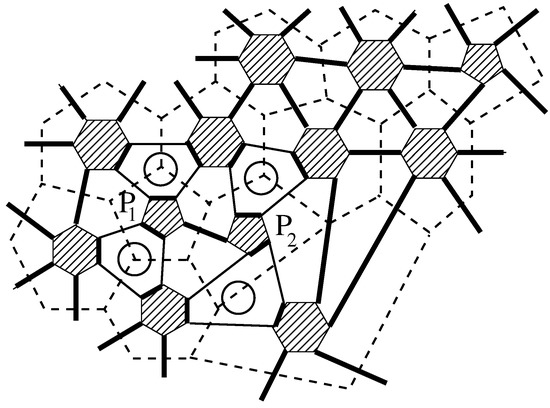
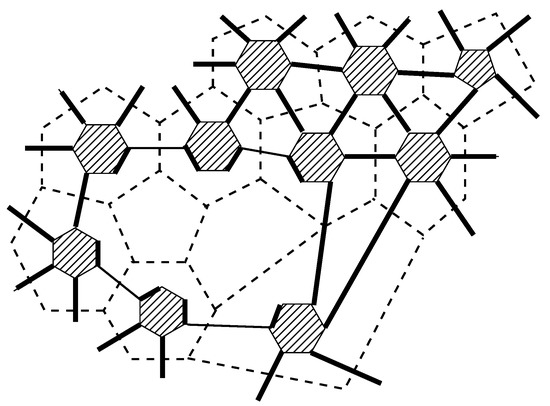
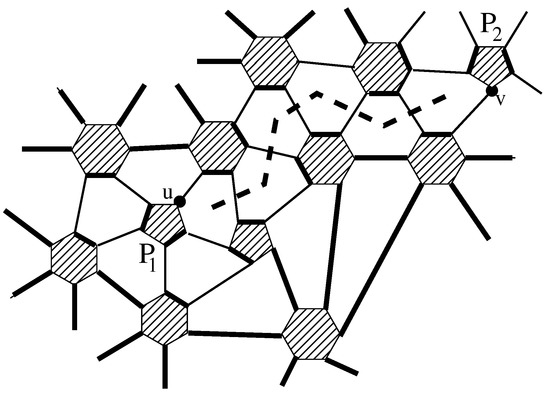
Let G be a leapfrog fullerene and , be two of its pentagonal faces, and M the canonical perfect matching in G. If and are close, at distance 2 in the dual graph of G, we have the situation shown in Figure 1. By flipping the edges on the four non-facial faces marked by circles, we obtain a perfect matching in ; the situation is shown in Figure 2. One can see that in , the vertices of are paired by the edges whose both ends belong to the two close pentagons. When, as shown in Figure 3, both and are removed from G, no vertices remain unpaired. Hence, has a perfect matching, and and form a nice pair.

Figure 2.
Flipping the edges on four hexagons adjacent to a pair of close pentagons.

Figure 3.
Any pair of close pentagons is nice.
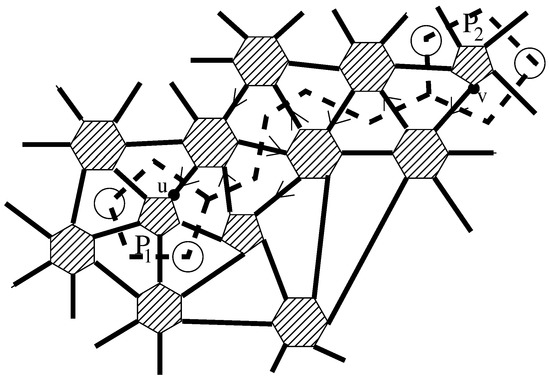
Let us now look at two remote pentagons in G. Each of the non-facial faces adjacent to and corresponds to a vertex of a pentagon in the original fullerene. Take the shortest path connecting two vertices on those pentagons in the original fullerene; the pentagons and the path are indicated by thick dashed lines in Figure 4. (We have removed all other edges of the original fullerene for the sake of clarity.) To this path corresponds a sequence of adjacent hexagons in G, such that shares an edge with , shares an edge with each of and for , and shares an edge with . Since the edges shared by the hexagons belong to M, and the edges of the terminal hexagons shared with the pentagons do not belong to M, it is possible to construct an M-alternating path P of odd length connecting a vertex u of to a vertex v in by choosing either three or five boundary edges of each . The chosen edges from M on P are indicated by arrows in Figure 4. By flipping the edges on this path and on the four hexagons indicated by circles in Figure 4, we obtain a matching, called , in G that leaves two vertices unsaturated, u on and v on , and matches no vertices from to vertices on or . The situation is shown in Figure 5. Deleting and now leaves a graph in which is a perfect matching. Hence, and form a nice pair, and the claim follows. □

Figure 4.
An M-alternating odd path connecting two remote pentagons.

Figure 5.
Any two remote pentagons form a nice pair.
Corollary 1.
The fraction of all fullerenes on vertices in which any two disjoint pentagons form a nice pair is bounded from below by for large values of n.
Proof.
It has been known for a long time [26] that the number of fullerene graphs on n vertices grows roughly as the ninth power of n; see [27] for a formal treatment. As each fullerene graph on n vertices gives rise to exactly one fullerene graph on vertices via the leapfrog transformation, the fraction of fullerenes on vertices which are leapfrog images of smaller fullerenes will asymptotically behave as for large values of n. The claim now follows since, in each of them, any two pentagons form a nice pair. □
4. Open Questions and Concluding Remarks
We have found in [6] that in all isolated pentagon (IP) fullerenes on 100 vertices at most, all pairs of pentagons are nice. In the previous section, we have found an infinite subclass of IP fullerenes with the same property—the leapfrog fullerenes. Further, all known fullerenes in which this is not the case have abutting pentagons. This suggests that in all IP fullerenes, all pairs of pentagons are nice. Hence, our first problem is:
Problem 1.
Is each pair of pentagons nice in all IP fullerenes?
The approach of the previous section relied on the existence of the canonical perfect matching in a leapfrog fullerene. As the existence of such matchings cannot be assumed in non-leapfrog IP fullerenes, a different approach might be needed for general IP fullerenes.
Another, less ambitious, but still interesting question is whether all pairs of pentagons are nice in IP fullerenes arising via some other transformations, such as, for example, chamfer and capra transformations. We know that such fullerenes allow perfect packings of stars and some other related graphs [28]. It is possible that those packings could be exploited in a way similar to the canonical perfect matchings for leapfrog fullerenes.
Problem 2.
What happens with fullerenes arising from smaller fullerenes via general Goldberg–Coxeter transformations? Is every pair of pentagons in such a fullerene G nice?
A further interesting problem could be to look at non-classical fullerenes, that is, the fullerenes containing facial cycles of length(s) different from five and six.
Problem 3.
What can be said about leapfrog (and other, more general) transforms of fullerenes containing heptagonal faces?
It is known that there are ordinary fullerene nanotubes containing non-nice pairs of pentagons [6]. It might be interesting to look at related structures that could be described as Y-branched carbon nanotubes [29].
Among the other interesting issues, we mention the transformations that do not increase the number of vertices but result in isomeric fullerene structures [30,31], migrations of pentagons on nanocones and other portions of the honeycomb lattice [32], fullerene dimer formation [33], and crystal formation involving fullerenes [34].
For other open questions, we refer the reader to [6].
Funding
This research was funded by Partial support of the Croatian Science Foundation via research project LightMol grant number HRZZ-IP-2016-06-1142.
Conflicts of Interest
The author declares no conflict of interest.
References
- Austin, S.J.; Fowler, P.W.; Hansen, P.; Monolopoulos, D.E.; Zheng, M. Fullerene isomers of C60. Kekulé counts versus stability. Chem. Phys. Lett. 1994, 228, 478–484. [Google Scholar] [CrossRef]
- Došlić, T. Cyclical edge-connectivity of fullerene graphs and (k,6)-cages. J. Math. Chem. 2003, 33, 103–112. [Google Scholar] [CrossRef]
- Kardoš, F.; Škrekovski, R. Cyclic edge-cuts in fullerene graphs. J. Math. Chem. 2008, 44, 121–132. [Google Scholar] [CrossRef]
- Kutnar, K.; Marušič, D. On cyclic edge-connectivity of fullerenes. Discrete Appl. Math. 2008, 156, 1661–1669. [Google Scholar] [CrossRef][Green Version]
- Qi, Z.; Zhang, H. A note on the cyclical edge-connectivity of fullerene graphs. J. Math. Chem. 2008, 43, 134–140. [Google Scholar] [CrossRef]
- Došlić, T. Nice pairs of odd cycles in fullerene graphs. J. Math. Chem. 2020, 58, 2204–2222. [Google Scholar] [CrossRef]
- de Carvalho, M.H.; Lucchesi, C.L.; Murty, U.S.R. Optimal ear decomposition of matching covered graphs. J. Combin. Theory Ser. B 2002, 85, 59–93. [Google Scholar] [CrossRef]
- de Carvalho, M.H.; Lucchesi, C.L.; Murty, U.S.R. On a conjecture of Lovász concerning bricks I. The Characteristic of a Matching Covered Graph. J. Combin. Theory Ser. B 2002, 85, 94–136. [Google Scholar] [CrossRef]
- de Carvalho, M.H.; Lucchesi, C.L.; Murty, U.S.R. On a conjecture of Lovász concerning bricks II. Bricks of finite characteristic. J. Combin. Theory Ser. B 2002, 85, 137–180. [Google Scholar] [CrossRef][Green Version]
- de Carvalho, M.H.; Lucchesi, C.L.; Murty, U.S.R. The perfect matching polytope and solid bricks. J. Combin. Theory Ser. B 2004, 92, 319–324. [Google Scholar] [CrossRef]
- de Carvalho, M.H.; Lucchesi, C.L.; Murty, U.S.R. Graphs with independent perfect matchings. J. Graph Theory 2005, 48, 19–50. [Google Scholar] [CrossRef]
- de Carvalho, M.H.; Lucchesi, C.L.; Murty, U.S.R. How to build a brick. Discrete Math. 2006, 306, 2383–2410. [Google Scholar] [CrossRef]
- Harary, F. Graph Theory; Addison-Wesley: Reading, MA, USA, 1969. [Google Scholar]
- Lovász, L.; Plummer, M.D. Matching Theory; North-Holland: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Grünbaum, B.; Motzkin, T.S. The number of hexagons and the simplicity of geodesics on certain polyhedra. Can. J. Math. 1963, 15, 744–751. [Google Scholar] [CrossRef]
- Fowler, P.W.; Manolopoulos, D.E. An Atlas of Fullerenes; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Schwerdtfeger, P.; Wirz, L.N.; Avery, J. The topology of fullerenes. WIRE: Comput. Mol. Sci. 2015, 5, 96–145. [Google Scholar] [CrossRef] [PubMed]
- Petersen, J. Die Theorie der regulären graphs. Acta Math. 1891, 15, 193–220. [Google Scholar] [CrossRef]
- Došlić, T. On some structural properties of fullerene graphs. J. Math. Chem. 2002, 31, 187–195. [Google Scholar] [CrossRef]
- Li, H.; Zhang, H. The isolated-pentagon rule and nice substructures in fullerenes. Ars Math. Contemp. 2018, 15, 487–497. [Google Scholar] [CrossRef]
- Ye, D.; Zhang, H. On k-resonant fullerene graphs. SIAM J. Discrete Math. 2009, 23, 1023–1044. [Google Scholar] [CrossRef]
- Diudea, M.V.; Stefu, M.; John, P.E.; Graovac, A. Generalized operations on maps. Croat. Chem. Acta 2006, 79, 355–362. [Google Scholar]
- Došlić, T. Leapfrog fullerenes have many perfect matchings. J. Math. Chem. 2008, 44, 1–4. [Google Scholar] [CrossRef]
- Došlić, T. Finding more perfect matchings in leapfrog fullerenes. J. Math. Chem. 2009, 45, 1130–1136. [Google Scholar] [CrossRef]
- King, R.B.; Diudea, M.V. The chirality of icosahedral fullerenes: A comparison of the tripling, (leapfrog), quadrupling (chamfering) and septupling (capra) transformations. J. Math. Chem. 2006, 39, 597–604. [Google Scholar] [CrossRef]
- Thurston, W.P. Shapes of polyhedra and triangulations of the sphere. Geom. Topol. Mono. 1998, 1, 511–549. [Google Scholar]
- Cioslowski, J. Note on the asymptotic isomer count of large fullerenes. J. Math. Chem. 2014, 52, 1–5. [Google Scholar] [CrossRef]
- Došlić, T.; Dehkordi, M.T.; Fath-Tabar, G.H. Packing stars in fullerenes. J. Math. Chem. 2020, 58, 2223–2244. [Google Scholar] [CrossRef]
- Nagy, P.; Ehlich, R.; Biró, L.P.; Gyulai, J. Y-branching of single walled carbon nanotubes. Appl. Phys. A 2000, 70, 481–483. [Google Scholar] [CrossRef]
- Astakhova, T.Y.; Vinogradov, G.A. Fullerene notation and isomerization operations. Fullerene Sci. Tech. 1997, 5, 1545–1562. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Ori, O. Skeletal rearrangements of the C240 fullerene: Efficient topological descriptors for monitoring Stone-Wales transformations. Mathematics 2020, 8, 968. [Google Scholar] [CrossRef]
- Ori, O.; Cataldo, F. Moving pentagons on nanocones. Fuller. Nanotub. Carbon Nanostruct. 2020, 28, 732–736. [Google Scholar] [CrossRef]
- Diudea, M.V.; Nagy, C.L.; Ursu, O.; Balaban, T.S. C60 dimers revisited. Fuller. Nanotub. Carbon Nanostruct. 2003, 11, 245–255. [Google Scholar] [CrossRef]
- Gadomski, A. Three types of computational soft-matter problems revisited, an own-selection-based opinion. Front. Phys. 2014, 2, 36. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).