A New HWMA Dispersion Control Chart with an Application to Wind Farm Data †
Abstract
:1. Introduction
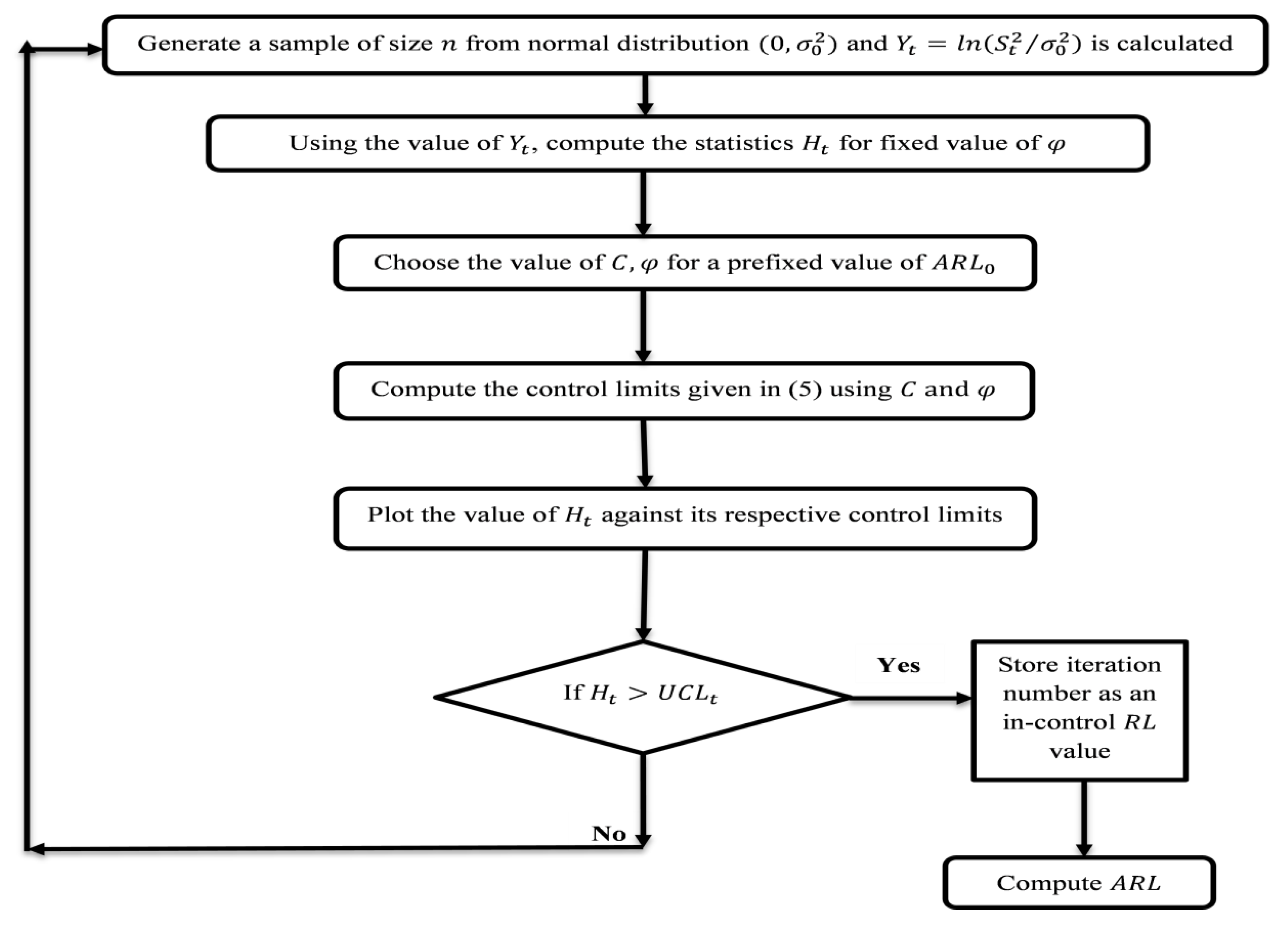
2. Design and Performance Evaluation of the Proposed Chart
3. Comparisons between Proposed and Existing Charts
Graphical Comparisons between Proposed and Existing Charts
4. Application: Monitoring of Daily Power Generation at Dhahran Wind Farm
Data Description
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Page, E.S. Continuous inspection schemes. Biometric 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Roberts, S.W. Control chart tests based on geometric moving averages. Technometrics 1959, 1, 239–250. [Google Scholar] [CrossRef]
- Shewhart, W.A. Economic control of quality of manufactured product. Van Nostrand N. Y. 1932, 27, 215–217. [Google Scholar]
- Montgomery, D.C. Introduction to Statistical Quality Control, 7th ed.; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Domangue, R.; Patch, S.C. Some omnibus exponentially weighted moving average statistical process monitoring schemes. Technometrics 1991, 33, 299–313. [Google Scholar] [CrossRef]
- Crowder, S.V.; Hamilton, M.D. An EWMA for monitoring a process standard deviation. J. Qual. Technol. 1992, 24, 12–21. [Google Scholar] [CrossRef]
- Castagliola, P. A new S2-EWMA control chart for monitoring the process variance. Qual. Reliab. Eng. Int. 2005, 21, 781–794. [Google Scholar] [CrossRef]
- Castagliola, P.; Celano, G.; Fichera, S. A new CUSUM-S2 control chart for monitoring the process variance. J. Qual. Mainte. Eng. 2009, 15, 344–357. [Google Scholar] [CrossRef]
- Shu, L.; Jiang, W. A new EWMA chart for monitoring process dispersion. J. Qual. Technol. 2008, 40, 319–331. [Google Scholar] [CrossRef]
- Huwang, L.; Huang, C.-J.; Wang, Y.-H.T. New EWMA control charts for monitoring process dispersion. Comput. Stat. Data Anal. 2010, 54, 2328–2342. [Google Scholar] [CrossRef]
- Abbas, N.; Riaz, M.; Does, R.J.M.M. CS-EWMA chart for monitoring process dispersion. Qual. Reliab. Eng. Int. 2013, 29, 653–663. [Google Scholar] [CrossRef]
- Zaman, B.; Abbas, N.; Riaz, M.; Lee, M.H. Mixed CUSUM-EWMA chart for monitoring process dispersion. Int. J. Adv. Manuf. Technol. 2016, 86, 3025–3039. [Google Scholar] [CrossRef]
- Ali, R.; Haq, A. New GWMA-CUSUM control chart for monitoring the process dispersion. Qual. Reliab. Eng. Int. 2018, 34, 997–1028. [Google Scholar]
- Abbas, N. Homogeneously weighted moving average control chart with an application in substrate manufacturing process. Comput. Ind. Eng. 2018, 120, 460–470. [Google Scholar] [CrossRef]
- Adegoke, N.A.; Smith, A.N.H.; Anderson, M.J.; Sanusi, R.A.; Pawley, M.D.M. Efficient homogeneously weighted moving average chart for monitoring process mean using an auxiliary variable. IEEE Access 2019, 7, 94021–94032. [Google Scholar] [CrossRef]
- Adegoke, N.A.; Abbasi, S.A.; Smith, A.N.H.; Anderson, M.J.; Pawley, M.D.M. A multivariate homogeneously weighted moving average control chart. IEEE Access 2019, 7, 9586–9597. [Google Scholar] [CrossRef]
- Nawaz, T.; Han, D. Monitoring the process location by using new ranked set sampling based memory control charts. Qual. Technol. Quanti. Manag. 2020, 17, 255–284. [Google Scholar] [CrossRef]
- Abid, M.; Shabbir, A.; Nazir, H.Z.; Sherwani, R.A.K.; Riaz, M. A double homogenously weighted moving average control chart for monitoring of the process mean. Qual. Reliab. Eng. Int. 2020, 36, 1513–1527. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2003. [Google Scholar]
- Said, S.A.; El-Amin, I.M.; Al-Shehri, A.M. Renewable energy potentials in Saudi Arabia. In Beirut regional Collaboration Workshop on Energy Efficiency and Renewable Energy Technology; American University of Beirut: Beirut, Lebanon, 2004; pp. 76–82. [Google Scholar]
- Shaahid, S.M.; Elhadidy, M.A. Wind and solar energy at Dhahran, Saudi Arabia. Renew. Energy 1994, 4, 441–445. [Google Scholar] [CrossRef]
- Wind Power Plant Project–Dumat Al Jandal. Available online: https://images.app.goo.gl/4t6QiQYvdDBYqehZ9 (accessed on 22 July 2019).







| RL Characteristic | ||||||
|---|---|---|---|---|---|---|
| 0.05 | 0.1 | 0.2 | 0.3 | 0.5 | ||
| 1 | ARL | 199.90 | 201.42 | 201.47 | 202.11 | 202.38 |
| MDRL | 113.00 | 154.00 | 149.00 | 146.00 | 141.50 | |
| SDRL | 246.86 | 182.73 | 183.48 | 188.57 | 200.84 | |
| 1.05 | ARL | 50.04 | 65.53 | 73.66 | 77.56 | 89.27 |
| MDRL | 29.00 | 51.00 | 58.00 | 58.00 | 64.00 | |
| SDRL | 58.62 | 57.67 | 61.46 | 69.86 | 85.98 | |
| 1.1 | ARL | 22.25 | 32.47 | 37.57 | 39.39 | 45.93 |
| MDRL | 12.00 | 26.00 | 30.00 | 31.00 | 33.00 | |
| SDRL | 25.80 | 27.70 | 30.35 | 33.26 | 42.84 | |
| 1.2 | ARL | 8.78 | 13.68 | 15.88 | 16.19 | 18.14 |
| MDRL | 5.00 | 11.00 | 13.00 | 13.00 | 14.00 | |
| SDRL | 9.61 | 11.82 | 12.25 | 12.82 | 16.05 | |
| 1.3 | ARL | 5.15 | 7.66 | 9.11 | 9.44 | 9.89 |
| MDRL | 4.00 | 6.00 | 8.00 | 8.00 | 8.00 | |
| SDRL | 5.14 | 6.63 | 6.78 | 7.20 | 8.38 | |
| 1.4 | ARL | 3.64 | 5.20 | 6.23 | 6.40 | 6.45 |
| MDRL | 3.00 | 4.00 | 5.00 | 5.00 | 5.00 | |
| SDRL | 3.35 | 4.30 | 4.55 | 4.73 | 5.19 | |
| 1.5 | ARL | 2.86 | 3.93 | 4.62 | 4.65 | 4.68 |
| MDRL | 2.00 | 3.00 | 4.00 | 4.00 | 4.00 | |
| SDRL | 2.40 | 3.16 | 3.38 | 3.38 | 3.67 | |
| 1.6 | ARL | 2.40 | 3.16 | 3.71 | 3.67 | 3.67 |
| MDRL | 1.00 | 3.00 | 3.00 | 3.00 | 3.00 | |
| SDRL | 1.96 | 2.46 | 2.64 | 2.58 | 2.70 | |
| 1.7 | ARL | 2.12 | 2.66 | 3.08 | 3.08 | 3.05 |
| MDRL | 1.00 | 2.00 | 3.00 | 3.00 | 3.00 | |
| SDRL | 1.65 | 2.01 | 2.14 | 2.11 | 2.17 | |
| 1.8 | ARL | 1.88 | 2.32 | 2.64 | 2.66 | 2.61 |
| MDRL | 1.00 | 1.00 | 2.00 | 2.00 | 2.00 | |
| SDRL | 1.43 | 1.70 | 1.85 | 1.83 | 1.81 | |
| 1.9 | ARL | 1.74 | 2.08 | 2.33 | 2.32 | 2.27 |
| MDRL | 1.00 | 1.00 | 2.00 | 2.00 | 2.00 | |
| SDRL | 1.24 | 1.51 | 1.60 | 1.56 | 1.49 | |
| 2 | ARL | 1.57 | 1.91 | 2.10 | 2.10 | 2.05 |
| MDRL | 1.00 | 1.00 | 1.00 | 2.00 | 2.00 | |
| SDRL | 1.09 | 1.35 | 1.40 | 1.37 | 1.30 | |
| 1.3 | 1.932 | 2.402 | 2.55 | 2.65 | ||
| RL Characteristic | ||||||
|---|---|---|---|---|---|---|
| 3 | 5 | 7 | 10 | 15 | ||
| 1 | ARL | 202.85 | 201.42 | 198.01 | 198.44 | 196.41 |
| MDRL | 143 | 154 | 153 | 158 | 155 | |
| SDRL | 209.11 | 182.73 | 176.45 | 170.88 | 167.69 | |
| 1.05 | ARL | 80.57 | 65.53 | 56.92 | 47.78 | 39.4 |
| MDRL | 60 | 51 | 46 | 39 | 33 | |
| SDRL | 77.68 | 57.67 | 48.25 | 39.29 | 31.72 | |
| 1.1 | ARL | 43.9 | 32.47 | 26.54 | 21.37 | 16.12 |
| MDRL | 33 | 26 | 22 | 18 | 13 | |
| SDRL | 41.44 | 27.7 | 22.2 | 17.61 | 13.21 | |
| 1.2 | ARL | 19.48 | 13.68 | 10.32 | 7.71 | 5.83 |
| MDRL | 14.5 | 11 | 8 | 6 | 5 | |
| SDRL | 18.45 | 11.82 | 8.7 | 6.28 | 4.58 | |
| 1.3 | ARL | 11.67 | 7.66 | 5.88 | 4.41 | 3.22 |
| MDRL | 8 | 6 | 5 | 4 | 3 | |
| SDRL | 10.84 | 6.63 | 4.76 | 3.45 | 2.35 | |
| 1.4 | ARL | 8.14 | 5.2 | 3.96 | 3.02 | 2.25 |
| MDRL | 6 | 4 | 3 | 3 | 1 | |
| SDRL | 7.54 | 4.3 | 3.11 | 2.24 | 1.56 | |
| 1.5 | ARL | 6.05 | 3.93 | 3.01 | 2.33 | 1.77 |
| MDRL | 4 | 3 | 3 | 1 | 1 | |
| SDRL | 5.5 | 3.16 | 2.26 | 1.65 | 1.17 | |
| 1.6 | ARL | 4.9 | 3.16 | 2.48 | 1.91 | 1.49 |
| MDRL | 4 | 3 | 2 | 1 | 1 | |
| SDRL | 4.34 | 2.46 | 1.78 | 1.3 | 0.91 | |
| 1.7 | ARL | 4.06 | 2.66 | 2.1 | 1.64 | 1.31 |
| MDRL | 3 | 2 | 1 | 1 | 1 | |
| SDRL | 3.51 | 2.01 | 1.47 | 1.06 | 0.73 | |
| 1.8 | ARL | 3.62 | 2.32 | 1.83 | 1.47 | 1.18 |
| MDRL | 3 | 1 | 1 | 1 | 1 | |
| SDRL | 3.05 | 1.7 | 1.27 | 0.9 | 0.56 | |
| 1.9 | ARL | 3.15 | 2.08 | 1.65 | 1.34 | 1.11 |
| MDRL | 3 | 1 | 1 | 1 | 1 | |
| SDRL | 2.6 | 1.51 | 1.09 | 0.77 | 0.44 | |
| 2 | ARL | 2.81 | 1.91 | 1.5 | 1.25 | 1.07 |
| MDRL | 2 | 1 | 1 | 1 | 1 | |
| SDRL | 2.25 | 1.35 | 0.95 | 0.66 | 0.35 | |
| 1.591 | 1.932 | 2.09 | 2.215 | 2.32 | ||
| 0.05 | 0.1 | 0.2 | 0.3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H-EWMA | H-EWMA | H-EWMA | H-EWMA | |||||||||
| 1 | 200.33 | 200.75 | 200.92 | 200.02 | 200.36 | 199.51 | 200.64 | 199.48 | 199.43 | 199.4 | 199.67 | 200.22 |
| 1.1 | 43.24 | 32.26 | 28.89 | 44.26 | 35.15 | 34.32 | 46.63 | 39.73 | 41.18 | 48.48 | 43.45 | 46.14 |
| 1.2 | 18.09 | 14.43 | 11.69 | 18.23 | 14.96 | 14.1 | 18.79 | 16.05 | 16.66 | 19.52 | 17.25 | 18.65 |
| 1.3 | 10.77 | 9.17 | 6.85 | 10.56 | 9.09 | 8.2 | 10.54 | 9.21 | 9.45 | 10.67 | 9.56 | 10.35 |
| 1.4 | 7.63 | 6.73 | 4.75 | 7.35 | 6.53 | 5.65 | 7.16 | 6.4 | 6.45 | 7.09 | 6.43 | 6.9 |
| 1.5 | 5.98 | 5.38 | 3.62 | 5.68 | 5.13 | 4.28 | 5.41 | 4.89 | 4.83 | 5.24 | 4.8 | 5.11 |
| 1.6 | 4.96 | 4.51 | 2.94 | 4.68 | 4.27 | 3.46 | 4.38 | 3.99 | 3.86 | 4.2 | 3.88 | 4.06 |
| 1.7 | 4.29 | 3.92 | 2.51 | 4.02 | 3.69 | 2.91 | 3.73 | 3.41 | 3.25 | 3.53 | 3.26 | 3.39 |
| 1.8 | 3.8 | 3.5 | 2.2 | 3.56 | 3.27 | 2.53 | 3.27 | 3 | 2.81 | 3.06 | 2.83 | 2.91 |
| 1.9 | 3.44 | 3.17 | 1.96 | 3.22 | 2.96 | 2.25 | 2.92 | 2.69 | 2.48 | 2.73 | 2.53 | 2.57 |
| 2 | 3.18 | 2.93 | 1.8 | 2.95 | 2.72 | 2.03 | 2.67 | 2.45 | 2.24 | 2.47 | 2.3 | 2.32 |
| 1.055 | 1.568 | 1.828 | 1.303 | 1.943 | 2.079 | 1.513 | 2.27 | 2.253 | 1.598 | 2.433 | 2.302 | |
| Subgroup | Example 1 | Example 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.6243 | 0.3376 | −0.9172 | 0.0709 | 0.5376 | −0.0199 | −0.0199 | 0.0000 | −0.0798 | −0.0798 | 0.0000 |
| 2 | 0.0718 | 0.3996 | −0.0596 | 1.3659 | 0.3227 | −0.3989 | −0.0389 | 0.0000 | −0.3989 | −0.1436 | 0.0000 |
| 3 | −0.0353 | −1.2937 | −0.0296 | 0.0709 | 0.6338 | −0.3989 | −0.0569 | 0.0000 | −0.3989 | −0.1947 | 0.0000 |
| 4 | −0.4403 | −1.4717 | 0.0898 | −0.4838 | 1.2130 | −0.3847 | −0.0598 | 0.0000 | −0.3422 | −0.1787 | 0.0000 |
| 5 | −0.7443 | −1.8528 | −0.1009 | 0.9281 | 1.8177 | −0.2703 | −0.0155 | 0.0357 | −0.0972 | 0.0222 | 0.1426 |
| 6 | −1.1330 | −1.6470 | 0.6685 | 1.3644 | −0.6021 | −0.0671 | 0.0105 | 0.0566 | 0.0231 | 0.1186 | 0.2051 |
| 7 | −1.6013 | −1.7784 | 0.6058 | 1.5148 | 0.2711 | 0.0450 | 0.0520 | 0.0901 | 0.1708 | 0.2632 | 0.3092 |
| 8 | −1.3388 | −1.4219 | 1.3121 | 1.1986 | 0.0989 | 0.1482 | 0.0810 | 0.1134 | 0.2244 | 0.3367 | 0.3587 |
| 9 | −0.1471 | −0.7052 | 0.6952 | 1.8248 | −0.2702 | 0.1741 | 0.0740 | 0.1079 | 0.1375 | 0.2578 | 0.2877 |
| 10 | 0.4738 | −1.2046 | 1.3146 | 1.5710 | 0.2134 | 0.1594 | 0.0785 | 0.1116 | 0.1601 | 0.2390 | 0.2664 |
| 11 | −0.6251 | −0.5070 | 2.4901 | 1.6751 | −0.0464 | 0.1907 | 0.1136 | 0.1399 | 0.1931 | 0.2565 | 0.2756 |
| 12 | −0.9566 | −0.1195 | −0.1200 | 0.4168 | 0.2475 | 0.1854 | 0.0880 | 0.0693 | 0.0601 | 0.1254 | 0.0000 |
| 13 | −1.2295 | 0.8355 | −0.9625 | −0.2670 | −0.4800 | 0.1367 | 0.0636 | 0.0434 | 0.0218 | 0.0206 | 0.0000 |
| 14 | −0.5131 | −0.8745 | 1.6919 | −0.6865 | −1.8279 | 0.1447 | 0.0897 | 0.0672 | 0.0954 | 0.0426 | 0.0310 |
| 15 | 0.6651 | −0.3131 | 3.1758 | −0.4326 | −0.1728 | 0.1952 | 0.1335 | 0.1051 | 0.1742 | 0.1365 | 0.1170 |
| 16 | 0.8609 | 1.2055 | 0.7537 | −0.5934 | 0.6171 | 0.1783 | 0.1069 | 0.0621 | 0.0145 | 0.0294 | 0.0000 |
| 17 | −0.0632 | −3.9879 | −0.3150 | −0.0427 | −0.2883 | 0.2258 | 0.1652 | 0.1126 | 0.4340 | 0.3891 | 0.3036 |
| 18 | −1.1750 | −0.0632 | −0.2966 | 0.2486 | 0.1488 | 0.2038 | 0.1370 | 0.0506 | 0.0707 | 0.2315 | 0.1070 |
| 19 | −1.8194 | −0.1347 | 2.6720 | −0.3043 | 0.6523 | 0.2487 | 0.1886 | 0.0976 | 0.4695 | 0.5303 | 0.3727 |
| 20 | −1.2295 | −1.6588 | 1.8223 | −1.1769 | 0.3310 | 0.2814 | 0.2219 | 0.1295 | 0.4724 | 0.7062 | 0.5346 |
| 21 | −0.3456 | −1.3377 | 0.7569 | 0.2470 | 0.6539 | 0.2474 | 0.1908 | 0.1081 | 0.2619 | 0.5895 | 0.4574 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riaz, M.; Abbasi, S.A.; Abid, M.; Hamzat, A.K. A New HWMA Dispersion Control Chart with an Application to Wind Farm Data. Mathematics 2020, 8, 2136. https://doi.org/10.3390/math8122136
Riaz M, Abbasi SA, Abid M, Hamzat AK. A New HWMA Dispersion Control Chart with an Application to Wind Farm Data. Mathematics. 2020; 8(12):2136. https://doi.org/10.3390/math8122136
Chicago/Turabian StyleRiaz, Muhammad, Saddam Akber Abbasi, Muhammad Abid, and Abdulhammed K. Hamzat. 2020. "A New HWMA Dispersion Control Chart with an Application to Wind Farm Data" Mathematics 8, no. 12: 2136. https://doi.org/10.3390/math8122136
APA StyleRiaz, M., Abbasi, S. A., Abid, M., & Hamzat, A. K. (2020). A New HWMA Dispersion Control Chart with an Application to Wind Farm Data. Mathematics, 8(12), 2136. https://doi.org/10.3390/math8122136





